Microsoft Word - 1-tit

УДК 681.3.06+519.68 ББК 32.973 В63

Воеводин В. В., Воеводин Вл. В.

В63 Параллельные вычисления. — СПб.: БХВ-Петербург, 2002. — 608 с: ил.

ISBN 5-94157-160-7

Книга известных российских ученых посвящена обсуждению ключевых проблем современных параллельных вычислений. С единых позиций рассматриваются архитектуры параллельных вычислительных систем, технологии параллельного программирования, численные методы решения задач. Вместе со строгим описанием основных положений теории информационной структуры программ и алгоритмов, книга содержит богатый справочный материал, необходимый для организации эффективного решения больших задач на компьютерах с параллельной архитектурой.

Для научных работников, инженеров, преподавателей, аспирантов и студентов естественнонаучных специальностей

УДК 681.3.06+519.68 ББК 32.973

Группа подготовки издания:

Главный редактор Екатерина Кондукова

Зам. главного редактора Анатолий Адаменко

Зав. редакцией Анна Кузьмина

Редактор Петр Науменко

Компьютерная верстка Натальи Смирновой

Корректор Наталия Першакова

Дизайн обложки Игоря Цырульникова

Зав. производством Николай Тверских

Лицензия ИД № 02429 от 24.07.00. Подписано в печать 23.09.02. Формат 70x100¹/i6- Печать офсетная. Усл. печ. л. 49,02. Тираж 3000 экз. Заказ № "БХВ-Петербург", 198005, Санкт-Петербург, Измайловский пр., 29.

Гигиеническое заключение на продукцию, товар № 77.99.02.953.Д.001537.03.02 от 13.03.2002 г. выдано Департаментом ГСЭН Минздрава России.

Отпечатано с готовых диапозитивов

в Академической типографии "Наука" РАН

199034, Санкт-Петербург, 9 линия, 12.

ISBN 5-94157-160-7 © Воеводин В. В., Воеводин Вл. В., 2002

Содержание

Предисловие.....................................................................................................1

Много ли надо знать о параллельных вычислениях?...........................................1

Часть I. Параллельные вычислительные системы..............................11

Глава 1. Что скрывают "обыкновенные" компьютеры.......................................13

§ 1.1. Немного об устройстве компьютера...........................................................14

Представление информации. Общее устройство компьютера. Операции и операнды. Команды. Управление. Арифметико-логическое устройство. Память. Устройство ввода/вывода. Центральный процессор. Вопросы и задания.

§ 1.2. Операции с числами.....................................................................................19

Двоичное представление чисел. Разряды. Фиксированная и плавающая запятая. Округление чисел. Ошибка округления. Сравнение представлений чисел. Вопросы и задания.

§ 1.3. Иерархия памяти...........................................................................................25

Различные виды памяти. Время доступа. Виртуальная память. Влияние на время решения задачи. Трудности работы с медленной памятью. Вопросы и задания.

§ 1.4. Языки программирования и программы....................................................31

Языки низкого и высокого уровня. Проблемно-ориентированные языки. Контроль эффективности программ. Компьютерная зависимость. Портабельность программ. Компиляторы и эффективность программ. Необходимость привлечения дополнительной информации. Вопросы и задания.

§ 1.5. Узкие места....................................................................................................37

Иллюстративная модель компьютера. Пиковая и реальная производительность. Взаимодействие отдельных узлов компьютера. Эффективность. Узкие места. Вопросы и задания.

Глава 2. Как повышают производительность компьютеров................................42

§ 2.1. Усложнение и наращивание аппаратных средств.....................................43

Уменьшение размеров. Скалярная, конвейерная и параллельная обработка. Иерархия памяти. Опережающий просмотр команд. Локальность вычислений и использования данных. Примеры. Вопросы и задания.

§ 2.2. Повышение интеллектуальности управления компьютером...................60

Закон Мура. Спецпроцессоры. Суперскалярные и VLlW-архитектуры. Коммутационные схемы. Топологии связей процессоров. SMP-компьютеры. Архитектуры NUMA и ccNUMA. Развитие программного обеспечения. Примеры. Вопросы и задания.

Содержание

§ 2.3. Система функциональных устройств..........................................................78

Простые и конвейерные устройства. Стоимость работы. Загруженность. Пиковая и реальная производительность. Эффективность. Различные соотношения. Законы Амдала и Густавсона—Барсиса. Взаимосвязь законов. Вопросы и задания.

Глава 3. Архитектура параллельных вычислительных систем............................94

§ 3.1. Классификация параллельных компьютеров и систем............................96

Классификация Флинна, Хокни, Фенга, Хендлера, Шнайдера, Скилликорна. Взаимосвязь классификаций. Архитектура компьютеров и структура задач. Вопросы и задания.

§ 3.2. Векторно-конвейерные компьютеры.........................................................114

Детальное рассмотрение компьютера Cray С90. Структура оперативной памяти. Регистровая структура. Функциональные устройства. Пиковая и реальная производительность. Вопросы и задания.

§ 3.3. Параллельные компьютеры с общей памятью.........................................134

Детальное рассмотрение компьютера HP Superdome. Ячейка компьютера. Локальные и удаленные ячейки. Процессор РА-8700. Работа с памятью. Вопросы и задания.

§ 3.4. Вычислительные системы с распределенной памятью............................142

Детальное рассмотрение компьютеров Cray T3D/T3E. Управляющие и вычислительные узлы. Процессорный элемент. Сетевой интерфейс. Сетевой маршрутизатор. Коммуникационная сеть. Память. Кластерные проекты. Вопросы и задания.

§ 3.5. Концепция GRID и метакомпьютинг.......................................................154

Метакомпьютер как огромная распределенная система. Особенности распределения задач и передачи данных. Различные проекты. Концепция GRID. Проблемы пользователей. Вопросы и задания.

§ 3.6. Производительность параллельных компьютеров....................................162

Сравнение вычислительных систем. Пиковая производительность и формат данных. Вычислительные и коммуникационные ядра. Тесты. Вопросы и задания.

Часть П. Параллельное программирование........................................179

Глава 4. Большие задачи и параллельные вычисления.....................................181

§ 4.1. Большие задачи и большие компьютеры..................................................183

Моделирование климатической системы. Обтекание летательных аппаратов. Математические модели и вычислительная техника. Огромные объемы вычислений и размеры памяти. Вопросы и задания.

§ 4.2. Граф алгоритма и параллельные вычисления...........................................191

Порядок вычислений. Граф алгоритма. Параллельные формы графа. Ярус и высота. Инвариантность к ошибкам округления. Граф алгоритма и информационное ядро. Параметризация в графе. Вопросы и задания.

§ 4.3. Концепция неограниченного параллелизма.............................................198

Параллельные алгоритмы. Принцип сдваивания. Примеры алгоритмов малой высоты. Ограниченность концепции. Новые алгоритмы — новые свойства. Трудности в проблеме портабельности. Вопросы и задания.

§ 4.4. Внутренний параллелизм............................................................................206

Преимущества внутреннего параллелизма. Примеры. Обнаружение новых свойств. Декомпозиция алгоритмов. Использование медленной памяти. Структура алгоритмов и программ. Вопросы и задания.

Содержание V

Глава 5. Технологии параллельного программирования....................................219

§ 5.1. Использование традиционных последовательных языков......................221

Обилие средств параллельного программирования. Трудности применения. Необходимость дополнительной информации. Системы программирования ОрепМР, DVM, трС. Примеры использования. Вопросы и задания.

§ 5.2. Системы программирования на основе передачи сообщений................268

Системы параллельного программирования Linda, MPI, MPI-2. Интерфейсы для последовательных языков Fortran, С, C++. Примеры использования. Вопросы и задания.

§ 5.3. Другие языки и системы программирования...........................................301

Т-система. Система программирования НОРМА. Приближенность к математическим записям. Примеры использования. Вопросы и задания.

Глава 6. Тонкая информационная структура программ.....................................320

§ 6.1. Графовые модели программ........................................................................324

Информационная структура программы. Операционная и информационная связь. Графы управления, операционно-логической истории, информационный, истории реализации, зависимостей, влияния. Минимальные графы зависимостей. Снова граф алгоритма. Примеры графов. Вопросы и задания.

§ 6.2. Выбор класса программ...............................................................................337

Статический анализ структуры программ. Статистическая значимость отдельных операторов. Линейный класс программ. Вопросы и задания.

§ 6.3. Графы зависимостей и минимальные графы............................................342

Опорные оператор, гнездо циклов, область. Пространства итераций. Лексикографический порядок. Типы зависимостей. Максимальный и минимальный графы зависимостей и их свойства. Теорема об информационном покрытии. Вопросы и задания.

§ 6.4. Простые и элементарные графы................................................................351

Простые и элементарные графы и программы. Расщепление минимальных графов на простые. Погружение минимального графа в объединение элементарных. Сведение к анализу элементарных программ. Вопросы и задания.

§ 6.5. Лексикографический порядок и i-свойство матриц...............................355

Лексикографический максимум в многограннике, /.-свойство матриц. Критерий лексикографического максимума. Дополнительные свойства матриц с /.-свойством. Вопросы и задания.

§ 6.6. Построение минимальных графов зависимостей.....................................363

Основная задача. Конструктивные алгоритмы построения элементарных, простых и минимальных графов зависимостей для программ из линейного класса. Вопросы и задания.

§ 6.7. Циклы ParDO и избыточные вычисления.................................................373

Лексикографически правильные графы. Параллельные множества. Параллельная структура программ. Критерий цикла ParDO. Избыточные вычисления и критерий их обнаружения. Вопросы и задания.

§ 6.8. Примеры.......................................................................................................378

Формализованное построение графов алгоритмов для конкретных программ. Сложнейшие графы алгоритмов для простейших программ. Зависимость параллельной структуры от порядка выполнения операций.

Содержание

Глава 7. Эквивалентные преобразования программ..........................................393

§ 7.1. Развертки графа............................................................................................394

Строгая и обобщенная развертки. Свойства разверток. Развертки и параллельные множества. Конструктивный алгоритм построения кусочно-линейных разверток. Выделение в графах строгих и нестрогих зависимостей. Вопросы и задания.

§ 7.2. Макрографы зависимостей.........................................................................404

Макровершины и макродуги. Укрупненное представление зависимостей. Развертки и декомпозиция алгоритмов. Распределенные вычисления. Работа с медленной памятью. Вопросы и задания.

§ 7.3. Эквивалентные программы.........................................................................408

Эквивалентные преобразования программ. Эквивалентные по вычислениям программы. Преобразования, гарантирующие эквивалентность. Вопросы и задания.

§ 7.4. Наиболее распространенные преобразования программ........................415

Перестановка циклов. Слияние циклов. Переупорядочивание операторов. Распределение цикла. Скашивание цикла. Расщепление пространства итераций. Выполнение итераций цикла в обратном порядке. Треугольные преобразования. Вопросы и задания.

§ 7.5. Две сопутствующие задачи..........................................................................421

Оценивание длины критического пути графа зависимостей. Распределение массивов по модулям памяти.

§ 7.6. Примеры.......................................................................................................426

Формализованное построение разверток и макрографов для конкретных программ. Определение циклов ParDO. Распределение массивов по модулям памяти. Эквивалентное преобразование подпрограммы OLDA из пакета тестов Perfect Club Benchmarks. Самые лучшие результаты. Система V-Ray.

Часть III. Смежные проблемы и применение.....................................441

Глава 8. Вычислительные системы и алгоритмы..............................................443

§ 8.1. Расширение и уточнение линейного класса.............................................448

Прямая подстановка. Вычисляемый цикл go to. Вычисляемые ветвления. Нелинейные индексные выражения. Уточнение описания внешних переменных. Подпрограммы и функции. Функции min и max. Прямое вычисление графов. Вопросы и задания.

§ 8.2. Граф-машина................................................................................................459

Локальность управления. Свойства различных реализаций. Гомоморфная свертка. Граф-машина и граф вычислительной системы. Сохранение временных режимов. Вопросы и задания.

§ 8.3. Регулярные и направленные графы...........................................................471

Итерационные процессы и регулярные графы. Расщепление бесконечного регулярного графа. Главный регулярный подграф. Критерий отсутствия контуров. Линейные развертки регулярного графа. Гомоморфная свертка регулярных графов. Вопросы и задания.

§ 8.4. Математические модели систолических массивов...................................482

Систолические массивы как вычислительные системы. Локальность управления. Минимальные коммуникационные связи. Реализация регулярных графов алгоритмов. Примеры построения систолических массивов для заданных алгоритмов. Вопросы и задания.

Содержание VII

§ 8.5. Математическая модель алгебраического вычислителя..........................499

Структура алгебраических задач. Спецпроцессор для алгебраических задач. Использование систолического массива для матричной операции А + ВС. Вопросы и задания.

§ 8.6. Матрицы и структура алгоритмов..............................................................503

Общие вычислительные процессы. Вариационная матрица алгоритма. Матрицы смежностей и инциденций. Критерий развертки. Уравновешенные графы. Критерий уравновешенности. Вопросы и задания.

§ 8.7. Новое применение сведений о структуре.....................................................511

Восстановление линейного функционала. Вычисление градиента. Анализ ошибок округления. Всюду вариационная матрица алгоритма. Вопросы и задания.

§ 8.8. Примеры.......................................................................................................528

Техника ускоренного вычисления градиента функции. Выполнение анализа ошибок по формальным правилам. Нахождение малых относительных эквивалентных возмущений.

Глава 9. Пользователь в среде параллелизма...................................................533

§ 9.1. Типичные ситуации в вопросах и ответах.................................................534

Конкретные вопросы из практики параллельного программирования. Исследование возникших ситуаций. Возможные идеи и пути решения. Что следует из перечисленных примеров? Вопросы и задания.

§ 9.2. Программный сервис в параллельных вычислениях...............................558

Почему в программе что-то не так? Компиляторы, отладчики, профилировщики, анализаторы, конверторы. Система V-Ray. Статические и динамические характеристики параллельных программ. Анализ структуры программ. Графовые структуры программ на практике. Вопросы и задания.

§ 9.3. Организационная поддержка пользователя..............................................581

Инфраструктура поддержки работы пользователей. Информационно-аналитический центр по параллельным вычислениям Parallel.ru. Вопросы и задания.

Заключение. Параллельные вычисления: интеграция от А до Я........................585

Список литературы........................................................................................588

Интернет-ресурсы..........................................................................................592

Предметный указатель...................................................................................593

Предисловие

Много ли надо знать

о параллельных вычислениях?

Ничего нельзя сказать о глубине лужи, если не попасть в нее.

Из законов Мерфи

В активе человечества имеется не так много изобретений, которые, едва возникнув, быстро распространяются по всему миру. Одним из них является компьютер. Появившись в середине двадцатого столетия, он через несколько десятков лет повсеместно стал незаменимым инструментом и надежным помощником в обработке самой разнообразной информации: цифровой, текстовой, визуальной, звуковой и др.

Известно, что первопричиной создания компьютеров была настоятельная необходимость быстрого проведения вычислительных работ, связанных с решением больших научно-технических задач в атомной физике, авиастроении, климатологии и т. п. Решение таких задач и сейчас остается главным стимулом совершенствования компьютеров. Однако в настоящее время основная сфера их применения связана с совсем иной деятельностью, в которой вычислительная составляющая либо отсутствует совсем, либо занимает небольшую часть.

Работа биржи, управление производством, офисные приложения, корпоративные информационные системы, процессы образования, игры, ведение домашнего хозяйства — это всего лишь отдельные примеры областей невычислительного использования компьютеров. В подобных областях вполне приемлемо применение персональных компьютеров и рабочих станций для достижения необходимых целей. Относительная простота процесса использования и комфортная программная среда формируют здесь устойчивое впечатление о компьютере как о весьма дружественном помощнике. И мало кто из пользователей такой техники догадывается и, тем более, знает, что все радикально меняется с переходом к решению больших и очень больших задач. Компьютеры становятся весьма сложными, куда-то пропадает дружественность интерфейса, программная среда переходит на жесткий командный язык и начинает требовать от пользователей предоставления такой информации, которая не всегда известна, и т. п.

Эта книга о больших и супербольших компьютерах и особенностях их использования. О тех проблемах, с которыми неизбежно приходится сталки-

Предисловие

ваться любому пользователю, вынужденному применять вычислительную технику на пределе ее возможностей.

Вообще говоря, большие задачи сами по себе не являются предметом нашего обсуждения, тем более, детального. Но иногда мы будем обращаться к ним явно, чтобы проиллюстрировать какие-то положения. Неявно же большие задачи буквально пронизывают всю книгу, т. к. любое обсуждение чаще всего предполагает, что решается именно большая задача. Формально характер обсуждения никак не связан с типом задач, хотя может ощущаться некоторая ориентация на научно-техническую сферу деятельности. Это объясняется всего лишь тем, что основное применение больших и супербольших компьютеров связано именно с данной сферой и потребности данной сферы оказывают наибольшее влияние на развитие компьютеров, по крайней мере, в настоящее время. Тем не менее, обсуждаемые в книге проблемы в одинаковой мере относятся к большим задачам как научно-техническим, так и любым другим, например, информационным.

Все, что связано с большими компьютерами и большими задачами, сопровождается характерным словом "параллельный": параллельные компьютеры, параллельные вычислительные системы, языки параллельного программирования, параллельные численные методы и т. п. В широкое употребление этот термин вошел почти сразу после появления первых компьютеров. Точнее, почти сразу после осознания того факта, что созданные компьютеры не в состоянии решить за приемлемое время многие задачи. Выход из создавшегося положения напрашивался сам собой. Если один компьютер не справляется с решением задачи за нужное время, то попробуем взять два, три, десять компьютеров и заставим их одновременно работать над различными частями общей задачи, надеясь получить соответствующее ускорение. Идея показалась плодотворной, и в научных исследованиях конкретное число объединяемых компьютеров довольно быстро превратилось в произвольное и даже сколь угодно большое число.

Объединение компьютеров в единую систему потянуло за собой множество следствий. Чтобы обеспечить отдельные компьютеры работой, необходимо исходную задачу разделить на фрагменты, которые можно выполнять независимо друг от друга. Так стали возникать специальные численные методы, допускающие возможность подобного разделения. Чтобы описать возможность одновременного выполнения разных фрагментов задачи на разных компьютерах, потребовались специальные языки программирования, специальные операционные системы и т. д. Постепенно такие слова, как "одновременный", "независимый" и похожие на них стали заменяться одним словом "параллельный". Всё это синонимы, если иметь в виду описание каких-то процессов, действий, фактов, состояний, не связанных друг с другом. Ничего иного слова "параллелизм" и "параллельный" в областях, относящихся к компьютерам, не означают.

Предисловие

Далеко не сразу удалось объединить большое число компьютеров. Первые компьютеры были слишком громоздкими, потребляли слишком много энергии, да и многие технологические проблемы комплексирования еще не нашли эффективного решения. Но со временем успехи микроэлектроники привели к тому, что важнейшие элементы компьютеров по многим своим параметрам, включая размеры и объем потребляемой энергии, стали меньше в тысячи и более раз. Идея объединения большого числа компьютеров в единую систему стала главенствовать в повышении общей производительности вычислительной техники. В одной из самых больших современных систем ASCI White объединено 8192 процессора. При этом достигаются весьма впечатляющие суммарные характеристики: пиковая производительность более 12 Тфлопс, оперативная память 4 Тбайт, дисковый массив 160 Тбайт. Но всем этим богатством нужно еще уметь воспользоваться.

Параллелизм на различных уровнях характерен для всех современных компьютеров от персональных до супербольших: одновременно функционирует множество процессоров, передаются данные по коммуникационной сети, работают устройства ввода/вывода, осуществляются другие действия. Любой параллелизм направлен на повышение эффективности работы компьютера. Некоторые его виды реализованы жестко в "железе" или обслуживающих программах и недоступны для воздействия на него рядовому пользователю. Но с помощью жесткой реализации не удается достичь наибольшей эффективности в большинстве случаев. Поэтому многие виды параллелизма реализуются в компьютерах гибко, и пользователю предоставляется возможность распоряжаться ими по собственному усмотрению.

Под термином "параллельные вычисления" как раз и понимается вся совокупность вопросов, относящихся к созданию ресурсов параллелизма в процессах решения задач и гибкому управлению реализацией этого параллелизма с целью достижения наибольшей эффективности использования вычислительной техники.

Вот уже более полувека параллельные вычисления привлекают внимание самых разных специалистов. Три обстоятельства поддерживают к ним постоянный интерес. Во-первых, это очень важная сфера деятельности. Занимаясь параллельными вычислениями, исследователь понимает, что он делает что-то, относящееся к самым большим задачам, самым большим компьютерам и, следовательно, находящееся на передовом фронте науки. Как минимум, близость к передовому фронту науки вдохновляет. Во-вторых, это очень обширная сфера деятельности. Она затрагивает разработку численных методов, изучение структурных свойств алгоритмов, создание новых языков программирования и многое другое, связанное с интерфейсом между пользователем и собственно компьютером. Параллельные вычисления тесно связаны и с самим процессом конструирования вычислительной техники. Структура алгоритмов подсказывает необходимость внесения в компьютер изменений, эффективно поддерживающих реализацию структур-

Предисловие

ных особенностей. Инженерные же новшества стимулируют разработку новых алгоритмов, эффективно эти новшества использующих. И, наконец, в-третьих. С формальных позиций рассматриваемая сфера деятельности легко доступна для исследований. Достаточно более или менее познакомиться с ее основами на уровне популярной литературы и уже можно делать содержательные выводы, возможно, даже никем не опубликованные.

Последнее обстоятельство придает характерную окраску исследованиям в области параллельных вычислений. Легкое освоение основных положений привлекает к параллельным вычислениям большое число специалистов из других областей. Это порождает немало новых задач, особенно на стыке вычислительной техники и приложений. Некоторые из них оказываются интересными и перспективными. Но, с другой стороны, простота освоения основ порождает массу легковесных результатов, что не делает параллельные вычисления привлекательной областью для серьезных исследований и не позволяет раскрыть все их богатство и многообразие связей.

В подтверждение сказанного приведем некоторые данные на начало 80-х годов прошедшего столетия. Это был период, когда в широкое использование стали поступать самые разнообразные компьютеры и вычислительные системы параллельной архитектуры. К этому времени только по проблемам их освоения было опубликовано более 5000 работ, и поток публикаций имел явную тенденцию к расширению. В данном потоке заметную часть составляли работы, связанные с обсуждением особенностей реализации параллельных численных методов, главным образом, по линейной алгебре. Интерес к методам линейной алгебры вполне понятен, т. к. они составляют основу процессов решения многих сложных проблем. Согласно данным, взятым из библиографических указателей на начало 80-х годов XX века, в области вычислительных методов линейной алгебры было опубликовано примерно 8000 работ. При этом около 120 ученых мира имели по этой тематике более чем по 10 работ. Казалось бы, что именно им и развивать параллельные методы линейной алгебры. Но среди них на тот период лишь около 10 человек имели по одной-две публикации, косвенно относящихся к параллельным численным методам и их применению на параллельных вычислительных системах. И только несколько человек имели публикации, прямо посвященные обсуждению этих проблем.

Интересно отметить, что в определенном смысле история повторяется. Аналогичной была ситуация на рубеже появления первых вычислительных машин. Тогда математики-алгоритмисты также принимали слабое участие в разработке численных методов и программ для компьютеров. Прошло много лет, прежде чем положение изменилось. Последствия же этого периода ощущаются до сих пор. В настоящее время вычислительное сообщество активно переходит на использование кластеров, больших многопроцессорных систем, неоднородных систем и систем, распределенных по значительной территории. И опять ведущая роль в освоении новейшей техники в целом

Предисловие

принадлежит не профессионалам в создании численных методов, а разработчикам языков программирования, компиляторов, операционных систем и просто лицам, которым необходимо решать задачи. К тому времени, когда математиками будет понято, как надо правильно реализовывать численные методы на новой технике, менять программную среду, скорее всего, будет поздно. Но именно от численных методов во многом зависит, насколько успешно используется вычислительная техника.

Планируя написание этой книги, мы понимали, что заведомо придется искать компромисс между многообразием сторон затрагиваемой проблемы и полнотой их описания. Удачен выбранный компромисс или нет — судить читателю. Мы лишь хотим сначала пояснить свою позицию. Возможно, что после этого будет легче понять как цели появления того или иного материала в книге, так и пути их достижения.

У разных специалистов, связанных с параллельной вычислительной техникой, разные взгляды на то, что представляют собой параллельные вычисления, где и какие акценты надо ставить при изложении материала. В этой книге мы попытались отразить позицию пользователей и те проблемы, с которыми им приходится сталкиваться. Говоря о пользователях, мы имеем в виду, прежде всего, тех из них, которые осваивают серийно выпускаемую технику, которые вынуждены изучать особенности этой техники, чтобы решать на ней реальные задачи более эффективно, и которым для достижения эффективности приходится многократно переписывать свои программы.

Это в значительной мере определило представленный в книге материал. Мы сразу отказались от искушения описать многие, в том числе, весьма красивые инженерные, программистские и математические идеи, оказавшиеся по каким-либо причинам либо нереализованными, либо апробированными недостаточно. Но даже при таком ограничении интересных идей и достижений, относящихся к параллельным вычислениям, оказалось немало. Отбор материала и структура его описания подчинены одной из целей книги — показу многообразия и глубины связей различных направлений деятельности в параллельных вычислениях с соседними областями. В первую очередь, с созданием вычислительной техники, разработкой программного обеспечения и математическими исследованиями.

С какой бы стороны не рассматривать параллельную вычислительную технику, главным стимулом ее развития было и остается повышение эффективности процессов решения больших и очень больших задач. Эффективность зависит от производительности компьютеров, размеров и структуры их памяти, пропускной способности каналов связи. Но в не меньшей, если не большей, степени она зависит также от уровня развития языков программирования, компиляторов, операционных систем, численных методов и многих сопутствующих математических исследований. Если с этой точки

Предисловие

зрения взглянуть на приоритеты пользователей, то они всегда связаны с выбором тех средств, которые позволяют решать задачи более эффективно.

Эффективность — понятие многоплановое. Это удобство использования техники и программного обеспечения, наличие необходимого интерфейса, простота доступа и многое другое. Но главное — это достижение близкой к пиковой производительности компьютеров. Данный фактор настолько важен, что всю историю развития вычислительной техники и связанных с ней областей можно описать как историю погони за наивысшей эффективностью решения задач.

Конечно, такой взгляд отражает точку зрения пользователей. Но ведь именно пользователям приходится "выжимать" все возможное из имеющихся у них средств и приводить в действие все "рычаги", чтобы достичь максимальной производительности компьютеров на своих конкретных задачах. Поэтому им нужно знать, где находятся явные и скрытые возможности повышения производительности и как наилучшим образом ими воспользоваться. Реальная производительность сложным образом зависит от всех составляющих процесса решения задач. Можно иметь высокопроизводительный компьютер. Но если компилятор создает не эффективный код, реальная производительность будет малой. Она будет малой и в том случае, если не эффективны используемые алгоритмы. Не эффективно работающая программа — это прямые потери производительности компьютера, средств на его приобретение, усилий на освоение и т. п. Таких потерь хотелось бы избежать или, по крайней мере, их минимизировать.

Проблемы пользователей нам известны не понаслышке. За плечами лежит более двадцати лет научной, производственной и педагогической деятельности в области параллельных вычислений. За это время освоены многие компьютеры и большие вычислительные системы. Было решено немало задач. Но не было ни одного случая, когда одна и та же программа эффективно реализовывалась без существенной переделки при переходе к другой технике. Конечно, хотя и трудно, но все же можно заново переписать программу, удовлетворяя требованиям языка программирования и штатного компилятора. Однако новую большую программу суперсложно сделать эффективно работающей.

Технология обнаружения узких мест процесса реализации программы плохо алгоритмизирована. Опыт показывает, что для повышения эффективности приходится рассматривать все этапы действий, начиная от постановки задачи и кончая изучением архитектуры компьютера, через выбор численного метода и алгоритма, тщательно учитывая особенности языка программирования и даже компилятора. Основной способ обнаружения узких мест — это метод проб и ошибок, сопровождающийся большим числом прогонов вариантов программы. Необходимость многих экспериментов объясняется скудностью информации, получаемой от компилятора после каждого прогона. К тому же

Предисловие

ни один компилятор не дает никаких гарантий относительно меры эффективности реализуемых им отдельных конструкций языка программирования. С самого начала пользователь ставится в такие условия, когда он не знает, как надо писать эффективные программы. Получить соответствующую информацию он может только на основе опыта, изучая почти как черный ящик влияние различных форм описания алгоритмов на эффективность.

Наши исследования показывают, что большинство из узких мест может быть объединено в три группы. Первая связана собственно с компьютером. На любом параллельном компьютере не все потоки данных обрабатываются одинаково. Какие-то из них реализуются предельно эффективно, какие-то достаточно плохо. Изучая особенности архитектуры компьютера, очень важно понять, что представляет собой те и другие потоки и описать их математически. Вторая определяется структурой связей между операциями программы. Не в каждой программе обязаны существовать фрагменты, реализуемые эффективно на конкретном компьютере. И, наконец, третья зависит от используемой в компиляторе технологии отображения программ в машинный код.

Если технология позволяет разложить программу на фрагменты, по которым почти всегда будет строиться эффективный код, то узких мест в этой группе может не быть. Такие технологии были разработаны для первых параллельных компьютеров. Но по мере усложнения вычислительной техники технологии компиляции становятся все менее и менее эффективными, и узких мест в третьей группе оказывается все больше и больше. Для больших распределенных систем узкие места компиляции начинают играть решающую роль в потере общей эффективности. Поэтому уже давно наметилось и теперь почти воплотилось в реальность "компромиссное" разделение труда: наименее алгоритмизированные и сложно реализуемые этапы компиляции, в первую очередь, расщепление программы на параллельные ветви вычислений, распределение данных по модулям памяти и организацию пересылок данных возлагаются на пользователя. Проблем от этого не стало меньше. Просто о том, о чем раньше заботились разработчики компиляторов, теперь должны беспокоиться сами пользователи.

Акцентированное внимание к узким местам процесса решения задач является характерной чертой настоящей книги. Узкие места описываются и изучаются практически всюду: в параллельных компьютерах и больших вычислительных системах, процессах работы многих функциональных устройств, конструировании численных методов, языках и системах программирования, различных приложениях и даже в работе пользователей. Особое внимание уделяется узким местам, связанным с выявлением параллельных структур алгоритмов и программ и их отображением на архитектуру компьютеров.

Исследуя различные вопросы параллельных вычислений, мы неоднократно убеждались в том, что все они связаны многими незримыми нитями как

Предисловие

между собой, так и с совершенно далекими от любого параллелизма областями знаний. Эти связи не лежат на поверхности, и почувствовать их можно, лишь поставив исследования на строгую математическую основу. И тогда начинает возникать ощущение, что параллельные вычисления своими корнями уходят во что-то очень фундаментальное. Возможно, это что-то есть информационная структура алгоритмов. Возможно, оно окажется чем-то иным. Но в любом случае появляется уверенность, что глубокое изучение параллельных вычислений приведет, в конце концов, к пониманию того, как должны быть устроены наши алгоритмы, компьютеры и программное обеспечение. Сейчас параллельные вычисления представляются гигантским айсбергом, верхушка которого исследована весьма основательно. Исследование же остальной его части только начинается. Перспективу этого процесса мы также попытались отразить в нашей книге.

Содержание книги и ее структура хорошо видны из подробного содержания. Поэтому сделаем по ней лишь несколько замечаний. В своей основе книга является монографией, поскольку в нее включено много уникального авторского материала. Однако содержание систематизировано таким образом, что книга может служить учебным пособием для студентов, аспирантов и специалистов, связанных в своей деятельности с направлением "Прикладная математика и информатика". Для ее чтения нужны минимальные начальные знания. Некоторые разделы доступны даже школьникам, владеющим навыками работы с компьютером. Вместе с тем, в книге также приводятся сведения очень высокой степени сложности, достойные внимания самых серьезных исследователей. Для облегчения знакомства с книгой каждая глава начинается с небольшого введения, поясняющего цель и особенности изложенного в ней материала. После ознакомления с новым материалом читателю предлагается ответить на вопросы и выполнить задания. Вопросы и задания, помеченные одной или двумя звездочками, относятся соответственно к сложным и очень сложным.

Создание учебного пособия широкого профиля по параллельным вычислениям — это, пожалуй, самая главная цель написания настоящей книги. Мы постарались с единых позиций не только рассказать об основах данного научного направления, но и показать его проблемы и перспективы развития. Конечно, по параллельным вычислениям имеется немало хороших книг и публикаций. Но все они, на наш взгляд, слишком фрагментарны и не создают цельного впечатления о рассматриваемой сфере деятельности, осуществляемой на стыке многих наук. Структура и форма изложения материала этой книги формировались довольно долго. Научные исследования позволили выделить опорные точки параллельных вычислений среди огромного числа общих результатов и наметить их связь между собой. В предварительных публикациях была предпринята попытка развить и систематизировать эти связи на основе строгих математических определений и выкладок. Различные фрагменты книги неоднократно обсуждались на конференциях, се-

Предисловие

минарах и в дискуссиях с коллегами. На основе отобранного материала в течение многих лет читаются основные и специальные курсы в Московском государственном университете им. М. В. Ломоносова, физико-техническом институте и международном государственном университете в г. Дубна. Решающим обстоятельством, повлиявшим на ускорение процесса написания книги, стало наше участие в молодежных научных школах. Необходимость создания учебных пособий по параллельным вычислениям там ощущалась особенно остро.

Заниматься параллельными вычислениями довольно сложно. Эту область за короткое время трудно освоить и, тем более, трудно получить хорошие результаты. Поэтому в коллективах, где проводятся подобные работы, имеет большое значение создание атмосферы поддержки, заинтересованности и терпеливости. Нам приятно выразить признательность академику Г. И. Мар-чуку, который такую атмосферу создал в институте вычислительной математики Российской академии наук и в течение многих лет поддерживал это направление исследований.

Мы благодарны академику В. А. Садовничему за столь же благоприятную атмосферу в Московском университете и поддержку работ научно-исследовательского вычислительного центра МГУ по созданию крупнейшего центра по высокопроизводительным вычислениям в системе вузов России. Многолетнее сотрудничество ИВМ РАН и НИВЦ МГУ в области параллельных вычислений позволило приобрести бесценный опыт как в решении больших задач, так и в правильной расстановке акцентов в процессах образования и подготовки высококвалифицированных кадров. Появление этой книги есть одно из следствий данного сотрудничества.

В процессе написания книги нам пришлось контактировать со многими коллегами. Некоторые из них предоставили свои материалы, помогающие лучше осветить отдельные разделы. С другими было просто полезно поговорить, чтобы сформировать нужную точку зрения. Всем им мы выражаем нашу признательность. Особенно отмечаем участие академика В. П. Дымникова, член-корреспондента А. В. Забродина, докторов физико-математических наук С. М. Абрамова, А. Н. Андрианова, А. Л. Ластовецкого, В. А. Крюкова, А. Н. Томилина, кандидатов физико-математических наук К. Н. Ефимкина, Н. А. Коновалова.

Мы выражаем благодарность Российскому фонду фундаментальных исследований и Министерству промышленности, науки и технологий Российской Федерации. Многие результаты, о которых говорится в книге, были получены в рамках выполнения грантов от этих организаций. Без поддержки этих организаций написать такую книгу было бы гораздо сложнее.

Мы благодарим представительство компании Hewlett-Packard в России за предоставленные материалы, возможность использования ее вычислительной техники, за внимание и постоянный интерес к нашей работе.

Предисловие

Мы исключительно благодарны А. И. Караваеву, прекрасно подготовившему все иллюстрации, использованные в данной книге. Наша искренняя благодарность сотрудникам лаборатории параллельных информационных технологий НИВЦ МГУ: кандидату физико-математических наук А. С. Антонову, А. Н. Андрееву и С. А. Жуматию за множество ценных замечаний по рукописи.

И, наконец, нашу особую признательность мы хотим выразить Т. С. Гамаюновой и С. Н. Воеводиной. Без их самоотверженной работы по набору текста, его проверке, подготовке оригинал-макета и коррекции материала книга могла бы не появиться в срок.

Параллельные вычисления — перспективная и динамично изменяющаяся область научной и прикладной деятельности. Мы надеемся, что выбрать правильный путь в ней поможет эта книга.

Валентин В. Воеводин и Владимир В. Воеводин

ЧАСТЬ I

Параллельные вычислительные системы

Глава 1

Что скрывают "обыкновенные" компьютеры

Внутри каждой большой задачи сидит маленькая, пытающаяся пробиться наружу.

Из законов Мерфи

В своем развитии персональные компьютеры достигли высокого уровня совершенства. Они компактны, обладают большой скоростью выполнения заданий и, что особенно важно, достаточно просты в обращении. Все эти качества привели к их широкому использованию, в том числе среди лиц, не имеющих специальной компьютерной подготовки. По существу персональный компьютер становится таким же привычным устройством, как пылесос, кухонный комбайн и телевизор. Он остается удобным инструментом до тех пор, пока не приходится решать очень большие задачи. Конечно, в этом случае можно попытаться использовать самый быстрый персональный компьютер с максимально большой памятью. Можно также перейти к использованию рабочей станции. Однако увеличение возможностей на этом пути все же ограничено. И тогда приходится обращаться к суперкомпьютерам.

Согласно распространенному мнению, суперкомпьютер — это такой компьютер, у которого все самое-самое: супербольшая скорость, супербольшая память, супербольшая цена. Это действительно так. Но, переходя от персонального компьютера к суперкомпьютеру, пользователю приходится также сталкиваться с очень большими трудностями в их использовании. Главное, на суперкомпьютерах отсутствует характерная для персональных компьютеров пользовательская среда. Оказывается, что использовать суперкомпьютер гораздо сложнее, чем персональный компьютер, а некоторые суперкомпьютеры даже очень сложно. Кроме этого, выясняется, что разных типов суперкомпьютеров довольно много, они не совместимы друг с другом, и на разных суперкомпьютерах совсем разные пользовательские среды. Взвесив предстоящие трудности, пользователи нередко отказываются от использования суперкомпьютеров вообще или переходят к более простым суперкомпьютерам. Если же пользователь все же решается использовать суперкомпьютер, ему важно понимать причины появления новых трудностей и пути их преодоления.

Современные суперкомпьютеры возникли не вдруг. Они являются продуктом длительного развития "обыкновенных" компьютеров, к которым, кстати, относится и типовой персональный компьютер. Эти "обыкновенные" компью-

Часть I. Параллельные вычислительные системы

теры имеют ряд принципиальных узких мест, которые не позволяют достичь сколь угодно большой скорости и иметь сколь угодно большую память. Стремление сделать компьютеры более мощными и развязать узкие места привело, в конце концов, к тем изменениям, которые превратили "обыкновенный" компьютер в суперкомпьютер. Узких мест в компьютерах много, много и способов их развязки. Это породило много типов суперкомпьютеров. К сожалению, за возросшие скорости и объемы памяти приходится платить. Для пользователей эта плата связана, в первую очередь, со значительным усложнением и ухудшением пользовательской среды. Многое из того невидимого, что делали "обыкновенные" компьютеры, на суперкомпьютерах пользователям надо делать самим. Просто потому, что проблемы эффективного обслуживания пользовательских задач стали настолько сложными, что пока их не научились хорошо решать в автоматическом режиме.

Чтобы лучше понять причины появления новых трудностей и, возможно, наметить в дальнейшем пути их преодоления, рассмотрим сначала, как устроен "обыкновенный" компьютер. Мы не будем заниматься детальным и, тем более, инженерным анализом. Лишь рассмотрим те узкие места, развязывание которых, с точки зрения пользователя, и превращает "обыкновенный" компьютер в суперкомпьютер с его достоинствами и недостатками.

§1.1. Немного об устройстве компьютера

За очень редким исключением во всех существующих компьютерах, как "обыкновенных", так и супер, реализована одна и та же конструктивная идея. Она состоит в том, что вся исходная и перерабатываемая информация хранится в компьютерах в форме некоторого множества двоичных разрядов или битое, а любое ее преобразование сводится, в конце концов, к преобразованию битов с помощью нескольких простых функций.

Сейчас нереально даже представить такую ситуацию, при которой пользователь записывает и читает свою информацию в двоичном виде, а также описывает ее преобразование как преобразование множества битов. В действительности он всегда общается с компьютером на каком-нибудь приемлемом для него языке. Часто пользователь даже не знает, какие процессы происходят в конкретном компьютере при решении его задач. Однако для нас очень важно помнить, что, тем не менее, все эти процессы в любом случае осуществляются на битовом уровне. Частично переход к битовому уровню и обратно выполняется автоматически с помощью аппаратных средств, частично программным путем. От того, насколько эффективно реализуются эти переходы, в немалой степени зависит успех в решении пользовательских задач.

Не с каждого входного языка разработчики компьютеров и его программного окружения могут автоматически организовать эффективные бинарные процессы. И тогда они начинают требовать от пользователя какие-то допол-

Глава 1. Что скрывают "обыкновенные" компьютеры

нительные сведения. Чаще всего дополнительные требования формулируются в специфических компьютерных терминах, не всегда очевидным образом связанных с задачей или методом ее решения. Все это усложняет как входной язык, так и всю процедуру общения с компьютером. Такая ситуация особенно характерна для суперкомпьютеров, но не так уж редко она возникает и в связи с "обыкновенными" компьютерами.

Основным информационным элементом в компьютере является слово. Каждое слово представляет собой упорядоченный набор битов. Слово может делиться на байты. Байт означает упорядоченный набор из 8 битов. Число битов в слове называется его длиной. В любом конкретном компьютере все слова имеют одну и ту же длину. В разных компьютерах длина слов может быть разной. Например, в персональном компьютере слово состоит из одного байта, в компьютере Сгау-1 оно состоит из 64 битов. Если в слове записана какая-то информация, то это означает, что в каждом бите слова зафиксировано одно из двух возможных его состояний 0 или 1. Совокупность состояний всех битов слова определяет содержимое слова. Устройство, в котором хранится все множество слов, обобщенно называется памятью. Оно может быть простым или сложным, однородным по устройству или разнородным в зависимости от типа или назначения компьютера. Все слова поименованы. Имя слова называется адресом. Структура адреса в определенном смысле отражает структуру памяти. Разные слова имеют разные адреса. Каждый адрес связан с конкретным физическим местом в памяти.

Если память устроена сложно и, к тому же, разнородна по своему строению, времена обращения к отдельным словам могут варьироваться в очень широких пределах, отличаясь друг от друга не только в разы, но и в десятки, сотни и даже тысячи раз. Это исключительно важное обстоятельство и оно нередко решающим образом определяет время решения задач. К различным вопросам эффективной работы с памятью мы будем возвращаться в этой книге неоднократно.

Основная задача любого компьютера состоит в преобразовании хранящейся в памяти информации. Она всегда реализуется как выполнение последовательности простых однозначных функций над содержимым отдельных слов. Как правило, все функции имеют не более двух аргументов. Функции могут использовать и/или изменять как слова целиком, так и их части. Вообще говоря, разные компьютеры могут иметь разные наборы исполняемых функций. Однако очень часто эти наборы функционально совпадают во многом или полностью, различаясь лишь техникой реализации. Наиболее распространенными функциями являются простейшие арифметические операции над числами (сложение, вычитание, умножение и т. д.) и логические операции булевой алгебры над битами слов (конъюнкция, дизъюнкция и т. д.). Обычно в компьютерной терминологии все функции называются операциями, а значение аргумента, иногда сам аргумент и даже адрес слова, где содержится аргумент, — операндами.

Часть I. Параллельные вычислительные системы

В компьютере операция реализуется в виде некоторой электронной схемы. Для обозначения реализаций этих схем используется самая различная терминология. Они называются чипом, устройством, процессором, сопроцессором и т. п. в зависимости от их сложности, связи друг с другом и даже вкуса конструктора. Мы будем использовать термин "устройство", оставляя другие названия для иных целей. Совокупность устройств, реализующих арифметические и логические операции, называется арифметико-логическим устройством (АЛУ).

Кроме операций над содержанием памяти, компьютер должен осуществлять также и все действия, связанные с организацией процесса преобразования информации. Возможные действия компьютера описываются системой машинных команд. Как и любая другая информация, машинная команда записывается как содержимое слова. В описании команды задаются код операции и те операнды, над которыми операция будет проводить действия. Некоторые машинные команды выполняют действия над словами, расположенными в строго определенном месте, например, в фиксированных регистрах. Такие команды не требуют явного указания операндов. Система команд всегда устроена таким образом, что выполнение каждой команды однозначно определяет следующую команду. Любой процесс преобразования информации описывается конкретной совокупностью машинных команд из числа возможных для данного компьютера. Эта совокупность называется машинным кодом или программой во внутреннем коде. Тем самым подчеркивается, что процесс описан программой на языке машинных команд, а не как-либо иначе.

Структура машинных команд всегда привязана к структуре компьютера и может быть совсем не похожей на структуру тех действий, которые пользователь предполагает выполнять. Как правило, свои действия пользователь описывает программами на языках высокого уровня. Компьютеры их "не понимают". Поэтому, чтобы программы могли быть выполнены, они должны быть переведены, прежде всего, в эквивалентный машинный код. Такой перевод осуществляют специальные программные системы, называемые компиляторами. Компиляторы очень сложны и выполняют очень большой объем работы. От того, как именно они преобразуют программы пользователя, решающим образом зависит эффективность реализации получаемого машинного кода и, следовательно, эффективность процесса решения задач.

До того как машинный код начнет исполняться, все команды и необходимые данные должны быть помещены или, как говорят, загружены в память. Это осуществляется с помощью специальных команд через так называемые устройства ввода. К ним относятся устройства считывания информации с дискеты и лазерных дисков, сканеры, клавиатура и т. п. Результаты работы компьютера выводятся из памяти также с помощью специальных команд через устройства вывода. К ним относятся устройства записи информации на дискеты и лазерные диски, графопостроители, принтеры и т. п. Сейчас

Глава 1. Что скрывают "обыкновенные" компьютеры

существует огромное разнообразие устройств ввода/вывода (УВВ). Но независимо от их конструктивных особенностей УВВ остаются самыми медленными устройствами компьютера. Это обстоятельство вызывает много трудных проблем, когда объем входной или выходной информации оказывается очень большим.

После загрузки в память машинного кода и данных компьютер может начинать свою работу. Руководство ею осуществляет устройство управления (УУ). Оно содержит необходимые регистры, счетчики и другие элементы, обеспечивающие управление перемещением информации между памятью, АЛ У, УВВ и другими частями компьютера. УУ должно решать две противоречивые задачи. С одной стороны, УУ должно работать достаточно быстро, чтобы не задерживать процесс решения задачи. С другой стороны, УУ должно управлять самыми различными устройствами, в том числе, удаленными друг от друга и работающими одновременно. Поэтому УУ всегда устроено по иерархическому и распределенному принципу. Самый быстрый уровень — это те электронные схемы, которые расшифровывают содержание очередной команды, выделяют код операции и адреса операторов, выбирают для анализа одну или несколько последующих команд. Другой уровень УУ — это, например, схемы, управляющие выполнением операций АЛУ. Совокупность устройства управления, арифметико-логического устройства и блока наиболее быстрой памяти называется центральным процессором.

Во всех современных компьютерах реализуются два способа управления: схемный и микропрограммный. Схемный используется тогда, когда возникает необходимость очень быстрого, но относительно простого управления. Микропрограммный — в случае сложного управления. В целом УУ занимает центральное место в управлении работой компьютера. Но оно обросло многими программными и микропрограммными системами, связанными с решением частных управленческих задач. Некоторые из них очень сложны. Например, система управления файлами по существу представляет собой специализированную вычислительную машину, которая имеет свою память и связана с памятью и магнитными дисками основного компьютера. Еще более сложной является система управления графической информацией и т. п. Совокупность программных систем, обеспечивающих управление работой компьютера, принято называть операционной системой. Для всех современных компьютеров операционная система неотделима от собственно компьютера и является его программным продолжением. Один и тот же компьютер может иметь несколько операционных систем. Например, для персональных компьютеров широко распространены операционные системы MS-DOS, Windows и Unix. Каждая из них имеет свои особенности и решает свои задачи.

Такова общая схема "обыкновенного" компьютера. Она представлена на рис 1.1. Конечно, эта схема идеализирована и лишь иллюстрирует связи между отдельными частями компьютера. Тем не менее, в ней отражено все то, что

Часть I. Параллельные вычислительные системы

мы будем обсуждать более детально, выявляя "узкие места". Отметим, что компьютеры подобного типа кроме названия "обыкновенный" имеют также названия "однопроцессорный", "фон-неймановской архитектуры" и др.

Перейдем теперь к более детальному обсуждению отдельных элементов "обыкновенного" компьютера.

УСТРОЙСТВА ВВОДА/ВЫВОДА

АРИФМЕТИКО-ЛОГИЧЕСКОЕ УСТРОЙСТВО

УСТРОЙСТВО УПРАВЛЕНИЯ

КОМПИЛЯТОР

ОПЕРАЦИОННАЯ СИСТЕМА

ПРОГРАММА

Рис. 1.1. Общая схема компьютера

Вопросы и задания

1. Приведите примеры физических, электрических и механических устройств, имеющих р = 2, 3, 8, 10 устойчивых состояний.

2. На основе предложенных устройств постройте схемы выполнения арифметических операций над целыми числами.

3. Исследуйте любой калькулятор как компьютер. Каковы в нем центральный процессор, память, операционная система, форма представления чисел?

4. Предположим, что компьютер имеет универсальный процессор и память объемом в 1 или 2 ячейки. Какие задачи можно решать на таком компьютере?

5. Знаете ли вы, что первые лекции об автоматизации процесса вычислений прочитаны английским математиком и экономистом Ч. Бэббиджем в 1840 г.?

6. Условный переход является одной из важнейших команд управления. Знаете ли вы, что впервые идея использовать условные переходы была высказана ирландским бухгалтером П. Лудгейтом в 1903 г.?

Глава 1. Что скрывают "обыкновенные" компьютеры

7. Рассмотрите любую систему машинных команд. С помощью команд, реализующих логические операции и операции безусловного перехода, составьте программу, реализующую операцию условного перехода.

8. Знаете ли вы, что первая вычислительная машина была построена немецким ученым К. Цузе в 1936 г. и была она механической?

9. Знаете ли вы, что первая отечественная электронная вычислительная машина МЭСМ была построена коллективом, возглавляемым академиком С. А. Лебедевым, в 1951 г.?

§ 1.2. Операции с числами

Есть одно обстоятельство, общее для всех компьютеров, осуществляющих работу с числами. Это — формы представления чисел. С одной стороны, они диктуются природой самих чисел. С другой — битовым представлением информации.

Известно [5], что любое вещественное число х ф 0 можно единственным образом представить в виде бесконечного ряда по степеням числа 2, т. е.

*=±Х^о'-²''- (i-i)

Здесь коэффициенты a_t принимают одно из значений 0 или 1, число b зависит от числа х и а/, = 1. При хранении чисел щ в компьютере их можно отождествлять с двоичными разрядами слова. Поэтому и коэффициенты a_tчасто называют двоичными разрядами числа х. При этом коэффициент щ называется /-ым разрядом. Вместо ряда (1.1) число х также записывают просто перечислением коэффициентов

x = ±a_ba_b-_h..ao,a-ia-₂..., (1.2)

иногда с указанием знака, иногда без него. Не всегда ставится и запятая, отделяющая коэффициенты при неотрицательных степенях двойки в (1.1) от коэффициентов при отрицательных степенях.

Никакие технические решения не дают возможность хранить все двоичные разряды числа, т. к. в общем случае их бесконечно много. Поэтому числа представляются лишь конечным набором старших разрядов. Другими словами, от числа (1.2) остается только набор коэффициентов аь...а₃ для некоторого s < Ь. Следовательно, любое число, имеющее в своем разложении (1.1) большое количество значащих разрядов, должно заменяться каким-то образом числом, имеющим отведенное количество разрядов. Эта операция замены называется округлением чисел. Разность между округленным и округляемым числами называется ошибкой округления.

Часть I. Параллельные вычислительные системы

Теоретически операция округления числа может быть либо однозначно определенной функцией округляемого числа, либо случайной функцией. Как случайная функция она реализуется в компьютерах исключительно редко, т. к. в этом случае невозможно при повторении расчетов получать одни и те же результаты. Как однозначно определенная функция операция округления может быть реализована самыми разными способами, к чему есть веские причины. Операция округления исключительно важна для пользователя. Чем меньше ошибка округления, тем в общем случае точнее результат. Наилучшее округление очевидно, и реализуется оно обычным "школьным" правилом. В этом случае ошибка округления никогда не превосходит половины последнего разряда в округленном числе. Но реализация данного правила в компьютере требует дополнительно и аппаратуры, и времени. В погоне за скоростью выполнения арифметических операций инженеры часто реализуют более простые операции округления. Иногда они делают это очень неудачно. Например, просто плохо была выполнена операция округления в первых моделях знаменитого компьютера Сгау-1. Только резкая критика со стороны пользователей заставила изменить операцию округления в последующих моделях.

Конечно, ошибки округления по отношению к самим числам являются малыми поправками. При выполнении различных операций они вносятся в результат почти всегда. И эти малые поправки радикально меняют свойства операций. Если при точном выполнении операции сложения, вычитания, умножения и деления обладают свойствами ассоциативности, коммутативности и дистрибутивности, то эти свойства при выполнении тех же операций с округлением пропадают. Факт, который доставляет очень много хлопот при конструировании численных методов.

Представление чисел в виде двоичных разложений (1.1), безусловно, продиктовано двоичным представлением любой информации в компьютерах. К сожалению, оно имеет ряд неустранимых изъянов. Доказано, в частности, что при выполнении таких арифметических операций, как сложение и вычитание, операция округления, реализованная по любому неслучайному правилу, дает ошибки с ненулевым смещением. Это приводит к ненулевым смещениям ошибок и в окончательных результатах, о чем не следует забывать. С точки зрения ошибок округления более привлекательным является разложение чисел по степеням числа 3. Подробнее с округлением чисел можно познакомиться в книге [5].

Если интересно знать, как реализована операция округления на конкретном компьютере, проведите на нем следующий эксперимент. При точных вычислениях рекуррентная формула

Уо = 1, У/t = (Ук-\/к)к, к>1

дает у_к = 1 для всех к. Не изменяя положения скобок, проведите расчеты по ней на компьютере в течение 10—15 минут и выведите для некоторых к значения ошибки

Ч = \Ук ~ 1|-

Глава 1. Что скрывают "обыкновенные" компьютеры

Здесь у_к есть реально вычисленная величина. Скорее всего, е^ будет линейно расти с ростом к. Но ведь некоторые задачи считаются часами, сутками и даже дольше. Теперь задайтесь вопросом о том, можно ли доверять полученному решению. Если возникли сомнения, вы на правильном пути. Тогда полистайте книгу [5] более внимательно.

Требование унифицированного выполнения арифметических операций приводит к унификации изображения чисел в компьютерах. Пусть для каждого числа отводится х двоичных разрядов памяти. Обычно они составляют слово или несколько слов. Прежде всего должно быть установлено взаимно однозначное соответствие между отдельными битами и двоичными разрядами числа. В зависимости от того, является ли это соответствие одним и тем же для всех чисел или зависит от числа, различают два основных способа представления чисел в компьютере, называемых соответственно представлением с фиксированной и плавающей запятой.

Предположим, что т двоичных разрядов памяти служат для изображения х последовательных разрядов чисел, причем положение запятой среди них фиксировано и является одним и тем же для всех чисел. Будем считать, что на изображение разрядов, стоящих слева от запятой, отводится г битов, где г > 0. Такой способ представления чисел называется представлением с фиксированной запятой. С помощью этого способа можно точно запомнить двоичное разложение любого из чисел, имеющих не более г ненулевых разрядов слева от запятой и не более \ — г ненулевых разрядов справа от запятой. Все эти числа лежат в диапазоне

-2^г<х< 2^Г.

Один из недостатков представления чисел с фиксированной запятой виден сразу. Если число много меньше 2^Г по модулю, то большая часть из отведенных х битов изображает старшие нулевые разряды и фактически не используется. Поэтому аппроксимация малых чисел числом с фиксированной запятой связана с большой относительной ошибкой. Однако для чисел, близких к 2^Г по модулю, используются все т битов. В этом случае относительная ошибка является минимальной. Абсолютная ошибка представления чисел с фиксированной запятой всегда лежит в одних и тех же пределах независимо от величины чисел. Достоинством представления чисел с фиксированной запятой является относительная простота алгоритмов сложения и умножения. По существу они ничем не отличаются от хорошо известных "школьных" алгоритмов выполнения этих операций.

Представление чисел с плавающей запятой заключается в следующем. Принимая во внимание (1.1), запишем число х в виде

х = а2^ь. (1.3)

Часть I. Параллельные вычислительные системы

Тогда будем иметь, что

1/2 < |я| < 1. (1.4)

Число а называется мантиссой числа х, число b — его двоичным порядком. Если х = О, то считается, что а = 0, а число b не определено. Пусть на изображение порядка без знака отводится г битов, на изображение мантиссы без знака % — г битов. Представив порядок и мантиссу как числа с фиксированной запятой, мы получаем представление числа х с плавающей запятой. При изображении мантиссы и порядка нет отмеченной выше потери относительной точности, т. к. в обоих случаях положение запятой строго определено. Порядок всегда является целым числом, а первый после запятой двоичный разряд мантиссы всегда равен 1. Порядок представляется точно. Мантисса будет точно представлена только для чисел, которые в двоичном разложении имеют не более % — г ненулевых разрядов. Все числа, которые могут быть представлены с плавающей запятой, всегда представляются с высокой относительной точностью. Это числа из диапазона

T^r <\х\<2^г~¹.

Минимальное положительное число со, которое можно представить с плавающей запятой, называется машинным нулем. Ясно, что в нашей трактовке представления чисел

ю = 2-²\ Все числа из диапазона

-Т¹' <х< Т¹'

изображаются нулем. В разных компьютерах под порядок и мантиссу отводятся разные числа разрядов. В частности, в упоминавшемся уже компьютере Сгау-1 на мантиссу со знаком выделено 49 разрядов, на двоичный порядок — 15 разрядов. Огромный диапазон представляемых чисел и большая их относительная точность, безусловно, определены ориентацией компьютера Cray-1 на научно-технические расчеты.

В современных компьютерах используются оба способа представления чисел. Операции над числами с фиксированной запятой выполняются быстрее, чем над числами с плавающей запятой. Это связано с тем, что при реализации операций с плавающей запятой по существу приходится выполнять все действия с парами чисел с фиксированной запятой. Рассмотрим два числа

х = а2^ь, у = c2^d

с плавающей запятой. Имеем

ху = {ас)Ъ^ь+<1).

Глава 1. Что скрывают "обыкновенные" компьютеры 23

Если 1/2 < \ас\ < 1, то мы сразу получаем представление числа ху в форме с плавающей запятой. Но если 1/4 < \ас\ < 1/2, то нужное представление числа ху будет другим. Именно,

ху = (2ас)2*+<4

Естественно, что при реализации операции умножения чисел с плавающей запятой обе ситуации должны осуществляться несколько по-разному. Поэтому в процессе реализации операции умножения чисел должны быть ветвления.

Еще более сложно осуществляется операция сложения чисел с плавающей запятой. Пусть для определенности b > d. Имеем

(х + у) = (а + с2^-Щ2^ь, (1.5)

причем всегда выполняется неравенство

\а+ с2^~^ь)\ < 2.

Если

\а + c2(^rf"*)| = О,

то представление (1.5) сразу дает форму числа х + у с плавающей запятой. Предположим теперь, что

2^Г~¹ < \а + с2^~^ь)\ < 2^Г

для какого-нибудь целого числа г. Представим число х + у в следующем виде:

х +у = ((а + с2(⁽'-^ь))2-^г)2(^ь+г). (1.6)

Так как выполняются соотношения

1/2 < \{а + c2(^rf-*))2-''| < 1,

то (1.6) дает форму с плавающей запятой для числа х + у. Здесь b + г есть порядок числа х + у, выражение

(а + с2^-^ь))2~^г

задает его мантиссу. Процесс реализации операции сложения также имеет ветвления, причем более сложные, чем у операции умножения.

Представление чисел с плавающей запятой оказывается предпочтительным в тех случаях, когда приходится иметь дело с числами из очень большого диапазона. Такая ситуация типична при проведении научно-технических расчетов. Однако довольно часто встречаются и другие ситуации. Например, в финансовых расчетах, задачах количественного учета заранее известен диапазон рассматриваемых чисел. Здесь вполне может использоваться представление чисел с фиксированной запятой. Необходимость экономии аппаратуры также приводит к фиксированной запятой. Умелое ее использование позволяет добиться большей скорости и большей точности решения задачи, чем использование плавающей запятой. Еще большего эффекта можно дос-

Часть I. Параллельные вычислительные системы

тичь путем разумного сочетания вычислений обоих типов. Однако мы не будем сколько-нибудь подробно останавливаться здесь на этих вопросах.

Устройства, выполняющие операции сложения/вычитания, называются сумматорами, выполняющие операции умножения — умножителями. Все эти устройства наряду с устройствами, реализующими логические операции, входят в состав АЛУ. Операции с фиксированной запятой выполняются быстрее аналогичных операций с плавающей запятой. Операции сложения выполняются быстрее операций умножения. Любые логические операции реализуются быстрее операций сложения/вычитания с фиксированной запятой. На каждом конкретном компьютере длительности выполнения стандартных операций отличаются друг от друга не более, чем в несколько раз.

Вопросы и задания

1. Докажите, что любое вещественное число х можно представить в виде троичного разложения

^х= X^fl/3''

/ = -оо

где числа a_t принимают одно из значений 0, 1, — 1.

2. Докажите, что знак числа х в п. 1 совпадает со знаком числа ab, если ab ф 0.

3. Обозначим через x_s число, получаемое из троичного разложения числа х отбрасыванием всех разрядов, начиная с (s — 1)-го. Докажите, что для троичного разложения x_s > х, если первый из ненулевых отброшенных разрядов отрицательный, и x_s < х, если он положительный.

4. Обладает ли двоичное разложение (1.1) аналогичным свойством?

5. Докажите, что число (1/2)3* не может быть задано конечной дробью по степеням числа 3.

6. Докажите, что в обозначениях пп. 3, 4 имеют место неулучшаемые оценки \х — x_s\ < 2^s для двоичного разложения и \х — x_s\ < (1/2)3* для троичного разложения.

7. В какой системе, двоичной или троичной, легче выполнять операцию округления, если стремиться к минимизации абсолютной ошибки?

8. Знаете ли вы, что первая в мире электронная вычислительная машина "Сетунь", работающая на троичной системе, была сконструирована в Московском университете к.т.н. Н. П. Брусенцовым?

9. Предложите какой-либо способ изображения чисел, отличный от способа с фиксированной или плавающей запятой. Насколько сложно при этом выполняются операции над числами?

10. Почему числа из интервала ( —со, со), где со есть машинный ноль, заменяются нулем, а не каким-либо другим числом?

Глава 1. Что скрывают "обыкновенные" компьютеры

11. Можно ли в представлении чисел с плавающей запятой вычислить число со ^!?

12. При точных вычислениях (1 + V2 )² = 3 + 2 V2 . Если подставить слева и справа вместо V2 любое его приближенное значение, то результаты всегда будут различными. Какое же из эквивалентных выражений (1 +V2 )² или 3 + 2V2 надо брать за основу вычислений?

13. Зависит ли состав множества приближенных решений задачи, определяемого порядком выполнения операций, от выбранного способа округления чисел?

§ 1.3. Иерархия памяти

Предположим, что на компьютере решается какая-нибудь очень большая задача, например, система линейных алгебраических уравнений с матрицей максимального размера. Если используется метод Гаусса, то исключать элементы можно в самых различных порядках. При этом общее число выполняемых арифметических операций остается одним и тем же или меняется не более чем в 2—3 раза. Однако, пропуская разные варианты метода для одной и той же системы, замечаем, что общее время решения задачи меняется в десятки раз и более. Другая реальная ситуация. Пусть зафиксирован какой-либо вариант метода Гаусса, но теперь решаются системы различных размеров. При этом ожидается, что общее время решения задачи будет меняться пропорционально общему числу арифметических операций. Но и в этом случае встречаются неожиданности. Иногда для некоторых порядков время решения задачи может оказаться существенно большим.

На общее время решения задачи влияет много факторов. Но главные из них — это время выполнения арифметических операций и время взаимодействия с памятью. В методах типа Гаусса вся совокупность арифметических операций известна заранее. Поэтому, если время решения задачи почему-то неоправданно возрастает, то, скорее всего, есть определенная неаккуратность в использовании памяти. А это означает, что имеются причины для более глубокого обсуждения строения памяти и принципов ее использования. Тем более, если возникает необходимость решать большие задачи.

Как бы ни была устроена память в компьютере, каждый бит информации моделируется простейшим техническим элементом, принимающим два состояния. Плотность расположения таких элементов исключительно высока. Например, в случае электронного устройства памяти число элементов на одном кристалле может достигать многих миллионов. Однако это не означает, что память можно сделать сколь угодно большой.

Главное требование к памяти — обеспечение малого времени доступа к отдельным словам. Вообще говоря, оно должно быть намного меньше, чем время выполнения операций над словами, в крайнем случае — соизмеримым с ним. Ту часть памяти, для которой характерное время доступа замет-

Часть /. Параллельные вычислительные системы

но меньше времени выполнения операций, называют быстрой, остальную — медленной. Большая часть образует адресуемую память, меньшая — неадресу емую. В адресуемой памяти каждое слово имеет адрес. Эта часть памяти доступна пользователю. Работая с ней, можно как записывать информацию, так и считывать. Она также называется оперативной памятью (ОП), а соответствующее техническое устройство — оперативным запоминающим устройством (ОЗУ).

Неадресуемая память недоступна пользователям. В ней различают постоянную память и сверхбыструю память. В постоянную память ничего нельзя записать, но из нее можно многократно считывать записанную ранее информацию. Обычно в ней хранятся команды запуска компьютера, различные служебные программы и т. п. Использование оптических технологий открывает возможность создания постоянной памяти огромных размеров. В этом случае в ней можно будет хранить, например, весь багаж библиотек программ широкого назначения.

Сверхбыстрая память отличается от оперативной существенно меньшим временем доступа. Чаще всего она имеет 1—2 уровня. Самый быстрый уровень — это регистровая память. Она имеет очень небольшой объем, измеряемый единицами или десятками слов. В ней хранятся те результаты выполнения операции, которые необходимы для реализации команды, непосредственно следующей за исполняемой. По существу регистровая память является неотъемлемой частью АЛУ. Почти такой же быстрой оказывается кэш-память. Она является своеобразным буфером между регистровой памятью и оперативной памятью. В современных компьютерах ее объем доходит до миллиона слов. В ней хранятся те результаты выполнения операции, которые могут потребоваться для реализации команд, вскоре следующих за исполняемыми. Управляет использованием сверхбыстрой памяти устройство управления. На стадии перевода программ в машинный код компилятор может выстраивать команды таким образом, чтобы эффект от использования сверхбыстрой памяти был максимальным. Но это делается не всегда.

Чтобы добиться малости времени доступа к оперативной памяти, необходимо выполнить много условий, в частности, минимизировать время прохождения управляющих сигналов к ее элементам. Среди прочего, в существующих технологиях это зависит от длин соединений. При большом числе элементов даже теоретически длины соединений нельзя сделать равномерно малыми. При этом неравномерность тем больше, чем больше число элементов. Уже одно это обстоятельство должно приводить к неоднородности памяти с точки зрения ее использования. При конструировании оперативного запоминающего устройства используют различные технические решения для уменьшения нежелательного эффекта большого разброса времени доступа. В частности, ОЗУ делают иерархическим, что соответствует делению памяти на кубы, блоки, секции, страницы и т. п. Чем выше уровень иерархии, тем

Глава 1. Что скрывают "обыкновенные" компьютеры

меньше разброс времен доступа к отдельным словам одного раздела памяти данного уровня. На самом высоком уровне выделяют группы слов, доступ к которым может быть осуществлен или одновременно, или с минимальной разностью времен. Чаще всего это слова с последовательными физическими адресами или адресами, меняющимися с постоянным шагом.

Таким образом, стремление сделать оперативную память "обыкновенного" компьютера достаточно большой приводит к усложнению ее структуры. В свою очередь, это неизбежно увеличивает разброс времен доступа к отдельным словам. Наилучший режим работы с оперативной памятью обычно поддерживается как операционными системами, так и компиляторами. Но для программ произвольного вида он не всегда может быть реализован. Чтобы его использовать, составитель программ должен соблюдать вполне определенные правила, о существовании которых следует узнать заранее.

Если для реализации алгоритма нужно не просто составить какую-нибудь программу, а добиться, чтобы она работала максимально быстро, то соблюдение этих правил может дать ощутимый эффект. Как уже отмечалось, многие компьютеры особенно быстро осуществляют доступ к словам с последовательными физическими адресами. Пусть, например, программа составляется на языке Fortran. С точки зрения этого языка безразлично, проводить обработку элементов массивов по строкам или столбцам. Безразлично это и с точки зрения сложности получаемой программы. Все различие сводится лишь к тому, что в одном случае мы имеем дело с преобразованием элементов каких-то матриц, а в другом — транспонированных к ним. Принимая во внимание специфику доступа к памяти, компиляторы с языка Fortran всегда располагают массивы в физической памяти последовательно по адресам, столбец за столбцом, слева направо и сверху вниз. Предположим, что реализуется алгоритм решения систем линейных алгебраических уравнений методом Гаусса. В этом случае время работы программы будет определяться ее трехмерными циклами. В зависимости от того, расположена матрица системы в массиве по столбцам или строкам, внутренние циклы программы будут также осуществлять обработку элементов массивов по столбцам или строкам. Времена реализации обоих вариантов могут различаться весьма заметно, иногда в несколько раз. Факт существенный, если речь идет о разработке оптимальных программ.

Проведенное обсуждение касается, главным образом, того случая, когда при решении задачи удается ограничиться лишь использованием достаточно быстрой оперативной памяти. Положение становится значительно сложнее, если приходится использовать медленную память.

В большинстве языков программирования отсутствует понятие размера памяти. Это связано с желанием не делать программы зависимыми от параметров компьютеров. Тем не менее, на каждом конкретном компьютере пользователю может быть предоставлена память лишь ограниченного разме-

Часть I. Параллельные вычислительные системы

ра. Стремление максимально увеличить ее размер приводит к необходимости использовать не только быструю оперативную память, но и медленную память. На современных компьютерах медленная память чаще всего реализуется на жестких дисках. Ее размеры во много раз больше размеров оперативной памяти. Однако во много раз больше у нее и время доступа. При решении предельно больших задач основную часть данных неизбежно приходится хранить в медленной памяти. Но в любом компьютере операции выполняются лишь над данными, находящимися в быстрой памяти. Поэтому в процессе решения больших задач нужно обязательно и, как правило, многократно переносить данные из медленной памяти в быструю и обратно. Это означает, что время решения больших задач определяется двумя составляющими: временем выполнения операций алгоритма и временем осуществления обменов между медленной и быстрой памятью. Основная проблема использования медленной памяти состоит в том, что неудачная организация обменов может привести к тому, что вторая составляющая будет превосходить первую в десятки, сотни и даже тысячи раз. Напомним, что неудачная организация работы с оперативной памятью может увеличить время реализации алгоритма только в несколько раз.

Квалифицированная организация обменов между медленной и быстрой памятью базируется на трех основных принципах: обращаться к медленной памяти как можно реже, переносить за обмен как можно больше данных, при каждом переносе в быструю память обрабатывать данные как можно дольше. Осуществить оптимальный баланс этих принципов — трудная задача. Чтобы не думать о ее решении, пользователю нередко предлагается работать с виртуальной памятью. Эта память условная. Она имеет вполне определенный размер и вполне определенную систему адресации слов. Виртуальная память может рассматриваться как однородная или иметь некоторую структуру. Для нее может быть разработана система правил предпочтительного размещения данных. Как конкретно отображается виртуальная память на физическую и как в действительности организуются обмены между медленной и быстрой памятью, зависит от соответствующих алгоритмов, заложенных в операционную систему. Кое-что об этих алгоритмах можно узнать из документации по компьютеру. Однако следует помнить, что, как правило, они универсальные и поэтому либо не учитывают совсем, либо учитывают очень слабо особенности конкретных программ.

Отсюда следует, что при решении больших задач нельзя безоговорочно доверять организацию обменов с медленной памятью операционной системе. Сначала лучше проверить качество ее работы с помощью следующего эксперимента. На каком-нибудь большом примере, отражающем существо решаемой задачи, нужно замерить в монопольном режиме астрономическое время реализации примера на компьютере и подсчитать время выполнения необходимых операций. Если первое время превышает второе не более чем в несколько раз, работу операционной системы по организации обменов

Глава 1. Что скрывают "обыкновенные" компьютеры

можно признать удовлетворительной для данного класса задач. В противном случае их надо организовывать самостоятельно, ориентируясь на вышеизложенные принципы. При этом стоит помнить, что не для каждой задачи время обменов с медленной памятью можно довести до низкого уровня.

В качестве подтверждения важности вопросов, касающихся обменов с медленной памятью при решении больших задач, рассмотрим один пример из истории разработки методов и программ для систем линейных алгебраических уравнений. Несмотря на его сорокалетнюю давность, он и сейчас остается весьма поучительным.

В середине 60-х годов прошлого столетия в нашей стране были широко распространены вычислительные машины типа М-20, построенные коллективом, возглавляемым академиком С. А. Лебедевым. По тем временам это были вполне современные компьютеры, обладающие производительностью около 20 тыс. операций в секунду. Однако их оперативная память была малой и позволяла решать системы линейных алгебраических уравнений с плотной матрицей порядка всего лишь 50—100. Требования практики заставляли искать способы решения систем значительно большего порядка. В качестве медленной памяти на этих машинах использовались магнитные барабаны. Они играли тогда такую же роль, какую сейчас в персональном компьютере играют жесткие диски. Естественно, с поправкой на объем хранимой информации. Под этот тип медленной памяти была разработана специальная блочная технология решения больших алгебраических задач [13]. Она позволяла с использованием только 300 слов оперативной памяти решать системы практически любого порядка. Точнее, такого порядка, при котором матрица и правая часть могли целиком разместиться в медленной памяти. При этом системы решались почти столь же быстро, как будто вся информация о них на самом деле была размещена в оперативной памяти. Созданные на основе данной технологии программы были весьма эффективны. В частности, на машинах типа М-20 они позволяли решать системы 200-го порядка всего за 9 минут.

В конце 60-х годов прошлого столетия появилась машина БЭСМ-6. Это была одна из лучших вычислительных машин в Европе. Она обладала производительностью около одного миллиона операций в секунду, т. е. была быстрее машин типа М-20 примерно в 50 раз. Разработана БЭСМ-6 была коллективом под руководством академика С. А. Лебедева, его заместителей В. А. Мельникова и Л. Н. Королева. Среди математического обеспечения машин БЭСМ-6 были и стандартные программы для решения системы линейных алгебраических уравнений большого порядка с использованием медленной памяти. Ожидалось, что с их помощью можно решать большие системы, если и не в 50, то хотя бы в несколько раз быстрее. Однако опытная проверка дала удивительные результаты. Система 200-го порядка решалась за 20 минут. Такова цена неаккуратного использования программиста-

Часть I. Параллельные вычислительные системы

ми медленной памяти. Конечно, со временем на машине БЭСМ-6 тоже появились хорошие программы. Но при этом пришлось вмешиваться в работу операционной системы.

Заметим, что М-20 и БЭСМ-6, эти пионеры вычислительной техники, относятся к классу "обыкновенных" компьютеров. Но все обсуждаемые выше проблемы являются актуальными и для современных компьютеров того же класса. В этом может легко убедиться каждый. Сравните производительность своего персонального компьютера и машины М-20. Теперь решите на своем компьютере систему линейных алгебраических уравнений 200-го порядка методом Гаусса и измерьте время ее решения. Далее сравните отношение производительностей и отношение времен решения систем для обоих компьютеров. И убедитесь, что сравнение далеко не в пользу вашего компьютера. Тогда резонно задать вопрос, почему же такое может произойти. Если же вы решите систему большого порядка с использованием жесткого диска в качестве медленной памяти, то результат сравнения с учетом различия в порядке систем окажется еще хуже. И снова задайте себе тот же вопрос. То, что здесь обсуждалось, как раз лежит в русле поиска ответа.

Вопросы и задания

1. Знаете ли вы, что в качестве внешней памяти первых электронных вычислительных машин использовалась магнитная лента?

2. Пусть вычисляются матрицы С = АВ и D = ВА как произведение двух квадратных матриц А и В порядка п. Предположим, что матрицы А, В, С, D располагаются во внешней памяти подряд соответственно по строкам, столбцам, строкам и строкам. Постройте соответствующие алгоритмы, если для их реализации можно использовать только О(п) ячеек оперативной памяти.

3. Что меняется в алгоритме вычисления матрицы D, если она должна быть расположена по столбцам?

4. Для пп. 2, 3 получите оценку времени работы с внешней памятью при вычислении матриц С, D, если в качестве внешней памяти используется магнитная лента.

5. Знаете ли вы, что впервые внешняя память на жестких дисках была разработана в 1956 г., каждый диск имел объем всего лишь в несколько мегабайт и размеры с письменный стол?

6. Для пп. 2, 3 получите оценку времени работы с внешней памятью при вычислении матриц С, D, если в качестве внешней памяти используется жесткий диск.

7. Знаете ли вы, что впервые концепция виртуальной памяти была реализована в 1962 г. на машине ATLAS?

8. Если вам доступен аппарат виртуальной памяти, вычислите матрицы С, D из пп. 2, 3 для самых больших значений п. Сравните времена реализации алгоритмов при одних и тех же значениях п, но разных расположениях матриц. Как вы можете объяснить различие времен?

Глава 1. Что скрывают "обыкновенные" компьютеры

§ 1.4. Языки программирования и программы

Мы уже говорили о том, что компьютер способен выполнять лишь программы, написанные в машинных командах. Однако программировать в машинных командах исключительно трудно. Прежде всего, из-за того, что структура команд чаще всего совсем не похожа на структуру тех действий, которыми пользователь предполагает описывать алгоритмы решения своих задач. Если составлять программы в машинных командах, пользователю неизбежно придется моделировать какими-то последовательностями команд каждое из своих действий. Но у этого способа программирования есть одно несомненное достоинство: он позволяет создавать самые эффективные программы. Объясняется это тем, что в данном случае имеется возможность тщательным образом учитывать совместно конкретные особенности как компьютера, так и задачи.

Рядовому пользователю не приходится программировать в машинных командах. У тех же специалистов, которым требуется создавать эффективные программы, такая потребность может появиться. Например, она часто возникает у разработчиков библиотек стандартных программ широкого назначения. Чтобы в какой-то мере облегчить труд таких специалистов, им предлагается программировать в некоторой системе символьного кодирования, называемой автокодом. По существу, это система тех же машинных команд, но с более удобной символикой. Кроме этого, в автокод могут быть введены дополнительные инструкции, моделирующие простейшие и наиболее часто встречающиеся комбинации машинных команд. Конечно, на компьютере имеется компилятор, который переводит программы, написанные на автокоде, в машинный код.

Автокод — это простейший язык программирования или, как его называют иначе, язык самого низкого уровня. Широко программировали на нем только на первых компьютерах. Массовое программирование на автокоде прекратилось по следующим причинам. Как отмечалось, программирование на нем очень трудоемко. Поэтому над автокодом стали создаваться различные языковые надстройки, называемые языками высокого уровня. Основная задача этих языков заключается в облегчении процесса программирования путем замены непонятных инструкций автокода другими инструкциями, более приближенными к пользовательским. Вершиной языков высокого уровня являются проблемно-ориентированные языки. Их инструкции позволяют пользователям писать программы просто в профессиональных терминах конкретных предметных областей. На каждом компьютере автокод, как правило, один. Языков высокого уровня, особенно проблемно-ориентированных, достаточно много. Компиляторы с них стали сложными иерархическими программными системами. Обратной стороной упрощения языков

Часть /. Параллельные вычислительные системы

программирования стало усложнение алгоритмов преобразования программ в машинный код и, как следствие, потеря программистом возможности контролировать эффективность создаваемых им программ. Это исключительно важное обстоятельство, и мы будем возвращаться к нему неоднократно, принимая во внимание нашу нацеленность на решение больших задач.

С точки зрения пользователя программировать на автокоде не только трудно, но и нецелесообразно из-за его ориентации на конкретный компьютер или, как говорят по другому, компьютерной зависимости. На разных моделях компьютеров автокоды разные. Универсального транслятора, переводящего программу из одного автокода в другой, не существует. Поэтому, переходя от одного типа компьютеров к другому, пользователю приходится переписывать заново все программы, написанные на автокоде. Этот процесс не только сверхсложный, но и крайне дорогой. Следовательно, одной из важнейших задач, стоящих перед разработчиками языков программирования высокого уровня, было создание языков, не зависящих от особенностей конкретных компьютеров. Такие языки появились в большом количестве. К ним относятся, например, Algol, Fortran, С и др. Они так и называются — машинно-независимые, что вроде бы подчеркивает их независимость от компьютеров. Еще их называют универсальными, что указывает на возможность описывать очень широкий круг алгоритмов.

Создание машинно-независимых языков программирования привело к появлению на рубеже 50—60-х годов прошлого столетия замечательной по своей красоте идеи. Традиционные описания алгоритмов в книгах нельзя без предварительного исследования перекладывать на любой компьютерный язык. Как правило, они неточны, содержат много недомолвок, допускают неоднозначность толкования и т. п. В частности, из-за предполагаемых свойств ассоциативности, коммутативности и дистрибутивности операций над числами в формулах отсутствуют многие скобки, определяющие порядок выполнения операций. Поэтому в действительности книжные описания содержат целое множество алгоритмов, на котором разброс отдельных свойств может быть очень большим. В результате, как правило, трудоемких исследований из данного множества выбирается какой-то один алгоритм, обладающий вполне приемлемыми характеристиками, и именно он программируется.

В программе любой алгоритм всегда описывается абсолютно точно. В его разработку вкладывается большой исследовательский труд. Чтобы избавить других специалистов от необходимости его повторять, надо этот труд сохранять. Программы на машинно-независимых языках высокого уровня как раз удобны для выполнения функций хранения. Идея состояла в том, чтобы на таких языках накапливать багаж хорошо отработанных алгоритмов и программ, а на каждом компьютере иметь компиляторы, переводящие программы с этих языков в машинный код. При этом вроде бы удавалось ре-

Глава 1. Что скрывают "обыкновенные" компьютеры

шить сразу две важные проблемы. Во-первых, сокращалось дублирование в программировании. И, во-вторых, автоматически решался вопрос о nopma-бельности программ, т. е. об их переносе с компьютера одного строения на компьютер другого строения. Вопрос, который был и остается весьма актуальным, т. к. компьютеры существенно меняют свое строение довольно часто. При реализации данной идеи функции по адаптации программ к особенностям конкретных компьютеров брали на себя компиляторы. Как следствие, пользователь освобождался от необходимости знать устройство и принципы функционирования как компьютеров, так и компиляторов.

В первые годы идея развивалась и реализовывалась очень бурно. Издавались многочисленные коллекции хорошо отработанных алгоритмов и программ из самых разных прикладных областей. Был налажен широкий обмен ими, в том числе, на международном уровне. Программы действительно легко переносились с одних компьютеров на другие. Постепенно и пользователи отходили от детального изучения компьютеров и компиляторов, ограничиваясь разработкой программ на машинно-независимых языках высокого уровня. Однако радужные надежды на длительный эффект от реализации обсуждаемой идеи довольно скоро стали меркнуть.

Причина оказалась простой и оказалась связана с несовершенством работы большинства компиляторов. Конечно, речь не идет о том, что они создают неправильные коды, хотя такое тоже случается. Дело в другом — ни один из компиляторов не гарантирует эффективность получаемых кодов. Вопрос об эффективности редко возникает при решении небольших задач. Такие задачи реализуются настолько быстро, что пользователь не замечает многие проблемы. Но различные аспекты эффективности программ, в первую очередь, скорость их реализации и точность получаемых решений становятся очень актуальными, если на компьютер ставятся большие и, тем более, предельно большие задачи.

Целью производства новых компьютеров является предоставление пользователям возможности решать задачи более эффективно, в первую очередь, более быстро. Поэтому, разрабатывая программы на языках высокого уровня, пользователь вправе рассчитывать на то, что время их реализации будет уменьшаться примерно так же, как растет производительность компьютеров. Кроме этого, он, конечно, предполагает, что программы на машинно-независимых языках будут действительно не зависеть от особенностей техники. Однако весь опыт развития компьютеров и связанных с ними компиляторов показывает, что в полной мере на это надеяться нельзя. Скорость реализации программ как функция производительности компьютеров оказалась на практике не линейной, а значительно более слабой, причем, чем сложнее устроен компьютер, тем она слабее. Программы на машинно-независимых языках показали зависимость от различных особенностей компьютеров. Постоянное же появление все новых и новых языков программирования без обеспечения каких-либо гарантий качества компилируемых программ лишь увеличивает сложность

Часть I. Параллельные вычислительные системы

решения многих проблем. На практике пользователь не может серьезно влиять на разработку языковой и системной среды компьютера. Но именно он ощущает на себе все ее огрехи. Ему и приходится с ней разбираться, хотя это совсем не его цель. Его цель — решать задачу.

Возникла странная ситуация. Пользователь самым прямым образом заинтересован в эффективности решения своих задач на компьютере. Для повышения эффективности он прилагает огромные усилия: меняет математические модели, разрабатывает новые численные методы, многократно переписывает программы и т. п. Но пользователь видит компьютер только через программное окружение, в первую очередь, через компилятор и операционную систему. Создавая и исполняя машинные коды, эти компоненты сильно влияют на эффективность реализации пользовательских программ. Однако с их помощью либо трудно, либо просто невозможно понять, где находятся узкие места созданного машинного кода и что необходимо изменить в конкретной программе на языке высокого уровня, чтобы повысить ее эффективность. Действительная информация, которую можно получить от компилятора и операционной системы после реализации программы, чаще всего оказывается настолько скудной и трудно воспринимаемой, что ею редко удается воспользоваться при выборе путей модернизации как самой программы, так и реализуемых ею алгоритмов.

Для пользователя вопрос взаимодействия с компьютером с целью поиска путей создания наиболее эффективных программ является очень актуальным. Но его решение почти полностью переложено на плечи самого пользователя. Штатное программное окружение компьютера не содержит никаких отладчиков, систем анализа структуры программ и т. п. Из описаний компилятора практически невозможно найти даже такую необходимую информацию, как эффективность работы в машинном коде отдельных, наиболее значимых конструкций языка высокого уровня. Есть много оснований упрекнуть создателей языков, компиляторов и операционных систем в недостаточном внимании к интересам разработчиков алгоритмов и программ. В таком упреке есть доля истины, т. к. интересы пользователей действительно затерялись среди многих других интересов системных программистов и перестали быть доминирующими. Однако надо также признать, что проблемы пользователей оказались совсем непростыми.

Одной из важнейших характеристик вычислительных процессов является точность получаемых результатов. Уже давно известно, что кроме общего описания процессов, на нее влияют форма представления чисел и способ выполнения операции округления. Эти факторы машинно-зависимые. Информация о них не воспринимается языками высокого уровня. Поэтому, строго говоря, такие языки даже по одной этой причине нельзя считать машинно-независимыми, т. к. на разных компьютерах могут допускаться разные представления чисел и разные способы выполнения округлений. В конечном счете, это может приводить, и на практике приводит, к достаточно

Глава 1. Что скрывают "обыкновенные" компьютеры

большому разбросу результатов реализаций одной и той же программы. Но тогда возникают многочисленные вопросы: "Какой смысл надо вкладывать в понятие машинно-независимый язык? Как разрабатывать алгоритмы и писать программы, чтобы хотя бы с какими-то оговорками их можно было рассматривать как машинно-независимые? Как трактовать результаты реализации программы с точки зрения точности?" И т. п.

Были предприняты значительные усилия, чтобы получить ответы на все эти вопросы. Унифицированы формы представления чисел. Разработаны стандарты на выполнение операции округления. Для многих алгоритмов получены оценки влияния ошибок округления. В целом же успехи невелики. Возможно, что главным достижением предпринятых усилий является осознание того, что при разработке численного программного обеспечения вопросы влияния ошибок округления нельзя игнорировать. Какое-то время казалось, что проблема точности является единственной принципиальной трудностью, связанной с реализацией алгоритмов на компьютерах разных типов. И хотя на легкое решение этой проблемы нельзя было рассчитывать, тем не менее, обозначились определенные перспективы. Постепенно как будто стала формироваться уверенность, что все же удастся создать на алгоритмических языках эффективное машинно-независимое численное программное обеспечение и, следовательно, довести до практического решения проблему портабельности программ.

Действительность пошатнула и эту уверенность. Было выяснено, что на множестве программ, эквивалентных с точки зрения пользователя по точности, числу арифметических операций и другим интересным для него характеристикам, разброс реальных времен реализации различных вариантов на конкретном компьютере остается очень большим. Причем не только для сложных программ, но и для самых простых. Например, программы решения систем линейных алгебраических уравнений с невырожденной треугольной матрицей, написанные на языке высокого уровня, могут давать существенно различные времена реализации просто в зависимости от того, осуществляются ли в них внутренние суммирования по возрастанию индексов или по их убыванию. Это означает, что пользователь принципиально не может выбрать заранее тот вариант программы на языке высокого уровня, который будет одинаково эффективен на разных компьютерах. Принципиально не может хотя бы потому, что такой вариант, скорее всего, не существует. Но это означает также, что языки программирования высокого уровня можно и по этой причине считать машинно-независимыми лишь условно.

Итак, чтобы получить оптимальный машинный код, необходимо, как минимум, предоставить компилятору описание всего множества вариантов программ, эквивалентных с точки зрения пользователя. Но на традиционных алгоритмических языках высокого уровня можно описать только один вариант. Отсюда вытекает два важных вывода. Во-первых, эффективно решить проблему портабельности программ, ориентируясь на использование

Часть /. Параллельные вычислительные системы

языков высокого уровня без предоставления дополнительной информации, невозможно. И, во-вторых, для построения программы, обеспечивающей оптимальный машинный код на конкретном компьютере, исключительно важно иметь возможность получения квалифицированной и достаточно полной информации со стороны компилятора и операционной системы на каждый прогон программы.

До тех пор пока такая возможность не будет реализована полностью, пользователям придется многократно переписывать свои программы в поисках оптимального варианта. Для уменьшения числа переписываний применяются различные приемы. Например, в программах выделяются вычислительные ядра, т. е. участки, на которые приходится основной объем вычислений. Эти ядра пишутся на автокоде. При переходе к новому компьютеру переписываются только они. Тем самым обеспечивается высокая эффективность программ. По такому принципу организованы такие популярные пакеты для решения задач линейной алгебры, как EISPACK, LINPACK, SCALAPACK и др. Вычислительные ядра в них организованы в специальную библиотеку программ BLAS, которая написана на автокоде и переписывается каждый раз при переходе к новому компьютеру. Как показал опыт, этот прием довольно дорогой и не всегда применим, особенно при создании больших программных комплексов. К тому же, как выяснилось, при переходе к компьютерам с принципиально иной архитектурой приходится переписывать не только вычислительные ядра, но и их оболочку.

Даже краткое обсуждение показало, что вопросы разработки эффективно реализуемых и долго используемых программ оказались исключительно трудными и интересными. Они потребовали не только создания языков высокого уровня, но и изучения структуры программ и алгоритмов, разработки новых технологий программирования, определения места и меры использования машинно-ориентированных языковых сред, совершенствования работы компиляторов и операционных систем и многого другого. Все эти вопросы никак не исчезают в связи с усовершенствованием компьютеров, а, наоборот, становятся все более и более актуальными.

Вопросы и задания

1. Знаете ли вы, что первые в мире программы составила дочь поэта Дж. Байрона графиня А. Лавлейс, и сделала она это для машины Ч. Беббиджа¹?

2. Знаете ли вы, что Fortran, один из первых языков программирования высокого уровня, был реализован в 1957 г.² и активно используется до настоящего времени?

¹ Чарльз Бэббидж (1792—1871) работал над созданием механического компьютера, программируемого с помощью перфокарт. Графиня Ада Августа Лавлейс, помимо написания программ, частично финансировала этот проект. — Ред.

² Fortran был разработан группой сотрудников фирмы IBM под руководством Джона Бэкуса. — Ред.

Глава 1. Что скрывают "обыкновенные" компьютеры

3. Знаете ли вы, что язык Фортран периодически подвергается ожесточенной критике со стороны разработчиков других языков программирования. Тем не менее, до сих пор в сфере научно-технических задач доля программ на языке Фортран и его диалектах превосходит долю программ на всех остальных языках программирования, вместе взятых. Как вы думаете, почему?

Исследуйте на устойчивость различные формы записи алгоритмов на языке высокого уровня для следующих задач:

4. Вычисление cosx через sinx при очень малых значениях х.

5. Вычисления sinx через tgx при очень больших значениях х.

6. Вычисление для больших я величины z = (2я)!!/(2я + 1)!!.

7. Вычисление величины v = х — Р(х)/Р\х) для многочлена Р(х) высокой степени при малых и больших значениях х.

8. Вычисление среднего арифметического большого количества чисел разных знаков.

9. Вычисление среднего геометрического большого количества больших положительных чисел.

10. Решение системы линейных алгебраических уравнений

х + л/2у = 1 л/3х + л/6у = л/3

при различных приближениях чисел л/2 , л/3 , ..., л/6.

11. Что меняется в заданиях 4—10, если вычисления осуществлять в режимах с фиксированной или плавающей запятой?

12. Можете ли вы гарантировать в предложенных решениях высокую относительную точность результата и если нет, то почему?

§ 1.5. Узкие места

Компьютеры постоянно совершенствуются. Главный вектор их развития — повышение производительности, т. е. возможности выполнять большее число операций в единицу времени. Данный вектор очень важен. Об этом говорит хотя бы тот факт, что в последние годы производительность компьютеров увеличивается на порядок примерно каждые пять лет. За производительность в компьютере отвечает, в первую очередь, арифметико-логическое устройство. Но оно занимает лишь около 20% всего оборудования. Следовательно, решая главную задачу — обеспечение пользователя информационно-вычислительными услугами, — компьютер решает и какие-то вспомогательные задачи, видимые или невидимые для пользователя. Меняется состав этих маленьких задач, меняются методы их решения. Вообще говоря, все они развиваются синхронно. Но иногда некоторые из маленьких задач или даже одна из них становится настолько критичной, что на определенном этапе развития компьютера оказывается самой главной, затмевая собой даже

Часть /. Параллельные вычислительные системы

компьютер в целом. Обо всем этом мы будем подробно говорить в главе 2. Чтобы лучше представлять, как и почему в процессе развития компьютера возникают различные узкие места, рассмотрим следующую иллюстративную модель.

Будем считать, что компьютер и его программное окружение есть некоторое предприятие широкого профиля по оказанию информационно-вычислительных услуг. Услугой является обработка какой-то совокупности данных. Потребители этих услуг — пользователи. Пользователь представляет предприятию согласованное с его требованиями техническое задание на услугу. Это — программа, написанная на том или ином языке. Отдавая заказ на конкретную услугу, пользователь, естественно, не хотел бы ничего знать о том, как предприятие будет ее реализовывать. Требования пользователя просты. Услуга должна быть выполнена правильно, быстро и дешево. На мелких услугах обычно так и бывает. Но если услуга масштабная, могут происходить сбои. Чаще всего предприятие не может обеспечить выполнение услуг в срок. Конечно, пользователь может обратиться в другое предприятие. Иногда это помогает. Однако нередко возникают и другие ситуации. Например, выполнение заказа в срок может потребовать от пользователя очень больших дополнительных затрат. Или может оказаться, что вообще ни одно из предприятий не берется за выполнение заказа. И тогда пользователю самому приходится разбираться, почему это происходит и что надо делать.

Любое предприятие по обеспечению информационно-вычислительными услугами организовано довольно сложно. Но всегда его ядром является производственный сектор. Это — арифметико-логическое устройство. В его составе имеется некоторый набор оборудования, такого как сумматоры, умножители, сопроцессоры и т. п. Все оно выполняет какие-то простейшие операции, вообще говоря, не имеющие прямого отношения к конечной услуге. Текущей организацией работы производственного отдела занимается сектор оперативного управления. Это — устройство управления. На предприятии существует склад для хранения исходных материалов, а также промежуточной и конечной продукции. Это — память. Структура склада разветвленная. Ее сложность объясняется необходимостью хранить самую разную по характеру использования продукцию. При работе производственного сектора появляются промежуточные результаты, которые будут востребованы им же или сразу, или почти сразу. Нет никакого смысла отсылать их в дальний угол склада, что неизбежно привело бы к общему замедлению процесса. Поэтому отдельные ячейки склада располагаются среди оборудования производственного сектора. Это — регистровая память. Другие рядом с ним. Это — кэш-память. Несколько дальше располагается быстрая оперативная память. И дальше всего — медленная память.

Одним из важнейших является технологический сектор. Именно он на основе технического задания разрабатывает план использования оборудования

Глава 1. Что скрывают "обыкновенные" компьютеры

производственного сектора, склада и некоторых других подразделений предприятия для реализации каждой конкретной услуги. Это — компилятор. Осуществление данного плана неизбежно требует перемещения различных объектов из одного места в другое. Обеспечением всех перемещений занимается транспортный сектор. Это — различные соединения, шины, каналы и т. п. И наконец, организует реальное выполнение работ в соответствии с разработанным планом организационный сектор. Это — операционная система.

Такова грубая модель устройства и процесса функционирования компьютера. В реальности все сложнее: отдельных подразделений в предприятии гораздо больше, функции между ними разделены не так четко и т. д. Тем не менее, даже на этой иллюстративной модели можно увидеть довольно много.

Вообще говоря, любой универсальный компьютер способен решить любую задачу, если только у него имеется достаточно памяти. Другое дело, что она может решаться настолько долго, что не хватит времени дождаться результатов. В рассмотренной модели видно, что время решения задачи определяется многими факторами. Главный из них — мощность оборудования производственного сектора. Но и от других секторов зависит немало. Если оборудование транспортного сектора несовершенно, перемещения объектов из одного места в другое будут осуществляться медленно. В этих условиях либо очень трудно, либо даже невозможно добиться высокой производительности всего предприятия. Если технологический сектор составит неэффективный план, требующий, например, больших накладных расходов, — эффект будет похожим. Очень многое зависит от того, как организационный сектор будет реализовывать план, предложенный технологическим сектором. Если из дальних углов склада необходимо часто перемещать большие количества объектов, то нерационально перемещать их малыми порциями. Гораздо эффективнее осуществлять перемещение большими группами. Как будет это организовано, зависит от решений, принимаемых организационным сектором. А эти решения, в частности, определяются структурой склада. И т. п.

Таким образом, работа нашего модельного предприятия по обеспечению пользователей информационно-вычислительными услугами зависит от действий всех секторов. Его базовая производительность определяется мощностью оборудования производственного сектора. Суммарная производительность всего оборудования этого сектора называется пиковой производительностью. Это — теоретическое понятие. Оно не учитывает никакие временные затраты от деятельности других секторов. Реальная производительность — это производительность предприятия, которую оно реально достигает при выполнении конкретной услуги. Вообще говоря, она может зависеть от вида услуги. Реальная производительность никогда не может превышать пиковую. Степень ее близости к пиковой говорит о степени согласованности работы секторов между собой и об эффективности работы предприятия в целом. Отношение реальной производительности к пиковой называется эффективностью работы предприятия. Свою долю в уменьшение

Часть I. Параллельные вычислительные системы

эффективности вносят все сектора. Одни больше, другие меньше, какие-то очень много.

Каждый из секторов решает свою маленькую задачу. И только вместе они способны сделать нечто большое. В процессе развития предприятия наступает момент, когда эволюционным путем уже нельзя поднять производительность. Тогда приходится проводить глобальную модернизацию. В первую очередь необходимо решить, как радикально увеличить пиковую производительность. Есть два пути, отработанные веками в самых разных отраслях. Грубо говоря, один из них связан с наращиванием однотипного оборудования, другой — с организацией конвейеров. В нашем случае годятся оба и даже их комбинация. Об этом мы также будем подробно говорить в главе 2. На период реконструкции производственного сектора его задача становится главной. Но затем неизбежно приходится модернизировать и все другие сектора. Главными становятся задачи реконструкции склада, транспортных путей, управления и т. д. Любая малая задача становится главной тогда, когда она оказывается самым узким местом в достижении наивысшей реальной производительности предприятия в целом.

Все сказанное, в том числе касающееся эффективности, имеет прямое отношение к любому компьютеру. Если на большинстве программ эффективность работы компьютера находится в пределах 0,5—1, ситуацию можно считать хорошей. Если же эффективность намного меньше, а задачи требуется решать как можно быстрее, приходится разбираться, где же теряется производительность и что надо сделать для ее повышения. Другими словами, надо установить узкие места процесса функционирования компьютера и его программного окружения в целом. Согласно рассмотренной модели, в первую очередь они могут определяться:

□ составом, принципом работы и временными характеристиками арифметико-логического устройства;

□ составом, размером и временными характеристиками памяти;

□ структурой и пропускной способностью коммуникационной среды;

□ компилятором, создающим неэффективные коды;

□ операционной системой, организующей неэффективную работу с памятью, особенно медленной.

Как мы увидим в дальнейшем, постоянное совершенствование именно перечисленных составляющих сделало возможным превращение "обыкновенного" компьютера в суперкомпьютер. Хотя и в суперкомпьютерах эти составляющие остаются потенциальными источниками возникновения узких мест.

Глава 1. Что скрывают "обыкновенные" компьютеры

Вопросы и задания

1. Предположим, что один землекоп может за час вырыть яму размером 1x1x1 м³и способен работать в таком режиме достаточно долго. За какое время бригада из 5, 10, 20 землекопов выроет яму размером 2x2 м² и глубиной 1 м?

2. Постройте график времени выполнения работы в зависимости от числа землекопов в бригаде.

3. Повторите задания пп. 1, 2 для ямы размером 10x10 м², глубиной 1 м и бригады из 10, 100 землекопов.

4. Чем принципиально различаются эти варианты?

5. Пусть предпринимается попытка увеличить реальную мощность производственного отдела из иллюстративной модели компьютера путем наращивания однотипного оборудования. Не кажется ли вам, что возникнет ситуация, аналогичная рассмотренной в пп. 1—4?

6. Для создания очень мощного компьютера часто объединяют вместе большое число персональных компьютеров. Пусть их будет п. Для обмена информацией между компьютерами необходимо создать коммуникационную сеть. Теоретически самый простой способ — соединить каждый компьютер с каждым прямыми связями, т. к. в этом случае информация вроде бы должна передаваться наиболее быстро. Всего потребуется п(п — 1) таких связей. Рассмотрите подобные коммуникационные сети для п = 3, 5, 8.

7. В реальных компьютерах величина п может достигать 10⁴—10⁵. Можете ли вы представить всю совокупность связей в этом случае, если они организованы согласно п. 6?

8. Пусть снова сверхмощный компьютер создается как объединение п персональных компьютеров. Построим неориентированный граф, в котором вершины символизируют персональные компьютеры, а ребра — прямые связи. Будем считать, что граф связный, т. е. для каждой пары вершин существует связывающая их цепь ребер. Такой граф называется коммуникационным. Исследуйте коммуникационный граф из п. 6.

9. Пусть в коммуникационном графе существуют не все ребра. Будем считать, что передача информации между персональными компьютерами может осуществляться вдоль любой цепи коммуникационного графа, связывающей соответствующие вершины. Постройте различные коммуникационные графы, уменьшая общее число ребер.

10. Если вам удалось построить коммуникационный граф, имеющий п вершин, п ребер и такой, что между любыми двумя вершинами существует цепь, состоящая не более чем из 21og₂« ребер, то вы на правильном пути. Соответствующие коммуникационные сети называются каскадными перестраиваемыми сетями.

Глава 2

Как повышают производительность компьютеров

Независимо от того, куда вы идете, это в гору и против ветра.

Из законов Мерфи

Замечено, что эмоциональное состояние человека, впервые сталкивающегося с суперкомпьютером, проходит несколько стадий. Сначала он испытывает что-то вроде эйфории, начитавшись рекламных данных о компьютере и находясь в предвкушении быстрого разрешения всех своих вычислительных проблем. После первого запуска своей программы у него возникает недоумение и подозрение, что что-то он сделал не так, поскольку реально достигнутая производительность слишком сильно отличается от ожидаемой. Он запускает программу повторно, но результат, если и меняется в лучшую сторону, то очень и очень слабо. Он идет к местному компьютерному гуру, и тут-то его поджидает настоящий удар. Сначала ему говорят, что полученные им 5% от пиковой производительности компьютера являются не таким уж и плохим результатом. А затем добавляют, что если он хочет "выжать" из такой вычислительной системы максимум, то для него вся работа только начинается. Нужно обойти возможные конфликты в памяти и постараться сбалансировать вычислительную нагрузку между процессорами. Необходимо подумать об оптимальном распределении данных, помочь компилятору разобраться со структурой программы, заменить последовательные части алгоритма на параллельные. Надо сделать еще много чего, что, вообще-то говоря, раньше совершенно не было свойственно работе прикладного программиста. И все прежние проблемы, характерные для последовательных компьютеров и традиционного последовательного программирования, разумеется, остаются...

Эту ситуацию заметили давно и предлагали различные способы ее решения. Изменялась архитектура компьютеров, развивалась среда программирования, но оставалось постоянным одно — "головная боль" прикладных программистов, решивших серьезно встать на путь параллельных вычислений. Оговоримся сразу, мы далеки от мысли кого-либо обвинять в такой ситуации. Инженерами и программистами проделана колоссальная работа, без которой и предмет нашего обсуждения не существовал бы. Просто область сложна сама по себе, да и жизнь постоянно вносит свои коррективы. Создавая кэш-память, которая прекрасно работает в одном микропроцессоре, никто и не подозревал, какие проблемы она принесет в многопроцессорных

Глава 2. Как повышают производительность компьютеров

системах. Только научились анализировать структуру исходного текста программ на Fortran, как появились языки С и C++, привнесшие значительные трудности в статический анализ параллельной структуры программ. Чуть ли не единственным достижением, постоянное развитие которого никак не задевает программиста, является увеличение тактовой частоты: программа работает быстрее, а он для этого ничего дополнительного не делает.

В той области, которая является предметом нашего исследования, всегда было и всегда будет очень много нового, непривычного, часто даже парадоксального. Во все времена для компьютеров, работающих на предельных скоростях, будут требоваться технологии, отличающиеся от "массовых", они всегда будут "на передовом крае", и, следовательно, они всегда будут вызывать трудности в использовании. Но для того и создана данная книга, чтобы показать возможные проблемы и пути их решения. Но это немного позже. В данной главе мы остановимся на базовых понятиях и посмотрим, как проходило развитие и каковы основные особенности современных компьютеров.

§ 2.1. Усложнение и наращивание аппаратных средств

Бесспорно, успехи микроэлектроники впечатляют. Согласно закону Мура, не имеющего строгого доказательства, но подтверждающегося уже не один десяток лет, производительность "обычных" компьютеров удваивается каждые полтора года. Однако попытаемся разобраться, только ли этими причинами определяются те рекордные показатели производительности, которыми обладают современные компьютеры. Обратимся к известным историческим фактам и проведем простое сравнение (рис. 2.1). На одном из первых компьютеров мира — EDSAC, появившемся в 1949 году и имевшем время такта 2 микросекунды, можно было выполнить 2« арифметических операций за 18« миллисекунд, т. е. в среднем 100 арифметических операций в секунду. Сравним эти данные, например, с характеристиками одного вычислительного узла современного суперкомпьютера Hewlett-Packard Superdome: время такта приблизительно 1,3 не (процессор РА-8700, 750 МГц), а пиковая производительность около 192 миллиардов арифметических операций в секунду.

EDS АС

1949 год

тактовая частота 0,5 МГц

1,5x10

HP Superdome

2001 год

770 МГц

производительность 10²оп/с 1,9х10⁹ ^> 1,9х10¹¹оп/с

Рис. 2.1. Увеличение производительности ЭВМ — за счет чего?

Часть /. Параллельные вычислительные системы

Что же получается? За полвека производительность компьютеров выросла почти в два миллиарда раз. При этом выигрыш в быстродействии, связанный с уменьшением времени такта с 2 мкс до 1,3 не, составляет лишь около 1500 раз. С этой цифрой естественно связать развитие микроэлектроники (что верно, конечно же, лишь в некотором приближении). Откуда же взялось остальное? Ответ достаточно очевиден — использование новых решений в архитектуре компьютеров, и среди них далеко не последнее место занимает принцип параллельной обработки данных, воплощающий идею одновременного выполнения нескольких действий.

Удивительно, но несмотря на все многообразие форм проявления параллелизма в архитектуре компьютеров, на обилие сопутствующих проблем, существует лишь два способа параллельной обработки данных, собственно параллелизм и конвейерность. Более того, оба способа интуитивно понятны, и нам необходимо сделать лишь небольшие пояснения.

Параллельная обработка

Предположим, что нам нужно найти сумму двух векторов, состоящих из 100 вещественных чисел каждый. В нашем распоряжении есть устройство, которое выполняет суммирование пары чисел за пять тактов работы компьютера. Устройство сделано так, что на все время выполнения данной операции оно блокируется, и никакой другой полезной работы выполнять не может. В таких условиях вся операция будет выполнена за 500 тактов. Развитие процесса обработки во времени схематично изображено на рис. 2.2.

Теперь допустим, что у нас есть два точно таких же устройства, которые могут работать одновременно и независимо друг от друга. Для простоты будем рассматривать идеальную ситуацию, когда нет никаких дополнительных накладных расходов, связанных с получением устройствами входных данных и сохранением результатов. Постоянно загружая каждое устройство элементами входных массивов, можно получить искомую сумму уже за 250 тактов (рис. 2.3) — ускорение выполнения работы в два раза. В случае 10 подобных устройств время получения результата составит всего 50 тактов, а в общем случае система из N устройств затратит на суммирование время около 500/Ж

Очень много примеров параллельной обработки можно найти и в нашей повседневной жизни: множество кассовых аппаратов в супермаркете, многополосное движение по оживленным автотрассам, бригада землекопов, несколько бензиновых колонок на автозаправочных станциях и т. п. Кстати, одним из пионеров в параллельной обработке был академик А. А. Самарский, выполнявший в начале 50-х годов прошлого столетия расчеты, необходимые для моделирования ядерных взрывов. Александр Андреевич решил эту задачу, посадив несколько десятков барышень с арифмометрами за столы. Барышни передавали данные друг другу просто на словах и отклады-

Глава 2. Как повышают производительность компьютеров

вали необходимые цифры на арифмометрах. С помощью вот такой "параллельной вычислительной системы", в частности, была рассчитана эволюция взрывной волны.

0-й такт

. b₄b₃b₂b^

1-й такт

2-й такт

■ b₅b₄b₃b₂

9l⁺6l

3-й такт

■ b₅b₄b₃b₂

9l⁺6l

4-й такт

5-й такт

■ b₅b₄b₃b₂

a₂+b₂

6-й такт

.b₅b₅b₄b₃

a₂+b₂

7-й такт

a₂+b₂

10-й такт

.b₅b₅b₄b₃

11 -й такт

.b₇b_eb₅b₄

Рис. 2.2. Суммирование векторов С = А + В с помощью последовательного устройства, выполняющего одну операцию за пять тактов

Часть I. Параллельные вычислительные системы

+ +

0-й такт

. b₅b₅b₄b₃


	a₂+6₂		^а1^+й1

1-й такт


	a₂+6₂		a^+bi

2-й такт


	a₂+b₂		a^+bi

3-й такт

.b₅b₅b₄b₃


	a₂+b₂		a^+bi

4-й такт


	a₂+b₂		a^+bi

5-й такт

.b_eb₇b_eb₅


	a₄⁺6₄		а₃^+йз

6-й такт

.b_sb₇b_eb₅


	a₄+6₄		а₃^+йз

7-й такт

.b_sb₇b₅b₅


	a₄+6₄		а₃^+йз

10-й такт

*W^a$^aS^a7


	а₆^+йб		а₅⁺Ь₅

11-й такт

.b₁₀b₉b_sb₇

Рис. 2.3. Суммирование векторов С = А + В с помощью двух одинаковых последовательных устройств, выполняющих операцию за пять тактов каждое

Конвейерная обработка

В предыдущем примере для выполнения одной операции сложения устройство блокировалось на пять тактов и никакой другой работы не выполняло. Оправдано ли это и можно ли организовать процесс обработки всех элемен-

Глава 2. Как повышают производительность компьютеров

тов входных массивов более эффективно? Для ответа на этот вопрос нужно вспомнить материал из предыдущей главы — представление вещественных чисел в компьютере. Сложение каждой пары чисел выполняется в виде последовательности микроопераций, таких как сравнение порядков, выравнивание порядков, сложение мантисс, нормализация и т. п. И что примечательно: в процессе обработки каждой пары входных данных микрооперации задействуются только один раз и всегда в одном и том же порядке: одна за другой. Это, в частности, означает, что если первая микрооперация выполнила свою работу и передала результаты второй, то для обработки текущей пары она больше не понадобится, и значит, она вполне может начинать обработку следующей ждущей на входе устройства пары аргументов.

Исходя их этих рассуждений, сконструируем устройство следующим образом. Каждую микрооперацию выделим в отдельную часть устройства и расположим их в порядке выполнения. В первый момент времени входные данные поступают для обработки первой частью. После выполнения первой микрооперации первая часть передает результаты свой работы второй части, а сама берет новую пару. Когда входные аргументы пройдут через все этапы обработки, на выходе устройства появится результат выполнения операции.

Такой способ организации вычислений и носит название конвейерной обработки. Каждая часть устройства называется ступенью конвейера, а общее число ступеней — длиной конвейера. Предположим, что для выполнения операции сложения вещественных чисел спроектировано конвейерное устройство, состоящее из пяти ступеней, срабатывающих за один такт каждая. Время выполнения одной операции конвейерным устройством равно сумме времен срабатывания всех ступеней конвейера. Это значит, что одна операция сложения двух чисел выполнится за пять тактов, т. е. за столько же времени, за сколько такая же операция выполнялась и на последовательном устройстве в предыдущем случае.

Теперь рассмотрим процесс сложения двух массивов (рис. 2.4). Как и прежде, через пять тактов будет получен результат сложения первой пары. Но заметим, что одновременно с первой парой прошли частичную обработку и другие элементы. Каждый последующий такт (!) на выходе конвейерного устройства будет появляться сумма очередных элементов. На выполнение всей операции потребуется 104 такта, вместо 500 тактов при использовании последовательного устройства — выигрыш во времени почти в пять раз.

Приблизительно так же будет и в общем случае. Если конвейерное устройство содержит / ступеней, а каждая ступень срабатывает за одну единицу времени, то время обработки п независимых операций этим устройством составит / + п — 1 единиц. Если это же устройство использовать в монопольном режиме (как последовательное), то время обработки будет равно Ып. В результате для больших значений п получили ускорение почти в / раз за счет использования конвейерной обработки данных.

48 Часть I. Параллельные вычислительные системы



... а₄а_ъа₂а_Л —> ... b₄b₃b₂b^ —►						—► 0-й такт
... а₄а_ъа₂а_Л —> ... b₄b₃b₂b^ —►
... а₅а₄а₃а₂ —> ...Ь₅Ь₄Ь_ЪЬ₂ —►	*^аА*					—► 1-й такт
... а₅а₄а₃а₂ —> ...Ь₅Ь₄Ь_ЪЬ₂ —►
■■■^аб^а5^а4^аз ^—■ -Ь_ЪЬ₅Ь₄Ь₃* —►	а₂Ь₂	*^аА*				—► 2-й такт
■■■^аб^а5^а4^аз ^—■ -Ь_ЪЬ₅Ь₄Ь₃* —►
■■■^a7^a6^a5^a4 ^—* ...b₇b₆b₅b₄ —►	^аз^ьз	а₂Ь₂	^аА			—► 3-й такт
■■■^a7^a6^a5^a4 ^—* ...b₇b₆b₅b₄ —►
■■■^a8^a7^a6^a5 ^—* -^Й8^Ь7⁶6^Ь5 ->•	^аА	^аз^ьз	з₂6₂	^ЭА		—► 4-й такт
■■■^a8^a7^a6^a5 ^—* -^Й8^Ь7⁶6^Ь5 ->•
... а_эа₈а₇а_е —> *■■■b_gb_ab₇b_e* —>	^а5^Й5	а₄Ь₄	^аз⁶з	з₂6₂	^аА	—► 5-й такт
... а_эа₈а₇а_е —> *■■■b_gb_ab₇b_e* —>
■■■^а10^а9^а8^а7 ^—* ...b₁₀b₉b_sb₇ —►	^а6^ь6	^а5^Й5	^аА	^аз⁶з	з₂6₂	—► с, 6-й такт
■■■^а10^а9^а8^а7 ^—* ...b₁₀b₉b_sb₇ —►
■■■ ^а11^а10^а9^а8 ~~* -⁶11^Ь10⁶9^Ь8 -*	а₇Ь₇	*^аА*	^Э5^Й5	а₄Ь₄	^аз⁶з	—► с₂ с, 7-й такт
■■■ ^а11^а10^а9^а8 ~~* -⁶11^Ь10⁶9^Ь8 -*
■■■ ^а12^а11^а10^а9 ~~*	*^аА*	а₇Ь₇	^аб⁶6	^Э5^Й5	а₄Ь₄	—► с₃ с₂ с₁ 8-й такт
■■■ ^а12^а11^а10^а9 ~~*

Рис. 2.4. Суммирование векторов С= Л + 5 с помощью

конвейерного устройства. Каждая из пяти ступеней

конвейера срабатывает за один такт

Заметим, что использование эпитетов "скалярный", "векторный" и "конвейерный" часто вызывает путаницу, поскольку многие из них применимы к близким по смыслу понятиям "обработка", "команда" и "устройство". Команда, у которой все аргументы должны быть только скалярными величинами, называется скалярной командой. Если хотя бы один аргумент команды может быть вектором, то такая команда называется векторной командой. Например, в системе команд компьютера Cray С90 есть скалярная команда A^scalсложения двух вещественных чисел S± и Sj с занесением результата в St,: A^scal S]_, S₂ -> Sj. Одновременно со скалярной командой предусмотрена и

Глава 2. Как повышают производительность компьютеров

команда A^vect для сложения двух векторов с занесением результата в третий: jvect y_h у₂ __>. j/₃ g зависимости от кода поступившей команды (A^scal или A^vect) процессор интерпретирует операнды либо как адреса скаляров, либо как адреса начала векторов.

Различие между скалярными и конвейерными устройствами мы уже обсудили чуть выше. Иногда в архитектуру процессора включают векторные устройства, ориентированные только на обработку векторов данных. В частности, в компьютере Cray С90 есть и конвейерное устройство UA {™_t^l, выполняющее только скалярные команды AI^scal сложения целых чисел, и векторное устройство UAfa? (также конвейерное), предназначенное для выполнения

только векторных команд целочисленного сложения AI^vect. Кстати, в отличие от целочисленных команд AI^scal и AI^vect, обсуждавшиеся ранее команды сложения вещественных чисел A^scal и A^vect в этом компьютере выполняются на одном и том же устройстве UA_Ka\.

Как и прежде, будем считать, что конвейерное устройство состоит из / ступеней, срабатывающих за один такт. Два вектора из п элементов можно либо сложить одной векторной командой, либо выполнить подряд п скалярных команд сложения элементов этих векторов. Если п скалярных команд одна за другой исполняются на таком устройстве, то, согласно общему закону, они будут обработаны за / + п — 1 тактов. Вместе с тем, на практике выдержать ритм, определяемый этой формулой, довольно сложно: каждый такт нужно обеспечивать новые входные данные, сохранять результат, проверять необходимость повторной итерации, быть может увеличивать значения индексов и т. д. и т. п. В итоге, необходимость выполнения множества вспомогательных операций приводит к тому, что становится невозможным каждый такт подавать входные данные на вход конвейерного устройства. В конвейере появляются "пузыри", а значит, на выходе уже не каждый такт появляются результаты, и эффективность работы устройства снижается.

При использовании векторных команд в формуле добавляется еще одно слагаемое: а + /+ п — 1, где а — это время, необходимое для инициализации векторной команды. Исполнение векторной команды не требует практически никаких вспомогательных действий, кроме момента ее инициализации или поддержки сегментации (см. § 3.2). Однако присутствие а определяет тот факт, что для небольших значений п соответствующие векторные команды выгоднее исполнять не в векторном, а в обычном скалярном режиме.

Поскольку ни а, ни / не зависят от значения п, то с увеличением длины входных векторов эффективность конвейерной обработки возрастает. Если под эффективностью обработки понимать реальную производительность Е конвейерного устройства, равную отношению числа выполненных операций п к

Часть I. Параллельные вычислительные системы

времени их выполнения t, то зависимость производительности от длины входных векторов определяется следующим соотношением:

р _ п _ п _ 1

У ~ Ко + / + я - 1) xj ■ _т + _(о + _/_ц

где т — это время такта работы компьютера.

На рис. 2.5 показан примерный вид этой зависимости. С увеличением числа входных данных реальная производительность конвейерного устройства все больше и больше приближается к его пиковой производительности. Однако у этого факта есть и исключительно важная обратная сторона — пиковая производительность любого конвейерного устройства никогда недостижима на практике.


	Е

		*( п ^*

Рис. 2.5. Зависимость производительности конвейерного устройства от длины входного набора данных

Сегодня параллелизмом в архитектуре компьютеров уже мало кого удивишь. Все современные микропроцессоры, будь то ALPHA 21264, Itanium, РА-8700 или Power 4, используют тот или иной вид параллельной обработки, реализованный в миниатюрных рамках одного кристалла. Вместе с тем, сами эти идеи появились очень давно. Изначально они внедрялись в самых передовых, а потому единичных, компьютерах своего времени. Затем после должной отработки технологии и удешевления производства они начинали использоваться в компьютерах среднего класса, и, наконец, сегодня все это в полном объеме воплощается в рабочих станциях и персональных компьютерах.

Для того чтобы убедиться, что все основные нововведения в архитектуре современных вычислительных систем используются еще со времен, когда ни микропроцессоров, ни понятия суперкомпьютеров еще не было, совершим маленький экскурс в историю, начав практически с момента рождения первых ЭВМ.

Глава 2. Как повышают производительность компьютеров

Первые компьютеры (EDSAC, EDVAC, UNIVAC, конец 40-х — начало 50-х годов XX столетия) для реализации принципа хранимой программы использовали ртутные линии задержки. При таком способе организации памяти разряды слова поступали для последующей обработки последовательно один за другим. Вполне естественно, что точно так же поразрядно выполнялись и арифметические операции, поэтому для сложения двух 32-разрядных чисел требовалось около 32 машинных тактов. Время разрядно-последовашельной памяти и разрядно-последовашельной арифметики в истории вычислительной техники.

С изобретением запоминающих устройств с произвольной выборкой данных стала реализуемой как разрядно-параллельная память, так и разрядно-параллельная арифметика. Все разряды слова одновременно считываются из памяти и участвуют в выполнении операции арифметико-логическим устройством. В 1953 году появилась машина IBM 701 — первая коммерческая ЭВМ, построенная на таком принципе. Однако наиболее удачной машиной этого класса стала выпущенная в 1955 году ЭВМ IBM 704, в которой была впервые применена память на ферритовых сердечниках и аппаратное АУ с плавающей точкой. Удивительный по тем временам коммерческий успех IBM 704 определялся продажей 150 (!) экземпляров этой машины.

Как в машине IBM 704, так и в других компьютерах того времени, все операции ввода/вывода осуществлялись через арифметико-логическое устройство. Внешних устройств было немного, но самое быстрое из них — лентопротяжное устройство, работало со скоростью около 15 000 символов в секунду, что было во много раз меньше скорости обработки данных процессором. Подобная организация вычислительных машин вела к существенному снижению производительности во время ввода и вывода информации. Одним из первых решений этой проблемы стало введение специализированной ЭВМ, называемой каналом ввода/вывода, которая позволяла АЛУ работать параллельно с устройствами ввода/вывода. В 1958 году к машине IBM 704 добавили шесть каналов ввода/вывода, что явилось основой для построения ЭВМ IBM 709.

Очень скоро стало понятно, что значительное повышение производительности компьютеров следует ожидать от использования принципов параллельной обработки данных в архитектуре компьютеров. В этом смысле исключительно интересным было выступление академика С. А. Лебедева на сессии Академии наук СССР в 1957 году [33], в котором он высказал массу идей, актуальных и сейчас: "Выполнение арифметических действий в значительной мере может быть совмещено по времени с обращением к памяти. При этом можно отказаться от стандартного цикла выполнения операций, когда вызов следующей команды производится после отсылки результата в запоминающее устройство, и производить выборку команд перед отсылкой результатов в запоминающее устройство...

Возможное ускорение работы машины за счет совмещения вызова команд и чисел по двум независимым каналам также может дать сокращение времени...

Часть /. Параллельные вычислительные системы

Помимо быстродействия арифметического устройства, существенным фактором, определяющим скорость работы машин, является время обращения к запоминающему устройству. Одним из решений уменьшения времени обращения к запоминающему устройству является создание дополнительной «сверхбыстродействующей памяти» сравнительно небольшой емкости. Создание такой «памяти» позволит сократить время для выполнения стандартных вычислений...

Некоторые весьма важные задачи, в особенности многомерные задачи математической физики, не могут успешно решаться при скоростях работы современных электронных вычислительных машин, и требуется существенное повышение их быстродействия.

Одним из возможных путей для решения таких задач может явиться параллельная работа нескольких машин, объединенных одним общим дополнительным устройством управления и с обеспечением возможности передачи кодов чисел с одной машины на другую. Однако может оказаться более целесообразным создание ряда параллельно работающих отдельных устройств машины. В такой машине должна иметься общая основная «память» для хранения чисел и команд, необходимых для решения задачи. Из этой «памяти» числа и команды, требующиеся для решения того или иного этапа задачи, поступают на ряд сверхбыстродействующих запоминающих устройств сравнительно небольшой емкости. Каждое такое сверхбыстродействующее запоминающее устройство связано со своим арифметическим устройством. Эти устройства имеют свое индивидуальное управление. Помимо этого, должно быть предусмотрено общее управление всей машиной в целом.

Для более полного использования арифметических устройств требуется, чтобы заполнение «сверхбыстродействующей памяти» из общей «памяти» машины осуществлялось одновременно с выполнением вычислений".

Знакомые идеи, не правда ли? Это удивительно, но факт — идеи, высказанные более 40 лет назад на заре развития вычислительной техники, находят свое активное воплощение в жизнь и сейчас.

Одной из первых машин, воплотивших идею повышения производительности за счет совмещения во времени различных этапов выполнения соседних команд, была система IBM STRETCH. Первый из семи построенных компьютеров этой серии был установлен в Лос-Аламосской национальной лаборатории США в 1961 году. Архитектура системы имела две принципиально важных особенности. Первая особенность — это опережающий просмотр для считывания, декодирования, вычисления адресов, а также предварительная выборка операндов нескольких команд.

Вторая особенность заключалась в разбиении памяти на два независимых банка, способных передавать данные в АЛУ независимо друг от друга (то есть опять-таки идеи параллелизма). Эта особенность, получившая название расслоение памяти, была позднее использована почти во всех больших вычислительных системах. Основная задача, решаемая в данном случае разра-

Глава 2. Как повышают производительность компьютеров

ботчиками компьютеров, состоит в согласовании скорости работы АЛУ и памяти. Это делается за счет разделения всей памяти на к независимых банков (иногда их называют секциями), что позволяет совместить во времени различные обращения к памяти. Одновременно вводится чередование адресов, при котором любые к подряд расположенных ячеек памяти с адресами Aq, Aq +1, ..., Aq + (к — 1) попадают в разные банки. При такой организации работа с подряд расположенными данными проходит максимально эффективно. На практике этот режим отвечает последовательной обработке элементов векторов или работе со строками/столбцами многомерных массивов (выбор между строками и столбцами определяется способом хранения многомерных массивов в каждом конкретном языке программирования, в частности, для двумерных массивов для языка Fortran — это столбцы, а для языка С — строки). Чаще всего число банков равно степени двойки: к = 2^т. В этом случае номер необходимого банка просто равен числу, записанному в т младших разрядах адреса.

Одновременно с проектом IBM STRETCH в 1956 году начался и другой известный проект, завершившийся запуском в 1962 году первого компьютера ATLAS. Наверняка, многие слышали о данном проекте, поскольку ATLAS по праву считается значительной вехой в истории развития вычислительной техники. Достаточно сказать, что в нем впервые была реализована мультипрограммная операционная система, основанная на виртуальной памяти и системе прерываний. Для нас же этот компьютер интересен, прежде всего, тем, что в нем впервые начали использовать конвейерный принцип обработки команд. Цикл обработки команды разбили на четыре ступени: выборка команды, вычисление адреса операнда, выборка операнда и выполнение операции. Это позволяло, в благоприятной ситуации, сократить среднее время выполнения команды с 6 до 1,6 мкс и увеличить производительность компьютера до 200 тысяч вещественных операций в секунду.

В 1964 году компания Control Data Corporation выпускает компьютер CDC-6600. Генеральным конструктором компьютера, а на то время и вице-президентом компании, был С. Крэй (Seymour Cray), создавший впоследствии множество уникальных суперкомпьютеров. Центральный процессор CDC-6600 содержал десять независимых функциональных устройств — параллелизм в явном виде. Все функциональные устройства могли работать одновременно друг с другом и являлись специализированными (устройства сложения с плавающей и фиксированной запятой (по одному), умножения (два устройства), деления, логических операций, сдвига и т. п.). Чтобы лучше почувствовать возможности суперкомпьютера того времени, приведем некоторые характеристики CDC-6600: время такта 100 не, память разбита на 32 банка по 4096 60-разрядных слов, средняя производительность 2—3 млн. операций в секунду.

В 1969 году Control Data Corporation выпускает компьютер CDC-7600 — усовершенствованный вариант модели CDC-6600. Центральный процессор нового компьютера содержит восемь независимых конвейерных функциональных устройств — одновременное использование и параллелизма, и конвейерности.

Часть I. Параллельные вычислительные системы

В отличие от предшественника, в CDC-7600 реализована двухуровневая память: вычислительная секция в обычном режиме работает со "сверхоперативной" памятью (64К 60-разрядных слов), куда при необходимости подкачиваются данные из основной памяти (512К 60-разрядных слов). Время такта CDC-7600 равно 27,5 не, средняя производительность 10—15 млн. операций в секунду.

Следующей важной вехой в развитии идей параллельной обработки данных, безусловно, явилось создание компьютера 1LL1AC IV. Матрица синхронно работающих процессоров — ключевая идея данного проекта. Архитектура компьютера 1LLIAC IV базировалась на концепции системы SOLOMON, описанной еще в 1962 году [61]. По начальному проекту основу 1LL1AC IV составляла матрица из 256 процессорных элементов, сгруппированных в четыре квадранта по 64 элемента в каждом (рис. 2.6). Планировалось, что вся система будет работать под общим управлением, однако в каждом квадранте находилось собственное устройство управления, выдающее команды для синхронно работающих процессорных элементов своего квадранта. Была предусмотрена возможность объединять два квадранта в один из 128 процессорных элементов или же рассматривать все четыре квадранта как единую матрицу 16x16. Время такта компьютера по проекту равнялось 40 не, а запланированная пиковая производительность 1 миллиард вещественных операций в секунду — фантастический по своим масштабам и сложности проект!



			СО ю ю см
1 квадрант на 64 ПЭ	II квадрант на 64 ПЭ	со со см
устройство управления	\| устройство управления


III квадрант на 64 ПЭ	IV квадрант на 64 ПЭ	СО со см
устройство управления	устройство управления

Рис. 2.6. Проект матричной системы ILLIAC IV

Глава 2. Как повышают производительность компьютеров

Однако чудеса в жизни редко случаются... Проект компьютера ILLIAC IV слишком опередил свое время, что и предопределило постоянные задержки и корректировки планов. Работа над системой началась в 1967 году. В 1972 году изготовили один квадрант из 64 процессорных элементов, который был установлен в научно-исследовательском центре NASA Ames (США). Наладка системы длилась до 1974 года, после чего ее сдали в эксплуатацию, но работы по доводке продолжались до 1975 года. В реальном использовании система находилась до 1982 года, после чего этот единственный изготовленный экземпляр нашел свое последнее пристанище в музее. Рассмотрим немного подробнее устройство компьютера.

Центральная часть компьютера состоит из устройства управления и матрицы из 64-х независимых идентичных процессорных элементов. Роль устройства управления выполняет простая вычислительная система небольшой производительности. Устройство управления выдает поток команд, синхронно исполняемый процессорными элементами. Каждый процессорный элемент — это арифметико-логическое устройство с собственной памятью объемом 2048 64-разрядных слов. Все процессорные элементы имели доступ только к своей локальной памяти. Для обмена данными в ходе выполнения программы каждый процессорный элемент мог использовать непосредственную связь с четырьмя соседями по схеме двумерного тора со сдвигом на единицу по вертикали (рис. 2.7).


			I
0	1	2	6	7
0	1	2	6	7


8	9	10		15
8	9	10		15


16	17
16	17
'	'
\|	\|
48	49			55
48	49			55


56	57	58	62	63
56	57	58	62	63
			I

УСТРОЙСТВО управления

Рис. 2.7. Процессорная матрица компьютера ILLIAC IV

Часть I. Параллельные вычислительные системы

Все процессорные элементы матрицы в каждый момент времени синхронно исполняют одну и ту же команду, выдаваемую устройством управления. Вместе с тем, с помощью битовой маски или специальных команд любой процессорный элемент можно перевести в пассивное состояние, запрещая выполнение поступающих команд.

Интересно, что помимо работы с 64-разрядными числами, процессорные элементы могут интерпретировать и обрабатывать данные уменьшенного формата, например, одно слово как два 32-разрядных числа или восемь однобайтовых. Этот дополнительный внутренний параллелизм позволяет обрабатывать 8-разрядные целочисленные данные со скоростью до 10 миллиардов байтовых операций в секунду.

Что же получилось в результате? Планировали матрицу из четырех квадрантов и 256 процессорных элементов, а сделали только один, проектное время такта по технологическим соображениям пришлось увеличить до 80 не, стоимость изготовления четвертой части системы оказалась в четыре раза выше, чем предусматривалось сначала, а ее реальная производительность достигала лишь 50 млн. вещественных операций в секунду. Полное фиаско? Ни в коей мере. Данный проект оказал огромное влияние как на архитектуру последующих поколений компьютеров, так и на развитие многих компонентов программного обеспечения параллельных вычислительных систем. Отработанные в рамках проекта технологии были использованы при создании систем РЕРЕ, BSP, ICL DAP и многих других. Идеи, заложенные в распараллеливающие компиляторы с языка Fortran, в частности, в IVTRAN, послужили основой для создания целого семейства компиляторов и разного рода программных анализаторов для появившихся позже параллельных компьютеров и супер-ЭВМ.

Идея включения векторных операций в систему команд компьютеров давно привлекала исследователей. Во-первых, использование векторных операций позволяет намного проще записать многие вычислительные фрагменты в терминах машинных команд. Если нужно сложить два вектора С = А + В, то отпадает необходимость в таких вспомогательных командах, как увеличение индекса, проверка условия выхода из цикла, перехода на начало тела цикла и многих других — достаточно воспользоваться соответствующей векторной командой. Код становится компактней, а эффективность соответствующих фрагментов, как правило, намного выше традиционных вариантов. Во-вторых, и это не менее важно, многие алгоритмы можно выразить в терминах векторных операций. И, наконец, в-третьих, подобные операции позволяют добиться максимального эффекта от использования конвейерных устройств.

Примеров успешных проектов вычислительных систем с использованием векторных команд немало. Одним из первых примеров явилась отечественная разработка компьютера Стрела, имеющего в системе команд "групповые операции". Более поздние варианты, появившиеся в конце 60-х годов про-

Глава 2. Как повышают производительность компьютеров

шлого века, это вычислительные системы ASC производства компании Texas Instruments и STAR 100 компании Control Data Corporation. Однако "классикой жанра", несомненно, является линия векторно-конвейерных суперкомпьютеров Cray.

В 1972 г. С. Крэй, вице-президент и генеральный конструктор многих машин, покидает компанию Control Data Corporation и основывает новую компанию Cray Research, которая в 1976 г. выпускает свой первый векторно-конвейерньш компьютер Сгау-1. Отличительными особенностями архитектуры данного компьютера являются векторные команды, независимые конвейерные функциональные устройства и развитая регистровая структура. Конвейерность и независимость функциональных устройств определили высокую теоретическую производительность компьютера (две операции за такт), векторные команды упростили путь к высокой производительности на практике (эффективная загрузка конвейеров), а работа функциональных устройств с регистрами сделала высокую производительность возможной даже при небольшом числе операций (исключительно малая латентность при запуске векторных команд).

Общие характеристики Сгау-1: время такта 12,5 не, 12 конвейерных функциональных устройств, причем все функциональные устройства могут работать одновременно и независимо друг от друга, оперативная память до 1 Мслова, пиковая производительность компьютера 160 млн. операций в секунду. В главе 3 мы будем детально разбирать архитектуру и особенности программирования векторно-конвейерного компьютера Cray С90, имеющего с Сгау-1 много общего в архитектуре, но появившегося на пятнадцать лет позже.

Анализируя архитектурные особенности компьютеров, мы неоднократно, хотя, быть может, и неявно, затрагивали очень важную проблему согласования скорости работы процессора и времени выборки данных из памяти. В одних компьютерах использовалось расслоение памяти, в других вводилась развитая регистровая структура, многоуровневая память, кэш-память или что-то еще, но в любом случае все подобные особенности организации памяти направлены на достижение одной цели — ускорить выборку команд и данных.

Давно было подмечено, что процесс выполнения большинства программ характеризуется двумя свойствами: локальностью вычислений и локальностью использования данных. И в том, и в другом случае следующий необходимый для работы программы объект (команда или операнд) расположен в оперативной памяти "недалеко" от предыдущего. Идеальный пример фрагмента программы с высокой локальностью вычислений — это цикл с телом из одного оператора и большим числом итераций. На практике многие программы обладают сразу двумя свойствами, и локальностью вычислений, и локальностью использования данных. Но, к сожалению, это ни в коей мере не является законом. Вызовы подпрограмм и функций, косвенная адресация массивов, неудачная работа с многомерными массивами и сложными сгрук-

Часть I. Параллельные вычислительные системы

турами данных, использование разного рода условных операторов — это лишь небольшой список причин, по которым свойства локальности в реальных программах могут значительно ослабевать.

Основной конструкцией в языках программирования, определяющей как локальность вычислений, так и локальность использования данных, являются циклы. В идеале, все тело цикла лучше поместить в более быструю память, поскольку на следующей итерации, скорее всего, нужно будет выполнить те же самые команды. Похожая ситуация и с данными: все то, что используется часто, лучше хранить на регистрах, у которых времена чтения/записи всегда согласованы со скоростью работы процессора. Однако удовольствие это очень дорогое и сколько-нибудь значительные объемы данных на регистрах держать невозможно. В такой ситуации будет использоваться следующий уровень в иерархии памяти, например, кэш-память. Если объема кэшпамяти не хватит, то можно задействовать следующий уровень и т. д. Аналогий этому факту очень много в повседневной жизни. Все самое необходимое мастер всегда держит под рукой на рабочем столе (регистры), часто используемые предметы хранятся здесь же в ящиках стола (кэш-память), основной набор инструментов лежит в шкафу недалеко от стола (основная память), за чем-то приходится иногда спускаться на склад (дисковая память), а что-то время от времени приходится заказывать даже из другой мастерской (архив на магнитной ленте).

Примеров конкретных реализаций различных уровней памяти можно привести очень много. Это регистры и регистровые файлы, кэш-память разных уровней, основная оперативная память, виртуальные диски, реализованные либо на отдельных участках основной оперативной памяти, либо на другой, более медленной памяти, жесткие диски, ленточные роботы и многое многое другое. А закон формирования иерархии памяти в каждом компьютере один: чем выше уровень в иерархии, тем выше скорость работы с данными, тем дороже (в пересчете на слово или байт) обходится память, поэтому объем каждого последующего уровня становится все меньше и меньше.

Эффективность использования иерархии памяти подметили давно. Так, даже в описанном выше компьютере ILLIAC IV уже можно выделить, по крайней мере, четыре уровня. Каждый процессорный элемент имел по 6 программно адресуемых регистров и собственную локальную оперативную память на 2048 слов. Для хранения данных использовались два жестких диска на 1 Гбит каждый, а для долговременного хранения предназначалась лазерная память с однократной записью емкостью в 10¹² бит (луч аргонового лазера выжигал отверстия в тонкой металлической пленке, укрепленной на барабане).

Безусловно, иерархия памяти не имеет прямого отношения к параллелизму. Но она относится к тем особенностям архитектуры компьютеров, которые имеют огромное значение для повышения их производительности, поэтому

Глава 2. Как повышают производительность компьютеров

ничего не сказать о ней мы, конечно же, не могли. Это тем более справедливо, если учесть, что в настоящее время подобная иерархия поддерживается везде, от суперкомпьютеров до персональных компьютеров.

Вопросы и задания

1. Каким соотношением связаны между собой время такта и тактовая частота компьютера?

2. Если время такта компьютера равно 2,5 не, и за каждый такт он может выполнять две операции, чему равна пиковая производительность этого компьютера?

3. Приведите примеры использования конвейерной и параллельной обработки из жизни школы или вуза.

4. Конвейерное устройство состоит из пяти ступеней. Времена срабатываний ступеней равны 1, 1, 2, 1 и 3 такта соответственно. С какой максимальной частотой на выходе данного устройства будут появляться результаты, если на его вход аргументы поступают без перебоев?

5. Меняется ли ответ задачи 4 в зависимости от того, в каком порядке идут ступени в таком устройстве?

6. За какое минимальное число тактов может быть выполнено 70 операций, если в распоряжении есть устройство, описанное в задаче 4?

7. В компьютере есть 7 параллельно работающих устройств, каждое из которых может выполнить операцию за 7 единиц времени. За какое минимальное время этот компьютер обработает 7 независимых операций?

8. Конвейерное устройство состоит из к ступеней, срабатывающих за я_ь п₂, , п_ктактов соответственно. За какое минимальное число тактов может быть выполнено m операций на таком устройстве?

9. В системе есть два универсальных процессора, выполняющих как операцию сложения, так и операцию умножения за один такт. Предположим, что операции чтения/записи данных происходят мгновенно и всегда есть место для сохранения промежуточных результатов. За какое минимальное число тактов в такой системе может быть выполнен следующий фрагмент программы?

а = с * d + е

Ь = v * t + и

f = х * у + Z

10. Знаете ли вы, что 100-летие со дня рождения академика С. А. Лебедева, одного из основателей российской школы вычислительной техники, 2 ноября 2002 года?

11. Знаете ли вы, что далеко не худшей модификацией модулей памяти на магнитных сердечниках были модули размером 12x12 см, содержащие тридцать два 32-разрядных слова?

12. Почему среднее время выполнения команды в компьютере ATLAS после введения в нем четырехступенчатой конвейерной обработки команд сократилось с 6 мке не до 1,5 мке, а до 1,6?

Часть I. Параллельные вычислительные системы

13. Почему пиковой производительности конвейерного компьютера нельзя точно достичь на практике?

14. Знаете ли вы, что для системы Сгау-1, отличавшейся невероятной по тем временам компактностью (диаметр центральной цилиндрической стойки 1,37 м, высота 1,98 м, диаметр в основании на уровне пола 2,74 м), требовалось два компрессора на 25 т хладагента и более 96 км шлейфов для внутренних соединений?

15. Знаете ли вы, что еще в 1967 году М. А. Карцевым был разработан проект вычислительного комплекса М-9 с производительностью около 1 миллиарда оп/с?

16. Какие уровни в иерархии памяти используются в современных компьютерах? Каковы их объемы?

§ 2.2. Повышение интеллектуальности управления компьютером

Итак, основной вывод предыдущего параграфа ясен — "параллелизм в архитектуре компьютеров — это не просто надолго, это навсегда". Современные технологии позволяют легко объединять тысячи процессоров в рамках одной вычислительной системы, и подобные компьютеры с терафлопной¹производительностью уже не самый интересный предмет для книги рекордов Гиннеса. Вместе с тем, весь опыт использования параллельных компьютеров показывает, что ситуация далека от идеальной. На практике почти всегда справедливо утверждение: "повышение степени параллелизма в архитектуре компьютера ведет как к росту его пиковой производительности, так одновременно и к увеличению разрыва между производительностью пиковой и реальной". Это и понятно. Не могут все программы одинаково эффективно использовать все 64 процессорных элемента компьютера ILL1AC IV. Если программа не поддается векторизации, она не сможет использовать всех преимуществ архитектуры семейства векторно-конвейерных машин Cray.

Иногда структура алгоритма не позволяет в принципе получить эффективную реализацию, но такая ситуация встречается не так часто. Чаще всего реальную производительность программы поднять можно, однако трудоемкость этого процесса сильно зависит от того, насколько развита поддержка параллелизма в аппаратно-программной среде вычислительной системы. Здесь важно все: операционные системы и компиляторы, технологии параллельного программирования и системы времени исполнения программ, поддержка параллелизма в процессоре и особенности работы с памятью. Если что-то не предусмотрено, то для получения эффективной программы пользователь должен сам позаботиться об этом: если компилятор плох, то писать на ассемблере, если на аппаратном уровне не решена проблема согласован-

Порядка 10¹² (триллион) операций с плавающей запятой. — Ред.

Глава 2. Как повышают производительность компьютеров

ности содержимого кэш-памяти разных процессоров, то регулярно в код вставлять функции, вызывающие сброс кэш-памяти, и т. п.

К настоящему моменту накопился значительный опыт поддержки параллелизма в программно-аппаратной среде компьютера, чему и будет посвящен данный параграф. Наряду со знакомством с "параллельной" составляющей этой среды, с пониманием того, что сопровождает решение задач на параллельном компьютере, не менее важна и обратная сторона вопроса. Если эффективность программы оказалось низкой, то в принципе причина может скрываться везде. Не стоит сразу ругать использованный алгоритм или свои способности программирования. Виновником может оказаться и плохой компилятор (или неверное его использование), и блокировки обращения к памяти на уровне аппаратуры, плохо реализованный параллельный ввод/вывод, конфликты при прохождении пакетов по коммуникационной среде — каждая составляющая программно-аппаратной среды компьютера вносит свой вклад в работу программы, а хороший он или плохой, вот с этим и надо разбираться.

Итак, первое, о чем стоит сказать, говоря о повышении эффективности работы программ, — это разработка спецпроцессоров. Перед разработчиками архитектуры компьютеров всегда встает дилемма: реализовывать ту или иную операцию на уровне аппаратуры или возложить эту функцию на программное обеспечение. Поддержка со стороны аппаратуры (специальная система команд процессора, особая структура памяти, разрядность, способы представления данных, топология внутрипроцессорных коммуникаций и т. п.) может дать значительный выигрыш в скорости выполнения определенного набора операций. Однако, если процессор исключительно эффективно обрабатывает байтовые целые числа, то совершенно не очевидно, что столь же эффективно он будет работать с вещественными числами с плавающей точкой или с большими массивами одноразрядных данных. Алгоритмы разные, а всего в архитектуре заранее предусмотреть невозможно, поэтому и приходится разработчикам искать компромисс между универсальностью и специализированностью. Об этом же заставляют задуматься и соображения относительно размеров вычислительных устройств и их стоимости.

В силу большой специализированное™ спецпроцессоров нужно очень аккуратно подходить к оценке показателей их производительности. Не редко проскакивают сообщения, которые многие склонны рассматривать как сенсационные: "разработан процессор, выполняющий X операций в секунду, в то время как лучшие современные образцы работают со скоростью в десятки и сотни раз меньшей". Типичная ситуация, в которой удалось эффектно смешать разные понятия и нигде не написать ничего неправильного. Просто "X операций в секунду" воспринимается как общий критерий производительности универсальных процессоров, хотя, как правило, имеются в виду операции специального вида. И сравнение идет с "лучшими современными образцами", что опять-таки ассоциируется с универсальными компьютера-

Часть /. Параллельные вычислительные системы

ми, придавая полученным результатам оттенок "значительного шага вперед" по сравнению с существующим уровнем.

Применений у спецпроцессоров много — обработка сигналов, распознавание речи, анализ изображений и сейсмологических данных, графические ускорители и т. п. Эффективно используя особенности конкретных алгоритмов, спецпроцессоры объединяют множество (сотни, тысячи, десятки тысяч) параллельно работающих элементарных функциональных устройств. Большой гибкости нет, зато есть огромная скорость работы. Одними из первых и широко используемыми до сих пор являются спецпроцессоры, построенные на основе аппаратной поддержки реализации быстрого преобразования Фурье.

Исключительно интересной оказалась идея воспользоваться скрытым от пользователя параллелизмом — параллелизмом на уровне машинных команд (Instruction-Level Parallelism). Выгод — масса, и среди главных стоит назвать отсутствие у пользователя необходимости в специальном параллельном программировании, и то, что проблемы с переносимостью, вообще говоря, остаются на уровне общих проблем переносимости программ в классе последовательных машин.

Существует два основных подхода к построению архитектуры процессоров, использующих параллелизм на уровне машинных команд. В обоих случаях предполагается, что процессор содержит несколько функциональных устройств, которые могут работать независимо друг от друга. Устройства могут быть одинаковыми, могут быть разными — в данном случае это неважно.

Суперскалярные процессоры не предполагают, что программа в терминах машинных команд будет включать в себя какую-либо информацию о содержащемся в ней параллелизме. Задача обнаружения параллелизма в машинном коде возлагается на аппаратуру, она же и строит соответствующую последовательность исполнения команд. В этом смысле код для суперскалярных процессоров не отражает точно ни природу аппаратного обеспечения, на котором он будет реализован, ни точного временного порядка, в котором будут выполняться команды.

VL1W-процессоры (Very Large Instruction Word) работают практически по правилам фоннеймановского компьютера. Разница лишь в том, что команда, выдаваемая процессору на каждом цикле, определяет не одну операцию, а сразу несколько. Команда VLlW-процессора состоит из набора полей, каждое из которых отвечает за свою операцию, например, за активизацию функциональных устройств, работу с памятью, операции с регистрами и т. п. Если какая-то часть процессора на данном этапе выполнения программы не востребована, то соответствующее поле команды не задействуется.

Примером компьютера с подобной архитектурой может служить компьютер АР-120В фирмы Floating Point Systems. Его первые поставки начались в 1976 году, а к 1980 году по всему миру было установлено более 1600 экземп-

Глава 2. Как повышают производительность компьютеров

ляров. Команда компьютера АР-120В состоит из 64 разрядов и управляет работой всех устройств машины. Каждый такт (167 не) выдается одна команда, что эквивалентно выполнению 6 миллионов команд в секунду. Поскольку каждая команда одновременно управляет многими операциями, то реальная производительность может быть выше. Все 64 разряда команды АР-120В делятся на шесть групп, отвечающих за свой набор операций: операции над 16-разрядными целочисленными данными и регистрами, сложение вещественных чисел, управление вводом/выводом, команды перехода, умножение вещественных чисел и команды работы с основной памятью.

Программа для VLlW-процессора всегда содержит точную информацию о параллелизме. Здесь компилятор всегда сам выявляет параллелизм в программе и явно сообщает аппаратуре, какие операции не зависят друг от друга. Код для VLlW-процессоров содержит точный план того, как процессор будет выполнять программу: когда будет выполнена каждая операция, какие функциональные устройства будут работать, какие регистры какие операнды будут содержать и т. п. Компилятор VL1W создает такой план имея полное представление о целевом VLlW-процессоре, чего, вообще говоря, нельзя сказать о компиляторах для суперскалярных машин.

Оба подхода имеют свои достоинства и недостатки, и не стоит противопоставлять простоту и ограниченные возможности архитектуры VL1W сложности и динамическим возможностям суперскалярных систем. Ясно, что создание плана выполнения операций во время компиляции важно для обеспечения высокой степени распараллеливания и в отношении суперскалярных систем. Также ясно и то, что во время компиляции существует неоднозначность, которую можно разрешить только во время выполнения программы с помощью динамических механизмов, свойственных суперскалярной архитектуре.

Большое влияние на развитие идей суперскалярной обработки еще в конце 50-х годов прошлого столетия оказал проект STRETCH фирмы IBM, и сейчас архитектура многих микропроцессоров построена по этому же принципу. Яркими представителями VLlW-компьютеров являются компьютеры семейств Multiflow и Cydra.

Оба изложенных принципа относятся к увеличению производительности отдельных процессоров, на основе которых, в свою очередь, могут строиться многопроцессорные конфигурации. Архитектура параллельных компьютеров за время существования компьютерной индустрии развивалась невероятными темпами и в самых разных направлениях. Убедиться в этом совсем не трудно, достаточно просмотреть, например, прекрасный обзор [24]. Однако, если отбросить детали и выделить общую идею построения большинства современных параллельных вычислительных систем, то останется лишь два класса.

Первый класс — это компьютеры с общей памятью. Системы, построенные по такому принципу, иногда называют мультипроцессорными системами или

Часть I. Параллельные вычислительные системы

просто мультипроцессорами. В системе присутствует несколько равноправных процессоров, имеющих одинаковый доступ к единой памяти (рис. 2.8). Все процессоры "разделяют" между собой общую память, отсюда еще одно название компьютеров этого класса — компьютеры с разделяемой памятью. Все процессоры работают с единым адресным пространством: если один процессор записал значение 79 в слово по адресу 1024, то другой процессор, прочитав слово, расположенное по адресу 1024, получит значение 79.


	Проц Проц ••• Проц

Память

Рис. 2.8. Параллельные компьютеры с общей памятью

Второй класс — это компьютеры с распределенной памятью, которые по аналогии с предыдущим классом иногда будем называть мультикомпьютерными системами (рис. 2.9). По сути дела, каждый вычислительный узел является полноценным компьютером со своим процессором, памятью, подсистемой ввода/вывода, операционной системой. В такой ситуации, если один процессор запишет значение 79 по адресу 1024, то это никак не повлияет на то, что по тому же адресу прочитает другой, поскольку каждый из них работает в своем адресном пространстве.


Проц	Проц	...	Проц
Память	Память	...	Память

Коммуникационная среда

Рис. 2.9. Параллельные компьютеры с распределенной памятью

К компьютерам с общей памятью относятся все системы класса Symmetric Multi Processors (SMP). В SMP все, кроме нескольких процессоров, в одном экземпляре: одна память, одна операционная система, одна подсистема ввода/вывода. Слово "симметричный" в названии архитектуры означает, что каждый процессор может делать все то, что и любой другой. Кстати, в настоящее время SMP часто рассматривают как альтернативное название для компьютеров с общей памятью, чему дополнительно способствуют два возможных варианта расшифровки данной аббревиатуры: Symmetric Multi Processors и Shared Memory Processors.

Глава 2. Как повышают производительность компьютеров

Эти два класса, компьютеры с общей и распределенной памятью, появились не случайно. Они отражают две основные задачи параллельных вычислений. Первая задача заключается в построении вычислительных систем с максимальной производительностью. Это легко позволяет сделать компьютеры с распределенной памятью. Уже сегодня существуют установки, объединяющие тысячи вычислительных узлов в рамках единой коммуникационной среды. Да что говорить, даже Интернет можно рассматривать как самый большой параллельный компьютер с распределенной памятью, объединяющий миллионы вычислительных узлов. Но как такие системы эффективно использовать? Как убрать большие накладные расходы, идущие на взаимодействие параллельно работающих процессоров? Как упростить разработку параллельных программ? Практически единственный способ программирования подобных систем — это использование систем обмена сообщениями, например, PVM или MPI, что не всегда просто. Отсюда возникает вторая задача — поиск методов разработки эффективного программного обеспечения для параллельных вычислительных систем. Данная задача немного проще решается для компьютеров с общей памятью. Накладные расходы на обмен данными между процессорами через общую память минимальны, а технологии программирования таких систем, как правило, проще. Проблема здесь в другом. По технологическим причинам не удается объединить большое число процессоров с единой оперативной памятью, а потому очень большую производительность на таких системах сегодня получить нельзя.

Заметим, что в обоих случаях много проблем вызывает система коммутации, связывающая либо процессоры с модулями памяти, либо процессоры между собой. Легко сказать, что 32 процессора имеют равный доступ к единой оперативной памяти или что 1024 процессора могут общаться каждый с каждым, а как это реализовать на практике? Рассмотрим некоторые способы организации коммуникационных систем в компьютерах.

Один из самых простых способов организации мультипроцессорных систем опирается на использование общей шины (рис. 2.10), к которой подключаются как процессоры, так и память. Сама шина состоит из какого-то числа линий, необходимых для передачи адресов, данных и управляющих сигналов между процессорами и памятью. Чтобы предотвратить одновременное обращение нескольких процессоров к памяти, используется та или иная схема арбитража, гарантирующая монопольное владение шиной захватившим ее устройством. Основная проблема таких систем заключается в том, что даже небольшое увеличение числа устройств на шине (4—5) очень быстро делает ее узким местом, вызывающим значительные задержки при обменах с памятью и катастрофическое падение производительности системы в целом.

Для построения более мощных систем необходимы другие подходы. Одним из них является разделение памяти на независимые модули и обеспечение возможности доступа разных процессоров к различным модулям одновре-

Часть I. Параллельные вычислительные системы

менно. Возможных решений может быть много, в частности, использование матричного коммутатора. Процессоры и модули памяти связываются так, как показано на рис. 2.11. На пересечении линий располагаются элементарные точечные переключатели, разрешающие или запрещающие передачу информации между процессорами и модулями памяти. Безусловным преимуществом такой организации является возможность одновременной работы процессоров с различными модулями памяти. Естественно, в ситуации, когда два процессора захотят работать с одним модулем памяти, один из них будет заблокирован. Недостатком матричных коммутаторов является большой объем необходимого оборудования, поскольку для связи п процессоров с п модулями памяти требуется п² элементарных переключателей. Во многих случаях это является слишком дорогим решением, что вынуждает разработчиков искать иные пути.

Процессоры Память

С С С

Шина

Рис. 2.10. Мультипроцессорная система с общей шиной

Модули памяти

0—0—0—0-

о—о—о—о-

0—0—0—0-

Точечные переключатели

Рис. 2.11. Мультипроцессорная система с матричным коммутатором

Альтернативным способом является использование каскадных переключателей, например, так, как это сделано в омега-сети. На рис. 2.12 показана сеть из четырех коммутаторов 2x2, организованная в два каскада. Каждый использованный коммутатор может соединить любой из двух своих входов с любым из двух своих выходов. Это свойство и использованная схема комму-

Глава 2. Как повышают производительность компьютеров

тации позволяют любому процессору вычислительной системы, показанной на этом рисунке, обращаться к любому модулю памяти. В общем случае для соединения я процессоров с п модулями памяти потребуется log₂« каскадов по я/2 коммутаторов в каждом, т. е. всего («log₂«)/2 коммутаторов. Для больших значений п эта величина намного лучше, чем я², однако появляется проблема другого рода — задержки. Каждый коммутатор не срабатывает мгновенно, т. к. на коммутацию входа с выходом на каждом каскаде требуется некоторое время. Опять ищется компромисс между дорогой коммуникационной системой с небольшим временем переключения и недорогой системой, но с большими задержками.


	с с с с						м м м м

Переключатели 2^х2

Рис. 2.12. Мультипроцессорная система с омега-сетью

Мы рассмотрели далеко не все варианты соединений процессоров с модулями памяти. Реально используемых схем коммутации процессоров в системах с распределенной памятью намного больше. По существу можно использовать и все уже рассмотренные варианты, и одновременно массу других. Простейший вариант топологии связи показан на рис. 2.13, а, где все вычислительные узлы объединены в одну линейку. Каждый узел системы, кроме первого и последнего, имеет по одному непосредственному соседу справа и слева. Для построения системы из я узлов требуется я — 1 соединение. Средняя длина пути между двумя узлами системы равна я/3. Можно уменьшить среднюю длину пути, если преобразовать линейку вычислительных узлов в кольцо (рис. 2.13, б). Добавив лишь одно дополнительное соединение первого узла с последним, мы на самом деле получили два дополнительных полезных свойства у новой топологии. Во-первых, средняя длина пути между двумя узлами сократилась с я/3 до я/6. Во-вторых, за счет того, что передача между любыми узлами уже может идти по двум независимым направлениям, увеличилась отказоустойчивость системы в целом. Пока все связи работоспособны, передача будет идти по кратчайшему пути. Но если нарушилась какая-либо одна связь, то возможна передача в противоположном направлении.

Часть I. Параллельные вычислительные системы

ОЧ!>Чз>Ч±)

Рис. 2.13. Мультикомпьютерные системы с топологиями связи: а — линейка; б — кольцо; в — звезда

Несмотря на явную ограниченность в непосредственных связях даже подобные простые "линейные" топологии хорошо соответствуют многим алгоритмам, в которых необходима связь лишь соседних процессов между собой. В частности, многие одномерные задачи математической физики (да и многомерные с делением области на одномерные) хорошо решаются подобными методами. Для таких задач никаких других топологий придумывать не надо. Но далеко не все задачи такие. Схему сдваивания или блочные методы линейной алгебры на таких топологиях эффективно реализовать не просто, поскольку неправильное размещение процессов по процессорам приведет к потере большей части времени на коммуникации. В идеальной ситуации пользователь не должен думать об этом, у него других проблем хватает, но на практике чудес не бывает. Сегодня по технологическим причинам нельзя сделать большие мультикомпьютерные системы, в которых каждый процессор имел бы непосредственную связь со всеми остальными. А раз так, то и здесь разработчикам вычислительных систем приходится искать компромисс между универсальностью и специализированностью, между сложностью и доступностью. Если класс задач заранее определен, то ситуация сильно об-

Глава 2. Как повышают производительность компьютеров

легчается, и результат может быть найден легко. Например, использование схемы распределения работы между параллельными процессами, аналогичной схеме клиент-сервер, при которой один головной процесс раздает задания подчиненным процессам (схема мастер/рабочие, или master/slaves), хорошо соответствует топологии "звезда" (рис. 2.13, в). Вычислительные узлы, расположенные в лучах звезды, не имеют непосредственной связи между собой. Но это нисколько не мешает эффективному взаимодействию процесса-мастера с подчиненными процессами при условии, что мастер расположен в центральном узле.

Выбор той или иной топологии связи процессоров в конкретной вычислительной системе может быть обусловлен самыми разными причинами. Это могут быть соображения стоимости, технологической реализуемости, простоты сборки и программирования, надежности, минимальности средней длины пути между узлами, минимальности максимального расстояния между узлами и др. Некоторые варианты показаны на рис. 2.14. Топология двумерной решетки (рис. 2.14, а) была использована в начале 90-х годов прошлого века при построении суперкомпьютера Intel Paragon на базе процессоров i860. В соответствии с топологией двумерного тора (рис. 2.14, б) могут быть соединены вычислительные узлы кластеров, использующих сеть SC1, предлагаемую компанией Dolphin Interconnect Solutions. Таким образом, в частности, построен один из кластеров НИВЦ МГУ. В настоящее время эта же компания Dolphin предлагает сетевые комплекты, позволяющие объединять узлы в трехмерный тор — чем меньше среднее расстояние между узлами, тем выше надежность. В этом смысле наилучшие показатели имеет топология, в которой каждый процессор имеет непосредственную связь со всеми остальными (рис. 2.14, в). Но о такой роскоши современный уровень технологии даже мечтать не позволяет: я — 1 соединение у каждого узла при общем числе связей я(я — 1)/2.

Иногда находятся исключительно интересные варианты, одним из которых является топология двоичного гиперкуба (рис. 2.14, г). В я-мерном пространстве рассмотрим лишь вершины единичного я-мерного куба, т. е. точки (jq, х₂, ..., х_п), в которых все координаты X/ могут быть равны либо 0, либо 1. В эти точки мы условно и поместим процессоры системы. Каждый процессор соединим с ближайшим непосредственным соседом вдоль каждого из я измерений. В результате получили я-мерный куб для системы из N = 2^ппроцессоров. Двумерный куб соответствует простому квадрату, а четырехмерный вариант условно изображен на рис. 2.14, г. В гиперкубе каждый процессор связан лишь с log₂7V непосредственными соседями, а не с N, как в случае полной связности. Заметим, что при всей кажущейся замысловатости гиперкуб имеет массу полезных свойств. Например, для каждого процессора очень просто определить всех его соседей: они отличаются от него лишь значением какой-либо одной координаты x_t. Каждая "грань" я-мерного гиперкуба является гиперкубом размерности я — 1. Максималь-

Часть I. Параллельные вычислительные системы

ное расстояние между вершинами «-мерного гиперкуба равно п. Гиперкуб симметричен относительно своих узлов: из каждого узла система выглядит одинаковой и не существует узлов, которым необходима специальная обработка. Отметим и то, что многие алгоритмы по своей структуре прекрасно соответствуют такой взаимосвязи между процессорами. В частности, "неудобная" для других топологий схема сдваивания очень хорошо ложится на гиперкуб, используя на каждом шаге алгоритма гиперкуб на единицу меньшей размерности.

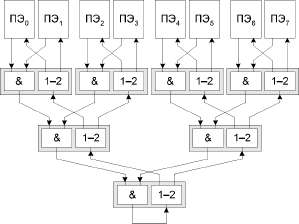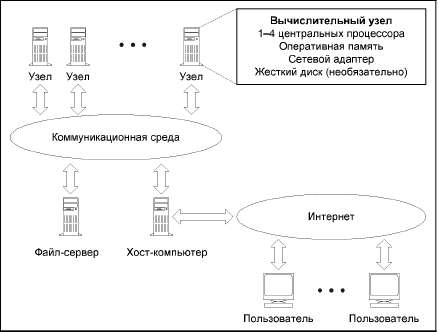1100

1101

юоо

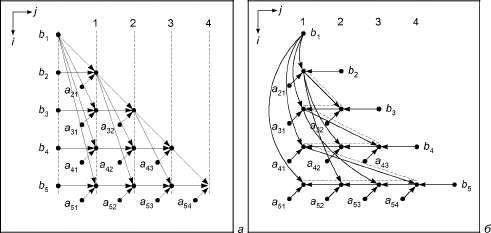0101

0001

Рис. 2.14. Варианты топологий связи процессоров: а — решетка; б — 2-тор; в — полная связь; г — гиперкуб

Одной из первых реальных многопроцессорных вычислительных систем с архитектурой гиперкуба стал компьютер Cosmic Cube, построенный в 1983 году в Калифорнийском технологическом институте на основе микропроцессоров Intel 8086/8087. В 1985 году фирма Intel выпустила первый промышленный гиперкуб. Это был компьютер iPSC (Intel Personal Supercomputer), в котором в качестве узловых процессоров были использованы микропроцессоры серии 80286/80287. В том же году был объявлен коммерческий гиперкуб NCUBE/ten фирмы NCUBE Corporation, содержащий до 1024 узлов.

В некоторых компьютерах гиперкуб использовался в комбинации с другими типами архитектур. В машинах серии Connection Machine фирмы Thinking

Глава 2. Как повышают производительность компьютеров

Machines использовалось до 2¹⁶ простых узлов. На одном кристалле этого компьютера находилось 16 узлов, имеющих связь каждый с каждым, а 2¹²таких кристаллов уже объединялись в 12-мерный гиперкуб.

Вернемся к обсуждению особенностей компьютеров с общей и распределенной памятью. Как мы уже видели, оба класса имеют свои достоинства, которые, правда, тут же плавно перетекают в их недостатки. Для компьютеров с общей памятью проще создавать параллельные программы, но их максимальная производительность сильно ограничивается небольшим числом процессоров. А для компьютеров с распределенной памятью все наоборот. Можно ли объединить достоинства этих двух классов? Одним из возможных направлений является проектирование компьютеров с архитектурой NUMA (Non Uniform Memory Access).

Почему проще писать параллельные программы для компьютеров с общей памятью? Потому что есть единое адресное пространство и пользователю не нужно заниматься организацией пересылок сообщений между процессами для обмена данными. Если создать механизм, который всю совокупную физическую память компьютера позволял бы программам пользователей рассматривать как единую адресуемую память, все стало бы намного проще.

По такому пути и пошли разработчики системы Cm*, создавшие еще в конце 70-х годов прошлого века первый NUMA-компьютер. Данный компьютер состоит из набора кластеров, соединенных друг с другом через межкластерную шину. Каждый кластер объединяет процессор, контроллер памяти, модуль памяти и, быть может, некоторые устройства ввода/вывода, соединенные между собой посредством локальной шины (рис. 2.15). Когда процессору нужно выполнить операции чтения или записи, он посылает запрос с нужным адресом своему контроллеру памяти. Контроллер анализирует старшие разряды адреса, по которым и определяет, в каком модуле хранятся нужные данные. Если адрес локальный, то запрос выставляется на локальную шину, в противном случае запрос для удаленного кластера отправляется через межкластерную шину. В таком режиме программа, хранящаяся в одном модуле памяти, может выполняться любым процессором системы. Единственное различие заключается в скорости выполнения. Все локальные ссылки отрабатываются намного быстрее, чем удаленные. Поэтому и процессор того кластера, где хранится программа, выполнит ее на порядок быстрее, чем любой другой.

От этой особенности и происходит название данного класса компьютеров — компьютеры с неоднородным доступом к памяти. В этом смысле иногда говорят, что классические SMP-компьютеры обладают архитектурой UMA (Uniform Memory Access), обеспечивая одинаковый доступ любого процессора к любому модулю памяти.

Часть I. Параллельные вычислительные системы

Кластер

CPU

I/O

...Л_______

Локальная шин

CPU

I/O

;

Локальная памят

CPU

I/O

к-----

-''

Контроллер памяти

Рис. 2.15. Схема вычислительной системы Cm*

Другим примером NUMA-компьютера являлся компьютер BBN Butterfly, который в максимальной конфигурации объединял 256 процессоров (рис. 2.16). Каждый вычислительный узел компьютера содержит процессор, локальную память и контроллер памяти, который определяет, является ли запрос к памяти локальным или его необходимо передать удаленному узлу через коммутатор Butterfly. С точки зрения программиста память является единой общей памятью, удаленные ссылки в которой реализуются немного дольше локальных (приблизительно 6 мкс для удаленных против 2 мкс для локальных).

По пути построения больших NUMA-компьютеров можно было бы смело идти вперед, если бы не одна неожиданная проблема — кэш-память отдельных процессоров. Кэш-память, которая помогает значительно ускорить работу отдельных процессоров, для многопроцессорных систем оказывается узким местом. В процессорах первых NUMA-компьютеров кэш-памяти не было, поэтому не было и такой проблемы. Но для современных микропроцессоров кэш является неотъемлемой составной частью. Причину нашего беспокойства очень легко объяснить. Предположим, что процессор Р\ сохранил значение х в ячейке q, а затем процессор Pi хочет прочитать содержимое той же ячейки q. Что получит процессор Р{! Конечно же, всем бы хотелось, чтобы он получил значение х, но как он его получит, если х попало в кэш процессора Р{> Эта проблема носит название проблемы согласования содержимого кэш-памяти (cache coherence problem, проблема

Глава 2. Как повышают производительность компьютеров

когерентности кэшей). Указанная проблема актуальна и для современных SMP-компьютеров, кэш процессоров которых также может вызвать несогласованность в использовании данных.

Переключатели

Рис. 2.16. Схема вычислительной системы BBN Butterfly

Для решения данной проблемы разработана специальная модификация NUMA-архитектуры — ccNUMA (cache coherent NUMA). He будем сейчас вдаваться в технические подробности множества протоколов, которые обеспечивают согласованность содержимого всех кэшей. Важно, что эта проблема решается и не ложится на плечи пользователей. Для пользователей важнее другой вопрос, насколько "неоднородна" архитектура NUMA? Если обращение к памяти другого узла требует на 5—10% больше времени, чем обращение к своей памяти, то это может и не вызвать никаких вопросов. Большинство пользователей будут относиться к такой системе, как к UMA (SMP), и практически все разработанные для SMP программы будут работать достаточно хорошо. Однако для современных NUMA систем это не так, и разница времени локального и удаленного доступа лежит в промежутке 200—700%. При такой разнице в скорости доступа для обеспечения должной

Часть I. Параллельные вычислительные системы

эффективности выполнения программ следует позаботиться о правильном расположении требуемых данных.

На основе архитектуры ccNUMA в настоящее время выпускается множество реальных систем, расширяющих возможности традиционных компьютеров с общей памятью. При этом, если конфигурации SMP серверов от ведущих производителей содержат 16—32—64 процессора, то их расширения с архитектурой ccNUMA уже объединяют до 256 процессоров и больше.

Одновременно с совершенствованием архитектуры проходило развитие и программного обеспечения параллельных компьютеров. Практика показала, что развитие аппаратной и программной составляющих параллельных вычислительных систем вообще нельзя рассматривать отдельно друг от друга. Новшества одной составляющей влекут изменения в другой. Хорошим примером тому может служить аппаратная поддержка барьерной синхронизации процессов в компьютерах семейства Cray T3D/T3E. Этот вид синхронизации часто используется в программах, однако его программная реализация требовала значительных накладных расходов — что нельзя было сделать эффективно на программном уровне, сделали на уровне аппаратуры (см. § 3.4).

Сейчас нас будут интересовать, в первую очередь, изменения в технологиях параллельного программирования. Конечно, в распоряжении современных программистов есть не только ассемблер или Fortran, создано много других систем и языков программирования. Однако в настоящее время проблема разработки эффективного параллельного программного обеспечения оказалась центральной проблемой параллельных вычислений в целом.

Итак, как же заставить несколько процессоров решать одну задачу? Этот вопрос возник одновременно с появлением первых параллельных компьютеров, и к настоящему моменту накоплен целый спектр различных технологий программирования. Подробное изложение конкретных технологий будет представлено в главе 5, здесь же мы ограничимся лишь описанием основных подходов.

Начнем с использования в традиционных языках программирования специальных комментариев, добавляющих "параллельную" специфику в изначально последовательные программы. Предположим, что вы работаете на век-торно-конвейерном компьютере Cray Т90. Вы знаете, что все итерации некоторого цикла программы независимы и, следовательно, его можно векторизовать, т. е. очень эффективно исполнить с помощью векторных команд на конвейерных функциональных устройствах. Если цикл простой, то компилятор и сам определит, возможность преобразования последовательного кода в параллельный. Если уверенности в высоком интеллекте компилятора нет, то перед заголовком цикла лучше вставить явное указание на отсутствие зависимости и возможность векторизации. В частности, для языка Fortran это выглядит так:

CDIR$ NODEPCHK

Глава 2. Как повышают производительность компьютеров

По правилу языка Fortran, буква 'С в первой позиции говорит о том, что вся строка является комментарием, последовательность 'dir$' указывает на то, что это спецкомментарий для компилятора, а часть 'nodepchk¹ как раз и говорит об отсутствии информационной зависимости между итерациями последующего цикла.

Следует отметить, что использование спецкомментариев не только добавляет возможность параллельного исполнения, но и полностью сохраняет исходный вариант программы. На практике это очень удобно — если компилятор ничего не знает о параллелизме, то все спецкомментарии он просто пропустит, взяв за основу последовательную семантику программы.

На использование комментариев опирается и широко распространенный в настоящее время стандарт ОрепМР. Основная ориентация сделана на работу с общей памятью, нитями (threads) и явным описанием параллелизма. В Fortran признаком спецкомментария ОрепМР является префикс !$омр, а в языке С используют директиву "#pragma omp". В настоящее время практически все ведущие производители SMP-компьютеров поддерживают ОрепМР в компиляторах на своих платформах.

Кроме использования комментариев для получения параллельной программы, часто идут на расширение существующих языков программирования. Вводятся дополнительные операторы и новые элементы описания переменных, позволяющие пользователю явно задавать параллельную структуру программы и в некоторых случаях управлять исполнением параллельной программы. Так, язык High Performance Fortran (HPF), помимо традиционных операторов Fortran и системы спецкомментариев, содержит новый оператор forall, введенный для описания параллельных циклов программы. Другим примером служит язык трС, разработанный в Институте системного программирования РАН как расширение ANSI С. Основное назначение трС — создание эффективных параллельных программ для неоднородных вычислительных систем.

Если нужно точнее отразить либо специфику архитектуры параллельных систем, либо свойства какого-то класса задач некоторой предметной области, то используют специальные языки параллельного программирования. Для программирования транспьютерных систем был создан язык Occam, для программирования потоковых машин был спроектирован язык однократного присваивания Sisal. Очень интересной и оригинальной разработкой является декларативный язык НОРМА, созданный под руководством И. Б. Задыхайло в Институте прикладной математики им. М. В. Келдыша РАН для описания решения вычислительных задач сеточными методами. Высокий уровень абстракции языка позволяет описывать задачи в нотации, близкой к исходной постановке проблемы математиком, что условно авторы языка называют программированием без программиста. Язык не содержит традиционных конструкций языков программирования, фиксирующих по-

Часть I. Параллельные вычислительные системы

рядок вычисления и тем самым скрывающих естественный параллелизм алгоритма.

С появлением массивно-параллельных компьютеров широкое распространение получили библиотеки и интерфейсы, поддерживающие взаимодействие параллельных процессов. Типичным представителем данного направления является интерфейс Message Passing Interface (MPI), реализация которого есть практически на каждой параллельной платформе, начиная от векторно-конвейерных супер-ЭВМ до кластеров и сетей персональных компьютеров. Программист сам явно определяет какие параллельные процессы приложения в каком месте программы и с какими процессами должны либо обмениваться данными, либо синхронизировать свою работу. Обычно адресные пространства параллельных процессов различны. В частности, такой идеологии следуют MPI и PVM. В других технологиях, например Shmem, допускается использование как локальных (private) переменных, так и общих (shared) переменных, доступных всем процессам приложения.

Несколько особняком стоит система Linda, добавляющая в любой последовательный язык лишь четыре дополнительные функции in, out, read и evai, что и позволяет создавать параллельные программы. К сожалению, простота заложенной идеи оборачивается большими проблемами в реализации, что делает данную красивую технологию скорее объектом академического интереса, чем практическим инструментом.

Часто на практике прикладные программисты вообще не используют никаких явных параллельных конструкций, обращаясь в критических по времени счета фрагментах к подпрограммам и функциям параллельных предметных библиотек. Весь параллелизм и вся оптимизация спрятаны в вызовах, а пользователю остается лишь написать внешнюю часть своей программы и грамотно воспользоваться стандартными блоками. Примерами подобных библиотек являются Lapack, ScaLapack, Cray Scientific Library, HP Mathematical Library, PETSc и многие другие.

И, наконец, последнее направление, о котором стоит сказать, это использование специализированных пакетов и программных комплексов. Как правило, в этом случае пользователю вообще не приходится программировать. Основная задача — это правильно указать все необходимые входные данные и правильно воспользоваться функциональностью пакета. Так, многие химики для выполнения квантово-химических расчетов на параллельных компьютерах пользуются пакетом GAMESS, не задумываясь о том, каким образом реализована параллельная обработка данных в самом пакете.

Подводя итог сказанному в двух параграфах этой главы, следует отдать должное тем большим изменениям, которые произошли в аппаратуре и программном обеспечении параллельных компьютеров за последние несколько десятков лет. Эти изменения, одни в большей степени, другие в меньшей, способствовали тому, что современные пользователи получили в свое распоряжение

Глава 2. Как повышают производительность компьютеров

мощнейшие вычислительные системы, способные решать совершенно неподъемные ранее вычислительные задачи. Но как показала практика, проблемы, характерные для параллельных вычислительных систем в целом, не исчезли, а перешли на другой уровень. Если на заре параллелизма стоял вопрос об эффективном использовании нескольких простых компьютеров, то сейчас речь идет об эффективности систем, состоящих из сотен и тысяч процессоров, каждый из которых сам по себе является сложной параллельной системой. Вопросы эффективности, пиковой и реальной производительности для таких систем выходят на передний план, поэтому следующий параграф будет посвящен теоретическим аспектам этих понятий.

Вопросы и задания

1. Две вычислительные системы отличаются только версиями установленных на них операционных систем. Могут ли на таких компьютерах отличаться времена работы одной и той же программы?

2. Возможна ли такая ситуация: в программе, содержащей 10 000 строк исходного текста, изменили только один символ, а время ее работы выросло в 10 раз?

3. Возможна ли такая ситуация: в программе, содержащей 10 000 строк исходного текста, изменили только один символ, после чего производительность, с которой ее выполнял компьютер, выросла в 10 раз?

4. Предположим, что спецпроцессор является матрицей синхронно работающих однобитных процессоров. Какие классы задач можно эффективно решать на таких спецпроцессорах?

5. Какого вида операции должен уметь быстро выполнять спецпроцессор, проектируемый для реализации быстрого преобразования Фурье?

6. Какие еще виды параллелизма на уровне машинных команд, кроме суперска-лярности и идей VLIW-обработки, используются в современных микропроцессорах?

7. Известно, что программа хорошо выполняется на суперскалярном процессоре с некоторым набором независимых функциональных устройств. Означает ли это, что та же самая программа будет хорошо выполняться на VLIW-процессоре, имеющем тот же набор устройств? Верно ли обратное?

8. Компилятор для какого процессора: суперскалярного или VLIW, должен быть более "интеллектуальным" для генерации эффективных программ?

9. Почему общую шину не используют для объединения большого числа процессоров?

10. Почему средняя длина пути между двумя узлами системы, в которой п процессоров соединены по топологии "линейка", равна я/3?

11. Приведите пример алгоритма, структура связей которого хорошо соответствует топологии "кольцо".

12. Какое минимальное число переключателей 4x4 необходимо для соединения 64 процессоров с помощью омега-сети?

Часть I. Параллельные вычислительные системы

13. Под расстоянием между двумя процессорами будем понимать минимальное число соединений, образующих путь между этими процессорами в данной топологии. Чему равно максимальное расстояние между процессорами в топологии "двумерный тор" отхя? Чему равно максимальное расстояние между процессорами в топологии "двумерная решетка" отхя?

14. Сколько непосредственных соседей имеет каждый процессор в топологии "трехмерный тор"? Чему равно максимальное расстояние между процессорами в топологии "трехмерный тор" 4x8x8?

15. Известно, что алгоритм хорошо отображался на топологию "кольцо". Можно ли гарантировать его хорошее отображение на топологию "гиперкуб"?

16. Что должен учитывать пользователь при переходе с SMP-компьютера на компьютер с архитектурой NUMA?

17. Что общего нужно учитывать при создании эффективных программ для компьютеров с архитектурой N UMA и компьютеров с распределенной памятью?

18. Напишите два варианта программы для любого доступного вам компьютера, показывающих, что правильное или неправильное использование кэш-памяти может привести к 10-кратной разнице во времени.

19. Какой компьютер содержит наибольшее число процессоров в последней редакции списка Тор500 самых мощных компьютеров мира?

20. Какая из технологий программирования, MPI или ОрепМР, лучше соответствует компьютерам с распределенной памятью? SMP-компьютерам?

§ 2.3. Система функциональных устройств

Любая вычислительная система есть работающая во времени совокупность функциональных устройств (ФУ). Для оценки качества ее работы вводятся различные характеристики. Рассмотрим их в рамках некоторой модели процесса работы устройств, вполне достаточной для практического применения. Мы не будем интересоваться содержательной частью операций, выполняемых функциональными устройствами. Они могут означать арифметические или логические функции, ввод/вывод данных, пересылку данных в память и извлечение данных из нее или что-либо иное. Более того, допускается, что при разных обращениях операции могут означать разные функции. Для нас сейчас важны лишь времена выполнения операций и то, на устройствах, какого типа они реализуются [9].

Пусть введена система отсчета времени и установлена его единица, например, секунда. Будем считать, что длительность выполнения операций измеряется в долях единицы. Все устройства, реальные или гипотетические, основные или вспомогательные, могут иметь любые времена срабатывания. Единственное существенное ограничение состоит в том, что все срабатывания одного и того же ФУ должны быть одинаковыми по длительности. Всегда мы будем интересоваться работой каких-то конкретных наборов ФУ. По

Глава 2. Как повышают производительность компьютеров

умолчанию будем предполагать, что все другие ФУ, необходимые для обеспечения процесса функционирования этих наборов, срабатывают мгновенно. Поэтому, если не сделаны специальные оговорки, мы не будем в таких случаях принимать во внимание факт их реального существования. Времена срабатываний изучаемых ФУ будем считать ненулевыми.

Назовем функциональное устройство простым, если никакая последующая операция не может начать выполняться раньше, чем закончится предыдущая. Простое ФУ может выполнять операции одного типа или разные операции. Разные ФУ могут выполнять операции, в том числе одинаковые, за разное время. Примером простого ФУ могут служить не конвейерные сумматоры или умножители. Эти ФУ реализуют только один тип операции. Простым устройством можно считать многофункциональный процессор, если он не способен выполнять различные операции одновременно, и мы не принимаем во внимание различия во временах реализации операций, предполагая, что они одинаковы. Основная черта простого ФУ только одна: оно монопольно использует свое оборудование для выполнения каждой отдельной операции.

В отличие от простого ФУ, конвейерное ФУ распределяет свое оборудование для одновременной реализации нескольких операций. Очень часто оно конструируется как линейная цепочка простых элементарных ФУ, имеющих одинаковые времена срабатывания. На этих элементарных ФУ последовательно реализуются отдельные этапы операций. В случае конвейерного ФУ, выполняющего операцию сложения чисел с плавающей запятой, соответствующие элементарные устройства последовательно реализуют такие операции, как сравнение порядков, сдвиг мантиссы, сложение мантисс и т. п. Тем не менее, ничто не мешает, например, считать конвейерным ФУ линейную цепочку универсальных процессоров. Принцип функционирования конвейерного ФУ остается одним и тем же. Сначала на первом элементарном ФУ выполняется первый этап первой операции, и результат передается второму элементарному ФУ. Затем на втором элементарном ФУ реализуется второй этап первой операции. Одновременно на освободившемся первом ФУ реализуется первый этап второй операции. После этого результат срабатывания второго ФУ передается третьему ФУ, результат срабатывания первого ФУ передается второму ФУ. Освободившееся первое ФУ готово для выполнения первого этапа третьей операции и т. д. После прохождения всех элементарных ФУ в конвейере операция оказывается выполненной. Элементарные ФУ называются ступенями конвейера, число ступеней в конвейере — длиной конвейера. Простое ФУ всегда можно считать конвейерным с длиной конвейера, равной 1. Как уже говорилось, конвейерное ФУ часто является линейной цепочкой простых ФУ, но возможны и более сложные конвейерные конструкции.

Поскольку уже конвейерное ФУ само является системой связанных устройств, необходимо установить наиболее общие принципы работы систем

Часть I. Параллельные вычислительные системы

ФУ. Будем считать, что любое ФУ не может одновременно выполнять операцию и сохранять результат предыдущего срабатывания, т. е. оно не имеет никакой собственной памяти. Однако будем допускать, что результат предыдущего срабатывания может сохраняться в ФУ до момента начала очередного его срабатывания, включая сам этот момент. После начала очередного срабатывания ФУ результат предыдущего срабатывания пропадает. Предположим, что все ФУ работают по индивидуальным командам. В момент подачи команды на входы конкретного ФУ передаются аргументы выполняемой операции либо как результаты срабатывания других ФУ с их выходов, либо как входные данные, либо как-нибудь иначе. Сейчас нам безразлично, как именно осуществляется их подача. Важно то, что в момент начала очередного срабатывания ФУ входные данные для этого ФУ доступны, а сам процесс подачи не приводит к задержке общего процесса. Конечно мы предполагаем, что программы, определяющие моменты начала срабатываний всех ФУ, составлены корректно и не приводят к тупиковым ситуациям.

При определении различных характеристик, связанных с работой ФУ, так или иначе приходится находить число операций, выполняемых за какое-то время. Это число должно быть целым. Если отрезок времени равен Т, а длительность операции есть т, то за время Т можно выполнить либо Т/т, либо — 1 операций, где символ есть ближайшее к * сверху целое

число. При больших по сравнению с т значениях Т величина — 1 при-

близительно равна Г/т. Чтобы в дальнейшем не загромождать выкладки и формулы символами целочисленности и различными членами малого порядка, мы будем всюду приводить результаты в главном, что эквивалентно переходу к пределу при Т⁷-» со. Говоря иначе, все характеристики и соотношения будут носить асимптотический характер, хотя об этом не будет напоминаться специально. Данное обстоятельство нисколько не снижает практическую ценность получаемых результатов, но делает их более наглядными.

Назовем стоимостью операции время ее реализации, а стоимостью работы — сумму стоимостей всех выполненных операций. Стоимость работы — это время последовательной реализации всех рассматриваемых операций на простых ФУ с аналогичными временами срабатываний. Загруженностью устройства на данном отрезке времени будем называть отношение стоимости реально выполненной работы к максимально возможной стоимости. Ясно, что загруженность р всегда удовлетворяет условиям 0 < р < 1. Имеет место также очевидное

Утверждение 2.1

Максимальная стоимость работы, которую можно выполнить за время Т, равна Г для простого ФУ и пТ для конвейерного ФУ длины п.

Будем называть реальной производительностью системы устройств количество операций, реально выполненных в среднем за единицу времени. Пиковой

Глава 2. Как повышают производительность компьютеров

производительностью будем называть максимальное количество операций, которое может быть выполнено той же системой за единицу времени при отсутствии связей между ФУ. Из определений вытекает, что как реальная, так и пиковая производительности системы суть суммы соответственно реальных и пиковых производительностей всех составляющих систему устройств.

Утверждение 2.2

Пусть система состоит из s устройств, в общем случае простых или конвейерных. Если устройства имеют пиковые производительности щ, ..., n_sv\ работают с загруженностями р_ь ..., p_s, то реальная производительность г системы выражается формулой

s ^r = ^Piⁿi. (2.1)

Поскольку реальная производительность системы равна сумме реальных производительностей всех ФУ, то достаточно доказать утверждение для одного устройства. Пусть для выполнения одной операции ФУ требует время х и за время Г выполнено ^операций. Независимо от того, каков тип устройства, стоимость выполненной работы равна TVx. Если устройство простое, то согласно утверждению 2.1 максимальная стоимость работы равна Т. Поэтому загруженность устройства равна Ni/T. По определению реальная производительность ФУ есть N/T, а его пиковая производительность — 1/т. И равенство (2.1) становится очевидным. Предположим теперь, что устройство конвейерное длины п. Согласно тому же утверждению 2.1 максимальная стоимость работы в данном случае равна пТ. Поэтому загруженность устройства равна Ni/nT. Реальная производительность снова есть N/T, а пиковая производительность будет равна л/т. И опять равенство (2.1) становится очевидным.

Если г, п, р суть соответственно реальная производительность, пиковая производительность и загруженность одного устройства, то имеет место равенство г = рк. Отсюда видно, что для достижения наибольшей реальной производительности устройства нужно обеспечить наибольшую его загруженность. Для практических целей понятие производительности наиболее важно потому, что именно оно показывает, насколько эффективно устройство выполняет полезную работу. По отношению к производительности понятие загруженности является вспомогательным. Тем не менее, оно полезно в силу того, что указывает путь повышения производительности, причем через вполне определенные действия.

Хотелось бы и для системы устройств ввести понятие загруженности, играющее аналогичную роль. Его можно определять по-разному. Например, как и для одного ФУ, можно было бы считать, что загруженность системы ФУ есть отношение стоимости реально выполненной работы к максимально

Часть /. Параллельные вычислительные системы

возможной стоимости. Такое определение вполне приемлемо и позволяет сделать ряд полезных выводов. Однако имеются и возражения. В этом определении медленные и быстрые устройства оказываются равноправными и если необходимо повысить загруженность системы, то не сразу видно, за счет какого ФУ это лучше сделать. К тому же, в данном случае не всегда будет иметь место равенство г = рпс соответствующими характеристиками системы.

Правильный путь введения понятия загруженности системы подсказывает соотношение (2.1). Пусть система состоит из s устройств, в общем случае простых или конвейерных. Если устройства имеют пиковые производительности %\ , ..., n_s и работают с загруженностями р\, ...,p_s, то будем считать по определению, что загруженность системы есть величина

P = Yj ^aiPi' ^а' = ~Г~ ■ (²-²)

7 = 1

Загруженность системы есть взвешенная сумма загруженностей отдельных устройств, т. к. из (2.2) следует, что

^а,- =1, а>0, \<i<s. (2.3)

/=i

Поэтому, как и должно быть для загруженности, выполняются неравенства О <р < 1. Из определения (2.2) с учетом (2.3) получаем, что для того, чтобы загруженность системы устройств равнялась 1, необходимо и достаточно, чтобы равнялись 1 загруженности каждого из устройств. Это вполне логично. Если система состоит из одного устройства, т. е. s = 1, то из (2.2) вытекает, что на ней понятия загруженности системы и загруженности устройства совпадают. Данный факт говорит о согласованности только что введенного понятия загруженности системы с ранее введенными понятиями. По определению, пиковая производительность л системы устройств равна 7ii+ ...+%• Следовательно, согласно (2.1), (2.2) всегда выполняется очень важное равенство

г=рп. (2.4)

Большое число ФУ, так же как и конвейерные ФУ, используются тогда, когда возникает потребность решить задачу быстрее. Чтобы понять, насколько быстрее это удается сделать, нужно ввести понятие "ускорение". Как и в случае загруженности, оно может вводиться различными способами, многообразие которых зависит от того, что с чем и как сравнивается. Нередко ускорение определяется, например, как отношение времени решения задачи на одном универсальном процессоре к времени решения той же задачи на системе из s таких же процессоров. Очевидно, что в наилучшей си-

Глава 2. Как повышают производительность компьютеров

туации ускорение может достигать s. Отношение ускорения к s называется эффективностью. Заметим, что подобное определение ускорения применимо только к системам, состоящим из одинаковых устройств, и не распространяется на смешанные системы. Понятие же "эффективность" в рассматриваемом случае просто совпадает с понятием загруженности. При введении понятия "ускорение" мы поступим иначе.

Пусть алгоритм реализуется за время Т на вычислительной системе из s устройств, в общем случае простых или конвейерных и имеющих пиковые производительности 7ti, ..., 7iy. Предположим, что ni <п₂ < ... <n_s. При реализации алгоритма система достигает реальной производительности г из (2.1). Будем сравнивать скорость работы системы со скоростью работы гипотетического простого универсального устройства, имеющего такую же пиковую производительность n_s, как самое быстрое ФУ системы, и обладающего возможностью выполнять те же операции, что все ФУ системы.

Итак, будем называть отношение R = r/щ ускорением реализации алгоритма на данной вычислительной системе или просто ускорением. Выбор в качестве гипотетического простого, а не какого-нибудь другого, например, конвейерного ФУ объясняется тем, что одно простое универсальное ФУ может быть полностью загружено на любом алгоритме. Принимая во внимание (2.1), имеем

R = ^---------. (2-5)

тахя,-

Анализ определяющего ускорение выражения (2.5) показывает, что ускорение системы, состоящей из s устройств, никогда не превосходит s и может достигать s в том и только в том случае, когда все устройства системы имеют одинаковые пиковые производительности и полностью загружены.

Подводя итог проведенным исследованиям, приведем для одного частного случая полезное, хотя и очевидное

Утверждение 2.3

Если система состоит из s устройств одинаковой пиковой производительности простых или конвейерных, то:

• загруженность системы равна среднему арифметическому загруженностей всех устройств;

• реальная производительность системы равна сумме реальных производи-тельностей всех устройств;

• пиковая производительность системы в s раз больше пиковой производительности одного устройства;

• ускорение системы равно сумме загруженностей всех устройств;

Часть I. Параллельные вычислительные системы

• если система состоит только из простых устройств, то ее ускорение равно отношению времени реализации алгоритма на одном универсальном простом устройстве с той же пиковой производительностью к времени реализации алгоритма на системе.

Пусть система устройств функционирует и показывает какую-то реальную производительность. Если производительность недостаточна, то в соответствии с (2.4) для ее повышения необходимо увеличить загруженность системы. Согласно (2.2) для этого, в свою очередь, нужно повысить загруженность любого устройства, у которого она еще не равна 1. Но остается открытым вопрос, всегда ли это можно сделать. Если устройство загружено не полностью, то его загруженность заведомо можно повысить в том случае, когда данное устройство не связано с другими. В случае же связанности устройств ситуация не очевидна.

Снова рассмотрим систему из s устройств. Не ограничивая общности, будем считать все устройства простыми, т. к. любое конвейерное ФУ всегда можно представить как линейную цепочку простых устройств. Допустим, что между устройствами установлены направленные связи, и они не меняются в процессе функционирования системы. Построим ориентированный мульти-граф, в котором вершины символизируют устройства, а дуги — связи между ними. Дугу из одной вершины будем проводить в другую в том и только том случае, когда результат каждого срабатывания устройства, соответствующего первой вершине, обязательно передается в качестве аргумента для очередного срабатывания устройству, соответствующему второй вершине. Назовем этот мультиграф графом системы. Предположим, что каким-то образом в систему введены все исходные данные и она начала функционировать согласно описанным ранее правилам. Если в процессе функционирования какие-то ФУ будут требовать для своих срабатываний другие исходные данные, то будем предполагать, что они подаются на входы ФУ без задержек. Исследуем максимальную производительность системы, т. е. ее максимально возможную реальную производительность при достаточно большом времени функционирования.

Утверждение 2.4

Пусть система состоит из s простых устройств с пиковыми производительно-стями щ ,..., щ, Если граф системы связный, то максимальная производительность /-_тах системы выражается формулой

W =^ПШ17Г₍, (2.6)

l<i<s

Предположим, что дуга графа системы идет из /-го ФУ в у'-ое ФУ. Пусть за достаточно большое время /-ое ФУ выполнило Nj операций, у'-ое ФУ — Nj операций. Каждый результат /-го ФУ обязательно является одним из аргументов очередного срабатывания у'-го ФУ. Поэтому количество операций, реализованныху'-ым ФУ за время Т, не может более, чем на 1, отличаться от

Глава 2. Как повышают производительность компьютеров

количества операций, реализованных /-ым ФУ, т. е. N,■ — 1 < Nj< N_t+ 1. Так как граф системы связный, то любые две вершины графа могут быть связаны цепью, составленной из дуг. Допустим, что граф системы содержит q дуг. Если k-ое ФУ за время Г выполнило N_k операций, а 1-ое ФУ — N/ операций, то из последних неравенств вытекает, что N/— q < N^< N/ + q для любых

к, I, 1 < к, I < s. Пусть устройства перенумерованы так, что tii < л₂<. ... < n_s. Принимая во внимание эту упорядоченность и полученные для числа выполняемых операций соотношения из (2.1), находим, что

_с ^Ni* | Ф ■

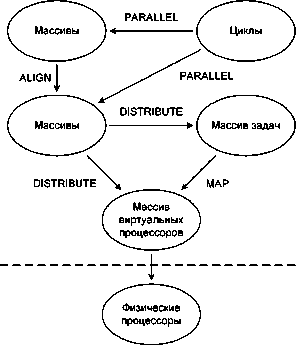Т Т

Вторые слагаемые в этих неравенствах стремятся к нулю при Т, стремящемся к бесконечности. Для всех к, 1 < к < s, обязаны выполняться неравенства N_k < ilk Т. В силу предполагаемой упорядоченности производительностей п_ки того, что все N^ асимптотически равны между собой, число операций, реализуемых каждым ФУ, будет асимптотически максимальным, если выполняется равенство TVi = ъ\Т. Это означает, что максимально возможная реальная производительность системы асимптотически будет равна sk\, что совпадает с (2.6).

Следствие

Пусть вычислительная система состоит из s простых устройств с пиковыми производительностями щ , ..., n_s. Если граф системы связный, то:

• асимптотически каждое из устройств выполняет одно и то же число операций;

• загруженность любого устройства не превосходит загруженности самого непроизводительного устройства;

• если загруженность какого-то устройства равна 1, то это — самое непроизводительное устройство;

• загруженность системы не превосходит


		S 1ГШ171/
		l<i<s
	-г max	s
		7 = 1
	превосходит
		s mini;
	-"max	_ l<i<s
	-"max	max л,-
		Ki<s

Часть /. Параллельные вычислительные системы

Установление всех приведенных здесь фактов осуществляется почти дословным повторением доказательства утверждения 2.4 и, естественно, использованием формул (2.2), (2.5).

Следствие (1-ый закон Амдала)

Производительность вычислительной системы, состоящей из связанных между собой устройств, в общем случае определяется самым непроизводительным ее устройством.

Заметим, что утверждение 2.4 указывает на одно из узких мест процесса функционирования системы. Некоторые узкие места вычислительных систем, описанные в литературе, так или иначе связываются с именем Амдала, американского специалиста в области вычислительной техники. Чтобы не терять узнаваемость различных фактов, мы не станем нарушать эту традицию и будем оставлять именными соответствующие утверждения, даже если они совсем простые. Возможно лишь несколько изменим формулировки, приспособив их к текущему изложению материала. Именно по этим причинам мы назвали 1-ым законом Амдала последнее следствие из утверждения 2.4.

Следствие

Пусть система состоит из простых устройств и граф системы связный. Асимптотическая производительность системы будет максимальной, если все устройства имеют одинаковые пиковые производительности.

Когда мы говорим о максимально возможной реальной производительности, то подразумеваем, что функционирование системы обеспечивается таким расписанием подачи команд, которое минимизирует простой устройств. Максимальная производительность может достигаться при разных режимах. В частности, как следует из утверждения 2.4, она достигается при синхронном режиме с тактом, обратно пропорциональным производительности самого медленного из ФУ, если, конечно, система состоит из простых устройств и граф системы связный. Пусть система состоит из s простых устройств одинаковой производительности. Тогда как в случае связанной системы, так и в случае не связанной, максимально возможная реальная производительность при больших временах функционирования оказывается одной и той же и равной ^-кратной пиковой производительности одного устройства.

Мы уже неоднократно убеждались в том, что различные характеристики процесса функционирования системы становятся лучше, если система состоит из устройств одинаковой производительности. Предположим, что все устройства, к тому же, простые и универсальные, т. е. на них можно выполнять различные операции. Пусть на такой системе реализуется некоторый алгоритм, а сама реализация соответствует какой-то его параллельной фор-

Глава 2. Как повышают производительность компьютеров

ме. О ней мы будем говорить детально в §4.2. Но здесь удобно привести некоторые факты, имеющие отношение как к параллельной форме, так и к функциональным устройствам. Допустим, что высота параллельной формы равна ш, ширина равна q и всего в алгоритме выполняется N операций.

Утверждение 2.5

В сформулированных условиях максимально возможное ускорение системы равно N/m.

Пусть система состоит из s устройств пиковой производительности п. Предположим, что за время Т реализации алгоритма на /-ом ФУ выполняется N_tопераций. По определению загруженность /-го ФУ равна Nj/n Т. Согласно (2.5) ускорение системы в данном случае равно

я пТ

При заданной производительности устройств время реализации одного яруса параллельной формы равно л^-1. Поэтому время Г реализации алгоритма не меньше, чем ш/п, и достигает этой величины, когда все ярусы реализуются подряд без пропусков. Следовательно, ускорение системы при любом числе устройств не будет превосходить N/m.

Следствие

Минимальное число устройств системы, при котором может быть достигнуто максимально возможное ускорение, равно ширине алгоритма.

Предположим, что по каким-либо причинам п операций из N мы вынуждены выполнять последовательно. Причины могут быть разными. Например, операции могут быть последовательно связаны информационно. И тогда без изменения алгоритма их нельзя реализовать иначе. Но вполне возможно, что мы просто не распознали параллелизм, имеющийся в той части алгоритма, которая описывается этими операциями. Отношение р = п/ N назовем долей последовательных вычислений.

Следствие (2-й закон Амдала)

Пусть система состоит из s одинаковых простых универсальных устройств. Предположим, что при выполнении параллельной части алгоритма все s устройств загружены полностью. Тогда максимально возможное ускорение равно

Я =-----------------. (²-⁷)

Р* + (1 - Р)

Часть /. Параллельные вычислительные системы

Обозначим через п пиковую производительность отдельного ФУ. Согласно утверждению 2.3:

Если всего выполняется N операций, то среди них pTV операций выполняется последовательно и (1 — p)7V параллельно на s устройствах по (1 — $)N/s операций на каждом. Не ограничивая общности, можно считать, что все последовательные операции выполняются на первом ФУ. Всего алгоритм реализуется за время

_т _ W + (1 - ®N/s

⁷i-------------------------------•

На параллельной части алгоритма работают как первое, так и все остальные устройства, тратя на это время

(1 - WA

¹ i

для 2 < / < п. Поэтому р! = 1 и

(1 - ют

^Р' P7V + (р - l)N/s ' Следовательно

R = 1 | V ⁽¹ " ®^N/S = ^S

£₂$_N + (I - p)_N/_s pj + (1 - p) *

Следствие (3-й закон Амдала)

Пусть система состоит из простых одинаковых универсальных устройств. При любом режиме работы ее ускорение не может превзойти обратной величины доли последовательных вычислений.

По поводу последнего следствия заметим лишь следующее. Если последовательно выполняются п операций, то число ярусов любой параллельной формы алгоритма не может быть меньше п. В условиях обозначений утверждения 2.5 это означает, что ш> п.

В проведенных исследованиях нигде не конкретизировалось содержание операций. В общем случае они могут быть как элементарными типа сложения или умножения, так и очень крупными, представляющими алгоритмы решения достаточно сложных задач. Современные вычислительные системы состоят из тысяч и даже десятков тысяч процессоров. Они вполне укладываются в рассмотренные модели. Системы с большим числом процессоров должны быть загружены достаточно полно. В противном случае нет стимула

Глава 2. Как повышают производительность компьютеров

их создавать. Исследования говорят о том, что в реализуемых на таких системах алгоритмах доля последовательных операций должна быть порядка десятых и сотых долей процента. О проблемах конструирования подобных алгоритмов мы будем говорить в §4.3.

В заключение отметим следующее. В обширной литературе, посвященной параллельным процессам и параллельным вычислительным системам, можно встретить много различных определений и законов, касающихся производительности, ускорения, эффективности и т. п. Как правило, новые определения и законы возникают тогда, когда старые в чем-то не устраивают исследователей. Однако ко всем таким "новациям" следует относиться очень осторожно. Довольно часто в попытке что-то "улучшить" скрываются какие-то узкие места, одни понятия подменяются другими, иногда просто проводятся ошибочные рассуждения.

В качестве иллюстрации сказанного рассмотрим примеры 1.5, 1.6 из [57], заменив в них обозначения и терминологию на используемые в данном параграфе. В этих примерах обсуждаются две оценки достигаемого ускорения. Обе они получаются в условиях, когда все устройства одинаковые, простые, универсальные. За ускорение берется отношение R = T\/T_s, где Т\ есть время реализации алгоритма на одном ФУ, T_s — на системе из s ФУ. Это согласуется с последним пунктом утверждения 2.3. В примере 1.5 анализируется оценка ускорения, вытекающая из второго закона Амдала. Именно,

R ^S

^Л pj + (1 - р)" <²-⁸)

Здесь R_A есть "оценка ускорения по Амдалу", которая полностью совпадает с (2.7). Далее говорится, что при р = 0,5 и s -> оо ускорение по Амдалу всего лишь приближается снизу к 2.

На этом основании делается вывод, что оценка ускорения по Амдалу очень пессимистична. Высказывается и причина этого, сводящаяся к тому, что якобы закон Амдала плохо учитывает "параллелизм по данным". Никаких строгих обоснований не приводится, но дается в подтверждение того, что имеются лучшие оценки, пример 1.6. Как "образец" рассуждений, выдержки из примера интересно привести полностью.

"Оценка Густавсона—Барсиса начинается с того же самого отношения T\/T_sдля ускорения, но использует совершенно другие предположения относительно 7\ и T_s. Пусть время реализации задачи с параллелизмом по данным на ^-устройствах нормировано единицей, т. е. T_s = 1. Но каково же Т\1

При реализации программы на одном устройстве нужно вычислить последовательную часть за время $T_S= р и параллельную часть за время 5(1 — р) T_s = (1 — р)5. Формула для 7\ есть просто сумма: 7\ = р + (1 — р)л. Подставляя 7\ и T_s в выражение для ускорения, мы получаем

Я_ГБ = s - (s - 1)р. (2.9)

Часть I. Параллельные вычислительные системы

Если р = 0,5, как в предыдущем примере, мы получаем Л_ГБ = s — (s — - 1)/2 =(s + 1)/2.

Результат примера 1.6 совсем иной, чем дает пессимистическое предсказание, исходя из закона Амдала".

Далее приводится красивый рис. 1.6, сравнивающий оценки ускорения как функции от р, даваемые формулами (2.8), (2.9), и демонстрирующий, конечно, существенное преимущество оценки (2.9). Объясняется это тем, что алгоритмы с параллелизмом по данным позволяют максимально использовать все устройства. По-видимому, столь успешное сравнение и дало основание присвоить оценке (2.9) именной идентификатор Л_ГБ — "оценка ускорения по Густавсону—Барсису".

В действительности, процитированные выдержки вызывают значительно больше вопросов, чем что-то проясняют. Главный из них сводится к правомочности сравнения формул (2.8) и (2.9) при одних и тех же значениях р. Обозначим через p^f величину р в (2.8), через р_ГБ величину р в (2.9). Напомним, что р^ есть отношение числа операций, выполняемых последовательно, к общему числу операций. Из цитаты "при реализации программы на одном устройстве нужно вычислить последовательную часть за время РгбТ? ⁼ Ргб ^и параллельную часть за время 5(1 — Ргб№⁼ (1 ^— Ргб)⁵" следует, что р_ГБ есть доля времени на выполнение последовательных операций при условии, что параллельная часть полностью занимает s устройств и общее время на последовательно-параллельное выполнение программы равно 1. Но ведь доля последовательно выполняемых операций и доля времени на их выполнение представляют совершенно разные понятия и просто так их нельзя полагать равными. Доля последовательных вычислений по определению не зависит от числа s используемых процессоров, а доля времени на их выполнение, опять же по определению, — зависит.

Поясним сказанное подробнее. Обозначим через т время выполнения одной операции. Если всего выполняется N операций, то пусть TV] означает число операций в последовательной части, a Nj — число операций в параллельной части. Так как на параллельной части все процессоры загружены полностью, то общее время реализации алгоритма равно

T=xNi + х-s

₂

Следовательно

^}тъ


N,	+ N₂	1		•>
	Ni			1
N_{	+ N₂	/s	1 +	1 N₂ 7tv7

(2.10)

Глава 2. Как повышают производительность компьютеров

Поэтому всегда имеем:

Ргб > Рл при s > 1 Ргб ~ Фа ^пР^и больших N₂/N\, /?гб ~ Рл ^ПР^И малых N₂/N\. Кроме этого, из (2.10) вытекает, что во всех случаях

о Фа

1 + С$ - 1)р^

Подставляя это выражение для р_ГБ в (2.9), получаем, что

l + (s-l)P_A ф_А+(1-р_А)

Таким образом, если учесть связь между р^ ^и Ргб> ^то оценки ускорения по Амдалу и по Густавсону—Барсису полностью совпадают. В частности, если взять p^ = 0,5, то эквивалентное значение р_ГБ должно быть равным не 0,5, как это берется в примере 1.6 из [57], a s/(s + 1). И тогда R-A ~ -^гб ⁼ 2s/(s + 1), что по обеим оценкам одинаково плохо.

Кроме того, что в [57] неверно сравниваются формулы (2.8) и (2.9), там же имеются и другие неточности. Например, без всяких на то оснований противопоставляются сфера применения формулы Амдала (2.8) и алгоритм с параллелизмом по данным. На самом деле, никаких причин для такого противопоставления нет. Алгоритмы с параллелизмом по данным характерны тем, что в параллельной части они распадаются на одинаковые по выполняемым операциям ветви. Это обстоятельство обеспечивает возможность загрузить одинаковым образом и полностью все ФУ системы при выполнении параллельной части. Но уж если такая возможность имеется, то независимо от причин, приведших к ее появлению, можно с одинаковым успехом применять как формулу Амдала, так и формулу Густавсона—Барсиса. Это мы уже показали выше. При правильном использовании параметра (3 никаких различий между обеими формулами нет.

Формулу Амдала следует применять для прогноза возможного ускорения. В данном случае величину р можно подсчитать, не пропуская программу на параллельной вычислительной системе. Формулу же Густавсона—Барсиса можно применять для оценивания достигнутого ускорения, не пропуская программу на однопроцессорном компьютере. Величина р при этом измеряется в процессе решения задачи.

С другими понятиями дело обстоит не лучше. Особенно много всяких псевдонаучных изысканий вокруг понятий пиковой и реальной производитель-ностей. Можно понять стремление создателей вычислительной техники использовать такое определение пиковой производительности, при котором

Часть I. Параллельные вычислительные системы

она будет как можно больше. Все-таки пиковая производительность является одной из основных характеристик. К тому же, пользователи интуитивно надеются, что чем больше пиковая производительность системы, тем задачи на ней решаются быстрее. Если читатель захочет детальнее понять различные подходы к определению пиковой производительности, мы рекомендуем ему предварительно познакомиться с работой [43]. В несколько вольном переводе ее название таково: "12 способов пудрить мозги с помощью пиковой производительности".

Вместо обсуждения понятия реальной производительности приведем следующий курьезный пример. Предположим, что система имеет два простых устройства одинаковой пиковой производительности. Пусть одно устройство есть сумматор, другое — умножитель. Допустим, что все обмены информацией осуществляются мгновенно и решается задача вычисления матрицы А = В + С при заданных матрицах В, С. Очевидно, что при естественном выполнении операции сложения матриц реальная производительность будет равна половине пиковой, т. к. умножитель не используется. Спрашивается: "Можно ли каким-то образом на данной задаче повысить реальную производительность?" Ответ: "Можно". Запишем равенство А = В + С в виде А = В + 1хС Умножение элементов матрицы С на 1 позволяет загрузить умножитель и формально реальная производительность увеличивается вдвое и сравнивается с пиковой.

Вам нужно такое увеличение производительности?

Несмотря на вроде бы очевидную курьезность рассмотренного примера, он приоткрывает, тем не менее, очень сложную и очень далекую от сколько-нибудь полного решения проблему. Для любой конкретной формулы или совокупности формул существует бесконечно много эквивалентных с точки зрения точных вычислений записей. Эквивалентные записи могут быть получены путем применения законов ассоциативности, коммутативности и дистрибутивности, с помощью приведения подобных членов, заменой 0 и 1 соответственно разностью и отношением каких-то равных выражений и т. п. На этом множестве порождается бесконечно много алгоритмов, также эквивалентных с точки зрения результатов, получаемых при точных вычислениях. Все такие алгоритмы в общем случае имеют разные вычислительные свойства, в частности, по числу операций, точности приближенных вычислений и т. д. Вспомните хотя бы алгоритмы вычисления определителя, основанные на использовании прямых формул, следующих из определения, и алгоритмы, основанные на преобразованиях Гаусса. Но все такие алгоритмы имеют и разные реализационные характеристики. Они дают разные загруженности, ускорения, времена реализации. Так что выбор среди эквивалентных подходящего алгоритма является сложной задачей, и только изредка этот выбор становится курьезом.

Глава 2. Как повышают производительность компьютеров

Вопросы и задания

1. Почему в конвейерных функциональных устройствах длительности срабатываний отдельных ступеней делают одинаковыми?

2. Пусть граф вычислительной системы есть ориентированное кольцо, все дуги которого направлены в одну сторону, например, по часовой стрелке. Покажите, что существуют различные временные режимы, при которых система будет функционировать.

3. Докажите, что в условиях п. 2 при одних и тех же входных данных разные временные режимы приводят к одним и тем же результатам.

4. Докажите, что в условиях п. 2 алгоритм, реализуемый вычислительной системой, расщепляется на независимые между собой ветви вычислений.

5. На сколько ветвей расщепляется алгоритм в п. 2?

6. Что имеется общего между отдельными ветвями?

7. Что меняется в ответах на пп. 2—6, если граф вычислительной системы состоит из двух ориентированных колец разного размера, имеющих одну общую вершину?

8. Что меняется в ответах на пп. 2—6, если граф вычислительной системы состоит из одного пути?

Глава 3

Архитектура параллельных вычислительных систем

Внутренняя согласованность ценится больше эффективной работы.

Из законов Мерфи

В процессе решения любой задачи на параллельном компьютере можно выделить следующие этапы: формулировка задачи, выбор метода ее решения, фиксация алгоритма, выбор технологии программирования, создание программы и, наконец, выполнение ее на том или ином компьютере. Все эти этапы важны и для обычных компьютеров, но при использовании параллельных вычислительных систем они приобретают особую значимость. Любой параллельный компьютер — это тщательно сбалансированная система, которая может дать фантастический результат. Такие компьютеры специально проектируются для того, чтобы работать с огромной производительностью. Но параллельные компьютеры не могут работать одинаково производительно на любых программах. Если структура программы не соответствует особенностям их архитектуры, то производительность неизбежно падает.

Указанное несоответствие может возникнуть на любом этапе решения задачи. Если на каком-либо одном шаге мы не учли особенностей целевого компьютера, то большой производительности на программе заведомо не будет. В самом деле, ориентация на векторно-конвейерный компьютер или вычислительный кластер с распределенной памятью во многом определит метод решения задачи. В одном случае в программе необходимо векторизовать внутренние циклы, а в другом надо думать о распараллеливании значительных фрагментов кода. И то, и другое свойство программ определяется свойствами заложенных в них методов. Не обладает выбранный метод такими свойствами, их не будет и в программе, а, значит, и не будет высокой производительности.

Параллельный компьютер стоит в конце всей цепочки, и поэтому его влияние прослеживается везде. Чем аккуратнее мы проходим каждый этап, чем больше структура программы соответствует особенностями архитектуры компьютера, тем выше его производительность и тем ближе она к его пиковым показателям. Все понимают, что достичь пиковой производительности невозможно. Этот показатель в сравнении с реальной производительностью скорее играет роль ориентира, показывая, насколько полно использованы

Глава 3. Архитектура параллельных вычислительных систем

возможности компьютера при выполнении той или иной реальной программы. Однако пик производительности вычисляется для случая, когда все работает с максимальной загрузкой, без конфликтов и ожиданий, т. е. в идеальных условиях. В реальности же все не так. Не так сложно построить компьютер с рекордными показателями пиковой производительности. Гораздо труднее предложить эффективный способ его использования, поскольку здесь уже нужно учитывать все предыдущие этапы в указанной выше цепочке.

Параллельные вычислительные системы развиваются очень быстро. С появлением вычислительных кластеров параллельные вычисления стали доступны многим. Если раньше параллельные компьютеры стояли в больших центрах, то сейчас кластер может собрать и поддерживать небольшая лаборатория. Стоимость кластерных решений значительно ниже стоимости традиционных суперкомпьютеров. Для их построения, как правило, используются массовые процессоры, стандартные сетевые технологии и свободно распространяемое программное обеспечение. Если есть желание, минимум средств и знаний, то принципиальных препятствий для построения собственной параллельной системы нет.

Интернет. Уникальное явление нашего времени. В рамках единой сети объединены миллионы компьютеров. А что, если их использовать для решения одной задачи? Это будет самый мощный параллельный компьютер в мире, намного превосходящий по пиковой производительности все компьютеры из списка Тор500, вместе взятые. Со временем Интернет дойдет до каждой квартиры, предоставляя всем выход в глобальную сеть. И в глобальную вычислительную сеть. Если вам нужно будет что-то посчитать, то вы подключаетесь к сети, даете задание и получаете результат. При этом совершенно не важно, где именно ваше задание было обработано. Отсюда и рождаются идеи построения метакомпьютера, включающего в себя многочисленные вычислительные ресурсы по всему миру.

Красивых идей при построении параллельных вычислительных систем очень много. В состав компьютеров входит все больше и больше всевозможных вычислительных узлов. Порой конструкторам приходится разрабатывать уникальные решения, чтобы все это множество устройств заставить согласованно работать вместе. Это правильно, на этом держится прогресс вычислительной техники. Не нужно только забывать главного. Погоня за внутренней согласованностью не должна становиться самоцелью. Любой параллельный компьютер является инструментом для решения реальных задач. В конечном счете, с этой точки зрения и нужно все оценивать. Если внутренняя согласованность в компьютере достигается во имя эффективного решения задач, то это оправдано. Если нет, то сразу возникает масса вопросов.

А что же мы имеем на практике? Об этом и рассказывает данная глава книги.

Часть I. Параллельные вычислительные системы

§ 3.1. Классификация параллельных компьютеров и систем

Уже по первым параграфам данной книги становится ясно, насколько много существует различных способов организации параллельных вычислительных систем. Здесь можно назвать векторно-конвейерные компьютеры, массивно-параллельные и матричные системы, компьютеры с широким командным словом, спецпроцессоры, кластеры, компьютеры с многопоточной архитектурой и т. п. В этот же список входят и те архитектуры, которые мы еще не обсуждали, например, систолические массивы или dataflow-компьютеры. Если же к подобным названиям для полноты описания добавить и сведения о таких важных параметрах, как организация памяти, топология связи между процессорами, синхронность работы отдельных устройств или способ исполнения операций, то число различных архитектур станет и вовсе необозримым.

Почему параллельных архитектур так много? Как они взаимосвязаны между собой? Какие основные факторы характеризуют каждую архитектуру? Поиск ответа на такие вопросы так или иначе приводит к необходимости классификации архитектур вычислительных систем [23]. Активные попытки в этом направлении начались после опубликования М. Флинном в конце 60-х годов прошлого столетия первого варианта классификации, который, кстати, используется и в настоящее время.

Вообще говоря, при введении классификации можно преследовать самые разные цели. С точки зрения главного инженера организации, где устанавливается компьютер, деление компьютеров по мощности потребляемой электроэнергии, конечно же, будет классификацией. Планово-финансовый отдел больше интересует стоимость. Если окажется, что установка двадцати компьютеров в локальной сети обойдется во столько же, во сколько и вось-мипроцессорный сервер с общей памятью, то для него это будут вычислительные системы одного класса. И правильно. Что заложили в основу классификации, такие следствия и получаем.

Ясно, что навести порядок в хаосе очень важно для лучшего понимания исследуемой предметной области. В самом деле, вспомним открытый в 1869 году Д. И. Менделеевым периодический закон. Выписав на карточках названия химических элементов и указав их важнейшие свойства, он сумел найти такое расположение, при котором четко прослеживалась закономерность в изменении свойств элементов, расположенных в каждом столбце и каждой строке. Теперь, зная положение элемента в таблице, он мог с большой степенью точности описать его свойства, не проводя с ним никаких непосредственных экспериментов. Другим, поистине фантастическим следствием, явилось то, что данный закон указал на несколько "белых пятен" в таблице и позволил предсказать не только существование, но и свойства пока неиз-

Глава 3. Архитектура параллельных вычислительных систем

вестных элементов. В 1875 году французский химик Поль Эмиль Ле-кок де Буабодран, изучая спектры минералов, открыл предсказанный Менделеевым галлий и впервые подробно описал его свойства. В свою очередь Менделеев, никогда прежде не видевший данного химического элемента, на основании введенной классификации смог и указать на ошибку в определении плотности галлия, и вычислить правильное значение.

Что-то похожее хотелось бы найти и для архитектур параллельных вычислительных систем. Главный вопрос — что заложить в основу классификации, может решаться по-разному. Однако с позиций наших исследований классификация должна давать ключ к пониманию того, как решать задачу эффективного отображения алгоритмов на архитектуру вычислительных систем. В некоторых случаях вводят описания классов компьютеров. На основе информации о принадлежности компьютера к конкретному классу пользователь сам принимает решение о способе записи алгоритма в терминах выбранной технологии параллельного программирования. Иногда в качестве классификации пытаются ввести формальное описание архитектуры, используя специальную нотацию. Такое направление интересно тем, что создается благоприятная основа для построения автоматизированных систем отображения. В самом деле, с одной стороны, есть формальное описание архитектуры целевого компьютера, с другой стороны, есть формальное описание алгоритма. Созданы условия для совместного исследования этих двух объектов и последующего синтеза оптимальной программы. Правда, результат очень сильно зависит как от качества введенных описаний, так и от методов их совместного исследования. О степени решенности даже упрощенного варианта данной проблемы читатель может судить по качеству компиляторов, работающих на существующих параллельных компьютерах.

Не стоит сбрасывать со счетов и тот факт, что удачная содержательная классификация может подсказать возможные пути совершенствования компьютеров. Трудно рассчитывать на нахождение нетривиальных "белых пятен", например, в классификации по стоимости или пиковой производительности. Однако размышления о возможной систематике с точки зрения простоты и технологичности программирования могут оказаться чрезвычайно полезными для определения направлений поиска новых архитектур.

Классификация М. Флинна (М. Flynn). По-видимому, самой ранней и наиболее известной является классификация архитектур вычислительных систем, предложенная в 1966 году М. Флинном. Классификация базируется на понятии потока, под которым понимается последовательность команд или данных, обрабатываемая процессором. На основе числа потоков команд и потоков данных Флинн выделяет четыре класса архитектур.

S1SD (Single Instruction stream/Single Data stream) — одиночный поток команд и одиночный поток данных (рис. 3.1). На рисунках, иллюстрирующих классификацию М. Флинна, использованы следующие обозначения:

Часть I. Параллельные вычислительные системы

ПР — это один или несколько процессорных элементов, УУ — устройство управления, ПД — память данных. К классу SISD относятся, прежде всего, классические последовательные машины или, иначе, машины фон-неймановского типа, например, PDP-11 или VAX 11/780. В таких машинах есть только один поток команд, все команды обрабатываются последовательно друг за другом и каждая команда инициирует одну скалярную операцию. Не имеет значения тот факт, что для увеличения скорости обработки команд и скорости выполнения арифметических операций может применяться конвейерная обработка: как машина CDC 6600 со скалярными функциональными устройствами, так и CDC 7600 с конвейерными попадают в этот класс.


	УУ	SISD

ПР			пд
			пд


	УУ	SIMD

пр ;			. .	пд
			' '

			' '

Рис. 3.1. Классы SISD и SIMD классификации М. Флинна

SIMD (Single Instruction stream/Multiple Data stream) — одиночный поток команд и множественный поток данных (см. рис. 3.1). В архитектурах подобного рода сохраняется один поток команд, включающий, в отличие от предыдущего класса, векторные команды. Это позволяет выполнять одну арифметическую операцию сразу над многими данными, например, над элементами вектора. Способ выполнения векторных операций не оговаривается, поэтому обработка элементов вектора может производиться либо процессорной матрицей, как в 1LL1AC IV, либо с помощью конвейера, как, например, в машине Сгау-1.

M1SD (Multiple Instruction stream/Single Data stream) — множественный поток команд и одиночный поток данных (рис. 3.2). Определение подразумевает наличие в архитектуре многих процессоров, обрабатывающих один и тот же поток данных. Однако ни Флинн, ни другие специалисты в области архитектуры компьютеров до сих пор не смогли представить убедительный пример реально существующей вычислительной системы, построенной на данном принципе. Ряд исследователей относят конвейерные машины к данному классу, однако это не нашло окончательного признания в научном сообществе. Будем считать, что пока данный класс пуст.

M1MD (Multiple Instruction stream/Multiple Data stream) — множественный поток команд и множественный поток данных (см. рис. 3.2). Этот класс

Глава 3. Архитектура параллельных вычислительных систем 99

предполагает, что в вычислительной системе есть несколько устройств обработки команд, объединенных в единый комплекс и работающих каждое со своим потоком команд и данных.


	УУ		MISD
		...
ПР				пд
				пд



	УУ		MIMD
		...
				. .	пд
ПР				' '

Рис. 3.2. Классы MISD и MIMD классификации М. Флинна

Итак, что же собой представляет каждый класс? В SISD, как уже говорилось, входят однопроцессорные последовательные компьютеры типа VAX 11/780. Однако многими критиками подмечено, что в этот класс можно включить и векторно-конвейерные машины, если рассматривать вектор как одно неделимое данное для соответствующей команды. В таком случае в этот класс попадут и такие системы, как Cray-1, CYBER 205, машины семейства FACOM VP и многие другие.

Бесспорными представителями класса S1MD считаются матрицы процессоров: 1LLIAC IV, 1CL DAP, Goodyear Aerospace МРР, Connection Machine 1 и т. п. В таких системах единое управляющее устройство контролирует множество процессорных элементов. Каждый процессорный элемент получает от устройства управления в каждый фиксированный момент времени одинаковую команду и выполняет ее над своими локальными данными. Для классических процессорных матриц никаких вопросов не возникает. Однако в этот же класс можно включить и векторно-конвейерные машины, например, Сгау-1. В этом случае каждый элемент вектора надо рассматривать как отдельный элемент потока данных.

Класс M1MD чрезвычайно широк, поскольку включает в себя всевозможные мультипроцессорные системы: Cm*, C.mmp, Cray Y-MP, Denelcor HEP, BBN Butterfly, Intel Paragon, Cray T3D и многие другие. Интересно то, что если конвейерную обработку рассматривать как выполнение последовательности различных команд (операций ступеней конвейера) не над одиночным векторным потоком данных, а над множественным скалярным потоком, то все рассмотренные выше векторно-конвейерные компьютеры можно расположить и в данном классе.

Предложенная схема классификации вплоть до настоящего времени является самой применяемой при начальной характеристике того или иного компьютера. Если говорится, что компьютер принадлежит классу S1MD или M1MD,

100

Часть I. Параллельные вычислительные системы

то сразу становится понятным базовый принцип его работы, и в некоторых случаях этого бывает достаточно. Однако видны и явные недостатки. В частности, некоторые заслуживающие внимания архитектуры, например dataflow и векторно-конвейерные машины, четко не вписываются в данную классификацию. Другой недостаток — это чрезмерная заполненность класса MIMD. Необходимо средство, более избирательно систематизирующее архитектуры, которые по Флинну попадают в один класс, но совершенно различны по числу процессоров, природе и топологии связи между ними, по способу организации памяти и, конечно же, по технологии программирования.

Классификация Р. Хокни (R. Hockney). Р. Хокни разработал свой подход к классификации для более детальной систематизации компьютеров, попадающих в класс MIMD по систематике М. Флинна. Как отмечалось выше, класс MIMD чрезвычайно широк и объединяет целое множество различных типов архитектур. Пытаясь систематизировать архитектуры внутри этого класса, Р. Хокни получил иерархическую структуру, представленную на рис. 3.3.

MIMD

переключаемые

конвейерные

с общей памятью

регулярные решетки

с распределенной памятью

гиперкубы

иерархические структуры

изменяющие конфигурацию

Рис. 3.3. Дополнительная классификация Р. Хокни класса MIMD

Основная идея классификации состоит в следующем. Множественный поток команд может быть обработан двумя способами: либо одним конвейерным устройством обработки, работающим в режиме разделения времени для отдельных потоков, либо каждый поток обрабатывается своим собственным устройством. Первая возможность используется в MIMD-компьютерах, которые автор называет конвейерными. Сюда можно отнести, например, процессорные модули в Denelcor HEP или компьютеры семейства Тега МТА.

Глава 3. Архитектура параллельных вычислительных систем

101

Архитектуры, использующие вторую возможность, в свою очередь, опять делятся на два класса. В первый класс попадают MIMD-компьютеры, в которых возможна прямая связь каждого процессора с каждым, реализуемая с помощью переключателя. Во втором классе находятся MIMD-компьютеры, в которых прямая связь каждого процессора возможна только с ближайшими соседями по сети, а взаимодействие удаленных процессоров поддерживается специальной системой маршрутизации.

Среди MIMD-машин с переключателем Хокни выделяет те, в которых вся память распределена среди процессоров как их локальная память (например, PASM, PRINGLE, IBM SP2 без SMP-узлов). В этом случае общение самих процессоров реализуется с помощью сложного переключателя, составляющего значительную часть компьютера. Такие машины носят название MIMD-машин с распределенной памятью. Если память это разделяемый ресурс, доступный всем процессорам через переключатель, то MIMD-машины являются системами с общей памятью (BBN Butterfly, Cray С90). В соответствии с типом переключателей можно проводить классификацию и далее: простой переключатель, многокаскадный переключатель, общая шина и т. п. Многие современные вычислительные системы имеют как общую разделяемую память, так и распределенную локальную. Такие системы автор рассматривает как гибридные MIMD с переключателем.

При рассмотрении MIMD-машин с сетевой структурой считается, что все они имеют распределенную память, а дальнейшая классификация проводится в соответствии с топологией сети: звездообразная сеть (ЮАР), регулярные решетки разной размерности (Intel Paragon, Cray T3D), гиперкубы (NCube, Intel iPSC), сети с иерархической структурой, такой как деревья, пирамиды, кластеры (Cm*, CEDAR) и, наконец, сети, изменяющие свою конфигурацию.

Заметим, что если архитектура компьютера спроектирована с использованием нескольких сетей с различной топологией, то, по всей видимости, по аналогии с гибридными MIMD-машинами с переключателями, их стоит назвать гибридными сетевыми MIMD-машинами, а использующие идеи разных классов — просто гибридными MIMD-машинами. Типичным представителем последней группы, в частности, является компьютер Connection Machine 2, имеющий на внешнем уровне топологию гиперкуба, каждый узел которого является кластером процессоров с полной связью.

Классификация Т. Фенга (Т. Feng). В 1972 году Т. Фенг предложил классифицировать вычислительные системы на основе двух простых характеристик. Первая — число п бит в машинном слове, обрабатываемых параллельно при выполнении машинных инструкций. Практически во всех современных компьютерах это число совпадает с длиной машинного слова. Вторая характеристика равна числу слов ш, обрабатываемых одновременно данной вычислительной системой. Немного изменив терминологию, функ-

102

Часть I. Параллельные вычислительные системы

ционирование любого компьютера можно представить как параллельную обработку п битовых слоев, на каждом из которых независимо преобразуются m бит. Опираясь на такую интерпретацию, вторую характеристику называют шириной битового слоя.

Каждую вычислительную систему С можно описать парой чисел (я, ш). Произведение Р = пхпг определяет интегральную характеристику потенциала параллельности архитектуры, которую Фенг назвал максимальной степенью параллелизма вычислительной системы. По существу, данное значение есть не что иное, как пиковая производительность, выраженная в других единицах. В период появления данной классификации, а это начало 70-х годов прошлого столетия, еще казалось возможным перенести понятие пиковой производительности как универсального средства сравнения и описания потенциальных возможностей компьютеров с традиционных последовательных машин на параллельные. Понимание того факта, что пиковая производительность сама по себе не столь важна, пришло позднее, и данный подход отражает, естественно, степень осмысления специфики параллельных вычислений того времени.

Рассмотрим компьютер Advanced Scientific Computer фирмы Texas Instruments (TI ASC). В основном режиме он работает с 64-разрядным словом, причем все разряды обрабатываются параллельно. Арифметико-логическое устройство имеет четыре одновременно работающих конвейера, содержащих по восемь ступеней. При такой организации 4x8 = 32 слова могут обрабатываться одновременно (то есть 32 бита в каждом битовом слое), и значит компьютер TI ASC может быть представлен в виде (64, 32).

На основе введенных понятий все вычислительные системы можно разделить на четыре класса.

Разрядно-последовательные, пословно-последовательные (п = т = 1). В каждый момент времени такие компьютеры обрабатывают только один двоичный разряд. Представителем данного класса служит давняя система MINIMA с естественным описанием (1, 1).

Разрядно-параллельные, пословно-последовательные (п > 1, т = 1). Большинство классических последовательных компьютеров, так же как и многие вычислительные системы, используемые сейчас, принадлежат к данному классу: IBM 701 с описанием (36, 1), PDP-11 с описанием (16, 1), IBM 360/50 и VAX 11/780 - обе с описанием (32, 1).

Разрядно-последовательные, пословно-параллельные (п = 1, т > 1). Как правило вычислительные системы данного класса состоят из большого числа одноразрядных процессорных элементов, каждый из которых может независимо от остальных обрабатывать свои данные. Типичными примерами служат STARAN (1, 256) и МРР (1, 16384) фирмы Goodyear Aerospace, прототип известной системы ILLIAC IV компьютер SOLOMON (1, 1024) и ICL DAP (1, 4096).

Глава 3. Архитектура параллельных вычислительных систем

103

Разрядно-параллельные, пословно-параллельные (я > 1, m > 1). Подавляющее большинство параллельных вычислительных систем, обрабатывая одновременно m х п двоичных разрядов, принадлежит именно к этому классу: ILL1AC IV (64, 64), TI ASC (64, 32), C.mmp (16, 16), CDC 6600 (60, 10), BBN Butterfly GP1000 (32, 256).

Недостатки предложенной классификации достаточно очевидны и связаны со способом вычисления ширины битового слоя ш. По существу Фенг не делает никакого различия между процессорными матрицами, векторно-конвейерными и многопроцессорными системами. Не делается акцент на том, за счет чего компьютер может одновременно обрабатывать более одного слова: множественности функциональных устройств, их конвейерности или же какого-то числа независимых процессоров. Если в системе N независимых процессоров имеют каждый по F конвейерных функциональных устройств с длиной конвейера L, то для вычисления ширины битового слоя надо просто найти произведение N х F х L.

Конечно же, опираясь на данную классификацию, достаточно трудно, а иногда и просто невозможно, осознать специфику той или иной вычислительной системы. Достоинством же можно считать введение единой числовой метрики для всех типов компьютеров, позволяющей сравнить любые два компьютера между собой.

Классификация В. Хендлера (W. Handler). В основу классификации В. Хенд-лер закладывает явное описание возможностей параллельной и конвейерной обработки информации вычислительной системой. При этом он намеренно не рассматривает различные способы связи между процессорами и блоками памяти, а считает, что коммуникационная сеть может быть нужным образом сконфигурирована и будет способна выдержать предполагаемую нагрузку.

Предложенная классификация базируется на различии между тремя уровнями обработки данных в процессе выполнения программ:

□ уровень выполнения программы; опираясь на счетчик команд и некоторые другие регистры, устройство управления (УУ) производит выборку и дешифрацию команд программы;

□ уровень выполнения команд; арифметико-логическое устройство компьютера (АЛУ) исполняет команду, выданную ему устройством управления;

□ уровень битовой обработки; все элементарные логические схемы процессора (ЭЛС) разбиваются на группы, необходимые для выполнения операций над одним двоичным разрядом.

Подобная схема выделения уровней предполагает, что вычислительная система содержит какое-то число процессоров, каждый со своим устройством управления. Каждое устройство управления связано с несколькими арифметико-логическими устройствами, исполняющими одну и ту же операцию в каждый конкретный момент времени. Наконец, каждое АЛУ объединяет

104

Часть I. Параллельные вычислительные системы

несколько групп элементарных логических схем, ассоциированных с обработкой одного двоичного разряда (число групп ЭЛС есть не что иное, как длина машинного слова). Если на какое-то время не рассматривать возможность конвейеризации, то число устройств управления к, число арифметико-логических устройств d в каждом устройстве управления и число групп ЭЛС w в каждом АЛУ составят тройку для описания данной вычислительной системы С: t(C) = (к, d, w).

В таких обозначениях описания некоторых хорошо известных вычислительных систем будут выглядеть следующим образом:

/(MINIMA) = (1,1,1);

/(IBM 701) = (1,1,36);

/(SOLOMON) = (1,1024,1);

/(ILLIAC IV) = (1,64,64);

/(STARAN) = (1,8192,1) — в полной конфигурации;

/(C.mmp) = (16,1,16) — основной режим работы;

/(PRIME) = (5,1,16);

/(BBN Butterfly GP1000) = (256,1,32).

Несмотря на то, что перечисленным системам присущ параллелизм разного рода, он без особого труда может быть отнесен к одному из трех выделенных уровней.

на каждой ступени слово из w бит


ЦП
			АЛУ
ЦП	_	УУ	:	^d
•			АЛУ

ФУ

w' ступеней конвейера

ФУ

d' ФУ могут быть сцеплены

к' ЦП из к могут работать в макроконвейере

Рис. 3.4. Уровни параллелизма в классификации В. Хендлера

Теперь можно расширить возможности описания, допустив возможность конвейерной обработки на каждом из уровней (рис. 3.4). В самом деле, кон-вейерность на самом нижнем уровне, т. е. на уровне ЭЛС, это конвейер-

Глава 3. Архитектура параллельных вычислительных систем

105

ность функциональных устройств. Если функциональное устройство обрабатывает w-разрядные слова на каждой из w' ступеней конвейера, то для характеристики параллелизма данного уровня естественно рассмотреть произведение w х w'. Знак "х" будем использовать на каждом уровне, чтобы отделить число, представляющее степень параллелизма, от числа ступеней в конвейере. Компьютер TI AS С имеет четыре конвейерных устройства по восемь ступеней в каждом для обработки 64-разрядных слов, следовательно, он может быть описан так:

CTIASC) = (1, 4, 64 х 8).

Следующий уровень конвейерной обработки — это конвейеризация на уровне команд. Предполагается, что в вычислительной системе есть несколько функциональных устройств, которые могут работать одновременно в режиме конвейера (для обозначения данной возможности часто используют другой термин — зацепление функциональных устройств). Классическим примером этому служат векторно-конвейерные компьютеры фирмы Cray Research. Другим примером является машина CDC 6600, содержащая десять независимых последовательных функциональных устройств, способных подавать результат своей работы на вход другим функциональным устройствам: ?(CDC 6600) = (1,1 х 10,60) (описан только центральный процессор без учета управляющих и периферийных подсистем).

Наконец, нам осталось рассмотреть конвейеризацию на самом верхнем уровне, известную как макроконвейер. Поток данных, проходя через один процессор, поступает на вход другому. Компьютер РЕРЕ, имея фактически три независимых системы из 288 устройств, описывается так:

?(РЕРЕ) = (1x3, 288, 32).

После расширения трехуровневой модели параллелизма средствами описания потенциальных возможностей конвейеризации каждая тройка

1(C) = (кх к', dx d\ wx w)

интерпретируется так:

П к — число процессоров (каждый со своим УУ), работающих параллельно;

□ к' — глубина макроконвейера из отдельных процессоров;

П d — число АЛУ в каждом процессоре, работающих параллельно;

П d' — глубина конвейера из функциональных устройств АЛУ;

П w — число разрядов в слове, обрабатываемых в АЛУ параллельно;

□ w' — число ступеней в конвейере функциональных устройств АЛУ.

Очевидна связь между классификацией Фенга и классификацией Хендлера: для получения максимальной степени параллелизма в терминах Фенга надо найти произведение всех шести величин в описании Хендлера. Здесь же за-

106

Часть I. Параллельные вычислительные системы

метим, что, заложив в основу своей схемы явное указание на присутствующий параллелизм и возможную конвейеризацию, Хендлер сразу снимает некоторые вопросы, характерные для схем Флинна и Фенга, по крайней мере, в плане описания векторно-конвейерных машин.

В дополнение к изложенному способу описания архитектур Хендлер предлагает использовать три операции, которые, будучи примененными к тройкам, позволят описать, во-первых, сложные структуры с подсистемами ввода/вывода, хост-компьютером или какими-то другими особенностями, и, во-вторых, возможные режимы функционирования вычислительных систем, поддерживаемые для оптимального соответствия структуре программ.

Первая операция (х) в каком-то смысле отражает конвейерный принцип обработки и предполагает последовательное прохождение данных сначала через первый ее аргумент-подсистему, а затем через второй. В частности, описание компьютера CDC 6600 можно уточнить следующим образом:

t(CDC 6600) = (10,1,12) х (1,1 х 10,60),

где первый аргумент отражает существование десяти 12-разрядных периферийных процессоров и тот факт, что любая программа должна сначала быть обработана одним из них и лишь после этого передана центральному процессору для исполнения. Аналогично можно получить описание машины РЕРЕ, принимая во внимание, что в качестве хост-компьютера она использует CDC 7600:

?(РЕРЕ) = t(CDC 7600) х (1 х 3, 288, 32) =

= (15, 1, 12) х (1, 1 х 9, 60) х (1 х 3, 288, 32).

Поток данных последовательно проходит через три подсистемы, что мы и отразили, соединив их знаком "х".

Заметим, что все подсистемы последнего примера достаточно сложны и по данному описанию могут представляться по-разному. Чтобы внести большую ясность, аналогично операции конвейерного исполнения, Хендлер вводит операцию параллельного исполнения (+), фиксирующую возможность независимого использования процессоров разными задачами, например:

/(4, d, w) = [(1, d, w) + (1, d, w) + (1, d, w) + (1, d, w)].

В случае CDC 7600 уточненная запись вида:

(15, 1, 12) х (1, 1 х 9, 60) =

= [(1, 1, 12) + ... + (1, 1, 12)] {15раз} х (1, 1 х 9, 60)

говорит о том, что каждая задача может захватить свой периферийный процессор, а затем одна за одной они будут поступать в центральный процессор.

И, наконец, третья операция — операция альтернативы (v), показывает возможные альтернативные режимы функционирования вычислительной сие-

Глава 3. Архитектура параллельных вычислительных систем

107

темы. Например, компьютер C.mmp может быть запрограммирован для использования в трех принципиально разных режимах:

t(C.mmp) = (16, 1, 16) v (1 х 16, 1,16) v (1, 16, 16).

Классификация Л. Шнайдера (L. Snyder). В 1988 году Л. Шнайдер предложил выделить этапы выборки и непосредственно исполнения в потоках команд и данных. Именно разделение потоков на адреса и их содержимое позволило описать такие ранее "неудобные" для классификации архитектуры, как компьютеры с длинным командным словом, систолические массивы и целый ряд других.

Введем необходимые для дальнейшего изложения понятия и обозначения. Назовем потоком ссылок S некоторой вычислительной системы конечное множество бесконечных последовательностей пар:

S= {(щ </,>) (д₂ <t₂>), (6, <и,>) (Ъ₂ <и₂>),

(с, <v,>) (с₂ <v₂>)},

где первый компонент каждой пары — это неотрицательное целое число, называемое адресом, второй компонент — это набор из п неотрицательных целых чисел, называемых значениями, причем п одинаково для всех наборов всех последовательностей. Например, пара (Ь₂ <и₂>) определяет адрес Ь₂и значение и₂. Если значения рассматривать как команды, то из потока ссылок получим поток команд I; если же значения интерпретировать как данные, то соответствующий поток — это поток данных В.

Интерпретация введенных понятий очень проста. Элементы каждой последовательности это адрес и его содержимое, выбираемое из памяти (или записываемое в память). Последовательность пар адрес—значение можно рассматривать как историю выполнения команд либо перемещения данных между процессором и памятью компьютера во время выполнения программы. Число инструкций, которое данный компьютер может выполнять одновременно, определяет число последовательностей в потоке команд. Аналогично, число различных данных, которое компьютер может обработать одновременно, определяет число последовательностей в потоке данных.

Пусть S произвольный поток ссылок. Последовательность адресов потока S, обозначаемая S_a, это последовательность наборов, сформированная из адресов каждой последовательности из S:

S_a = <ai b_x ci>, <a₂ b₂ c₂>.

Последовательность значений потока S, обозначаемая S_v, это последовательность наборов, сформированная из значений каждой последовательности из S:

S_v = <ti ui vi>, <t₂ u₂ v₂>.

Если S_x — последовательность элементов, где каждый элемент является набором из п чисел, то для обозначения "ширины" последовательности будем пользоваться обозначением: w(S_x) = п.

108

Часть I. Параллельные вычислительные системы

Из определений S_a, S_v и w следует, что если S это поток ссылок со значениями из п чисел, то w{S_a) = \ S\ и w{S_v) = n\S\, где | S\ обозначает мощность множества S.

Каждую пару (I, В) с потоком команд / и потоком данных В будем называть вычислительным шаблоном, а все компьютеры будем разбивать на классы в зависимости от того, какой шаблон они могут исполнить. В самом деле, компьютер может исполнить шаблон (I, В), если он в состоянии:

П выдать w{I_a) адресов команд для одновременной выборки из памяти;

□ декодировать и проинтерпретировать одновременно w(I_v) команд;

□ выдать одновременно w(B_a) адресов операндов;

□ выполнить одновременно w(B_v) операций над различными данными.

Если все эти условия выполнены, то компьютер может быть описан как Iw(ia)w(iv)D_w(Da)w(Dv)- Рассмотрим классическую последовательную машину. Согласно классификации Флинна, она попадает в класс SISD, следовательно |/| = \В\ = 1 и w(I_a) = w{B_a) = 1. Из-за того, что в подобного рода компьютерах команды декодируются последовательно, следует равенство w(I_v) = 1, а последовательное исполнение команд дает w(B_v) = 1. Поэтому описание однопроцессорной машины с фоннеймановской архитектурой будет выглядеть так: 1\\В\\.

Теперь возьмем две машины из класса SIMD: Goodyear Aerospace МРР и ILLIAC IV, причем не будем принимать во внимание разницу в способах обработки данных отдельными процессорными элементами. Единственный поток команд означает |/| = 1 для обеих машин. Аналогично последовательной машине, для потока команд получаем равенство w(I_a) = w(I_v) = 1. Далее, вспомним, что для доступа к операндам устройство управления МРР рассылает один и тот же адрес всем процессорным элементам, поэтому в этой терминологии МРР имеет единственную последовательность в потоке данных, т. е. \В\ = 1. Однако затем выборка данных из памяти и последующая обработка осуществляются в каждом процессорном элементе, поэтому w(B_v) = 16 384, а вся система МРР может быть описана /i₍iA₍i6 384-

В ILLIAC IV устройство управления, так же, как и в МРР, рассылает один и тот же адрес всем процессорным элементам, однако каждый из них может получить свой уникальный адрес, добавляя содержимое локального индексного регистра. Это означает, что \В\ = 64 и в системе присутствуют 64 потока адресов данных, определяющих одиночные потоки операндов, т. е. w(B_a) = w(B_v) = 64. Суммируя сказанное, приходим к описанию ILLIAC IV:

Л,1-064,64-

Для более детальной классификации Шнайдер вводит три предопределенных значения, которые могут принимать величины w(I_a), w(I_v), w(B_a) и w(B_v):

П s — значение равно 1;

Глава 3. Архитектура параллельных вычислительных систем

109

П с — значение от 1 до некоторой (небольшой) константы;

П m — значение от 1 до произвольно большого конечного числа.

В частности, в этих обозначениях фоннеймановская машина принадлежит к классу I_SSB_SS.

Несмотря на то, что и с и m в принципе не имеют определенной верхней границы, они отражают разные свойства архитектуры компьютера. Описатель с предполагает жесткие ограничения сверху со стороны аппаратуры, и соответствующий параметр не может быть значительно увеличен относительно простыми средствами. Примером может служить число инструкций, упакованных в командном слове VLIW-компьютера. С другой стороны, описатель m используется тогда, когда обозначаемая величина может быть легко изменена, т. е. другими словами, компьютер по данному параметру масштабируем. Например, относительная простота увеличения числа процессорных элементов в системе МРР является основанием для того, чтобы отнести ее к классу I_ssD_sm.

Конечно же, различие между с и т в достаточной мере условное и, как правило, порождает массу вопросов. Например, как описать машину, в которой процессоры связаны через общую шину? С одной стороны, нет никаких принципиальных ограничений на число подключаемых процессоров. Однако каждый дополнительный процессор увеличивает загруженность шины, и при достижении некоторого порога подключение новых процессоров бессмысленно. С помощью какого символа описать такую систему: с или т? Мы оставляем данный вопрос открытым.

На основе этих обозначений можно выделить следующие классы компьютеров:

□ I_SSD_SS — классические машины фоннеймановского типа;

□ I_SSD_SC — фоннеймановские машины, в которых заложена возможность выбирать данные, расположенные с разным смещением относительно одного и того же адреса и над которыми будет выполнена одна и та же операция. Примером могут служить компьютеры, имеющие команды типа одновременного выполнения двух операций сложения над данными в формате полуслова, расположенными по указанному адресу;

□ I_ssD_sm — SIMD-компьютеры без возможности получения уникального адреса для данных в каждом процессорном элементе. Сюда входят, например, МРР, Connection Machine 1 и систолические массивы;

□ I_ssD_mm — это SIMD-компьютеры, имеющие возможность независимой модификации адресов операндов в каждом процессорном элементе, например, ILLIAC IV и Connection Machine 2;

□ I_SCD_CC — вычислительные системы, выбирающие и исполняющие одновременно несколько команд, для доступа к которым используется один адрес. Типичным примером являются VLIW-компьютеры;

□ I_mmD_mm — к этому классу относятся все компьютеры типа MIMD.

110

Часть I. Параллельные вычислительные системы

Достаточно ясно, что не нужно рассматривать все возможные комбинации описателей s, с и ш, т. к. архитектура реальных компьютеров накладывает ряд вполне разумных ограничений, в частности w(I_a) < w(I_v) и w(D_a) < w(D_v).

Подводя итог, можно отметить два положительных момента в классификации Шнайдера: более избирательная систематизация SIMD-компьютеров и возможность описания нетрадиционных архитектур типа систолических массивов или компьютеров с длинным командным словом. Вместе с тем, почти все вычислительные системы типа MIMD опять попали в один и тот же класс I_mmD_mm. Это означает, что критерий классификации, основанный лишь на потоках команд и данных без учета распределенности памяти и топологии межпроцессорной связи, слишком слаб для подобных систем.

Классификация Д. Скилликорна (D. Skillicorn). В 1989 году была сделана очередная попытка расширить классификацию Флинна и тем самым преодолеть ее недостатки. Д. Скилликорн разработал подход, пригодный для описания свойств многопроцессорных систем и некоторых нетрадиционных архитектур, в частности, dataflow.

Предлагается рассматривать архитектуру любого компьютера, как абстрактную структуру, состоящую из четырех компонентов:

□ процессор команд (IP — Instruction Processor) — функциональное устройство, работающее как интерпретатор команд; в системе, вообще говоря, может отсутствовать;

□ процессор данных (DP — Data Processor) — функциональное устройство, работающее как преобразователь данных в соответствии с арифметическими операциями;

□ иерархия памяти (IM — Instruction Memory, DM — Data Memory) — запоминающее устройство, в котором хранятся данные и команды, пересылаемые между процессорами;

□ переключатель — абстрактное устройство, обеспечивающее связь между процессорами и памятью.

Функции процессора команд во многом схожи с функциями устройств управления последовательных машин и, согласно Д. Скилликорну, сводятся к следующим. На основе своего состояния и полученной от DP информации IP выполняет такие действия: определяет адрес команды, которая будет выполняться следующей; осуществляет доступ к IM для выборки команды; получает и декодирует выбранную команду; сообщает DP команду, которую надо выполнить; определяет адреса операндов и посылает их в DP; получает от DP информацию о результате выполнения команды.

Функции процессора данных делают его во многом похожим на арифметическое устройство традиционных процессоров. DP получает от IP команду, которую надо выполнить; получает от IP адреса операндов; выбирает one-

Глава 3. Архитектура параллельных вычислительных систем

111

ранды из DM; выполняет команду; запоминает результат в DM; возвращает в IP информацию о состоянии после выполнения команды.

команды

информация о состоянии


	■ц
п
1=1
т
m
>
о
Ь£		1

Память данных

Память команд

Рис. 3.5. Фоннеймановская архитектура в терминах классификации Д. Скилликорна

Структура традиционной фон-неймановской архитектуры в терминах таким образом определенных основных частей компьютера показана на рис. 3.5. Это один из самых простых видов архитектуры, не содержащих переключателей. Для описания сложных параллельных вычислительных систем Д. Скилликорн зафиксировал четыре типа переключателей без какой-либо явной связи с типом устройств, которые они соединяют:

□ 1 — 1 — переключатель такого типа связывает пару функциональных устройств;

П п — п — переключатель связывает каждое устройство из одного множества устройств с соответствующим ему устройством из другого множества, т. е. фиксирует попарную связь;

П 1 — п — переключатель соединяет одно выделенное устройство со всеми функциональными устройствами из некоторого набора;

□ п х п — каждое функциональное устройство одного множества может быть связано с любым устройством другого множества, и наоборот.

Примеров подобных переключателей можно привести много. Так, все матричные процессоры имеют переключатель типа 1-я для связи единственного процессора команд со всеми процессорами данных. В компьютерах семейства Connection Machine каждый процессор данных имеет свою локальную память, следовательно, такая связь будет описываться как п — п. В то же время, каждый процессор команд может связаться с любым другим процессором, что отвечает описанию пхп.

112

Часть /. Параллельные вычислительные системы

Классификация Д. Скилликорна строится на основе следующих восьми характеристик:

□ количество процессоров команд IP;

□ число запоминающих устройств (модулей памяти) команд IM;

□ тип переключателя между IP и IM;

□ количество процессоров данных DP;

□ число запоминающих устройств (модулей памяти) данных DM;

□ тип переключателя между DP и DM;

□ тип переключателя между IP и DP;

□ тип переключателя между DP и DP.

Рассмотрим компьютер Connection Machine 2. В терминах данных характеристик его можно описать следующим образом:

(1, 1, 1 — 1, п, п, п — п, 1 — п, п х п).

Условное изображение его архитектуры приведено на рис. 3.6.

п хп SW *

п: 1

Память данных

Память команд

Рис. 3.6. Архитектура Connection Machine 2 в классификации Д. Скилликорна

Для сильно связанных мультипроцессоров типа BBN Butterfly ситуация иная. Такие системы состоят из множества процессоров, соединенных с модулями памяти с помощью переключателя. Задержка при доступе любого процессора к любому модулю памяти примерно одинакова. Связь и синхронизация между процессорами осуществляется через общие (разделяемые) переменные. Описание таких машин в рамках данной классификации выглядит так:

(л, п, п — п, п, п, п х п, п — п, нет).

Глава 3. Архитектура параллельных вычислительных систем

113

Саму архитектуру можно изобразить так, как показано на рис. 3.7.

SW Г


L j	<	.••
		.••	-------г^-*
				-
				-

Память данных

Память команд

Рис. 3.7. Архитектура BBN Butterfly в классификации Д. Скилликорна

Используя введенные характеристики и предполагая, что рассмотрение количественных характеристик можно ограничить только тремя возможными вариантами значений: 0, 1 и я (то есть больше единицы), можно получить различные классы архитектур.

Интересно, что среди сформулированных Скилликорном целей, которым должна служить хорошо построенная классификация архитектур, есть и такая: "классификация должна показывать, за счет каких структурных особенностей достигается увеличение производительности различных вычислительных систем". Эта цель очень созвучна целям наших исследований. Когда пользователь приходит на новую вычислительную систему, то, как правило, ему известна лишь ее пиковая производительность. Однако этого явно недостаточно. Если ему действительно нужна высокая производительность, то, хочет он этого или нет, ему придется иметь дело с целым спектром смежных вопросов. Практически все они связаны с особенностями архитектуры компьютера. Вот тут-то и пригодилась бы хорошая классификация.

Попадание компьютера в тот или иной класс сразу давало бы пользователю информацию об особенностях его программирования, методах достижения высокой производительности, причинах низкой производительности. Косвенно такую информацию получить можно, но только в самых общих чертах. В частности, все компьютеры в первом приближении можно поделить на компьютеры с общей и распределенной памятью. Для компьютеров с общей памятью пользователю не нужно заботиться о распределении данных, а для программирования можно использовать простую технологию ОрепМР. На компьютерах с распределенной памятью ему, скорее всего, придется работать в терминах MPI и самому заботиться о распределении и пересылках данных. В общих чертах все верно, но, честно говоря, только в самых об-

114

Часть I. Параллельные вычислительные системы

щих. В таком описании опущено слишком много важных деталей, без которых составление эффективных параллельных программ просто невозможно. Раз эти детали существенны, то они должны быть отражены в классификации. Компьютеров много, деталей еще больше, отсюда и множество классификаций, и интерес к данной проблеме в целом.

Вопросы и задания

1. Может ли быть полезной на практике классификация компьютеров по их стоимости (весу, размеру, отказоустойчивости)? Если да, то для какого класса пользователей?

2. Может ли быть полезной на практике классификация компьютеров по их пиковой производительности? Если да, то для какого класса пользователей?

3. К какому классу по классификации Флинна можно отнести современные компьютеры с общей памятью, например, HP Superdome?

4. К каким классам по классификации Флинна можно отнести суперскалярные и VLIW-процессоры?

5. Приведите примеры современных компьютеров класса SIMD.

6. Опишите с помощью метрики Фенга первые 10 компьютеров из списка Тор500. Проделайте то же самое с помощью подходов Хендлера, Шнайдера, Скилликорна.

7. Как соотносятся друг с другом классификации Хендлера и Флинна?

8. Попробуйте найти взаимосвязь между изложенными в данном параграфе различными классификациями компьютеров.

9. *Какие параметры архитектуры параллельного компьютера нужно знать пользователю для создания эффективных программ? Предложите классификацию компьютеров, опираясь на выделенные параметры.

10. *В данном параграфе мы говорили о подходах к классификации компьютеров. Предложите классификацию технологий параллельного программирования, разработанных к настоящему времени.

§ 3.2. Векторно-конвейерные компьютеры

С появлением в 1976 году компьютера Сгау-1 началась история векторно-конвейерных вычислительных систем. Архитектура оказалась настолько удачной, что компьютер дал начало целому семейству машин, а его название стало нарицательным для обозначения сверхмощной вычислительной техники. Поскольку компьютеры этого семейства по праву считаются классическими представителями мира суперкомпьютеров, с них мы и начнем изучение различных классов архитектур.

С середины 90-х годов прошлого века векторные компьютеры стали заметно сдавать позиции, уступая свои места массивно-параллельным компьютерам с распределенной памятью. Это и понятно. Соотношение цена/производи-

Глава 3. Архитектура параллельных вычислительных систем

115

тельность для уникальных систем не может конкурировать с продукцией массового производства, а именно этот параметр для многих является решающим. Поговаривали даже о закате векторного направления в целом. Однако в марте 2002 года корпорация NEC объявила о завершении основных работ по созданию параллельной вычислительной системы "the Earth Simulator", основу которой составляют векторные процессоры! Система состоит из 640 вычислительных узлов, в каждом узле по 8 векторных процессоров, что дает 5120 процессоров во всей системе в целом. Поскольку пиковая производительность одного процессора составляет 8 Гфлопс, то для всего компьютера эта величина превышает 40 Тфлопс. Производительность на тесте L1NPACK составила 35,6 Тфлопс, т. е. 89% от пика — прекрасный показатель! Так что говорить о неперспективности данного направления в развитии вычислительной техники явно рано.

Секция межпроцессорного взаимодействия

......................._........._........._........._..............:.....t.....:.............._........

проц₀


"л		Регистр маски вектора		1\| Векторные регистры

		Регистр ДЛИНЫ вектора
				ч----------------•
		Т-регистры
		Т-регистры	<^	S-регистры
				S-регистры
		В-регистры		I J
		В-регистры	*г+	А-регистры
-у				А-регистры

	>	Буферы команд		Блок управления вв./выв.

Векторные ФУ

ПРОЦ,

ФУ обработки

вещественных

чисел

Память

Скалярные ФУ

проц₁₄

> Адресные ФУ

проц₁₅

ПРОЦ_;

Секция ввода/вывода

Внешние устройства Рис. 3.8. Общая схема компьютера Cray С90

В качестве объекта для детального изучения возьмем компьютер Cray С90, в архитектуре которого есть все характерные особенности компьютеров данного класса [18]. Его последователь Cray Т90 имеет такую же структуру, от-

116

Часть I. Параллельные вычислительные системы

личаясь лишь некоторыми количественными характеристиками. Описание компьютера будем вести с той степенью детальности, которая необходима для выделения ключевых особенностей и узких мест архитектуры. Знание именно этих параметров нам понадобится позднее для анализа эффективности функционирования реальных параллельных программ.

Итак, Cray С90 — это векторно-конвейерный компьютер, появившийся на рынке вычислительной техники в самом начале 90-х годов прошлого века. В максимальной конфигурации Cray С90 содержит 16 процессоров, работающих над общей памятью. Время такта компьютера равно 4,1 не, что соответствует тактовой частоте почти 250 МГц. На рис. 3.8 показана общая схема данного компьютера с более детальным представлением структуры одного процессора. Поскольку все процессоры одинаковы, то не имеет значения, какой именно процессор изображать детально.

Все процессоры компьютера Cray С90 не только одинаковы, но и равноправны по отношению ко всем разделяемым ресурсам: памяти, секции ввода/вывода и секции межпроцессорного взаимодействия. Рассмотрим кратко их особенности.

Структура оперативной памяти

Оперативная память Cray С90 разделяется всеми процессорами и секцией ввода/вывода. Каждое слово памяти состоит из 80-ти разрядов: 64 разряда для хранения данных и 16 вспомогательных разрядов для коррекции ошибок. Для увеличения скорости выборки данных вся память разделена на множество банков, которые могут работать одновременно.

Каждый процессор имеет доступ к оперативной памяти через четыре порта с пропускной способностью два слова за один такт каждый. Один из портов всегда связан с секцией ввода/вывода, и, по крайней мере, один из портов всегда выделен под операцию записи. Подобная архитектура хорошо подходит для выполнения векторных операций с не более чем двумя входными векторами.

В максимальной конфигурации реализовано расслоение памяти компьютера на 1024 банка: каждая из 8 секций разделена на 8 подсекций, а каждая подсекция на 16 банков (рис. 3.9). Последовательные адреса идут с чередованием по каждому из данных параметров:

адрес 0 — в 0-й секции, 0-й подсекции, 0-м банке;

адрес 1-е 1-й секции, 0-й подсекции, 0-м банке;

адрес 2-е 2-й секции, 0-й подсекции, 0-м банке;

адрес 8 — в 0-й секции, 1-й подсекции, 0-м банке; адрес 9 — в 1-й секции, 1-й подсекции, 0-м банке;

Глава 3. Архитектура параллельных вычислительных систем

117

адрес 63 — в 7-й секции, 7-й подсекции, 0-м банке; адрес 64 — в 0-й секции, 0-й подсекции, 1-м банке; адрес 65 — в 1-й секции, 0-й подсекции, 1-м банке;


Цо 8 секций	В каждой секции до 8 подсекций	В каждой подсекц до 16 банков	ли
секция 0	секция 3, подсекция 0	секция 3, подсекция 3 -	-банк 0
секция 0	секция 3, подсекция 0	секция 3, подсекция 3 -	-банк 1
секция 1	секция 3, подсекция 1	секция 3, подсекция 3 -	-банк 1
	секция 3, подсекция 1	секция 3, подсекция 3 -	-банк 2
	секция 3, подсекция 2	секция 3, подсекция 3 -	-банк 2
секция 2	секция 3, подсекция 2
секция 2	секция 3, подсекция 3
секция 3
секция 3




	секция 3, подсекция 7
	секция 3, подсекция 7


секция 7




		секция 3, подсекция 3 -	■банк15

Рис. 3.9. Расслоение памяти компьютера Cray С90

При одновременном обращении к одной и той же секции возникает конфликт, который разрешается за 1 такт. В этом случае один из запросов продолжает обрабатываться, а другой просто блокируется на один такт. Если происходит одновременное обращение к одной и той же подсекции одной секции, время на разрешение конфликта уже может достигать 6 тактов. Ясно, что максимальное число конфликтов будет происходить при постоянном обращении к одной и той же подсекции одной и той же секции. Это заведомо произойдет при выполнении процессором векторной операции над данными, расположенными с шагом, кратным 64. Этот же пример является иллюстрацией того факта, что даже при выполнении одной программы на одном процессоре Cray С90 конфликты возможны.

Вместе с тем, подобная структура памяти ориентирована на максимально быструю обработку наиболее типичных случаев. Операции чтения/записи последовательно расположенных данных проходят без возникновения конфликтов. В частности, все одномерные массивы будут обрабатываться именно так. Аналогичная ситуация и при выборке данных с любым нечетным шагом — конфликтов так же не возникнет. В общем случае, чем большей степени двойки кратен шаг выборки данных, тем больше времени требуется на разрешение возникающих конфликтов.

118

Часть I. Параллельные вычислительные системы

Секция ввода/вывода

Этой части компьютера не будем уделять много внимания. Скажем лишь, что он поддерживает три типа каналов для работы с внешними устройствами, которые различаются скоростью передачи данных:

□ Low-speed (LOSP) channels — 6 Мбайт/с;

□ High-speed (HISP) channels — 200 Мбайт/с;

□ Very high-speed (VHISP) channels — 1800 Мбайт/с.

Секция межпроцессорного взаимодействия

Основное назначение данной секции заключается в передаче данных и управляющей информации между процессорами для синхронизации их совместной работы организации взаимодействия друг с другом. Секция межпроцессорного взаимодействия содержит разделяемые регистры и семафоры, объединенные в одинаковые группы — кластеры. Каждый кластер состоит из восьми 32-разрядных разделяемых адресных регистров (SB), восьми 64-разрядных разделяемых скалярных регистров (ST) и 32 однобитовых семафоров. Число кластеров в системе определяется конфигурацией компьютера.

Теперь перейдем к описанию структуры отдельного процессора. Все процессоры имеют одинаковую вычислительную секцию, состоящую из регистров и функциональных устройств (ФУ). Различные регистры и функциональные устройства могут хранить и обрабатывать три класса данных: адреса, скаляры и векторы.

Регистровая структура процессора

Каждый процессор имеет набор основных и набор промежуточных регистров. К основным регистрам относятся адресные регистры А, скалярные регистры S и векторные регистры V. Промежуточные регистры В и Т, играющие роль промежуточного хранилища между памятью и основными регистрами, предусмотрены для регистров А и S соответственно. Все основные регистры связаны с памятью и функциональными устройствами, а регистры А и S имеют дополнительную связь с соответствующими промежуточными регистрами. Промежуточные регистры связаны только с памятью и основными регистрами, непосредственной связи с функциональными устройствами у них нет. Здесь же заметим, что и традиционной кэш-памяти в данном компьютере нет.

В структуре компьютера предусмотрено 8 адресных регистров в основном наборе А, и 64 регистра в промежуточном наборе В. Адресные регистры предназначены для хранения и вычисления адресов, индексации, указания величины сдвигов, числа итераций циклов и т. д. Все регистры данной группы имеют по 32 разряда.

Как и в случае адресных регистров, в основном наборе скалярных регистров S содержится 8 регистров, и еще 64 регистра в промежуточном наборе Т.

Глава 3. Архитектура параллельных вычислительных систем

119

Эти регистры предназначены для хранения аргументов и результатов скалярной арифметики, но могут содержать операнды для векторных команд. Это значит, что скалярные регистры используются для выполнения как скалярных, так и векторных команд. Все скалярные регистры 64-разрядные.

Каждый векторный К-регистр может содержать до 128 64-разрядных слов. Всего в процессоре содержится 8 векторных регистров. Промежуточных регистров для набора V нет. Векторные регистры используются только для выполнения векторных команд.

Для поддержки выполнения векторных команд предусмотрено два дополнительных регистра VL и VM. Регистр длины вектора VL содержит реальную длину векторов, хранящихся в векторных регистрах и участвующих в векторной операции. Данный регистр содержит 8 разрядов. Регистр маски вектора VM состоит из 128 разрядов и позволяет выполнять векторную операцию не над всеми элементами входных векторов. Если разряд маски равен 1, то операция над соответствующими элементами будет выполнена, в противном случае — нет. Данная возможность исключительно полезна при векторизации фрагментов, содержащих условные операторы.

Функциональные устройства

Все функциональные устройства у компьютера Cray С90 являются конвейерными. Число ступеней у них различно, однако каждая ступень каждого устройства всегда срабатывает за один такт. Это, в частности, означает, что при полной загрузке все устройства могут выдавать результат каждый такт (см. §2.1). Кроме этого, все функциональные устройства независимы и могут работать одновременно друг с другом.

Функциональные устройства данного компьютера делятся на четыре группы: адресные, скалярные, векторные и функциональные устройства для выполнения операций над вещественными числами.

Два адресных функциональных устройства предназначены для выполнения сложения/вычитания и умножения 32-разрядных целых чисел. Скалярных устройств в процессоре всегда четыре. Они используются для целочисленного сложения/вычитания, логических поразрядных операций, для выполнения операций сдвига и нахождения числа нулей до первой единицы в слове. Скалярные устройства оперируют с 64-разрядными данными и предназначены для выполнения только скалярных команд.

Число векторных устройств в зависимости от конфигурации компьютера меняется от пяти до семи. В их число могут входить устройства для целочисленного сложения/вычитания, сдвига, логических поразрядных операций, устройство для нахождения числа нулей до первой единицы в слове, для умножения битовых матриц. Некоторые из перечисленных устройств могут быть продублированы. Все векторные функциональные устройства предназначены для выполнения только векторных команд.

120

Часть I. Параллельные вычислительные системы

Три функциональных устройства для вещественной арифметики работают с 64-разрядными числами, представленными в форме с плавающей запятой. Они предназначены для сложения/вычитания, умножения и нахождения обратной величины числа. Отдельного устройства для выполнения явной операции деления вещественных чисел нет. Все устройства данной группы могут выполнять как векторные, так и скалярные команды.

Интересно, что в каждой группе функциональных устройств предусмотрено устройство для выполнения операций сложения. Однако в каждом случае формат операций разный. Адресное функциональное устройство выполняет скалярное сложение 32-разрядых целых чисел. Скалярное устройство предназначено для скалярного сложения целых 64-разрядных чисел. Устройство сложения из векторной группы выполняет операции над векторами из 64-разрядных целых чисел. Устройство сложения из последней группы используется как для обычного сложения двух вещественных чисел, так и для сложения векторов. Каждой из этих разновидностей соответствует своя команда в системе команд компьютера Cray С90, по коду которой аппаратура может "понять", на устройстве какой группы необходимо выполнять ту или иную операцию. Подобная ситуация возникает не только для сложения. Можно сказать, что она характерна для архитектуры компьютера в целом и проявляется во многих других операциях.

Выполнение векторных операций в данном компьютере обладает интересной особенностью. Все конвейеры во всех векторных устройствах и устройствах для вещественной арифметики продублированы (рис. 3.10). Элементы входных векторов с четными номерами всегда поступают на конвейер 0, а элементы входных векторов с нечетными номерами — на конвейер 1. В начальный момент времени нулевые элементы векторных регистров V\ и V₂ поступают на первую ступень конвейера 0, и одновременно с этим первые элементы векторных регистров V\ и Vj поступают на первую ступень конвейера 1. На следующем такте результат первой ступени перемещается на вторую, а на первую ступень конвейеров 0 и 1 поступают вторые и третьи элементы векторных регистров V\ и V₂. Аналогично раскладываются результаты в регистре К₃: с конвейера 0 они записываются в элементы с четными номерами, а с конвейера 1 — с нечетными. В результате функциональное устройство при максимальной загрузке на каждом такте выдает уже не один результат, а два.

В скалярных операциях, использующих функциональные устройства для вещественной арифметики, работает только один конвейер 0.

Архитектура Cray С90 позволяет использовать регистр результатов одной векторной операции в качестве входного регистра для последующей векторной операции. Выход одной операции сразу подается на вход другой, причем последняя не обязана ждать завершения первой, а, начиная с некоторого момента, будет работать одновременно с ней. Подобная ситуация называется зацеплением векторных операций. Вообще говоря, глубина зацепления может быть любой, например, чтение векторов, выполнение операции сложения, выполнение операции умножения, запись векторов.

Глава 3. Архитектура параллельных вычислительных систем

121

Векторный регистр V.,

Векторный регистр V₃

Конвейер О

Конвейер 1

Векторный регистр V₂

Рис. 3.10. Выполнение векторных операций в компьютере Cray С90

Основное назначение зацепления состоит опять-таки в увеличении скорости обработки данных. В самом деле, предположим, что нам нужно выполнить операцию вида А/ = Bj + Q х d, где каждый входной вектор содержит по п элементов. Пусть в нашем распоряжении есть функциональные устройства сложения и умножения, содержащие по 1\ и lj ступеней соответственно. Если выполнять исходную операцию традиционным способом, т. е. сначала векторную операцию умножения, а затем сложения, то вся операция будет реализована за 4 + /2 + 2 х п — 2 тактов. Если для той же операции воспользоваться режимом с зацеплением, то по сути получится один конвейер длиной 1\ + /2, а значит и время выполнения всей операции сократится до 4 + I2 + п — 1. При больших значениях п время реализации операции по сравнению с обычным способом уменьшится почти в два раза. Эта ситуация схематично показана на рис. 3.11.


с, — of —»■ C,xd—>• В,- —		-»• С,хс/	с,. —»• d —>		-,
	X			X

			В,. —»■		— Л
	+

Рис. 3.11. Зацепление векторных операций

122

Часть I. Параллельные вычислительные системы

Секция управления процессора

Команды выбираются из оперативной памяти блоками и заносятся в буфера команд, откуда затем они выбираются для исполнения. Если необходимой для исполнения команды нет в текущем буфере, она ищется в других буферах. Если требуемой команды в буферах не оказалось, то происходит выборка очередного блока.

Такова основа архитектуры компьютера Cray С90. Нетрудно видеть, что идеи параллельной обработки пронизывают все ее составные части. Среди основных особенностей архитектуры, дающих заметный вклад в ускорение выполнения программ, можно назвать следующие.

□ Конвейеризация выполнения команд. Все основные операции, выполняемые процессором, т. е. обращение в память, обработка команд и выполнение инструкций функциональными устройствами являются конвейерными.

□ Независимость функциональных устройств. Функциональные устройства в Cray С90 являются независимыми, поэтому несколько операций могут выполняться одновременно.

□ Векторная обработка. Векторная обработка увеличивает скорость и эффективность обработки за счет того, что обработка целого набора (вектора) данных выполняется одной командой. Скорость выполнения операций в векторном режиме может быть в 10—15 раз выше скорости скалярной обработки.

□ Зацепление функциональных устройств. Возможность выполнения нескольких векторных операций в режиме "макроконвейера" дает дополнительный выигрыш в скорости их обработки.

□ Многопроцессорная обработка. В максимальной конфигурации компьютер может содержать до 16 независимых процессоров. Эти процессоры могут быть использованы по-разному. В частности, они могут выполнять несколько независимых программ, но могут и все быть назначены на выполнение одной программы.

Пиковая производительность Cray С90

Зная архитектуру компьютера, легко посчитать его пиковую производительность. Поскольку нас, прежде всего, интересует скорость выполнения операций над вещественными числами, то нужно максимально загрузить функциональные устройства для вещественной арифметики. Операция нахождения обратной величины сама по себе используется редко, а в операции деления ей дополнительно требуется операция умножения. Поэтому для определения пиковой производительности компьютера будем задействовать только устройства умножения и сложения. Для получения максимальной производительности их нужно использовать в режиме с зацеплением. Именно так

Глава 3. Архитектура параллельных вычислительных систем

123

мы уже поступали, когда речь шла о реализации операции вида A_t = B_t + Q х d. Если дополнительно учесть, что каждое такое устройство для выполнения векторной операции использует два внутренних конвейера, то система из двух устройств будет выдавать результат четырех операций за такт. Время такта компьютера равно 4,1 не, поэтому пиковая производительность одного процессора Cray С90 составит почти 1 Гфлопс или 10⁹ операций в секунду. Если одновременно работают все 16 процессоров компьютера, то пиковая производительность увеличивается до 16 Гфлопс.

Мы разобрали основные особенности архитектуры данного компьютера, из чего стало понятно, почему он считает так быстро. Однако для понимания того, как для него нужно писать эффективные программы, нужно изучить и его другую сторону. Нужно выделить те факторы, которые снижают его производительность на реальных программах. Не сделав этого шага, нам будет трудно понять, что в программе следует изменить, чтобы производительность увеличить. Анализу эффективности выполнения программ на данном компьютере будет посвящена оставшаяся часть параграфа.

Первое, что нам нужно сделать, — это определиться с терминологией. Компьютер обладает векторно-конвейерной архитектурой. Основной выигрыш во времени можно получить за счет использования векторного режима обработки. Некоторый фрагмент программы может быть обработан в векторном режиме, если для его выполнения могут быть использованы векторные команды из системы команд компьютера. Если весь фрагмент программы удалось заменить векторными командами, то говорят о его полной векторизации. В противном случае мы имеем дело с частичной векторизацией или невозможностью векторизации фрагмента вовсе. Процесс поиска подходящих фрагментов в программе и их замена векторными командами называется векторизацией программы. Пример векторизуемого фрагмента может выглядеть так:

DO i = 1, n

C(i) = A(i) + B(i) END DO

Для данного фрагмента компилятор сгенерирует последовательность векторных команд: загрузка векторов а и в из памяти в векторные регистры, векторная операция сложения, запись содержимого векторного регистра в память.

Однако далеко не любой фрагмент программы можно векторизовать. Для этого необходимо выполнение двух условий. Первое — это наличие векторов-аргументов. Второе условие немного сложнее и заключается в том, что над всеми элементами векторов должны выполняться одинаковые, независимые операции, для которых существуют аналогичные векторные команды в системе команд компьютера. Поясним введенные понятия немного подробнее.

124

Часть /. Параллельные вычислительные системы

Под вектором будем понимать упорядоченный набор однотипных данных, все элементы которого размещены в памяти компьютера с одинаковым смещением друг относительно друга. Простейшим примером векторов в программах служат одномерные массивы. Другим примером могут служить строки и столбцы матриц. Для языка Fortran расстояние между соседними элементами одного столбца матрицы равно единице, а между соседними элементами одной строки — размерности матрицы. Для языка С строки и столбцы меняются местами. Диагональ квадратной матрицы также является примером вектора, поскольку расстояние между всеми ее элементами одинаково и равно размерности матрицы плюс единица. Наконец, весь многомерный массив целиком также можно считать одним вектором с длиной, равной произведению всех размерностей массива. Этот список можно продолжать и далее, и в любой программе, использующей регулярные структуры данных, можно найти массу различных примеров векторов.

В то же время вся поддиагональная часть двумерной матрицы вектором не является. Связано это с тем, что расстояние между элементами этого набора данных в памяти компьютера не является каким-либо одним постоянным числом.

Кроме векторов, в векторизуемом фрагменте могут использоваться и простые переменные. Поскольку в системе команд компьютера Cray С90 есть векторные команды, в которых некоторые аргументы могут быть скалярами, то векторизация следующего фрагмента никаких проблем не вызовет:

DO i = 1, n

B(i) = A(i) + s END DO

Основными кандидатами для векторизации являются самые внутренние циклы всех циклических конструкций программы. Именно они задают перебор "одномерных" наборов данных, которые, в частности, могут быть векторами. Но работа с векторами еще не является достаточным условием для векторизации. Рассмотрим следующий пример:

DO i = 1, n

A(i) = A(i-l) + B(i) END DO

Вычисление i-го элемента массива а не может начаться, пока не будет вычислен предыдущий элемент. Но в таком случае теряет всякий смысл использование конвейерной обработки! Мы не можем загрузить данные на первую ступень конвейера, пока результат не выйдет из устройства. В данном примере существует зависимость между операциями, которая и будет препятствовать векторизации. Именно поэтому мы говорили о возможности векторизации лишь при условии существования одинаковых и независимых операций.

Глава 3. Архитектура параллельных вычислительных систем

125

Рассмотрим еще один пример:

DO i = 1, n

A(i) = Funct( A(i), B(i)) END DO

В явном виде такой фрагмент также не может быть векторизован. Компилятор не знает, какая операция соответствует вызову пользовательской функции Funct, и, следовательно, он не знает, на какие векторные команды можно заменить данный фрагмент. В некоторых случаях компилятор может получить дополнительную информацию, если проведет межпроцедурный анализ, выяснит содержание функции Funct и выполнит in-line подстановку.

На этом краткое введение в векторизацию программ мы закончим и перейдем к анализу узких мест в архитектуре компьютера Cray С90. Основное, что нам предстоит выяснить, какие особенности архитектуры необходимо учитывать при написании действительно эффективных программ для данного компьютера.

Анализ факторов, снижающих реальную производительность компьютеров, начнем с обсуждения уже известного нам закона Амдала. Одна из его интерпретаций сводится к тому, что время работы программы определяется ее самой медленной частью. В самом деле, предположим, что одна половина некоторой программы — это сугубо последовательные вычисления, которые невозможно векторизовать. Тогда вне зависимости от свойств другой половины, которая может быть идеально векторизована и, скажем, выполнена мгновенно, ускорения работы всей программы более чем в два раза мы не получим.

Влияние данного фактора надо оценивать с двух сторон. Во-первых, по природе самого алгоритма все множество операций программы Q разбивается на последовательные операции Qi и операции Q₂, исполняемые в векторном режиме. Если доля последовательных операций велика, то программист сразу должен быть готов к тому, что большого ускорения он никакими средствами не получит и, быть может, следует уже на этом этапе подумать об изменении алгоритма.

Во-вторых, не следует сбрасывать со счетов и качество компилятора. Он вполне может не распознать векторизуемость отдельных конструкций, сгенерировать для них скалярный код и, тем самым, часть "потенциально хороших" операций из Q₂ перенести в Qj.

Следующие два фактора, снижающие производительность компьютера на реальных программах, определяют принципиальную невозможность достижения пиковой производительности на векторно-конвейерных устройств. Это время разгона векторной команды и секционирование длинных векторов. Для инициализации векторной команды требуется несколько тактов, после чего начинается заполнение конвейера и лишь через некоторое время появ-

126

Часть I. Параллельные вычислительные системы

ляются первые результаты. Только после этого устройство каждый такт будет выдавать результат, и его производительность асимптотически будет приближаться к пиковой. Но лишь приближаться. Точного значения пиковой производительности никогда получено не будет.

Теперь вспомним устройство векторных регистров. Каждый регистр содержит 128 элементов. Для запуска векторной команды длинный входной вектор необходимо разбить на секции по 128 элементов. Секцию вектора, целиком расположенную в регистре, уже можно обрабатывать с помощью векторных команд. Такая технология работы с длинными векторами предполагает, что векторизуемый цикл исходной программы должен быть преобразован в двумерное гнездо циклов. Внешний цикл последовательно перебирает секции, а внутренний работает только с элементами текущей секции. Именно внутренний цикл реально и подлежит векторизации. На практике не стоит пугаться этой процедуры, поскольку она полностью выполняется компилятором.

На переход от обработки одной секции к другой требуется пусть и небольшое, но время, а это опять лишняя задержка и опять падение производительности. Если время разгона влияет только при старте, то секционирование немного снижает производительность во всех точках, кратных 128. Это снижение небольшое и с увеличением длины векторов его относительное влияние становится все меньше и меньше, асимптотически приближаясь к малой константе.

Для того чтобы немного почувствовать влияние этих факторов, рассмотрим следующий фрагмент программы.

DO i = 1, n

A(i) = B(i) *s + C(i) END DO

В табл. 3.1 показана производительность компьютера Cray С90 на данном фрагменте в зависимости от длины входных векторов, т. е. от значения п. Необходимо отметить, что приведенные здесь и далее значения производительности на практике могут немного меняться в зависимости от текущей загрузки компьютера и некоторых других факторов. Эти значения нужно рассматривать скорее как ориентир, а не как абсолютный показатель.

Таблица 3.1. Производительность Cray С90 на операции Ai = B_tx s + Q


	Длина вектора Производительность (Мфлопс)	Длина Производительность вектора (Мфлопс)
	1 7,0 2 14,0	150 413,2 256 548,0

Глава 3. Архитектура параллельных вычислительных систем

127

Таблица 3.1 (окончание)


Длина вектора	Производительность (Мфлопс)	Длина вектора	Производительность (Мфлопс)
4	27,6	257	491,0
16	100,5	512	659,2
32	181,9	1024	720,4
128	433,7	2048	768,0
129	364,3	8192	802,0

И время начального разгона, и секционирование относятся к накладным расходам на организацию векторных операций на конвейерных функциональных устройствах. Показанная зависимость явно стимулирует к работе с длинными векторами данных, т. к. с ростом длины вектора доля накладных расходов в общем времени выполнения операции быстро падает. Одновременно заметим, что очень короткие циклы выгоднее выполнять не в векторном режиме, а в скалярном, поскольку не будет необходимости тратить дополнительное время на инициализацию векторных команд.

Конфликты при обращении в память у компьютеров серии Cray С90 полностью определяются аппаратными особенностями организации доступа к оперативной памяти. Наибольшее время на разрешение конфликтов требуется при выборке данных с шагом 64, когда постоянно совпадают номера и секций, и подсекций. С другой стороны, выборка с любым нечетным шагом проходит без конфликтов вообще, и в этом смысле она эквивалентна выборке с шагом единица. Для оценки влияния конфликтов при доступе в память рассмотрим следующий пример:

DO i = 1, n х k, k

A(i) = B(i) *s + C(i) END DO

В данном примере происходит выполнение векторной операции A_t = Bj х х s + Q над векторами длины п в режиме с зацеплением. Значение переменной к определяет шаг, с которым данные выбираются из памяти. Рассматривая выше аналогичный пример для шага, равного единице, мы видели, насколько важным параметром для производительности является длина векторов. Чтобы этот параметр сейчас не мешал, мы сделаем число операций для любого значения к одинаковым, положив верхнюю границу цикла равной п х к. Производительность компьютера Cray С90 на данной операции для «=1000 показана в табл. 3.2.

128

Часть I. Параллельные вычислительные системы

Таблица 3.2. Влияние конфликтов в памяти на производительность Cray С90

Шаг по памяти Производительность (Мфлопс)


	1	705,2
	2	444,6
	4	274,6
	8	142,8
	16	84,5
	32	44,3
	64	22,6
	128	22,6

Как мы видим, производительность падает катастрофически, достигая минимума с шага 64. А причина этому одна — структура фрагмента плохо соответствует особенностям архитектуры компьютера.

Еще одной неприятной стороной конфликтов при обращении к памяти является то, что проявляться они могут совершенно по-разному. В предыдущем примере конфликты возникали при использовании цикла с четным шагом. Но такая ситуация слишком очевидна, и опытного программиста она насторожит сразу. Вместе с тем, казалось бы, не должно быть никаких причин для беспокойства при работе фрагмента следующего вида:

DO i = 1, n DO j = 1, n DO k = 1, n

X(i,j,k) = X(i,j,k)+P(k,i)*Y(k,j) END DO END DO END DO

Зависимости между итерациями цикла нет, используются одновременно операции сложения и умножения, внутренний цикл с параметром к легко векторизуется. Однако все не так безобидно, как кажется. Решающее значение имеет то, каким образом описан массив х. Предположим, что описание имеет вид:

DIMENSION Х(40,40,Ю00)

По определению Фортрана массивы хранятся в памяти "по столбцам". Следовательно, при изменении последнего индексного выражения на единицу реальное смещение по памяти будет равно произведению размеров массива по предыдущим размерностям. Для нашего примера расстояние в памяти

Глава 3. Архитектура параллельных вычислительных систем

129

между соседними элементами x(i,j,k) и x(i,j,k+i) равно 40 х 40 = 1600. Но, используя другое разложение на множители, число 1600 можно представить произведением 25 х 64! Это число кратно наихудшему шагу для выборки из памяти, поэтому число конфликтов будет максимальным. Можно ли избавиться от конфликтов? Как ни странно, это сделать чрезвычайно легко. Достаточно лишь изменить описание массива, добавив единицу к первым двум размерностям:

DIMENSION Х(41,41Д000)

Расстояние между соседними элементами x(i,j,k) и х(i, j,k+i) становится нечетным числом и конфликты исчезают. Немного увеличив объем массива, мы сделали выборку из памяти максимально эффективной. Точно такой же пример можно привести и для языка С, достаточно строки и столбцы поменять местами.

Еще один пример возможного появления конфликтов — это использование косвенной адресации. Рассмотрим следующий фрагмент:

DO i = 1, n

XYZ ( IX(i) ) = XYZ(IX(i))+P(i)*Y(i) END DO

В зависимости от того, к каким элементам массива xyz реально происходит обращение, число конфликтов будет меняться. Их может не быть вовсе, если, например, ix(i) всегда равно i. Если же предположить, что ix(i) равно некоторому одному и тому же числу для всех i, то число конфликтов будет максимальным (на каждой итерации будет происходить обращение к одному и тому же элементу массива, т. е. будет обращение к одной и той же подсекции одной и той же секции).

Следующие три фактора, снижающие производительность Cray С90, определяются тем, что перед началом выполнения любой операции данные должны быть занесены в регистры. Для этого в архитектуре компьютера предусмотрены три независимых канала передачи данных, два из которых могут работать на чтение из памяти, а третий на запись. Такая структура хорошо подходит для операций, требующих не более двух входных векторов. Примером операции служит, в частности, операция А_{= Д х s +Q, на которой компьютер может работать в режиме с зацеплением и, следовательно, показывать хорошие значения производительности.

Однако операции с тремя векторными аргументами, например, A_t = B_t х Q + D_hуже не могут быть реализованы столь же эффективно. Часть времени будет неизбежно потрачено впустую на ожидание подкачки третьего аргумента для запуска операции с зацеплением. Это является прямым следствием ограниченной пропускной способности тракта процессор—память (memory bottleneck). С одной стороны, максимальная производительность достигается на операции с зацеплением, требующей три аргумента, а, с другой сторо-

130

Часть I. Параллельные вычислительные системы

ны, на чтение одновременно могут работать лишь два канала. В табл. 3.3 приведена производительность компьютера на указанной выше векторной операции, требующей три входных вектора В, С, D, в зависимости от их длины.

Таблица 3.3. Производительность Cray С90 на операции Д = В, х Q + Ц

Длина вектора Производительность (Мфлопс)

10 57,0

100 278,3

1000 435,3

12801 445,0

Теперь предположим, что пропускная способность каналов не является узким местом. В этом случае на предварительное занесение данных в регистры все равно требуется некоторое дополнительное время. Архитектура компьютера такова, что нам необходимо использовать векторные регистры перед выполнением операций. Как следствие, требуемые для этого операции чтения/записи будут неизбежно снижать общую производительность. Довольно часто влияние данного фактора можно заметно ослабить, если повторно используемые вектора один раз загрузить в регистры, выполнить все построенные на их основе выражения, а уже затем перейти к оставшейся части программы.

Рассмотрим следующий фрагмент программы:

DO j = 1, 120

DO i = 1, n

D(i) = D(i) + s*P(i,j-U + t*P(i,j)

END DO END DO

Для векторизации внутреннего цикла фрагмента нет никаких препятствий. На каждой из 120 итераций по j для выполнения векторной операции требуется считать три входных вектора d (i), р (i, j -1) и p (i, j), и записать один выходной d (i). Следовательно, за время работы всего фрагмента будет выполнено 120 х 3 = 360 операций чтения векторов и 120 операций записи.

Сделаем несложное эквивалентное преобразование данного фрагмента. Явно выпишем каждые две последовательные итерации цикла по j, приведя его к следующему виду:

DO j = 1, 120, 2 DO i = 1, n

Глава 3. Архитектура параллельных вычислительных систем

131

D(i) = D(i)+s*P(i,j-l)+t*P(i,j)+s*P(i,j)+t*P(i,j+1) END DO END DO

Теперь на каждой из 60 итераций внешнего цикла потребуется четыре входных вектора D(i), P(i,j-l), P(i,j), P(i,j+l) и, опять же, один выходной D(i). Суммарно, для нового варианта фрагмента будет выполнено 60 х 4 = = 240 операций чтения и 60 операций записи. Выигрыш очевиден. Преобразование подобного рода носит название раскрутки цикла. Оно имеет максимальный эффект в том случае, когда на соседних итерациях цикла используются одни и те же данные. В табл. 3.4 показана производительность компьютера на данном фрагменте в зависимости от глубины раскрутки. Значение п равно 128.

Таблица 3.4. Зависимость производительности Cray С90 от глубины раскрутки

Глубина раскрутки Производительность (Мфлопс)

1 612,9

2 731,6

3 780,7

4 807,7

Теоретически, с увеличением глубины раскрутки растет и производительность, приближаясь в пределе к некоторому значению. Однако на практике максимальный эффект достигается где-то на первых шагах, а затем производительность либо остается примерно одинаковой, либо падает. Основная причина данного несоответствия теории и практики заключается в том, что компьютеры Cray С90 имеют сильно ограниченный набор векторных регистров: 8 регистров по 128 слов в каждом. Как правило, увеличение глубины раскрутки ведет к увеличению числа входных векторов. Так было и в нашем случае. Фрагмент в исходной форме требовал по три входных вектора на каждой итерации внешнего цикла. Раскрутка глубиной 2 привела к необходимости загрузки четырех векторов, для раскрутки на глубину 3 потребуется пять векторов и т. д. Каждый дополнительный вектор предполагает наличие дополнительного регистра, что с увеличением глубины раскрутки станет узким местом.

Теперь вспомним, что значение пиковой производительности вычислялось при условии одновременной работы всех функциональных устройств. Предположим, что некоторый алгоритм выполняет одинаковое число операций сложения и умножения. Пусть сначала должны выполниться все операции сложения, и лишь после этого операции умножения. В такой ситуации в каждый момент времени в компьютере будут задействованы только устройства

132

Часть /. Параллельные вычислительные системы

одного типа. Более половины от пиковой производительности получить нельзя. Присутствующая несбалансированность в использовании функциональных устройств является серьезным фактором, сильно снижающим реальную производительность компьютера. Соответствующие данные можно найти в табл. 3.5.

Таблица 3.5. Производительность Cray С90 на различных операциях


Длина вектора	Производительность		на	операции (Мф	лопс)
	а,= bj+q	a,= b,l с,		а,= si bj+ t	а,= s/ Ь,х t
10	35,5	24,8		49,7	46,1
100	202,9	88,4		197,4	166,5
1000	343,8	117,2		283,8	215,9

В наборе функциональных устройств нет устройства деления. Для выполнения данной операции используется устройство вычисления обратной величины и устройство умножения. Отсюда сразу следует, что производительность фрагмента в терминах операций деления будет очень низкой. Это полностью подтверждает столбец табл. 3.5, соответствующий операции щ= bj/q. Кроме этого, использование деления вместе с операцией сложения немного выгоднее, чем с умножением. Это явно видно из последних двух столбцов таблицы.

Часто структура программы бывает такова, что в ней постоянно происходит передача управления из одной части в другую. Возможными причинами этому могут служить частое обращение к различным небольшим подпрограммам и функциям, либо просто запутанная структура управления из-за большого числа переходов. Следствием такой структуры станет частая перезагрузка буферов команд, и, следовательно, возникнут дополнительные накладные расходы. Наилучший результат достигается в том случае, если весь фрагмент кода помещается в одном буфере команд. Незначительные потери производительности будут у фрагментов, расположенных в нескольких буферах. Если же перезагрузка частая, т. е. фрагмент или программа обладают малой локальностью вычислений, то производительность может меняться в очень широких пределах.

На этом мы закончим обсуждение негативных факторов и перейдем к выводам. Что следует из проведенного анализа архитектуры суперкомпьютера Cray С90? Выводов можно сделать много, но главный из них помогает понять причину крайне низкой производительности неоптимизированных программ. Это, в частности, в полной мере относится к программам, перенесенным с традиционных последовательных компьютеров. Дело в том, что на производительность реальных программ одновременно оказывают влияние в той или иной степени ВСЕ перечисленные выше факторы. В самом де-

Глава 3. Архитектура параллельных вычислительных систем

133

ле, программы не бывают векторизуемыми на все 100%. Всегда есть некоторая последовательная инициализация, ввод/вывод или что-то подобное. Вместе с этим, обязательно будет присутствовать какое-то число конфликтов в памяти, быть может легкая несбалансированность в использовании функциональных устройств. Для части операций может не хватать каналов чтения/записи, векторных регистров и т. д. по всем изложенным выше факторам. Не стоит сбрасывать со счетов и влияние компилятора, который вполне мог что-то не векторизовать или что-то сделать неоптимально.

Предположим, что влияние каждого отдельного фактора в программе позволяет достичь 85% пиковой производительности. Примем самую простую модель, в которой суммарное влияние оценивается произведением коэффициентов для каждого фактора. Поскольку мы уже выделили 10 факторов, что дает суммарный эффект 0,85¹⁰ или менее, чем до 0,2 от пика! Если мы хотим добиться хорошей производительности данного компьютера, то необходимо принимать во внимание все указанные выше факторы одновременно, минимизируя их суммарное проявление в программе. Безусловно, это сделать можно, но это трудная работа. Работа, которую нельзя недооценивать, и большую часть которой лучше выполнить на этапе планирования алгоритма и составления программы.

Но не стоит думать, что разобранный нами компьютер столь уж плох. Ни в коей мере. Напротив, линия векторно-конвейерных компьютеров Cray занимает первые места по простоте достижения относительно высокой реальной производительности в сравнении с другими архитектурами. Все классы компьютеров обладают целым набором подобных факторов, и мы это увидим в последующих параграфах. Главное — это знать не только то, почему компьютер считает быстро, но и то, что в его архитектуре мешает достигать высокой производительности.

Вопросы и задания

1. Предположим, что слово компьютера состоит из 64 разрядов. Память может работать с ошибками. Сколько необходимо дополнительных разрядов, чтобы (а) обнаруживать возникшую одиночную ошибку в слове и (б) исправлять одиночную ошибку?

2. Будет ли являться вектором совокупность данных, расположенных в столбцах матрицы, начиная со второго по пятый включительно? Рассмотреть языки Fortran и С.

3. Если бы каждый процессор компьютера Cray С90 имел по одному универсальному каналу связи с памятью, могли бы возникнуть конфликты в памяти?

4. Пропускная способность каждого канала процессора равна двум словам за такт. Почему пропускная способность в одно слово за такт была бы явно недостаточной при существующей архитектуре процессора Cray С90?

134

Часть I. Параллельные вычислительные системы

5. В состав секции межпроцессорного взаимодействия компьютера Cray С90 входят семафоры. Что такое семафор? Для чего он служит? Какого рода операции применяют к семафорам?

6. Почему для векторных регистров не предусмотрено промежуточного набора, аналогичного промежуточным регистрам Т и В1

7. Зачем нужно зацепление векторных операций?

8. Для векторизации лучше всего подходят самые внутренние циклы. Какие конструкции программы лучше всего подходят для распараллеливания программы между несколькими процессорами компьютера Cray С90?

9. Что мешает векторизации цикла, содержащего вызов подпрограммы?

10. Что мешает векторизации цикла типа WHILE?

11. В программе необходима работа с векторами длиной 129. Производительность компьютера Cray С90 на векторах длиной 256 намного больше, чем на векторах длиной 129. Значит ли это, что для уменьшения времени выполнения программы нужно просто перейти от векторов длины 129 к векторам длины 256?

12. Может ли некоторый одномерный векторизуемый цикл в скалярном режиме исполняться быстрее, чем в векторном режиме?

13. Приведите другие возможные формы проявления в различных конструкциях языков программирования конфликтов при обращении к памяти.

§ 3.3. Параллельные компьютеры с общей памятью

К компьютерам с общей памятью у пользователей всегда было неоднозначное отношение. С одной стороны, программирование компьютеров этого класса значительно проще, чем, скажем, программирование вычислительных кластеров с распределенной памятью. В самом деле, не нужно думать о распределении массивов, внутренний параллелизм программ описывается просто, процесс отладки идет быстрее. С другой стороны, классические представители этого класса имеют и два недостатка: небольшое число процессоров и очень высокую стоимость.

Чтобы увеличить число процессоров, но сохранить возможность работы в рамках единого адресного пространства, предлагались различные решения (см. § 2.2). Одним из распространенных вариантов является решение на основе архитектуры ccNUMA (cache coherent Non Uniform Memory Access). В такой архитектуре память всего компьютера физически распределена, что значительно увеличивает потенциал его масштабируемости. Вместе с тем, память логически остается общей. Это дает возможность использования всех технологий и методов программирования, созданных для SMP-компью-теров. Дополнительно в такой архитектуре содержимое кэш-памяти отдельных процессоров на уровне аппаратуры согласуется с содержимым опера-

Глава 3. Архитектура параллельных вычислительных систем

135

тивной памяти (решается проблема когерентности кэшей, cache coherence problem). Значительно увеличивая число процессоров по сравнению с SMP-компьютерами, архитектура ccNUMA привносит дополнительную особенность, несвойственную компьютерам с общей памятью. Время обращения к памяти зависит от того, является ли это обращением к локальной или удаленной памяти. Процесс написания программ остается прежним, и физическая распределенность памяти программисту не видна. Однако ясно, что эффективность программ напрямую зависит от степени "неоднородности" доступа к памяти.

Проведем исследование архитектуры компьютеров данного класса на примере вычислительной системы Hewlett-Packard Superdome. Компьютер появился в 2000 году, а в ноябрьской редакции списка Тор500 2001 года им уже были заняты 147 позиций.

Компьютер HP Superdome в стандартной комплектации может объединять от 2 до 64 процессоров с возможностью последующего расширения системы. Все процессоры имеют доступ к общей памяти, организованной в соответствии с архитектурой ccNUMA. Это означает, что, во-первых, все процессы могут работать в едином адресном пространстве, адресуя любой байт памяти посредством обычных операций чтения/записи. Во-вторых, доступ к локальной памяти в системе будет идти немного быстрее, чем доступ к удаленной памяти. В-третьих, проблемы возможного несоответствия данных, вызванные кэш-памятью процессоров, решены на уровне аппаратуры.

В максимальной конфигурации Superdome может содержать до 256 Гбайт оперативной памяти. Ближайшие планы компании — реализовать возможность наращивания памяти компьютера до 1 Тбайта.

Архитектура компьютера спроектирована таким образом, что в ней могут использоваться несколько типов микропроцессоров. Это, конечно же, традиционные для вычислительных систем Hewlett-Packard процессоры семейства РА: РА-8600 и РА-8700. Вместе с тем, система полностью подготовлена и к использованию процессоров следующего поколения с архитектурой 1А-64, разработанной совместно компаниями HP и Intel. При замене существующих процессоров на процессоры 1А-64 гарантируется двоичная совместимость приложений на системном уровне. В дальнейшем, если другого не оговорено, будем рассматривать конфигурации HP Superdome на базе процессора РА-8700.

Основу архитектуры компьютера HP Superdome составляют вычислительные ячейки (cells), связанные иерархической системой переключателей. Каждая ячейка является симметричным мультипроцессором, реализованным на одной плате, в котором есть все необходимые компоненты (рис. 3.12):

□ процессоры (до 4-х);

□ оперативная память (до 16 Гбайт);

136

Часть I. Параллельные вычислительные системы

П контроллер ячейки;

□ преобразователи питания;

□ связь с подсистемой ввода/вывода (опционально).

Интересно, что ячейки Superdome во многом похожи на аналогичные архитектурные элементы других современных ccNUMA компьютеров. В Superdome таким элементом является ячейка, в семействе SGI Origin 3x00 это узел (node), а в компьютерах серии Compaq AlphaServer GS320 — QBB (Quad Building Block). Во всех системах в каждом элементе содержится по четыре процессора.



		память	память
		1	t
РА-8700	<-►	контроллер ячейки		*

РА-8700	<-►

РА-8700	<-►

РА-8700	<-►
		А

контроллер ввода/вывода

к коммутатору Рис. 3.12. Структура ячейки компьютера HP Superdome

Центральное место в архитектуре ячейки Superdome занимает контроллер ячейки. Несмотря на столь обыденное название, контроллер — это сложнейшее устройство, состоящее из 24 миллионов транзисторов. Для каждого процессора ячейки есть собственный порт в контроллере. Обмен данными между каждым процессором и контроллером идет со скоростью 2 Гбайт/с.

Память ячейки имеет емкость от 2 до 16 Гбайт. Конструктивно она разделена на два банка, каждый из которых имеет свой порт в контроллере ячейки. Скорость обмена данными между контроллером и каждым банком составляет 2 Гбайт/с, что дает суммарную пропускную способность тракта контроллер—память 4 Гбайт/с.

Соединение контроллера ячейки с контроллером устройств ввода/вывода (12 слотов РС1) устанавливается опционально.

Один порт контроллера ячейки всегда связан с внешним коммутатором. Он предназначен для обмена процессоров ячейки с другим процессорами системы. Скорость работы этого порта равна 8 Гбайт/с.

Выполняя интерфейсные функции между процессорами, памятью, другими ячейками и внешним миром, контроллер ячейки отвечает и за когерентность кэш-памяти процессоров.

Глава 3. Архитектура параллельных вычислительных систем

137

Ячейка — это базовый четырехпроцессорный блок компьютера. В 64-процессорной конфигурации Superdome состоит из двух стоек, в каждой стойке по 32 процессора (рис. 3.13).

Стойка 1 ячейка—


		Стойка 2

О.	о. о го 2 2 о	-с -с -с ч	ячейка
О.

ГО			ячейка
ГО
			ячейка
О
			ячейка

О.	о. о го 2 5 о	-с -с -с ч	ячейка
О.
ГО			ячейка
ГО
			ячейка
о
о
			ячейка

ячейка ячейка

ячейка

Рис. 3.13. Общая структура компьютера HP Superdome

Каждая стойка содержит по два восьмипортовых неблокирующих коммутатора. Все порты коммутаторов работают со скоростью 8 Гбайт/с. К каждому коммутатору подключаются четыре ячейки. Три порта коммутатора задействованы для связи с другими коммутаторами системы (один в этой же стойке, и два коммутатора — в другой). Оставшийся порт зарезервирован для связи с другими системами HP Superdome, что дает потенциальную возможность для формирования многоузловой конфигурации компьютера с общим числом процессоров больше 64.

Одним из центральных вопросов любой вычислительной системы с архитектурой ccNUMA является разница во времени при обращении процессора к локальным и удаленным ячейкам памяти. В идеале хотелось бы, чтобы этой разницы, как в SMP-компьютере, не было вовсе. Однако в таком случае система заведомо будет плохо масштабируемой. В компьютере HP Superdome возможны три вида задержек при обращении процессора к памяти, являющихся своего рода платой за высокую масштабируемость системы в целом:

□ процессор и память располагаются в одной ячейке; в этом случае задержка минимальна;

□ процессор и память располагаются в разных ячейках, но обе эти ячейки подсоединены к одному и тому же коммутатору;

□ процессор и память располагаются в разных ячейках, причем обе эти ячейки подсоединены к разным коммутаторам; в этом случае запрос должен пройти через два коммутатора и задержки будут максимальными.

138

Часть I. Параллельные вычислительные системы

Ясно, что величина задержки зависит не только от взаимного расположения процессора и памяти, но и от числа процессоров. Не менее важным параметром является и характер вычислительной нагрузки. Например, задержка может меняться в зависимости от числа одновременно работающих приложений. В табл. 3.6 показана зависимость задержки от числа процессоров в двух характерных ситуациях. В первом случае работают однонитевые приложения, а во втором — многонитевая программа. В отличие от первого случая, во втором случае появляются дополнительные затраты, необходимые для поддержания когерентности кэш-памяти процессоров. В обоих случаях приводятся усредненные показатели задержки. Предполагается, что запросы к памяти распределены равномерно.

Таблица 3.6. Задержка в зависимости от числа процессоров и загрузки

Число процессоров Однонитевые программы, Многонитевая программа,

не не

4 174 235

8 208 266

16 228 296

32 261 336

64 275 360

Для рассмотренных видов нагрузки, при сделанных выше предположениях о распределении запросов к памяти, показанные результаты являются очень неплохими. В самом деле, коэффициент увеличения задержки при переходе от минимальной 4-процессорной конфигурации к 64-процессорной составил лишь 1,6 раза. Это значит, что во многих случаях пользователь вправе надеяться на эффективную реализацию своих программ, созданных им для традиционных SMP-компьютеров.

Компьютер HP Superdome имеет массу интересных особенностей. В частности, программно-аппаратная среда компьютера позволяет его настроить различным образом. Superdome может быть классическим единым компьютером с общей памятью. Однако его можно сконфигурировать и таким образом, что он будет являться совокупностью независимых разделов (nPartitions), работающих под различными операционными системами, в частности, под HP UX, Linux и Windows 2000. Организация эффективной работы с большим числом внешних устройств, возможности "горячей" замены всех основных компонентов аппаратуры, резервирование, мониторинг базовых параметров — все это останется за рамками нашего обсуждения.

Изучив особенности архитектуры HP Superdome в целом, кратко рассмотрим структуру используемого в нем процессора РА-8700. Если мы хотим

Глава 3. Архитектура параллельных вычислительных систем

139

эффективно использовать всю систему, необходимо, хотя бы в общих чертах, иметь представление об особенностях ее базовой компоненты.

Процессор имеет тактовую частоту 750 МГц. Работая с максимальной загрузкой, он может выполнять четыре арифметические операции за такт. Эти два параметра определяют значение его пиковой производительности — 3 Гфлопс. Отсюда получается и значение пиковой производительности базовой 64-процессорной системы HP Superdome — 192 Гфлопс.

Процессор РА-8700 обладает суперскалярной архитектурой. На каждом такте он выполняет столько операций, сколько (1) позволяет информационная структура кода и (2) сколько в данный момент есть доступных функциональных устройств. Всего процессор РА-8700 содержит 10 функциональных устройств: четыре устройства для целочисленной арифметики и логики, четыре устройства для работы с вещественной арифметикой и два устройства для операций чтения/записи. На каждом такте устройство выборки команд может считывать 4 команды из кэш-памяти команд.

Начиная с РА-8500, процессоры данного семейства имеют большую кэшпамять первого уровня L1, реализованную прямо на кристалле. В РА-8700 объем кэш-памяти равен 2,25 Мбайт, из которых 1,5 Мбайт отводится под кэш данных, а оставшиеся 0,75 Мбайт — это кэш команд. Вся кэш-память процессора является множественно-ассоциативной с 4 каналами (4-way set-associative cache).

В целом область использования компьютеров HP Superdome исключительно широка. Достаточно сказать, что две крупные инсталляции данного компьютера в России соответствуют различным задачам и областям. Один 64-процессорный компьютер HP Superdome установлен в Межведомственном суперкомпьютерном центре для решения широкого спектра научно-технических задач, а 72-процессорная конфигурация работает в Сбербанке России.

В заключение, как и в предыдущем параграфе, выделим те особенности вычислительных систем с общей памятью, которые снижают их производительность на реальных программах. Не должно складываться впечатление, что каждый параграф данной главы мы хотим закончить на пессимистической ноте. Однако воспринимать реальность нужно с открытыми глазами, четко представляя не только преимущества использования параллельных компьютеров, но и подводные камни, встречающиеся на этом пути.

Закон Амдала носит универсальный характер, поэтому он упоминается вместе со всеми параллельными системами. Не являются исключением и компьютеры с общей памятью. Если в программе 20% всех операций должны выполняться строго последовательно, то ускорения больше 5 получить нельзя вне зависимости от числа использованных процессоров (влияние кэшпамяти сейчас не рассматривается). Это нужно учитывать и перед адаптацией старой последовательной программы к такой архитектуре, и в процессе проектирования нового параллельного кода.

140

Часть I. Параллельные вычислительные системы

Для компьютеров с общей памятью дополнительно следует принять в расчет и такие соображения. Наличие физической общей памяти стимулирует к использованию моделей параллельных программ также с общей памятью. Это вполне естественно и оправданно. Однако в этом случае возникают дополнительные участки последовательного кода, связанные с синхронизацией доступа к общим данным, например, критические секции. Относительно подобных конструкций в описании соответствующей технологии программирования может и не быть никакого предостережения, однако реально эти фрагменты будут последовательными участками кода.

Работа с памятью является очень тонким местом в системах данного класса. Одну из причин снижения производительности — неоднородность доступа к памяти, мы уже обсуждали. Степень неоднородности на уровне 5—10% серьезных проблем не создаст. Однако разница во времени доступа к локальной и удаленной памяти в несколько раз потребует от пользователя очень аккуратного программирования. В этом случае ему придется решать вопросы, аналогичные распределению данных для систем с распределенной памятью. Другую причину — конфликты при обращении к памяти — мы детально не разбирали, но она также характерна для многих SMP-систем.

Наличие кэш-памяти у каждого процессора тоже привносит свои дополнительные особенности. Наиболее существенная из них состоит в необходимости обеспечения согласованности содержимого кэш-памяти. Отсюда появились и первые две буквы в аббревиатуре ccNUMA. Чем реже вовлекается аппаратура в решение этой проблемы, тем меньше накладных расходов сопровождает выполнение программы. По этой же причине во многих системах с общей памятью существует режим выполнения параллельной программы с привязкой процессов к процессорам.

Сбалансированность вычислительной нагрузки также характерна для параллельных систем, как и закон Амдала. В случае систем с общей памятью ситуация упрощается тем, что практически всегда системы являются однородными. Они содержат одинаковые процессоры, поэтому о сложной стратегии распределения работы речь, как правило, не идет.

Любой современный процессор имеет сложную архитектуру, объединяющую и несколько уровней памяти, и множество функциональных устройств. Реальная производительность отдельного процессора может отличаться от его же пиковой в десятки раз. Чем выше степень использования возможностей каждого процессора, тем выше общая производительность вычислительной системы.

И опять, как и в предыдущем параграфе, перечисление особенностей компьютера, влияющих на его производительность, можно продолжать и далее. Здесь они свои, но опять-таки все они в той или иной мере проявляются в каждой программе. Отсюда и проблемы с низкой производительностью, отсюда и потенциальные проблемы у пользователей. Проблемы решаемые, но их нужно ясно представлять, чтобы выбрать правильный способ решения.

Глава 3. Архитектура параллельных вычислительных систем 141

Вопросы и задания

1. Назовите преимущества и недостатки двух систем: 16-процессорной системы с общей памятью и 16-процессорного вычислительного кластера, построенных на базе одних и тех же процессоров.

2. Чему равна пиковая производительность 16-процессорного компьютера с общей памятью HP Superdome и 16-процессорного вычислительного кластера, построенных на базе процессоров РА-8700 / 750 МГц? Попробуйте оценить стоимость каждого решения. Какие преимущества имеет более дорогое решение?

3. Проведите исследование методов организации доступа к общей памяти в современных SMP-серверах.

4. Выделите основные особенности и характерные черты архитектуры IA-64. Какие современные процессоры построены в соответствии с этой архитектурой?

5. Сколько процессоров содержат современные SMP-компьютеры, имеющие наилучшее соотношение цена/производительность? Проведите исследование по разным типам процессоров и систем.

6. Какое соотношение между объемами памяти на различных уровнях иерархии характерно для современных SMP-компьютеров? Для вычислительных систем с архитектурой ccNUMA?

7. Какое соотношение между скоростью выполнения арифметических операций и скоростью обмена с основной памятью характерно для современных SMP-компьютеров?

8. Напишите тестовую программу, которая автоматически определяет соотношение между скоростью выполнения арифметических операций и скоростью обмена с различными уровнями памяти.

9. Напишите тестовую программу, которая автоматически определяет разницу во времени обращения к локальной и удаленной памяти для вычислительных систем с архитектурой ccNUMA.

10. Напишите программу, работающую с максимальной производительностью на любой доступной вам вычислительной системе с общей памятью. Постройте зависимость производительности от числа процессоров.

11. Добавьте в вычислительное ядро программы из предыдущего вопроса использование массивов (если их там не было). Постройте зависимость производительности вычислительной системы с общей памятью от числа процессоров и размеров используемых массивов.

12. Исследуйте зависимость производительности вычислительной системы с общей памятью, показываемой на тестах из предыдущих двух вопросов, от нагрузки на других процессорах системы.

142

Часть /. Параллельные вычислительные системы

§ 3.4. Вычислительные системы с распределенной памятью

Идея построения вычислительных систем данного класса очень проста. Берется какое-то количество вычислительных узлов, которые объединяются друг с другом некоторой коммуникационной средой. Каждый вычислительный узел имеет один или несколько процессоров и свою собственную локальную память, разделяемую этими процессорами. Распределенность памяти означает то, что каждый процессор имеет непосредственный доступ только к локальной памяти своего узла. Доступ к данным, расположенным в памяти других узлов, выполняется дольше и другими, более сложными способами. В последнее время в качестве узлов все чаще и чаще используют полнофункциональные компьютеры, содержащие, например, и собственные внешние устройства. Коммуникационная среда может специально проектироваться для данной вычислительной системы либо быть стандартной сетью, доступной на рынке.

Преимуществ у такой схемы организации параллельных компьютеров много. В частности, покупатель может достаточно точно подобрать конфигурацию в зависимости от имеющегося бюджета и своих потребностей в вычислительной мощности. Соотношение цена/производительность у систем с распределенной памятью ниже, чем у компьютеров других классов. И главное, такая схема дает возможность практически неограниченно наращивать число процессоров в системе и увеличивать ее производительность. Большое число подключаемых процессоров даже определило специальное название для систем данного класса: компьютеры с массовым параллелизмом или массивно-параллельные компьютеры. Уже сейчас в мире существуют десятки компьютеров, в составе которых работает более тысячи процессоров.

Широкое распространение компьютеры с такой архитектурой получили с начала 90-х годов прошлого столетия. Среди них можно назвать Intel Paragon, IBM SP1/SP2, Cray T3D/T3E и ряд других. По большому счету, различие между ними состоит в используемых процессорах и организации коммуникационной среды. Компьютер Intel Paragon был построен на основе процессоров Intel i860, расположенных в узлах прямоугольной двумерной решетки. В вычислительных узлах IBM SP по мере развития данного семейства использовалось несколько процессоров, в частности, PowerPC, P2SC и POWER3. Их взаимодействие идет через иерархическую систему высокопроизводительных коммутаторов, что дает потенциальную возможность общения каждого узла с каждым. Семейство компьютеров Cray T3D/T3E опирается на процессоры DEC Alpha и топологию трехмерного тора.

Данный параграф мы начнем с описания архитектуры компьютеров семейства Cray T3D/T3E. Являясь представителями обсуждаемого класса вычис-

Глава 3. Архитектура параллельных вычислительных систем

143

лительных систем, эти компьютеры обладают рядом интересных дополнительных особенностей, что и предопределило наш выбор.

Итак, компьютеры Cray T3D/T3E — это массивно-параллельные компьютеры с распределенной памятью, объединяющие в максимальной конфигурации более 2000 процессоров. Как и любые компьютеры данного класса, они содержат два основных компонента: узлы и коммуникационную среду.

Все узлы компьютера делятся на три группы. Когда пользователь подключается к компьютеру, то он попадает на управляющие узлы. Эти узлы работают в многопользовательском режиме, на этих же узлах выполняются однопроцессорные программы и работают командные файлы. Узлы операционной системы недоступны пользователям напрямую. Эти узлы поддерживают выполнение многих системных сервисных функций ОС, в частности, работу с файловой системой. Вычислительные узлы компьютера предназначены для выполнения программ пользователя в монопольном режиме. При запуске программе выделяется требуемое число узлов, которые за ней закрепляются вплоть до момента ее завершения. Гарантируется, что никакая программа не сможет занять вычислительные узлы, на которых уже работает другая программа. Число узлов каждого типа зависит от конфигурации системы. В частности, данные, взятые из двух реальных конфигураций Cray ТЗЕ, выглядят так: 24/16/576 или 7/5/260 (управляющие узлы/ узлы ОС/ вычислительные узлы).

Каждый узел последних моделей состоит из процессорного элемента (ПЭ) и сетевого интерфейса. Процессорный элемент содержит один процессор Alpha, локальную память и вспомогательные подсистемы. В модели Cray ТЗЕ-1200Е использовались микропроцессоры DEC Alpha 21164/600 МГц. В модели Cray ТЗЕ-1350 в узлах используются микропроцессоры Alpha 21164А (EV5.6) с тактовой частотой 675 МГц и пиковой производительностью 1,35 Гфлопс. Интересно, что компьютеры серии Cray T3D содержали в каждом узле по два независимых процессора DEC Alpha 21064/150 МГц.

Локальная память каждого процессорного элемента является частью физически распределенной, но логически разделяемой памяти всего компьютера. Память физически распределена, т. к. каждый ПЭ содержит свою локальную память. В то же время память разделяется всеми ПЭ, поскольку любой ПЭ через свой сетевой интерфейс может обращаться к памяти любого другого ПЭ, не прерывая его работы.

Сетевой интерфейс узла связан с соответствующим сетевым маршрутизатором, который является частью коммуникационной сети. Все маршрутизаторы расположены в узлах трехмерной целочисленной прямоугольной решетки и соединены между собой в соответствии с топологией трехмерного тора (рис. 3.14). Это означает, что каждый узел имеет шесть непосредственных соседей вне зависимости от того, где он расположен: внутри параллелепипеда, на ребре, на грани или в его вершине.

144

Часть I. Параллельные вычислительные системы

Рис. 3.14. Коммуникационная решетка компьютера Cray ТЗЕ

Подобная организация коммуникационной сети имеет много достоинств, среди которых отметим два. Во-первых, это возможность выбора альтернативного маршрута для обхода поврежденных связей. А во-вторых, быстрая связь граничных узлов и небольшое среднее число перемещений по тору при взаимодействии разных ПЭ.

Каждая элементарная связь между двумя узлами — это два однонаправленных канала передачи данных, что допускает одновременный обмен данными в противоположных направлениях. В модели Cray ТЗЕ-1200Е максимальная скорость передачи данных между узлами равна 480 Мбайт/с, латентность на уровне аппаратуры составляет менее 1 мкс.

Коммуникационная сеть образует трехмерную решетку, соединяя сетевые маршрутизаторы узлов в направлениях X, Y, Z. Выбор маршрута для обмена данными между двумя узлами А к В происходит следующим образом. Отталкиваясь от вершины А, сетевые маршрутизаторы сначала выполняют смещение по измерению X до тех пор, пока координата очередного транзитного узла и вершины В по измерению X не станут равными. Затем аналогичная процедура выполняется по Y, а в конце по Z(cm. рис. 3.14). Так как смещение может быть как положительным, так и отрицательным, то этот механизм помогает минимизировать число перемещений по сети и обойти поврежденные связи. Сетевые маршрутизаторы спроектированы таким образом, чтобы осуществлять параллельный транзит данных по каждому из трех измерений X, Ya Z одновременно.

Безусловно, интересной особенностью архитектуры компьютера является аппаратная поддержка барьерной синхронизации. Барьер — это точка в программе, при достижении которой каждый процесс должен ждать до тех пор, пока остальные процессы также не дойдут до барьера. Лишь после этого события все процессы могут продолжать работу дальше. Данный вид синхронизации часто

Глава 3. Архитектура параллельных вычислительных систем

145

используется в программах, но его реализация средствами системы программирования сопровождается большими накладными расходами. Поддержка барьеров в аппаратуре позволяет свести эти расходы к минимуму.

Рис. 3.15. Барьерная синхронизация в компьютерах Cray T3D/T3E

В схемах поддержки каждого ПЭ предусмотрено несколько входных и выходных регистров синхронизации. Каждый разряд этих регистров соединен со своей независимой цепью реализации барьера. Все цепи синхронизации одинаковы, а их общее число зависит от конфигурации компьютера. Каждая цепь строится по принципу двоичного дерева на основе двух типов устройств (рис. 3.15). Одни устройства реализуют логическое умножение ("&"), а другие выполняют дублирование входа на два своих выхода ("1—2"). Выход последнего устройства "&" является входом первого устройства дублирования "1—2". Устройства дублирования по своей цепи распространяют полученные значения по всем ПЭ, записывая их в соответствующий разряд выходного регистра.

Рассмотрим работу одной цепи. В исходном состоянии соответствующий разряд входного и выходного регистра каждого ПЭ равен нулю. Появление единицы в выходном разряде ПЭ будет сигнализировать о достижении барьера всеми процессами. Как только процесс доходит до барьера, то разряд входного регистра соответствующего ПЭ переопределяется в единицу. На выходе любого устройства "&" единица появится только в том случае, если оба входа содержат единицу. Если какой-либо процесс еще не дошел до барьера, то ноль на входе этого ПЭ пройдет по цепочке устройств логического умножения и определит ноль на выходе последнего устройства "&". Следовательно, нули будут и в выходных разрядах каждого ПЭ. Как только последний процесс записал единицу в свой входной разряд, единица появ-

146

Часть I. Параллельные вычислительные системы

ляется на выходе последнего устройства "&" и разносится цепью устройств дублирования по выходным разрядам на каждом ПЭ. По значению выходного разряда каждый процесс узнает, что все остальные процессы дошли до точки барьерной синхронизации.

Эти же цепи в компьютерах данного семейства используются и по-другому. Если все устройства логического умножения в схеме заменить устройствами логического сложения, то получится цепь для реализации механизма "Эврика". На выходе любого устройства логического сложения единица появится в том случае, если единица есть хотя бы на одном его входе. Это значит, что как только один ПЭ записал единицу во входной регистр, эта единица распространяется всем ПЭ, сигнализируя о некотором событии на исходном ПЭ. Самая очевидная область применения данного механизма — это задачи поиска.

Помимо традиционных суперкомпьютеров типа Cray ТЗЕ или IBM SP, класс компьютеров с распределенной памятью в последнее время активно расширяется за счет вычислительных кластеров. Сразу оговоримся, что в компьютерной литературе понятие "кластер" употребляется в различных значениях. В частности, "кластерная" технология используется для повышения скорости работы и надежности серверов баз данных или Web-серверов. Здесь мы будем говорить только о кластерах, ориентированных на решение задач вычислительного характера.

Классические суперкомпьютеры всегда ассоциировались с чем-то большим: огромные размеры, гигантская производительность, большая память и, конечно же, колоссальная стоимость. Сама по себе высокая стоимость удивления не вызывает. Уникальные решения, да еще и с рекордными характеристиками, не могут быть дешевыми. Однако прогресс в электронике внес серьезные коррективы. В середине 90-х годов прошлого века на рынке появились недорогие и эффективные микропроцессоры и коммуникационные решения. Появилась реальная возможность создавать установки "суперкомпьютерного" класса из составных частей массового производства. Это и предопределило появление кластерных вычислительных систем, являющихся отдельным направлением развития компьютеров с массовым параллелизмом.

Если говорить кратко, то вычислительный кластер есть совокупность компьютеров, объединенных в рамках некоторой сети для решения одной задачи (рис. 3.16). В качестве вычислительных узлов обычно используются доступные на рынке однопроцессорные компьютеры, двух- или четырех-процессорные SMP-серверы. Каждый узел работает под управлением своей копии операционной системы, в качестве которой чаще всего используются стандартные ОС: Linux, Windows NT, Solaris и т. п. Состав и мощность узлов могут меняться даже в рамках одного кластера, что дает возможность создавать неоднородные системы. Выбор конкретной коммуникационной среды определяется многими факторами: особенностями класса решаемых задач,

Глава 3. Архитектура параллельных вычислительных систем

147

доступным финансированием, необходимостью последующего расширения кластера и т. п. Возможно включение в конфигурацию кластера специализированных компьютеров, например, файл-сервера. Как правило, предоставляется возможность удаленного доступа на кластер через Интернет.

Рис. 3.16. Общая схема вычислительного кластера

Ясно, что простор для творчества при проектировании кластеров огромен. Узлы могут не содержать локальных дисков, коммуникационная среда может одновременно использовать различные сетевые технологии, узлы не обязаны быть одинаковыми и т. д. Рассматривая крайние точки, кластером можно считать как пару ПК, связанных локальной 10-мегабитной Ethernet-сетью, так и вычислительную систему, создаваемую в рамках проекта Cplant в Национальной лаборатории Sandia: 1400 рабочих станций на базе процессоров Alpha объединены высокоскоростной сетью Myrinet. Чтобы лучше почувствовать масштаб и технологию существующих систем, сделаем краткий обзор наиболее интересных современных кластерных установок.

Кластерные проекты

Один из первых проектов, давший имя целому классу параллельных систем — Beowulf-кластеры, возник в центре NASA Goddard Space Flight Center

148

Часть I. Параллельные вычислительные системы

(GSFC). Проект Beowulf стартовал летом 1994 года, и вскоре был собран 16-процессорный кластер на процессорах Intel 486DX4/100 МГц. На каждом узле было установлено по 16 Мбайт оперативной памяти и по 3 сетевых карты для обычной сети Ethernet. Для работы в такой конфигурации были разработаны специальные драйверы, распределяющие трафик между доступными сетевыми картами.

Позже в GSFC был собран кластер TheHlVE — Highly-parallel Integrated Virtual Environment, структура которого показана на рис. 3.17. Этот кластер состоит из четырех подкластеров Е, В, G, и DL, объединяя 332 процессора и два выделенных хост-компьютера. Все узлы данного кластера работают под управлением Red Hat Linux.

QO DO

Fast Ethernet

Fast Ethernet G DL

64 Dual P-Pro

Gigabit Ethernet

66 Dual P-Pro

Gigabit Ethernet

Myrinet

16 Dual 10 Quad Pill Xeon Pill Xeon

Рис. 3.17. Структура кластера TheHlVE

В 1998 году в Лос-Аламосской национальной лаборатории на базе процессоров Alpha 21164А с тактовой частотой 533 МГц был создан Linux-кластер Avalon. Первоначально Avalon состоял из 68 процессоров, затем их число было увеличено до 140. В каждом узле установлено по 256 Мбайт оперативной памяти, жесткий диск на 3 Гбайт и сетевой адаптер Fast Ethernet. Общая стоимость проекта Avalon составила 313 тысяч долларов. Показанная кластером производительность на тесте L1NPACK — 47,7 Гфлопс, позволила ему занять 114 место в 12-й редакции списка Тор500 рядом с 152-процессорной системой IBM RS/6000 SP. В том же 1998 году на самой престижной конференции в области высокопроизводительных вычислений Supercomputing'98 создатели Avalon представили доклад "Avalon: An Alpha/Linux Cluster Achieves 10 Gflops for $150k", получивший первую премию в номинации "Наилучшее соотношение цена/производительность" ("1998 Gordon Bell Price/Performance Prize").

Глава 3. Архитектура параллельных вычислительных систем

149

В апреле 2000 года в рамках проекта АСЗ в Корнелльском университете для проведения биомедицинских исследований был установлен кластер Velocity+. Он состоит из 64 узлов с четырьмя процессорами Intel Pentium III каждый. Узлы работают под управлением Windows 2000 и объединены сетью

cLAN.

Проект LoBoS (Lots of Boxes on Shelfes) реализован в Национальном Институте здоровья США в апреле 1997 года. Он интересен использованием в качестве коммуникационной среды технологии Gigabit Ethernet. Сначала кластер состоял из 47 узлов с двумя процессорами Intel Pentium Pro/200 МГц, 128 Мбайт оперативной памяти и диском на 1,2 Гбайт на каждом узле. В 1998 году был реализован следующий этап проекта — LoBoS2, в ходе которого узлы были преобразованы в настольные компьютеры с сохранением объединения в кластер. Сейчас LoBoS2 состоит из 100 вычислительных узлов, содержащих по два процессора Pentium П/450 МГц, 256 Мбайт оперативной и 9 Гбайт дисковой памяти. Дополнительно к кластеру подключены 4 управляющих компьютера с общим RAID-массивом объемом 1,2 Тбайт.

Интересной разработкой стал в 2000 году кластер KLAT2 (Kentucky Linux Athlon Testbed 2). Система KLAT2 состоит из 64 бездисковых узлов с процессорами AMD Athlon/700 МГц и оперативной памятью 128 Мбайт на каждом. Программное обеспечение, компиляторы и математические библиотеки (SCALAPACK, BLACS и ATLAS) были доработаны для эффективного использования технологии 3D-Now! процессоров AMD. Эта работа позволила существенно увеличить производительность системы в целом. Значительный интерес представляет и использованное сетевое решение, названное "Flat Neighbourhood Network" (FNN). В каждом узле установлено четыре сетевых адаптера Fast Ethernet, а узлы соединяются с помощью девяти 32-портовых коммутаторов. При этом для любых двух узлов всегда есть прямое соединение через один из коммутаторов, но нет необходимости в соединении всех узлов через единый коммутатор. Благодаря оптимизации программного обеспечения под архитектуру AMD и топологии FNN удалось добиться рекордного соотношения цена/производительность на тесте LINPACK — 650 долларов за 1 Гфлопс.

Идея разбиения кластера на разделы получила интересное воплощение в проекте Chiba City, реализованном в Аргонской Национальной лаборатории. Главный раздел содержит 256 вычислительных узлов, на каждом из которых установлено по два процессора Pentium Ш/500 МГц, 512 Мбайт оперативной памяти и локальный диск объемом 9 Гбайт. Кроме вычислительного раздела в систему входят: раздел визуализации (32 компьютера IBM Intellistation с графическими картами Matrox Millenium G400, 512 Мбайт оперативной памяти и дисками 300 Гбайт), раздел хранения данных (8 серверов IBM Netfinity 7000 с процессорами Хеоп/500 МГц и дисками по

150

Часть I. Параллельные вычислительные системы

300 Гбайт) и управляющий раздел (12 компьютеров IBM Netfinity 500). Все они объединены сетью Myrinet, которая используется для поддержки параллельных приложений. Для управляющих и служебных целей используются сети Gigabit Ethernet и Fast Ethernet. Все разделы делятся на "города" (towns) по 32 компьютера. Каждый из них имеет своего "мэра", который локально обслуживает свой "город", снижая нагрузку на служебную сеть и обеспечивая быстрый доступ к локальным ресурсам.

Сеть Myrinet 2000

128 CPUs

А V

Сеть Fast Ethernet

Сеть Gigabit Ethernet

Управляющий компьютер

Файл-сервер

Резервный

управляющий

компьютер

Рис. 3.18. Структура суперкомпьютера МВС-1000М

Кластером является и суперкомпьютер МВС-1000М, установленный в Межведомственном суперкомпьютерном центре в Москве (http://www.jscc.ru). Компьютер состоит из шести базовых блоков, содержащих по 64 двухпроцессорных модуля (рис. 3.18). Каждый модуль имеет два процессора Alpha 21264/667 МГц (кэш-память второго уровня 4 Мбайт), 2 Гбайт оперативной памяти, разделяемой процессорами модуля, жесткий диск. Общее число процессоров в системе равно 768, а пиковая производительность МВС-1000М превышает 1 Тфлопс.

Все модули МВС-1000М связаны двумя независимыми сетями. Сеть Myrinet 2000 используется программами пользователей для обмена данными в процессе вычислений. При использовании МР1 пропускная способность каналов сети достигает значений 110—170 Мбайт/с. Сеть Fast Ethernet используется операционной системой для выполнения сервисных функций.

Глава 3. Архитектура параллельных вычислительных систем

151

Коммуникационные технологии построения кластеров

Понятно, что различных вариантов построения кластеров очень много. Одно из существенных различий лежит в используемой сетевой технологии, выбор которой определяется, прежде всего, классом решаемых задач.

Первоначально Beowulf-кластеры строились на базе обычной 10-мегабитной сети Ethernet. Сегодня часто используется сеть Fast Ethernet, как правило, на базе коммутаторов. Основное достоинство такого решения — это низкая стоимость. Вместе с тем, большие накладные расходы на передачу сообщений в рамках Fast Ethernet приводят к серьезным ограничениям на спектр задач, эффективно решаемых на таких кластерах. Если от кластера требуется большая универсальность, то нужно переходить на другие, более производительные коммуникационные технологии. Исходя из соображений стоимости, производительности и масштабируемости, разработчики кластерных систем делают выбор между Fast Ethernet, Gigabit Ethernet, SCI, Myrinet, cLAN, ServerNet и рядом других сетевых технологий (основные параметры коммуникационных технологий можно найти, например, на http://www.Parallel.ru).

Пропускная способность

Узел 1

Узел 2

Рис. 3.19. Латентность и пропускная способность коммуникационной среды

Какими же числовыми характеристиками выражается производительность коммуникационных сетей в кластерных системах? Необходимых пользователю характеристик две: латентность и пропускная способность сети. Латентность — это время начальной задержки при посылке сообщений. Пропускная способность сети определяется скоростью передачи информации по каналам связи (рис. 3.19). Если в программе много маленьких сообщений, то сильно скажется латентность. Если сообщения передаются большими порциями, то важна высокая пропускная способность каналов связи. Из-за латентности максимальная скорость передачи по сети не может быть достигнута на сообщениях с небольшой длиной.

152

Часть I. Параллельные вычислительные системы

На практике пользователям не столько важны заявляемые производителем пиковые характеристики, сколько реальные показатели, достигаемые на уровне приложений. После вызова пользователем функции посылки сообщения Send() сообщение последовательно проходит через целый набор слоев, определяемых особенностями организации программного обеспечения и аппаратуры. Этим, в частности, определяются и множество вариаций на тему латентности реальных систем. Установили MPI на компьютере плохо, латентность будет большая, купили дешевую сетевую карту от неизвестного производителя, ждите дальнейших сюрпризов.

В заключение параграфа давайте попробуем и для данного класса компьютеров выделить факторы, снижающие производительность вычислительных систем с распределенной памятью на реальных программах.

Начнем с уже упоминавшегося ранее закона Амдала. Для компьютеров данного класса он играет очень большую роль. В самом деле, если предположить, что в программе есть лишь 2% последовательных операций, то рассчитывать на более чем 50-кратное ускорение работы программы не приходится. Теперь попробуйте критически взглянуть на свою программу. Скорее всего, в ней есть инициализация, операции ввода/вывода, какие-то сугубо последовательные участки. Оцените их долю на фоне всей программы и на мгновенье предположите, что вы получили доступ к вычислительной системе из 1000 процессоров. После вычисления верхней границы для ускорения программы на такой системе, думаем, станет ясно, что недооценивать влияние закона Амдала никак нельзя.

Поскольку компьютеры данного класса имеют распределенную память, то взаимодействие процессоров между собой осуществляется с помощью передачи сообщений. Отсюда два других замедляющих фактора — латентность и скорость передачи данных по каналам коммуникационной среды. В зависимости от коммуникационной структуры программы степень влияния этих факторов может сильно меняться.

Если аппаратура или программное обеспечение не поддерживают возможности асинхронной посылки сообщений на фоне вычислений, то возникнут неизбежные накладные расходы, связанные с ожиданием полного завершения взаимодействия параллельных процессов.

Для достижения эффективной параллельной обработки необходимо добиться максимально равномерной загрузки всех процессоров. Если равномерности нет, то часть процессоров неизбежно будет простаивать, ожидая остальных, хотя в это время они вполне могли бы выполнять полезную работу. Данная проблема решается проще, если вычислительная система однородна. Очень большие трудности возникают при переходе на неоднородные системы, в которых есть значительное различие либо между вычислительными узлами, либо между каналами связи.

Существенный фактор — это реальная производительность одного процессора вычислительной системы. Разные модели микропроцессоров могут поддерживать несколько уровней кэш-памяти, иметь специализированные функ-

Глава 3. Архитектура параллельных вычислительных систем

153

циональные устройства и т. п. Возьмем хотя бы иерархию памяти компьютера Cray ТЗЕ: регистры процессора, кэш-память 1-го уровня, кэш-память 2-го уровня, локальная память процессора, удаленная память другого процессора. Эффективное использование такой структуры требует особого внимания при выборе подхода к решению задачи.

Дополнительно каждый микропроцессор может иметь элементы векторно-конвейерной архитектуры. В этом случае ему будут присущи многие факторы, которые мы обсуждали в конце § 3.2.

К сожалению, как и прежде, на работе каждой конкретной программы в той или иной мере сказываются все эти факторы. Однако в отличие от компьютеров других классов, суммарное воздействие изложенных здесь факторов может снизить реальную производительность не в десятки, а в сотни и даже тысячи раз по сравнению с пиковой. Потенциал компьютеров этого класса огромен, добиться на них можно очень многого. Однако могут потребоваться значительные усилия. Все этапы в решении каждой задачи, начиная от выбора метода до записи программы, нужно продумывать очень аккуратно.

Крайняя точка — Интернет. Его тоже можно рассматривать как компьютер с распределенной памятью. Причем, как самый мощный в мире компьютер. Попробуйте найти способ решения ваших задач на таком компьютере.

Вопросы и задания

1. Многие параллельные вычислительные системы с распределенной памятью в качестве узлов используют SMP-компьютеры. Какими свойствами должен обладать алгоритм решения задачи, ориентированный на использование компьютера с такой архитектурой?

2. Есть две системы. У одной быстрые процессоры и медленные каналы связи, а у другой — медленные процессоры и быстрые связи. В чем преимущества и недостатки каждой системы? На какой системе программы будут иметь лучшую масштабируемость?

3. Приведите пример реальной вычислительной системы с распределенной памятью и коммуникационной сетью, имеющей топологию двумерного тора.

4. Сколько компьютеров, входящих в последнюю редакцию списка Тор500, имеют в своем составе более 1000 процессоров? Сколько среди них компьютеров с распределенной памятью?

5. Сколько процессорных элементов объединяет компьютер Cray ТЗЕ, коммуникационная решетка которого имеет размеры 3x4x5? A Cray T3D с такой же решеткой?

6. Коммуникационная решетка компьютера Cray ТЗЕ имеет размеры 3x4x5. Укажите непосредственных соседей узла, расположенного в вершине (на верхней грани, на ребре).

7. Расстоянием между двумя узлами А и В компьютера Cray ТЗЕ назовем длину минимального пути (по числу ребер), соединяющих А и В. Рассмотрим все возможные конфигурации коммуникационной решетки, состоящей из 64 узлов. Для каждой конфигурации определим максимум среди расстояний по всем парам

154

Часть I. Параллельные вычислительные системы

узлов. Чему равен минимум среди указанных максимальных расстояний? А для решетки из 1024 узлов?

8. Могут ли в компьютере Cray ТЗЕ маршруты передачи сообщений от вычислительного узла А к узлу В и, наоборот, от В к А быть различными? Одинаковыми?

9. Предложите способ программной реализации барьерной синхронизации с помощью любой доступной технологии параллельного программирования. Сколько времени требуется на выполнение одного барьера на доступном вам компьютере?

10. В чем вы видите слабые стороны вычислительных кластеров по сравнению с традиционными суперкомпьютерами?

11. Что понимается под словами "масштабируемость кластера"?

12. Могут ли в одном кластере вычислительные узлы работать под управлением различных операционных систем?

13. Есть ли смысл в одном кластере использовать несколько различных сетевых технологий?

14. Предположим, что в качестве узла кластера используется процессор Intel Pentium III (IV). Приведите пример фрагмента программы, разная форма записи которого приводит к различию в производительности процессора в 10 раз (алгоритм изменяться не должен).

15. Сколько кластерных систем присутствует в текущей редакции списка Тор500?

16. *Предположим, что необходимо сделать кластер для максимально эффективного выполнения теста LINPACK. Какую архитектуру вы предложите для такого кластера? Какова структура одного процессора, коммуникационной среды, каково соотношение между скоростью работы процессора и пропускной способностью сети?

17. Какой должна быть архитектура кластера, чтобы соответствовать структуре задачи, решаемой вами в настоящий момент на параллельном компьютере?

§ 3.5. Концепция GRID и метакомпьютинг

В предыдущих параграфах мы рассмотрели несколько классов параллельных вычислительных систем. Это были компьютеры с общей памятью (Cray С90, Hewlett-Packard Superdome), массивно-параллельные компьютеры с распределенной памятью (Cray T3D/T3E), вычислительные кластеры различной конфигурации. Если все первые параллельные системы были достоянием отдельных мощных фирм и корпораций, то сегодня ситуация резко изменилась. Вычислительный кластер можно собрать практически в любой лаборатории, отталкиваясь от потребностей в вычислительной мощности и доступного бюджета. Для целого класса задач, где не предполагается тесного взаимодействия между параллельными процессами, решение на основе обычных рабочих станций и сети Fast Ethernet будет вполне эффективным. Но чем такое решение отличается от обычной локальной сети современного предприятия? С точки зрения прикладного программиста почти ничем. Если у него появится возможность использования подобной сети для решения своих задач, то для него такая конфигурация и будет параллельным компьютером.

Глава 3. Архитектура параллельных вычислительных систем

155

Продолжая идею дальше, любые вычислительные устройства можно считать параллельной вычислительной системой, если они работают одновременно и их можно использовать для решения одной задачи. Под это определение попадают как барышни с арифмометрами, которыми руководил академик А. А. Самарский при расчете первых ядерных взрывов (см. § 2.1), так и компьютеры в сети Интернет. Способ организации параллельных вычислений в каждом случае может быть своим, потенциальные возможности систем могут сильно различаться, но принципиальная возможность параллельного решения задач должна присутствовать.

В этом смысле уникальные возможности дает сеть Интернет, которую можно рассматривать как самый большой компьютер в мире. Никакая вычислительная система не может сравниться ни по пиковой производительности, ни по объему оперативной или дисковой памяти с теми суммарными ресурсами, которыми обладают компьютеры, подключенные к Интернету. Компьютер, состоящий из компьютеров, своего рода метакомпьютер. Отсюда происходит и специальное название для процесса организации вычислений на такой вычислительной системе — мешакомпьюшинг. В принципе, совершенно не обязательно рассматривать именно Интернет в качестве коммуникационной среды метакомпьютера, эту роль может выполнять любая сетевая технология. В данном случае для нас важен принцип, а возможностей для технической реализации сейчас существует предостаточно. Вместе с тем, к Интернету всегда был и будет особый интерес, поскольку никакая отдельная вычислительная система не сравнится по своей мощности с потенциальными возможностями глобальной сети.

Конструктивные идеи использования распределенных вычислительных ресурсов для решения сложных задач появились относительно недавно. Первые прототипы реальных систем метакомпьютинга стали доступными с середины 90-х годов прошлого века. Некоторые системы претендовали на универсальность, часть из них была сразу ориентирована на решение конкретных задач, где-то ставка делалась на использование выделенных высокопроизводительных сетей и специальных протоколов, а где-то за основу брались обычные каналы и работа по протоколу HTTP. Вот лишь несколько примеров.

Расширение MPI для поддержки распределенных вычислений PACX-MPI. Поддерживается объединение в единый метакомпьютер нескольких МРР-систем, возможно с различными реализациями MPI. Передача данных между МРР производится через Интернет с помощью TCP/IP. На конференции Supercomputing в 1998 году продемонстрировано совместное использование средствами PACX-MPI двух 512-процессорных суперкомпьютеров Cray ТЗЕ, находящихся в университете Штутгарта (Германия) и в Питтсбургском суперкомпьютерном центре (США).

Система Condor распределяет задачи по существующей корпоративной сети рабочих станций, используя то время, когда компьютеры простаивают без

156

Часть I. Параллельные вычислительные системы

нагрузки, например, ночью. Программное обеспечение системы Condor распространяется свободно. В настоящее время поддерживаются все основные платформы: SGI, Solaris, Linux, HP-UX, Digital Unix, Windows NT. Детальное описание и необходимые дистрибутивы можно найти на сайте проекта http://www.cs.wisc.edu/condor/.

Проект SETI@home (Search for Extraterrestrial Intelligence) — поиск внеземных цивилизаций с помощью распределенной обработки данных, поступающих с радиотелескопа. Присоединиться к проекту может любой желающий, загрузив на свой компьютер программу обработки радиосигналов. Доступны клиентские программы для Windows, Mac, UNIX, OS/2. С момента старта проекта в мае 1999 года по май 2002 года для участия в проекте зарегистрировались более 3,7 миллионов человек. Согласно приводимой на сайте статистике суммарная производительность задействованных в проекте компьютеров во много раз превосходит производительность всех компьютеров из списка Тор500. Адрес проекта http://setiathome.ssl.berkeley.edu/.

Distributed.net также является одним из самых больших объединений пользователей Интернета, предоставляющих свои компьютеры для решения сложных задач в распределенном режиме. Основные проекты связаны с задачами определения шифров (RSA Challenges). С момента начала проекта в нем зарегистрировались около 200 тыс. человек. Адрес этого проекта http://www.Distributed.net/.

GIMPS — Great Internet Mersenne Prime Search. Поиск простых чисел Mep-сена, т. е. простых чисел вида 2^Р— 1, где Р является простым числом. В ноябре 2001 года в рамках данного проекта было найдено максимальное на данное время число Мерсена 2¹³ ⁴⁶⁶ ⁹¹⁷ — 1. Десятки тысяч компьютеров по всему миру, отдавая часть своих вычислительных ресурсов, работали над этой задачей два с половиной года. Организация Electronic Frontier Foundation предлагает приз в $100 000 за нахождение простого числа Мерсена, содержащего 10 миллионов цифр. Адрес проекта http://mersenne.org/.

Проект Globus изначально зародился в Аргонской национальной лаборатории и сейчас получил широкое признание во всем мире. Целью проекта является создание средств для организации глобальной информационно-вычислительной среды. В рамках проекта разработан целый ряд программных средств и систем, в частности, единообразный интерфейс к различным локальным системам распределения нагрузки, системы аутентификации, коммуникационная библиотека Nexus, средства контроля и мониторинга и др. Разработанные средства распространяются свободно в виде пакета Globus Toolkit вместе с исходными текстами. В настоящее время Globus взят за основу в множестве других масштабных проектов, таких как National Technology Grid, Information Power Grid и European DataGrid. Дополнительную информацию можно найти на сайте http://www.globus.org/.

Глава 3. Архитектура параллельных вычислительных систем 157

Прогресс в сетевых технологиях последних лет колоссален. Гигабитные линии связи между компьютерами, разнесенными на сотни километров, становятся обычной реальностью. Объединив различные вычислительные системы в рамках единой сети, можно сформировать специальную вычислительную среду. Какие-то компьютеры могут подключаться или отключаться, но, с точки зрения пользователя, эта виртуальная среда является единым метакомпьютером. Работая в такой среде, пользователь лишь выдает задание на решение задачи, а остальное метакомпьютер делает сам: ищет доступные вычислительные ресурсы, отслеживает их работоспособность, осуществляет передачу данных, если требуется, то выполняет преобразование данных в формат компьютера, на котором будет выполняться задача, и т. п. Пользователь может даже и не узнать, ресурсы какого именно компьютера были ему предоставлены. А, по большому счету, часто ли вам это нужно знать? Если потребовались вычислительные мощности для решения задачи, то вы подключаетесь к метакомпьютеру, выдаете задание и получаете результат. Все.

Здесь существует почти полная аналогия с электрической сетью. Подключая электрический чайник к розетке, вы не задумываетесь, какая станция производит электроэнергию. Вам нужен ресурс, вы им пользуетесь. Кстати, по аналогии именно с электрической сетью распределенная вычислительная среда в англоязычной литературе получила название Grid или "вычислительная сеть". В дальнейшем, слова Grid и метакомпьютер мы будем использовать как синонимы.

Продолжая аналогию с электрической сетью, на метакомпьютер хотелось бы перенести не только название, но и такой же простой способ взаимодействия с ним пользователя. Но вот тут-то и возникают основные проблемы, которые определяются сложностью организации самого метакомпьютера. В отличие от традиционного компьютера метакомпьютер имеет целый набор присущих только ему особенностей:

□ метакомпьютер обладает огромными ресурсами, которые несравнимы с ресурсами обычных компьютеров. Это касается практически всех параметров: число доступных процессоров, объем памяти, число активных приложений, пользователей и т. п.;

□ метакомпьютер является распределенным по своей природе. Компоненты метакомпьютера могут быть удалены друг от друга на сотни и тысячи километров, что неизбежно вызовет большую латентность и, следовательно, скажется на оперативности их взаимодействия;

□ метакомпьютер может динамически менять конфигурацию. Какие-то компьютеры к нему подсоединяются и делегируют права на использование своих ресурсов, какие-то отключаются и становятся недоступными. Но для пользователя работа с метакомпьютером должна быть прозрачной. Задача системы поддержки работы метакомпьютера состоит в поиске

158

Часть I. Параллельные вычислительные системы

подходящих ресурсов, проверке их работоспособности, в распределении поступающих задач вне зависимости от текущей конфигурации метаком-пьютера в целом;

□ метакомпьютер неоднороден. При распределении заданий нужно учитывать особенности операционных систем, входящих в его состав. Разные системы поддерживают различные системы команд и форматы представления данных. Различные системы в разное время могут иметь различную загрузку, связь с вычислительными системами идет по каналам с различной пропускной способностью. Наконец, в состав метакомпьютера могут входить системы с принципиально различной архитектурой, начиная с домашних персональных компьютеров, заканчивая мощнейшими системами из списка Тор500;

□ метакомпьютер объединяет ресурсы различных организаций. Политика доступа и использования конкретных ресурсов может сильно меняться в зависимости от их принадлежности к той или иной организации. Метакомпьютер не принадлежит никому, поэтому политика его администрирования может быть определена лишь в самых общих чертах. Вместе с тем, согласованность работы огромного числа составных частей метакомпьютера предполагает обязательную стандартизацию работы всех его служб и сервисов.

Говоря о метакомпьютере, следует четко представлять, что речь идет не только об аппаратной части и не столько об аппаратной части, сколько о его инфраструктуре [49]. В комплексе должны рассматриваться такие вопросы, как средства и модели программирования, распределение и диспетчеризация заданий, технологии организации доступа к метакомпьютеру, интерфейс с пользователями, безопасность, надежность, политика администрирования, средства доступа и технологии распределенного хранения данных, мониторинг состояния различных подсистем метакомпьютера и многие другие. Представьте себе, как заставить десятки миллионов различных электронных устройств, составляющих метакомпьютер, работать согласованно над заданиями десятков тысяч пользователей в течение продолжительного времени? Фантастически сложная задача, масштабное решение которой было невозможным еще десять лет назад.

В настоящее время идет активное обсуждение различных стратегий построения метакомпьютера. Однако многие вопросы до сих пор недостаточно проработаны, часть предложенных технологий еще находится на стадии апробации, не всегда используется единая терминология. Ситуация в данной области развивается чрезвычайно быстро. В данной книге мы решили основное внимание уделить не детальному описанию каких-либо конкретных систем или технологий метакомпьютинга, а обсуждению базовых принципов и идей вычислительной компоненты сети. Много полезной информации о текущем состоянии работ в данной области можно найти на сайтах http://www.globus.org, http://www.gridforum.org и др.

Глава 3. Архитектура параллельных вычислительных систем

159

Несмотря на кажущуюся вычурность и нереальность создаваемой глобальной вычислительной системы, область применения метакомпьютера обширна. В рамках метакомпьютера объединяются колоссальные вычислительные ресурсы. Это делает реальным решение таких задач, к которым раньше нельзя было даже подступиться. Биоинженерия — это одна из таких областей. Для определения пространственной структуры одной макромолекулы на одной современной рабочей станции требуется несколько дней, однако общее число необходимых численных экспериментов для различных соединений исчисляется сотнями тысяч. Мощности никакой традиционной вычислительной системы для решения такой задачи не хватит, а суммарные ресурсы метакомпьютера могут помочь. Другое направление применения — это обеспечение высокой скорости обработки большого потока слабо связанных друг с другом или вовсе независимых задач. Типичными примерами задач данного направления является проведение огромного числа расчетов на завершающем этапе проектирования сложных электронных приборов [49] или же традиционные задачи криптографии. Смежным направлением является проведение вычислений по требованию (on-demand computing). Для многих организаций экономически невыгодно держать у себя высокопроизводительные компьютеры, поскольку потребности в проведении больших расчетов возникают лишь эпизодически, а стоимость приобретения и сопровождения такого оборудования велика.

В данном ряду стоит особо отметить задачи распределенного хранения и обработки данных. Реально массивы данных могут быть географически удалены друг от друга и распределены по большому числу разного рода хранилищ и баз данных. Несмотря на разобщенность, все эти данные могут потребоваться в рамках единого эксперимента, что предъявляет к метаком-пьютеру серьезные требования не только вычислительного, но и коммуникационного характера.

Характерной задачей из данной области является создание информационной инфраструктуры для поддержки экспериментов в физике высоких энергий. В 2006—2007 годах в Европейской организации ядерных исследований (CERN) планируется ввести в строй мощный ускоритель — Большой Ад-ронный Коллайдер. Четыре физические установки данного проекта в течение 15—20 лет будут ежегодно собирать данные объемом порядка нескольких Пбайт (10¹⁵ байт). Во время экспериментов данные будут поступать со скоростью от 100 Мбайт/с до 1 Гбайт/с. Оптимальная схема хранения и последующая эффективная обработка собранных данных тысячами участников эксперимента из разных стран мира является исключительно сложной задачей. Принято решение создать иерархическую распределенную систему региональных центров, что позволит снять колоссальную нагрузку на вычислительные мощности и системы хранения CERN.

Создаваемая система включает несколько уровней иерархии, причем на возможности каждого уровня накладываются очень жесткие требования.

160

Часть I. Параллельные вычислительные системы

Компьютерные ресурсы каждого центра должны быть адекватны поставленным перед ними задачам. Так, например, основной центр в CERN должен обеспечивать задачи по созданию баз данных по экспериментам. Ресурсы этого центра в 2007 году должны находиться на уровне: мощность вычислительных кластеров 2500К Speclnt95, объем дискового хранилища 2,5 Пбайт, хранилище на лентах объемом 10—15 Пбайт. При этом каждый год ленточное хранилище должно увеличивать свой ресурс на 10—15 Пбайт, а дисковый массив должен увеличиваться на 20%. Для обеспечения работы физиков всего мира с этими данными создается распределенная система (DataGrid), поэтому сетевые соединения CERN с региональными центрами первого уровня должны быть порядка 1—2 Гбит/с. Суммарные мощности центров первого уровня будут соответствовать мощности основного центра в CERN (то же верно и для суммарной мощности центров второго уровня по отношению к центрам первого уровня). Предполагается создать 5—6 центров первого уровня на каждый из 4-х экспериментов (ALICE, ATLAS, CMS и LHCb), и около 25—30 центров второго уровня.

Большая часть центров будет удалена друг от друга на значительное расстояние, что требует соответствующей технологии удаленной работы с данными эксперимента. Принято решение в качестве основы для построения инфраструктуры эксперимента использовать Grid-технологии и объединить все центры в рамки единого метакомпьютера. Предполагается разработать специализированное программное обеспечение для эффективного доступа к данным эксперимента, позволяющее кэшировать, тиражировать и передавать данные в неоднородной среде метакомпьютера. В качестве технологической основы выбрана система Globus.

Запланированная работа исключительно масштабна. Она предполагает создание большого числа сложных программных подсистем различного уровня для обеспечения прозрачного доступа к распределенным данным, управления рабочей нагрузкой вычислительных систем, эффективного управления данными, построение систем оперативного мониторинга и т. п. Много интересных деталей данного проекта можно найти на сайте http://www.eu-datagrid.org/.

Удачных примеров использования идей метакомпьютинга для решения реальных задач уже сейчас можно привести немало. Но, к сожалению, все эти работы уникальны и настолько трудоемки, что до массового использования еще очень далеко. Легко было сказать, опираясь на аналогию с электрической сетью: "Подключайся и используй". На практике возникает огромное количество действительно серьезных проблем. Часть проблем касается вопросов политического и экономического характера. Без решения и урегулирования таких вопросов не обойтись и их надо обязательно учитывать, поскольку масштаб работ по метакомпьютингу быстро выходит на межгосударственный уровень. Большой спектр проблем лежит перед создателями самого метакомпьютера и поддерживающих его работу систем. Это и

Глава 3. Архитектура параллельных вычислительных систем

161

понятно: задача сложная, во многом новая и необычная, с небольшим числом готовых наработок и пока явным недостатком опыта.

Однако еще больше проблем появится перед пользователями. Как создавать программы для систем метакомпьютинга на настоящий момент — не ясно. На какую модель программирования ориентироваться пользователю? В рамках метакомпьютера могут использоваться все существующие в настоящее время архитектуры. В одних узлах используются системы программирования с явной передачей сообщений, в других ставка делается на многопотоковую обработку, третьи опираются на понятие общей памяти, четвертые используют векторную обработку данных и т. д. Как обеспечить правильный подбор распределенных вычислительных ресурсов в зависимости от свойств конкретной программы или алгоритма? Данная задача представляется исключительно сложной, поскольку затрагивает практически весь спектр вопросов, характерных для параллельных вычислений в целом.

Для небольшого класса многократно используемых программ уже сейчас удалось найти подходящее решение. С помощью специально спроектированных средств оформляется Web-интерфейс к программе, которая предварительно подготовлена специалистами к выполнению в рамках некоторой системы метакомпьютинга. Пользователь не занимается программированием, а задает свои входные данные и запускает задачу на счет, не заботясь о том, где и как реально программа будет выполнена. Через какое-то время система возвращает ему результат. Сейчас существует несколько систем подобного класса, например, система UNICORE (http://www.fz-juelich.de/unicore/).

Реальная работа по созданию и апробации систем метакомпьютинга активно идет по многим направлениям. Многие ведущие компании взяли Globus Toolkit в качестве стандарта для создания Grid-приложений, создавая программную инфраструктуру для своих платформ. Создаются глобальные полигоны, объединяющие в рамках супервысокоскоростных сетей значительные распределенные вычислительные ресурсы. Проводятся серии экспериментов, направленных на отработку новых сетевых технологий, методов диспетчеризации и мониторинга в распределенной вычислительной среде, интерфейса с пользователем, моделей и методов программирования. Потенциал направления, безусловно, огромен, но число нерешенных проблем пока перевешивает реальный эффект. Сейчас все находится в стадии становления. Нет сомнений, что в будущем ситуация изменится.

Вопросы и задания

1. Сколько компьютеров в сети вашей организации? Какова их суммарная производительность? Что нужно сделать, чтобы их можно было бы использовать в режиме единого параллельного компьютера?

2. Чем отличается программирование вычислительного кластера и метакомпьютера с точки зрения прикладного программиста?

162

Часть I. Параллельные вычислительные системы

3. Как вычислить пиковую производительность метакомпьютера?

4. Назовите 10 причин, снижающих производительность метакомпьютера на реальных программах.

5. Предположим, что метакомпьютер объединяет только кластеры, состоящие из SMP-узлов. Какие технологии параллельного программирования можно было бы использовать для его программирования?

6. Попробуйте составить проект вычислительного портала в сети Интернет, предоставляющего максимальное число услуг и сервисов вычислительного характера.

7. Что нужно знать метакомпьютеру для оптимального подбора необходимых вычислительных ресурсов под конкретную программу или алгоритм?

8. Какие проблемы появятся при разработке компилятора для метакомпьютера?

9. Какие вопросы, связанные с обеспечением информационной безопасности, придется решать при создании метакомпьютера?

10. Как метакомпьютер может решить вопрос о целесообразности передачи программы для проведения вычислений на удаленных ресурсах?

11. Назовите конкретные задачи (или области) в химии, физике, астрономии и других науках, для которых использование метакомпьютера было бы эффективно.

12. Сделайте Web-интерфейс к своей параллельной программе с возможностью задания входных параметров и запуска программы на различных конфигурациях доступного параллельного компьютера.

13. Как, в дополнение к предыдущему вопросу, на основе Web-технологий сделать систему online-визуализации динамики исполнения параллельной программы?

§ 3.6. Производительность параллельных компьютеров

Оценивать и сравнивать всегда было делом трудным и неблагодарным. Вы потратите массу сил и времени на выработку критериев и проведение анализа, но обязательно найдется человек, с точки зрения которого результаты должны быть точно противоположными. Сколько людей — столько мнений. Желание получить объективную оценку немедленно наталкивается на множество субъективных факторов: разные постановки задачи, разные критерии сравнения, разные цели оценивания и т. п. Более того, любая оценка невольно приводит к сравнению, к явному или неявному ранжированию, выделению лучших и самых лучших. В этом вопросе редко удается прийти к единодушному согласию, поскольку убеждают только железные, неоспоримые факты. Какое яйцо лучше: свежее или "с душком"? Ответ очевиден. Но, видимо, вы также воспитаны на европейской кухне. Любители восточной кухни над вопросом задумаются...

Необходимость оценки производительности и последующего сравнения компьютеров появилась практически одновременно с их рождением. Какой

Глава 3. Архитектура параллельных вычислительных систем

163

компьютер выбрать? Какому компьютеру отдать предпочтение? На каком компьютере задача будет решаться быстрее? Подобные вопросы задавались пользователями всегда и будут задаваться ими еще долго. Казалось бы, что тут сложного, запусти программу и проверь. Но не все так просто. Перенос параллельной программы на новую платформу требует времени, зачастую значительного. Много попыток в таких условиях не сделаешь, да и не всегда есть свободный доступ к новой платформе. А если на новом компьютере должен работать набор программ, как быть в такой ситуации?

Хотелось бы иметь простую единую методику априорного сравнения вычислительных систем между собой. В идеальной ситуации вычислять бы для каждой системы по некоторому закону одно число, которое и явилось его обобщенной характеристикой. Со сравнением компьютеров проблем не стало бы, с выбором тоже.

Сопоставить одно число каждому компьютеру можно по-разному. Например, можно вычислить это значение, опираясь на параметры самого компьютера. С этой точки зрения, естественной характеристикой любого компьютера является его пиковая производительность. Данное значение определяет тот максимум, на который способен компьютер. Вычисляется оно очень просто. Для этого достаточно предположить, что все устройства компьютера работают в максимально производительном режиме. Если в процессоре есть два конвейерных устройства, то рассматривается режим, когда оба конвейера одновременно работают с максимальной нагрузкой. Если в компьютере есть 1000 таких процессоров, то пиковая производительность одного процессора просто умножается на 1000.

Иногда пиковую производительность компьютера называют его теоретической производительностью. Этот нюанс в названии лишний раз подчеркивает тот факт, что производительность компьютера на любой реальной программе никогда не только не превысит этого порога, но и не достигнет его точно.

Пиковая производительность компьютера вычисляется однозначно, спорить тут не о чем, и уже этим данная характеристика хороша. Более того, подсознательно всегда возникает связь между пиковой производительностью компьютера и его возможностями в решении задач. Чем больше пиковая производительность, тем, вроде бы, быстрее пользователь сможет решить свою задачу. В целом данный тезис не лишен некоторого смысла, но лишь некоторого и даже "очень некоторого". Полагаться на него полностью нельзя ни в коем случае. С момента появления первых параллельных компьютеров пользователи убедились, что разброс в значениях реальной производительности может быть огромным. На одних задачах удавалось получать 90% от пиковой производительности, а на других лишь 2%. Если кто-то мог использовать независимость и конвейерность всех функциональных устройств компьютера CDC 7600, то производительность получалась высокой. Если в вычислениях были информационные зависимости, то конвейерность не использовалась, и произво-

164

Часть I. Параллельные вычислительные системы

дительность снижалась. Если в алгоритме явно преобладал один тип операций, то часть устройств простаивала, вызывая дальнейшее падение производительности. Об этом мы уже начинали говорить в § 2.3.

Структура программы и архитектура компьютера тесно связаны. Пользователя не интересуют потенциальные возможности вычислительной системы. Ему нужно решить его конкретную задачу. Именно с этой точки зрения он и хочет оценить "качество" компьютера. Для обработки данных эксперимента в физике высоких энергий не требуется высокоскоростной коммуникационной среды. Главное — это большое число вычислительных узлов. Для таких целей вполне подойдет локальная 10-мегабитная сеть организации из ста рабочих станций. Ее можно рассматривать в качестве параллельного компьютера, и ночью целиком отдавать под такие задачи. Теперь попробуйте на таком компьютере запустить серьезную модель расчета изменения климата. Скорее всего, никакого ускорения решения задачи не будет. Имеем компьютер, с хорошим показателем пиковой производительности. Но для одних задач он подходит идеально, а для других никуда не годится.

Традиционно используются два способа оценки пиковой производительности компьютера. Один из них опирается на число команд, выполняемых компьютером в единицу времени. Единицей измерения, как правило, является MIPS (Million Instructions Per Second). Для определенного класса приложений такой подход является вполне приемлемым, поскольку общее представление о скорости работы компьютера получить можно. Но, опять-таки, только самое общее. Производительность, выраженная в MIPS, говорит о скорости выполнения компьютером своих же инструкций. Но в какое число инструкций отобразится программа пользователя или отдельный ее оператор? Заранее не ясно. К тому же, каждая программа обладает своей спецификой, число команд той или иной группы от программы к программе может меняться очень сильно. В этом контексте данная характеристика действительно дает лишь самое общее представление о производительности компьютера.

Интересный эффект в оценке производительности компьютера на основе MIPS наблюдается в компьютерах, в которых для выполнения вещественной арифметики применяются сопроцессоры. В самом деле, операции над числами, представленными в форме с плавающей запятой, выполняются дольше простых управляющих инструкций. Если такие операции выполняются без сопроцессора в режиме эмуляции, то срабатывает целое множество небольших инструкций. Время эмуляции намного больше, чем выполнение операции сопроцессором, но каждая небольшая инструкция срабатывает быстрее, чем команда сопроцессору. Вот и получается, что использование сопроцессора уменьшает время работы программы, зато в режиме эмуляции производительность компьютера, выраженная в MIPS, может оказаться значительно больше.

Глава 3. Архитектура параллельных вычислительных систем

165

При обсуждении производительности компьютера не менее важен и вопрос о формате используемых данных. Если процессор за один такт может выполнять операции над 32-разрядными вещественными числами, то его же производительность при работе с 64-разрядной арифметикой может упасть во много раз. Известно, что первый матричный компьютер ILLIAC IV мог выполнять до 10 миллиардов операций в секунду. И это в 1974 году! Если брать за основу только цифры, то впечатляет. А если посмотреть вглубь, то окажется, что это верно лишь для простых команд, оперирующих с байтами. Помимо работы с 64-разрядными числами, процессорные элементы 1LL1AC IV могли интерпретировать и обрабатывать данные уменьшенного формата. Например, одно слово они могли рассматривать как два 32-разрядных числа или восемь однобайтовых. Именно этот дополнительный внутренний параллелизм и позволял получить столь внушительные характеристики.

Для задач вычислительного характера, в которых важна высокая скорость выполнения операций над вещественными числами, подход к определению производительности также не должен опираться на скорость выполнения машинных инструкций. Во многих случаях операции над вещественными числами выполняются медленнее, чем, скажем, управляющие или регистровые операции. За время выполнения одной операции умножения двух чисел в форме с плавающей запятой может выполниться десяток простых инструкций. Это послужило причиной введения другого способа измерения пиковой производительности: число вещественных операций, выполняемых компьютером в единицу времени. Единицу измерения назвали Flops, что является сокращением от Floating point operations per second. Такой способ, безусловно, ближе и понятнее пользователю. Операция а + b в тексте программы всегда соответствует одной операции сложения в коде программы. Пользователь знает вычислительную сложность своей программы, а на основе этой характеристики может получить нижнюю оценку времени ее выполнения.

Да, к сожалению, оценка будет только нижней. В этом и кроется причина недовольства и разочарований. Взяв за ориентир пиковую производительность компьютера, пользователь рассчитывает и на своей программе получить столько же. Совершенно не учитывается тот факт, что пиковая производительность получается при работе компьютера в идеальных условиях. Нет конфликтов при обращении к памяти, все берется с регистров, все устройства постоянно и равномерно загружены и т. п. Но в жизни так бывает очень редко. В каждой программе пользователя есть свои особенности, которые эти идеальные условия нарушают, обнажая узкие места архитектуры. Особенности структуры процессора, система команд, состав функциональных устройств, строение и объем кэш-памяти, архитектура подсистемы доступа в память, реализация ввода/вывода — все это, и не только это, может повлиять на выполнение реальной программы. Причем заметим, мы перечислили только части аппаратуры, а говорить надо о программно-аппаратной среде выполнения программ в целом. Если для компьютера нет эффектив-

166

Часть I. Параллельные вычислительные системы

ных компиляторов, то пиковая производительность будет вводить в заблуждение еще сильнее.

Значит нужно отойти от характеристик аппаратуры и оценить эффективность работы программно-аппаратной среды на фиксированном наборе задач. Бессмысленно для каждого компьютера показывать свой набор. Разработчики без труда придумают такие программы, на которых их компьютер достигает производительности, близкой к пиковой. Такие примеры никого не убедят. Набор тестовых программ должен быть зафиксирован. Эти программы будут играть роль эталона, по которому будут судить о возможностях вычислительной системы.

Такие попытки неоднократно предпринимались. На основе различных критериев формировались тестовые наборы программ или фиксировались отдельные эталонные программы (такие программы иногда называют бенчмарками, отталкиваясь от английского слова benchmark). Программы запускались на различных системах, замерялись те или иные параметры, на основе которых в последствии проводилось сравнение компьютеров между собой. В дальнейшем изложении для подобных программ мы чаще всего будем использовать слово тест, делая акцент не на проверке правильности работы чего-либо, а на тестировании эффективности работы вычислительной системы.

Что имело бы смысл взять в качестве подобного теста? Что-то несложное и известное всем. Таким тестом стал LINPACK. Эта программа предназначена для решения системы линейных алгебраических уравнений с плотной матрицей с выбором главного элемента по строке. Простой алгоритм, регулярные структуры данных, значительная вычислительная емкость, возможность получения показателей производительности, близких к пиковым, — все эти черты сделали тест исключительно популярным.

Этот тест рассматривается в трех вариантах. В первом варианте решается система с матрицей размера 100x100. Предоставляется уже готовый исходный текст, в который не разрешается вносить никаких изменений. Изначально предполагалось, что запрет внесения изменений в программу не позволит использовать каких-либо специфических особенностей аппаратуры, и показатели производительности будут сильно занижены. В настоящее время ситуация полностью изменилась. Матрица столь небольшого размера легко помещается целиком в кэш-память современного процессора (нужно лишь 80 Кбайт), что завышает его характеристики.

Во втором варианте теста размер матрицы увеличивается до 1000x1000. Разрешается как внесение изменений в текст подпрограммы, реализующей заложенный авторами метод решения системы, так и изменение самого метода. Единственное ограничение — это использование стандартной вызывающей части теста, которая выполняет инициализацию матрицы, вызывает подпрограмму решения системы и проверяет корректность результатов.

Глава 3. Архитектура параллельных вычислительных систем

167

В этой же части вычисляется и показанная компьютером производительность, исходя из формулы для числа операций 2«³/3 + 2п² (п — это размер матрицы), вне зависимости от вычислительной сложности реально использованного алгоритма.

В данном варианте достигались значения производительности, близкие к пиковой. Этому способствовали и значительный размер матрицы, и возможность внесения изменений в программу или алгоритм. Отсюда появилось и специальное название данного варианта — LINPACK ТРР, Toward Peak Performance.

С появлением больших массивно-параллельных компьютеров вопрос подбора размера матрицы стал исключительно актуальным. На матрицах 100x100 или 1000x1000 никаких разумных показателей получить не удавалось. Эти задачи были слишком малы. Матрица размера 1000x1000 занимает лишь 0,01—0,001% всей доступной оперативной памяти компьютера. Первые эксперименты с тестом LINPACK на реальных массивно-параллельных компьютерах показали, что и фиксировать какой-либо один размер задачи тоже нельзя. В результате в третьем варианте теста было разрешено использовать изложенную во втором варианте методику для матриц сколь угодно большого размера. Сколько есть оперативной памяти на всех вычислительных узлах системы, столько и можно использовать. Для современных компьютеров размер матрицы уже перевалил за миллион, поэтому такой шаг был просто необходим.

Для работы теста LINPACK на вычислительных системах с распределенной памятью была создана специальная версия HPL (High-Performance LINPACK). В отличие от стандартной реализации, в HPL пользователь может управлять большим числом параметров для достижения высокой производительности на своей установке.

В настоящее время LINPACK используется для формирования списка Тор500 — пятисот самых мощных компьютеров мира (www.top500.org). Кроме пиковой производительности R_peak для каждой системы указывается величина R_max, равная производительности компьютера на тесте LINPACK с матрицей максимального для данного компьютера размера N_max. По значению R_max отсортирован весь список. Как показывает анализ представленных данных, величина R_max составляет 50—70% от значения Rp^. Интерес для анализа функционирования компьютера представляет и указанное в каждой строке значение N^/₂, показывающее, на матрице какого размера достигается половина производительности R_max.

Что же показывают данные теста LINPACK? Только одно — насколько хорошо компьютер может решать системы уравнений с плотной матрицей указанным методом. Поскольку задача имеет хорошие свойства, то и корреляция производительности на тесте LINPACK с пиковой производительностью компьютера высока. Операции ввода/вывода не затрагиваются, отношение

168

Часть I. Параллельные вычислительные системы

числа выполненных операций к объему используемых данных высокое, регулярность структур данных и вычислений, простая коммуникационная схема, относительно небольшой объем передач между процессорами и другие свойства программы делают данный тест "удобным". Безусловно, по данным этого теста можно получить много полезной информации о вычислительной системе и с этим никто не спорит. Но нужно ясно понимать и то, что высокая производительность на LINPACK совершенно не означает того, что и на вашей конкретной программе будет достигнута высокая производительность.

Интересное свойство LINPACK связано с законом Мура. Согласно этому закону производительность вычислительных систем удваивается каждые 18 месяцев. Не имея строгих доказательств, этот закон, тем не менее, подтверждается уже не один десяток лет. Согласно закону, объем памяти увеличивается в четыре раза каждые три года. Это позволит каждые три года удваивать размер используемой матрицы. За эти же три года производительность компьютеров вырастет в четыре раза. Поскольку вычислительная сложность теста LINPACK есть куб от размера матрицы, то время выполнения третьего варианта теста должно удваиваться каждые три года. Получается, что фиксировать размер матрицы нельзя, а использование матриц максимального размера со временем приведет к очень большим затратам. Желателен компромисс, который пока не найден.

В любом случае ясно то, что данных одного теста LINPACK для получения всей картины о возможностях компьютера мало. Неплохим дополнением к тесту LINPACK является набор тестов STREAM. Этот набор содержит четыре небольших цикла, работающих с очень длинными векторами. Основное назначение тестов STREAM состоит в оценке сбалансированности скорости работы процессора и скорости доступа к памяти.

Ключевыми в тесте являются следующие четыре операции:

a(i) = b(i) a(i) = q * b(i) a(i) = b(i) + c(i) a(i) = b(i) + q * c(i)

Размеры массивов подбираются таким образом, чтобы ни один из них целиком не попадал в кэш-память. Форма записи тестовой программы исключает возможность повторного использования данных, что также могло бы исказить реальную картину. Результатом работы тестов являются вычисленные значения реальной скорости передачи данных и производительности.

Первый тест предназначен для определения скорости передачи данных в отсутствии какой-либо арифметики. Во втором тесте добавлена одна дополнительная операция. Поскольку вторым аргументом является скалярная переменная, то объем передаваемых данных между процессором и памятью

Глава 3. Архитектура параллельных вычислительных систем

169

останется на прежнем уровне. Возможное различие в получаемых результатах будет определяться способностью компьютера выполнять арифметические операции с одновременным доступом к памяти. В третьем тесте появляется второй входной вектор, что увеличивает нагрузку на тракт процессор—память. В последнем тесте добавляется еще одна операция. Все тесты работают с 64-разрядными вещественными числами.

Предполагается, что в хорошо сбалансированной архитектуре скорость выполнения арифметических операций должна быть согласована со скоростью доступа в память. В современных высокопроизводительных системах это выполняется, но, как правило, только при работе с верхними уровнями иерархии памяти. Если попали данные в кэш-первого уровня, то все будет хорошо. А что делать в других случаях? Именно по этой причине тесты STREAM работают с очень большими векторами, хранящимися в основной оперативной памяти. Попробуйте на доступной вам системе провести следующий эксперимент. С помощью, например, четвертого теста определите реальную скорость передачи данных между процессором и памятью. Разделите пиковую производительность компьютера на только что полученное значение. Чем больше полученное вами число, тем менее сбалансированы в архитектуре скорости обработки и передачи данных (меньше единицы данное значение бывает далеко не всегда).

Характеристики компьютеров, полученные на тех или иных тестах, всегда вызывали и будут вызывать недоверие и критику. Единственная характеристика, которая по-настоящему интересует пользователя — это насколько эффективно компьютер будет выполнять его собственную программу. Каждая программа уникальна. В каждой программе своя смесь команд, задействую-щая определенные компоненты вычислительной системы. Повторить или смоделировать поведение каждой программы тест не может, поэтому и остается у пользователя сомнение в адекватности полученных характеристик.

Это в полной мере касается таких простых тестов, как LINPACK или STREAM. Однако, если задуматься, то возникает замкнутый круг. С одной стороны, тесты должны быть легко переносимыми с платформы на платформу, а потому должны быть простыми. Чтобы поместиться в памяти каждого компьютера, структуры данных должны быть небольшими. Более того, чтобы получить широкое признание, тест должен иметь понятную формулировку решаемой задачи. Перемножение матриц, метод Гаусса решения системы линейных уравнений, быстрое преобразование Фурье, метод Монте-Карло — это все доступно, компактно, используется многими, легко переносится. С другой стороны, к подобным программам всегда было отношение, как к чему-то несерьезному, как к "игрушкам". Фиксированный размер задачи, характерное вычислительное ядро, отсутствие интенсивного ввода/вывода, упрощенный код и другие свойства тестов дают веские основания для подобного отношения. Доля истины в таких рассуждениях, безусловно, есть. Жизнь всегда намного богаче и разнообразнее, чем теория.

170

Часть I. Параллельные вычислительные системы

Точно так же и реальные программы по отношению к тестам. Что же в результате мы имеем? Средства для оценки производительности компьютеров необходимы. Чтобы использоваться широко, они должны быть простыми. Простые тесты не дают полной картины и в каждом случае нужно использовать дополнительные средства. Простота необходима, но простота не приводит к искомому результату.

Одно из возможных направлений выхода из данной ситуации состоит в формировании набора взаимодополняющих тестов. Если одно число не может адекватно охарактеризовать вычислительную систему, можно попытаться это сделать с помощью набора чисел. Тестовые программы могут браться из разных предметных областей и делать акцент на различных особенностях архитектуры. Часть программ может быть модельными приложениями, а часть может представлять реальные промышленные приложения. Ясно, что принципы формирования таких наборов могут быть самыми разными.

Одним из первых пакетов, построенных на таких принципах, стал набор из 24 Ливерморских циклов (The Livermore Fortran Kernels, LFK) [59]. В его состав вошли вычислительные ядра прикладных программ, используемых в Ливерморской национальной лаборатории США. Все включенные в пакет фрагменты программ являются простыми циклическими конструкциями, разобраться в которых не составляет никакого труда. Часть циклов представляют собой типичные вычислительные блоки типа скалярного произведения, рекурсий или вычисления значения полиномов. Другая часть содержит часто используемые конструкции языка Fortran. Некоторые циклы содержат фрагменты, эффективная компиляция которых может быть затруднена. Примеры трех тестовых конструкций показаны ниже.

С*** KERNEL 1 HYDRO FRAGMENT

cdir$ ivdep

DO 1 k = 1, n 1 X(k) = Q + Y(k) * (R * ZX(k+10) + T * ZX(k+ll))

C*** KERNEL 9 INTEGRATE PREDICTORS

DO 9 k = 1, n

PX(l,k) = DM28*PX(13,k) + DM27*PX(12,k) + DM26*PX(11,k) +

1 DM25*PX(10,k) + DM24*PX( 9,k) + DM23*PX( 8,k) +

2 DM22*PX( 7,k) + C0*(PX( 5,k) + PX(6,k))+ PX(3,k) 9 CONTINUE

C*** KERNEL 20 DISCRETE ORDINATES TRANSPORT: RECURRENCE

Глава 3. Архитектура параллельных вычислительных систем 171

dw = 0.200dO cdir$ novector с

DO 20 к = 1, n

di = Y(k) - G(k)/( XX(k)+DK)

dn = dw

IF( di.NE.0.0) dn = MAX( S,MIN( Z(k)/di, T))

X(k) = ((W(k)+V(k)*dn)* XX(k)+U(k))/(VX(k)+V(k)*dn)

XX(k+l) = (X(k) - XX(k) ) *dn+ XX (k) 20 CONTINUE cdir$ vector с

Все тесты LFK очень маленькие, и это характерное свойство пакета в целом. В некоторых тестах содержатся явные указания компилятору. Например, в тесте 1 стоит директива ivdep, которая говорит об отсутствии информационной зависимости в цикле и достаточно большом числе итераций цикла, при котором векторизация заведомо будет иметь смысл. В тесте 20 есть директива novector, препятствующая использованию векторных команд компилятором во фрагменте вплоть до последующей директивы vector.

Первые версии LFK появились в начале 70-х годов прошлого столетия. Столь раннее возникновение пакета определило его основную направленность — измерение производительности отдельных процессоров. Значительную популярность Ливерморские циклы приобрели на векторно-конвейерных машинах, что, впрочем, легко объяснимо. Формирование набора тестов в виде небольших циклических конструкций хорошо подходило компьютерам этого класса, находившегося в то время на волне высокопроизводительных вычислений.

Интересно, что Ливерморские циклы использовались исследователями в разных целях. Выполнив данный тест на каком-либо перспективном компьютере, можно было приблизительно оценить, насколько хорошо или плохо будут работать характерные вычислительные конструкции. Для этого пакет и создавался. Вместе с тем, Ливерморские циклы широко применялись в качестве теста для компиляторов. Конструкции простые, результат легко оценить и проверить, а для высокопроизводительных компьютеров высокое качество генерируемого кода является исключительно важным требованием.

Пакет тестов PERFECT Club Benchmarks (Performance Evaluation for Cost-effective Transformations) появился в конце 80-х годов прошлого века [45]. Он состоит из тринадцати программ, общим объемом более 50 000 строк на языке Fortran-77. Практически все программы являются реальными приложениями, взятыми из различных предметных областей: вычислительная

172

Часть I. Параллельные вычислительные системы

гидродинамика, прогноз погоды, обработка сигналов, моделирование распространения вредных примесей в атмосфере, квантовая механика и др. В этом и состояла основная идея — работать, по возможности, не с модельными, а с реальными, живыми программами. Результаты были получены на многих компьютерах и дали богатейший материал для исследований. Программы данного пакета тестировали если и не все, то очень многие параметры вычислительных систем.

Однако пакет PERFECT Club Benchmarks не получил широкого распространения. С момента его появления часто высказывалось мнение, что сам процесс адаптации программ пакета к новому компьютеру является нетривиальной задачей. Во многих случаях процесс тестирования выполнялся на порядок быстрее процесса адаптации пакета. С появлением параллельных компьютеров с распределенной памятью ситуация ухудшилась. Потребовались соответствующие версии программ этого пакета. Но попробуйте взять уже готовое приложение, изначально не предназначенное для распараллеливания, состоящее из 5000—10 000 строк, и переписать его, скажем, в терминах МР1 или PVM. Переписать "как-нибудь" не сложно, но что такие тесты покажут, какие выводы из их работы можно будет сделать? Если возможность векторизации и адаптация программ для векторно-конвейерных компьютеров еще как-то просматривалась, то перенос программ пакета на компьютеры с распределенной памятью оказался неразрешимой задачей. Кстати, результаты адаптации программы TRFD из пакета PERFECT Club Benchmarks приведены в примере 7.6 из § 7.6. Интересное исследование структуры программы FL052Q из этого же пакета с описанием методики ее распараллеливания можно найти в [3].

Наибольшую известность среди наборов тестов получил пакет NAS Parallel Benchmarks (NPB). В состав пакета входят две группы тестов, отражающих различные стороны реальных программ вычислительной гидродинамики. Пять программ представляют типичные вычислительные ядра, а три программы являются модельными приложениями. Такой состав пакета разумен и вполне оправдан. На вычислительных ядрах можно оценить эффективность выполнения компьютером базовых фрагментов многих реальных программ. Но поскольку никакое ядро само по себе не заменит всей программы целиком, то в состав пакета были включены упрощенные варианты реальных приложений. По сравнению с реальными аналогами эти приложения имеют более регулярную структуру и реализуют упрощенную модель, что явилось результатом компромисса между "реальностью" тестов и сложностью их переноса с компьютера на компьютер.

Ключевыми в вычислительных ядрах пакета являются следующие операции.

□ ЕР (Embarrassingly Parallel). Каждым параллельным процессом выполняется генерация большого числа псевдослучайных чисел. Взаимодействие процессов требуется только в конце получения очередной порции чисел.

Глава 3. Архитектура параллельных вычислительных систем

173

П IS (Integer Sort). Вариант сортировки большого массива целых чисел.

□ FT (Fourier Transform). Быстрое преобразование Фурье на трехмерной решетке.

□ MG (MultiGrid). Решение трехмерного уравнения Пуассона на основе многосеточного метода.

□ CG (Conjugate Gradient). Реализация метода сопряженных градиентов для нахождения наименьшего собственного значения разреженной симметричной положительно определенной матрицы.

Модельные приложения отражают решение систем дифференциальных уравнений в частных производных на логически структурированных сетках с использованием трех различных неявных методов релаксации.

□ Тест LU включает схему симметричной последовательной верхней релаксации, отражая решение регулярно разреженных, блочных (5x5), нижних и верхних треугольных систем.

□ Тест SP содержит решение последовательности независимых скалярных пятидиагональных систем, каждая из которых ориентирована вдоль трех взаимно ортогональных направлений в вычислительном пространстве.

□ Тест ВТ близок к тесту SP, отличаясь, в основном, решением блочных (5x5) трехдиагональных систем вместо скалярных пятидиагональных систем. Как в ВТ, так и в SP используются варианты классического неявного метода попеременных направлений.

В процессе своего развития, пакет прошел два этапа. Основное различие этапов заключается в правилах написания и адаптации тестов для новых компьютеров. Первая версия NPB 1.0 фиксировала только постановку решаемых задач, входные данные и результаты вычислений для проверки корректности расчетов. Для каждой конкретной вычислительной системы исследователи могли выбрать наиболее подходящий метод, структуры данных, способ организации программы. Конечно же, некоторые ограничения все же накладывались. В частности, запрещалось явное программирование на ассемблере, поскольку это смещало акценты в целях и задачах тестирования. Но в целом предоставленная возможность выбора, с помощью которого можно было учесть особенности архитектуры компьютера, является оправданной.

По большому числу компьютеров были получены интересные результаты, но тестирование в таком виде не прижилось. Основных причин было две. Во-первых, это высокая трудоемкость создания варианта тестов для каждой новой вычислительной платформы. По сути дела, каждый раз тесты писались заинтересованным коллективом заново. Здесь же кроется и вторая причина — как сравнивать данные проведенного тестирования? Какую полезную информацию сможет почерпнуть пользователь из такого тестирования? В случае хорошего результата можно было сказать только одно: существует коллектив, который может эффективно решить поставленную задачу

174

Часть /. Параллельные вычислительные системы

на данном компьютере. Очень часто такой коллектив формировался из числа сотрудников компании, производящей тестируемый компьютер. Сроки создания теста не понятны, трудоемкость процесса не ясна, исходные тексты, как правило, не распространялись, для оценки были доступны только конечные цифры. Это скорее напоминало соревнование фирм-производителей, которые по сравнению с обычными пользователями работали в заведомо идеальных условиях. По сути полученные цифры являлись аналогом пиковой производительности, но уже применительно к конкретной задаче, поскольку производительности выше этого значения пользователь не получит. Подобные соображения привели к созданию последующей версии пакета NPB.

Начиная с версии NPB 2.0, появившейся в конце 1995 года, фиксировались алгоритмы и исходные тексты для всех тестов. Основная ориентация делалась на параллельные компьютеры с большим числом процессоров и распределенной иерархической памятью. В качестве средств программирования использовались Fortran 77 и MPI. Ко всем исходным текстам предоставили свободный доступ, что позволило собрать данные для большого числа вычислительных систем.

Изменилась и методика тестирования. В отличие от первой версии в NPB 2.0 разрешалось лишь два уровня оптимизации. Первый уровень не допускал никаких изменений исходного текста, а на втором уровне можно было изменить не более 5% кода. Чаще всего на практике рассматривается первый уровень.

Со временем и в тестах NPB столкнулись с проблемой подбора разумного размера задачи для больших вычислительных систем. В описании тестов теперь фигурируют пять различных классов решаемых задач, на практике чаще всего используются три старших класса: А, В и С.

Обе версии тестов NPB в совокупности дают прекрасный материал для анализа эффективности функционирования вычислительных систем. Результаты первой версии дают профессионально полученную верхнюю оценку производительности для каждого теста. Эта работа была выполнена экспертами очень высокой квалификации. Данные второй версии пакета NPB показывают значения, которые будут характерны для, скажем так, "грамотного" пользователя. Сравнение этих величин дает много полезной информации. В частности, увидев верхнюю оценку, можно сразу понять, стоит ли тратить усилия на дальнейшую оптимизацию кода.

Очень важно и то, что различные тесты пакета NPB позволяют по-разному взглянуть на характеристики программно-аппаратной среды вычислительной системы. В частности, тесты IS и FT требуют не только эффективной реализации глобальных операций, но и высокой пропускной способности сети для передачи больших сообщений. Тест LU характерен передачей большого числа относительно небольших сообщений, что накладывает же-

Глава 3. Архитектура параллельных вычислительных систем

175

сткие ограничения на величину латентности коммуникационной среды. Тест SP отличается малой степенью повторного использования данных, поэтому для него важна большая пропускная способность тракта процессор-память. Напротив, тесты ВТ и LU значительную часть времени тратят на обращение плотных матриц 5x5, поэтому для них важнее эффективная работа кэш-памяти и оптимальное использование регистров.

Этот же набор тестов показал, насколько важной характеристикой является коммуникационный профиль приложений. На небольших параллельных компьютерах коммуникационный профиль программ был не столь интересен. С распространением вычислительных систем, содержащих десятки и сотни процессоров, это понятие вышло на передний план. Длина сообщений, интенсивность передачи сообщений в разные моменты времени работы программы, топология передач сообщений между процессорами, накладные расходы на организацию взаимодействия, масштабируемость коммуникационной структуры программы, структура синхронных и асинхронных посылок — эти и ряд других характеристик определяют коммуникационный профиль приложения.

Детальный анализ коммуникационного профиля тестов пакета NPB дает очень много полезной информации. В частности, взаимодействие параллельных процессов в тестах FT и IS опирается на коллективные операции, в тестах ВТ и SP используются асинхронные пересылки, а тесты LU и MG построены на основе синхронной передачи сообщений. Для тестов SP и ВТ характерен большой объем данных, пересылаемых с каждого процессора, для LU и MG свойственна небольшая средняя длина сообщений. Для многих тестов пакета разница между минимальной и максимальной длиной сообщений составляет несколько порядков. Подобное исследование и описание коммуникационных свойств пакета NPB можно найти, например, в [66].

При всех положительных свойствах пакета NAS Parallel Benchmarks, полной картины о производительности компьютера он все же не дает. Безусловно, NPB является одним из лучших наборов тестов, предназначенных для анализа эффективности параллельных вычислительных систем. Однако у пакета есть и большой недостаток — его поддержкой в настоящее время никто не занимается...

Среди известных тестов, используемых сегодня для оценки производительности компьютеров, можно назвать тесты SPEC. Держателем тестов SPEC является Standard Performance Evaluation Corporation. Это некоммерческий консорциум, в который входят производители вычислительных систем и программного обеспечения, учебные и научные организации. Основная задача консорциума состоит в разработке тестов для самых разных программно-аппаратных сред, моделирующих реальные рабочие нагрузки. В состав тестового набора входят тесты вычислительного характера, тесты скорости работы системы в качестве Web-серверов, почтовых серверов, тесты графи-

176

Часть I. Параллельные вычислительные системы

ческих подсистем и многие другие. В их состав включен и пакет SPEChpc96, призванный отразить оценку производительности многопроцессорных вычислительных систем. Состав тестов часто меняется, что вызвано желанием консорциума оперативно отражать последние достижения в развитии вычислительной техники.

В середине 2001 года появился пакет программ SPEC ОМРМ2001, предназначенный для измерения производительности параллельных систем с общей памятью, содержащих от 4 до 32 процессоров. Измерение проводится на программах, записанных в терминах ОрепМР. Последователем данного пакета является SPEC OMPL2001, расширяющий число процессоров в тестируемой конфигурации компьютера до 512.

Но так уж сложилось, что тесты SPEC, в основном, используются для оценки производительности традиционных систем. Здесь у разработчиков есть большой опыт, задача более обозримая, разработаны методики. Широкого признания в мире параллельных компьютеров тесты SPEC пока не получили.

Как мы уже видели, одна из серьезных проблем многих тестов состоит в аккуратном подборе размера задачи. Так было с тестом L1NPACK, для которого рассматривались варианты матриц 100x100, 300x300, 1000x1000 и матрицы максимального размера, помещающиеся в память компьютера. Так было с пакетом NPB, включающим пять характерных размеров задач. Одной из первых удачных попыток решить проблему подбора размера задачи стал тест HINT, изменяющий вычислительную нагрузку в процессе своей работы [51]. Данное свойство позволяет тесту HINT оценить эффективность работы компьютера в различных режимах работы с памятью (регистры, кэш, основная память), что абсолютно не было свойственно тестам с фиксированным размером задачи. Эта же особенность дает возможность получать многие характеристики рассмотренных выше тестов SPEC, L1NPACK и NPB на основе результатов работы теста HINT.

Однако что бы ни говорили создатели тестовых пакетов и программ, скепсис по поводу получаемых с помощью бенчмарков результатов у пользователей пока остается. Во многом это связано с тем, что тестирование не дает полного представления о работе компьютера в различных режимах. Любой тест приоткрывает лишь часть общей картины. Результат его работы можно условно считать точкой в пространстве, описывающем поведение компьютера в целом. Если рассматривается набор тестов, например, NPB, то в пространстве будем иметь несколько точек. Ясно, что кардинально это проблему не решает. Объем полученной выборки не может быть сравним со всем многообразием вариантов поведения тестируемого компьютера на реальных программах и наборах данных.

Хорошим вариантом для описания свойств компьютера можно было бы считать возможность выделения в таком пространстве некоторого набора характерных опорных точек. Но что считать характерной точкой и как ин-

Глава 3. Архитектура параллельных вычислительных систем

177

терполировать поведение компьютера на конкретной программе по значениям базовых параметров в выделенных характерных точках? Другой способ описания можно попытаться найти через определение функциональной зависимости свойств компьютера от параметров его программно-аппаратной среды. Однако в аналитическом виде достаточно точные оценки получить крайне сложно, а на методы вычислительного характера в настоящее время опирается только тест HINT.

Поскольку никакое одно число или даже набор чисел не будут универсальной характеристикой производительности компьютера, то при необходимости получения истинной картины о свойствах компьютера идут по пути комплексного тестирования программно-аппаратной среды в целом. Определяют параметры работы вычислительного комплекса на большом наборе программ, имеющих различные вычислительно-коммуникационные характеристики. Такая работа, как правило, тяжела и трудоемка, но другого пути в настоящий момент нет. В зависимости от целей тестирования выделяют и используют следующие уровни:

□ базовый уровень программного обеспечения: тестирование эффективности работы операционной системы, компиляторов и систем программирования. Этот уровень рассматривается далеко не всегда, но нужно учесть, что все последующие действия будут "видны" через призму данного уровня (если компилятор плох, то хороших результатов не будет ни на одном другом уровне);

□ базовый уровень аппаратуры: определение скорости выполнения элементарных операций, скорости обмена между различными уровнями иерархии памяти и объемы доступной памяти на каждом уровне (определение объемов важно для последующей интерпретации результатов);

□ уровень операций ввода/вывода: анализ эффективности различных режимов чтения и записи данных при работе с внешними устройствами, определение скорости выполнения основных операций с файлами и целесообразности выполнения асинхронных операций ввода/вывода;

□ базовый коммуникационный уровень: определение параметров среды взаимодействия параллельных процессов, эффективности выполнения основных коммуникационных процедур и примитивов синхронизации. В настоящее время этот уровень чаще всего подразумевает определение латентности и скорости передачи данных по коммуникационной сети в различных режимах, а также тестирование эффективности работы конструкций MPI;

□ коммуникационный уровень приложений: исследование эффективности отображения различных логических топологий процессов на коммуникационную среду, получение и анализ коммуникационных профилей характерных параллельных программ;

178

Часть I. Параллельные вычислительные системы

П уровень модельных приложений: определение характеристик компьютера при выполнении простых программ различной структуры;

□ уровень приложений: комплексная проверка характеристик компьютера при выполнении реальных программ.

Ясно, что задача определения производительности параллельных компьютеров сложна и на сегодня еще далека от своего решения. Слишком много параметров, зачастую противоречивых, приходится учитывать при конструировании реальных бенчмарков. Состав операций, коммуникационный профиль, требуемый размер памяти на каждом уровне иерархии, простота переноса между вычислительными платформами, время работы, базовые вычислительные конструкции, простота интерпретации результатов — все это, как и многое другое, должно приниматься в расчет авторами тестов.

Ситуация не простая. Но, с другой стороны, задача ясна, необходима и до сих пор еще не решена — так ли это плохо? Цель определена и есть большое поле для деятельности...

Вопросы и задания

1. Почему цена компьютеров не может служить основой критерия для оценки их производительности?

2. Сравните пиковую производительность какого-либо современного спецпроцессора с пиковой производительностью универсального микропроцессора. С какой производительностью универсальный процессор будет выполнять "наиболее удобные" для спецпроцессора операции?

3. Возьмите любой современный микропроцессор. Чему равна его производительность, измеренная на пакетах LINPACK, SPEC, STREAM? Как эти данные соотносятся с его пиковой производительностью?

4. Какие преимущества и недостатки в использовании программы перемножения двух матриц в качестве бенчмарка для параллельных вычислительных систем?

5. Перечислите, какими свойствами должен обладать хороший бенчмарк для параллельных вычислительных систем?

6. Напишите тестовую программу, определяющую размер кэш-памяти первого и второго уровней и объем доступной оперативной памяти.

7. Подумайте, какие другие задачи можно было бы использовать в качестве теста, аналогично задаче решения системы уравнений в тесте LINPACK?

8. Напишите программу, которая показывает, насколько может изменяться производительность процессора в зависимости от расположения данных в его памяти.

9. Постройте и проанализируйте коммуникационный профиль вашей параллельной программы. Определите основные источники затрат на коммуникации.

10. Выделите типичные коммуникационные схемы параллельных программ. Напишите тест, реализующий данные схемы и сравните эффективность их работы в различных средах.

ЧАСТЬ II

Параллельное программирование

Глава 4

Большие задачи

и параллельные вычисления

Если у веревки есть один конец, значит у нее должен быть и другой.

Из законов Мерфи

Если создают большие вычислительные системы, значит они для чего-то нужны. Это что-то — большие задачи, которые постоянно возникают в самых различных сферах деятельности. Практическая потребность или просто любознательность всегда ставили перед человеком трудные вопросы, на которые нужно было получать ответы. Строится высотное задание в опасной зоне. Выдержит ли оно сильные ветровые нагрузки и колебания почвы? Проектируется новый тип самолета. Как он будет вести себя при различных режимах полета? Уже сейчас зафиксировано потепление климата на нашей планете и отмечены негативные последствия этого явления. А каким будет климат через сто и более лет?

Подобного рода вопросы сотнями и тысячами возникают в каждой области. Уже давно разработаны общие принципы поиска ответов. Первое, что пытаются сделать, — это построить математическую модель, адекватно отражающую изучаемое явление или объект. Как правило, математическая модель представляет собой некоторую совокупность дифференциальных, интегральных, алгебраических или каких-то других соотношений, определенных в области, так или иначе связанной с предметом исследований. Решения этих соотношений и должны давать ответы на поставленные вопросы.

Как следует из предыдущих глав, существующие компьютеры сами по себе не могут решить ни одной содержательной задачи. Они способны выполнять лишь небольшое число очень простых действий. Вся их интеллектуальная сила определяется программами, составленными человеком. Программы также реализуют последовательности простых действий. Но эти действия целенаправленные. Поэтому искусство решать задачи на компьютере есть искусство превращения процесса поиска решения в процесс выполнения последовательности простых действий. Называется такое искусство разработкой алгоритмов.

Если математическая модель построена, то следующее, что надо сделать, — это разработать алгоритм решения задачи, описывающей модель. Довольно часто в его основе лежит принцип дискретизации изучаемого объекта и, если необходимо, окружающей его среды. Исследуемый объект и среда разби-

182

Часть II. Параллельное программирование

ваются на отдельные элементы и на эти элементы переносятся связи, диктуемые математической моделью. В результате получаются системы уравнений с очень большим числом неизвестных. В простейших случаях число неизвестных пропорционально числу элементов. Для сложных моделей оно на несколько десятичных порядков больше. Вообще говоря, чем мельче выбирать элементы разбиения, тем точнее получается результат. В большинстве задач уровень разбиения определяется только возможностью компьютера решить возникающую систему уравнений за разумное время. Но в некоторых задачах, таких как изучение структуры белковых соединений, расшифровка геномов живых организмов, разбиение по самой сути может доходить до уровня отдельных атомов. И тогда вычислительные проблемы становятся исключительно сложными даже для самых мощных компьютеров, в том числе, параллельной архитектуры.

Во все времена были задачи, решение которых находилось на грани возможностей существовавших средств. Вплоть до середины двадцатого столетия единственным вычислительным средством был человек, вооруженный в лучшем случае арифмометром или электрической счетной машиной. Решение наиболее крупных задач требовало привлечения до сотни и более расчетчиков. Так как вычисления они проводили одновременно, то по существу такой коллектив своими действиями моделировал работу многопроцессорной вычислительной системы. Роль отдельного процессора в этой системе выполнял отдельный человек. При подобной организации вычислений никак не могло появиться большое число крупных задач. Их просто некому было считать. Поэтому еще 50—60 лет назад весьма распространенным являлось мнение, что несколько мощных компьютеров смогут решить все практически необходимые задачи.

История опровергла эти прогнозы. Компьютеры оказались настолько эффективным инструментом, что новые и очень крупные задачи стали возникать не только в традиционных для вычислений областях, но даже в таких, где раньше большие вычислительные работы не проводились. Например, в военном деле, управлении, биологии и т. п. К тому же, использование компьютеров освободило человека от нудного и скрупулезного труда, связанного с выполнением операций. Это позволило ему направить свой интеллект на постановку новых задач, построение математических моделей, разработку алгоритмов и при этом не бояться больших объемов вычислений. Подобные обстоятельства и привели к массовой загрузке компьютеров решением самых разных проблем, в том числе, очень крупных. Случилось то, что и должно было случиться: за исключением начального периода развития компьютеров спрос на самые большие вычислительные мощности всегда опережал и опережает предложение таких мощностей. Другое дело, что реализовать как спрос, так и предложение оказалось трудно.

Большие задачи и компьютеры представляют две взаимосвязанные сферы деятельности, два конца одной веревки. Если был один конец — большие

Глава 4. Большие задачи и параллельные вычисления

183

задачи, значит должен был появиться и другой — компьютеры. Потребность в решении больших задач заставляет создавать более совершенные компьютеры. В свою очередь, более совершенные компьютеры позволяют улучшать математические модели и ставить еще большие задачи. В конце концов, обыкновенные компьютеры превратились в параллельные. Задачи от этого параллельными не стали, но начали развиваться алгоритмы с параллельной структурой вычислений. В результате опять появилась возможность увеличить размеры решаемых задач. Теперь на очереди стоят оптические и квантовые компьютеры. Конца этому процессу не видно.

§ 4.1. Большие задачи и большие компьютеры

На примере проблем моделирования климатической системы и исследования обтекания летательных аппаратов покажем, как возникают очень большие задачи и что за этим следует дальше.

В современном понимании климатическая система включает в себя атмосферу, океан, сушу, криосферу и биоту [26]. Климатом называется ансамбль состояний, который система проходит за достаточно большой промежуток времени. Климатическая модель — это математическая модель, описывающая климатическую систему. В основе климатической модели лежат уравнения динамики сплошной среды и уравнения равновесной термодинамики. Кроме этого, в модели описываются все энергозначимые физические процессы: перенос излучения в атмосфере, фазовые переходы воды, облака и конвенция, перенос малых газовых примесей и их трансформация, мелкомасштабная турбулентная диффузия тепла и диссипация кинетической энергии и многое другое. В целом модель представляет систему трехмерных нелинейных уравнений с частными производными. Решения этой системы должны воспроизводить все важные характеристики ансамбля состояний реальной климатической системы.

Даже без дальнейших уточнений понятно, что климатическая модель исключительно сложна. Работая с ней, приходится принимать во внимание ряд серьезных обстоятельств. В отличие от многих естественных наук, в климате нельзя поставить глобальный натурный целенаправленный эксперимент. Следовательно, единственный путь изучения климата — это проводить численные эксперименты с математической моделью и сравнивать модельные результаты с результатами наблюдений. Однако и здесь не все так просто. Математические модели для разных составляющих климатической системы развиты не одинаково. Исторически первой стала создаваться модель атмосферы. Она и в настоящее время является наиболее развитой. К тому же, за сотни лет наблюдений за ее состоянием накопилось довольно много эмпирических данных. Так что в атмосфере есть с чем сравнивать

184

Часть II. Параллельное программирование

модельные результаты. Для других составляющих климатической системы результатов наблюдений существенно меньше. Слабее развиты и соответствующие математические модели. По существу только начинает создаваться модель биоты.

Общая модель климата пока еще далека от своего завершения. Не во всем даже ясно, как могла бы выглядеть совместная идеальная модель. Чтобы приблизить климатическую модель к реальности, приходится проводить очень много численных экспериментов и на основе анализа результатов вносить в нее коррективы. Как правило, пока эксперименты проводятся с моделями для отдельных составляющих климата или для некоторых их комбинаций. Наиболее часто рассматривается совместная модель атмосферы и океана. Недостающие данные от других составляющих берутся либо из результатов наблюдений, либо из каких-то других соображений.

Важнейшей проблемой современности является проблема изменения климата под влиянием изменения концентрации малых газовых составляющих, таких как углекислый газ, озон и др. Как уже отмечалось, климатический прогноз может быть осуществлен только с помощью численных экспериментов над моделью. Поэтому ясно, что для того чтобы научиться предсказывать изменение климата в будущем, уже сегодня надо иметь возможность проводить большой объем вычислений. Попробуем хотя бы как-то его оценить.

Рассмотрим модель атмосферы как важнейшей составляющей климата и предположим, что мы интересуемся развитием атмосферных процессов на протяжении, например, 100 лет. При построении алгоритмов нахождения численных решений используется упоминавшийся ранее принцип дискретизации. Общее число элементов, на которые разбивается атмосфера в современных моделях, определяется сеткой с шагом в 1° по широте и долготе на всей поверхности земного шара и 40 слоями по высоте. Это дает около 2,6х10⁶ элементов. Каждый элемент описывается примерно 10 компонентами. Следовательно, в любой фиксированный момент времени состояние атмосферы на земном шаре характеризуется ансамблем из 2,6х10⁷ чисел. Условия обработки численных результатов требуют нахождения всех ансамблей через каждые 10 минут, т. е. за период 100 лет необходимо определить около 5,3х10⁴ ансамблей. Итого, только за один численный эксперимент приходится вычислять 1,4х10¹⁴ значимых результатов промежуточных вычислений. Если теперь принять во внимание, что для получения и дальнейшей обработки каждого промежуточного результата нужно выполнить 10²— 10³ арифметических операций, то это означает, что для проведения одного численного эксперимента с глобальной моделью атмосферы необходимо выполнить порядка 10¹⁶—10¹⁷ арифметических операций с плавающей запятой.

Таким образом, вычислительная система с производительностью 10¹² операций в секунду будет осуществлять такой эксперимент при полной своей загрузке и эффективном программировании в течение нескольких часов. Ис-

Глава 4. Большие задачи и параллельные вычисления

185

пользование полной климатической модели увеличивает это время, как минимум, на порядок. Еще на порядок может увеличиться время за счет не лучшего программирования и накладных расходов при компиляции программ и т. п. А сколько нужно проводить подобных экспериментов! Поэтому вычислительная система с триллионной скоростью совсем не кажется излишне быстрой с точки зрения потребностей изучения климатических проблем.

Большой объем вычислений в климатической модели и важность связанных с ней выводов для различных сфер деятельности человека являются постоянными стимулами в деле совершенствования вычислительной техники. Так, на заре ее развития одним из следствий необходимости разработки эффективного вычислительного инструмента для решения задач прогноза погоды стало создание Дж. фон Нейманом самой теории построения "обыкновенного" компьютера. В нашумевших в свое время проектах вычислительных систем пятого поколения и во многих современных амбициозных проектах климатические модели постоянно фигурируют как потребители очень больших скоростей счета. Наконец, существуют проекты построения вычислительных систем огромной производительности, предназначенных специально для решения климатических проблем.

Имеется и обратное влияние. Развитие вычислительной техники позволяет решать задачи все больших размеров. Корректное решение больших задач заставляет развивать новые разделы математики. Как уже говорилось, изучение предсказуемости климата требует определения решения системы дифференциальных уравнений на очень большом отрезке времени. Но это имеет смысл делать лишь в том случае, когда решение обладает определенной устойчивостью к малым возмущениям. Одна из составляющих климатической системы, а именно атмосфера, относится к классу так называемых открытых (то есть имеющих внешний приток энергии и ее диссипацию) нелинейных систем, траектории которых неустойчивы поточечно. Такие системы имеют совершенно особое свойство. При больших временах их решения оказываются вблизи некоторого многообразия относительно небольшой размерности. Открытие данного свойства послужило сильным толчком к развитию теории нелинейных диссипативных систем методами качественной теории дифференциальных уравнений. В свою очередь, это существенно усложнило вычислительные задачи, возникающие при климатическом прогнозе, что опять требует больших вычислительных мощностей.

Приведенные доводы, скорее всего, убедили читателя, что для исследования климата действительно нужна очень мощная вычислительная система. Тем более, что климат нельзя изучать, выполняя над ним целенаправленные эксперименты. Однако остается вопрос, насколько много необходимо иметь таких систем. Ведь основная деятельность человека связана с созданием материальных объектов, с чем или над чем можно проводить натурные эксперименты. Например, летательные аппараты можно испытывать в аэродина-

186

Часть II. Параллельное программирование

мических трубах, материалы — на стендах, сооружения — на макетах и т. п. Конечно, здесь также нужно проводить какие-то расчеты. Но стоит ли для этих целей использовать вычислительные системы, стоящие не один миллион долларов? Возможно, для подобных расчетов достаточно ограничиться хорошим персональным компьютером или рабочей станцией?

Ответ зависит от конкретной ситуации. Возьмем для примера такую проблему, как разработка ядерного оружия. Пока не был установлен мораторий на ядерные испытания, натурные эксперименты давали много информации о путях совершенствования оружия. И хотя при этом приходилось проводить очень большой объем вычислений, все же удавалось обходиться вычислительной техникой не самого высокого уровня. После вступления моратория в силу остался единственный путь совершенствования оружия — это проведение численных экспериментов с математической моделью. По своей сложности соответствующая модель сопоставима с климатической и для работы с ней уже нужна самая мощная вычислительная техника. В аналогичном положении находится ядерная энергетика. А такая проблема, как расшифровка генома человека. Здесь также невозможны никакие глобальные эксперименты и опять нужна мощная техника. Вообще, оказывается, что проблем, где невозможно или трудно проводить натурные эксперименты, не так уж мало. Это — экономика, экология, астрофизика, медицина и т. д. При этом часто возникают очень большие задачи.

Интересно отметить, что даже там, где натурные эксперименты являются привычным инструментом исследования, большие вычислительные системы начинают активно использоваться. Рассмотрим, например, проблему выбора компоновки летательного аппарата, обладающего минимальным лобовым сопротивлением, максимально возможными значениями аэродинамического качества и допустимого коэффициента подъемной силы при благоприятных характеристиках устойчивости и управляемости в эксплуатационных режимах. Для ее решения традиционно использовались продувки отдельных деталей аппарата или его модели в аэродинамических трубах. Но вот несколько цифр [37]. При создании в начале века самолета братьев Райт эксперименты в аэродинамических трубах обошлись в несколько десятков тысяч долларов, бомбардировщик 40-х гг. прошлого столетия потребовал миллион, а корабль многоразового использования "Шатл" — 100 млн. долларов. Столь же сильно возрастает время продувки в расчете на одну трубу — почти 10 лет для современного аэробуса. Однако несмотря на огромные денежные и временные затраты, продувки в аэродинамических трубах не дают полной картины обтекания хотя бы просто потому, что обдуваемый образец нельзя окружить датчиками во всех точках. Для преодоления этих трудностей также пришлось обратиться к численным экспериментам с математической моделью [28].

Определять аэродинамические характеристики летательного аппарата нужно уже на стадии проектирования. Необходимо также давать оценку различным вариантам компоновки, оптимизировать геометрические параметры, опре-

Глава 4. Большие задачи и параллельные вычисления

187

делять внешний облик с наилучшими характеристиками. Знание соответствующих данных нужно и в процессе летных испытаний при анализе их результатов для выработки рекомендаций по устранению выявленных недостатков. Эта задача не может быть решена без информации о характере обтекания элементов аппарата и знания поля течения в целом. Как уже говорилось, экспериментальное получение такой информации по мере усложнения летательных аппаратов становится все более труднодоступным делом.

В практике работы конструкторских организаций используются инженерные методы расчета, основанные на упрощенных математических моделях. Эти методы пригодны на самых ранних этапах проектирования. Они не могут учесть деталей течения, необходимых на углубленных этапах проектирования, и не могут обеспечить требуемую точность расчетов. В большой области изменения физических параметров упрощенные модели вообще не применимы. Для углубленной стадии проектирования летательных аппаратов перспективными являются математические модели, основанные на нестационарных пространственных уравнениях динамики невязкого, нетеплопроводного газа, в том числе, учитывающие уравнения состояния и уравнения вязкого пограничного слоя между поверхностью аппарата и обтекаемой средой. Модели принципиально различаются для случаев сверхзвукового и дозвукового набегающего потока. Вообще говоря, случай дозвукового обтекания сложнее, т. к. около летательного аппарата возможно образование местных сверхзвуковых зон. Все части аппарата здесь взаимно влияют друг на друга, и задача должна решаться глобально, т. е. во всей области, окружающей летательный аппарат. Именно для расчета дозвуковых течений необходимо использовать вычислительные системы высокой производительности с большим объемом памяти.

Приведем некоторые данные конкретного расчета, взятые из той же работы [28]. Рассчитывались различные варианты дозвукового обтекания летательного аппарата сложной конструкции. Математическая модель требует задания граничных условий на бесконечности. Реально, область исследования берется конечной. Однако из-за обратного влияния границы ее удаление от объекта должно быть значительным по всем направлениям. На практике это составляет десятки длин размера аппарата. Таким образом, область исследования оказывается трехмерной и весьма большой. При построении алгоритмов нахождения численных решений опять используется принцип дискретизации. Из-за сложной конфигурации летательного аппарата разбиение выбирается очень неоднородным. Общее число элементов, на которые разбивается область, определяется сеткой с числом шагов порядка 10² по каждому измерению, т. е. всего будет порядка 10⁶ элементов. В каждой точке надо знать 5 величин. Следовательно, на одном временном слое число неизвестных будет равно 5х10⁶. Для изучения нестационарного режима приходится искать решения в 10²—10⁴ слоях по времени. Поэтому одних только значимых результатов промежуточных вычислений необходимо найти около

188

Часть II. Параллельное программирование

10⁹—10^п. Для получения каждого из них и дальнейшей его обработки нужно выполнить 10²—10³ арифметических операций. И это только для одного варианта компоновки и режима обтекания. А всего требуется провести расчеты для десятков вариантов. Приближенные оценки показывают, что общее число операций для решения задачи обтекания летательного аппарата в рамках современной модели составляет величину 10¹⁵—10¹⁶. Для достижения реального времени выполнения таких расчетов быстродействие вычислительной системы должно быть не менее 10⁹—10¹⁰ арифметических операций с плавающей запятой в секунду при оперативной памяти не менее 10⁹ слов.

Успехи в численном решении задач обтекания позволили создать комбинированную технологию разработки летательных аппаратов. Теперь основные эксперименты, особенно на начальной стадии проектирования, проводятся с математической моделью. Они позволяют достаточно достоверно определить оптимальную компоновку, проанализировать все стадии процесса обтекания, выявить потенциально опасные режимы полета и многое другое. Все это дает возможность снизить до минимума дорогостоящие натурные эксперименты в аэродинамических трубах и сделать их более целенаправленными. Конечно, численные эксперименты на высокопроизводительных вычислительных системах тоже обходятся недешево. Но все же они значительно дешевле, чем натурные эксперименты. Кроме этого, их стоимость постоянно снижается. Например, по данным США она уменьшается в 10 раз каждые 10 лет. Объединение численных и натурных экспериментов в единый технологический процесс привело к принципиально новому уровню аэродинамического проектирования. В результате значительно возросло качество, уменьшились стоимость, сроки проектирования и время испытаний летательных аппаратов. Совершенствование математических моделей сделает этот процесс еще более эффективным. Как и в примере с климатом, более совершенные модели потребуют применения более мощных вычислительных систем. В свою очередь, появление новых систем опять даст толчок совершенствованию моделей и т. д. Снова убеждаемся в том, что большие задачи и большие вычислительные системы с точки зрения их развития оказывают влияние друг на друга.

В рассмотренной проблеме выбора компоновки летательного аппарата легко увидеть нечто большее, имеющее отношение к самым различным областям деятельности человека. В самом деле, при создании тех или иных изделий, механизмов и сооружений, так же как и при проведении многих научных экспериментов весь процесс от возникновения идеи до ее реализации можно грубо разбить на следующие этапы. Сначала каким-то способом разрабатывается общий проект и готовится технологическая документация. Затем строится опытный образец или его макет. И, наконец, проводится испытание. По его результатам в опытный образец вносятся изменения и снова проводится испытание. Цикл образец—испытание—образец повторяется до тех пор, пока опытный образец не станет действующим, удовлетворяя всем

Глава 4. Большие задачи и параллельные вычисления

189

заложенным в проект требованиям. Проведение каждого испытания и внесение очередных изменений в опытный образец почти всегда требует много денег и много времени. Поэтому одна из общих задач заключается в том, чтобы на пути превращения опытного образца в действующий сократить до минимума как число испытаний, так и их стоимость и время проведения. По существу это можно сделать единственным способом — заменить часть натурных экспериментов или большинство из них, а в идеале даже все, экспериментами с математическими моделями. Значимость численных экспериментов в общем процессе зависит от качества модели. Если она хорошо отражает создаваемый или изучаемый объект, натурные эксперименты оказываются необходимыми достаточно редко, что, в свою очередь, приводит к большим материальным и временным выгодам. В этой ситуации весь процесс во многом превращается в своего рода компьютерную игру, в которой можно посмотреть различные варианты решений, обнаружить и исследовать узкие места, выбрать оптимальный вариант, проанализировать последствия такого выбора и т. д. И лишь изредка отдельные решения придется проверять на натурных экспериментах. Это обстоятельство, безусловно, стимулирует создание самых совершенных математических моделей в различных областях.

Очевидно, что использование математических моделей невозможно без применения вычислительной техники. Но оказывается, что для очень многих случаев нужна не просто какая-нибудь техника, а именно высокопроизводительная. В самом деле, изучаем ли мы процесс добычи нефти, или прочность кузова автомобиля, или процессы преобразования электрической энергии в больших трансформаторах и т. п., — исследуемые объекты являются трехмерными. Чтобы получить приемлемую точность численного решения, объект нужно покрыть сеткой не менее чем 100x100x100 узлов. В каждой точке сетки нужно определить 5—20 функций. Если изучается нестационарное поведение объекта, то состояние всего ансамбля значений функций нужно определить в 10²—10⁴ моментах времени. Поэтому только значимых результатов промежуточных вычислений для подобных объектов нужно получить порядка 10⁹—10¹¹. Теперь надо принять во внимание, что на вычисление и обработку каждого из промежуточных результатов, как показывает практика, требуется в среднем выполнить 10²—10³ арифметических операций. И вот мы уже видим, что для проведения только одного варианта численного эксперимента число операций порядка 10¹¹—10¹⁴ является вполне рядовым. А теперь учтем необходимое число вариантов, накладные расходы на время решения задачи, появляющиеся за счет качества программирования, компиляции и работы операционной системы. И сразу становится ясно, что скорость вычислительной техники должна измеряться миллиардами операций в секунду. Такая техника стоит недешево. Тем не менее, как говорится, игра стоит свеч.

190

Часть II. Параллельное программирование

Мы неоднократно подчеркивали влияние больших задач на развитие вычислительной техники и наоборот. Постепенно в эту сферу втягивается много чего другого. Развитие математического моделирования приводит к более сложным описаниям моделей. Для их осмысления и разработки принципов исследования приходится привлекать новейшие достижения из самых разных областей математики. Дискретизация задач приводит к системам уравнений с огромным числом неизвестных. Прежние методы их решения не всегда оказываются пригодными по соображениям точности, скорости, требуемой памяти, структуре алгоритмов и т. п. Возникают и реализуются новые идеи в области вычислительной математики. В конечном счете, для более совершенных математических моделей создаются новые методы реализации численных экспериментов. Как правило, они требуют больших вычислительных затрат и снова не хватает вычислительных мощностей. А далее опять все идет по кругу, о чем уже не один раз говорилось выше.

Решаясь на регулярное использование численных экспериментов, приходится заботиться о качестве их проведения. Оно определяется многими факторами. Этапы, которые проходит каждый эксперимент, укрупненно отражены на рис. 4.1 Данным рисунком мы хотим подчеркнуть простую мысль: если хотя бы один из этапов на рис. 4.1 окажется неэффективным, то неэффективным будет и весь численный эксперимент.


	ИССЛЕДУЕМОЕ ЯВЛЕНИЕ ИЛИ ОБЪЕКТ
	1
	МАТЕМАТИЧЕСКАЯ МОДЕЛЬ			РЕЗУЛЬТАТ
	▼
	ЧИСЛЕННЫЙ МЕТОД			АНАЛИЗ

				ВЫЧИСЛЕНИИ
	1
	ПРОГРАММА			КОМПЬЮТЕР
	1
	КОМПИЛЯТОР			ОПЕРАЦИОННАЯ СИСТЕМА

Рис. 4.1. Этапы численного эксперимента

Следовательно, внимательному изучению должны подвергаться все этапы численного эксперимента. Это важно понять, запомнить и постоянно реали-зовывать на практике. Не правда ли, очень похоже на закон Амдала, о котором упоминалось в связи с производительностью вычислительных систем?

Глава 4. Большие задачи и параллельные вычисления

191

Вопросы и задания

1. Допустим, что перемножаются две квадратные матрицы. Какие появятся особенности в организации вычислительных процессов, если взять матрицы максимального размера и стараться решить задачу по возможности быстрее? Рассмотрите варианты вычислительных систем:

1.1. С общей памятью и универсальными процессорами.

1.2. С общей памятью и конвейерными сумматорами, умножителями и делителями.

1.3. С распределенной памятью и универсальными процессорами.

1.4. С распределенной памятью и конвейерными сумматорами, умножителями и делителями.

2. Проделайте то же самое для решения системы линейных алгебраических уравнений методом Гаусса.

3. Что меняется во втором задании, если делители не будут конвейерными?

§ 4.2. Граф алгоритма

и параллельные вычисления

Любая программа для "обыкновенного" компьютера описывает некоторое семейство алгоритмов. Выбор конкретного алгоритма при ее реализации определяется тем, как срабатывают условные операторы. Состав и порядок выполнения остальных операторов строго задается самой программой. Если в программе отсутствуют условные операторы, то программа изначально описывает только один алгоритм. В свою очередь, срабатывания условных операторов зависят исключительно от входных данных. Поэтому "обыкновенный" компьютер всегда выполняет какую-то последовательность действий, которая однозначно определена программой и входными данными. Более того, для одной и той же программы эта последовательность будет одной и той же на любых моделях "обыкновенного" компьютера. Тем самым заведомо однозначно определяется результат. Все это является, в конечном счете, следствием того, что в любом "обыкновенном" компьютере в любой момент времени может реализоваться только одна операция. Любая другая операция в этот момент может лишь проходить стадию подготовки к реализации.

Иначе обстоит дело на вычислительных системах параллельной архитектуры. Теперь в каждый момент времени может выполняться целый ансамбль операций, не зависящих друг от друга. На любой конкретной параллельной системе программа и входные данные однозначно определяют как состав ансамблей, так и их последовательность. Но на разных системах ансамбли и последовательности могут быть разными. Чтобы, тем не менее, гарантировать получение однозначного результата, порядок выполнения всей совокупности операций должен подчиняться некоторому условию.

192

Часть II. Параллельное программирование

Как на "обыкновенном", так и на параллельном компьютере решение задачи находится в результате выполнения множества простых операций. Все операции имеют небольшое число аргументов. Обычно их не более двух. В качестве конкретных значений аргументов операции берутся либо входные данные, либо результаты выполнения других операций. Соответствие, какие результаты какими являются аргументами, устанавливается разработчиком программы. Ясно, что любая операция — потребитель аргументов не может начать выполняться раньше, чем закончится выполнение всех операций — поставщиков для нее аргументов. Тем самым на множестве всех операций разработчик программы явно или неявно устанавливает частичный порядок. Для любых двух операций порядок определяет одну из возможностей: либо указывает, какая из операций должна выполняться раньше, либо констатирует, что обе операции могут выполняться независимо друг от друга. При одном и том же частичном порядке общий временной порядок всего множества операций может быть различным. Несколько позже мы покажем, что любой из этих порядков дает один и тот же результат. Поэтому сохранение частичного порядка, заданного программой, и есть то условие, выполнение которого гарантирует однозначность результата. В рамках одного и того же частичного порядка возможен выбор любой реализации.

Дадим сказанному следующую трактовку. Пусть при фиксированных входных данных программа описывает некоторый алгоритм. Построим ориентированный граф. В качестве вершин возьмем любое множество, например, множество точек арифметического пространства, на которое взаимнооднозначно отображается множество всех операций алгоритма. Возьмем любую пару вершин и, v. Допустим, что согласно описанному выше частичному порядку операция, соответствующая вершине и, должна поставлять аргумент операции, соответствующей вершине v. Тогда проведем дугу из вершины и в вершину v. Если соответствующие операции могут выполняться независимо друг от друга, дугу проводить не будем. В случае, когда аргументом операции является начальное данное или результат операции нигде не используется, возможны различные договоренности. Например, можно считать, что соответствующие дуги отсутствуют. Или предполагать, что все входные данные и результаты вводятся и выводятся через специальные устройства ввода/вывода. В этом случае вершины графа, отвечающие таким операциям, и только они не будут иметь соответственно входящие и выходящие дуги. Мы будем поступать в зависимости от обстоятельств. Построенный таким образом граф можно было бы назвать графом информационной зависимости реализации алгоритма при фиксированных входных данных. Однако такое название слишком громоздко. Поэтому будем называть его в дальнейшем просто графом алгоритма. Независимо от способа построения ориентированного графа, те его вершины, которые не имеют ни одной входящей или выходящей дуги, будем называть соответственно входными или выходными вершинами графа.

Глава 4. Большие задачи и параллельные вычисления

193

Это понятие требует некоторого пояснения. Граф алгоритма почти всегда зависит от входных данньгх. Даже если в программе отсутствуют условные операторы, он будет зависеть от размеров массивов, т. к. они определяют общее число выполняемых операций и, следовательно, общее число вершин графа. Так что в действительности граф алгоритма почти всегда есть параметризованный граф. От значений параметров зависит, конечно, не только число вершин, но и вся совокупность дуг. Если программа не имеет условных операторов, то как ее саму, так и описанный ею алгоритм будем называть детерминированными. В противном случае будем называть их недетерминированными. Имеется одно принципиальное отличие графа детерминированного алгоритма от графа недетерминированного алгоритма. Для детерминированного алгоритма всегда существует взаимно-однозначное соответствие между всеми операциями описывающей его программы и всеми вершинами графа алгоритма. Для недетерминированного алгоритма взаимно-однозначного соответствия при всех значениях параметров, т. е. входных данных, нет. Можно лишь утверждать, что в этом случае при каждом наборе значений параметров существует взаимно-однозначное соответствие между каким-то подмножеством всех операций программы и вершинами графа. Разным значениям параметров могут соответствовать разные подмножества.

В дальнейшем, если не сделаны дополнительные оговорки, мы будем рассматривать детерминированные алгоритмы и программы. Причин для введения этого ограничения довольно много. Во-первых, они устроены проще и, естественно, начать исследования именно с них. Во-вторых, класс детерминированных алгоритмов и программ весьма широк сам по себе. Далее, многие формально недетерминированные алгоритмы в действительности являются почти детерминированными. Например, в том случае, когда ветвления охватывают конечное число операций, не зависящее от значений входных данных. Такие ветвления можно погрузить в более крупные операции, имеющие, тем не менее, конечное число аргументов. И, наконец, если ветвления охватывают большие детерминированные фрагменты, то все равно исследование графа алгоритма сводится к исследованию этих фрагментов.

Введенный в рассмотрение граф алгоритма есть ориентированный ациклический мультиграф. Его ацикличность следует из того, что в любых программах реализуются только явные вычисления и никакая величина не может определяться через саму себя. Даже если в программе имеются рекурсивные выражения, то это всего лишь удобная форма описания однотипных вычислений. При каждом обращении к рекурсии на самом деле реализуются разные операции. В общем случае граф алгоритма есть мультиграф, т. е. две вершины могут быть связаны несколькими дугами. Это будет тогда, когда в качестве разных аргументов одной и той же операции используется одна и та же величина. Будем применять для обозначения графа стандартную символику G= (V, Е), где V— множество вершин, Е— множество дуг графа G.

194

Часть II. Параллельное программирование

Итак, каждое описание алгоритма порождает ориентированный ациклический мультиграф. Верно и обратное. Если задан ориентированный ациклический мультиграф, то его всегда можно рассматривать как граф некоторого алгоритма. Для этого каждой вершине нужно поставить в соответствие любую однозначную операцию, имеющую столько аргументов, сколько дуг входит в вершину. Поэтому между алгоритмами и рассматриваемыми графами есть определенное взаимное соответствие.

Утверждение 4.1

Пусть задан ориентированный ациклический граф, имеющий п вершин. Существует число s < п, для которого все вершины графа можно так пометить одним из индексов 1, 2, ..., s, что если дуга из вершины с индексом / идет в вершину с индексом/ то /</.

Выберем в графе любое число вершин, не имеющих предшествующих, и пометим их индексом 1. Удалим из графа помеченные вершины и инцидентные им дуги. Оставшийся граф также является ациклическим. Выберем в нем любое число вершин, не имеющих предшествующих и пометим их индексом 2. Продолжая этот процесс, в конце концов, исчерпаем весь граф. Так как при каждом шаге помечается не менее одной вершины, то число различных индексов не превышает числа вершин графа.

Отсюда следует, что никакие две вершины с одним и тем же индексом не связаны дугой. Минимальное число индексов, которым можно пометить все вершины графа, на 1 больше длины его критического пути. И, наконец, для любого целого числа s, не превосходящего общего числа вершин, но большего длины критического пути, существует такая разметка вершин графа, при которой используются все s индексов.

Граф, размеченный в соответствии с утверждением 4.1, называется строгой параллельной формой графа. Если в параллельной форме некоторая вершина помечена индексом к, то это означает, что длины всех путей, оканчивающихся в данной вершине, меньше к. Существует строгая параллельная форма, при которой максимальная из длин путей, оканчивающихся в вершине с индексом к, равна к — 1. Для этой параллельной формы число используемых индексов на 1 больше длины критического пути графа. Среди подобных параллельных форм существует такая, в которой все входные вершины находятся в группе с одним индексом, равным 1. Эта строгая параллельная форма называется канонической. Для заданного графа его каноническая параллельная форма единственна. Группа вершин, имеющих одинаковые индексы, называется ярусом параллельной формы, а число вершин в группе — шириной яруса. Число ярусов в параллельной форме называется высотой параллельной формы, а максимальная ширина ярусов — ее шириной. Параллельная форма минимальной высоты называется максимальной. Слово "максимальная" здесь означает, что в этой параллельной форме в ярусах нахо-

Глава 4. Большие задачи и параллельные вычисления

195

дится в определенном смысле максимальное число вершин. Все канонические параллельные формы являются максимальными.

Заметим, что формулировка утверждения 4.1 остается в силе, если неравенство / < j заменить неравенством / < j. Однако ни одно из следствий уже выполняться не будет. Граф, размеченный таким образом, называется обобщенной параллельной формой. Соответственно вводятся понятия обобщенный ярус, ширина обобщенного яруса и т. п. В исследованиях, связанных с параллельными формами, обобщенные параллельные формы играют роль замыкания множества строгих параллельных форм.

Теперь допустим, что алгоритм реализуется на синхронном компьютере, "обыкновенном" или параллельном. Пусть для простоты все операции выполняются за одно и то же время, равное 1. Пренебрежем всеми остальными временными потерями и будем считать, что операции начинают выполняться сразу, как только оказываются готовыми их аргументы, без каких-либо простоев. Предположим, что алгоритм начинает реализовываться в нулевой момент времени. Тогда каждой операции можно присвоить индекс, равный моменту окончания ее выполнения. Если эти индексы перенести на соответствующие вершины графа алгоритма, то ясно, что мы получим его строгую параллельную форму. При этом номер яруса означает момент времени, когда заканчивают выполняться соответствующие ему операции. Все операции одного яруса выполняются независимо друг от друга, а число этих операций совпадает с шириной яруса. Высота параллельной формы есть время реализации алгоритма и т. п. Совершенно очевидна связь между различными синхронными реализациями алгоритма и различными строгими параллельными формами его графа. В частности, если алгоритм реализуется на "обыкновенном" компьютере, то этому соответствует параллельная форма, в которой все ярусы имеют ширину, равную 1. В данном случае параллельная форма называется линейной и говорят, что граф упорядочен линейно.

Параллельные формы графа алгоритма удобно изображать на листе бумаги, если ось абсцисс считать осью времени, а вершины откладывать по оси ординат соответственно времени окончания выполнения операций. Если построить аналогичный чертеж для любого реального или гипотетического компьютера, синхронного или асинхронного, то видно, что в проведенных рассуждениях мало что меняется. Лишь ярусы параллельной формы будут размываться во времени. Но как бы они не размывались, их всегда можно привести к синхронной форме с единичным временем выполнения операций, перемещая вершины и соответствующие им дуги параллельно оси абсцисс. Для этого отметим не только моменты окончания выполнения операций, но и моменты их начала. Ярусы параллельной формы будем строить следующим образом. В первый ярус объединим максимальное число вершин, не имеющих входящих дуг и соответствующих операциям с непустым пересечением временных интервалов их выполнения. Эти вершины заведо-

196

Часть II. Параллельное программирование

мо не связаны друг с другом какими-либо дугами. Удалим из графа алгоритма вершины первого яруса и инцидентные им дуги. Для оставшейся части графа выделим аналогичную группу вершин и будем считать ее вторым ярусом параллельной формы и т. д.

Таким образом, между различными реализациями одного и того же алгоритма на различных компьютерах и различными параллельными формами графа алгоритма существует определенное взаимное соответствие. Зная граф алгоритма и его параллельные формы, можно понять, каков запас параллелизма в алгоритме и как его лучше реализовать на конкретном компьютере параллельной архитектуры. Вот почему мы будем уделять очень много внимания как построению графа алгоритма, так и нахождению его параллельных форм.

В дальнейшем терминологию, относящуюся к параллельным формам графа алгоритма, будем часто переносить и на сам алгоритм, говоря о параллельной форме алгоритма, ярусах алгоритма, высоте параллельной формы алгоритма. Минимальную высоту параллельных форм алгоритма будем называть высотой алгоритма и т. д. Другими словами, будем сразу считать вершинами графа операции самого алгоритма, а дугами — отношения частичного порядка между операциями. Это не дает никаких новых знаний по существу, но позволяет избегать громоздких фраз за счет исключения длинных последовательностей слов типа "множество операций, соответствующих такому-то множеству вершин графа алгоритма". Обычным же графом алгоритма удобнее пользоваться в иллюстративных рисунках и чертежах.

Наконец, покажем, что независимо от того, какая параллельная форма алгоритма реализуется на компьютере, результат реализации будет одним и тем же.

Утверждение 4.2

Пусть при выполнении операции ошибки округления определяются только значениями аргументов. Тогда при одних и тех же входных данных все реализации алгоритма, соответствующие одному и тому же частичному порядку на операциях, дают один и тот же результат, включая всю совокупность ошибок округления.

Рассмотрим каноническую параллельную форму алгоритма. Операции любого яруса не зависят друг от друга. Аргументами операций 1-го яруса являются только входные данные. Они не зависят от времени выполнения операций. Поэтому все операции 1-го яруса дают результаты, не зависящие от того, когда реально выполняются эти операции. Аргументами операций 2-го яруса являются или входные данные, или результаты выполнения операций 1-го яруса. В соответствии со сказанным, все они не зависят от времени выполнения операций. Поэтому операции 2-го яруса также дают результаты, не зависящие от того, когда реально выполняются эти операции. Продолжая последовательно по ярусам это доказательство, убеждаемся в справедливости утверждения.

Глава 4. Большие задачи и параллельные вычисления

197

Заметим, что та последовательность выполнения операций, которая диктуется программой, записанной на последовательном языке, определяет на множестве операций линейный порядок. Конечно, он сохраняет и частичный порядок, о котором говорилось выше. Но в общем случае на множестве операций существуют и другие линейные порядки, сохраняющие тот же частичный порядок. Согласно утверждению 4.2, все они будут давать один и тот же результат. Следовательно, фиксация последовательного порядка выполнения операций при задании алгоритма, вообще говоря, является избыточным действием. Значительно "экономичнее" задавать граф алгоритма или какую-нибудь его строгую параллельную форму, лучше всего — каноническую. Тем более, что для реализации алгоритмов на параллельных вычислительных системах нужна именно такая информация. Однако за многие годы существования "обыкновенных" компьютеров накопилось столько много прикладного программного обеспечения на последовательных языках, что не может даже идти речи о его переписывании вручную. Поэтому необходимо развивать теорию и строить инструментальные системы, помогающие очищать записи алгоритмов от последовательных "излишеств", что, в конечном счете, и сводится к построению графа алгоритма и нахождению его параллельных форм. Как мы увидим в дальнейшем, это очень непростая задача.

По нашему мнению, граф алгоритма представляет самое основное ядро идеи разработчика, содержащейся в записи алгоритма. Разработчик алгоритма мог знать это ядро. Вполне возможно, что он был вынужден замаскировать его из-за того, что язык описания алгоритма не давал возможность эффективно изобразить данное ядро. Но как показывает практика, в подавляющем большинстве случаев это ядро алгоритма для разработчика неизвестно. Более того, как правило, он даже и не думает о его существовании. Все становится понятным, если принять во внимание, что граф алгоритма есть не просто ядро алгоритма, а является его информационным ядром. До недавнего времени знания о том, как распространяется информация при реализации алгоритмов, не имели практической ценности. Поэтому неудивительно, что не было особого стремления их получать. Появление параллельных вычислительных систем сделало эти знания исключительно нужными. Вот они и стали развиваться.

Вопросы и задания

1. Если на множестве операций меняется частичный порядок, то может ли новый алгоритм быть эквивалентным исходному?

2. Может ли минимальное значение числа ярусов обобщенной параллельной формы характеризовать структуру алгоритма?

3. Пусть для одной и той же задачи алгоритмы дают решения с разными ошибками округления. Могут ли такие алгоритмы иметь одни и те же параллельные формы?

198

Часть II. Параллельное программирование

4. Приведите примеры разных алгоритмов, предназначенных для решения разных задач, но имеющих, тем не менее, одинаковые графы.

5. Пусть для одной и той же задачи алгоритмы дают решения с одними и теми же ошибками округления при всех входных данных. Могут ли такие алгоритмы иметь разные графы?

6. Используя унарные и бинарные операции, постройте графы следующих алгоритмов:

6.1. Быстрое преобразование Фурье.

6.2. Решение системы линейных алгебраических уравнений с треугольной матрицей методом обратной подстановки.

6.3. Решение системы линейных алгебраических уравнений с квадратной матрицей методом Гаусса.

6.4. Обращение матрицы методом Жордана.

6.5. Любой метод перемножения двух квадратных матриц порядка п, требующий менее п³ умножений.

§ 4.3. Концепция неограниченного параллелизма

Внедрение первых компьютеров в практику показало, что их мощности недостаточны для решения многих крупных задач. Технологические возможности того времени не могли обеспечить необходимый уровень производительности. Довольно скоро возникла и стала успешно развиваться новая идея его повышения. Она связывала увеличение производительности с объединением в одну систему нескольких компьютеров или процессоров, функционирующих одновременно. Вот несколько характерных примеров, часть из которых уже обсуждалась ранее [35]. В 1958 г. появилась вычислительная система PILOT, объединяющая три независимых компьютера в одном комплексе. В 1962 г. вошла в строй система Burroughs D825, включающая до 4 идентичных процессоров, работающих над общей памятью. В 1964 г. была построена система CDC 6600. Она содержала неоднородную совокупность арифметико-логических устройств. Каждое из них выполняло только часть команд из всего набора, но все они могли функционировать одновременно. В 1972 г. появился матричный компьютер 1LL1AC IV, содержащий уже 64 элементарных процессора. По существу с этих компьютеров и началась эра параллельных вычислительных систем.

Заметим, что поводом для возникновения самой идеи вычислительных систем параллельной архитектуры послужило не только несовершенство элементной базы и архитектуры первых компьютеров. Это несовершенство было относительным, но оно не позволяло поднять производительность "обыкновенных" компьютеров до уровня, необходимого для решения наиболее крупных задач. А идея была значительно более глубокой. Она наметила

Глава 4. Большие задачи и параллельные вычисления

199

перспективы будущего развития вычислительной техники. Сейчас, спустя несколько десятилетий, параллелизм в вычислительных системах не перестал быть актуальным. Несмотря на огромный прогресс в развитии как элементной базы, так и архитектуры компьютеров, "обыкновенные" компьютеры снова не позволяют достичь производительности, необходимой для решения наиболее крупных задач, но уже сегодняшнего дня.

Независимо от того, как устроены реальные или гипотетические параллельные вычислительные системы, все они базируются на одной и той же методологической основе. Именно, каждая такая система имеет какое-то число функциональных устройств, которые могут работать независимо друг от друга и способны, к тому же, выполнять операции алгоритма. Это означает, что для того, чтобы алгоритм мог быть реализуем на параллельной системе, он должен быть представим в виде последовательности ансамблей операций. Все операции одного ансамбля должны быть независимыми и обладать возможностью быть выполненными одновременно на имеющихся в системе функциональных устройствах. Используя терминологию предыдущего параграфа, эту мысль можно выразить иначе: алгоритм должен иметь параллельную форму, ширина ярусов которой в среднем соизмерима с числом функциональных устройств системы. В общем случае, чем больше ярусов, ширина которых равна числу независимых устройств, тем выше реальная производительность параллельной вычислительной системы на данном алгоритме.

Создание параллельных вычислительных систем потребовало разработки математической концепции построения параллельных алгоритмов, т. е. алгоритмов, приспособленных к реализации на подобных системах. Эта концепция стала развиваться в конце 50-х — начале 60-х годов прошлого столетия. В то время о структуре параллельных вычислительных систем и путях их развития было мало чего известно. Разве только то, что в таких системах одновременно может работать много устройств. Быстрое развитие элементной базы подсказывало, что число устройств вроде бы вскоре может стать очень большим. Концепция получила название концепции неограниченного параллелизма. В ее основе явно или неявно лежит предположение, что алгоритм реализуется на параллельной вычислительной системе, не накладывающей на него никаких ограничений. Считалось, что процессоров может быть сколь угодно много, все они универсальные, работают в синхронном режиме, имеют общую память, любые передачи информации осуществляются мгновенно и без конфликтов. В терминах предыдущего параграфа это означало, что основная цель концепции неограниченного параллелизма сводилась к построению алгоритмов минимальной высоты, т. к. в такой модели вычислений именно высота определяет время реализации алгоритмов.

Концепция неограниченного параллелизма отражает уровень математических знаний того времени в области параллельных вычислений. Она имеет как свои недостатки, так и свои достоинства. Рассмотрим некоторые результаты, полученные на ее основе.

200

Часть II. Параллельное программирование

Для решения одной и той же задачи могут применяться алгоритмы, имеющие различную параллельную сложность. Среди них могут быть и алгоритмы наименьшей высоты. Рассмотрим важный пример вычисления произведения п чисел О], а₂, ..., а„, в котором отчетливо видна идея, играющая большую роль в построении алгоритмов малой высоты.

Пусть п = 8. Обычная схема, реализующая процесс последовательного умножения, выглядит следующим образом:

Данные Я] а₂ «з ^а4 ^а5 ^аб ^ai ^а&

Ярус 1 а\й₂

Ярус 2 (а]Д₂)^аз

Ярус 3 (Я]Й2Яз)^й4

Ярус 4 (а1й₂аз^й4)^й5

Ярус 5 (Я1Й2Яз^й4^й5)^й6 Ярус 6 (я_]Я₂Яз^й4^й5^йб)^й7 Ярус 7 (Я1Й2Яз^й4^й5^й6^й7)^й8

Высота параллельной формы равна 7, ширина равна 1. Если вычислительная система имеет более одного процессора, то при данной схеме вычислений все они, кроме одного, на всех шагах будут простаивать. Следующая параллельная форма другого алгоритма вычисления произведения чисел использует процессоры более эффективно:

Данные а\ а₂ «з ^а4 ^а5 ^аб ^а1 ^а&

Ярус 1 Я]Д₂ ^аз ^а4 ^а5 ^ав ^а1 ^а&

Ярус 2 (Я1Я₂)(Я₃ ^й4) («5 «б) («7 «8)

Ярус 3 (й^Яз^) ^^fl5 ^ав ^а1 ^а%)

Высота параллельной формы равна 3, ширина равна 4. Существенное снижение высоты произошло за счет более полной загруженности процессоров выполнением полезной работы.

Последняя схема очевидным образом распространяется на случай произвольного п. Для ее реализации необходимо на каждом ярусе осуществлять максимально возможное число произведений непересекающихся пар чисел, взятых на предыдущем ярусе. В общем случае высота параллельной формы равна Tlog2« 1 , где ГоЛ означает ближайшее к а сверху целое число. Эта параллельная форма реализуется на [п/2] процессорах, но в ней загруженность процессоров уменьшается от яруса к ярусу. Процесс построения чисел каждого яруса по описанной схеме называется процессом сдваивания.

Очевидно, что с помощью процесса сдваивания можно строить алгоритмы логарифмической высоты не только для многократного применения операции умножения чисел, но и для любой ассоциативной операции, например,

Глава 4. Большие задачи и параллельные вычисления

201

сложения чисел, умножения матриц и т. п. Обратим внимание, что алгоритм последовательного применения операции и алгоритм сдваивания — это принципиально разные алгоритмы, хотя они и требуют для своих реализаций выполнения одного и того же числа операций. Им нужны не только разные числа процессоров, но и разные коммуникационные сети. В них по-разному сказывается влияние ошибок округления и для них по-разному пишутся программы. В общем случае, у них все разное, в том числе, и графы алгоритмов. На рис. 4.2 для я = 8 вверху представлен граф последовательного применения операции, внизу — граф для принципа сдваивания. Начальные вершины символизируют ввод данных.

Рис. 4.2. Последовательный граф и граф сдваивания

Рассмотренный пример подсказывает один вывод, весьма важный в методологическом отношении.

Утверждение 4.3

Пусть функция существенно зависит от п переменных и представлена как суперпозиция конечного числа операций, имеющих не более р аргументов. Предположим, что ее значения вычисляются с помощью какого-либо алгоритма с использованием тех же операций. Если без учета ввода данных высота алгоритма равна s, то s > logyz.

Рассмотрим каноническую параллельную форму графа алгоритма. Пусть на нулевом ярусе расположены вершины, соответствующие вводу значений входных переменных. На s-ом ярусе находится одна конечная вершина. Так как у всех вершин не более р входящих дуг, то на (s — 1)-ом ярусе имеется не более р вершин, на (s — 2)-ом ярусе не более р² вершин и т. д. На нулевом ярусе будет находиться не более p^s вершин. Ясно, что p^s> п. Поэтому s > logp п.

Таким образом, если какая-нибудь задача определяется п входными данными, то мы не можем рассчитывать в общем случае на существование алго-

202

Часть II. Параллельное программирование

ритма ее решения с высотой менее log п. Если получен алгоритм высоты порядка log^a п, где a > 0, то такой алгоритм мы должны считать эффективным с точки зрения времени его реализации на параллельной вычислительной системе. Если, конечно, не принимать во внимание все другие аспекты реализации.

Пусть вектор у вычисляется как произведение квадратной матрицы А и вектора х порядка п. Если y_h ay, Xj суть элементы соответствующих векторов и матрицы, то для всех / имеем

у: =^yL^au^xJ-

Предположим, что вычислительная система имеет п² процессоров. Тогда на первом шаге можно параллельно вычислить все п² произведений a^xj, а затем, используя схему сдваивания для сложения, за Г log2«l шагов вычислить параллельно все п сумм, определяющих координаты вектора у. Следовательно, можно построить алгоритм вычисления произведения квадратной матрицы и вектора порядка п высоты порядка log₂«. При этом ширина алгоритма равна п². Процессоры используются неравномерно. Только на первом шаге задействованы все процессоры. Затем число работающих процессоров на каждом шаге уменьшается вдвое. Нельзя согласно утверждению 4.3 построить алгоритм, имеющий меньшую высоту. Но существуют алгоритмы, имеющие при логарифмической высоте несколько меньшую ширину.

Задачу вычисления произведения двух матриц порядка п можно рассматривать как задачу вычисления п произведений одной матрицы и п независимых векторов порядка п, считая векторами столбцы второй матрицы. Если все эти произведения вычислять параллельно по описанному алгоритму, то полученный алгоритм будет иметь высоту порядка log2« и ширину я³. Снова процессоры используются неравномерно, и опять нельзя построить алгоритм, имеющий меньшую высоту, но существуют алгоритмы, имеющие при логарифмической высоте несколько меньшую ширину.

Обратим внимание на следующее обстоятельство. Если пытаться реализовы-вать описанные алгоритмы по ярусам канонической параллельной формы, то возникает необходимость одновременной рассылки одних и тех же данных по многим процессорам. Такую операцию нельзя осуществить очень быстро. Поэтому в реальных условиях временные затраты на рассылки приводят к значительному замедлению процессов вычислений.

Построение параллельных алгоритмов наименьшей высоты для матрично-векторных сумм и произведений не вызвало никаких затруднений. Это может создать впечатление, что такие алгоритмы легко строятся и для других матрично-векторных задач. Подобное впечатление, конечно, не верно. Рассмотренные алгоритмы скорее являются исключением, чем правилом.

Глава 4. Большие задачи и параллельные вычисления

203

Рассмотрим в соответствии с [39] процесс вычисления векторов x_h 1 < / < s, при заданных векторах xq, х~\, , х~_г ₊ \ с помощью линейных рекуррентных соотношений следующего вида:

Xj = AftXj _]+...+ AjpCj -_r + bj. (4.1)

Здесь Ay, bj — заданные матрицы и векторы порядка п, при я = 1 они становятся числами. Предположим, что мы хотим построить при фиксированном s параллельный алгоритм вычисления векторов Х]_, x_s по возможности меньшей высоты. Очевидно, что, используя порядка п²г процессоров, правую часть соотношений (4.1) можно вычислить примерно за log₂ nr шагов. Это дает параллельный алгоритм высоты порядка s log2 nr. Однако совсем не очевидно, как построить алгоритм с существенно более слабой зависимостью высоты от s. Не очевидно даже, что вообще существуют такие алгоритмы.

Рекуррентные соотношения (4.1) можно записать несколько иначе — через матрицы и векторы большего порядка:

^xi-r+l 1


	Е	*••^Air-\^Air"i* ..0 0 0
	0 • 0 .	-Е 0 0 .. Е 0 1

Х,-_₂

Обозначим матрицу через Q_h вектор слева через y_t. Тогда будем иметь

У1 = Qiyi - 1 = ... = (Qt Qi -1 Q\) Уо, l<i<s.

Матрицы Qi и векторы y_t имеют порядок nr + 1. Согласно алгоритму сдваивания, все произведения (Q,(2i) Уо можно вычислить за Tlog2(5 + 1)1 макрошагов, используя при этом as + 1щ макропроцессоров, выполняющих в качестве макрооперации умножение двух матриц порядка nr + 1. Принимая во внимание построенный параллельный алгоритм для нахождения произведения двух матриц, теперь легко построить параллельный алгоритм для вычисления всех векторов jq, ..., x_s с высотой порядка log₂ s х log₂nr и шириной порядка (nrfs. Этот алгоритм получил название процесса рекуррентного сдваивания.

Описанный процесс принципиально отличается от алгоритма, основанного на прямом вычислении векторов х_г- из (4.1). Оба алгоритма дают одни и те же результаты только в условиях точных вычислений. На основе использования рекуррентных соотношений типа (4.1) построены очень многие численные методы линейной алгебры, математической физики и анализа. Процесс рекуррентного сдваивания указывает путь понимания того, что можно ожидать от этих методов с точки зрения построения алгоритмов малой высоты, если использовать большое число процессоров. Предположим, напри-

204 Часть II. Параллельное программирование

мер, что решается система линейных алгебраических уравнений с невырожденной треугольной матрицей порядка п. За один параллельный шаг, используя около п²/1 процессоров, можно сделать равными 1 все диагональные элементы матрицы, разделив на них коэффициенты соответствующих уравнений. Решая систему с помощью обратной подстановки, сразу получаем для неизвестных рекуррентные соотношения типа (4.1), где все матрицы и векторы представляют числа, х₀ = 0, г = i, s = п. Следовательно, используя процесс рекуррентного сдваивания, можно решить треугольную систему за 0(log₂²n) параллельных шагов, задействовав 0(«³) процессоров.

Пусть, наконец, рассматривается задача вычисления обратной матрицы А~^]для квадратной матрицы А порядка п. В основе построения быстрого параллельного алгоритма лежит следующая идея. Обозначимся.) = X" + с\Х^п ~ ^] + + ... + с_п характеристический многочлен матрицы А. Известно, что ДА) = О согласно теореме Кели-Гамильтона. Поэтому

А~¹ =- — (А^п-¹+с₁А"-²+... + с_п _УЕ). (4.2)

Если Xj — корни характеристического многочлена и ^ — следы матриц А^к, то известно, что X_t и % связаны так называемыми соотношениями Ньютона, представляющими относительно с^ систему линейных алгебраических уравнений с треугольной матрицей. Именно,

5_Х 2 S₂ •?! 3


^с1		*1
^с2		*2
с₃	=	S3
*^Сп*		s_n

(4.3)

_^sn-l^sn-2 ••••^$1 ^п.

Параллельный алгоритм определения матрицы А~^] состоит из следующих этапов. Сначала по схеме сдваивания находятся все степени матрицы А от первой до (п — 1)-й. Этот этап имеет log₂« макрошагов, где каждый макро-шаг есть вычисление не более я/2 произведений двух матриц порядка п.

Весь первый этап может быть выполнен за 0(log2²«) параллельных шагов на 0(п⁴) процессорах. На втором этапе за 0(log2«) шагов при использовании 0(п²) процессоров вычисляются все следы s^ матриц А^к. На третьем этапе за 0(log2²n) шагов на 0(п³) процессорах находятся коэффициенты с^ характеристического многочлена путем решения треугольной системы (4.3). На четвертом этапе матрица А^-1 определяется согласно формуле (4.2) за 0(log2«) параллельных шагов с использованием 0(п³) процессоров. В целом параллельный алгоритм вычисления матрицы А~¹ имеет высоту 0(log2²«) и ширину 0(п⁴). В настоящее время для решения этой задачи неизвестны алгоритмы существенно меньшей высоты. Ширина же может быть уменьшена.

Глава 4. Большие задачи и параллельные вычисления

205

Если решается система линейных алгебраических уравнений Ах = Ь с квадратной невырожденной матрицей А порядка п, то параллельный алгоритм строится очень просто. Представим решение х системы в виде х=А~^]Ь. Сначала за 0(log₂²n) параллельных шагов, используя 0(п⁴) процессоров, находим матрицу А~^]. Затем за 0(log₂«) параллельных шагов, используя 0(п²) процессоров, находим решение х как произведение матрицы А~^] и вектора Ъ.

В рамках концепции неограниченного параллелизма построено немало алгоритмов небольшой высоты. С некоторыми из них можно познакомиться в работе [39] и процитированной там литературе. Но мы не будем обсуждать их здесь детально. Причина очень проста: подавляющее большинство этих алгоритмов оказались на практике несостоятельными. Огромное число требуемых процессоров, сложные информационные связи между операциями, катастрофическая численная неустойчивость, большое число конфликтов в памяти — вот лишь некоторые из "подводных камней" быстрых параллельных алгоритмов. Их практическая несостоятельность видна из анализа типового численного программного обеспечения существующих параллельных систем. По существу, оно почти целиком состоит из программ, реализующих те же методы, которые хорошо зарекомендовали себя при реализации на последовательных компьютерах. Реально в какой-то мере используется только принцип сдваивания для вычисления сумм и произведений многих чисел. Подробное обсуждение концепции неограниченного параллелизма можно найти в книге [9].

Несмотря на отмеченные недостатки, мы сочли уместным хотя бы кратко упомянуть об этой концепции в данной книге. Все-таки, она отражает заметный период в истории изучения параллелизма в вычислениях. К тому же, концепция оказалась исключительно живучей. Предельная абстрагирован-ность от реалий устройства и использования вычислительной техники сделала ее привлекательной для проведения исследований, главным образом, чисто математических. Однако на сегодняшний день все достижения в рамках концепции неограниченного параллелизма скорее представляют набор отдельных изобретений в области численных методов, чем систематически развивающуюся область математики. Тем не менее, вполне возможно, что здесь еще не сказано последнее слово, и к построению быстрых параллельных алгоритмов все же будет разработан более систематизированный подход.

Вопросы и задания

1. Используя унарные и бинарные операции, постройте параллельные алгоритмы малой высоты для следующих задач:

1.1. Вычисление значения многочлена в точке.

1.2. Решение системы линейных алгебраических уравнений с трехдиагональной матрицей.

206

Часть II. Параллельное программирование

1.3. Решение системы линейных алгебраических уравнений с двухдиагональной матрицей.

1.4. Обращение двухдиагональной матрицы.

1.5. Решение системы линейных алгебраических уравнений с блочной двухдиагональной матрицей блочного порядка m и порядком блоков, равным п.

2. **Пусть дан любой детерминированный алгоритм, использующий лишь операции сложения, умножения и деления чисел. Опишите класс математически эквивалентных алгоритмов, полученных из данного путем применения законов ассоциативности, коммутативности и дистрибутивности, а также приведения подобных членов и замены подобными членами чисел 0 и 1. На этом классе попытайтесь установить алгоритмы минимальной и максимальной сложности как по отдельным операциям, так и по операциям в целом, в том числе параллельную сложность.

3. В условиях п. 2 для следующих задач с матрицами порядка п постройте алгоритмы, использующие О(па), 0 < а < 3, операций умножения, и исследуйте структуру соответствующих графов:

3.1. *Перемножение двух квадратных матриц.

3.2. *Решение системы линейных алгебраических уравнений с квадратной матрицей.

3.3. *Если в пп. 3.1, 3.2 вам удалось построить алгоритмы, в которых а = log₂7, вы на правильном пути. Соответствующие алгоритмы называются алгоритмами Штрассена.

3.4. Сравните графы алгоритмов Штрассена с графом алгоритма быстрого преобразования Фурье.

§ 4.4. Внутренний параллелизм

В процессе длительного использования последовательных компьютеров был накоплен и тщательно отработан огромный багаж численных методов и программ. Появление параллельных компьютеров вроде бы должно было привести к созданию новых методов. Но этого не произошло. Попытка разработать специальные параллельные методы, в частности, методы малой высоты, оказалась на практике несостоятельной. Естественно, возникает вопрос, как же тогда решать задачи на параллельных компьютерах и можно ли на этих компьютерах использовать старый алгоритмический и программный багаж? Как это часто бывает, ответ был найден простым по форме и совсем не простым по реализации. В терминах § 4.2 он сводится к следующему. Возьмем любой подходящий алгоритм, записанный в виде математических соотношений, последовательных программ или каким-либо иным способом. Допустим, что по этой записи для него удалось построить граф алгоритма. Предположим, что для этого графа обнаружена параллельная форма с достаточной шириной ярусов. Тогда рассматриваемый алгоритм, по крайней мере, принципиально можно реализовать на параллельном компьютере. Очень важно, что согласно утверждению 4.2 параллельная реализация алгоритма

Глава 4. Большие задачи и параллельные вычисления

207

будет иметь такие же вычислительные свойства, как и любая другая. В частности, если исходный алгоритм был численно устойчив, то он останется таким же и в параллельной форме. Подобный параллелизм в алгоритмах стали называть внутренним.

Оказалось, что в старых, давно используемых и хорошо отработанных алгоритмах довольно часто удается обнаружить хороший запас внутреннего параллелизма. Использование внутреннего параллелизма имеет очевидное достоинство, т. к. не нужно тратить дополнительные усилия на изучение вычислительных свойств вновь создаваемых алгоритмов. Недостатки также очевидны из-за необходимости определять и исследовать графы алгоритмов. В тех случаях, когда внутреннего параллелизма какого-либо алгоритма недостаточно для эффективного использования конкретного параллельного компьютера, приходится заменять его другим алгоритмом, имеющим лучшие свойства параллелизма. К счастью, для очень многих задач уже разработано большое количество различных алгоритмов. Поэтому подобрать подходящий алгоритм почти всегда удается. Правда, осуществить этот выбор не так легко, т. к. нужно знать параллельную структуру алгоритмов. А она-то как раз неизвестна. Поэтому понятно, насколько актуальными являются сведения о параллельных свойствах алгоритмов, а также знания, позволяющие эти сведения получать.

Рассмотрим некоторые примеры. Пусть решается классическая задача вычисления произведения А = ВС двух квадратных матриц В, С порядка п. Будем считать элементы матриц А, В, С числами и обозначим их ay, b_ik, сщ. Согласно определению операции умножения матриц имеем

^a>j = X ^b>k ^ckj, /, У = 1, 2, ..., п. (4.4)

к = 1

Эти формулы довольно часто используются для непосредственного вычисления элементов матрицы А. Сами по себе они не определяют алгоритм однозначно, т. к. не определен порядок суммирования произведений b_ikc_kj под знаком суммы. Однако заметим, что явно виден параллелизм вычислений. Выражается он отсутствием указания о соблюдении какого-либо порядка перебора индексов /, j.

Если операции сложения и умножения чисел выполняются точно, то все порядки суммирования в (4.4) эквивалентны и приводят к одному и тому же результату. Пусть из каких-то соображений выбран следующий алгоритм реализации формул (4.4):

а/)=0, _а.Ш = _афк -1) + _bikCkh _и _у; _к = i_; ₂, ..., п, (4.5)

^аЧ = ^ач^п)-

208

Часть II. Параллельное программирование

Снова явно указан параллелизм перебора индексов /, j. Однако по индексу к параллелизма нет, т. к. этот индекс должен перебираться последовательно от 1 до п, что следует из средней формулы (4.5).

Построим теперь граф алгоритма (4.5). Будем считать, что вершины графа соответствуют операциям вида a + be, где a, b, с элементы того же кольца, которому принадлежат элементы матриц А, В, С. Для наглядности их можно рассматривать как числа, хотя ничто не мешает им быть, например, квадратными матрицами одного порядка. При построении графа природу элементов а, Ь, с учитывать не будем. Не будем также сначала показывать в графе вершины и инцидентные им дуги, связанные с вводом элементов матриц В, С и с присвоением элементам матрицы А вычисленных значений «/"Л Чтобы не вносить в исследование графа алгоритма неоправданные дополнительные трудности, вершины графа нельзя располагать произвольно. Приемлемый способ их расположения подсказывает сама форма записи (4.5). Рассмотрим прямоугольную решетку в трехмерном пространстве с координатами /, j, к. Во все целочисленные узлы решетки для 1 < /, j, к < п поместим вершины графа. Анализируя запись (4.5), нетрудно убедиться в том, что в вершину с координатами /, j, к для к > 1 будет передаваться результат выполнения операции, соответствующей вершине с координатами i,j, к — 1.


к i	< i i	i i i i	i i i	i

Рис. 4.3. Графы перемножения матриц

Граф алгоритма устроен достаточно просто. Он распадается на п² не связанных между собой подграфов. Каждый подграф содержит п вершин и представляет один путь, расположенный параллельно оси к. Как и следовало ожидать, в графе отражен тот же параллелизм, который был явно указан в записях (4.4), (4.5) Для л = 2 граф алгоритма представлен на рис 4.3, а. В полном графе имеется множественная рассылка данных. Элемент Ь^ рассылается по всем вершинам, имеющим те же самые значения координат /, к.

Глава 4. Большие задачи и параллельные вычисления

209

Элемент сщ рассылается по всем вершинам, имеющим те же самые координаты к, j. Для я = 2 эти рассылки показаны на рис. 4.3, б. Все вершины соответствуют операциям вида a + be. Однако при к = 1 они выполняются несколько иначе, чем при к ф 1. Именно, в этих случаях аргумент а не является результатом какой-либо операции, а всегда полагается равным 0. Ничто не мешает 0 считать входным данным алгоритма и рассылать его по всем вершинам при к = 1.

Этот пример хорошо иллюстрирует, насколько важно правильно выбрать способ расположения вершин графа алгоритма. Если, например, расположить вершины на прямой линии, да еще без какой-либо связи с индексами /, j, к из (4.5), то вряд ли в таком графе удалось бы разглядеть параллелизм. При выбранном расположении вершин параллелизм очевиден. Более того, легко описать любой ярус любой параллельной формы. Это есть множество вершин, не содержащее при фиксированных /, j более одной вершины. Ярусы канонической параллельной формы представляют множество вершин, лежащих на гиперплоскости к = const. Поэтому вполне естественно ожидать, что нам придется связывать способ расположения вершин с системой индексов, используемых в записи алгоритма. Данный пример такую зависимость уже наметил.

Заметим, что если суммирование в (4.4) выполнять по схеме сдваивания, то граф алгоритма станет совсем другим. Именно, каждый путь в графе на рис. 4.3, а должен быть заменен на нижний граф на рис. 4.2. Новый граф уже труднее разместить в трехмерном пространстве. Но ведь и записать суммирование по принципу сдваивания, используя один индекс, значительно сложнее.

Пусть теперь решается система линейных алгебраических уравнений Ах = b с невырожденной треугольной матрицей А порядка п методом обратной подстановки. Обозначим через ay, b_h x_t элементы матрицы, правой части и вектор-решения. Предположим для определенности, что матрица А левая треугольная с диагональными элементами, равными 1. Тогда имеем

/'-1 xi = b\, Xj = bj — 2^ayXj, 2 < i < n. (4.6)

7 = 1

Эта запись также не определяет алгоритм однозначно, т. к. не определен порядок суммирования. Рассмотрим, например, последовательное суммирование по возрастанию индекса j. Соответствующий алгоритм можно записать следующим образом

_xfj) = _xij - О - _aijXjJ - 1), / = i, ₂, ..., n, j = 1, 2, ..., / - 1, (4.7)

xt=xf'-^l\

Основная операция алгоритма имеет вид a — be. Выполняется она для всех допустимых значений индексов /, j. Все остальные операции осуществляют присваивание. Опять неэффективна простая перенумерация операций при

210

Часть II. Параллельное программирование

построении графа алгоритма. В декартовой системе координат с осями /, j построим прямоугольную координатную сетку с шагом 1 и поместим в узлы сетки при 2 < i < п, 1 <j<i — 1 вершины графа, соответствующие операциям a — be. Анализируя связи между операциями, построим граф алгоритма, включив в него также вершины, символизирующие ввод входных данных ay и bj. Этот граф для случая я = 5 представлен на рис. 4.4, а. Верхняя угловая вершина находится в точке с координатами /= 1, j= 0. На этом рисунке показана одна из максимальных параллельных форм. Ее ярусы отмечены пунктирными линиями. Параллельная форма становится канонической, если вершины, соответствующие вводу элементов ау, поместить в первый ярус. Общее число ярусов, содержащих операции типа а — be, равно п — 1. Операции ввода элементов вектора b расположены в первом ярусе.

Рис. 4.4. Графы для треугольных систем

Если при вычислении суммы в (4.6) мы останавливаемся по каким-то соображениям на последовательном способе суммирования, то выбор суммирования именно по возрастанию индекса j был сделан, вообще говоря, случайно. Так как в этом выборе пока не видно каких-либо преимуществ, то можно построить алгоритм обратной подстановки с суммированием по убыванию индекса/ Соответствующий алгоритм таков:

xfb = b_h

xff> = дс//⁺¹> - ayxff), i = 1, 2, ..., я, j = i~ 1, / - 2, ..., 1, (4.8)

x_t=xP.

Его граф для случая n = 5 представлен на рис. 4.4, б. Теперь верхняя угловая вершина находится в точке с координатами / = 1,у = 1.

Глава 4. Большие задачи и параллельные вычисления

211

Пытаясь размещать вершины, соответствующие операциям типа a — be, по ярусам хотя бы какой-нибудь параллельной формы, мы обнаруживаем, что теперь в каждом ярусе всегда может находиться только одна вершина. Объясняется это тем, что все вершины графа на рис. 4.4, # лежат на одном пути. Этот путь показан пунктирными стрелками. Поэтому общее число ярусов в графе алгоритма (4.8), содержащих операции вида a — dc, всегда равно (п² — — п + 2)/2, что намного больше, чем я — 1 ярус в графе алгоритма (4.7).

Полученный результат трудно было ожидать. Действительно, оба алгоритма (4.7) и (4.8), предназначены для решения одной и той же задачи. Они построены на одних и тех же формулах (4.6) и в отношении точных вычислений эквивалентны. Оба алгоритма совершенно одинаковы с точки зрения их реализации на однопроцессорных компьютерах, т. к. требуют выполнения одинакового числа операций умножения и вычитания и одинакового объема памяти. На классе треугольных систем оба алгоритма даже эквивалентны с точки зрения влияния ошибок округления.

Тем не менее, графы обоих алгоритмов принципиально отличаются друг от друга. Если эти алгоритмы реализовывать на параллельной вычислительной системе, имеющей п универсальных процессоров, то алгоритм (4.7) можно реализовать за время, пропорциональное п, а алгоритм (4.8) — только за время, пропорциональное п². В первом случае средняя загруженность процессоров близка к 0,5, во втором случае она близка к 0.

Таким образом, алгоритмы, совершенно одинаковые с точки зрения реализации на "обыкновенных" компьютерах, могут быть принципиально различными с точки зрения реализации на параллельных компьютерах.

Воспользовавшись данным примером, подчеркнем, что в этом факте, собственно говоря, и заключается основная трудность математического освоения параллельных компьютеров. Специалисты различного профиля, работающие на "обыкновенных" компьютерах в течение многих лет, привыкли оценивать алгоритмы, главным образом, через три их характеристики: число операций, объем требуемой памяти и точность. На этих характеристиках было построено практически все: основные параметры вычислительной техники, процесс обучения вычислительному делу, создание численных методов и алгоритмов, оценка эффективности, разработка языков и трансляторов и многое другое.

Создание параллельных вычислительных систем дополнительно потребовало от алгоритмов принципиально других свойств и характеристик, знание которых для последовательных компьютеров было просто не нужно. Нет никаких оснований предполагать, что складывавшиеся годами и десятилетиями стереотипы отношения к вычислительной технике и конструированию алгоритмов изменятся достаточно быстро. Инерция в этом процессе исключительно велика. Вот почему важно не только исследовать алгоритмы более глубоко и основательно. Особенно необходимо создавать конструктивную методологию для выявления и изучения параллельных свойств алгоритмов.

212

Часть II. Параллельное программирование

Среди многих задач линейной алгебры, возникающих при решении уравнений математической физики сеточными методами, часто встречается задача решения систем линейных алгебраических уравнений с блочно-двухдиа-гональными матрицами. При этом внедиагональные блоки представляют собой диагональные матрицы, диагональные блоки — двухдиагональные матрицы. Будем считать для определенности, что матрица системы является левой треугольной. Пусть она имеет блочный порядок m и порядок блоков, равный п. Итак, рассмотрим систему линейных алгебраических уравнений Аи = /следующего вида:

А А А

А А


ГА]		РЧ
А		А
А	=	А
_А,_		F *_ m _*

Аи - 1А

где


*^ъ\к*
^eu Ь_1к		0
е₂к	hk	-1, к Ь„к _		•>	А =
0	е„-	-1, к Ь„к _		•>	А =
		~«А			f\k
	А =	^и2к	, А =		flk
		*^Unk_*			fnk _

4к

Чк

¹Ък

(4.9)

¹пк

Решение блочно-двухдиагональной системы (4.9) определяется рекуррентно: £4 = ДГЧА-А-1А-1), 1<к<т, (4.10)

если положить Щ = 0, Bq = 0. Макрооперация X = В ^_1(F — BY) вычисляет вектор X по векторам F, Yu матрицам В, В. Построим граф алгоритма (4.9), считая, что каждая из его вершин соответствует данной макрооперации. Очевидно, он будет таким, как показано на рис. 4.5. Большие размеры вершин и дуг на рисунке подчеркивают, что операции являются сложными и передается сложная информация.

Глава 4. Большие задачи и параллельные вычисления

213

е, D₀=0 В₂ D, В_т D_m_,

Рис. 4.5. Макрограф для блочно-двухдиагональной системы

Из строения графа сразу видно, что если алгоритм (4.10) рассматривать как последовательность матрично-векторных операций, то он является строго последовательным и не распараллеливается. Практически не распараллеливается и каждая макрооперация в отдельности. Она также представляет решение двухдиагональной системы. Поэтому распараллеливаться может только процесс вычисления правой части системы, если, конечно, данную систему снова решать аналогично (4.10).

Из этих фактов можно было бы сделать вывод о невозможности хорошего распараллеливания алгоритма решения рассматриваемой системы (4.9). Однако такой вывод был бы преждевременным.

Исследуем поэлементную запись алгоритма решения блочно-двухдиагональной системы. С учетом введенных ранее обозначений элементов матриц и векторов имеем:

^uik ⁼ (fik~ ^ei - 1, k^ui - 1, к ~ Ф, к - I^м/, к - \)^ik > (4 11)

к = 1,2, ..., т, i = 1, 2, ..., п.

При этом предполагается, что м_/0 = щ_к = е_0/( = d^ = 0 для всех /, к. В записи (4.11) основной и, по существу, единственной является скалярная операция

u=b~^l(f- ex- dy), (4.12)

которая вычисляет величину и по величинам f, е, х, у, b, d. Опять неэффективна простая перенумерация операций. Для построения графа алгоритма рассмотрим прямоугольную решетку, узлы которой имеют целочисленные координаты /, к. Во все узлы решетки для 1 < / < я, \ < к < т поместим вершины графа и будем считать, что они соответствуют операции (4.12). Не будем указывать вершины, поставляющие входные данные и нулевые значения некоторых аргументов. Анализируя запись (4.11), нетрудно убедиться в том, что в вершину с координатами /, к будут передаваться результаты выполнения операций, соответствующих вершинам с координатами / — 1, к и /, к — 1. Вся остальная информация, необходимая для реализации операции с координатами /, к, является входной и нужна для реализации только этой операции. В графе данного алгоритма нет множественной рассылки входных данных типа той, которая имела место в алгоритме (4.5).

214

Часть II. Параллельное программирование

Для случая п = 5, m = 9 граф алгоритма представлен на рис. 4.6. Из него следует, что вопреки возможным ожиданиям граф алгоритма прекрасно распараллеливается. Пунктирными линиями отмечены ярусы максимальной параллельной формы. Понятно, что высота алгоритма без учета ввода входных данных равна m + п +1, ширина алгоритма равна min(m, п). На рис. 4.7 в этом же графе пунктирными линиями обведены группы вершин. Каждая из таких групп соответствует одной вершине графа, представленного на рис. 4.5. Они же являются ярусами обобщенной параллельной формы. Из этих рисунков видно, каким образом хорошо распараллеливаемый алгоритм может превратиться в нераспараллеливаемый при неудачном укрупнении операций.

Рис. 4.6. Граф для блочно-двухдиагональной системы

Рис. 4.7. Ярусы обобщенной параллельной формы

Глава 4. Большие задачи и параллельные вычисления

215

Рассмотрим, наконец, решение краевой задачи для одномерного уравнения теплопроводности. Пусть требуется найти решение и {у, z),

где

Эй Э²и „ „

ду dz²и(0, Z) = cp(z), и(у, 0) = и₀(у), и(у, 1) = и_{(у). Построим равномерную сетку с шагом h по z и шагом т по у. Предположим, что по тем или иным причинам выбрана явная схема

_uf - «у^_1) _ «<!_-/> - Ц~^ + ^и№ т ~ а² '

Пусть алгоритм реализуется в соответствии с формулой

uf = „y-D +^(_w('-/⁾ -²"У^_1) +"5+~i¹⁾>- ^(4ЛЗ)

Для построения графа алгоритма введем прямоугольную систему координат с осями /, j. Переменные у, z связаны с переменными /, j соотношениями

у = т/, z = hj.

Поместим в каждый узел целочисленной решетки вершину графа и будем считать ее соответствующей скалярной операции

<й = а(1-Ц-) + Аг(Ь + с), (4.14)

А² А²

выполняемой для разных значений аргументов а, Ь, с. Для случая h = 1/8, х = 7/6 граф алгоритма представлен на обоих рис. 4.8, а, б. На границе области расположены вершины, символизирующие ввод начальных данных и граничных значений.

На данном примере мы хотим затронуть очень важный вопрос, касающийся реализации алгоритмов на любых компьютерах. До сих пор мы связывали ее с выполнением операций по ярусам параллельных форм. Конечно, операции одного яруса не зависят друг от друга и их действительно можно реали-зовывать на разных устройствах одновременно. Но эффективность такой организации параллельных вычислений может оказаться очень низкой. На рис. 4.8, а пунктирными линиями показаны все ярусы максимальной параллельной формы алгоритма (4.13). Предположим, что операции реализуются по этим ярусам. Каждая операция вида (4.14) одного яруса требует трех аргументов. Они являются результатами выполнения операций на предыдущем ярусе. Если данные, полученные на одном ярусе, могут быстро извлекаться из памяти, то никаких серьезных проблем с реализацией алгоритма по ярусам параллельной формы не возникает. Однако для больших многомерных

216

Часть II. Параллельное программирование

задач ярусы оказываются столь масштабными, что информация о них может не поместиться в быстрой памяти. Тогда для ее размещения приходится использовать медленную память. Для этой памяти время выборки одного числа существенно превышает время выполнения базовой операции (4.14). Это означает, что при переходе к очередному ярусу время, затраченное на выполнение операций, окажется значительно меньше времени взаимодействия с памятью. Чем меньше отношение времени выполнения операций ко времени доступа к памяти, тем меньше эффективность реализации алгоритма (4.13) по ярусам параллельной формы. В этом случае большая часть времени работы параллельного компьютера будет тратиться на осуществление обменов с медленной памятью, а не на собственно счет.

Рис. 4.8. Микро- и макропараллелизм в графе

Можно ли каким-либо способом повысить эффективность использования медленной памяти в алгоритме (4.13) и, если можно, то как? Ответ на данный вопрос дает более детальное изучение графа алгоритма. Заметим, что в графе алгоритма (4.13), кроме строгой параллельной формы с горизонтальными ярусами на рис. 4.8, а, существуют параллельные формы, строгие и обобщенные, с наклонными ярусами. Например, обобщенные параллельные формы можно получить, сгруппировав в ярусы вершины на прямых / + j = const и / — j = const. На рис. 4.8, б пунктирными линиями показаны некоторые из этих ярусов. Отмеченные ярусы разбивают область задания графа на многогранники. Алгоритм (4.13) теперь можно реализовывать по полученным многогранникам, в том числе, параллельно. При этом одному процессору всегда поручается выполнение всех операций, относящихся к одному многограннику. При параллельной реализации сначала выполняются

Глава 4. Большие задачи и параллельные вычисления

217

операции, соответствующие нижним заштрихованным многогранникам на рис. 4.8, б. Затем параллельно выполняются операции, соответствующие соседним незаштрихованным многогранникам, и т. д.

В новом процессе операции одного многогранника становятся макрооперацией. Время выполнения макрооперации определяется числом вершин в многограннике, что примерно пропорционально его площади. Информационную связь между собой многогранники осуществляют через вершины, лежащие около границ. Следовательно, время на извлечение из памяти информации, необходимой для реализации макрооперации, определяется длиной границы многогранника. Размеры многогранников можно выбирать произвольно. Они зависят только от того, какие ярусы обобщенных параллельных форм формируют их границы. Всегда можно выбрать такое разбиение области задания графа, при котором для большинства многогранников отношение длин границ к их площадям будет сколь угодно малым. При реализации таких макроопераций влияние времени доступа к медленной памяти будет снижено очень сильно.

До сих пор параллельные формы алгоритмов применялись только для выявления множеств независимых операций. Как показывает данный пример, они могут также быть полезными для исследования возможности эффективного использования медленной памяти. Подчеркнем, что проведенные выше рассуждения одинаково пригодны как для параллельных компьютеров, так и для "обыкновенных".

Рассмотренные выше примеры убедительно показали, что во многих алгоритмах действительно имеется хороший запас параллелизма. Ключевым моментом в его выявлении или установлении факта, что он отсутствует, является знание графов алгоритмов и их параллельных форм. Более того, оказалось, что графы алгоритмов и их параллельные формы можно успешно применять для решения и других вопросов, связанных с реализацией алгоритмов на компьютерах, причем необязательно параллельных. Однако все рассмотренные примеры были относительно простыми, а графы алгоритмов почти очевидными. Тем не менее, на этих примерах удалось нащупать некоторые принципы проведения исследований структуры алгоритмов. Чтобы теперь перейти к существенно более сложным алгоритмам, необходимо намеченную методологию поставить на фундаментальную теоретическую основу. Но об этом мы будем говорить в следующих главах.

Вопросы и задания

Исследуйте внутренний параллелизм в следующих алгоритмах:

1. Схема Горнера вычисления значения многочлена в точке.

2. Быстрое параллельное вычисление значения многочлена в точке.

218

Часть II. Параллельное программирование

3. Решение системы линейных алгебраических уравнений с двухдиагональной матрицей методом обратной подстановки.

4. Быстрое параллельное решение системы линейных алгебраических уравнений с двухдиагональной матрицей.

5. Вычисление произведения А^Т(В + В⁷)А, где А, В — квадратные матрицы.

6. Рекуррентное вычисление значений Ujj_k = F(Uj _ ^_к, u-ц _ iд, иц_к _ j) для произвольной функции F(x, у, z)-

7. Решение системы линейных алгебраических уравнений методом Гаусса.

8. Решение системы линейных алгебраических уравнений методом Жордана.

9. Быстрое преобразование Фурье.

10. Перемножение матриц методом Штрассена.

Глава 5

Технологии параллельного программирования

Все, что начинается хорошо, кончается плохо. Все, что начинается плохо, кончается еще хуже.

Из законов Мерфи

Итак, вы приступаете к созданию параллельной программы. Желание есть, задача ясна, метод выбран, целевой компьютер, скорее всего, тоже определен. Осталось только все мысли выразить в той или иной форме, понятной для этого компьютера. Чем руководствоваться, если собственного опыта пока мало, а априорной информации о доступных технологиях параллельного программирования явно недостаточно? Наводящих соображений может быть много, но в результате вы все равно будете вынуждены пойти на компромисс, делая выбор между временем разработки программы, ее эффективностью и переносимостью, интенсивностью последующего использования программы, необходимостью ее дальнейшего развития. Не вдаваясь в детали выбора, попробуйте для начала оценить, насколько важны для вас следующие три характеристики.

Основное назначение параллельных компьютеров — это быстро решать задачи. Если технология программирования по разным причинам не позволяет в полной мере использовать весь потенциал вычислительной системы, то нужно ли тратить усилия на ее освоение? Не будем сейчас обсуждать причины. Ясно то, что возможность создания эффективных программ является серьезным аргументом в выборе средств программирования.

Технология может давать пользователю полный контроль над использованием ресурсов вычислительной системы и ходом выполнения его программы. Для этого ему предлагается набор из нескольких сотен конструкций и функций, предназначенных "на все случаи жизни". Он может создать действительно эффективную программу, если правильно воспользуется предложенными средствами. Но захочет ли он это делать? Не стоит забывать, что он должен решать свою задачу из своей предметной области, где и своих проблем хватает. Маловероятно, что физик, химик, геолог или эколог с большой радостью захочет осваивать новую специальность, связанную с параллельным программированием. Возможность быстрого создания параллельных программ должна приниматься в расчет наравне с другими факторами.

Вычислительная техника меняется очень быстро. Предположим, что была найдена технология, позволяющая быстро создавать эффективные парал-

220

Часть II. Параллельное программирование

дельные программы. Что произойдет через пару лет, когда появится новое поколение компьютеров? Возможных вариантов развития событий два. Первый вариант — разработанные прежде программы были "одноразовыми" и сейчас ими уже никто не интересуется. Бывает и так. Однако, как правило, в параллельные программы вкладывается слишком много средств (времени, усилий, финансовых затрат), чтобы просто так об этом забыть и начать разработку заново. Хочется перенести накопленный багаж на новую компьютерную платформу. Скорее всего, на новом компьютере старая программа рано или поздно работать будет, и даже будет давать правильный результат. Но дает ли выбранная технология гарантии сохранения эффективности параллельной программы при ее переносе с одного компьютера на другой? Скорее всего, нет. Программу для новой платформы нужно оптимизировать заново. А тут еще разработчики новой платформы предлагают вам очередную новую технологию программирования, которая опять позволит создать выдающуюся программу для данного компьютера. Программы переписываются, и так по кругу в течении многих лет.

Выбор технологии параллельного программирования — это и в самом деле вопрос не простой. Если попытаться сделать обзор средств, которые могут помочь в решении задач на параллельном компьютере, то даже поверхностный анализ приведет к списку из более 100 наименований: НОРМА, Т-система, ARCH, А++/Р++, ABCL, Adl, Ada, ATLAS, Aztec, BIP, BLACS, BSPlib, BlockSolve95, BERT 77, CVM, Counterpoint, CC++, Charm/Charm++, Cilk, CFX, Cray MPP Fortran, Concurrent Clean, Converse, CODE, DOUG, DEEP, DVM, Erlang, EDPEPPS, F1DAP, FFTW, FLUENT, FM, F—, Fortran 90/95, Fortran D95, Fortran M, Fx, FORGE, GA, GALOPPS, GAMESS, Guassian, GRADE, Haskell, HPVM, HPF, HPC, HPC++, HeNCE, 1CC, JIAJIA, JOSTLE, KELP, КАР, LAPACK, LPARX, Linda, Maisie, Mentat, mpC, MPC++, MP1, MPL, Modula-3, NAG, Nastran, NESL, NAMD, OOMP1, OpenMP, Occam, Orca, Opus, P4, Para++, ParJava, Parsec, Parallaxis, Phantom, Phosphorus, Pict, pC++, P-Sparslib, P1M, ParMETIS, PARPACK, PBLAS, PETSc, PGAPack, PLAPACK, PIPS, Pthreads, PVM, Quarks, Reactor, ShMem, SVMlib, Sisal, SR, sC++, ScaLAPACK, SPRNG, TOOPS, TreadMan, Treadmarks, TRAPPER, uC++, Vienna Fortran, VAST, ZPL.

В некоторых случаях выбор определяется просто. Например, вполне жизненной является ситуация, когда воспользоваться можно только тем, что установлено на доступном вам компьютере. Другой аргумент звучит так: "... все используют МР1, поэтому и я тоже буду...". Если есть возможность и желание сделать осознанный выбор, это обязательно нужно делать. Посоветуйтесь со специалистами. Проблемы в дальнейшем возникнут в любом случае, вопрос только насколько быстро и в каком объеме. Если выбор будет правильным, проблем будет меньше. Если неправильным, то тоже не отчаивайтесь, будет возможность подумать о выборе еще раз. Сделав выбор несколько раз, вы станете специалистом в данной области, забудете о своих

Глава 5. Технологии параллельного программирования

221

прежних интересах, скажем, о квантовой химии или вычислительной гидродинамике. Не исключено, что в итоге вы сможете предложить свою технологию и найти ответ на центральный вопрос параллельных вычислений: "Как создавать эффективные программы для параллельных компьютеров?"

В данной главе мы рассмотрим различные подходы к программированию параллельных компьютеров. Одни широко используются на практике, другие интересны своей идеей, третьи лаконичны и выразительны. Хотелось показать широкий спектр существующих средств, но и не сводить описание каждой технологии до одного абзаца текста. Противоречивая задача. Однако надеемся, что после изучения каждого раздела вы сможете не только проводить качественное сравнение технологий, но и самостоятельно писать содержательные программы.

Знакомясь с различными системами параллельного программирования, обязательно обратите внимание на следующее обстоятельство. Если вы решаете учебные задачи или производственные задачи небольшого размера, вам почти наверняка не придется задумываться об эффективности использования параллельной вычислительной техники. В этом случае выбор системы программирования практически не имеет значения. Используйте то, что вам больше нравится. Но как только вы начнете решать большие задачи и, особенно, предельно большие многовариантные задачи, вопрос эффективности может оказаться ключевым.

Очень скоро станет ясно, что при использовании любой системы параллельного программирования желание повысить производительность вычислительной техники на вашей задаче сопровождается тем, что от вас требуется все больше и больше каких-то новых сведений о структуре задачи, программы или алгоритма. Ни одна система параллельного программирования не гарантирует высокую эффективность вычислительных процессов без предоставления дополнительных сведений.

Все эти сведения нетрадиционны и нетривиальны. Не очень даже ясно, в какой форме они должны быть предоставлены. О том, как получать такие сведения, мы будем подробно говорить в главах 6 к 7. Возможно, что описываемые ниже системы параллельного программирования, а также опыт их использования приведут, в конце концов, к созданию дружественных по отношению к пользователям, высокоэффективных систем общения со сложной вычислительной техникой.

§ 5.1. Использование традиционных последовательных языков

Вариантом, на который согласились бы многие пользователи параллельных вычислительных систем, является использование традиционных последовательных языков программирования. Вариант не идеальный, но преимуществ

222

Часть II. Параллельное программирование

и в самом деле много: сохраняется весь уже созданный программный багаж, программист продолжает мыслить в привычных для него терминах, а всю дополнительную работу по адаптации программы к архитектуре параллельных компьютеров выполняет компилятор. На первый взгляд все кажется вполне реальным, однако попробуем оценить сложность задачи автоматического распараллеливания программ компилятором.

Предположим, что мы хотим получить эффективную программу для параллельного компьютера с распределенной памятью. Мы специально сделали акцент на эффективности программы, поскольку именно в этом и состоит основная задача. Получить какой-нибудь исполняемый код не составляет никакой проблемы: для этого достаточно, например, просто скомпилировать программу для одного процессора. Но тогда зачем использовать параллельный компьютер, если при запуске на любой конфигурации всегда реально задейст-вуется лишь один процессор, и время работы программы не уменьшается?

Чтобы полностью использовать потенциал данной архитектуры, необходимо решить три основные задачи:

□ найти в программе ветви вычислений, которые можно исполнять параллельно;

□ распределить данные по модулям локальной памяти процессоров;

□ согласовать распределение данных с параллелизмом вычислений.

Если не решить первую задачу, то бессмысленно использовать многопроцессорные конфигурации компьютера. Если решена первая, но не решены последние две задачи, то все время работы программы может уйти на обмен данными между процессорами. В таком случае про масштабируемость программы можно забыть.

Указанные задачи в самом деле крайне сложны. Построить эффективные алгоритмы их решения даже для узкого класса программ очень не просто, в чем читатель легко убедится сам, если рассмотрит несколько реальных примеров.

Попробуем немного упростить ситуацию, и будем рассматривать параллельные компьютеры с общей памятью. Казалось бы, остается лишь задача определения потенциального параллелизма программы, но все ли так просто? Рассмотрим следующий фрагмент программы, состоящий всего из трех (!) строк:

DO 10 i = 1, n DO 10 j = 1, n 10 U(i + j) = U(2*n -i-j+1) * q + p

Какие итерации данной циклической конструкции являются независимыми, и можно ли фрагмент исполнять в параллельном режиме? Несмотря на исключительно маленький размер исходного текста, вопрос совсем не триви-

Глава 5. Технологии параллельного программирования

223

альный. Прежде, чем читать дальше, попробуйте найти ответ самостоятельно, хотя из общих соображений уже ясно, что если задается вопрос "можно ли?..", то ответом будет — "можно".

Рис. 5.1. Информационная структура фрагмента при п = 10

На рис. 5.1 показана информационная структура данного фрагмента для случая п = 10. По рисунку можно сразу определить, что ни один из циклов не является параллельным. Однако даже имея под рукой этот рисунок, непросто определить, что исходный фрагмент можно преобразовать к эквивалентной форме, в которой оба внутренних цикла уже будут параллельными:

DO 10 i = 1, n

DO 20 j = 1, n - i 20 U(i + j) = U(2*n - i - j + l)*q + p

DO 30 j = n - i + 1, n 30 U(i + j) = U(2*n - i - j + l)*q + p 10 continue .

224

Часть II. Параллельное программирование

Если исходный фрагмент (п = 1000) выполнить на векторно-конвейерном компьютере Cray С90, то его производительность составит около 20 Мфлопс при пиковой производительности почти в 1 Гфлопс. Основная причина низкой производительности заключается в том, что компилятор не может самостоятельно найти такую эквивалентную форму фрагмента, в которой все итерации внутреннего цикла были бы независимы, и, следовательно, он не может векторизовать фрагмент. Одновременно заметим, что производительность этого же компьютера на преобразованном фрагменте уже составит около 420 Мфлопс. И фрагмент состоит всего из трех строк, и все индексные выражения и границы циклов заданы явно, но определить параллельные свойства совсем не просто...

Рассмотрим теперь такой фрагмент:

DO 10 i = 1, n 10 U(i) = Func(U, i)

где Func — это функция пользователя. Чтобы ответить на вопрос, являются ли итерации цикла независимыми, компилятор должен определить, не используются ли функцией Func элементы массива и. Если в теле данной функции где-то используется, например, элемент u(i - 1), то итерации зависимы. Если сама функция Func явно не использует массив и, но в ее теле где-то стоит вызов другой функции, которая в свою очередь и использует элемент и (i - 1), то итерации цикла опять-таки будут зависимы. В общем случае, компилятор должен уметь анализировать цепочки вызовов произвольной длины и выполнять полный межпроцедурный анализ. В некоторых случаях это сделать можно, но в общем случае задача крайне сложна.

А какой вывод может сделать компилятор о независимости итераций такого фрагмента:

DO 10 i = 1, n 10 U(i) = A(i) + U(IU(i) )

Если нет никакой априорной информации о значениях элементов массива косвенной адресации iu, а чаще всего ее нет, то ничего определенного сказать нельзя. Во всяком случае, поскольку параллельная реализация может привести к изменению результата, то компилятор "для надежности" сгенерирует последовательный код. Компилятор плохой? Нет, просто в данном случае он ничего иного в принципе сделать не может.

Подобных примеров, когда компиляторам сложно определить истинную структуру фрагмента, а значит и сложно получить его эффективную параллельную реализацию, можно привести много. Наверное, не стоит сильно винить компиляторы в неспособности решения возникающих проблем. Даже в теории полностью проанализировать произвольный фрагмент, записанный в соответствии с правилами языка программирования, невозможно. Если архитектура компьютеров не очень сложна, то компиляторы вполне в

Глава 5. Технологии параллельного программирования

225

состоянии сгенерировать эффективный код и с обычных последовательных программ. В противном случае компилятору необходимы "подсказки", содержащие указания на те или иные свойства программ.

Подсказки компилятору могут быть выражены в разной форме. В одних случаях используются специальные директивы, записанные в комментариях, в других случаях в язык вводятся новые конструкции, часто используются дополнительные служебные функции или предопределенные переменные среды окружения. Типичная связка: традиционный последовательный язык + какая-либо комбинация из только что рассмотренных способов. На использовании специальных директив в комментариях к тексту программы основано и одно из самых известных расширений языка Fortran для работы на параллельных компьютерах — High Performance Fortran (HPF). В середине 90-х годов прошлого столетия с HPF были связаны очень большие надежды, поскольку язык был сразу ориентирован на разработку переносимых параллельных программ. Появление HPF по времени совпало с периодом бурного развития компьютеров с массовым параллелизмом, и проблема переносимости программ стала исключительно актуальной. Однако на этом пути не удалось найти приемлемого решения. Сложность конструкций HPF оказалась непреодолимым препятствием на пути создания по-настоящему эффективных компиляторов, что, естественно, предопределило отказ от него со стороны пользователей.

Технология программирования ОрепМР

Одним из наиболее популярных средств программирования компьютеров с общей памятью, построенных на подобных принципах, в настоящее время является технология ОрепМР. За основу берется последовательная программа, а для создания ее параллельной версии пользователю предоставляется набор директив, процедур и переменных окружения. Стандарт ОрепМР разработан для языков Fortran (77, 90, и 95), С и C++ и поддерживается практически всеми производителями больших вычислительных систем. Реализации стандарта доступны как на многих UNIX-платформах, так и в среде Windows NT. Поскольку все основные конструкции для этих языков похожи, то рассказ о данной технологии мы будем вести на примере только одного из них, а именно на примере языка Fortran.

Как в рамках правил ОрепМР пользователь должен представлять свою параллельную программу? Весь текст программы разбит на последовательные и параллельные области (рис. 5.2). В начальный момент времени порождается нить-мастер или "основная" нить, которая начинает выполнение программы со стартовой точки. Здесь следует сразу оговориться, почему вместо традиционного для параллельного программирования термина "процесс" появился новый термин — "нить" {thread, легковесный процесс, иногда "поток"). Технология ОрепМР опирается на понятие общей памяти, и поэтому она, в значительной степени, ориентирована на SMP-компьютеры. На

226

Часть II. Параллельное программирование

подобных архитектурах возможна эффективная поддержка нитей, исполняющихся на различных процессорах, что позволяет избежать значительных накладных расходов на поддержку классических UNIX-процессов.

ч------------------ последовательная секция

<------- параллельная секция

<------------------ последовательная секция

ПП...П <--------- параллельная секция

ч------------------ последовательная секция

Рис. 5.2. ОрепМР: процесс исполнения программы

Основная нить и только она исполняет все последовательные области программы. Для поддержки параллелизма используется схема FORK/JOIN. При входе в параллельную область нить-мастер порождает дополнительные нити (выполняется операция FORK). После порождения каждая нить получает свой уникальный номер, причем нить-мастер всегда имеет номер 0. Все порожденные нити исполняют один и тот же код, соответствующий параллельной области. При выходе из параллельной области основная нить дожидается завершения остальных нитей, и дальнейшее выполнение программы продолжает только она (выполняется операция JOIN).

В параллельной области все переменные программы разделяются на два класса: общие (SHARED) и локальные (PRIVATE). Общие переменные всегда существуют лишь в одном экземпляре для всей программы и доступны всем нитям под одним и тем же именем. Объявление локальных переменных вызывает порождение своего экземпляра каждой переменной для каждой нити. Изменение нитью значения своей локальной переменной, естественно, никак не влияет на изменение значения этой же локальной переменной в других нитях.

По существу, только что рассмотренные понятия областей программы и классов переменных определяют общую идею написания параллельной программы в рамках ОрепМР: некоторые фрагменты текста программы объявляются параллельными областями; именно эти области и только они исполняются набором нитей, которые могут работать как с общими, так и с локальными переменными. Все остальное — это конкретизация деталей и описание особенностей реализации данной идеи на практике.

Глава 5. Технологии параллельного программирования

227

Рассмотрим базовые положения и основные конструкции ОрепМР. Все директивы ОрепМР располагаются в комментариях и начинаются с одной из следующих комбинаций: !$омр, с$омр или *$омр (напомним, что строка, начинающаяся с одного из символов '! ', ' с' или ' *' по правилам языка Fortran считается комментарием). В дальнейшем изложении при описании конкретных директив для сокращения записи мы иногда будем опускать эти префиксы, хотя в реальных программах они, конечно же, всегда должны присутствовать. Все переменные среды окружения и функции, относящиеся к ОрепМР, начинаются с префикса омр_.

Описание параллельных областей. Для определения параллельных областей программы используется пара директив

!$ОМР PARALLEL

<параллельный код программы> !$ОМР END PARALLEL

Для выполнения кода, расположенного между данными директивами, нитью-мастером дополнительно порождается omp_num_threads - 1 нитей, где omp_num_threads — это переменная окружения, значение которой пользователь задает перед запуском программы и, вообще говоря, может изменять. Нить-мастер всегда получает номер 0. Все нити исполняют код, заключенный между данными директивами.

После end parallel автоматически происходит неявная синхронизация всех нитей. Как только все нити доходят до этой точки, нить-мастер продолжает выполнение последующей части программы, а остальные нити уничтожаются.

Параллельные секции могут быть вложенными одна в другую. По умолчанию, вложенная параллельная секция исполняется одной нитью. Необходимую стратегию обработки вложенных секций определяет переменная omp_nested, значение которой можно изменить с помощью функции omp_set_nested.

Число нитей в параллельной секции можно менять. Если значение переменной

OMP_DYNAMIC раВНО 1, ТО С ПОМОЩЬЮ фуНКЦИИ OMP_SET_NUM_THREADS ПОЛЬЗО-

ватель может изменить значение переменной omp_num_threads, а значит и число порождаемых при входе в параллельную секцию нитей. Значение переменной OMP_DYNAMIC Контролируется функцией OMP_SET_DYNAMIC.

Необходимость порождения нитей и параллельного исполнения кода параллельной секции пользователь может определять динамически с помощью дополнительной опции if в директиве:

!$ОМР PARALLEL IF(<условие>)

Если <условие> не выполнено, то директива не срабатывает и продолжается обработка программы в прежнем режиме.

Мы уже говорили о том, что все порожденные нити исполняют один и тот же код. Теперь нужно обсудить вопрос, как разумным образом распределить

228

Часть II. Параллельное программирование

между ними работу. Для распределения работы в рамках ОрепМР можно использовать четыре варианта:

□ программирование на низком уровне;

□ директива do для параллельного выполнения циклов;

□ директива sections для параллельного выполнения независимых фрагментов программы;

□ директива single для однократного выполнения участка кода. Программирование на низком уровне предполагает распределение работы с

ПОМОЩЬЮ фуНКЦИЙ OMP_GET_THREAD_NUM И OMP_GET_NUM_THREADS, ВОЗВра-

щающих номер нити и общее количество порожденных нитей соответственно. Например, если написать фрагмент вида:

IF(OMP_GET_THREAD_NUM() .EQ. 3) THEN

<индивидуальный код для нити с номером 3> ELSE

<код для всех остальных нитей> ENDIF

то часть программы между директивами if. . .else будет выполнена только нитью с номером 3, а часть между else. . .endif — всеми остальными. Как и прежде, исходный код остается одинаковым для всех нитей. Однако реальная передача управления в нем будет идти для разных нитей по-разному, поскольку функция omp_get_thread_num () возвратит значение 3 только для нити с номером 3.

Если в параллельной секции встретился оператор цикла, то согласно общему правилу он будет выполнен всеми нитями, т. е. каждая нить выполнит все итерации данного цикла.

Для распределения итераций цикла между нитями нужно использовать директиву do:

!$ОМР DO [опция [[,] опция]...]

<о!о-цикл> [!$ОМР END DO]

Данная директива относится к идущему следом за ней оператору do.

□ Опция schedule определяет конкретный способ распределения итераций данного цикла по нитям.

□ static [,m] — блочно-циклическое распределение итераций. Первый блок из m итераций выполняет первая нить, второй блок — вторая и т. д. до последней нити, затем распределение снова начинается с первой нити. Если значение m не указано, то все множество итераций делится на

Глава 5. Технологии параллельного программирования

229

непрерывные куски примерно одинакового размера, и таким образом полученные куски распределяются между нитями.

□ dynamic [,m] — динамическое распределение итераций с фиксированным размером блока. Сначала все нити получают порции из m итераций, а затем каждая нить, заканчивающая свою работу, получает следующую порцию, содержащую также m итераций. Если значение m не указано, оно принимается равным единице.

□ guided [,m] — динамическое распределение итераций блоками уменьшающегося размера. Сначала размер выделяемых блоков берется достаточно большим, а в процессе работы программы он все время уменьшается. Минимальный размер блока итераций равен т. Размер первоначально выделяемого блока зависит от реализации. Если значение m не указано, оно принимается равным единице. В ряде случаев такое распределение позволяет аккуратнее разделить работу и сбалансировать загрузку нитей.

□ runtime — способ распределения итераций цикла выбирается во время работы программы в зависимости от значения переменной omp_schedule.

Выбранный способ распределения итераций указывается в скобках после опции schedule, например:

!$ОМР DO SCHEDULE (DYNAMIC, 10)

В данном примере будет использоваться динамическое распределение итераций блоками по 10 итераций.

В конце параллельного цикла происходит неявная барьерная синхронизация параллельно работающих нитей: их дальнейшее выполнение происходит только тогда, когда все они достигнут данной точки. Если в подобной задержке нет необходимости, то завершающая директива end do nowait позволяет нитям, уже дошедшим до конца цикла, продолжить выполнение без синхронизации с остальными. Если директива end do в явном виде не указана, то в конце параллельного цикла синхронизация все равно будет выполнена.

На организацию параллельных циклов накладывается несколько естественных ограничений. В частности, предполагается, что корректная программа не должна зависеть от того, какая именно нить какую итерацию параллельного цикла выполнит. Нельзя использовать побочный выход из параллельного цикла. Размер блока итераций, указанный в опции schedule, не должен изменяться в рамках цикла.

Рассмотрим следующий пример. Будем предполагать, что он расположен в параллельной секции программы.

!$ОМР DO SCHEDULE (STATIC, 2) DO i = 1, n DO j = 1, m

230

Часть II. Параллельное программирование

A(i, j) = (B(i, j - 1) + B(i - 1, j)) /2.0

END DO END DO !$OMP END DO

В данном примере внешний цикл объявлен параллельным, причем будет использовано блочно-циклическое распределение итераций по две итерации в блоке. Относительно внутреннего цикла никаких указаний нет, поэтому он будет выполняться последовательно каждой нитью.

Параллелизм на уровне независимых фрагментов оформляется в ОрепМР с помощью парной директивы sections. . .end sections и какого-то числа директив section, расположенных внутри этой пары. Например:

!$ОМР SECTIONS !$ОМР SECTION

<фрагмент 1> !$ОМР SECTION

<фрагмент 2> !$ОМР SECTION

<фрагментЗ> !$ОМР END SECTIONS

В данном примере программист описал, что все три фрагмента можно исполнять параллельно. Каждый из таких фрагментов будет выполнен только один раз какой-либо одной нитью. Если число нитей больше числа секций, то какие нити для каких секций задействовать, а какие нити не использовать вовсе, решают авторы конкретной реализации ОрепМР. В конце конструкции предполагается неявная синхронизация работы нитей. Если в подобной синхронизации нет необходимости, то может быть использована директива END SECTIONS nowait.

В директивах do и sections можно использовать опции firstprivate и lastprivate, каждую со своим списком переменных. Эти опции управляют инициализацией локальных переменных перед входом в данные конструкции, а также определяют те значения, которые переменные будут иметь после завершения параллельного цикла и обработки секций.

Если в параллельной секции какой-либо участок кода должен быть выполнен лишь один раз, то его нужно поставить между директивами single...end single. Подобная необходимость часто возникает при работе с общими переменными. Указанный участок будет выполнен только одной нитью. Если в конце не указана директива end single nowait, то выполнится неявная синхронизация всех нитей.

Одно из базовых понятий ОрепМР — классы переменных. Все переменные, используемые в параллельной секции, могут быть либо общими, либо ло-

Глава 5. Технологии параллельного программирования

231

кальными. Общие переменные описываются директивой shared, а локальные — директивой private. Каждая общая переменная существует лишь в одном экземпляре и доступна для каждой нити под одним и тем же именем. Для каждой локальной переменной в каждой нити существует отдельный экземпляр данной переменной, доступный только этой нити.

Предположим, что следующий фрагмент расположен в параллельной секции:

I = OMP_GET_THREAD_NUM() PRINT *, I

Если переменная i в данной параллельной секции была описана как локальная, то на выходе будет получен весь набор чисел от 0 до omp_num_threads - 1. Числа будут идти, вообще говоря, в произвольном порядке, но каждое число встретится только один раз. Если же переменная i была объявлена общей, то единственное, что можно сказать с уверенностью — мы получим последовательность из omp_num_threads чисел, лежащих в диапазоне от 0 до omp_num_threads - 1 каждое. Сколько и каких именно чисел будет в последовательности, заранее сказать нельзя. В предельном случае это может быть даже набор из omp_num_threads одинаковых чисел 1₀. В самом деле, предположим, что все процессы, кроме процесса i₀, выполнили в каком-то порядке первый оператор. Затем их выполнение по какой-то причине было приостановлено. В это время процесс с номером i₀присвоил это значение переменной i, а поскольку данная переменная является общей, то одно и то же значение в последствии и будет выведено каждой нитью. Чтобы избежать подобной неопределенности, программист должен сам следить за корректностью использования общих переменных различными нитями.

Рассмотрим следующий пример программы.

PROGRAM HELLO

INTEGER NTHREADS, TID, OMP_GET_NUM_THREADS, +OMP_GET_THREAD_NUM

С Порождение нитей с локальными переменными !$ОМР PARALLEL PRIVATE(NTHREADS, TID)

С Получить и напечатать свой номер TID = OMP_GET_THREAD_NUM() PRINT *, 'Hello World from thread = ', TID

С Участок кода для нити-мастера IF (TID .EQ. 0) THEN

232

Часть II. Параллельное программирование

NTHREADS = OMP_GET_NUM_THREADS()

PRINT *, 'Number of threads = ', NTHREADS

ENDIF

С Завершение параллельной секции !$ОМР END PARALLEL END

Каждая нить выполнит фрагмент кода, представляющий параллельную секцию, и напечатает приветствие вместе с номером нити. Дополнительно, нить-мастер напечатает общее число порожденных нитей. В объявлении параллельной секции явно указано, что переменные nthreads и tid являются локальными. Для определения общего числа нитей и их номеров использованы библиотечные функции omp_get_num_threads и omp_get_thread_num.

Теперь рассмотрим программу сложения векторов.

PROGRAM VEC_ADD_DO INTEGER N, CHUNK, I PARAMETER (N = 1000) PARAMETER (CHUNK =100) REAL A(N), B(N), C(N)

! Инициализация массивов DO I = 1, N

A(I) = I * 1.0 B(I) = A(I) END DO

!$OMP PARALLEL SHARED(A,B,C,N) PRIVATE(I) !$OMP DO SCHEDULE(DYNAMIC,CHUNK)

DO I = 1, N

C(I) = A(I) + B(I)

END DO !$OMP END DO NOWAIT

!$OMP END PARALLEL END

В данном примере массивы а, в, с и переменная n объявлены общими. Переменная i является локальной, каждый процесс будет иметь свою копию данной переменной. Итерации параллельного цикла будут распределяться между нитями динамически. Размер блоков фиксирован и равен chunk.

Глава 5. Технологии параллельного программирования 233

Синхронизации нитей в конце параллельного цикла не будет, т. к. использована КОНСТРУКЦИЯ NOWAIT.

Целый набор директив в ОрепМР предназначен для синхронизации работы нитей. Самый распространенный и простой способ синхронизации — это барьер. Он оформляется с помощью директивы

!$ОМР BARRIER

Все нити, дойдя до этой директивы, останавливаются и ждут пока все оставшиеся нити не дойдут до этой точки программы, после чего все нити продолжают работать дальше.

Пара директив master. . .end master выделяет участок кода, который будет выполнен только нитью-мастером. Остальные нити просто пропускают данный участок и продолжают работу с оператора, расположенного следом за директивой end master. Неявной синхронизации данная директива не предполагает.

С помощью директив

!$ОМР CRITICAL [ (<имя_критической_секции>) ]

!$ОМР END CRITICAL [ (< имя_ критической_секции >) ]

оформляется критическая секция программы. В каждый момент времени в критической секции может находиться не более одной нити. Если критическая секция уже выполняется какой-либо нитью Pq, то все другие нити, выполнившие директиву critical для секции с данным именем, будут заблокированы, пока нить Pq не закончит выполнение данной критической секции. Как только Pq выполнит директиву end critical, одна из заблокированных на входе нитей войдет в секцию. Если на входе в критическую секцию стояло несколько нитей, то случайным образом выбирается одна из них, а остальные заблокированные нити продолжают ожидание. Все неименованные критические секции условно ассоциируются с одним и тем же именем. Все критические секции, имеющие одно и то же имя, рассматриваются единой секцией.

Модифицируем приведенный выше пример, связанный с печатью номера нити, следующим образом:

!$ОМР CRITICAL

I = OMP_GET_THREAD_NUM()

PRINT *, I !$OMP END CRITICAL

Даже в том случае, если переменная i будет объявлена общей, все равно на выходе гарантированно появятся все числа от 0 до omp_num_threads - 1.

234

Часть II. Параллельное программирование

Теперь посмотрим, есть ли разница между данным фрагментом, в котором используется критическая секция и общая переменная i, и фрагментом без критической секции с локальной переменной I. Результат, как мы только что видели, может различаться лишь в порядке появления чисел. Наборы чисел будут одинаковыми. Однако в исполнении этих фрагментов разница существенная. Если есть критическая секция, то в каждый момент времени фрагмент будет обрабатываться лишь какой-либо одной нитью. Остальные нити, даже если они уже подошли к данной точке программы и готовы к работе, будут ожидать своей очереди. Если критической секции нет, то все нити могут одновременно выполнить данный участок кода. С одной стороны, критические секции предоставляют удобный механизм для работы с общими переменными. Но, с другой стороны, пользоваться им нужно осмотрительно, поскольку критические секции добавляют последовательные участки кода в параллельную программу, что может снизить ее эффективность.

Частым случаем использования критических секций на практике является обновление общих переменных. Например, если переменная sum является общей и оператор вида sum = sum + Expr находится в параллельной секции программы, то при одновременном выполнении данного оператора несколькими нитями можно получить некорректный результат. Чтобы избежать такой ситуации, можно воспользоваться механизмом критических секций или специально предусмотренной для таких случаев директивой atomic:

!$ОМР ATOMIC

SUM = SUM + Expr

Данная директива относится только к идущему непосредственно за ней оператору. В данном примере atomic гарантирует корректную работу с общей переменной sum.

Поскольку в современных параллельных вычислительных системах может использоваться сложная структура и иерархия памяти, пользователь должен иметь гарантии того, что в необходимые ему моменты времени каждая нить будет видеть единый согласованный образ памяти. Именно для этих целей и предназначена директива

!$ОМР FLUSH [ список_переменных ]

Выполнение данной директивы предполагает, что значения всех переменных, временно хранящиеся в регистрах, будут занесены в основную память, все изменения переменных, сделанные нитями во время их работы, станут видимы остальным нитям, если какая-то информация хранится в буферах вывода, то буферы будут сброшены, и т. п. Поскольку выполнение данной директивы в полном объеме может повлечь значительные накладные расходы, а в какой-то момент нужна гарантия согласованного представления не всех, а лишь отдельных переменных, то эти переменные можно явно перечислить списком.

Глава 5. Технологии параллельного программирования

235

Мы не будем детальнее разбирать конструкции данной технологии. Читатель сможет найти полные тексты спецификаций ОрепМР для языков Fortran, С и C++ на сайте http://www.openmp.org.

Чем привлекательна технология ОрепМР? Можно отметить несколько моментов, среди которых стоит особо подчеркнуть два. Во-первых, технология изначально спроектирована таким образом, чтобы пользователь мог работать с единым текстом для параллельной и последовательной программ. Обычный компилятор на последовательной машине директивы ОрепМР просто "не замечает", поскольку они расположены в комментариях. Единственным источником проблем могут стать переменные окружения и специальные функции. Однако для них в спецификациях стандарта предусмотрены специальные "заглушки", гарантирующие корректную работу ОрепМР-программы в последовательном случае. Для этого нужно только перекомпилировать программу и подключить другую библиотеку.

Другим достоинством ОрепМР является возможность постепенного, "инкре-ментного" распараллеливания программы. Взяв за основу последовательный код, пользователь шаг за шагом добавляет новые директивы, описывающие новые параллельные конструкции. Нет необходимости сразу писать параллельную программу целиком, ее создание ведется последовательно. Это упрощает как процесс программирования, так и отладку.

Система программирования DVM

Модель, положенная в основу языков параллельного программирования Fortran-DVM [53] и C-DVM [30], объединяет элементы моделей параллелизма по данным и управлению. Базирующаяся на этих языках DVM-система разработки параллельных программ создана в Институте прикладной математики им. М. В. Келдыша РАН.

DVM-система состоит из пяти основных компонентов: компиляторы с языков Fortran-DVM и C-DVM, система поддержки выполнения параллельных программ, отладчик параллельных программ, анализатор производительности, предсказатель производительности.

При проектировании DVM-системы авторы опирались на следующие принципы.

□ Система должна базироваться на высокоуровневой модели выполнения параллельной программы, удобной и понятной для программиста, привыкшего программировать на последовательных языках.

□ Спецификации параллелизма должны быть прозрачными для обычных компиляторов. Программа на языках Fortran-DVM и C-DVM, помимо описания алгоритма средствами традиционных языков Fortran 77 или С, содержит спецификации параллелизма — правила параллельного выполнения этого алгоритма. Эти спецификации, которые по-другому на-

236

Часть II. Параллельное программирование

зывают директивами, должны быть "невидимы" для стандартных компиляторов.

□ Языки параллельного программирования должны представлять собой традиционные языки последовательного программирования, расширенные спецификациями параллелизма. Эти языки должны предлагать программисту модель программирования, близкую к модели выполнения. Знание программистом модели выполнения его программы и ее близость к модели программирования существенно упрощает для него анализ производительности программы и проведение ее модификаций, направленных на достижение приемлемой эффективности.

□ Основная работа по реализации модели выполнения параллельной программы (например, распределение данных и вычислений) должна осуществляться динамически системой поддержки выполнения DVM-программ. Это позволяет обеспечить динамическую настройку DVM-программ при их запуске на параметры приложения и конфигурацию параллельного компьютера.

Следствием последнего пункта является то, что программист может иметь один вариант программы для выполнения как на последовательных и параллельных компьютерах различной конфигурации, так и на неоднородных сетях ЭВМ. Это значительно облегчает отладку и дальнейшее сопровождение программы.

Таковы общие принципы. Параллельная программа на исходном языке Fortran-DVM (C-DVM) превращается DVM-препроцессором в обычную программу на языке Fortran 77 (С) с вызовами функций системы поддержки. Поскольку основой для организации межпроцессорного взаимодействия в системе поддержки является MPI, то программа может выполняться всюду, где есть MPI и компиляторы с языков С и Fortran 77. Этим поддерживается высокая степень переносимости. В будущем планируется автоматическое преобразование DVM-программ в ОрепМР-программы.

Для языка Fortran все DVM-директивы оформлены в виде строк комментариев, начинающихся с cdvm$, *dvm$ или idvm$. В языке С директивы DVM оформляются в виде макросов. Семантика директив в языках Fortran и С практически одинакова, что позволяет иметь на компьютере единую систему поддержки выполнения DVM-программ.

Модель выполнения DVM-программы можно описать следующим образом.

DVM-программа исполняется на виртуальной многопроцессорной системе. Виртуальной многопроцессорной системой называется та машина, которая предоставляется программе пользователя аппаратурой и базовым системным программным обеспечением. Для распределенной вычислительной системы примером такой машины может служить MPI-машина. В этом случае виртуальная многопроцессорная система — это группа MPI-процессов, которые

Глава 5. Технологии параллельного программирования

237

создаются при запуске параллельной программы на выполнение. Другим примером виртуальной системы является PVM.

Виртуальная многопроцессорная система всегда представляется в виде многомерной решетки процессоров. Число процессоров виртуальной многопроцессорной системы и конкретный способ ее представления задаются при запуске DVM-программы.

В момент запуска DVM-программа начинает свое выполнение с первого оператора программы сразу на всех процессорах виртуальной многопроцессорной системы. В это время в DVM-программе существует единственный поток управления (единственная ветвь).

В любой DVM-программе могут быть использованы два уровня параллелизма. На верхнем уровне в программе описывается какое-то число независимых ветвей (задач), которые могут выполняться параллельно. Задачи DVM — это независимые по данным крупные блоки программы. В конце ветвей допускается выполнение глобальной редукционной операции. В рамках каждой ветви могут дополнительно выделяться параллельные циклы. Никакой другой иерархии параллелизма DVM не допускает, и описать в теле параллельного цикла еще несколько независимых ветвей нельзя.

При входе в параллельную конструкцию, т. е. в параллельный цикл или в область параллельных задач, поток управления разбивается на некоторое количество независимых потоков, каждый из которых определяет процесс вычислений на соответствующих процессорах. При выходе из параллельной конструкции потоки управления на всех процессорах вновь становятся одинаковыми.

Все переменные DVM-программы размножаются по всем процессорам. Это означает, что на каждом процессоре будет своя локальная копия каждой переменной, с которой и будет происходить работа. Исключение составляют лишь специально указанные "распределенные" массивы, способ физического расположения которых определяется соответствующей директивой.

Любой оператор присваивания DVM-программы выполняется в соответствии с правилом собственных вычислений. Это означает, что он будет выполнен тем процессором, на котором распределена переменная, стоящая в левой части оператора присваивания.

Любая DVM-программа работает в соответствии с моделью SPMD на всех выделенных ей процессорах.

Основные конструкции DVM

Общая схема отображения программы и взаимосвязь основных понятий показана на рис. 5.3. Отображение виртуальных процессоров на физические осуществляется средствами операционной системы.

238

Часть II. Параллельное программирование

Рис. 5.3. Отображение последовательной программы в системе DVM

Распределение массивов. Для распределения массивов в системе DVM используется директива distribute. Данная директива имеет описательный статус и может быть использована в неисполняемой части программы аналогично операторам real, dimension и т. п. Рассмотрим отображение одномерного массива.

CDVM$ DISTRIBUTE имя-массива (формат) [ONTO Т(п)]

где поле формат может принимать одно из нескольких значений:

□ block — отображение равными блоками;

□ wgt_block(wb,nwb) — отображение взвешенными (неравными) блоками;

□ * — отображение целым измерением.

Предположим, что при запуске программы задана линейка виртуальных процессоров p(np). При отображении равными блоками измерение массива разбивается на np равных блоков, причем i-ый блок отображается на виртуальный процессор р (i). При отображении взвешенными блоками задается вектор весов wb размера nwb для каждой точки (или группы соседних точек) измерения распределяемого массива. Измерение массива делится на np блоков так, чтобы минимизировать отклонение веса каждого блока (суммы ве-

Глава 5. Технологии параллельного программирования

239

сов точек блока) от среднего значения. Такое отображение позволяет точнее сбалансировать загрузку процессоров. Отображение целым измерением означает, что измерение не будет распределяться между процессорами.

Если присутствует опция onto т (п), то массив отображается на ту часть линейки процессоров р (np) , на которую отображена n-ая задача вектора задач т.

Распределение многомерного массива осуществляется через независимое распределение каждого его измерения. При этом число распределенных измерений массива не может превышать числа измерений решетки виртуальных процессоров.

Выравнивание массивов. Для создания эффективных программ мало задать распределение массивов. Во многих случаях требуется отобразить несколько массивов согласованно друг с другом. Причин для этого много. Например, согласованное распределение потребуется для массивов, которым присваиваются новые значения в одном цикле, поскольку в противном случае не удастся соблюсти правило собственных вычислений. Согласованное отображение нескольких массивов нужно и для того, чтобы уменьшить количество общих данных, доступ к которым требует существенных накладных расходов.

Для организации согласованного отображения нескольких массивов используется механизм выравнивания одного массива относительно другого с помощью ДИреКТИВЫ ALIGN.

Рассмотрим следующий фрагмент программы.

REAL A(N), B(N) CDVM$ DISTRIBUTE A (BLOCK) CDVM$ DISTRIBUTE В (BLOCK)

DO i = nl, n2 B(i) = A(f (i)) END DO

Пусть owN(B(i)) обозначает виртуальный процессор, на который распределен элемент в (i). В соответствии с правилом собственных вычислений оператор на i-й итерации цикла будет выполняться на процессоре owN(B(i)). Если элемент A(f (i)) будет распределен на процессор owN(B(i)), то для каждого витка цикла все данные будут распределены на одном процессоре. Чтобы обеспечить такую локализацию данных, необходимо вместо директивы

CDVM$ DISTRIBUTE В (BLOCK)

применить директиву выравнивания массивов

CDVM$ ALIGN B(i) WITH A(f(i))

Директива устанавливает соответствие между элементами в (i) и а (f (i)), при котором они будут распределены на один и тот же процессор.

240

Часть II. Параллельное программирование

В любой момент можно динамически изменять текущее распределение данных с помощью директив redistribute и realign. Однако пользоваться такой возможностью нужно аккуратно, поскольку перераспределение может потребовать значительных затрат времени.

Параллельное выполнение циклов. Директива параллельного выполнения циклов parallel встроена в язык Fortran в виде спецкомментария следующего вида:

CDVM$ PARALLEL (/;, ..., i_m) ON A(L_h ..., L_n)

где /j — это управляющие параметры циклов /и-мерного тесно вложенного гнезда циклов, расположенного сразу после данной директивы, L_k = a_kxij + b_k— это линейная функция от управляющего параметра у'-го цикла, а— это идентификатор массива данных или вектора задач (1 <j<m, 1 < к < п). Все управляющие параметры циклов перечисляются в том порядке, в каком расположены циклы в тексте программы.

Данная директива устанавливает соответствие между итерацией многомерного цикла с индексами (/_ь ..., i_m) и элементом A(L_y, ..., L_n). Итерация цикла (/_ь ..., i_m) будет выполняться тем процессором, на который отображен элемент массива A(L_y,..., L_n).

Рассмотрим следующий пример.

CDVM$ PARALLEL (i) ON B(i) DO i = nl, n2

CALL XSUM(A, B, i, nl, n2) END DO

Данная директива говорит о том, что каждая итерация i₀ будет выполнена тем процессором, на который распределен элемент B(i₀).

Здесь следует сделать несколько дополнительных замечаний о выполнении операторов присваивания DVM-программы. Основной закон — это правило собственных вычислений. Оператор всегда должен выполняться тем процессором, на котором расположена переменная, стоящая в левой части. Та переменная, которой присваивается значение, определяет процессор, выполняющий оператор. Следствием этого факта является то, что с помощью перераспределения данных можно управлять балансировкой вычислительной нагрузки между процессорами.

Предположим, что в тексте программы есть такой фрагмент:

DO i = 1, n

B(i) = A(i) + C(i) END DO

Если перед циклом нет директивы parallel, то данный цикл будет выполняться всеми процессорами по правилу собственных вычислений. При этом

Глава 5. Технологии параллельного программирования

241

возможны две ситуации. Если массив в не является распределенным, то он размножен по всем процессорам, и, следовательно, все процессоры выполнят весь цикл полностью от первой итерации до последней. Если массив в является распределенным, то каждый процессор выполнит только те итерации /, для которых элементы в (i) распределены именно на этот процессор.

Теперь предположим, что перед циклом расположена директива parallel. Каждый процессор выполнит те итерации, которые предписаны данной директивой в соответствии с ее частью on. Однако для корректной работы программы предписание директивы должно полностью соответствовать правилу собственных вычислений. Явная избыточность? В некотором смысле — да, но она необходима для получения эффективных программ. Если есть директива parallel, то компилятор не вставляет никаких проверок на принадлежность вычисляемого элемента данному процессору. Каждый процессор выполняет только ту порцию итераций, которая предписана директивой. Во главу ставится эффективность, а за корректностью программы должен следить пользователь. Если директивы parallel нет, то для соблюдения правила собственных вычислений перед каждым оператором компилятор автоматически вставит дополнительную проверку. Будет гарантия корректности работы программы за счет снижения эффективности ее работы.

Отображение задач. Директива map встроена в язык Fortran в следующем виде:

CDVM$ MAP T\n) ONTO Щу.1₂, -, jy.ji)

где T{n) — это я-ая задача вектора задач Г, a P{ii.i₂, ■■■, j\-j₂) — это секция решетки виртуальных процессоров.

Директива map специфицирует то, что n-ая задача вектора Т будет выполняться секцией виртуальных процессоров P(iyi₂, —, Л72)- Все отображенные на эту задачу массивы (директива distribute) и вычисления (директива parallel) будут автоматически отображены на ту же секцию виртуальных процессоров P(i_y:i₂, ...,jy.j₂).

Что касается задач, то в DVM существуют две формы отображения блоков программы на задачи. Статическая форма является прямым аналогом параллельных секций во многих других языках, в частности, директивы sections в ОрепМР. Статическая форма отображения выглядит, например, так:

С описание массива задач

CDVM$ TASK MB (3)

CDVM$ TASK_REGION MB CDVM$ ON MB(1)

CALL JAC0BY(A1, Bl, M, N1 + 1) CDVM$ END ON

242

Часть II. Параллельное программирование

CDVM$ ON MB (2)

CALL JACOBY(A2, B2, Ml + 1, N2 + 1) CDVM$ END ON CDVM$ ON MB(3)

CALL JACOBY(A3, ВЗ, M2, N2) CDVM$ END ON CDVM$ END TASK_REGION

В динамической форме итерация цикла отображается на задачу. Эта спецификация синтаксически похожа на обычную директиву параллельного цикла, но существует семантическое отличие. В параллельном цикле на каждом процессоре из решетки виртуальных процессоров выполняется непрерывный диапазон итераций цикла, а в цикле параллельных задач каждая итерация цикла выполняется на секции данной решетки. Пример динамической формы отображения блоков программы на задачи может быть таким:

CDVM$ TASK_REGION MB CDVM$ PARALLEL (I) ON MB (I) DO I = 1, NT

END DO CDVM$ END_TASK REGION

Общие данные. Общими данными в системе DVM считаются те данные, которые вычисляются на одних процессорах, а используются на других. Все общие данные в DVM делятся на четыре группы: "соседние" общие данные, REMOTE-данные, "редукционные" данные и across-данные.

"Соседние" общие данные. Рассмотрим следующий фрагмент программы

CDVM$ PARALLEL (i) ON B(i), SHAD0W_RENEW (A(dl:d2)) DO i = 1 + dl, N - d2

B(i) = A(i - dl) + A(i + d2) END DO

Необходимые каждому процессору общие данные размещены на соседних виртуальных процессорах. Спецификация shadow_renew указывает, что в данном цикле используются новые значения общих данных из массива а, значение dl указывает размер требуемых данных от левого соседа, a d2 — от правого. Для доступа к данным, размещенным на других процессорах, используются так называемые теневые грани массива. Теневую грань пользователь может представлять себе буфером, который является непрерывным продолжением локальной секции массива в памяти процессора. Перед выполнением цикла требуемые данные автоматически пересылаются с соседних процессоров в теневые грани массива а на каждом процессоре. Доступ к

Глава 5. Технологии параллельного программирования

243

этим данным при выполнении цикла производится обычным образом и ничем не отличается от доступа к данным, изначально размещенным на процессорах. Фраза "может представлять себе буфером..." появилась не случайно, т. к. в конкретных реализациях это может быть не так. Например, в системах с общей памятью реализация теневых граней может осуществляться просто через синхронизацию доступа к соответствующим частям массива. Дополнительно в DVM предусмотрена и асинхронная форма данной спецификации, которая позволяет совместить вычисления и пересылку данных в теневые грани.

REMOTE-данные. Иногда доступ к удаленным данным требует заведения специальных буферов и соответствующей замены ссылок на массив, через которые происходят обращения к удаленным элементам массива.

Рассмотрим следующий фрагмент программы.

DIMENSION А(100,100), В(100,100) СТОМ$ DISTRIBUTE (*,BLOCK) :: А CDVM$ ALIGN B(I, J) WITH A(I, J)

CDVM$ REMOTE_ACCESS (А (50, 50))

С замена А(50, 50) ссылкой на буфер на всех процессорах OWN(X) и С рассылка значения А(50, 50) по всем процессорам X = А(50, 50)

CDVM$ REMOTE_ACCESS (В(100, 100))

С пересылка значения В (100, 100) в буфер процессора OWN(A(l, 1) А(1, 1) = В(100, 100)

CDVM$ PARALLEL (I, J) ON A (I, J) , REMOTE_ACCESS (B(I, n) ) С рассылка значений В(I, п) по процессорам OWN(A(I, J)) DO I = 1, 100 DO J = 1, 100

A(I,J) = B(I,J) + B(I,n) END DO END DO

Первые две директивы remote_access описывают удаленные ссылки для отдельных операторов. Директива remote_access в параллельном цикле специфицирует удаленные данные (элементы n-го столбца матрицы в) для всех процессоров, на которых выполняется цикл. При этом на каждый процессор будет переслана только необходимая ему часть столбца матрицы в.

244

Часть II. Параллельное программирование

Редукционные данные. Данные этой группы появляются при выполнении разного рода глобальных операций. Сначала операция выполняется на каждом процессоре на основе тех данных, которые на нем размещены. Частичный результат заносится в редукционную переменную процессора. Затем по редукционным переменным вычисляется результат глобальной операции.

Рассмотрим следующий фрагмент программы.

CDVM$ PARALLEL (I) ON B(I), REDUCTION (SUM(s)) DO I = 1, n

S = S + B(I) END DO

Имеющаяся зависимость по переменной s, вообще говоря, требует последовательного выполнения итераций цикла с передачей значения переменной s от каждого отработавшего процессора к следующему. Но если ситуация позволяет пренебречь отсутствием ассоциативности у машинных операций сложения, то такой цикл можно эффективно распараллелить. Для этого на каждом процессоре вводятся локальные копии переменной s, в которых при параллельном выполнении цикла будут храниться частичные суммы. После выполнения цикла суммирование всех частичных сумм даст искомую глобальную сумму.

Подобные общие данные называются редукционными. При их спецификации необходимо указать и ту редукционную операцию, которую требуется выполнить после цикла для объединения частичных результатов, посчитанных на каждом процессоре. Аналогично приведенному примеру можно поступить для распараллеливания циклов, в которых вычисляется, например, максимальное или минимальное значение элементов массива, произведение элементов массива или выполняется ряд других операций.

ACROSS-данные. Рассмотрим фрагмент программы, в котором пересчитыва-ются элементы массива в.

CDVM$ PARALLEL (I) ON B(I), ACROSS (B(dl:d2)) DO I = 1 + dl, n - d2

B(I) = B(I - dl) + B(I + d2) END DO

Указанные в директиве элементы массива в являются ACROSS-данными. В отличие от соседних общих данных, across-данные используются и обновляются в одном и том же цикле, определяя информационную зависимость. Параметры dl и d2 указывают размеры общих данных на соседних процессорах слева и справа соответственно. Подобная зависимость по данным опять-таки требует последовательного выполнения итераций цикла с передачей значений обновленных общих данных от одного процессора другому. Однако в некоторых случаях можно эффективно распараллелить такой цикл, если организо-

Глава 5. Технологии параллельного программирования

245

вать его конвейерное выполнение. Это, в частности, можно сделать, когда двумерный цикл распределен по одному измерению на линейку процессоров. Идея конвейерного выполнения заключается в том, что первый процессор выполняет часть "своих" итераций цикла и передает следующему процессору соответствующую порцию обновленных общих данных. После получения этих данных второй процессор начинает выполнять "свои" итерации цикла параллельно с выполнением первым процессором второй порции итераций, и т. д. Оптимальное число итераций в порции зависит от общего количества итераций цикла, времени выполнения каждой итерации, числа процессоров, а также латентности и пропускной способности коммуникационной среды. Система поддержки DVM-программ обеспечивает автоматическую передачу обновленных общих данных между процессорами.

Как мы видим, DVM-программа может выполняться на любом количестве процессоров, начиная с одного процессора. Это является следствием того, что директивы параллелизма в DVM не зависят ни от количества процессоров, ни от конкретных номеров процессоров. Единственным исключением является уровень задач. По требованию директивы map пользователь обязан явно описать массив виртуальных процессоров. При этом количество процессоров, описанных в программе, не должно превышать количества процессоров, задаваемых при запуске программы. Эта согласованность легко достигается использованием встроенной функции number_of_processors о, значением которой является количество процессоров, задаваемых при запуске программы.

В заключение рассмотрим пример параллельной программы на языке Fortran-DVM, реализующей алгоритм Якоби для решения сеточных уравнений.

PROGRAM JAC_DVM

PARAMETER (L = 8, ITMAX = 20) REAL A(L, L) , B(L, L) CDVM$ DISTRIBUTE (BLOCK, BLOCK) :: A CDVM$ ALIGN В (I, J) WITH A (I, J) С массивы А и В распределяются блоками

PRINT *, *********** TEST JACOBI **********' DO IT = 1, ITMAX CDVM$ PARALLEL (J, I) ON A (I, J ) DO J = 2, L - 1 DO I = 2, L - 1

A(I, J) = B(I, J) END DO END DO CDVM$ PARALLEL (J, I) ON В (I, J) , SHADOW_RENEW (A)

246

Часть II. Параллельное программирование

С двумерный параллельный цикл, итерация (j, i) выполняется, С на том процессоре, где размещен элемент B(i, j) С копирование теневых элементов массива А С с соседних процессоров перед выполнением цикла DO J = 2, L - 1 DO I = 2, L - 1

B(I, J) = (A(I - 1, J) + A(I, J - 1) + * A(I + 1, J) + A(I, J + 1) )/4

END DO END DO END DO

OPEN (3, FILE = 'JACOBI.DAT', FORM = 'FORMATTED') WRITE (3,*)B CLOSE (3) END

Массив а распределяется на двумерную решетку виртуальных процессоров, поскольку количество форматов block определяет и количество измерений решетки процессоров. При запуске программы на выполнение может быть задана любая конкретная двумерная решетка процессоров. На рис. 5.4 показано отображение массива а на процессорную решетку 3x3. Согласно директиве align, элемент в (I, j) будет распределен на тот же процессор, где размещен и элемент массива а (i, j).

Обе директивы parallel описывают распределение итераций цикла, согласованное с распределением массивов айв: итерация цикла с индексами (J, I) будет выполняться на том же процессоре, где размещены элементы A(i,j) и B(i, j). Перестановка индексов вызвана только особенностью распределения памяти в языке Fortran. Из соображений эффективности внутренний цикл лучше организовать так, чтобы он перебирал расположенные подряд элементы столбца (в C-DVM такая перестановка не потребуется).

Для второй директивы parallel необходимо описать общие теневые данные. Ширина теневых граней определяется разницей индексных выражений элементов массивов, расположенных в левой и правой частях оператора присваивания. Для данного примера ширина всех граней равна 1. Схема обмена теневыми данными для одного процессора показана на рис. 5.4.

Отладка и оптимизация DVM-программ. Для отладки DVM-программ авторы системы разработали как набор инструментальных средств, так и специальную технологию отладки. Функциональная отладка DVM-программ [31] осуществляется поэтапно. Сначала программа отлаживается на рабочей станции как обычная последовательная программа с использованием штатных средств отладки. Затем на той же рабочей станции программа пропускается в специальном режиме для проверки DVM-указаний. Это позволяет

Глава 5. Технологии параллельного программирования

247

выявить их правильность и полноту. На следующем этапе программа может быть пропущена на параллельной машине в режиме сравнения промежуточных результатов ее параллельного выполнения с эталонными результатами, полученными при ее последовательном выполнении.


Ац	А₁₂	A-I3	А₁₄
А₂₁	А₂₂	^А23	А₂₄
Лл	^32	A33	^34
А₄1	А₄₂	A43


		2
А13	^А,4	Al5	Al6	А₁₇
^А23	А₂₄	^А25	^А26	А₂₇
Азз/				А37
	^А34	А35	Д ^Н36


(	А₄₄	А45	А46


	3
Ai6	А₁₇	Al8
^А26	А₂₇	^А28
Азб	А37	Азе
	А₄₇	А48


Лл	А32	Азз
А₄1	А₄₂	А43	А₄₄
А₅1	А52	А53	А54
^А61	^А62	^А63	^А64
А₇₁	А₇₂	А73

А А А

63/ 64 65


	^37	А38
А46	А₄₇	А48
А56	А₅₇	А58
^А66	^А67	^А68
	А₇₇	А78

А74 А₇₅


Аб1	Аб2	Абз
А₇₁	А₇₂	А73	А₇₄
Aei	^A82	\з	\л



	Аб4	Аб5	Абб	У
А73				\
	А₇₄	А₇₅	А76

Авз	Ав4	Ав5	Авб	\l


	Аб7	Аб8
А76	А₇₇	А78
Авб	Ав7	\в

□

Локальные части массива

□

Теневые элементы

Рис. 5.4. Отображение массива А(8, 8) на процессорную решетку 3x3

Для отладки программы на реальной параллельной машине используются средства трассировки, позволяющие зафиксировать последовательность обращений к переменным и их значения, а также последовательность вызовов функций системы поддержки выполнения DVM-программ.

Повысить эффективность DVM-программ помогает анализатор производительности, который позволяет пользователю получить информацию об основных показателях эффективности выполнения его программы или ее частей на параллельной системе. Для повышения эффективности программ можно использовать специальный инструмент — предсказатель производи-

248

Часть II. Параллельное программирование

тельности. Он позволяет на рабочей станции смоделировать выполнение DVM-программы на параллельной ЭВМ с заданными заранее параметрами (топология коммуникационной сети, ее латентность и пропускная способность, а также производительность процессоров) и спрогнозировать для такой системы характеристики выполнения программы.

В настоящее время система DVM может использоваться на рабочих станциях SGI, HP, IBM, SUN, на персональных ЭВМ с операционными системами UNIX и Windows 95/98/2000/NT. Система установлена и работает на таких параллельных вычислительных системах, как МВС-1000М, МВС-1000/200, Parsytec СС, Convex SPP 1600, на вычислительных кластерах НИВЦ МГУ и в других организациях.

Исходные тексты системы, библиотеки выполняемых программ, документация, примеры и другие материалы доступны через Интернет по адресу http://www.keldysh.ru/dvm/.

Система программирования трС

Язык трС является, по-видимому, первым языком высокого уровня, разработанным специально для программирования неоднородных сетей. Он позволяет программисту определить все основные свойства параллельного алгоритма, влияющие на скорость его выполнения в неоднородной вычислительной среде. Необходимое число параллельных процессов, объем вычислений и передаваемых данных в рамках каждого процесса, сценарий взаимодействия процессов и многие другие характеристики доступны программисту для создания эффективных программ. Важно и то, что трС позволяет менять эти характеристики динамически во время выполнения программы. При этом информация, извлеченная из описания параллельного алгоритма, вместе с данными о реальной производительности процессоров и коммуникационных каналов, помогает системе программирования трС найти эффективный способ отображения процессов mpC-программы на компьютеры сети.

Язык и система программирования трС разработана в Институте системного программирования РАН. Детали описания и текущее состояние проекта можно найти в [32] или на сайте http://www.ispras.ru/~mpc.

Основы программирования на трС. Язык программирования трС является строгим расширением языка С, ориентированным на параллельные вычисления на неоднородных сетях. mpC-программа — это множество параллельных процессов, взаимодействующих посредством неявной передачи сообщений. Используя язык трС, программист явно нигде не указывает, сколько процессов составляют программу и на каких компьютерах эти процессы выполняются. Это делается уже пользователем программы в момент ее запуска внешними по отношению к языку средствами. Исходный код на трС, составленный в соответствии с моделью SPMD, управляет лишь тем, какие именно вычисления выполняются каждым из процессов программы.

Глава 5. Технологии параллельного программирования

249

Группе процессов, совместно выполняющих некоторый параллельный алгоритм, в языке трС соответствует понятие сети. Сеть в трС — это механизм, позволяющий программисту абстрагироваться от реальных физических процессов параллельной программы. В простейшем случае сетью является множество виртуальных процессоров. Определение сети в программе вызывает создание группы реальных процессов, представляющей эту сеть: каждому виртуальному процессору соответствует отдельный процесс параллельной программы. Заметим, что в разные моменты времени выполнения параллельной программы один и тот же реальный параллельный процесс может представлять различные виртуальные процессоры различных сетей.

Определив один раз сеть, программист вызывает отображение ее виртуальных процессоров на реальные процессы параллельной программы, и это отображение сохраняется на все время жизни сети. Рассмотрим следующий пример.

#include <mpc.h>#define N 3int [*]main() {net SimpleNet(N) mynet; [mynet ]MPC_Printf("Hello, world!\n");}

В программе сначала определяется сеть mynet, состоящая из n виртуальных процессоров, а затем на этой сети вызывается библиотечная функция MPC_Printf. Выполнение данной программы заключается в параллельном вызове функции MPC_Printf теми n процессами программы, на которые отображены виртуальные процессоры сети mynet. Это отображение осуществляется системой программирования языка трС во время выполнения программы. Выполнение функции MPC_Printf каждым процессом заключается в посылке сообщения "Hello, world!" на терминал пользователя, с которого была запущена эта программа. В результате пользователь увидит n приветствий "Hello, world! " — по одному от каждого вовлеченного процесса.

Спецификатор [*] перед именем main в определении главной функции говорит, что код этой функции в обязательном порядке выполняется всеми процессами параллельной программы. Такие функции в трС называются базовыми. Корректная работа таких функций возможна только при условии их вызова всеми процессами параллельной программы. Контроль за корректностью вызовов базовых функций осуществляется компилятором. В отличие от функции main, для корректной работы функции MPC_Printf, вообще говоря, не требуется ее вызова всеми процессами параллельной программы. Более того, вполне осмысленным и корректным является вызов этой функции любым отдельно взятым процессом параллельной программы. Такие функции в трС называются узловыми. Узловые функции не связаны явно ни с заданием параллелизма, ни с взаимодействием процессов. Они могут быть вызваны как отдельным процессом параллельной программы, так и группой процессов.

Перейдем к следующему примеру.

#include <mpc.h>

#include <sys/utsname.h>#define N 3int [*]main() { net SimpleNet(N) mynet;

250

Часть II. Параллельное программирование

struct utsname [mynet]un; [mynet ] uname (Sun) ;

[mynet]MPC_Printf("Hello world! I'm on \"%s\".\n",

un.nodename);}

Данная программа выводит на терминал пользователя более содержательные послания от тех процессов параллельной программы, на которые отображаются виртуальные процессоры сети mynet. Кроме приветствия "Hello, world!", процесс сообщает имя компьютера, на котором он выполняется. Для этого в программе определяется переменная un, распределенная по сети mynet. Только процессы, соответствующие виртуальным процессорам сети mynet, содержат в своей памяти копию этой переменной. Эти же процессы выполняют вызов функции uname, что специфицируется конструкцией [mynet] перед именем функции. После этого поле nodename в каждой копии распределенной структуры un будет содержать ссылку на имя того компьютера, на котором соответствующий процесс выполняется. В дальнейшем локальные копии распределенных переменных иногда будем называть проекциями переменных на процессах или виртуальных процессорах.

Время жизни сети mynet, как и время жизни переменной un, ограничено блоком, в котором эта сеть определяется. При выходе из этого блока все процессы программы, захваченные под виртуальные процессоры сети mynet, освобождаются и могут быть использованы при создании других сетей. Такие сети называются в трС автоматическими. В отличие от автоматических, время жизни статических сетей ограничено лишь временем выполнения программы. Статические и автоматические сети в трС полностью аналогичны статическим и автоматическим переменным в языке С.

Следующие две программы демонстрируют различие статических и автоматических сетей. Программы выглядят практически идентичными. Обе они циклически выполняют блок, включающий определение сети и выполнение уже знакомых вычислений на этой сети. Единственным, но существенным, отличием является то, что в первой программе определяется автоматическая сеть, а во второй — статическая. Первая программа выглядит так.

#include <mpc.h> #include <sys/utsname.h> idefine Nmin 3

idefine Nmax 5int [*]main() { repl n; for(n = Nmin; n <= Nmax; n++) { auto net SimpleNet(n) anet;

struct utsname [anet]un; [anet]uname(&un); [anet]MPC_Printf("An autom.network of %d; I'm on %s.\n", [anet]n, un.nodename); } }

Глава 5. Технологии параллельного программирования

251

При входе в блок на первом витке цикла создается автоматическая сеть из трех виртуальных процессоров (n = Nmin = з), которая при выходе из цикла уничтожается. При входе в блок на втором витке цикла создается новая автоматическая сеть уже из четырех виртуальных процессоров, которая также прекращает свое существование при выходе из блока. К моменту выполнения повторной инициализации цикла (операция п++) эта 4-процессорная сеть уже не существует. Наконец, на последнем витке при входе в блок создается автоматическая сеть из пяти виртуальных процессоров (n = Nmax = 5). Поскольку каждый раз сеть создается заново, то на каждой итерации цикла имена компьютеров, выдаваемые функцией MPC_Printf, могут быть различными.

Заметим, что переменная п в данном примере распределена по всем процессам параллельной программы. Ее определение содержит ключевое слово repl, сокращение от replicated. Оно информирует компилятор о том, что значения этой переменной у разных процессов параллельной программы равны между собой. Другими словами, проекции данной переменной на всех процессах имеют одно и то же значение. Такие распределенные переменные называются в трС размазанными, а значение размазанной переменной называется размазанным значением. Компилятор с языка трС контролирует объявленное программистом свойство размазанности и предупреждает обо всех случаях, когда оно может быть нарушено.

Теперь рассмотрим тот же пример, но уже с использованием статической сети.

#include <mpc.h> #include <sys/utsname.h> idefine N rain 3

idefine N max 5int [*]main() {repl n; for(n = Nmin; n <= N max; n++) { static net SimpleNet(n) snet; struct utsname [snet]un; [snet]uname(&un);

[snet]MPC_Printf("A static network of %d; I'm on %s.\n", [snet]n, un.nodename); } }

При входе в блок на первом витке цикла создается сеть из трех виртуальных процессоров. Однако при выходе из блока она не уничтожается, а просто перестает быть видимой. В этом случае блок является не областью существования сети, а областью ее видимости, как это и предписано для конструкций языка С. Во время выполнения повторной инициализации и проверки условия цикла эта статическая 3-процессорная сеть существует, но недоступна. При повторных входах в блок на последующих витках цикла никакие

252

Часть II. Параллельное программирование

новые сети не создаются, а просто становится видна та статическая сеть из трех виртуальных процессоров, которая была создана при первом входе в блок вне зависимости от значения переменной п. Имя anet из предыдущего примера на разных витках цикла обозначало совершенно разные сети. Имя snet данного примера на каждой итерации обозначает одну и ту же сеть, существующую с момента первого входа в блок, в котором она определяется, и до конца выполнения программы. Это же подтверждает и выдача, содержащая на каждой итерации один и тот же набор имен компьютеров.

Важнейшим атрибутом сети является ее тип. Это обязательная часть определения любой сети. Всякому определению сети должно предшествовать определение соответствующего сетевого типа. В рассмотренных нами примерах определение сетевого типа simpieNet находится среди прочих стандартных определений языка трС в файле mpc.h и включается в программу с помощью директивы препроцессора #inciude. Определение simpieNet выглядит следующим образом:

nettype SimpieNet(int n) { coord I = n;

};

Определение вводит имя сетевого типа simpieNet, параметризованного целым параметром п. В теле определения объявляется координатная переменная I, изменяющаяся в пределах от о до п - 1. Тип simpieNet является простейшим параметризованным сетевым типом и соответствует сетям, состоящим из п виртуальных процессоров, упорядоченных в соответствии со своим номером.

Рассмотрим следующую программу.

#include <mpc.h>#define N 5int [*]main() { net SimpieNet(N) mynet;

int [mynet]my_coordinate;

my_coordinate = I coordof mynet;

if(my_coordinate%2 = 0) [mynet]MPC_Printf("Hello, even world!\n");

else [mynet]MPC_Printf("Hello, odd world!\n"); }

Данная программа демонстрирует, каким образом можно запрограммировать выполнение различных вычислений виртуальными процессорами с различными координатами. В программе используется бинарная операция coordof, левым операндом которой в этом примере является координатная переменная i, а правым сеть mynet. Результатом выполнения операции будет целое значение, распределенное по сети mynet. После выполнения присваивания my_coordinate = i coordof mynet значения проекций переменной my_coordinate будут равны координатам соответствующих виртуальных процессоров в сети mynet. В результате виртуальные процессоры с четными

Глава 5. Технологии параллельного программирования

253

координатами выведут на терминал пользователя приветствие

"Hello, even world!", а виртуальные процессоры с нечетными координатами напишут "Hello, odd world!".

Сети в языке трС не являются абсолютно не зависимыми друг от друга. Каждая вновь создаваемая сеть имеет в точности один виртуальный процессор, общий с уже существующими сетями. Этот виртуальный процессор называется родителем создаваемой сети и является тем связующим звеном, через которое передаются результаты вычислений на сети в случае прекращения ее существования. Родитель сети явно или неявно специфицируется ее определением.

До сих пор ни одна из сетей не была определена с явным указанием родителя. Во всех случаях родитель специфицировался неявно, и этим родителем был виртуальный хост-процессор. В любой момент выполнения любой трС-программы гарантируется существование предопределенной сети host, состоящей из единственного виртуального процессора, отображаемого на хост-процесс. Рассмотрим следующую программу.

#include <mpc.h>nettype AnotherSimpleNet(int n) { coord I = n; parent [0];

};

idefine N 3int [*]main() { net AnotherSimpleNet(N) [host]mynet; [mynet] MPC_Printf("Hello, world!\n");}

Эта программа полностью эквивалентна самой первой программе. Разница лишь в том, что в определении сети неявная спецификация родителя сети заменена на явную. Еще одно различие можно найти в определении сетевого типа. Там добавлена строка, явно специфицирующая координаты родителя в сетях этого типа (по умолчанию родитель имеет нулевые координаты в создаваемой сети). Если бы нам по какой-то причине понадобилось, чтобы родитель сети mynet имел не наименьшую, а наибольшую координату, то в определении сетевого типа AnotherSimpleNet вместо спецификации parent [0] следовало бы использовать спецификацию parent [п - 1].

Естественным развитием общей идеологии трС является функция MPCBarrier, которая позволяет синхронизировать работу виртуальных процессоров любой сети. В частности, программа

#include <mpc.h> idefine N 5 int [ * ] main () {

net SimpleNet(N) mynet; [mynet]: {

int my_coordinate;

254

Часть II. Параллельное программирование

my_coordinate = I coordof mynet; if(my_coordinate%2 = 0)

MPC_Printf("Hello, even world!\n"); ( [(N)mynet])MPC_Barrier(); if(my_coordinate%2 = 1)

MPC_Printf("Hello, odd world!\n"); } }

выводит сообщения от виртуальных процессоров с нечетными координатами на терминал пользователя только после того, как будут выведены сообщения от всех виртуальных процессоров с четными координатами. Одновременно заметим, что в этой программе на барьере ждут только процессы, реализующие сеть mynet.

Вызов функции MPC_Barrier в предыдущей программе выглядит несколько необычно. Действительно, эта функция принципиально отличается от всех функций, которые встречались до сих пор, и представляет собой сетевую функцию. В отличие от базовых функций, которые всегда выполняются всеми процессами параллельной программы, сетевые функции выполняются на сетях и, следовательно, могут выполняться параллельно с другими сетевыми или узловыми функциями. По сути, сетевые функции являются полным аналогом базовых, но применительно к конкретным сетям. Верно и обратное утверждение: базовая функция это та же сетевая функция, только примененная не к конкретной сети, а к всеобъемлющей сети с именем '*'.

Различие базовых, сетевых и узловых функций определяется степенью интегрированное™ процессов, выполняющих каждый вид функций. Наиболее интегрированные — это базовые функции. Все процессы программы выполняют код базовой функции. Это обязательно. Именно поэтому бессмысленно говорить о параллельном вызове двух базовых функций. Наименее интегрированными являются узловые функции. Это обычные последовательные функции, которые могут выполняться как отдельным процессом, так и несколькими процессами. Узловые функции не описывают параллельных вычислений и коммуникаций между процессами. Между базовыми и узловыми функциями расположены сетевые функции. Сетевая функция описывает вычисления и коммуникации на некоторой абстрактной сети, являющейся ее формальным параметром. Две сетевые функции можно вызвать одновременно на двух непересекающихся сетях, и они будут выполняться параллельно. Это означает, что аппарат узловых и сетевых функций поддерживает параллелизм задач.

Дополнительно сетевые функции обеспечивают модульное параллельное программирование. Программист может реализовать тот или иной параллельный алгоритм в виде сетевой функции, а все остальные могут использо-

Глава 5. Технологии параллельного программирования

255

вать такую программную единицу в своих приложениях параллельно с другими вычислениями и коммуникациями без знания ее исходного кода.

Здесь же заметим, что все переменные, описанные в функции обычным образом, считаются распределенными по той же сети, на которой задана и сама функция.

Описание библиотечной функции MPC_Barrier, находящееся в файле mpc.h, выглядит следующим образом:

int [net SimpleNet(n) w] MPC_Barrier(void);

Любая сетевая функция имеет специальный сетевой формальный параметр. Этот параметр является сетью, на которой вызывается сетевая функция. В случае функции MPC_Barrier описание сетевого параметра имеет вид:

net SimpleNet(n) w

Данное описание, наряду с формальной сетью w, на которой выполняется функция MPC_Barrier, вводит параметр п — число виртуальных процессоров этой сети.

Если бы функция MPC_Barrier не была библиотечной, она могла бы быть определена, например, так:

int [net SimpleNet(n) w] MPC_Barrier(void) { int [w:parent]bs[n], [w]b = 1; bs[] = b; b = bs [ ] ;

}

В теле функции определяется автоматический массив bs из п элементов. Данный массив является динамическим, но язык трС это допускает. Массив распределен по сети, являющейся родителем сети w (это специфицируется с помощью конструкции [w:parent], помещенной перед именем массива в его определении). Здесь же определяется распределенная по сети w переменная ь. Следующая за этим определением пара операторов реализует барьер для виртуальных процессоров сети w. Каждый процесс, кроме процесса, собирающего значения массива bs, выполнит первый оператор и сразу перейдет к выполнению второго. Однако процесс, собирающий значения bs, не начнет выполнение второго оператора, пока полностью не закончит выполнение первого. Это произойдет только тогда, когда все процессы передадут ему свои значения. После этого он перейдет к выполнению второго оператора, разблокировав стоящие на втором операторе процессы и завершив барьерную синхронизацию.

Следует оговориться, что для данной реализации барьера распределенность массива bs именно по родителю сети w несущественна. Важно лишь, чтобы сбор и рассылка данных выполнялись на одном и том же процессоре.

256

Часть II. Параллельное программирование

Вызов сетевой функции MPC_Barrier в предыдущем примере задает как фактический сетевой аргумент — сеть mynet, на которой в действительности вызывается функция, так и фактическое значение единственного параметра сетевого типа simpieNet. Последнее, на первый взгляд, кажется избыточным. Однако надо учесть, что фактическим сетевым аргументом функции MPC_Barrier может быть сеть любого типа, а не только типа simpieNet. По существу, функция MPC_Barrier лишь интерпретирует ту совокупность процессов, на которой она вызвана, как сеть типа simpieNet.

Основным средством для неявного описания обменов данными в языке трС являются подсети — подмножество виртуальных процессоров некоторой сети. Рассмотрим следующую программу.

#include <string.h> #include <mpc.h> #include <sys/utsname.h>

nettype Mesh(int m, int n) { coord I = m, J = n; parent [0,0]; };

idefine MAXLEN 256 int [ * ] main () {

net Mesh(2,3) [host]mynet; [mynet]: {

struct utsname un;

char me[MAXLEN], neighbour[MAXLEN]; subnet [mynet:I == 0]rowO, [mynet:I == 1]rowl; uname(Sun);

strcpy(me, un.nodename); [rowO]neighbour[] = [rowl]me[]; [rowl]neighbour[] = [row0]me[]; MPC_Printf("I'm (%d, %d) from \"%s\"\n"

"My neighbour (%d, %d) is on \"%s\".\n\n", I coordof mynet, J coorlof mynet, me, (I coordof mynet + 1)%2, J coordof mynet, neighbour); } }

В данной программе каждый виртуальный процессор сети mynet типа Mesh (2,3) выводит на терминал пользователя имя компьютера, на котором

Глава 5. Технологии параллельного программирования

257

его разместила система программирования трС, и имя компьютера, на который система поместила ближайший виртуальный процессор с соседней строки. Для этого определяются две подсети rowO и rowl сети mynet. Подсеть rowO соответствует нулевой строке решетки виртуальных процессоров сети mynet (этот факт специфицируется с помощью конструкции [mynet:i == 0]). Аналогично, подсеть rowl соответствует первой строке решетки виртуальных процессоров сети mynet. В общем случае логические выражения, выделяющие виртуальные процессоры подсетей, могут быть довольно сложными. Например, выражение i<j&&j%2==o выделяет виртуальные процессоры решетки, расположенные над главной диагональю в четных столбцах.

Выполнение присваивания [rowO]neighbourп = [rowl]men заключается в параллельной пересылке содержимого соответствующей проекции массива те от каждого у'-го виртуального процессора строки rowl каждому у'-му виртуальному процессору строки rowO с последующим его присваиванием соответствующей проекции массива neighbour. Аналогично, выполнение присваивания [rowl]neighbour[] = [row0]me[] заключается в параллельной пересылке содержимого проекций массива те от виртуальных процессоров подсети rowO соответствующим виртуальным процессорам подсети rowl с последующим их присваиванием проекциям массива neighbour. В результате проекция распределенного массива neighbour на виртуальный процессор сети mynet с координатами (0,у) содержит имя компьютера, на котором система программирования разместила виртуальный процессор с координатами (1,у). Проекция массива neighbour на виртуальный процессор с координатами (1,у) содержит имя компьютера, на котором оказался виртуальный процессор с координатами (0,у).

Используемые в этой программе подсети, соответствующие строкам решетки процессоров сети mynet, можно было бы определить и неявно, без объявления подсети subnet. Соответствующие присваивания выглядели бы так:

[mynet:1 == 0]neighbour[] = [mynet:I == l]me[]; [mynet:I == 1]neighbour[] = [mynet:I == 0]me[];

В данном случае использование неявно определенных подсетей вполне оправдано, поскольку упрощает программу без потери эффективности или функциональных возможностей. Однако без явного определения подсети не всегда можно обойтись, в частности, сетевые функции нельзя вызывать на неявно определенных подсетях.

Определение сети вызывает отображение ее виртуальных процессоров на реальные процессы параллельной программы, которое сохраняется на все время жизни сети. На основании чего система программирования трС осуществляет это отображение, и каким образом программист может этим отображением управлять? Основная цель параллельных вычислений — это ускорение решения задачи. Поэтому критерием при отображении виртуаль-

258

Часть II. Параллельное программирование

ных процессоров сети на реальные процессы является минимизация времени выполнения соответствующей параллельной программы. При выполнении этого отображения mpC-система опирается как на информацию о конфигурации и производительности компонентов параллельной вычислительной системы, выполняющей программу, так и на информацию об объеме вычислений, которые предстоит выполнить различным виртуальным процессорам определяемой сети.

В рассмотренных до сих пор примерах объемы вычислений нигде не фигурировали. Поэтому система программирования по умолчанию считала, что всем виртуальным процессорам всех определяемых сетей предстояло выполнять одинаковые объемы вычислений. Исходя из этого, она старалась отобразить их таким образом, чтобы общее число виртуальных процессоров, отображенных в данный момент на различные реальные процессоры было бы приблизительно пропорционально мощности этих процессоров. При таком отображении все процессы, представляющие виртуальные процессоры сети, выполняют вычисления приблизительно с одной скоростью. Если объемы вычислений между точками синхронизации или обмена данными окажутся приблизительно одинаковыми, то процессы в этих точках не будут простаивать в ожидании друг друга, и параллельная программа получится сбалансированной.

Такое отображение было вполне приемлемым для всех уже рассмотренных нами программ. Однако в случае значительных различий в объемах вычислений, выполняемых разными виртуальными процессорами, подобное распределение может привести к существенному замедлению программы.

Язык трС предоставляет программисту средства для спецификации относительных объемов вычислений, выполняемых виртуальными процессорами сети. Рассмотрим схему программы расчета массы металлической конструкции, сваренной из N неоднородных рельсов.

typedef struct {double length; double width; double heigth; double mass;} rail; nettype HeteroNet(int n, double v[n]) { coord I = n; node { I >= 0: v[I];}; parent [0]; };

double MassOfRail(double 1, double w, double h, double delta) { double m, x, y, z; for(m =0., x = 0.; x < 1; x + = delta)

Глава 5. Технологии параллельного программирования 259

for (у =0.; у < w; у + = delta) for(z =0.; z < h; z + = delta) m + = Density(x,y,z); return m*delta*delta*delta;

}

int [*]main(int [host]argc, char **[host]argv) { repl N = [host]atoi(argv[1]); static rail [host]s[[host]N]; repl double volumes[N]; int [host]i; repl j;

[host]InitializeSteelHedgehog(s, [host]N); for (j = 0; j < N; j++)

volumes[j] = s[j].length*s[j].width*s[j].heigth;

recon MassOfRail(0.2, 0.04, 0.05, 0.005); { net HeteroNet(N, volumes) mynet; [mynet]: {

rail r; r = s [ ] ;

r.mass = RailMass(r.length, r.width, r.height, DELTA); [host]printf("The total weight is %g kg\n", [host] ((r.mass) [ + ])); } } }

В данной программе определяется сетевой тип HeteroNet, имеющий два параметра. Первый параметр является целым скалярным параметром п и задает число виртуальных процессоров сети. Второй векторный параметр v состоит из п элементов типа double. Именно этот параметр используется при спецификации относительных объемов вычислений, выполняемых различными виртуальными процессорами. Определение сетевого типа HeteroNet содержит необычное объявление node {i >= о: v [ i ]}, которое читается следующим образом: для любого i >= о относительный объем вычислений, выполняемых виртуальным процессором с координатой i, задается значением v[i].

260

Часть II. Параллельное программирование

Для параллельного вычисления общей массы металлического "ежа" создается сеть mynet, состоящая из N виртуальных процессоров, каждый из которых вычисляет массу одного из этих рельсов. Вычисление массы рельса осуществляется интегрированием с фиксированным шагом заданной функции плотности Density по объему рельса. Очевидно, что объем вычислений для нахождения массы рельса пропорционален объему этого рельса. Поэтому, в определении сети mynet в качестве второго фактического параметра сетевого типа HeteroNet используется размазанный массив volumes, /-и элемент которого содержит объем /-го рельса. Этим специфицируется, что объем вычислений, выполняемый /-м виртуальным процессором сети mynet, пропорционален объему рельса, массу которого этот виртуальный процессор рассчитывает.

Отображение виртуальных процессоров на компьютеры основывается на информации об их производительности. По умолчанию система программирования языка трС использует одну и ту же методику оценки производительности для всех участвующих в выполнении программы реальных процессоров. Эта оценка получается в результате выполнения специальной тестовой параллельной программы при установке mpC-системы в конкретной параллельной вычислительной среде. Такая оценка является довольно грубой и может значительно отличаться от реальной производительности, достигаемой процессорами при выполнении конкретного кода. Именно поэтому язык трС предоставляет специальный оператор гесоп, позволяющий программисту изменять оценку производительности компьютеров, настраивая ее на те вычисления, которые будут в действительности выполняться.

В последнем примере этот оператор стоит непосредственно перед определением сети mynet. Выполнение его заключается в том, что все физические процессоры, назначенные программе, параллельно выполняют специфицированный в этом операторе код (вызов функции RaiiMass с фактическими аргументами 20.о, 4.0, 5.0 и 0.5). Время, затраченное каждым из процессоров на выполнение этого кода, используется для обновления оценки их производительности. Основной объем вычислений, выполняемый каждым из виртуальных процессоров сети mynet, как раз и приходится на вызов функции RaiiMass. Поэтому при создании этой сети система будет основываться на реальной производительности физических процессоров, достигаемой ими на этой части программы.

Важным обстоятельством является и то, что оператор гесоп позволяет обновлять оценку производительности процессоров во время выполнения программы. В частности, это можно сделать непосредственно перед тем моментом, когда оценка будет использоваться системой программирования. Это особенно важно, если параллельная вычислительная система используется одновременно и для других вычислений. Реальная производительность процессоров, достигаемая при выполнении параллельной программы, может

Глава 5. Технологии параллельного программирования

261

меняться в больших пределах в зависимости от их загрузки другими, внешними по отношению к этой программе, вычислениями. Использование оператора гесоп позволяет создавать параллельные программы, реагирующие на изменение загрузки системы: вычисления перераспределяются по процессорам в соответствии с их фактической производительностью на момент выполнения этих действий.

До сих пор при описании неоднородных параллельных алгоритмов мы не учитывали ни затраты на передачу данных, ни способа взаимодействия процессов при выполнении алгоритма. Следующие два примера иллюстрируют соответствующие возможности языка трС.

Первая программа моделирует движение нескольких больших, удаленных друг от друга групп тел под влиянием гравитационного притяжения. Поскольку сила притяжения быстро падает с увеличением расстояния, действие большой группы тел можно приближенно заменить воздействием одного эквивалентного тела. Это позволяет естественным образом распараллелить вычисления, когда за каждую группу тел будет отвечать свой параллельный процесс. Этот процесс хранит атрибуты всех тел своей группы, а также суммарную массу и координаты центров масс других групп.

Параллельная программа будет реализовывать следующий алгоритм:

Инициализация всех групп на хост-процессе Рассылка групп по процессам Параллельное вычисление масс групп Обмен массами групп между процессами while (1) {

Визуализация групп хост-процессом

Параллельное вычисление центров масс групп

Обмен центрами масс между процессами

Параллельное обновление атрибутов групп

Сбор групп на хост-процессе }

Предполагается, что каждая итерация основного цикла алгоритма вычисляет новые координаты всех тел через некоторый фиксированный интервал времени.

Ядром программы, реализующей этот алгоритм, является следующее определение сетевого типа:

nettype Galaxy(m, k, n[m]) { coord I = m;

node { I >= 0: bench* ( (n[I]/k) * (n [I]/k) ) ; } ; link { I > 0 : length*(n[I]*sizeof(Body)) [I] - > [0]; };

262

Часть II. Параллельное программирование

parent [0]; scheme { int i ;

par (i = 0; i < m; i++) 100%% [i]; par (i = 1; i < m; i++) 100%% [i] - > [0]; }; };

Первая строка вводит имя Galaxy этого сетевого типа и список формальных параметров — целые скалярные параметры m и к, а также векторный параметр п, состоящий из m целых чисел. Следующая строка объявляет координатную переменную i, изменяющуюся в пределах от о до m - 1. Далее виртуальные процессоры привязываются к этой системе координат, и описываются абсолютные объемы вычислений, которые должны быть выполнены этими виртуальными процессорами. В качестве единицы измерения используется объем вычислений, необходимый для расчета группы из к тел. Предполагается, что /-и элемент векторного параметра п равен числу тел в группе, обрабатываемой /-ым виртуальным процессором. Число операций, необходимое для обработки одной группы, пропорционально квадрату числа тел в этой группе. Поэтому, объем вычислений, выполняемый /-ым виртуальным процессором в (n[i]/k)² раз отличается от объема вычислений, принятого за единицу (это и записано в соответствующей строке).

Следующая строка специфицирует объемы данных в байтах, передаваемые между виртуальными процессорами во время выполнения алгоритма. Она просто говорит, что /-Й виртуальный процессор посылает атрибуты всех своих тел виртуальному хост-процессору. Заметим, что данное определение описывает в точности одну итерацию основного цикла алгоритма. Это является достаточно хорошим приближением, поскольку практически все вычисления и обмены данными сосредоточены в этом цикле. Исходя из этого, общее время выполнения алгоритма приблизительно равно времени выполнения одной итерации, умноженному на общее число итераций.

Наконец, блок scheme описывает, как именно виртуальные процессоры взаимодействуют во время выполнения алгоритма. Сначала все виртуальные процессоры параллельно выполняют все 100% вычислений. Затем все виртуальные процессоры, кроме хоста, параллельно посылают 100% тех данных, которые должны быть посланы виртуальному хост-процессору.

Наиболее важными фрагментами остального кода этой mpC-программы являются следующие:

void [*] main(int [host]argc, char **[host]argv)

{

TestGroup[] = (*AllGroups[0]) [] ;

Глава 5. Технологии параллельного программирования

263

recon Update_group(TestGroup, TestGroupSize); {

net GalaxyNet(NofG, TestGroupSize, NofB) g;

} }

Оператор recon использует вызов функции update_Group с фактическими параметрами TestGroup и TestGroupSize для обновления оценки производительности физических процессоров, выполняющих программу. Основная часть общего объема вычислений, выполняемых каждым виртуальным процессором, приходится на вызов функции update_Group. Поэтому полученная оценка производительности реальных процессоров будет близка к их реальной производительности, достигаемой при выполнении этой программы. Следующая строка определяет абстрактную сеть g типа GalaxyNet с фактическими параметрами NofG — фактическое число групп, TestGroupSize — размер группы, используемой в тестовом коде, и NofB — массив из NofG элементов, содержащих фактическое число тел в группах. Остальные вычисления и коммуникации будут выполняться на этой абстрактной сети. Система программирования трС отобразит виртуальные процессоры абстрактной сети g на реальные параллельные процессы, составляющие параллельную программу. При выполнении этого отображения система программирования использует информацию о конфигурации и производительности физических процессоров и коммуникационных каналов, а также информацию об описанном параллельном алгоритме.

Следующая программа умножает матрицу А на транспонированную матрицу В, т. е. выполняет матричную операцию С = АВ^Т, где А а В являются плотными квадратными матрицами размера n х п. Программа реализует неоднородную одномерную версию параллельного алгоритма, используемого в пакете ScaLAPACK для умножения матриц. Алгоритм можно описать следующим образом.

□ Каждый элемент матрицы С — это квадратный блок размера г х г. Единицей вычисления является вычисление одного блока, т. е. умножение матрицы г х п на матрицу п х г. Для простоты предположим, что п делится нацело на г.

П Матрицы А, В и С одинаковым образом разбиты на р горизонтальных полос, где р — это число процессоров. Каждый процессор отвечает за вычисление своей полосы результирующей матрицы С.

П На каждом шаге алгоритма рассылается строка блоков матрицы В, представляющая собой блочный столбец матрицы В^т. Все процессоры параллельно вычисляют соответствующую часть блочного столбца матрицы С.

264 Часть II. Параллельное программирование

П Все блоки матрицы С требуют одинакового количества арифметических операций, и каждый процессор выполняет объем работы, пропорциональный числу выделенных ему блоков. Чтобы сбалансировать нагрузку процессоров, площадь полосы, отображенной на каждый процессор, должна быть пропорциональна его скорости.

Следующее определение сетевого типа ParaiieiAxBT описывает этот алгоритм.

nettype ParaiieiAxBT(int р, int n, int r, int t, int d[p]) { coord I = p;

node { I >= 0: bench*(d[I]*n/r/t); }; link (J = p) {

I! = J: length*(d[J]*n*sizeof(double)) [J] - > [I]; };

parent [0]; scheme {

int i, j, PivotProcessor = 0, PivotRow = 0; for(i = 0; i < n/r; i++, PivotRow + = r) {

if(PivotRow >= d[PivotProcessor]) {

PivotProcessor++; PivotRow = 0; }

for (j = 0; j < p; j ++) if(j! = PivotProcessor) (100.*r/d[PivotProcessor])%%[PivotProcessor] - > [j]; par(j = 0; j < p; j ++) (100.*r/n)%%[j]; }

}; };

Предполагается, что тестовый код, используемый для оценки скорости реальных процессоров, умножает матрицу г х п на матрицу n х t, где t мало по сравнению с п и делится нацело на г. Предполагается также, что /-и элемент вектора d равен числу строк в полоске матрицы С, отображенной на /-и виртуальный процессор абстрактной сети, выполняющей этот алгоритм. Соответственно, объявление node специфицирует, что объем вычислений, выполняемых /-м виртуальным процессором в d[i]*n/r/t раз больше, чем объем вычислений, выполняемых тестовым кодом.

Глава 5. Технологии параллельного программирования

265

Объявление link содержит информацию о том, что каждый виртуальный процессор посылает свою полосу матрицы В всем остальным виртуальным процессорам.

Объявление scheme специфицирует n/г последовательных шагов этого алгоритма. На каждом шаге, виртуальный процессор PivotProcessor, который хранит ведущую строку, посылает ее остальным виртуальным процессорам. При этом выполняется r/d [PivotProcessor] х100% объема передач от всего объема данных, передаваемых по соответствующему коммуникационному каналу. Затем все виртуальные процессоры параллельно вычисляют соответствующую часть блочного столбца матрицы С, выполняя r/n х 100% объема вычислений каждый.

Наиболее интересными фрагментами остального кода этой программы являются:

recon SerialAxBT (а, Ь, с, г, n, t) ;

[host] : {

int j ;

struct {int p; double time;} min;

double time;

for(j = 1; j <= p; j ++) {

Partition(j, powers, d, n, r);

time = timeof(net ParallelAxBT(j, n, r, t, d) w); if (time < min. time) { min.p = j; min.t ime = t ime; } }

p = min.p; }

Partition (p, powers, d, n, r); {

net ParallelAxBT(p, n, r, t, d) w;

repl [w]N, [w]i;

int [w]myN;

N = [w]n;

myN = ([w]d)[I coordof w];

266

Часть II. Параллельное программирование

М : {

double A[myN/r] [г] [N] , ВТ [myN/r] [г] [N] , C[myN/r] [г] [N] , Brow[r] [N] ;

repl PivotProcessor, RelPivotRow, AbsPivotRow;

for(AbsPivotRow = 0, RelPivotRow = 0, PivotProcessor = 0; AbsPivotRow < N; RelPivotRow + = r, AbsPivotRow + = r)

{

if(RelPivotRow >= d[PivotProcessor]) { PivotProcessor ++; RelPivotRow = 0;

}

Brow[] = [w:I == PivotProcessor]ВТ[RelPivotRow/r][];

for(i = 0; i < myN/r; i ++)

SerialAxBT(A[i][0],Brow[0],C[j][0] +

AbsPivotRow,r,N,r); } } }

Оператор recon обновляет оценку производительности реальных процессоров, используя последовательное умножение тестовой матрицы г х п на тестовую матрицу п х t с помощью функции seriaiAxBT (вычисления, выполняемые каждым из виртуальных процессоров как раз, в основном, и приходятся на вызов функции SeriaiAxBT).

Следующий блок, выполняемый виртуальным хост-процессором, вычисляет оптимальное число физических процессоров, вовлеченных в параллельное умножение матриц. Операция timeof оценивает время выполнения алгоритма, специфицируемого его операндом — некоторым конкретным типом сети, без его фактического выполнения. Вычисленное значение переменной р будет использовано в качестве числа процессоров.

Определение сети w вызывает отображение ее виртуальных процессоров на физические процессоры таким образом, чтобы минимизировать время выполнения программы. Блок, следующий за определением сети w и выполняемый этой сетью, реализует алгоритм параллельного умножения матриц. Основные свойства этого алгоритма были описаны в определении сетевого типа ParallelAxBT.

Глава 5. Технологии параллельного программирования

267

Вопросы и задания

1. Какие конструкции языка С препятствуют автоматическому распараллеливанию программ?

2. Отвечая на предыдущий вопрос, вы сформировали список конструкций, препятствующих автоматическому распараллеливанию программ. Внимательно проанализируйте полученный список и подумайте, верно ли такое утверждение: "Любую программу, в которой нет конструкций из списка, можно автоматически распараллелить"?

3. В цикле содержится вызов функции. Какие конструкции языков необходимо учитывать, чтобы определить, являются ли все итерации данного цикла независимыми или нет? Рассмотрите языки С и Fortran.

4. Какой вычислительной системе лучше соответствует технология ОрепМР: вычислительному кластеру из рабочих станций или SMP-компьютеру?

5. Чем отличаются понятия "процесс" и "нить"?

6. Верно ли утверждение: "OpenMP-программы работают согласно модели Single Program Multiple Data (SPMD)?"

7. Чем различаются общие и локальные переменные в последовательной секции ОрепМР-программы?

8. Допускает ли ОрепМР изменение числа параллельных нитей по ходу работы программы?

9. Как будет обрабатываться такая конструкция: в параллельном цикле стоит вызов функции, в теле которой так же есть параллельный цикл?

10. Почему в ОрепМР нет конструкций, аналогичных директивам DVM ALIGN и

DISTRIBUTE?

11. Предположим, что в ОрепМР не было бы директивы BARRIER. Смоделируйте барьерную синхронизацию нитей с помощью других средств ОрепМР, в частности, с помощью механизма критических секций.

12. Можно ли автоматически конвертировать DVM-программу в программу на ОрепМР?

13. Напишите с помощью ОрепМР, DVM и трС программы перемножения двух матриц, решения системы линейных уравнений методом Гаусса, нахождения обратной матрицы. Проанализируйте выполненную работу с точки зрения эффективности полученных программ, простоты написания программ, переносимости программ.

14. Проанализируйте, что общего и чем различаются классы переменных в ОрепМР, DVM и трС.

15. Для чего в DVM введена директива ALIGN?

16. Сравните модели выполнения параллельных циклов в ОрепМР и DVM.

17. Для нахождения суммы элементов вектора в рамках ОрепМР при сложении частичных сумм можно воспользоваться критической секцией. Как выполнить эту же операцию в DVM?

268

Часть II. Параллельное программирование

18. Какая связь между понятиями "реальный процесс", "реальный процессор" и "виртуальный процессор" в трС?

19. Что общего и чем различаются базовые, сетевые и узловые функции трС?

20. Что общего и чем различаются распределенные и размазанные переменные в трС?

21. Какие конструкции и понятия трС отражают ориентацию данной системы на программирование неоднородных вычислительных систем?

22. Каким образом реализуется обмен данными между узлами сети в трС?

23. С помощью каких средств можно оперативно отслеживать изменение загрузки различных узлов вычислительной сети, на которой работает трС-программа?

24. Попробуйте выделить сильные и слабые стороны каждой из технологий OpenMP, DVM и трС.

§ 5.2. Системы программирования на основе передачи сообщений

Широкое распространение компьютеров с распределенной памятью определило и появление соответствующих систем программирования. Как правило, в таких системах отсутствует единое адресное пространство, и для обмена данными между параллельными процессами используется явная передача сообщений через коммуникационную среду. Отдельные процессы описываются с помощью традиционных языков программирования, а для организации их взаимодействия вводятся дополнительные функции. По этой причине практически все системы программирования, основанные на явной передаче сообщений, существуют не в виде новых языков, а в виде интерфейсов и библиотек.

К настоящему времени примеров известных систем программирования на основе передачи сообщений накопилось довольно много: Shmem, Linda, PVM, MPI и др. В данном параграфе мы остановимся лишь на двух из них. Сначала мы расскажем о системе Linda, простой и красивой по своей идее системе программирования. Затем остановимся на наиболее используемой в настоящее время системе MPI.

Система параллельного программирования Linda

Система Linda разработана в середине 80-х годов прошлого века в Йельском университете, США [50]. Идея ее построения исключительно проста, а потому красива и очень привлекательна. Параллельная программа есть множество параллельных процессов, где каждый процесс работает как обычная последовательная программа. Все процессы имеют доступ к общей памяти, единицей хранения в которой является кортеж. Отсюда происходит и специальное название для общей памяти — пространство кортежей. Каждый

Глава 5. Технологии параллельного программирования

269

кортеж — это взятая в скобки упорядоченная последовательность значений, разделенных запятыми. Например,

("Hello", 42, 3.14), (5, FALSE, 97, 1024, 2), ("worker", 5)

Так, первый кортеж этого примера состоит из строки "Hello", элемента целого типа 42 и вещественного числа 3.14. Во втором кортеже есть элемент целого типа 5, элемент логического типа false и три целых числа. Последний кортеж состоит из двух элементов: строки "worker" и целого числа 5. Количество элементов в кортеже, вообще говоря, может быть любым, однако конкретные реализации могут накладывать ограничения. Если первым элементом кортежа является строка, то эта строка называется именем кортежа.

Все процессы работают с пространством кортежей по принципу: поместить кортеж, забрать, скопировать. В отличие от традиционной памяти, процесс может забрать кортеж из пространства кортежей, после чего данный кортеж станет недоступным остальным процессам. В отличие от традиционной памяти, если в пространство кортежей положить два кортежа с одним и тем же именем, то не произойдет привычного для нас "обновления" значения переменной — в пространстве кортежей окажется два кортежа с одним и тем же именем. В отличие от традиционной памяти, изменить кортеж непосредственно в пространстве нельзя. Для изменения значений элементов кортежа его нужно сначала оттуда изъять, затем процесс, изъявший кортеж, может изменить значения его элементов, и вновь поместить измененный кортеж в память. В отличие от других систем программирования, процессы в системе Linda никогда не взаимодействуют друг с другом явно, и их общение всегда идет через пространство кортежей.

Интересно заметить, что по замыслу создателей системы Linda в любой последовательный язык достаточно добавить лишь четыре новые функции, после чего он становится средством параллельного программирования! Эти функции и составляют систему Linda: три для операций над кортежами и пространством кортежей и одна функция для порождения параллельных процессов. Для определенности, дальнейшее обсуждение системы и ее функций будем вести с использованием языка С.

Функция оит помещает кортеж в пространство кортежей. Например,

out ("GoProcess", 5);

помещает в пространство кортежей кортеж ("GoProcess", 5). Если такой кортеж уже есть в пространстве кортежей, то появится второй, что в принципе позволяет иметь сколь угодно много экземпляров одинаковых кортежей. По этой же причине с помощью функции out нельзя изменить кортеж, уже находящийся в пространстве. Для этого кортеж должен быть сначала оттуда изъят, затем изменен и после этого помещен назад. Функция out никогда не блокирует выполнивший ее процесс.

270

Часть II. Параллельное программирование

Функция in ищет подходящий кортеж в пространстве кортежей, присваивает значения его элементов элементам своего параметра-кортежа и удаляет найденный кортеж из пространства кортежей. Например,

in("P", int i, FALSE);

Этой функции соответствует любой кортеж, который состоит из трех элементов: значением первого элемента является строка "Р", второй элемент может быть любым целым числом, а третий должен иметь значение false. Подходящим кортежем считается кортеж, имеющий столько же элементов того же типа, и, если указано конкретное значение, то и такое же значение. В данном примере подходящими кортежами могут быть ("Р", 5, false) или ("р",

135, FALSE) И Т. П., НО Не ("Р", 7.2, FALSE) ИЛИ ("Ргос", 5, FALSE). ПОСКОЛЬКУ основной способ выборки данных из пространства кортежей опирается не на адрес, а на совпадении значений отдельных полей, то само пространство кортежей можно считать виртуальной общей ассоциативной памятью.

Если параметру функции in соответствуют несколько кортежей, случайным образом выбирается один из них. После нахождения кортеж удаляется из пространства кортежей, а неопределенным формальным элементам параметра-кортежа, содержащимся в вызове данной функции, присваиваются соответствующие значения. В нашем примере переменной i присвоится 5 или 135. Если в пространстве кортежей ни один кортеж не соответствует функции, то вызвавший ее процесс блокируется до тех пор, пока соответствующий кортеж в пространстве не появится.

Элемент кортежа в функции in считается формальным, если перед ним стоит определитель типа. Если используется переменная без типа, то берется ее значение и элемент рассматривается как фактический параметр. Например, во фрагменте программы

int i = 5;

in ("Р", i, FALSE);

функции in, в отличие от предыдущего примера, соответствует только кортеж ("Р", 5, FALSE).

Если переменная описана до вызова функции и ее надо использовать как формальный элемент кортежа, нужно использовать ключевое слово formal или знак ?. Например, во фрагменте программы

j = 15;

in ("Р", ?i, j);

последнюю строку можно заменить и на оператор in ("Р", formal i, j). В этом примере функции in будет соответствовать, например, кортеж ("Р", 6, 15), но не ("Р", 6, 12). Конечно же, формальными могут быть и несколько элементов кортежа одновременно:

in ("Add If", int i, bool b);

Глава 5. Технологии параллельного программирования

271

Если после такого вызова функции в пространстве кортежей будет найден кортеж ("Add_if", 100, true), то переменной i присвоится значение юо, а переменной ь — значение true.

Функция read отличается от функции in лишь тем, что выбранный кортеж не удаляется из пространства кортежей. Все остальное точно так же, как и у функции in. Этой функцией удобно пользоваться в том случае, когда значения переменных менять не нужно, но к ним необходим параллельный доступ из нескольких процессов. Иногда вместо обозначения read для данной функции используют обозначение rd.

Функция eval похожа на функцию out. Разница заключается в том, что для вычисления значения каждого поля, содержащего обращение к какой-либо функции, порождается отдельный параллельный процесс. На основе вычисленных значений функций, найденных в полях, eval формирует результирующий кортеж и помещает его в пространство кортежей. Например,

eval ("hello", funct(z), TRUE, 3.1415);

При обработке данного вызова система создаст новый процесс для вычисления функции funct (z). Когда процесс закончится и будет получено значение w = funct (z), в пространство кортежей будет добавлен кортеж ("hello", w, true, 3.1415). Функция, вызвавшая eval, не ожидает завершения порожденного параллельного процесса и продолжает свою работу дальше. Следует отметить и то, что пользователь не может явно управлять размещением порожденных параллельных процессов на доступных ему процессорных устройствах — это Linda делает самостоятельно.

Порядок вычисления полей в кортеже заранее не определен. Не следует использовать запись вида out ("string", i++, i), поскольку непонятно, будет ли выполнен инкремент i до вычисления значения третьего элемента или после. Аналогично, в операторе in ("string2", ?j, ?a[j]) нельзя предсказать, какое значение переменной j будет использовано в третьем элементе. Это может быть значение, полученное после выполнения операции ?j, либо значение, присвоенное переменной до выполнения данного оператора.

Параллельная программа в системе Linda считается завершенной, если все порожденные процессы завершились или все они заблокированы функциями in И read.

По сути дела, описание системы закончено, и теперь можно привести несколько небольших примеров. Мы уже говорили о том, что параллельные процессы в системе Linda напрямую друг с другом не общаются, своего уникального номера-идентификатора не имеют и общего числа параллельно работающих процессов-соседей, вообще говоря, не знают. Однако если у пользователя есть в этом необходимость, то такую ситуацию очень просто смоделировать. Программа в самом начале вызывает функцию out:

out("Next", 1);

272

Часть II. Параллельное программирование

Этот кортеж будет играть роль "эстафетной палочки", передаваемой от процесса процессу: каждый порождаемый параллельный процесс первым делом выполнит следующую последовательность:

in ("Next", ?My_Id); out("Next", My_Id+l) ;

Первый оператор изымает данный кортеж из пространства, на его основе процесс получает свой номер My_id, и затем кортеж с номером для следующего процесса помещается в пространство. Заметим, что использование функции in в данном случае позволяет гарантировать монопольную работу с данным кортежем только одного процесса в каждый момент времени. После такой процедуры каждый процесс получит свой уникальный номер, а число уже порожденных процессов всегда можно определить, например, с помощью такого оператора:

read("Next", ?Num_Processes) ;

Теперь рассмотрим возможную схему организации программы для перемножения С = АВ двух квадратных матриц размера n х п. Инициализирующий процесс использует функцию out и помещает в пространство кортежей исходные строки матрицы А и столбцы матрицы В:

for(i =1; i <= N; ++i) {

out ("A", i, <i-H строка A>); out("B", i, <±-u столбец B>);

}

Для порождения Nproc идентичных параллельных процессов можно воспользоваться следующим фрагментом:

for(i =0; i < Nproc; ++i)

eval("ParProc", get_elem_result());

Входные данные готовы, и нахождение всех N¹ элементов Су результирующей матрицы можно выполнять в любом порядке. Главное — это распределить работу между процессами, для чего процесс, инициирующий вычисления, в пространство помещает следующий кортеж:

out("NextElementCij", 1);

Второй элемент данного кортежа всегда будет показывать, какой из N² элементов Су предстоит вычислить следующим. Базовый вычислительный блок функции get_eiem_resuit () будет содержать приведенный далее фрагмент:

in ("NextElementCij", ? NextElement); if(NextElement < N*N)

out("NextElementCij ", NextElement + 1) ;

Nrow = (NextElement - 1) / N + 1; /* определим номер строки */

Ncol = (NextElement - 1) % N + 1; /* определим номер столбца */

Глава 5. Технологии параллельного программирования

273

В результате выполнения данного фрагмента для элемента с номером NextEiement процесс определит его местоположение в результирующей матрице: номер строки Nrow и столбца Ncoi. Заметим, что если вычисляется последний элемент, то кортеж с именем "NextEiementcij" в пространство не возвращается. Когда в конце работы программы процессы обратятся к этому кортежу, они будут заблокированы, что не помешает нормальному завершению программы. И, наконец, для вычисления элемента Су каждый процесс get_elem_result выполнит следующий фрагмент:

read("A", Nrow, ?row); read("В", Ncol, ?col); out("result", Nrow, Ncol, DotProduct(row,col));

где DotProduct — это функция, которая реализует скалярное произведение. Таким образом, каждый элемент произведения окажется в отдельном кортеже в пространстве кортежей. Завершающий процесс соберет результат, поместив кортежи в соответствующие элементы матрицы С:

for (irow = 0; irow < N; irow++) for (icol = 0; icol < N; icol++)

in("result", irow + 1, icol + 1, ?C[irow][icol]);

He имея в системе Linda никаких явных средств для синхронизации процессов, совсем не сложно их смоделировать самим. Предположим, что в некоторой точке нужно выполнить барьерную синхронизацию N процессов. Какой-то один процесс, например, стартовый, заранее помещает в пространство кортеж ("ForBarrier", N). Подходя к точке синхронизации, каждый процесс выполняет следующий фрагмент, который и будет выполнять функции барьера:

in("ForBarrier", ? Bar); Bar = Bar - 1; if(Bar != 0) {

out("ForBarrier", Bar);

read("Barrier"); } else

out("Barrier");

Если кортеж с именем "ForBarrier" есть в пространстве, то процесс его изымает, в противном случае блокируется до его появления. Анализируя второй элемент данного кортежа, процесс выполняет одно из двух действий. Если есть процессы, которые еще не дошли до данной точки, то он возвращает кортеж в пространство с уменьшенным на единицу вторым элементом и встает на ожидание кортежа "Barrier". В противном случае он сам помещает кортеж в пространство "Barrier", который для всех является сигналом к продолжению работы.

274

Часть II. Параллельное программирование

Очень просто с помощью системы Linda написать программу, работающую по схеме мастер/рабочие (master/slaves). Процесс-мастер порождает какое-то число одинаковых процессов-рабочих, распределяет между ними работу и собирает результат. Текст подобной программы показан ниже.

main(argc, argv)

int argc;

char *argv[];

{

int nworker, j , hello();

nworker = atoi (argv[l]);

for (j = 0; j < nworker; j++)

eval ("worker", hello(j)); for(j = 0; j < nworker; j++)

in("done"); printf("Hello_world is finished.\n"); }

int hello (num) /** function hello **/

int num;

{

printf("Hello world from number %d.\n", num);

out("done");

return(0);

}

В целом, сильные и слабые стороны системы Linda понятны. Простота и стройность концепции системы является основным ее козырем. Однако эти же факторы оборачиваются большой проблемой на практике. Как эффективно поддерживать пространство кортежей? Если вычислительная система обладает распределенной памятью, то общение процессов через пространство кортежей заведомо будет сопровождаться большими накладными расходами. Если процесс выполняет функции read или in, то как среди потенциально огромного числа кортежей в пространстве быстро найти подходящий? Подобные проблемы пытаются решить разными способами, например, введением нескольких именованных пространств, но все предлагаемые решения либо усложняют систему, либо являются эффективными только для узкого класса программ.

Вместе с тем, некоторые прикладные пакеты построены именно на основе системы Linda. Удачным примером можно считать реализацию популярного пакета для квантово-химических расчетов Gaussian.

Глава 5. Технологии параллельного программирования

275

Современное состояние и дополнительную информацию по системе Linda можно найти на сайте http://www.cs.yale.edu/Linda/linda.html.

Система программирования MPI

Наиболее распространенной технологией программирования параллельных компьютеров с распределенной памятью в настоящее время является МР1. Мы уже говорили о том, что основным способом взаимодействия параллельных процессов в таких системах является передача сообщений друг другу. Это и отражено в названии данной технологии — Message Passing Interface. Стандарт МР1 фиксирует интерфейс, который должны соблюдать как система программирования МР1 на каждой вычислительной системе, так и пользователь при создании своих программ. Современные реализации чаще всего соответствуют стандарту МР1 версии 1.1. В 1997—1998 годах появился стандарт МР1-2.0, значительно расширивший функциональность предыдущей версии. Однако до сих пор этот вариант МР1 не получил широкого распространения. Везде далее, если иного не оговорено, мы будем иметь дело со стандартом 1.1.

МР1 поддерживает работу с языками С и Fortran. В данной книге все примеры и описания всех функций будут даны с использованием языка С. Однако это совершенно не является принципиальным, поскольку основные идеи МР1 и правила оформления отдельных конструкций для этих языков во многом схожи.

Полная версия интерфейса содержит описание более 120 функций. Если описывать его полностью, то этому нужно посвящать отдельную книгу. Наша задача — объяснить идею технологии и помочь освоить необходимые на практике компоненты. Наиболее употребимые функции мы опишем. Но если у читателя возникнут какие-либо вопросы по стандарту или желание узнать последние новости о развитии технологии МР1, мы советуем обратиться к сайту http://www.mpiforum.org.

Интерфейс поддерживает создание параллельных программ в стиле M1MD, что подразумевает объединение процессов с различными исходными текстами. Однако на практике программисты гораздо чаще используют SPMD-модель, в рамках которой для всех параллельных процессов используется один и тот же код. В настоящее время все больше и больше реализаций МР1 поддерживают работу с нитями.

Все дополнительные объекты: имена функций, константы, предопределенные типы данных и т. п., используемые в МР1, имеют префикс mpi_. Например, функция посылки сообщения от одного процесса другому имеет имя MPi_send. Если пользователь не будет использовать в программе имен с таким префиксом, то конфликтов с объектами МР1 заведомо не будет. Все описания интерфейса МР1 собраны в файле mpi.h, поэтому в начале МР1-программы должна стоять директива #inciude <mpi. h>.

276

Часть II. Параллельное программирование

MPI-программа — это множество параллельных взаимодействующих процессов. Все процессы порождаются один раз, образуя параллельную часть программы. В ходе выполнения MPI-программы порождение дополнительных процессов или уничтожение существующих не допускается.

Каждый процесс работает в своем адресном пространстве, никаких общих переменных или данных в MPI нет. Основным способом взаимодействия между процессами является явная посылка сообщений.

Для локализации взаимодействия параллельных процессов программы можно создавать группы процессов, предоставляя им отдельную среду для общения — коммуникатор. Состав образуемых групп произволен. Группы могут полностью входить одна в другую, не пересекаться или пересекаться частично. При старте программы всегда считается, что все порожденные процессы работают в рамках всеобъемлющего коммуникатора, имеющего предопределенное имя mpi_comm_world. Этот коммуникатор существует всегда и служит для взаимодействия всех процессов MPI-программы.

Каждый процесс MPI-программы имеет уникальный атрибут номер процесса, который является целым неотрицательным числом. С помощью этого атрибута происходит значительная часть взаимодействия процессов между собой. Ясно, что в одном и том же коммуникаторе все процессы имеют различные номера. Но поскольку процесс может одновременно входить в разные коммуникаторы, то его номер в одном коммуникаторе может отличаться от его номера в другом. Отсюда два основных атрибута процесса: коммуникатор и номер в коммуникаторе.

Если группа содержит п процессов, то номер любого процесса в данной группе лежит в пределах от 0 до я — 1. Подобная линейная нумерация не всегда адекватно отражает логическую взаимосвязь процессов приложения. Например, по смыслу задачи процессы могут располагаться в узлах прямоугольной решетки и взаимодействовать только со своими непосредственными соседями. Такую ситуацию пользователь может легко отразить в своей программе, описав соответствующую виртуальную топологию процессов. Эта информация может оказаться полезной при отображении процессов программы на физические процессоры вычислительной системы. Сам процесс отображения в MPI никак не специфицируется, однако система поддержки MPI в ряде случаев может значительно уменьшить коммуникационные накладные расходы, если воспользуется знанием виртуальной топологии.

Основным способом общения процессов между собой является посылка сообщений. Сообщение — это набор данных некоторого типа. Каждое сообщение имеет несколько атрибутов, в частности, номер процесса-отправителя, номер процесса-получателя, идентификатор сообщения и др. Одним из важных атрибутов сообщения является его идентификатор или тэг. По идентификатору процесс, принимающий сообщение, например, может различить два сообщения, пришедшие к нему от одного и того же процесса. Сам иден-

Глава 5. Технологии параллельного программирования

277

тификатор сообщения является целым неотрицательным числом, лежащим в диапазоне от 0 до 32 767. Для работы с атрибутами сообщений введена структура MPi_status, поля которой дают доступ к значениям атрибутов.

На практике сообщение чаще всего является набором однотипных данных, расположенных подряд друг за другом в некотором буфере. Такое сообщение может состоять, например, из двухсот целых чисел, которые пользователь разместил в соответствующем целочисленном векторе. Это типичная ситуация, на нее ориентировано большинство функций MPI, однако такая ситуация имеет, по крайней мере, два ограничения. Во-первых, иногда необходимо составить сообщение из разнотипных данных. Конечно же, можно отдельным сообщением послать количество вещественных чисел, содержащихся в последующем сообщении, но это может быть и неудобно программисту, и не столь эффективно. Во-вторых, не всегда посылаемые данные занимают непрерывную область в памяти. Если в Fortran элементы столбцов матрицы расположены в памяти друг за другом, то элементы строк уже идут с некоторым шагом. Чтобы послать строку, данные нужно сначала упаковать, передать, а затем вновь распаковать.

Чтобы снять указанные ограничения, в MPI предусмотрен механизм для введения производных типов данных (derived datatypes). Описав состав и схему размещения в памяти посылаемых данных, пользователь в дальнейшем работает с такими типами так же, как и со стандартными типами данных MPI.

Поскольку собственные типы данных и виртуальные топологии процессов используются на практике не очень часто, то в данной книге мы не будем их описывать подробно.

Общие функции MPI

Прежде чем переходить к описанию конкретных функций, сделаем несколько общих замечаний. При описании функций мы всегда будем пользоваться словом оит для обозначения выходных параметров, через которые функция возвращает результаты. Даже если результатом работы функции является одно число, оно будет возвращено через один из параметров. Связано это с тем, что практически все функции MPI возвращают в качестве своего значения информацию об успешности завершения. В случае успешного выполнения функция вернет значение mpi_success, иначе — код ошибки. Вид ошибки, которая произошла при выполнении функции, можно будет понять из описания каждой функции. Предопределенные возвращаемые значения, соответствующие различным ошибочным ситуациям, определены в файле mpi.h. В дальнейшем при описании конкретных функций, если ничего специально не сказано, то возвращаемое функцией значение будет подчиняться именно этому правилу.

Далее мы рассмотрим общие функции MPI, необходимые практически в каждой программе.

278

Часть II. Параллельное программирование

int MPI_Init(int *argc, char ***argv)

Инициализация параллельной части программы. Все другие функции MPI могут быть вызваны только после вызова MPiinit. Необычный тип аргументов MPi_init предусмотрен для того, чтобы иметь возможность передать всем процессам аргументы функции main.

Инициализация параллельной части для каждого приложения должна выполняться только один раз. Поскольку для сложных приложений, которые состоят из многих модулей и пишутся разными людьми, это отследить трудно, введена дополнительная функция MPi_initiaiized:

MPI_Initialized (int *flag)

Здесь out flag — признак инициализации параллельной части программы.

Если функция MPi_init уже была вызвана, то через параметр flag возвращается значение 1, в противном случае 0.

int MPI_Finalize(void)

Завершение параллельной части приложения. Все последующие обращения к любым MPI-функциям, в том числе к MPiinit, запрещены. К моменту вызова MPi_Finaiize каждым процессом программы все действия, требующие его участия в обмене сообщениями, должны быть завершены.

Общая схема MPI-программы выглядит так:

main(int argc, char **argv) {

MPI_Init(Sargc, Sargv);

MPI_Finalize();

}

int MPI_Comm_size(MPI_Comm comm, int *size)

□ comm — идентификатор коммуникатора;

□ out size — число процессов в коммуникаторе comm.

Определение общего числа параллельных процессов в коммуникаторе comm. Результат возвращается через параметр size, для чего функции передается адрес этой переменной. Поскольку коммуникатор является сложной структурой, перед ним стоит имя предопределенного типа MPi_comm, определенного в файле mpi.h.

int MPI_Comm_rank(MPI_Comm comm, int *rank)

□ comm — идентификатор коммуникатора;

□ out rank — номер процесса в коммуникаторе comm.

Глава 5. Технологии параллельного программирования

279

Определение номера процесса в коммуникаторе comm. Если функция MPi_comm_size для того же коммуникатора comm вернула значение size, то значение, возвращаемое функцией MPi_comm_rank через переменную rank, лежит в диапазоне oTOflosize-i.

double MPI_Wtime(void)

Эта функция возвращает астрономическое время в секундах (вещественное число), прошедшее с некоторого момента в прошлом. Если некоторый участок программы окружить вызовами данной функции, то разность возвращаемых значений покажет время работы данного участка. Гарантируется, что момент времени, используемый в качестве точки отсчета, не будет изменен за время существования процесса. Заметим, что эта функция возвращает результат своей работы не через параметры, а явным образом.

Простейший пример программы, в которой использованы описанные выше функции, выглядит так:

main(int argc, char **argv) {

int me, size;

MPI_Init(Sargc, Sargv); MPI_Comm_rank(MPI_COMM_WORLD, &me); MPI_Comm_size(MPI_COMM_WORLD, Ssize); printf("Process %d size %d \n", me, size);

MPI_Finalize();

}

Строка, соответствующая функции printf, будет выведена столько раз, сколько процессов было порождено при вызове MPiinit. Порядок появления строк заранее не определен и может быть, вообще говоря, любым. Гарантируется только то, что содержимое отдельных строк не будет перемешано друг с другом.

Прием/передача сообщений между отдельными процессами

Все функции передачи сообщений в MPI делятся на две группы. В одну группу входят функции, которые предназначены для взаимодействия двух процессов программы. Такие операции называются индивидуальным или операциями типа "точка-точка". Функции другой группы предполагают, что в операцию должны быть вовлечены все процессы некоторого коммуникатора. Такие операции называются коллективными.

280

Часть II. Параллельное программирование

Начнем описание функций обмена сообщениями с обсуждения операций типа "точка-точка". Все функции данной группы, в свою очередь, также делятся на два класса: функции с блокировкой (с синхронизацией) и функции без блокировки (асинхронные).

Прием/передача сообщений с блокировкой задаются конструкциями следующего вида.

int MPI_Send(void *buf, int count, MPI_Datatype datatype, int dest, int msgtag, MPI_Comm comm)

□ buf — адрес начала буфера с посылаемым сообщением;

□ count — число передаваемых элементов в сообщении;

□ datatype — тип передаваемых элементов;

□ dest — номер процесса-получателя;

□ msgtag — идентификатор сообщения;

□ comm — идентификатор коммуникатора.

Блокирующая посылка сообщения с идентификатором msgtag, состоящего из count элементов типа datatype, процессу с номером dest. Все элементы посылаемого сообщения расположены подряд в буфере buf. Значение count может быть нулем. Разрешается передавать сообщение самому себе. Тип передаваемых элементов datatype должен указываться с помощью предопределенных констант типа, например, mpi_int, mpi_long, mpi_short,

MPI_LONG_DOUBLE, MPI_CHAR, MPI_UNSIGNED_CHAR, MPI_FLOAT ИЛИ С ПОМОЩЬЮ

введенных производных типов. Для каждого типа данных языков Fortran и С есть своя константа. Полный список предопределенных имен типов можно найти в файле mpi.h.

Блокировка гарантирует корректность повторного использования всех параметров после возврата из подпрограммы. Это означает, что после возврата из данной функции можно использовать любые присутствующие в вызове функции переменные без опасения испортить передаваемое сообщение. Выбор способа осуществления этой гарантии: копирование в промежуточный буфер или непосредственная передача процессу dest, остается за разработчиками конкретной реализации MPI.

Следует специально отметить, что возврат из функции MPi_send не означает ни того, что сообщение получено процессом dest, ни того, что сообщение покинуло процессорный элемент, на котором выполняется процесс, запустивший MPisend. Предоставляется только гарантия безопасного изменения переменных, использованных в вызове данной функции.

Подобная неопределенность далеко не всегда устраивает пользователя. Чтобы расширить возможности передачи сообщений, в MPI введены дополни-

Глава 5. Технологии параллельного программирования

281

тельные три функции. Все параметры у этих функций такие же, как и у функции MPi_send, однако у каждой из них есть своя особенность.

MPi_Bsend — передача сообщения с буферизацией. Если прием посылаемого сообщения еще не был инициализирован процессом-получателем, то сообщение будет записано в буфер и произойдет немедленный возврат из функции. Выполнение данной функции никак не зависит от соответствующего вызова функции приема сообщения. Тем не менее, функция может вернуть код ошибки, если места под буфер недостаточно.

MPi_ssend — передача сообщения с синхронизацией. Выход из данной функции произойдет только тогда, когда прием посылаемого сообщения будет инициализирован процессом-получателем. Таким образом, завершение передачи с синхронизацией говорит не только о возможности повторного использования буфера, но и о гарантированном достижении процессом-получателем точки приема сообщения в программе. Если прием сообщения также выполняется с блокировкой, то функция MPissend сохраняет семантику блокирующих вызовов.

MPi_Rsend — передача сообщения по готовности. Данной функцией можно пользоваться только в том случае, если процесс-получатель уже инициировал прием сообщения. В противном случае вызов функции, вообще говоря, является ошибочным и результат ее выполнения не определен. Во многих реализациях функция MPi_Rsend сокращает протокол взаимодействия между отправителем и получателем, уменьшая накладные расходы на организацию передачи.

int MPI_Recv(void *buf, int count, MPI_Datatype datatype, int source, int msgtag, MPI_Comm comm, MPI_Status *status)

□ out buf — адрес начала буфера для приема сообщения;

□ count — максимальное число элементов в принимаемом сообщении;

□ datatype — тип элементов принимаемого сообщения;

□ source — номер процесса-отправителя;

□ msgtag — идентификатор принимаемого сообщения;

□ comm — идентификатор коммуникатора;

□ out status — параметры принятого сообщения.

Прием сообщения с идентификатором msgtag от процесса source с блокировкой. Число элементов в принимаемом сообщении не должно превосходить значения count. Если число принятых элементов меньше значения count, то гарантируется, что в буфере buf изменятся только элементы, соответствующие элементам принятого сообщения. Если нужно узнать точное число элементов в принимаемом сообщении, то можно воспользоваться функциями MPI_Probe ИЛИ MPI_Get_count.

282

Часть II. Параллельное программирование

Блокировка гарантирует, что после возврата из функции все элементы сообщения уже будут приняты и расположены в буфере buf.

Ниже приведен пример программы, в которой нулевой процесс посылает сообщение процессу с номером один и ждет от него ответа. Если программа будет запущена с большим числом процессов, то реально выполнять пересылки все равно станут только нулевой и первый процессы. Остальные процессы после их порождения функцией MPi_init сразу завершатся, выполнив функцию MPI_Finalize.

#include "mpi.h" #include <stdio.h>

int main(argc,argv)

int argc;

char *argv[]; {

int numtasks, rank, dest, src, re, tag=l;

char inmsg, outmsg='x';

MPI_Status Stat;

MPI_Init(Sargc,Sargv);

MPI_Comm_size(MPI_COMM_WORLD, Snumtasks);

MPI_Comm_rank(MPI_COMM_WORLD, Srank);

if (rank ==0) { dest = 1; src = 1;

re = MPI_Send(&outmsg, 1, MPI_CHAR, dest, tag, MPI_COMM_WORLD); re = MPI_Recv(&inmsg, 1, MPI_CHAR, src, tag, MPI_COMM_WORLD, SStat); } else

if (rank == 1) { dest = 0; src = 0; re = MPI_Recv(&inmsg, 1, MPI_CHAR, src, tag, MPI_COMM_WORLD,

SStat); re = MPI_Send(&outmsg, 1, MPI_CHAR, dest, tag, MPI_COMM_WORLD); } MPI_Finalize (); }

Глава 5. Технологии параллельного программирования

283

В следующем примере каждый процесс с четным номером посылает сообщение своему соседу с номером, на единицу большим. Дополнительно поставлена проверка для процесса с максимальным номером, чтобы он не послал сообщение несуществующему процессу. Показана только схема программы.

main(int argc, char **argv)

{

int me, size;

int SOME_TAG=0;

MPI_Status status;

MPI_Init (Sargc, Sargv); MPI_Comm_rank (MPI_COMM_WORLD, &me); MPI_Comm_size (MPI_COMM_WORLD, Ssize); if ( (me % 2) == 0) {

if ((me+1) < size) /* посылают все процессы, кроме последнего */ MPI_Send (..., me+1, SOME_TAG, MPI_COMM_WORLD); } else

MPI_Recv (..., me-1, SOME_TAG, MPI_COMM_WORLD, Sstatus);

MPI_Finalize();

}

При приеме сообщения в качестве номера процесса-отправителя можно указать предопределенную константу mpi_any_source — признак того, что подходит сообщение от любого процесса. В качестве идентификатора принимаемого сообщения можно указать константу mpi_any_tag — это признак того, что подходит сообщение с любым идентификатором. При одновременном использовании этих двух констант будет принято любое сообщение от любого процесса.

Параметры принятого сообщения всегда можно определить по соответствующим полям структуры status. Предопределенный тип MPi_status описан в файле mpi.h. В языке С параметр status является структурой, содержащей поля с именами mpi_source, mpi_tag и mpi_error. Реальные значения номера процесса-отправителя, идентификатора сообщения и кода ошибки доступны через status.mpi_source, status.mpi_tag и status.mpi_error. В языке Fortran параметр status является целочисленным массивом размера mpi_status_size. Константы mpi_source, mpi_tag и mpi_error являются индексами по данному массиву для доступа к значениям соответствующих полей, например, status (mpi_source) .

284

Часть II. Параллельное программирование

Обратим внимание на некоторую несимметричность операций посылки и приема сообщений. С помощью константы mpi_any_source можно принять сообщение от любого процесса. Однако в случае посылки данных требуется явно указать номер принимающего процесса.

В стандарте оговорено, что если один процесс последовательно посылает два сообщения другому процессу, и оба эти сообщения соответствуют одному и тому же вызову MPi_Recv, то первым будет принято сообщение, которое было отправлено раньше. Вместе с тем, если два сообщения были одновременно отправлены разными процессами и оба сообщения соответствуют одному и тому же вызову MPi_Recv, то порядок их получения принимающим процессом заранее не определен.

MPI не гарантирует выполнения свойства "справедливости" при распределении приходящих сообщений. Предположим, что процесс Р\ послал сообщение, которое может быть принято процессом Р₂. Однако прием может не произойти, в принципе, сколь угодно долгое время. Такое возможно, например, если процесс Р₃ постоянно посылает сообщения процессу Р₂, также подходящие под шаблон mpi Recv.

Процесс 1 Процесс 2

MPI Send MPI Send

•-•• X ■"■■

MPI Recv MPI Recv

Рис. 5.5. Тупиковая ситуация при использовании блокирующих функций

Последнее замечание относительно использования блокирующих функций приема и посылки связано с возможным возникновением тупиковой ситуации. Предположим, что работают два параллельных процесса и они хотят обменяться данными. Было бы вполне естественно в каждом процессе сначала воспользоваться функцией MPi_send, а затем MPi_Recv (схематично эта ситуация изображена на рис. 5.5). Но именно этого и не стоит делать. Дело в том, что мы заранее не знаем, как реализована функция MPi_send. Если разработчики для гарантии корректного повторного использования буфера посылки заложили схему, при которой посылающий процесс ждет начала приема, то возникнет классический тупик. Первый процесс не может вернуться из функции посылки, поскольку второй не начинает прием сообщения. А второй процесс не может начать прием сообщения, поскольку сам по похожей причине застрял на посылке. Выход из этой ситуации прост. Нуж-

Глава 5. Технологии параллельного программирования

285

но использовать либо неблокирующие функции приема/передачи, либо функцию совмещенной передачи и приема. Оба варианта мы обсудим ниже.

int MPI_Get_count(MPI_Status *status, MPI_Datatype datatype, int *count)

□ status — параметры принятого сообщения;

□ datatype — тип элементов принятого сообщения;

□ out count — число элементов сообщения.

По значению параметра status данная функция определяет число уже принятых (после обращения к MPi_Recv) или принимаемых (после обращения к MPi_Probe или MPi_iprobe) элементов сообщения типа datatype. Данная функция, в частности, необходима для определения размера области памяти, выделяемой для хранения принимаемого сообщения.

int MPI_Probe(int source, int msgtag, MPI_Comm comm, MPI_Status *status)

□ source — номер процесса-отправителя или mpi_any_source;

□ msgtag — идентификатор ожидаемого сообщения или mpi_any_tag;

□ comm — идентификатор коммуникатора;

□ out status — параметры найденного подходящего сообщения.

Получение информации о структуре ожидаемого сообщения с блокировкой. Возврата из функции не произойдет до тех пор, пока сообщение с подходящим идентификатором и номером процесса-отправителя не будет доступно для получения. Атрибуты доступного сообщения можно определить обычным образом с помощью параметра status. Следует особо обратить внимание на то, что функция определяет только факт прихода сообщения, но реально его не принимает.

Прием/передача сообщений без блокировки. В отличие от функций с блокировкой, возврат из функций данной группы происходит сразу без какой-либо блокировки процессов. На фоне дальнейшего выполнения программы одновременно происходит и обработка асинхронно запущенной операции. В принципе, данная возможность исключительно полезна для создания эффективных программ. В самом деле, программист знает, что в некоторый момент ему потребуется массив, который вычисляет другой процесс. Он заранее выставляет в программе асинхронный запрос на получение данного массива, а до того момента, когда массив реально потребуется, он может выполнять любую другую полезную работу. Опять же, во многих случаях совершенно не обязательно дожидаться окончания посылки сообщения для выполнения последующих вычислений.

Если есть возможность операции приема/передачи сообщений скрыть на фоне вычислений, то этим, вроде бы, надо безоговорочно пользоваться. Однако на практике не все согласуется с теорией. Многое зависит от конкретной реализации. К сожалению, далеко не всегда асинхронные операции эффективно поддерживаются аппаратурой и системным окружением. Поэтому

286

Часть II. Параллельное программирование

не стоит удивляться, если эффект от выполнения вычислений на фоне пересылок окажется нулевым. Стандарт стандартом, но вы работаете в конкретной среде, на конкретной вычислительной системе. А справедливости ради заметим, что стандарт эффективности и не обещал...

Сделанные замечания касаются только вопросов эффективности. В отношении предоставляемой функциональности асинхронные операции исключительно полезны, поэтому они присутствуют практически в каждой реальной программе.

int MPI_Isend(void *buf, int count, MPI_Datatype datatype, int dest, int msgtag, MPI_Comm comm, MPI_Request *request)

□ buf — адрес начала буфера с посылаемым сообщением;

□ count — число передаваемых элементов в сообщении;

□ datatype — тип передаваемых элементов;

□ dest — номер процесса-получателя;

□ msgtag — идентификатор сообщения;

□ comm — идентификатор коммуникатора;

□ out request — идентификатор асинхронной операции.

Передача сообщения аналогична вызову MPisend, однако возврат из функции MPi_isend происходит сразу после инициализации процесса передачи без ожидания обработки всего сообщения, находящегося в буфере buf. Это означает, что нельзя что-то записывать в данный буфер без получения дополнительной информации, подтверждающей завершение посылки. Определить тот момент времени, когда можно повторно использовать буфер buf без опасения испортить передаваемое сообщение, можно с помощью параметра request И функций MPI_Wait И MPI_Test.

Аналогично трем модификациям функции MPi_send, предусмотрены три дополнительных варианта функций MPI_Ibsend, MPI_Issend, MPI_Irsend. К изложенной выше семантике работы этих функций добавляется асинхронность.

int MPI_Irecv(void *buf, int count, MPI_Datatype datatype, int source, int msgtag, MPI_Comm comm, MPI_Request *request)

□ out buf — адрес начала буфера для приема сообщения;

□ count — максимальное число элементов в принимаемом сообщении;

□ datatype — тип элементов принимаемого сообщения;

□ source — номер процесса-отправителя;

□ msgtag — идентификатор принимаемого сообщения;

□ comm — идентификатор коммуникатора;

□ out request — идентификатор операции асинхронного приема сообщения.

Глава 5. Технологии параллельного программирования

287

Прием сообщения, аналогичный MPiRecv, однако возврат из функции происходит сразу после инициализации процесса приема без ожидания получения и записи всего сообщения в буфере buf. Окончание процесса приема можно определить с помощью параметра request и процедур типа MPi_wait И MPI_Test.

Сообщение, отправленное любой из функций MPi_send, MPi_isend и любой из трех их модификаций, может быть принято любой из процедур MPi_Recv

И MPI_Irecv.

С помощью данной функции легко обойти возможную тупиковую ситуацию, показанную на рис. 5.5. Заменим вызов функции приема сообщения с блокировкой на вызов функции MPiirecv. Расположим его перед вызовом функции MPi_send, т. е. преобразуем фрагмент:

MPI_Send (...) MPI_Recv(...)

следующим образом

MPI_Irecv (...) MPI_Send (...)

В такой ситуации тупик гарантированно не возникнет, поскольку к моменту вызова функции MPisend запрос на прием сообщения уже будет выставлен.

int MPI_Wait(MPI_Request *request, MPI_Status *status)

□ request — идентификатор операции асинхронного приема или передачи;

□ out status — параметры сообщения.

Ожидание завершения асинхронной операции, ассоциированной с идентификатором request И запущенной функциями MPI_Isend ИЛИ MPI_Irecv. Пока асинхронная операция не будет завершена, процесс, выполнивший функцию MPi_wait, будет заблокирован. Если речь идет о приеме, атрибуты и длину принятого сообщения можно определить обычным образом с помощью параметра status.

int MPI_Waitall(int count, MPI_Request *requests, MPI_Status *statuses)

□ count — число идентификаторов асинхронных операций;

□ requests — идентификаторы операций асинхронного приема или передачи;

□ out statuses — параметры сообщений.

288

Часть II. Параллельное программирование

Выполнение процесса блокируется до тех пор, пока все операции обмена, ассоциированные с указанными идентификаторами, не будут завершены. Если во время одной или нескольких операций обмена возникли ошибки, то поле ошибки в элементах массива statuses будет установлено в соответствующее значение.

Ниже показан пример программы, в которой все процессы обмениваются сообщениями с ближайшими соседями в соответствии с топологией кольца.

#include "mpi.h" #include <stdio.h>

int main(argc,argv)

int argc;

char *argv[]; {

int numtasks, rank, next, prev, buf[2], tagl=l, tag2=2;

MPI_Request reqs[4];

MPI_Status stats [4];

MPI_In.it (Sargc, &argv) ;

MPI_Comm_size(MPI_COMM_WORLD, Snumtasks);

MPI_Comm_rank(MPI_COMM_WORLD, Srank);

prev = rank - 1;

next = rank+1;

if (rank == 0) prev = numtasks - 1;

if (rank == (numtasks - 1)) next = 0;

MPI_Irecv(&buf[0], 1, MPI_INT, prev, tagl, MPI_COMM_WORLD,

&reqs[0]); MPI_Irecv(&buf[1], 1, MPI_INT, next, tag2, MPI_COMM_WORLD, &reqs[1]);

MPI_Isend(&rank, 1, MPI_INT, prev, tag2, MPI_COMM_WORLD, &reqs[2]); MPI_Isend(&rank, 1, MPI_INT, next, tagl, MPI_COMM_WORLD, &reqs[3]);

MPI_Waitall(4, reqs, stats);

MPI_Finalize();

}

Глава 5. Технологии параллельного программирования

289

int MPI_Waitany( int count, MPI_Request *requests, int *index, MPI_Status *status)

□ count — число идентификаторов асинхронных операций;

□ requests — идентификаторы операций асинхронного приема или передачи;

□ out index — номер завершенной операции обмена;

□ out status — параметры сообщения.

Выполнение процесса блокируется до тех пор, пока какая-либо асинхронная операция обмена, ассоциированная с указанными идентификаторами, не будет завершена. Если завершились несколько операций, то случайным образом будет выбрана одна из них. Параметр index содержит номер элемента в массиве requests, содержащего идентификатор завершенной операции.

int MPI_Waitsome( int incount, MPI_Request *requests, int *outcount, int *indexes, MPI_Status *statuses)

□ incount — число идентификаторов асинхронных операций;

□ requests — идентификаторы операций асинхронного приема или передачи;

□ out out count — число идентификаторов завершившихся операций обмена;

□ out indexes — массив номеров завершившихся операций обмена;

□ out statuses — параметры завершившихся операций приема сообщений.

Выполнение процесса блокируется до тех пор, пока одна из операций обмена, ассоциированных с указанными идентификаторами, не будет завершена. Параметр out count содержит число завершенных операций, а первые outcount элементов массива indexes содержат номера элементов массива requests с их идентификаторами. Первые outcount элементов массива statuses содержат параметры завершенных операций.

int MPI_Test(MPI_Request *request, int *flag, MPI_Status *status)

□ request — идентификатор операции асинхронного приема или передачи;

□ out flag — признак завершенности операции обмена;

□ out status — параметры сообщения.

Проверка завершенности асинхронных функций MPi_isend или MPi_irecv, ассоциированных с идентификатором request. В параметре flag функция MPiTest возвращает значение 1, если соответствующая операция завершена, и значение 0 в противном случае. Если завершена процедура приема, то атрибуты и длину полученного сообщения можно определить обычным образом с помощью параметра status.

int MPI_Testall( int count, MPI_Request *requests, int *flag, MPI_Status *statuses)

□ count — число идентификаторов асинхронных операций;

□ requests — идентификаторы операций асинхронного приема или передачи;

290

Часть II. Параллельное программирование

П out flag — признак завершенности операций обмена;

□ out statuses — параметры сообщений.

В параметре flag функция возвращает значение 1, если все операции, ассоциированные с указанными идентификаторами, завершены. В этом случае параметры сообщений будут указаны в массиве statuses. Если какая-либо из операций не завершилась, то возвращается 0, и определенность элементов массива statuses не гарантируется.

int MPI_Testany(int count, MPI_Request *requests, int *index, int *flag, MPI_Status *status)

□ count — число идентификаторов асинхронных операций;

□ requests — идентификаторы операций асинхронного приема или передачи;

□ out index — номер завершенной операции обмена;

□ out flag — признак завершенности операции обмена;

□ out status — параметры сообщения.

Если к моменту вызова функции MPi_Testany хотя бы одна из операций асинхронного обмена завершилась, то в параметре flag возвращается значение 1, index содержит номер соответствующего элемента в массиве requests, a status — параметры сообщения. В противном случае в параметре flag будет возвращено значение 0.

int MPI_Testsome( int incount, MPI_Request *requests, int *outcount, int *indexes, MPI_Status *statuses)

□ incount — число идентификаторов асинхронных операций;

□ requests — идентификаторы операций асинхронного приема или передачи;

□ out outcount — число идентификаторов завершившихся операций обмена;

□ out indexes — массив номеров завершившихся операций обмена;

□ out statuses — параметры завершившихся операций приема сообщений.

Данная функция работает так же, как и MPi_waitsome, за исключением того, что возврат происходит немедленно. Если ни одна из указанных операций не завершилась, то значение outcount будет равно нулю.

int MPI_Iprobe( int source, int msgtag, MPI_Comm comm, int *flag, MPI_Status *status)

□ source — номер процесса-отправителя или mpi_any_source;

□ msgtag — идентификатор ожидаемого сообщения или mpi_any_tag;

□ comm — идентификатор коммуникатора;

Глава 5. Технологии параллельного программирования

291

П out flag — признак завершенности операции обмена;

□ out status — параметры подходящего сообщения.

Получение информации о поступлении и структуре ожидаемого сообщения без блокировки. В параметре flag возвращается значение 1, если сообщение с подходящими атрибутами уже может быть принято (в этом случае ее действие полностью аналогично MPi_Probe), и значение 0, если сообщения с указанными атрибутами еще нет.

Объединение запросов на взаимодействие. Процедуры данной группы позволяют снизить накладные расходы, возникающие в рамках одного процессора при обработке приема/передачи и перемещении необходимой информации между процессом и сетевым контроллером. Несколько запросов на прием и/или передачу могут объединяться вместе для того, чтобы далее их можно было бы запустить одной командой. Способ приема сообщения никак не зависит от способа его посылки: сообщение, отправленное с помощью объединения запросов либо обычным способом, может быть принято как обычным способом, так и с помощью объединения запросов.

int MPI_Send_init( void *buf, int count, MPI_Datatype datatype, int dest, int msgtag, MPI_Comm comm, MPI_Request *request)

□ buf — адрес начала буфера с посылаемым сообщением;

□ count — число передаваемых элементов в сообщении;

□ datatype — тип передаваемых элементов;

□ dest — номер процесса-получателя;

□ msgtag — идентификатор сообщения;

□ comm — идентификатор коммуникатора;

□ out request — идентификатор асинхронной передачи.

Формирование запроса на выполнение пересылки данных. Все параметры точно такие же, как и у подпрограммы MPi_isend, однако, в отличие от нее, пересылка не начинается до вызова подпрограммы MPi_startaii. Как и прежде, дополнительно предусмотрены варианты и для трех модификаций

ПОСЫЛКИ сообщений: MPI_Bsend_init, MPI_Ssend_init, MPI_Rsend_init.

int MPI_Recv_init( void *buf, int count, MPI_Datatype datatype, int source, int msgtag, MPI_Comm comm, MPI_Request *request)

□ out buf — адрес начала буфера приема сообщения;

□ count — число принимаемых элементов в сообщении;

□ datatype — тип принимаемых элементов;

□ source — номер процесса-отправителя;

□ msgtag — идентификатор сообщения;

292

Часть II. Параллельное программирование

П comm — идентификатор коммуникатора;

□ out request — идентификатор асинхронного приема.

Формирование запроса на выполнение приема сообщения. Все параметры точно такие же, как и у функции MPi_irecv, однако, в отличие от нее, реальный прием не начинается до вызова функции MPi_startaii.

MPI_Startall(int count, MPI_Request *requests)

□ count — число запросов на взаимодействие;

□ out requests — массив идентификаторов приема/передачи.

Запуск всех отложенных операций передачи и приема, ассоциированных с элементами массива запросов requests и инициированных функциями MPi_Recv_init, MPi_send_init или ее тремя модификациями. Все отложенные взаимодействия запускаются в режиме без блокировки, а их завершение можно определить обычным образом с помощью функций семейств MPI_Wait И MPI_Test.

Совмещенные прием и передача сообщений. Совмещение приема и передачи сообщений между процессами позволяет легко обходить множество подводных камней, связанных с возможными тупиковыми ситуациями. Предположим, что в линейке процессов необходимо организовать обмен данными между /-м и / + 1-м процессами. Если воспользоваться стандартными блокирующими функциями посылки сообщений, то возможен тупик, обсуждавшийся ранее. Один из способов обхода такой ситуации состоит в использовании функции совмещенного приема и передачи.

int MPI_Sendrecv( void *sbuf, int scount, MPI_Datatype stype, int dest, int stag, void *rbuf, int rcount, MPI_Datatype rtype, int source, MPI_Datatype rtag, MPI_Comm comm, MPI_Status *status)

□ sbuf — адрес начала буфера с посылаемым сообщением;

□ scount — число передаваемых элементов в сообщении;

□ stype — тип передаваемых элементов;

□ dest — номер процесса-получателя;

□ stag — идентификатор посылаемого сообщения;

□ out rbuf — адрес начала буфера приема сообщения;

□ rcount — число принимаемых элементов сообщения;

□ rtype — тип принимаемых элементов;

□ source — номер процесса-отправителя;

□ rtag — идентификатор принимаемого сообщения;

□ comm — идентификатор коммуникатора;

□ out status — параметры принятого сообщения.

Глава 5. Технологии параллельного программирования

293

Данная операция объединяет в едином запросе посылку и прием сообщений. Естественно, что реализация этой функции гарантирует отсутствие тупиков, которые могли бы возникнуть между процессами при использовании

обыЧНЫХ блокирующих Операций MPI_Send и MPI_Recv.

Принимающий и отправляющий процессы могут являться одним и тем же процессом. Буфера приема и посылки обязательно должны быть различными. Сообщение, отправленное операцией MPi_sendrecv, может быть принято обычным образом, и точно так же операция MPi_sendrecv может принять сообщение, отправленное обычной операцией MPisend.

Коллективные взаимодействия процессов

В операциях коллективного взаимодействия процессов участвуют все процессы коммуникатора. Соответствующая процедура должна быть вызвана каждым процессом, быть может, со своим набором параметров. Возврат из процедуры коллективного взаимодействия может произойти в тот момент, когда участие процесса в данной операции уже закончено. Как и для блокирующих процедур, возврат означает то, что разрешен свободный доступ к буферу приема или посылки. Асинхронных коллективных операций в MPI нет.

В коллективных операциях можно использовать те же коммуникаторы, что и были использованы для операций типа "точка-точка". MPI гарантирует, что сообщения, вызванные коллективными операциями, никак не повлияют и не пересекутся с сообщениями, появившимися в результате индивидуального взаимодействия процессов.

Вообще говоря, нельзя рассчитывать на синхронизацию процессов с помощью коллективных операций. Если какой-то процесс уже завершил свое участие в коллективной операции, то это не означает ни того, что данная операция завершена другими процессами коммуникатора, ни даже того, что она ими начата (конечно же, если это возможно по смыслу операции).

В коллективных операциях не используются идентификаторы сообщений.

int MPI_Bcast(void *buf, int count, MPI_Datatype datatype, int source, MPI_Comm comm)

□ out buf — адрес начала буфера посылки сообщения;

□ count — число передаваемых элементов в сообщении;

□ datatype — тип передаваемых элементов;

□ source — номер рассылающего процесса;

□ comm — идентификатор коммуникатора.

Рассылка сообщения от процесса source всем процессам, включая рассылающий процесс. При возврате из процедуры содержимое буфера buf процесса source будет скопировано в локальный буфер каждого процесса коммуникатора comm. Значения параметров count, datatype, source И comm

294

Часть II. Параллельное программирование

должны быть одинаковыми у всех процессов. В результате выполнения следующего оператора всеми процессами коммуникатора comm:

MPI_Bcast (array, 100, MPI_INT, 0, comm);

первые сто целых чисел из массива array нулевого процесса будут скопированы в локальные буфера array каждого процесса.

int MPI_Gather( void *sbuf, int scount, MPI_Datatype stype, void *rbuf, int rcount, MPI_Datatype rtype, int dest, MPI_Comm comm)

□ sbuf — адрес начала буфера посылки;

□ scount — число элементов в посылаемом сообщении;

□ stype — тип элементов отсылаемого сообщения;

□ out rbuf — адрес начала буфера сборки данных;

□ rcount — число элементов в принимаемом сообщении;

□ rtype — тип элементов принимаемого сообщения;

□ dest — номер процесса, на котором происходит сборка данных;

□ comm — идентификатор коммуникатора.

Сборка данных со всех процессов в буфере rbuf процесса dest. Каждый процесс, включая dest, посылает содержимое своего буфера sbuf процессу dest. Собирающий процесс сохраняет данные в буфере rbuf, располагая их в порядке возрастания номеров процессов. На процессе dest существенными являются значения всех параметров, а на всех остальных процессах — только значения параметров sbuf, scount, stype, dest и comm. Значения параметров dest и comm должны быть одинаковыми у всех процессов. Параметр rcount у процесса dest обозначает число элементов типа rtype, принимаемых не от всех процессов в сумме, а от каждого процесса. С помощью похожей функции MPiGatherv можно принимать от процессов массивы данных различной длины.

int MPI_Scatter(void *sbuf, int scount, MPI_Datatype stype, void *rbuf, int rcount, MPI_Datatype rtype, int source, MPI_Comm comm)

□ sbuf — адрес начала буфера посылки;

□ scount — число элементов в посылаемом сообщении;

□ stype — тип элементов отсылаемого сообщения;

□ out rbuf — адрес начала буфера сборки данных;

□ rcount — число элементов в принимаемом сообщении;

□ rtype — тип элементов принимаемого сообщения;

□ source — номер процесса, на котором происходит сборка данных;

□ comm — идентификатор коммуникатора.

Глава 5. Технологии параллельного программирования

295

Функция MPi_scatter по своему действию является обратной к MPi_Gather. Процесс source рассылает порции данных из массива sbuf всем п процессам приложения. Можно считать, что массив sbuf делится на п равных частей, состоящих из scount элементов типа stype, после чего /-я часть посылается /-му процессу. На процессе source существенными являются значения всех параметров, а на всех остальных процессах — только значения параметров rbuf, rcount, rtype, source и comm. Значения параметров source и comm должны быть одинаковыми у всех процессов.

Аналогично функции MPi_Gatherv, с помощью функции MPi_Scatterv процессам можно отослать порции данных различной длины.

В следующем примере показано использование функции MPi_scatter для рассылки строк массива. Напомним, что в языке С, в отличие от Fortran, массивы хранятся в памяти по строкам.

#include "mpi.h" #include <stdio.h> idefine SIZE 4

int main(argc,argv)

int argc;

char *argv[];

{

int numtasks, rank, sendcount, recvcount, source;

float sendbuf[SIZE] [SIZE] = {

{1.0, 2.0, 3.0, 4.0},

{5.0, 6.0, 7.0, 8.0},

{9.0, 10.0, 11.0, 12.0},

{13.0, 14.0, 15.0, 16.0} }; float recvbuf[SIZE];

MPI_Init(Sargc,Sargv); MPI_Comm_rank(MPI_COMM_WORLD, Srank); MPI_Comm_size(MPI_COMM_WORLD, Snumtasks);

if (numtasks == SIZE) { source = 1; sendcount = SIZE; recvcount = SIZE;

MPI_Scatter(sendbuf, sendcount, MPI_FLOAT, recvbuf, recvcount, MPI_FLOAT, source, MPI_COMM_WORLD);

296

Часть II. Параллельное программирование

printf("rank= %d Results: %f %f %f %f\n", rank, recvbuf[0],

recvbuf[l], recvbuf[2], recvbuf[3]); } else

printf("Число процессов должно быть равно %d. \n", SIZE);

MPI_Finalize();

}

К коллективным операциям относятся и редукционные операции. Такие операции предполагают, что на каждом процессе хранятся некоторые данные, над которыми необходимо выполнить единую операцию, например, операцию сложения чисел или операцию нахождения максимального значения. Операция может быть либо предопределенной операцией MPI, либо операцией, определенной пользователем. Каждая предопределенная операция имеет свое имя, например, mpi_max, mpi_min, mpi_sum, mpi_prod и т. п.

int MPI_Allreduce( void *sbuf, void *rbuf, int count, MPI_Datatype datatype, MPI_Op op, MPI_Comm comm)

□ sbuf — адрес начала буфера для аргументов операции ор;

□ out rbuf — адрес начала буфера для результата операции ор;

□ count — число аргументов у каждого процесса;

□ datatype — тип аргументов;

□ ор — идентификатор глобальной операции;

□ comm — идентификатор коммуникатора.

Данная функция задает выполнение count независимых глобальных операций ор. Предполагается, что в буфере sbuf каждого процесса расположено count аргументов, имеющих тип datatype. Первые элементы массивов sbuf участвуют в первой операции ор, вторые элементы массивов sbuf участвуют во второй операции ор и т. д. Результаты выполнения всех count операций записываются в буфер rbuf на каждом процессе. Значения параметров count, datatype, ор и comm у всех процессов должны быть одинаковыми. Из соображений эффективности реализации предполагается, что операция ор обладает свойствами ассоциативности и коммутативности.

int MPI_Reduce( void *sbuf, void *rbuf, int count, MPI_Datatype datatype, MPI_Op op, int root, MPI_Comm comm)

□ sbuf — адрес начала буфера для аргументов;

□ out rbuf — адрес начала буфера для результата;

□ count — число аргументов у каждого процесса;

□ datatype — тип аргументов;

Глава 5. Технологии параллельного программирования

297

П ор — идентификатор глобальной операции;

□ root — процесс-получатель результата;

□ comm — идентификатор коммуникатора.

Функция аналогична предыдущей, но результат операции будет записан в буфер rbuf не у всех процессов, а только у процесса root.

Синхронизация процессов

Синхронизация процессов в MPI осуществляется с помощью единственной функции MPl_Barrier.

int MPI_Barrier (MPI_Comm comm)

comm — идентификатор коммуникатора.

Функция блокирует работу вызвавших ее процессов до тех пор, пока все оставшиеся процессы коммуникатора comm также не выполнят эту процедуру. Только после того, как последний процесс коммуникатора выполнит данную функцию, все процессы будут разблокированы и продолжат выполнение дальше. Данная функция является коллективной. Все процессы должны вызвать MPi_Barrier, хотя реально исполненные вызовы различными процессами коммуникатора могут быть расположены в разных местах программы.

Работа с группами процессов

Несмотря на то, что в MPI есть значительное множество функций, ориентированных на работу с коммуникаторами и группами процессов, мы не будем подробно останавливаться на данном разделе. Представленная функциональность позволяет сравнить состав групп, определить их пересечение, объединение, добавить процессы в группу, удалить группу и т. д. В качестве примера приведем лишь один способ образования новых групп на основе существующих.

int MPI_Comm_split(MPI_Comm comm, int color, int key, MPI_Comm *newcomm)

□ comm — идентификатор существующего коммуникатора;

□ color — признак разделения на группы;

□ key — параметр, определяющий нумерацию в новых группах;

□ out newcomm — идентификатор нового коммуникатора.

Данная процедура разбивает все множество процессов, входящих в группу comm, на непересекающиеся подгруппы — одну подгруппу на каждое значение параметра color. Значение параметра color должно быть неотрицательным целым числом. Каждая новая подгруппа содержит все процессы, у которых параметр color имеет одно и то же значение, т. е. в каждой новой подгруппе будут собраны все процессы "одного цвета". Всем процессам подгруппы будет возвращено одно и то же значение newcomm. Параметр key определяет нумерацию в новой подгруппе.

298

Часть II. Параллельное программирование

Предположим, что нужно разделить все процессы программы на две подгруппы в зависимости от того, является ли номер процесса четным или нечетным. В этом случае в поле color достаточно поместить выражение My_ioi%2, где My_id — это номер процесса. Значением данного выражения может быть либо 0, либо 1. Все процессы с четными номерами автоматически попадут в одну группу, а процессы с нечетными в другую.

int MPI_Comm_fгее (MPI_Comm comm)

out comm — идентификатор коммуникатора.

Появление нового коммуникатора всегда вызывает создание новой структуры данных. Если созданный коммуникатор больше не нужен, то соответствующую область памяти необходимо освободить. Данная функция уничтожает коммуникатор, ассоциированный с идентификатором comm, который после возвращения из функции будет иметь значение mpi_comm_null.

Дальнейшее развитие интерфейса. Стандарт MPI-2

В 1998 году была завершена основная часть работы, связанная с подготовкой новой версии MPI-2. Функциональность интерфейса новой версии значительно расширилась. Однако до сих пор лишь очень немногие производители параллельной вычислительной техники поддерживают данный стандарт, ожидая, по всей видимости, широкого признания пользователями новой версии.

А для пользователей этот вопрос не столь очевиден, как кажется. С одной стороны, в новом стандарте отражены, казалось бы, только разумные конструкции, необходимые на практике. Возьмем, например, параллельный ввод/вывод. Для большого класса задач операции подобного типа всегда были узким местом и адекватные средства просто необходимы. Но, с другой стороны, пользователям не дается никаких гарантий, что такие конструкции будут эффективно реализованы. Будут ли они тратить свои силы для очередного переписывания программ в новых терминах? Далеко не факт...

Мы не будем столь же детально описывать функции нового стандарта. Отметим лишь основные изменения, сделанные в MPI-2 по сравнению с предыдущими версиями.

Динамическое порождение процессов. В новом стандарте отошли от прежней статической модели параллельной программы. Ранее в программе один раз порождалось некоторое фиксированное число параллельных процессов, которое в процессе работы не изменялось. В модели, заложенной в MPI-2, разрешается создание и уничтожение процессов по ходу выполнения программы. Предусмотрен специальный механизм, позволяющий устанавливать связь между только что порожденными процессами и уже работающей частью MPI-программы. Более того, в MPI-2 есть возможность установить связь между двумя приложениями даже в том случае, когда ни одно из них не было инициатором запуска другого.

Одностороннее взаимодействие процессов. Обмен сообщениями по традиционной схеме send/Receive не всегда является удобным. Иногда активной

Глава 5. Технологии параллельного программирования

299

стороной вполне может быть только один процесс. Если он знает, какому процессу нужно передать данные и где их разместить, то зачем требовать активности получателя? Аналогично и в случае приема сообщений. Практика показала, что схема Put /Get для многих приложений является более приемлемой, что и послужило поводом для ее включения в MPI-2. Следует учесть, что схема Put /Get особенно актуальна на компьютерах с общей памятью, которые активно появляются в последнее время.

Параллельный ввод/вывод. MPI-2 предоставляет специальный интерфейс для работы процессов с файловой системой.

Расширенные коллективные операции. Во многие коллективные операции добавлена возможность взаимодействия между процессами, входящими в разные коммуникаторы. Например, в стандартной операции рассылки сообщения MPi_Bcast рассылающий процесс может взаимодействовать с процессами другого коммуникатора. Другой пример расширения: многие коллективные операции внутри коммуникатора в MPI-2 могут выполняться в режиме in_piace, при котором входные и выходные буфера совпадают.

Интерфейс для C++. Представленные в MPI-1 интерфейсы для языков Fortran и С расширены интерфейсом для C++.

Полный вариант описания стандарта MPI-2, а также планы его развития, можно найти на сайте http://www.mpiforum.org.

Вопросы и задания

1. Что общего и в чем различия между традиционной общей памятью в SMP-компьютерах и пространством кортежей в системе Linda?

2. В программе необходимо использовать критическую секцию. Как реализовать критическую секцию в рамках системы Linda?

3. Продумайте детали реализации системы Linda в Linux-кластере. Укажите возможные узкие места, влияющие на эффективность выполнения программ.

4. Необходимо написать программу для компьютера с общей памятью. Чему отдать предпочтение: ОрепМР или Linda? Сравните данные технологии с различных точек зрения.

5. С использованием системы Linda напишите программу, реализующую сложение элементов вектора по схеме сдваивания.

6. Можно ли написать автоматический конвертор, преобразующий программы из ОрепМР в систему Linda и наоборот?

7. Можно ли написать автоматический конвертор, преобразующий программы из MPI в систему Linda и наоборот?

8. В распоряжении программистов есть, с одной стороны, MPI и ОрепМР, а с другой стороны, компьютеры с общей и распределенной памятью. Какая технология программирования какой архитектуре лучше соответствует?

300

Часть II. Параллельное программирование

9. Чем отличаются процессы в MPI и в системе Linda?

10. Что означает в MPI посылка и прием сообщения с блокировкой?

11. Всем MPI-процессам надо обменяться сообщениями "по кольцу". Найдите такой способ организации программы, который бы гарантировал отсутствие тупиковой ситуации. Как сделать то же самое, но с использованием только блокирующих операций MPl_Send и MPl_Recv?

12. Верно ли, что в коллективных операциях участвуют все процессы приложения?

13. Могут ли каким-то образом общаться процессы, принадлежащие разным коммуникаторам?

14. Верно ли, что никакие два процесса программы не могут иметь одинаковые номера?

15. Сравните технологии программирования MPI и DVM с различных точек зрения.

16. Какая взаимосвязь между понятиями виртуальной топологии процессов в MPI и сетью в трС? Каково назначение этих конструкций?

17. Можно ли в MPI-программе учесть возможную неоднородность вычислительной системы?

18. Почему в MPI нет механизма критических секций?

19. Почему использование асинхронных операций обмена сообщениями, выполняющихся на фоне вычислений, вместо операций с блокировкой необязательно приведет к ускорению программы?

20. Можно ли в MPI принять сообщение, не зная точно номера посылающего процесса?

21. Известно, что MPI не гарантирует справедливости в распределении приходящих сообщений. Как в схеме мастер/рабочие гарантировать регулярную загрузку и регулярное обслуживание каждого подчиненного процесса?

22. Как в MPI определить размер буфера, необходимого для приема сообщения?

23. Какие особенности программно-аппаратной среды компьютера могут быть использованы системой поддержки MPI для эффективного выполнения функции

MPI_Startall?

24. Какое выражение нужно поместить на место параметра color функции MPl_Comm_split, чтобы группу из 100 процессов разделить на две подгруппы с номерами от 0 до 40 и от 41 до 99?

25. Реализуйте с использованием MPI метод Якоби по схеме DVM-программы, приведенной в предыдущем параграфе. Сравните полученную MPI-программу с аналогичной DVM-программой. Какие достоинства есть у каждой из этих программ?

26. Объясните, в каких случаях вы отдали бы предпочтение именно системе Linda, MPI, OpenMP, DVM, mpC?

Глава 5. Технологии параллельного программирования

301

§ 5.3. Другие языки

и системы программирования

У ученых всегда было много идей, на основе чего можно было бы построить новые системы программирования. Одни идеи отражали особенности архитектуры компьютеров, другие опирались на различные разделы математики или теоретического программирования, третьи отталкивались от предметной области решаемых задач. В качестве примеров подобных систем можно назвать Sisal, Haskell, Cilk, Т-система, НОРМА и др. Систем много, но не надо забывать, что реальное распространение систем всегда определяли три фактора: простота программирования, эффективность программ, переносимость программ. Да, задача создания системы программирования, удовлетворяющей всем этим требованиям, пока не решена. Но потому мы и решили включить данный параграф в книгу, чтобы показать, насколько интересными и неожиданными могут оказаться идеи, на базе которых можно создавать новые системы. Если возникнет желание работать в данном направлении, то не нужно сразу отказываться от, казалось бы, безумных идей. Возможно, что именно на стыке различных областей и будет найден разумный вариант, удовлетворяющий всем необходимым условиям.

В данном параграфе мы расскажем про две российские разработки: Т-сис-тему и язык НОРМА. Одна предлагает подход к автоматическому динамическому распараллеливанию программ, а другая позволяет программировать практически в терминах математических формул.

Т-система

В этом разделе мы рассмотрим ключевые аспекты технологии автоматического динамического распараллеливания программ, известной как Т-система [42]. Разработка Т-системы была начата в Институте программных систем РАН (г. Переславль-Залесский) в конце 80-х годов прошлого столетия.

Наиболее характерной чертой Т-системы является использование парадигмы функционального программирования для обеспечения динамического распараллеливания программ. На этой основе удалось найти и реализовать в Т-системе интересные формы для организации параллельных вычислений, в частности, для синхронизации или распределения нагрузки. Вместе с тем, функциональный стиль Т-системы удалось удачно совместить с традиционными языками программирования с помощью расширений языков С, C++ или языка Fortran. Явные параллельные конструкции в языке отсутствуют, и программист в тексте явно не указывает, какие части программы следует выполнять параллельно.

Базовые принципы Т-системы опираются на результаты общей теории функционального программирования. Для их пояснения можно не вдаваться

302

Часть II. Параллельное программирование

в детали теории, а воспользоваться простой аналогией. Предположим, что у нас есть сложное арифметическое выражение, включающее много подвыражений, заключенных в скобки. Все эти подвыражения можно вычислять в любом порядке, и в каждом случае мы получим один и тот же результат (конечно же, рассматривается не машинная, а точная арифметика без ошибок округления). В теории функционального программирования этот закон арифметики обобщается на произвольные рекурсивные функции.

Такой подход дает прямой метод для распараллеливания функциональных программ, построенных из "чистых" функций. Чистые функции — это одно из базовых понятий Т-системы, обозначающее функции без побочных эффектов. В каждый момент времени необходимо выделять готовые к вычислению "подвыражения" и распределять их по имеющимся процессорам. За основу берется граф, узлы которого представляют вызванные функции, а дуги соответствуют отношению "подвыражение—выражение".

Оказывается, что для добавления функциональной семантики в традиционный язык программирования достаточно ввести понятие неготового значения. В языке С это достигается введением дополнительного атрибута у описания переменных. Новое ключевое слово tvai в описании "tvai int i" определяет переменную, значение которой может быть целым числом или неготовым значением (пока не посчитанным). Для обозначения функций без побочных эффектов дополнительно используется слово tfun, выход Т-функции обозначается словом tout и т. д.

Рассмотрим простой пример.

tfun void tmain(...) { tvai int x, у, z, b = 1; int w, t, a = 5;

G(a, b, &x, &y, &z); /* результаты принимаем в x, у, z */ b = z; У = a; w = a; t = b+a*w;

}

Предположим, что функция G является чистой и имеет атрибут tfun. Будем исполнять пример "по шагам". Комментарии будут относиться к моменту завершения срабатывания очередного оператора.

1. G(a, b, &х, &у, &z). Поскольку функция g является чистой, то она может быть выполнена параллельно с основной программой. После выполнения этого оператора Т-система на основе данного вызова функции g оформит новую порцию работы, готовую к параллельному исполнению.

Глава 5. Технологии параллельного программирования

303

Вне зависимости от того, будет ли эта порция выполняться немедленно или же по каким-то причинам ее выполнение будет отложено, система перейдет к выполнению следующего оператора. Переменные х, у, z получат статус неготовых переменных и будут содержать неготовые значения.

2. ь = z. Теперь и переменная ь стала неготовой, а система без какой-либо задержки будет исполнять программу дальше. Этот пример служит иллюстрацией к тому, что неготовые значения можно копировать. Одновременно мы изменили состав потребителей результатов функции с. Теперь третий результат должен быть передан как в переменную z, так и в переменную ь. Заметим, что неготовность переменной ь в данный момент, конечно же, никак не влияет на то значение ь, которое было использовано в качестве аргумента функции g.

3. у = а. Переменная а — обычная, поэтому переменная у из "неготовой" станет "готовой" и получит то значение, которое имела переменная а.

4. w = а. Этот оператор проблем не вызывает, поскольку в нем использованы только обычные переменные.

5. t = b+a*w. На этом операторе выполнение фрагмента будет заблокировано до тех пор, пока функция g не вернет результат в переменную ь. Неготовые значения можно копировать, что и было сделано во втором операторе, но никаких других операций над ними выполнять нельзя.

Относительно данного фрагмента остался неясным лишь один вопрос. Может сложиться впечатление, что из-за третьего оператора фрагмент не будет обладать детерминированным поведением. В самом деле, если оператор "у = а" выполнится раньше завершения функции с, то значение переменной у будет определяться функцией g, а если позже, то переменная у получит значение а.

На самом деле детерминированность обеспечена. После выполнения данного оператора значение у всегда будет равно значению а. В начале обработки оператора "у = а" происходит блокировка переменной у. Выполняется проверка значения переменной и, если значение является неготовым, то выставляется отказ от ожидаемого значения и разрыв связи с его поставщиком. В нашем случае это отказ от выходного значения функции g. После всех этих проверок и выполнения оператора блокировка с переменной снимается. Такая последовательность гарантирует детерминированность поведения программы и обеспечивает привычную семантику: после выполнения "у = а" значение у будет равно значению а.

Диалект языка С, полученный добавлением новых ключевых слов, носит название ТС. Новый язык позволяет использовать привычную для многих программистов императивную нотацию для записи программ в функциональном стиле.

304

Часть II. Параллельное программирование

Чтобы ознакомиться с базовыми конструкциями Т-системы и языка ТС, рассмотрим два простых примера: вычисление чисел Фибоначчи и рекурсивный обход древовидной структуры данных.

Рассмотрим задачу нахождения «-ого числа Фибоначчи. Вычисление опирается на определение чисел Фибоначчи:

\1, если п = 1 или п = 2;

"1Л-1+Л-2. "^³-

Текст программы решения этой задачи с использованием Т-системы показан ниже. Номера строк, конечно же, не являются частью Т-системы. Они нам понадобятся в дальнейшем для пояснения различных конструкций программы.

001 iinclude <tc.h> 002

003 #include <stdio.h>

004 #include <stdlib.h> 005

007 unsigned cfib (unsigned _n)

008 {

009 return _n < 2 ? _n : cfib(_n - 1) + cfib(_n - 2);

010 } 011

012 tfun void fib (unsigned _n, tout unsigned *_res)

013 {

014 if (_n < 32) {

015 *_res = cfib(_n);

016 } else {

017 tval unsigned resl, res2;

018 fib(_n - 1, &resl);

019 fib(_n - 2, &res2);

020 *_res = resl + res2;

021 }

022 } 023

024 int tmain (int argc, char* argv[])

025 {

026 unsigned n;

027 tval unsigned res;

028 if (argc < 2) {

Глава 5. Технологии параллельного программирования

305

029 terrprint(

030 "Usage:\n"

031 "gr_fib <number>\n"

032 ) ;

033 return - 1;

034 }

035 n = (unsigned)atoi(argv[l]);

036 fib(n, &res);

037 (unsigned)res;

038 terrprint("fib(%u) = %u\n", n, res);

039 return 0;

040 }

В программе с помощью ключевого слова tvai определены переменные resi, res2 и res, способные хранить как обычное, так и неготовое значение. В тот момент, когда их адреса передаются в Т-функцию fib, а это вызовы fib в строках 18, 19 и 36, выполнение вызывающей функции не останавливается, и она продолжает работать дальше. Поскольку второй формальный параметр Т-функции fib имеет описание tout, то в моменты вызовов соответствующая переменная resi, res2 и res становится "неготовой". Она будет содержать то самое специальное неготовое значение. Когда вызванная функция fib вычислит результат и вернет его в переменную (строка 15 или 20), это значение будет заменено обычным "готовым" значением.

Обращение к неготовым переменным за их значением блокирует процесс вычисления функции. Например, такое может произойти в строке 20, где стоит обращение к переменным resi и res2. В строках 18 и 19 не требуется знания значения переменных resi и res2, поэтому оба вызова Т-функций fib будут выполнены без блокировки, и их вычисление может происходить параллельно.

Порожденные в процессе работы программы вызовы Т-функций fib (строки 18, 19 и 36) формируют независимые порции работы (гранулы параллелизма), готовые к вычислению. Все порции помещаются в очередь, откуда вычислительные процессы-исполнители получают для себя работу. Т-функции в тексте программы указывают шаблоны потенциальных параллельных фрагментов кода. Реальные параллельные фрагменты появляются и обрабатываются Т-системой во время работы программы, как результат реальных вызовов Т-функций.

Условный оператор, стоящий в строке 14, выполняет две задачи. С одной стороны, нужно в какой-то момент времени остановить образование новых порций работы и начать формировать окончательный результат. В этом смысле здесь полная аналогия с обычными рекурсивными функциями. С другой стороны, все формируемые порции работы должны быть достаточ-

306

Часть II. Параллельное программирование

но весомыми. Нужно скрыть накладные расходы, вызываемые передачей очередной порции какому-либо процессу, что можно сделать через увеличение объема вычислений. Из этих соображений и появилась константа 32 в данной строке.

Ясно, что неготовые переменные в Т-системе являются основным средством синхронизации. Существенно различаются ситуации обращения к неготовым переменным на чтение (доступ за значением) и на запись (доступ для присваивания):

□ при чтении неготовой переменной происходит блокировка процесса вычисления, выполнившего такое обращение; его ожидание продлится до тех пор, пока переменная не получит готового значения; исключение составляют лишь операции копирования (присваивания) неготовых переменных, при выполнении которых блокировки не возникает;

□ при записи обычного значения в неготовую переменную она становится готовой для всех своих потребителей, а ранее заблокированные на данной переменной процессы выходят из состояния блокировки.

Теперь рассмотрим программу рекурсивного обхода дерева, которая проиллюстрирует работу с удаленными указателями.

001 iinclude <tc.h> 002

003 #include <stdio.h>

004 #include <stdlib.h> 005

006 struct tree {

007 struct tree tptr left;

008 struct tree tptr right;

009 int value;

010 }; 011

012 struct tree tptr create_tree(int deep) {

013 struct tree tptr res = tnew(struct tree);

014 res->value = 1;

015 if (deep <= 1) {

016 res ->left = NULL;

017 res ->right = NULL;

018 } else {

019 res->left = create_tree(deep - 1);

020 res ->right = create_tree(deep-1);

021 }

022 tvalidate(*res);

Глава 5. Технологии параллельного программирования

307

023 return res;

024 }

025 tfun void tsum(const struct tree tptr _tree,

026 tout int *_res) {

027 tval int left_sum, right_sum; 028

029 if (_tree->left != NULL) {

030 tsum(_tree->left, &left_sum);

031 } else {

032 left_sum = _tree->value;

033 }

034 if (_tree->right != NULL) {

035 tsum(_tree->right, &right_sum);

036 } else {

037 right_sum = _tree->value;

038 }

039 *_res = left_sum + right_sum;

040 } 041

042 int tmain (int argc, char* argv[])

043 {

044 struct tree tptr tree = create_tree(12);

045 tval int sum;

046 tsum(tree, &sum) ;

047 terrprint("sum = %u\n", sum); 04 8 return 0;

049 }

В этой программе дерево структур с типом tree сначала порождается функцией create_tree, а затем обходится в рекурсивной функции tsum. Как и в предыдущем примере, происходит распараллеливание в каждом узле дерева: сначала порождаются вызовы для левой и правой ветви, и лишь затем происходит обращение к результатам обхода.

Ключевое слово tptr служит для описания глобальных ссылок на неготовые переменные. При операции чтения данных по Т-указателю может происходить ожидание готовности значения и его подгрузка из узла вычислительной системы, в котором расположено значение, в узел, где произошло обращение по Т-указателю. При операции записи значение передается в нужный узел системы, и там значение записывается в соответствующую Т-пере-менную, делая ее готовой.

308

Часть II. Параллельное программирование

Практика использования Т-системы рекомендует следующую последовательность шагов в процессе разработки программ на языке ТС.

1. Разработка дизайна кода. На этом этапе решается вопрос о том, какие фрагменты алгоритма будут реализованы на языке ТС в виде Т-функций, а какие реализованы в виде привычного последовательно исполняемого кода на стандартных языках последовательного программирования С, C++ или Fortran.

2. Реализация и первичная отладка на однопроцессорном компьютере. Разработанная ТС-программа отлаживается на обычном однопроцессорном компьютере в последовательном режиме без использования Т-системы. Для этого все новые ключевые слова, добавленные в язык С, автоматически переопределяются с помощью соответствующих макросов (например: tptr определятеся как "*"; tvai — как "пусто" и т. п.).

3. Отладка на многопроцессорных установках. После отладки ТС-программы на однопроцессорном компьютере в последовательном режиме следует полнофункциональная отладка в параллельной вычислительной среде.

4. Оптимизация. Последний этап, на котором с помощью трассировки, профилировки и других средств производится оптимизация программы, характерен для любой технологии параллельного программирования.

Ясно, что по сравнению с другими системами параллельного программирования преимущества Т-системы наиболее отчетливо проявляются в двух ситуациях. Первая ситуация характерна тем, что до выполнения программы нет точной информации о том, как сбалансировать работу параллельных процессов. Вторая ситуация возникает тогда, когда вычислительная схема программы близка к функциональной модели и может быть эффективно представлена с помощью совокупности функций, рекурсивно вызывающих друг друга. Сильной стороной Т-системы является и то, что она в значительной степени освобождает программиста от многих традиционных забот, характерных для параллельного программирования. Явная организация параллельных фрагментов программы, их распределение по узлам кластера, синхронизация работы фрагментов, явные операции обмена данными между ними — все это Т-система берет на себя.

Но, как обычно, недостатки являются продолжением достоинств. Существует масса подводных камней, о которых явно не говорится, но которые нужно четко представлять. Типичный пример — это вызов Т-функции, который может вызвать пересылку данных из одного узла кластера в другой. Внешне ничего подозрительного нет, а накладные расходы могут оказаться очень большими. Если этот фактор на этапе проектирования программы не учесть, то с ее эффективностью могут возникнуть большие проблемы. Балансировка вычислительной нагрузки лежит на системе, но гарантии оптимальности она не дает. Опять-таки, при реализации программ для Т-системы программист обязан изложить алгоритм в функциональном сти-

Глава 5. Технологии параллельного программирования

309

ле и описать программу в виде набора чистых Т-функций. Это нельзя назвать неудобным, но это, по крайней мере, непривычно. На программисте лежит и выбор оптимального размера потенциально параллельных фрагментов. Очень маленькая вычислительная сложность Т-функций может привести к чрезмерным накладным расходам. Слишком большая вычислительная сложность может привести к малому количеству порождаемых в процессе параллельных фрагментов и, как следствие, к неравномерной загрузке вычислительных узлов системы.

Система программирования НОРМА

Язык НОРМА является специализированным непроцедурным языком, предназначенным для спецификации задач вычислительного характера, в частности, задач математической физики. Все конструкции языка носят декларативный характер и описывают правила вычисления значений. Основное назначение языка состоит в автоматизации процесса разработки программ. Программист работает "почти" в терминах математических формул, что значительно упрощает его работу. Задача транслятора усложняется. Помимо традиционных задач, в частности, синтаксического и семантического анализа, он выполняет синтез выходной программы.

Идеи, позволяющие автоматически строить программу по спецификации задачи, были сформулированы И. Б. Задыхайло в работе [29] еще в 1963 году. Дальнейшее их развитие привело к появлению языка НОРМА и нескольких версий транслятора для различных платформ.

Первоначально термин НОРМА расшифровывался как Непроцедурное Описание Разностных Моделей Алгоритмов. В последствии появилась и другая трактовка: НОРМАльный уровень общения прикладного математика с компьютером. Разработчик прикладных программ абстрагируется от особенностей конкретных компьютеров и мыслит в привычных терминах своей предметной области. Отталкиваясь от конкретных потребностей Института прикладной математики им. М. В. Келдыша РАН, авторы языка старались максимально упростить решение класса задач математической физики. Специфика предметной области — это ориентация на сеточные методы. Именно этот факт наложил значительный отпечаток как на концепцию языка, так и на все его основные конструкции.

В записи программы на языке НОРМА не требуется никакой информации о порядке выполнения операций. Порядок предложений языка может быть произвольным. Язык позволяет формулировать запрос на вычисления, не уточняя, каким именно образом вычисления следует организовать. Все информационные связи выявляются и учитываются транслятором-синтезатором на этапах анализа исходной программы и синтеза выходного текста. На трансляторе лежит и выбор конкретного способа организации вычислений. В частности, на этапе синтеза результирующей программы он может сгенерировать как последовательный, так и параллельный код.

310

Часть II. Параллельное программирование

Выбор высокого уровня языка НОРМА определяет его характерную черту — это язык с однократным присваиванием. Каждая переменная может принимать значение только один раз. Такие понятия, как память, побочный эффект, оператор присваивания и управляющие операторы в языке НОРМА отсутствуют просто "по определению". Во всех традиционных языках программирования эти понятия есть, поскольку с их помощью нужно формулировать конкретный алгоритм с учетом вопросов экономии и распределения памяти, порядка выполнения операторов и т. п. Запись на языке НОРМА, по существу, является записью численного метода решения конкретной задачи.

Важно и то, что в записи на языке НОРМА отсутствуют избыточные информационные связи. Такие связи обычно накладываются в процессе программирования, причем особенно отчетливо это проявляется при оптимизации алгоритмов и программ. Мы уже имели возможность убедиться, что определение точной информационной структуры программ является сложной задачей. НОРМА позволяет опустить этап последовательного программирования, а для генерации параллельной программы предлагает сразу отталкиваться от записи в терминах математических формул. С этой точки зрения было бы очень интересно исследовать потенциал языка НОРМА для программирования dataflow-компьютеров.

Полученные результаты были использованы авторами при создании реального транслятора-синтезатора. По описанию на языке НОРМА он позволяет получать выходные программы как для последовательных компьютеров, так и для параллельных вычислительных систем с распределенной и общей памятью. Выходные программы могут быть записаны на языках Fortran MPI, Fortran PVM, Fortran 77 и других диалектах Fortran.

Описание языка мы дадим по рабочему стандарту [2] и данным сайта http://www.keldysh.ru/norma.

Программа на языке НОРМА состоит из одного или нескольких разделов. Разделы могут быть трех видов — главный раздел, простой раздел и раздел-функция. Вид раздела определяется ключевыми словами main part, part и function соответственно. Разделы могут вызывать друг друга по имени и передавать данные при помощи механизма формальных и фактических параметров, либо через внешние файлы при помощи описаний input и output. Рекурсивные вызовы разделов запрещены.

Все имена, описанные в разделе, локализованы в этом разделе. Понятие глобальных переменных в языке НОРМА отсутствует.

Параметры, указанные в списке формальных параметров до ключевого слова result, являются исходными данными. Все параметры, перечисленные после данного ключевого слова, являются результатами вычислений. Один и тот же параметр не может одновременно быть исходным и результатом: это приводит к повторному присваиванию значений переменным, что в языке

Глава 5. Технологии параллельного программирования

311

НОРМА запрещено. В разделе-функции ключевое слово result не используется, поскольку результат вычисления функции связывается с именем и типом функции.

В теле раздела могут быть заданы описания, операторы и итерации. Порядок их расположения, вообще говоря, произвольный — возможные ограничения определяются при описании входного языка транслятора.

Базовым понятием языка НОРМА является область. Область — это совокупность целочисленных наборов вида

{/ь ..., /„}, п > 0, /}•> 0,у'= 1...Л,

задающих координаты точек в «-мерном индексном пространстве. С каждой осью координат «-мерного пространства задачи связывается имя индекса.

Ключевым понятием при описании областей является понятие одномерной области. Одномерная область служит для задания диапазона точек на некоторой оси координат индексного пространства. В простейшем случае при описании одномерной области указывается имя одномерной области, имя индекса и границы изменения значений индекса. Например, следующие два описания языка НОРМА

ks : (к = 1..п). js : (j = 1..10) .

вводят две одномерные области. В первом случае верхняя граница задана с помощью параметра п (значения всех параметров должны быть описаны в разделе описания параметров). Во втором случае размерность указана явно. Границами диапазона являются целые положительные константные выражения, построенные из целых констант, параметров области и арифметических операций.

Многомерная область строится при помощи операции произведения областей, обозначаемой знаком ",-". Пример описания двумерной области, полученной с помощью операции произведения одномерных областей DirK и DirL, показан ниже:

Square: (DirK: (k=1..15) ; DirL: (1=1..5))

Введенная прямоугольная область square является подмножеством двумерного индексного пространства. В нее входят точки, у которых первая координата имеет значение от 1 до 15, а вторая — от 1 до 5.

Операция ",-" произведения прямоугольных областей А к В обладает свойством коммутативности, т. е. А ; В = В ; А. Это, в частности, означает, что порядок направлений индексного пространства при описании области не фиксируется. Если порядок направлений индексного пространства необходимо зафиксировать, то задаются описания индексов областей с помощью ключевого слова INDEX.

312

Часть II. Параллельное программирование

Необязательно все области описывать явно, можно воспользоваться уже введенными именами. Так, описание

NewGrid: (ks;j s).

определяет область через определенные выше одномерные области ks и js.

Введенные области можно изменять. Модификация областей может состоять в добавлении некоторого числа точек, в удалении точек или изменении диапазона. Модификация двух первых типов описывается при помощи функций границ left (п) и right (п). Функция left применяется к левой границе диапазона, а функция right — к правой границе диапазона. Знак "+" перед функцией означает, что к одномерной области добавляются точки, знак "-" — что из одномерной области удаляются точки. Обе эти функции имеют лишь один параметр п, определяющий число точек, которые необходимо удалить или добавить к области. В качестве фактического параметра функций left и right может быть задана только целая положительная константа. Обращение к функциям допустимо лишь в контексте с именем одномерной области, задающей модифицируемый диапазон. Предположим, что в программе было описание:

DirK:(k=l..15)

Тогда область DirKm, состоящую из точек к=з..18, можно задать следующим образом:

DirKm: DirK-LEFT(2)+RIGHT(3)

Можно изменить составляющую одномерную область путем явного переопределения диапазона. Для этого в модификации надо указать имя индекса и его новое значение. Предположим, что в программе было описание:

Square: (DirK:(k=l..15); DirL: (1=1..9) )

Для модификации сделанного описания и определения области, в которой один индекс будет по-прежнему меняться от 1 до 15, а другой уже от 10 до 22, можно воспользоваться такой конструкцией:

SquareNew: Square/l=10..22

Возможна модификация области при помощи простых соотношений, связывающих индексы области. Например, описания

KL: ((к=1..10);(1=1..10)). Diagonal: KL/k=l

задают область Diagonal, СОСТОЯЩУЮ ИЗ точек (k=l,l=l), (k=2,l=2), (k=3,l=3) , ..., (k=10,l=10) .

Следует отметить, что область определяет только значения координат точек индексного пространства, а не значения расчетных величин в этих точках. Если требуется вычислить значения величины Yy, i,j= 1...Я на некоторой

Глава 5. Технологии параллельного программирования

313

сетке Ху, i,j = l...n, введенной при решении задачи формулой Ху = F(i,j), то следует выполнить следующую последовательность шагов:

1. Описать область, состоящую из точек i, j=i.. .п.

2. Описать на этой области величины х и у.

3. Задать на этой области правило вычисления значений сетки Ху = F(i, j) и правило вычисления значений Yy= G{Xy).

Помимо явного описания областей, в языке НОРМА предусмотрена возможность задания условных областей. Входят или не входят точки индексного пространства в условную область определяется тем, выполняется или не выполняется некоторое условие. Идея задания условной области проста. Ранее определенная область D разбивается на две непересекающиеся подобласти D\ и В₂. Первая подобласть состоит из точек области D, в которых заданное условие принимает значение истина, а вторая подобласть из точек, в которых условие принимает значение ложь. Возьмем предыдущее описание области square и на его основе зададим условные области:

Squarel, Square2: Square/ x[k,1] - y[k,l]<eps

Данное описание задает разбиение исходной области square на две подобласти Squarel И Square2, причем Squarel П Square2=0, а SquarelUSquare2=Square. Подобласть Squarel СОСТОИТ ИЗ тех точек Square,

для которых условие х [к, 1] - у [к, l] <eps принимает значение истина, а подобласть square2 из точек, в которых условие принимает значение ложь.

В языке определены два класса величин: скалярные величины (скаляры) и величины на области. Описание ставит в соответствие каждой величине уникальное в текущем разделе имя, а также задает тип величины: real, integer или double. Пример описания скаляров может быть таким:

VARIABLE kl,k2 INTEGER VARIABLE pi DOUBLE

Каждая величина на области связывается с указанной в описании областью. Эта область определяет имена индексов, которые могут использоваться в индексных выражениях при обращении к данной величине. Порядок указания индексных выражений не является существенным. Для индексов не требуется специального описания, т. к. они вводятся при описании областей.

Опять воспользуемся прежним описанием области square и введем на его основе величины на области:

Square: (DirK:(k=l..15); DirL: (1=1..9) )

VARIABLE Xsum, Y DEFINED ON Square,

OneDimK DEFINED ON DirK, OneDimL DEFINED ON DirL

Приведенные описания определяют величины xsum и y на области square. Обе эти величины могут иметь в индексных выражениях индексы к и l. Be-

314

Часть II. Параллельное программирование

личины oneDimK и oneDimL определены на областях DirK и DirL, поэтому и в индексных выражениях они могут иметь индексы к и 1 соответственно.

Поскольку порядок направлений индексного пространства при описании области не фиксируется, то обращения y [ к - 1,1+1] иу[1+1,к - 1] эквивалентны. Кроме того, при обращении к величине на области действует правило задания индексов по умолчанию: индексные выражения, совпадающие с именем индекса, могут быть опущены. Именно поэтому все обращения xsum[k,i], xsum[k], Xsum[i] и Xsum к величине Xsum эквивалентны. Если необходимо одно индексное направление связать с другим, то это нужно делать явно. Например, диагональные элементы матрицы y можно определить как y [ k, i=к ] или просто y [ 1=к ].

В языке НОРМА определены лишь три вида операторов: скалярный оператор, оператор assume и вызов раздела.

Скалярный оператор предназначен для вычисления арифметических значений скаляров. По существу, это аналог оператора присваивания в традиционных языках программирования, в левой части которого указывается имя скаляра, а в правой части — скалярное арифметическое выражение. Например:

s = 234

рр = 12+x+SQRT(s+8)

Переприсваивание в скалярном операторе запрещено, поэтому оператор вида к = к - 1 по определению является неверным.

Оператор assume используется для вычисления арифметических значений величин, определенных на областях. Семантика этого оператора определяется следующим образом. Рассмотрим соотношение, записанное в условном виде так:

FOR D(ii, ..., /„) ASSUME

yl — J7\ V j\ V h (1th pr

^lndexL(,\...,i_m) ^T\^AbviexR*(i_h,...J„y •"' Index* «(<',,..., /„)' '

где:

□ D(i\, —, i_n) — область оператора assume;

□ (/'i, ..., /„) — индексы области d;

□ X^Jq ,l<q <k — имена величин, определенных на области;

□ IndexZ (i_p), 1 < р < п — индексные выражения левой части;

□ lndexR^Jg(i\, ..., i„) — индексные выражения правой части;

□ F — функция, вычисляемая в правой части;

□ Other — это другие термы правой части.

Глава 5. Технологии параллельного программирования

315

Каждое такое соотношение задает правило F вычисления значений величины X из левой части по значениям величин X^Л ,..., X^h и термов Other из правой части. Происходит это следующим образом:

□ определяются все точки (щ, ..., a_n) е D(i\, ..., /„);

□ для каждой точки (д_]5 ..., a„) е В требуется вычислить значение величины X из левой части в точке IndexZ(c₁, ..., а„);

П для каждой точки (а\, ..., a_n) е D вычисляются значения индексных выражений h\.dsxR^J,(a\, ..., а„) всех величин X^lq, \<q<k, входящих в правую часть соотношения, и определяется множество аргументов правой части:

□ если в некоторый момент времени для некоторой точки (щ, ..., а„) е В все аргументы из X вычислены, то возможно вычисление значения величины Х^&хКа , а )^из левой части; если не все аргументы определены,

то вычисление данной точки в данный момент невозможно (но это не означает, что оно вообще невозможно).

Данный оператор однозначно определяет правило для вычисления значений величины. При этом он не требует немедленного выполнения вычисления в данном месте программы и не задает порядка или способа вычисления. Оператор не содержит никакой информации о последовательном или параллельном исполнении. Рассмотрим уже знакомые нам описания:

Square: (DirK:(k=l..15); DirL: (1=1..9) ) VARIABLE Xsum, Y DEFINED ON Square,

Оператор вида

FOR Square ASSUME Xsum = 0

задает обнуление 135 элементов величины xsum. Способ реализации этого запроса в языке НОРМА не фиксируется. Поскольку НОРМА является языком однократного присваивания, то следующий оператор является некорректным:

FOR Square ASSUME Xsum = Xsum+Y

По сути, основную идею языка НОРМА мы описали. Незатронутыми остались разделы языка, связанные с заданием режима последовательного вычисления, детали вызовов разделов программы и обращений к функциям, интерфейс с языком Fortran и специальная конструкция iteration, позволяющая задать итеративный вычислительный процесс. На понимание общей концепции языка они не влияют, а при необходимости читатель всегда может найти недостающие подробности в [2].

316

Часть II. Параллельное программирование

Рассмотрим пример программы, записанной на языке НОРМА для решения системы линейных уравнений методом Гаусса—Жордана. Расчетные формулы метода можно записать в следующем виде:


m₀,ij	= °tj
*%i =*	h
^mW	= m_t-\	,ij/m_t-\,t,t
^rt,t =	r_t._ht/m_t._htj
^mW	= m_t-\	*,ij- Щ-\,1*	<?x	^mW
*^rt,i =*	n-\,i-	-mt-\,i,t*	^rV
*Xj= ,*	*^rN,i*

i=l...N j=l...N

i= 1...N

j=l...N t=l...N

t= 1...N

j = 1...N i = 1..J -l,t+ 1...N t = 1...N

t=\...N i= 1..J- 1, t+ 1...N

i= 1...N

Текст программы приведен ниже. Нумерация строк не является элементом языка, а используется лишь для последующего объяснения смысла операторов.

1 MAIN PART Gauss.

2 BEGIN

3 INDEX k,l.

4 ks : (k=l..n).

5 Is : (1=1..n).

6 kls : (ks; Is) .

7 VARIABLE a DEFINED ON kls.

8 VARIABLE b, x DEFINED ON ks.

9 INPUT a(FILE='gauss') ON kls,

10 b(FILE='gauss') ON ks.

11 DOMAIN PARAMETERS n=4.

12 COMPUTE Calculate(a ON kls, b ON ks RESULT x ON ks).

13 OUTPUT x(FILE='gauss.out',TAB(10),'Решение:^?,STR(1)) ON ks.

14 END PART.

15 PART Calculate.

16 a,b RESULT x

! Раздел вычислений

17 BEGIN

18 INDEX i,j

19 so : (ijs: (is: (i=l..n); js: (j=l..n));ts: (t=0..n)).

20 slo:(ts;is). s:so/ts-LEFT(1). si:slo/t=l..n.

21 VARIABLE a DEFINED ON ijs.

22 VARIABLE b, x DEFINED ON is.

23 VARIABLE m DEFINED ON SO.

Глава 5. Технологии параллельного программирования

317

24 VARIABLE г DEFINED ON slo.

25 DOMAIN PARAMETERS n=4.

26 DISTRIBUTION INDEX i=2..8, j=l.

27 FOR so/t=0 ASSUME m=a.

28 FOR slo/t=0 ASSUME r=b.

29 sa,sb:s/i=t. sal,sbl:sl/i=t.

30 MACRO INDEX ti [t - l,i=t].

31 MACRO INDEX tij [ti,j=t].

32 FOR sa ASSUME m = m[ti] / m[tij].

33 FOR sal ASSUME r = r[ti] / m[tij].

34 FOR sb ASSUME m = m[t - 1] - m[t - 1,j=t] * m[i=t].

35 FOR sbl ASSUME r = r[t - 1] - m[t - l,j=t] * r[i=t].

36 FOR is ASSUME x = r[t=n].

37 END PART

Прокомментируем операторы программы. Используемые ниже номера совпадают с нумерацией строк программы.

(1) Заголовок главного раздела программы Gauss.

(2) Начало главного раздела.

(3) Описание индексов областей.

(4—6) Определение одномерных областей is, js и многомерной области ijs, на которых определены начальные данные задачи.

(7—8) Описание переменных а, ь и х, где а — матрица коэффициентов системы, ь — столбец свободных членов, х — результат решения системы.

(9—10) Ввод начальных данных из файла gauss.dat.

(11) Задание параметра областей.

(12) Вызов раздела calculate, осуществляющего расчет.

(13) Вывод результата в файл gauss.out.

(14) Конец главного раздела.

(15) Заголовок простого раздела calculate.

(16) Обозначение входных (а, Ь) и выходных (х) параметров раздела.

(17) Начало простого раздела.

(18) Описание индексов областей.

(19) Определяется многомерная область so, состоящая из областей ts и ijs. Область ijs, в свою очередь, состоит из is и js.

318 Часть II. Параллельное программирование

(20) Определяются безусловная область sio и области s, si с помощью

операций модификации области.

(21—22) Описание переменных, являющихся параметрами раздела.

(23—24) Описание переменных m и г, участвующих в расчете.

(25) Задание размерности областей.

(26) Описание индексов распределения. (27—28) Задание начальных значений m и г.

(29) Описание вспомогательных условных областей sa, sb, sal, sbi.

(30—31) Описания индексных конструкций, которые служит для сокращения записи сложных индексных выражений.

(32—36) Вычисления для соответствующих расчетных формул.

(37) Конец раздела.

В чем особенность данной работы и данного направления в целом? В 1990 году вышла в свет работа А. Н. Андрианова, К. Н. Ефимкина, И. Б. Задыхайло "Непроцедурный язык НОРМА и методы его реализации", обобщившая некоторые предыдущие работы авторов. Об этой работе упоминается в [2]. Внешне это выглядело как появление еще одного языка, направленного на создание пользовательской среды, удобной для разработки прикладных программ. Однако в действительности данная работа принципиально отличалась от большинства других работ. В ней впервые было ясно сказано, что в основу языка программирования для параллельных компьютеров может быть положено описание математических соотношений без указания в нем какого-либо параллелизма или сведений об архитектуре вычислительных машин. Это позволяет снять целый ряд трудностей. Математические соотношения как язык описания заданий наиболее близки разработчикам численных методов и прикладным программистам. Сохраняется весь внутренний параллелизм реализуемого алгоритма. Математические соотношения не используют понятие памяти, в них отсутствует пересчет значений переменных. Для таких языков существующая технология определения параллелизма в программах реализуется значительно проще.

Перспективное направление, на котором в дальнейшем будет получено еще немало интересных результатов.

Вопросы и задания

1. Приведите примеры алгоритмов, для которых использование Т-системы было бы вполне естественным.

2. Приведите примеры алгоритмов, структура которых плохо соответствует "духу" Т-системы.

Глава 5. Технологии параллельного программирования

319

3. Опишите, что должен учитывать и как должен быть устроен анализатор, определяющий "чистоту" функций? Рассмотрите случаи языков Fortran и С отдельно.

4. Напишите программу нахождения определенного интеграла методом прямоугольников с использованием Т-системы. Как будет выглядеть эта же программа в терминах MPI, OpenMP, DVM, mpC, Linda, языка НОРМА?

5. Проведите численные эксперименты на любой доступной вам параллельной системе с указанными в предыдущем вопросе программами. Проведите анализ полученных результатов.

6. Какие операции допустимы над неготовыми переменными в Т-системе?

7. Как реализовать Т-систему на базе системы Linda?

8. Как вы понимаете словосочетание "функциональное программирование"?

9. Что означают термины "декларативный язык", "императивный язык", "непроцедурный язык"?

10. Для каких задач язык НОРМА подходит хорошо, а для каких его использование не будет выглядеть естественным?

11. Почему в программе на языке НОРМА не может быть побочных эффектов?

12. Какие проблемы возникнут на пути автоматического конвертирования операторов assume языка НОРМА в запись на МР1?

13. Напишите программу перемножения двух матриц с использованием языка НОРМА

14. В чем преимущество записи алгоритма с помощью математических формул перед записью, скажем, на языке Fortran для исследования параллельных свойств этого алгоритма?

15. **Напишите систему, которая по фрагменту на языке С (Fortran) восстанавливает заложенные в него математические соотношения.

Глава 6

Тонкая информационная структура программ

Всегда не хватает времени, чтобы

выполнить работу как надо, но на то,

чтобы ее переделать, время находится.

Из законов Мерфи

Данная глава является достаточно трудной для чтения. Тем не менее, мы посчитали необходимым включить ее в эту книгу. Несколько мотивов стали побудительными для такого решения.

Как свидетельствует история, развитие и использование вычислительной техники постоянно сопровождается одним малоприятным явлением, держащим в напряжении пользователей компьютеров, в особенности наиболее активную их часть. Меняются языки программирования, совершенствуются пользовательские среды. Но каждый раз, как только появляются компьютеры нового типа, приходится модернизировать прикладное программное обеспечение. Иногда изменения незначительны, но чаще всего они оказываются радикальными. Несмотря на оптимистические заверения разработчиков новых языков программирования, в настоящее время нельзя быть уверенным, что программы, написанные на любом из них, будут широко востребованы хотя бы в течение ближайших 3—5 лет. Поэтому необходимо признать тот факт, что еще долгое время пользователи будут вынуждены видоизменять свои программы, подстраивая их под особенности компьютеров. Это обстоятельство заставляет думать о том, как облегчить такой труд. Но прежде всего нужно понять, в каком же направлении следует думать.

Начиная с 60-х годов прошлого столетия увеличение быстродействия компьютеров определяется не столько уменьшением тактового периода элементной базы, сколько принятием новых решений в архитектуре вычислительных систем. При этом ускорение вычислений достигается за счет отображения характерных особенностей программ и алгоритмов в аппаратуре. Уже на раннем этапе были подмечены локальность счета и частое использование лишь небольшого числа данных, выделены основные элементы программ — циклы, ветвления, процедуры и т. п. Это сразу нашло отражение в буферах команд и регистрах, кэш-памяти, аппаратурной организации стека и во многом другом. Одновременно решалась и задача выравнивания скоростей работы различных узлов вычислительных систем (вспомните 1-й закон Амдала как одно из следствий утверждения 2.4. Одни аппаратур-

Глава 6. Тонкая информационная структура программ

321

ные решения практически не требовали программной поддержки (кэшпамять), другим необходима динамическая поддержка (виртуальная память), а третьим было достаточно предварительного распределения работы на этапе компиляции после проведения статического анализа программ (прямо адресуемые регистры). Во всем этом проявлялась вполне определенная тенденция: характерные особенности вычислений рано или поздно находили свое отражение в архитектурных особенностях компьютеров, а дополнительные аппаратурные возможности стимулировали развитие новых алгоритмов. В конечном счете задачи решались более эффективно.

Совсем не просто выделить характерные особенности вычислений и доказать, что они требуют аппаратурной поддержки. Не всегда легко оценить и аппаратурные новшества. В связи с этим приведем два примера. В § 4.4 было рассмотрено решение систем линейных алгебраических уравнений с левой треугольной матрицей методом обратной подстановки с порядком суммирования по возрастанию и убыванию индексов. Напомним, что оба алгоритма имели принципиальные различия в свойствах параллельности вычислений. Однако будет совсем не правильно считать характерным свойством проявления параллелизма именно суммирование в порядке возрастания индексов. Ведь если рассмотреть аналогичную задачу с правой треугольной матрицей, то все будет наоборот. Другой пример. В 1953 г. была введена в эксплуатацию отечественная вычислительная машина "Стрела", созданная под руководством известных конструкторов Ю. Я. Базилевского и Б. И. Рамеева. Наряду с обычными машинными командами она имела и так называемые групповые команды. Они позволяли достаточно просто записывать группы операций над содержимым ячеек памяти, номера которых представляли арифметические прогрессии. Исполнялись групповые команды в среднем несколько быстрее, чем те же группы команд, оформленные программно. Однако это ускорение достигалось не за счет использования конвейерности вычислений, а за счет аппаратурной поддержки организации соответствующих циклов. Если бы в то время математики смогли разглядеть в групповых операциях то, что теперь называется векторными операциями, и доказать, что они отражают характерные особенности вычислений, вполне возможно, что первые векторные компьютеры появились бы значительно раньше. Не говоря уже о том, что значительно раньше началось бы внедрение идей параллелизма и конвейерности в разработку новых численных методов. Но групповые операции не получили тогда должного развития. Время было упущено.

В период безраздельного господства однопроцессорных компьютеров интерес к выявлению особенностей вычислительных процессов со стороны как инженеров, так и математиков был исключительно эпизодическим и не касался фундаментальных основ строения алгоритмов и программ. Все изменилось с появлением вычислительных систем параллельной архитектуры. Эти системы потребовали совсем иной организации вычислений, обобщен-

322

Часть II. Параллельное программирование

но называемой теперь "параллельными вычислениями". Очень скоро стало ясно, что имеющихся знаний недостаточно для обеспечения эффективного функционирования новой техники. Этому были свои причины.

В течение нескольких десятилетий концепция однопроцессорных компьютеров обращала внимание разработчиков алгоритмов и программ только на две характеристики, связанные с вычислительной техникой, — это общее число операций и объем требуемой памяти. Даже такой важный фактор, как влияние ошибок округления, чаще всего в конкретных разработках выпадал из сферы внимания. Что же касается структурных свойств алгоритмов, например, таких как модульность, то их изучение так и не вышло из зачаточного состояния. Все это в конечном счете привело к тому, что к моменту широкого внедрения параллельных вычислительных систем в практику решения больших задач вычислительная математика оказалась без нужного багажа знаний. Без нужного багажа знаний оказались и смежные науки, в частности, связанные с разработкой алгоритмических языков, компиляторов и архитектуры вычислительных систем.

Можно возражать против таких выводов. Но, подбирая аргументы, давайте перечислять не только достижения. Давайте задавать вопросы, на которые не можем найти ответы. Попробуем докопаться до причин, мешающих их получить. И тогда станет ясно, как мало мы знаем в области параллельных вычислений.

О том, что в этой области действительно имеются серьезные проблемы, говорят и такие факты. Количество работ, посвященных распараллеливанию, на текущий момент исчисляется тысячами. Однако до сих пор не так уже много ясности в том, что же реально сделано, как это можно использовать, где узкие места и что надо делать дальше. Конечно, создано программное обеспечение для конкретных параллельных систем. Однако появление новых систем снова приводит к необходимости пересматривать методы и программы. Созданы компиляторы для новой техники. Но по общему признанию работают они не очень эффективно и полученные с их помощью программы не позволяют полностью использовать возможности параллельных систем.

Некоторую завесу над причиной многочисленных трудностей приоткрывает работа [67]. В ней на большом фактическом материале авторы проанализировали методы выявления параллелизма, заложенные в компиляторы для параллельных вычислительных систем начала 90-х годов прошлого столетия. Оказалось, что сфера применения каждого из методов очень узка. В целом же при анализе индексных выражений компиляторы "спотыкаются" примерно в 85% случаев. Это говорит о том, что при несомненных достижениях в вопросах конструирования высокопроизводительных параллельных систем того времени технология организации на них самих вычислительных процессов была на относительно низком уровне.

Глава 6. Тонкая информационная структура программ

323

С тех пор прошло более 10 лет. За это время появилось много новых идей как в распараллеливании вычислений, так и в организации параллельных процессов. Но ситуация в общем изменяется мало. Для пользователя она скорее даже ухудшается. Языки программирования становятся зависящими от особенностей архитектур вычислительных систем и начинают приобретать черты языков низкого уровня. Например, такие языки, как PVM и MPI по существу уже являются коммуникационными автокодами, хотя и на макроуровне. На пользователя все в большей степени перекладывается забота об эффективности организации вычислительных процессов, включая обнаружение в программах и алгоритмах необходимых свойств параллельности и коммуникационных свойств.

Постоянная нехватка должной поддержки со стороны языков программирования, компиляторов и операционных систем в обеспечении эффективности процессов решения задач привела к созданию специализированных программных комплексов по анализу пользовательских программ и их преобразованию под требования конкретных параллельных языков программирования и собственно паралельных вычислительных систем. Эти комплексы реализуются на автономных компьютерах и не связаны с компиляторами целевых вычислительных систем. Поэтому на них могут быть реализованы самые передовые методы исследования и преобразования программ. Представляя собою автономные программные системы, указанные комплексы оказались удобным инструментом для выполнения различных работ, когда программы одного вида нужно перевести в эквивалентные программы другого вида. Среди зарубежных автономных систем наиболее известна система Parafrase и созданная на ее основе серия пакетов КАР [47, 52, 58], а также система Forge [62]. Среди отечественных — система V-Ray [65].

Работа с автономными системами по исследованию и преобразованию пользовательских программ выявила ряд интересных обстоятельств. Во-первых, с помощью таких систем можно значительно уменьшить время реализации программ на параллельных вычислительных системах. По сравнению с тем временем, которое показывают программы, пропущенные через штатные компиляторы без предварительной оптимизации, почти всегда удается получать ускорение в несколько раз. Ускорение удается получать даже в тех случаях, когда программы предварительно оптимизируются вручную. Как правило, оно тем больше, чем больше и сложнее исходные пользовательские программы. Во-вторых, для достижения предельно возможного ускорения приходится применять существенно более сложные методы исследования и преобразования программ, чем те, которые традиционно включаются в компиляторы. Сейчас они настолько сложны, что об их ручном применении не может быть и речи. Однако для компьютерного и, тем более, автономного использования эти методы вполне приемлемы. И, наконец, работа с автономными системами отчетливо высветила тот факт, что для успешного освоения

324

Часть II. Параллельное программирование

вычислительных систем параллельной архитектуры пользователям необходимо иметь возможность получать самые подробные сведения о самых различных деталях структуры своих алгоритмов и программ.

Настоящая глава посвящена фундаментальным основам построения методов для получения и использования таких сведений. Эти основы связаны с изучением тонкой информационной структуры алгоритмов и программ, другими словами, информационных связей на уровне отдельных операций или отдельных срабатываний отдельных операторов. В обсуждении затрагиваемых вопросов мы не будем следовать исторической линии, а изложим свою собственную концепцию. На наш взгляд, она достаточно четко построена и впитала в себя лучшее из разрозненных результатов и идей, полученных к настоящему времени. Эта концепция является тем стержнем, опираясь на который, можно оценить место каждого конкретного результата или идеи и понять, как все они связаны друг с другом.

Развивая наши исследования, мы будем уделять особое внимание анализу записей алгоритмов с помощью математических соотношений и в виде программ на последовательных языках. Объясняется это тем, что именно в этих формах записана большая часть мирового багажа алгоритмических знаний. К данному багажу приходится обращаться очень часто и не только в связи с освоением вычислительной техники параллельной архитектуры. Поэтому всегда полезно знать о нем как можно больше. Наш основной интерес будет связан, конечно, с анализом этого багажа с точки зрения выявления возможностей лучшей организации параллельных вычислительных процессов. Проводя анализ, мы будем формально изучать только тексты программ и описывающие алгоритмы математические соотношения и без особых оговорок не будем использовать какие-либо дополнительные сведения.

§ 6.1. Графовые модели программ

В главе 4 мы уже касались вопроса использования математических моделей для изучения некоторых явлений. Модели возникают естественным образом, если по каким-либо причинам явления не поддаются точному описанию, по крайней мере, на момент исследования. Почти всегда это имеет место при изучении природных явлений. В этом случае модель впитывает в себя имеющиеся сведения о конкретном явлении, а детальное ее изучение позволяет обнаруживать либо новые черты явления, либо факты несоответствия модели явлению. Однако нередко возникают другие ситуации, когда об изучаемом явлении или объекте вроде бы должно быть известно все, т. к. оно описано абсолютно точно. Тем не менее, и в этих случаях приходится использовать модели. Только теперь они вводятся не из-за нехватки сведений, касающихся описания, а по иным причинам. Например, если само описание очень сложно с точки зрения применяемого аппарата исследова-

Глава 6. Тонкая информационная структура программ

325

ний, или требуется найти какой-либо простой критерий, характеризующий некоторое свойство, или когда, вообще, не очень ясно, что придется исследовать в будущем, а аппарат исследований надо создавать уже сегодня, и т. п. Конечно, как сами модели, так и уровни их сложности могут быть самыми разными. Но в данной ситуации считается обязательным выполнение следующего требования: если какое-то искомое свойство обнаружено в модели, то оно же должно присутствовать и в изучаемом явлении или объекте, возможно, с какой-то известной или проверяемой точностью. Типичным примером такой ситуации является случай, когда явление приближенно описывается моделью, представляющей систему дифференциальных уравнений, а эта модель, в свою очередь, аппроксимируется моделью, представляющей систему алгебраических уравнений.

Нашей ближайшей целью является рассмотрение моделей для программ на последовательных языках программирования. Как объекты исследований программы описаны абсолютно точно. Но даже с точки зрения их реализации на однопроцессорных компьютерах возникает много вопросов, ответы на которые не видны из текста программ. Например, как провести такую реорганизацию программы, чтобы минимизировать число используемых переменных, наилучшим образом использовать кэш-память, минимизировать число обменов с медленной памятью и др. При выявлении в программах скрытого параллелизма и свойств, необходимых для эффективного его использования, вопросов возникает еще больше.

Эти и подобные им вопросы связаны со знанием явных или скрытых свойств программы, определяющих ее строение или, как говорят иначе, ее информационную структуру. Мы будем считать, что информационная структура программы есть совокупность сведений о том, как отдельные элементы программы связаны между собой. Конечно, такое определение вряд ли можно назвать точным. Но его и нельзя существенно улучшить. Дело в том, что любой последовательный язык определяет некоторый класс алгоритмов, причем достаточно широкий. Программа на этом языке есть не что иное, как запись одного из алгоритмов. Понятие алгоритма является в математике первичным и его нельзя строго определить через другие понятия. Поэтому нельзя в общем случае и строго определить, как устроены алгоритмы. Любая попытка "точнее" определить понятие структуры программы неизбежно будет связана с сужением множества изучаемых ее свойств.

В основе изучения информационной структуры программ уже давно сформировались два подхода. Первый называется денотационным и опирается на исследование состояния памяти программ. В практических приложениях он используется редко. По этой причине мы его рассматривать не будем. Второй подход называется операционным. Исполнение (развитие) любой программы представляется в виде набора выполненных действий (операций), некоторым образом связанных между собой. Содержание действий, их вы-

326

Часть II. Параллельное программирование

числительная мощность и способ связи в рамках данного подхода не фиксируются. Они определяются в каждом конкретном случае по-своему в зависимости от целей исследования. Операционный подход в практических приложениях используется очень часто. Более того, он очевидным образом порождает класс моделей программ, называемых графовыми. В этом классе каждая модель представляет граф, в котором вершины соответствуют каким-то множествам действий программы, а дуги (ребра) так или иначе связаны с отношениями между ними. Диапазон уровней сложности графовых моделей огромен. Отдельная вершина может представлять и программу целиком, и какие-то ее большие или малые фрагменты и даже отдельные элементарные операции. И на все это накладывается многообразие связей. С такими моделями мы будем иметь дело в настоящей главе.

Опираясь на аксиоматику операционного подхода, в любой программе можно выделить два типа действий, которые, следуя [27], будем называть преобразователями и распознавателями. Преобразователи осуществляют переработку информации, а распознаватели определяют последовательность срабатываний преобразователей в процессе работы программы. Первому типу действий соответствуют, например, операторы присваивания. Их левая часть определяет область памяти программы, подвергающейся воздействию преобразователя, а переменные из правой части показывают на необходимые для выполнения данного действия аргументы. Второму типу действий в программе отвечают альтернативные операторы: условные, разного рода переключатели и т. п. Основное их назначение состоит в выборе одной из нескольких возможных альтернатив дальнейшего следования.

Везде далее будем предполагать, что множества операторов, соответствующих этим двум типам действий, не пересекаются. В реальных программах это не всегда так. Условное выражение альтернативного оператора вправе содержать вызов функции, которая помимо выполнения своих внутренних действий может иметь побочный эффект, влияющий на дальнейший ход развития программы. Другим примером может служить оператор присваивания, правая часть которого содержит в качестве терма условное арифметическое выражение. Такие примеры в явном виде не допускают строгого деления на преобразователи и распознаватели. Однако с помощью очевидных элементарных преобразований, канонизирующих тексты программ, они могут быть приведены к нужной форме.

Рассмотрим иллюстративный пример, к которому будем обращаться несколько раз. Пусть решается система линейных алгебраических уравнений Ах = b с левой двухдиагональной матрицей порядка п. Обозначим через оь ..., а_п диагональные элементы матрицы А, через cj, ..., с„ — ее поддиаго-нальные элементы, через by, ..., b„ — правые части, через х\, ..., х„ — координаты решения. Допустим, что необходимо найти максимальную коорди-

Глава 6. Тонкая информационная структура программ

327

нату вектора-решения. Соответствующий алгоритм может быть записан в следующем виде, например, на языке типа Fortran:

1 у = by/а_у

2 х=у

3 DO / = 2, n

4 х = (bj — срс)/ау (6.1)

5 if (x<y) go to 7

6 у =x

7 END DO

После выполнения программы значение переменной у будет равно максимальному из чисел х\, ..., х_п. Здесь операторы с метками 1, 2, 4, б являются преобразователями, операторы с метками з, 5, 7 — распознавателями.

Между действиями программы устанавливаются, как правило, два типа отношений. Первый тип определяется фактом выполнения одного действия непосредственно за другим. Если какие-либо два действия находятся в этом отношении, то будем говорить, что между ними установлена связь по управлению или операционная связь. Второй тип связан с использованием одним действием в качестве аргументов результатов выполнения других действий. Он определяет информационную связь. Оба типа отношений в общем случае вводят на множестве действий частичный порядок.

Каждому оператору исходной программы поставим в соответствие вершину графа — экземпляр преобразователя или распознавателя в зависимости от типа оператора. Получим множество вершин, между которыми согласно исходной программе определим отношение, соответствующее передаче управления. Если текст программы допускает выполнение одного оператора непосредственно за другим, то соответствующие вершины соединим дугой, направленной от предшественника к последователю. Получим граф, который обычно называется графом управления, управляющим графом, графом передач управления или просто графом программы [27]. Его основным свойством является независимость от входных данных программы. Множества вершин и дуг для каждой программы фиксированы и образуют единственный граф. Этот граф задает одну из моделей программы. На рис. 6.1 он представлен для примера (6.1).

•--------*т--------*+--------*ш--------*■

12 3 4 5 6 7

Рис. 6.1. Управляющий граф

328

Часть II. Параллельное программирование

Отталкиваясь от графа управления, можно получить другие модели программ. Если забыть о конкретном содержании каждой вершины и обозначить ее просто некоторым символом, то получим схему Мартынюка. Если, кроме этого, каждому входу и выходу оператора (аргументу и результату) сопоставить символы переменных (ячеек памяти), то схема Мартынюка преобразуется в схему Лаврова. Схемы Мартынюка очень часто используются при оптимизирующих преобразованиях программ, т. к. являются удобным средством исследования их логической структуры. С помощью схем Лаврова удалось, например, найти решение задачи минимизации числа переменных.

Теперь предположим, что каким-то образом мы определили начальные данные программы и наблюдаем за ее выполнением на обычном последовательном вычислителе. Каждое срабатывание каждого оператора (а оно необязательно будет единственным) будем фиксировать отдельной вершиной. Получим множество, которое количественно почти всегда будет отличаться от множества вершин графа управления. В отличие от графа управления, в данном случае порядок непосредственного срабатывания операторов можно определить точно. Соединив вершины дугами передач управления, получим ориентированный граф, носящий название операционно-логической истории программы [27]. Он представляет единственный путь от начальной вершины к конечной. По существу это не что иное, как последовательность срабатывания преобразователей и распознавателей исходной программы при заданных входных данных. В операционно-логической истории от входных данных зависит практически все: общее число вершин, количество вершин, соответствующих одному оператору, и даже набор присутствующих преобразователей и распознавателей. Граф управления свободен от подобных кон-кретностей. На рис. 6.2 представлена операционно-логическая история программы (6.1) для случая п = 3, Ъ\ = 0, Ь₂ = Ьт, = ау = а₂ — «з ⁼ ^с2 ⁼ ^сз ⁼ 1-

Рис. 6.2. Операционно-логическая история

На рис. 6.3 представлена операционно-логическая история той же программы (6.1), но для других входных данных п = 3, by = О, Ъ₂ = с₂ = — 1,

h = «1 = а₂ = а_ъ = с₃ = 1.

Рис. 6.3. Другие входные данные

Глава 6. Тонкая информационная структура программ

329

Преобразуем операционно-логическую историю следующим образом: все вершины, отвечающие одному оператору программы, объединим в одну с сохранением входных и выходных дуг и ликвидацией образующихся кратных дуг. Легко проверить, что полученный граф является подграфом графа управления программы, соответствующим конкретным входным данным. Объединяя подобным образом все операционно-логические истории программы вместе, мы можем, тем не менее, не получить всего графа управления. Такая ситуация является в некотором смысле вырожденной и говорит о плохом проектировании исходной программы. Однако на практике она вполне реальна. Объединяя графы на рис. 6.2, 6.3, мы получим граф на рис. 6.1.

Изменим графовую основу. Будем среди операторов принимать во внимание только преобразователи, а в качестве отношения между ними брать отношение информационной зависимости. Построим сначала граф, в котором вершины соответствуют операторам-преобразователям. Две вершины соединим информационной дугой, если между какими-нибудь срабатываниями соответствующих операторов теоретически возможна информационная связь. Полученный граф называется информационным графом программы [27]. Как и в случае графа управления информационный граф не зависит от входных данных. В нем могут быть "лишние" дуги, которые не реализуются либо при конкретных входных данных, либо совместно с другими дугами. Информационный граф также представляет одну из моделей программы. Но в отличие от графа управления эта модель применяется на практике очень часто. В частности, она использовалась в упоминавшихся ранее системе Parafrase и серии пакетов КАР. На рис 6.4 представлен информационный граф программы (6.1).

•---------->т----------£*£--------->т

12 4 6

Рис. 6.4. Информационный граф

Снова каким-то образом определим начальные данные программы и будем наблюдать за ее выполнением на последовательном вычислителе. Каждое срабатывание каждого оператора-преобразователя будем фиксировать отдельной вершиной. Соединив вершины дугами передач информации, мы получим ориентированный граф, называемый историей реализации программы [27]. На рис. 6.5, 6.6 представлены истории реализации программы (6.1) для случаев входных данных, соответствующих рис. 6.2, 6.3.

Объединив эти истории, мы получим информационный граф программы (6.1), представленный на рис. 6.4.

330

Часть II. Параллельное программирование


					• 2	4	• 6
				• 1
1	2	4	6	• 1

Рис. 6.5. История реализации

Рис. 6.6. Другие входные данные

Таким образом, мы имеем четыре основные графовые модели. Это — граф управления, информационный граф, операционно-логическая история и история реализации. Первые две модели не зависят от входных данных и строятся непосредственно по тексту программы. Две последние модели для своего построения формально требуют слежения за выполнением всех операторов. Понятно, что сложность построения моделей возрастает в порядке указанного перечисления. Первые две модели давно и успешно применяются на практике. Последние две модели до недавнего времени применялись, главным образом, в теоретических исследованиях, что связано, естественно, со сложностью их практического построения. Достоинством всех моделей является то, что они существуют для всех программ. На основе этих моделей можно строить различные смешанные модели, в которых одни фрагменты программы представляются информационным графом или графом управления, а другие — той или иной историей. Существуют преобразования, переводящие одни модели в другие [16].

Среди рассмотренных моделей как в теоретическом отношении, так и в отношении возможных перспектив практического применения наибольший интерес представляет история реализации программы. Зная эту модель, можно получить, наверное, любые сведения, касающиеся процессов реализации описанного программой алгоритма. Например, определить множества независимых друг от друга операций, найти подходящее распределение операций по процессорам вычислительной системы, обнаружить различные узкие места и т. п. Сказанное не покажется большим преувеличением, если обратить внимание на совпадение истории реализации программы с введенным в § 4.2 графом алгоритма. Конечно, имеется в виду алгоритм, описанный рассматриваемой программой. С некоторыми из задач вокруг графа алгоритма мы уже сталкивались ранее.

Чтобы на основе графа алгоритма решать какие-то задачи, необходимо иметь соответствующий аппарат. Граф алгоритма, как и история реализации программы, не подчеркивают в своих определениях какие-либо специфиче-

Глава 6. Тонкая информационная структура программ

331

ские особенности. Кажется, что мы должны их рассматривать как произвольные ориентированные ациклические графы. Действительно, любой такой граф может быть графом некоторого алгоритма, который при подходящем выборе языка программирования может быть описан некоторой программой. Но основной аппарат для решения задач с произвольными графами связан с перебором возможных вариантов. И главная цель выбора метода исследования состоит в минимизации числа переборов.

Допустим, что решается задача построения максимальной параллельной формы графа алгоритма. Если граф имеет m дуг, то легко предложить метод, дающий эту форму за число переборов порядка ш². Схема метода похожа на доказательство утверждения 4.1. С точки зрения теории графов это — хороший результат. Однако заметим, что исходный алгоритм реализуется на однопроцессорном компьютере за время, пропорциональное ш. Следовательно, время исследования параллельной структуры алгоритма будет намного превышать время его реализации. Ситуация оказывается значительно хуже, если рассмотреть задачу оптимального размещения операций по процессорам вычислительной системы. Согласно [25], наиболее интересные варианты этой задачи относятся к так называемым NP-полным задачам, для решения которых уже требуется выполнить порядка ш\ переборов.

Тратить столь большое время на исследование структуры алгоритма стоит только в том случае, если результаты исследования будут использоваться многократно. Но здесь нас поджидает еще одна неприятность. Снова напомним, что граф алгоритма в общем случае зависит от входных данных. В частности, от размеров используемых матриц, шагов сетки и т. п. Поэтому любое описанное исследование мы можем провести только для фиксированных значений входных данных. Различных значений входных данных, как правило, бесконечно много и заранее совсем не ясно, как результаты исследований при разных значениях входных данных связаны между собой. Все это, в конце концов, сводит на нет сколько-нибудь значимую возможность исследования графа алгоритма как произвольного графа. Возможно, что именно поэтому, возникнув достаточно давно, такое понятие, как история реализации программы, долгое время не могло превратиться в конструктивный инструмент изучения структуры алгоритмов и программ.

Но правомерно ли все-таки всегда граф алгоритма и, соответственно, историю реализации программы рассматривать как произвольные графы? Если допустить, что граф алгоритма является произвольным, то записать алгоритм можно, лишь записав независимо друг от друга все операции и связи между ними. Длина записи в этом случае окажется пропорциональной числу операций. В практической деятельности не приходится иметь дело с большими алгоритмами подобного рода, в первую очередь, именно потому, что их невозможно записать в компактном виде. Поэтому используемые в действительности алгоритмы нельзя отнести к произвольным. Они обладают рядом характерных отличий, связанных с существованием периодически

332

Часть II. Параллельное программирование

повторяемых участков вычислений. Следовательно, есть основания предполагать, что изучая реальные алгоритмы и выделяя их специфику, удастся избежать при исследовании структуры алгоритмов NP-сложности больших дискретных задач. NP-сложность — это та реальная опасность, которая может возникнуть при неудачном выборе метода исследований.

В §4.4 мы рассмотрели несколько примеров графов простых алгоритмов. Все они в той или иной мере оказались устроенными регулярно. Поэтому, например, выявить в них параллелизм удалось легко. Вся эта регулярность и легкость связана только с тем, что вершины графа алгоритма были расположены не хаотически в каком-то случайном пространстве, а в том пространстве и в тех его точках, которые задавали множества индексов, используемых для описания алгоритмов. Если бы вершины графов даже таких простых примеров были расположены беспорядочно, то вряд ли в них удалось бы разглядеть хотя бы какой-нибудь параллелизм.

Понимание того, что для эффективного изучения структуры алгоритмов и программ необходима более тесная связь графовых моделей с формами записи алгоритмов, пришло довольно давно. Однако разнообразие возникающих идей было невелико. Все они "крутились" вокруг следующих положений:

□ необходимо изучать структуру на уровне отдельных операций;

□ для успешного изучения структуры необходимо согласовывать размещение вершин графов с множеством индексов, используемых для описания алгоритма;

□ необходимо научиться как можно точнее определять по тексту программы информационные связи между отдельными операциями.

Одними из первых работ, затрагивающих эти положения, были работы Л. Лампорта [55, 56]. Объектом исследований в них были тесно вложенные циклы на языке Fortran. Здесь впервые введено новое понятие "пространство итераций". Это есть множество целочисленных точек, координаты которых совпадают с координатами допустимых значений параметров циклов тесно вложенного гнезда. Именно в этих точках надо размещать операции, представляющие отдельные срабатывания тела гнезда циклов. Тем самым по существу была предложена модель "координатного" размещения истории реализации программ. Важным моментом явилось также то, что было продемонстрировано достоинство такого размещения. Предложенные в работах методы координат и гиперплоскостей оказались настолько удобными для проведения аналитического изучения параллелизма, что были включены в ряд параллелизующих компиляторов для преобразования тесно вложенных гнезд циклов к "параллельному" виду.

Несмотря на сказанное, работы Л. Лампорта имели скорее методологическое, чем практическое значение. Они убедительно показали, в каком направлении следует двигаться в исследовании структуры алгоритмов и про-

Глава 6. Тонкая информационная структура программ

333

грамм, но уровень продвижения был не очень большим. Тесно вложенные гнезда циклов представляют очень узкий класс программ, которые даже в качестве фрагментов встречаются не так уж часто. Но для них все понятия имеют прекрасные геометрические интерпретации. Собственно говоря, эти интерпретации и являются зерном работ и составляют, на наш взгляд, основную их ценность. К сожалению, "геометрия" тесно вложенных гнезд циклов не распространяется непосредственно на более сложный класс программ. Затруднение вызывает даже распространение такого простого понятия, как пространство итераций, не говоря уже о более сложных понятиях типа гиперплоскости. Аналитическая часть работ Л. Лампорта является слабой. Все доказанные утверждения, в том числе, относящиеся к определению информационных связей между операциями, предполагают достаточно жесткие ограничения на тело исследуемых циклических конструкций.

Трудности определения информационных связей между операциями по тексту программы привели к появлению большого числа работ, связанных с графовыми моделями иного типа, называемыми графами зависимостей. В этих моделях отношение информационной связи заменяется значительно более широким отношением зависимости. Именно, две операции или два оператора называются зависимыми, если при их выполнении имеют место обращения к одной и той же переменной (ячейке памяти). Так как информационная связь также реализуется через обращение к одной переменной, то ясно, что она есть частный случай зависимости. Очевидно, что устанавливать факт зависимости значительно проще, чем факт информационной связи. Во всех этих моделях мы, как правило, имеем дело только с операторами-преобразователями .

В примере (6.1) имеются две изменяемые переменные х а у. Если в качестве вершин графа зависимостей взять операторы-преобразователи с метками 1, 2, 4, б, то получим граф, представленный на рис. 6.7.

12 4 6

Рис. 6.7. Общий граф зависимостей

Как и положено, информационный граф на рис. 6.4 является его подграфом. Обратим внимание на то, что переменные х и у в примере (6.1) в разных операторах играют разную роль: где-то они определяют аргументы, где-то результат. На рис. 6.7 разделение ролей не отмечено. К этому вопросу мы еще вернемся.

334

Часть II. Параллельное программирование

Как и в рассмотренных ранее моделях многое зависит от того, представляют ли вершины графов зависимостей операторы или отдельные срабатывания операторов. Допустим, что осуществляется суммирование чисел О], ..., a_n. Один из алгоритмов последовательного суммирования записывается так:

15 = 0

(6.2)

DO / = 1, И

2 s = s + а,

END DO

Если построить граф зависимостей, в котором вершины являются операторами, то поскольку имеется только одна изменяемая переменная s, он будет таким, как на рис. 6.8.

Построим теперь для примера (6.2) граф зависимостей, считая вершины отдельными срабатываниями операторов. Для п = 4 он представлен на рис. 6.9.


/-	^==		~^Г^	Ч
/-	^==	*S^⁵**	~^Г^	Ч
0	1	"==г	*-•**	4
0	1	2	3	4

Рис. 6.8. Зависимость между операторами

Рис. 6.9. Зависимость между операциями

Заметим, что в вершину с номером п входит п дуг, в вершину с номером я — 1 входит л — 1 дуг и т. д. Большое число входящих дуг в графах зависимостей в общем случае оказывается платой за легкость проверки выполнения отношения зависимостей. Об этом мы также будем еще говорить. А пока данный факт только отметим.

Одной из первых работ, в которой достаточно четко описывается понятие зависимости и его использование для преобразования программ, является работа [60]. Всего предложено достаточно много графов зависимостей. Они отличаются друг от друга различием типов анализируемых программ — от тесно вложенных гнезд циклов до программ общего вида, разнообразием содержания вершин — от операторов программы до отдельных их срабатываний или, другими словами, до отдельных операций, а также разнообразием видов и количеств описывающих зависимости дуг. Некоторые из графов зависимостей активно использовались в параллелизующих компиляторах.

Близко к графам зависимостей стоит граф влияния [6]. Будем говорить, что одна операция влияет на другую, если изменением значения переменной, которую вычисляет первая операция, можно изменить значение перемен-

Глава 6. Тонкая информационная структура программ

335

ной, которую вычисляет вторая операция. Построим ориентированный граф. Будем считать операции вершинами графа. Соединим дугой каждую из пар вершин, в которых одна из соответствующих им операций влияет на другую. Пусть направление дуги совпадает с направлением влияния. Такой граф и будем называть графом влияния. Для примера (6.2) граф влияния при п = 4 совпадает с графом зависимостей на рис. 6.9. Но в общем случае эти графы различны. Отношения управления, информационной связи и зависимости не являются транзитивными. В отличие от них отношение влияния транзитивно. За исключением вырожденных случаев история реализации программ есть остовный подграф графа влияния. Более того, граф влияния оказывается транзитивным замыканием истории реализации. Сама же история реализации по отношению к графу влияния представляет его минимальный по числу дуг подграф, обладающий следующим свойством: в обоих графах любые две вершины либо связаны путем, либо не связаны одновременно. К подобным минимальным графам мы будем обращаться постоянно. История реализации программы (6.2) представлена на рис. 6.10.

•------*•------**------>•------*•

12 2 2 2

Рис. 6.10. Минимальный граф зависимостей

Как мы уже неоднократно отмечали, среди графовых моделей история реализации программы наиболее интересна. Понятно, что она также является одним из графов зависимостей. Поэтому исследования графов зависимостей вроде бы должны были приближать к лучшему пониманию того, как в действительности устроена история реализации. Однако долгое время эти приближения были настолько грубыми, что в отношении истории реализации программы не удавалось получить никаких существенно новых сведений.

Для того чтобы установить самые интересные факты, касающиеся структуры алгоритма, необходимо исследовать его описания в терминах самых "мелких" операций, которые, тем не менее, все еще воспринимаются исследователями. В вычислительных задачах такими операциями, как правило, являются числовые операции умножения, сложения, деления и т. п. Для нас сейчас важно то, что все они имеют малое число аргументов. Обычно их один-два. Следовательно, в этих случаях история реализации программы должна обладать очень важным свойством. Именно, в каждую ее вершину входит конечное число дуг, не зависящее от общего числа вершин в истории. Общий недостаток большинства работ по графам зависимостей как в прошлом, так и сейчас заключается в том, что прямо или косвенно в них рассматриваются только такие ситуации, в которых число дуг, в среднем вхо-

336

Часть II. Параллельное программирование

дящее в одну вершину, не ограничивается сверху равномерно по входным данным и поэтому может быть очень большим. История реализации программы в подобных работах может изучаться, в основном, через ее погружение в большие графы. Но в графах, имеющих много лишних дуг, изучение свойств истории возможно лишь через какие-то достаточные критерии. При всей своей полезности область практического применения достаточных критериев весьма ограничена. С их помощью нельзя гарантировать выполнение многих условий, они не указывают пути преодоления узких мест, связанных с невыполнением критериев, и т. п.

Впервые общие принципы метода построения по тексту программы точной истории ее реализации были изложены в книге [9]. В этой книге история называлась решетчатым графом алгоритма. Детали метода описаны в работе [15] и книгах [10, 64], где история реализации программы уже выступает под именем графа алгоритма. В книгах [10, 11, 64] детально изучены алгебраические свойства графов алгоритмов. В книге [6] и работах [8, 12] описаны различные применения графа алгоритма. На основе разработанной методологии построения, исследования и применения графа алгоритма и связанных с ним других графов создана практически работающая автономная система V-Ray. С некоторыми результатами ее использования можно познакомиться в работе [65] и далее в этой книге.

Данная глава посвящена различным аспектам исследования программ, связанным с историями их реализаций. Мы будем называть всюду такие истории графами алгоритмов. Как уже отмечалось, формально между понятиями истории реализации программы и графа алгоритма, описанного той же программой, нет различий. Но нам кажется, что название "граф алгоритма" лучше отражает суть дела. Например, один и тот же алгоритм может быть описан на одном и том же языке разными программами. Соответствующие истории формально также будут разными, если для расположения вершин использовать один и тот же принцип. Однако как графы все истории изоморфны между собой. Следовательно, они скорее отражают не программы, а описываемый ими алгоритм. История реализации есть графовая модель программы. Слово "граф" в названии "граф алгоритма" подчеркивает это обстоятельство. Можно привести и другие аргументы в пользу использования названия "граф алгоритма".

Вопросы и задания

1. Что означает случай, когда в программе нет преобразователей? Имеют ли смысл такие программы?

2. Что означает случай, когда в программе нет распознавателей? Имеют ли смысл такие программы?

3. Как выглядят управляющие и информационные графы для пп. 1, 2?

Глава 6. Тонкая информационная структура программ

337

4. Что означает несвязность управляющего или информационного графа с точки зрения параллельных вычислений?

5. Может ли быть управляющий граф несвязным, а информационный граф связным и наоборот?

6. Докажите, что если информационный граф несвязный, то граф алгоритма также несвязный?

7. Верно ли аналогичное утверждение относительно управляющего графа?

8. Докажите, что если пересечение множеств переменных, находящихся в правых и левых частях преобразователей, пустое, то граф алгоритма также пустой, т. е. не имеет ни одной дуги.

9. Если граф алгоритма пустой, то означает ли это пустоту управляющего и/или информационного графа?

10. Приведите примеры, когда граф влияния не совпадает с графом зависимостей.

11. Приведите примеры, когда граф алгоритма связный, а граф влияния пустой.

§ 6.2. Выбор класса программ

По определению, граф алгоритма существует для любой программы. Как этого ни хотелось бы, трудно даже поверить в то, что удастся разработать эффективный метод его построения и исследования для любой программы. Поэтому можно лишь надеяться, что мы сможем указать достаточно широкий класс программ, для которого, в свою очередь, сможем выполнить все намеченное. Но прежде всего необходимо определиться с языком описания программ.

В качестве средства описания алгоритмов выберем подмножество языка Fortran. Этот выбор объясняется следующими соображениями. Мы будем изучать тонкую структуру алгоритмов на уровне связей между отдельными операциями. Тонкая структура весьма чувствительна к мельчайшим изменениям алгоритма. Например, уже отмечалось, что изменение порядка выполнения операций в пределах действия законов коммутативности, ассоциативности и дистрибутивности при точных вычислениях может очень сильно изменить результат, если реально операции приходится выполнять в условиях влияния ошибок округления. Поэтому порядок выполнения операций алгоритма должен быть описан максимально точно. Обязательность описания порядка присутствует в языках программирования. Этому условию удовлетворяет не один язык Fortran, но и такие популярные в настоящее время языки как С\С++ и ряд других. Дополнительным аргументом в пользу выбора языка Fortran является то, что именно на нем записана большая часть алгоритмического багажа в мире. Несмотря на многочисленные попытки разработчиков новых языков программирования "похоронить" язык Fortran, он продолжает активно использоваться до сих пор, особенно в сфере решения научно-технических задач. К тому же, этот язык близок по сво-

338

Часть II. Параллельное программирование

ей форме к математическим соотношениям, к которым мы планируем обратиться позднее. И, наконец, забегая несколько вперед, скажем, что будем использовать такое подмножество языка Fortran, которое с точностью до обозначений присутствует во всех языках программирования. В этих условиях выбор языка почти безразличен.

Однако совсем не безразличен выбор класса программ. Интуитивно ясно, что он должен существенно отличаться от тесно вложенных гнезд циклов. Но совсем не ясно, в какую сторону и насколько. Чтобы ответить на многочисленные вопросы, были собраны данные по реально используемым программам с помощью специальной системы статистического анализа [17]. В качестве объекта исследований был взят набор программ на Fortran, написанных для решения задач минимизации, линейной алгебры и математической физики. Суммарный объем выборки составил более 12 000 инструкций языка. В работе над исследуемыми программами, т. е. в их написании и отладке, принимало участие достаточно много людей из разных коллективов. Поэтому случайные отклонения, вызванные индивидуальными стилями программирования, не могли сильно повлиять на итоговую статистику. Статистика собиралась так, чтобы получить информацию о наиболее типичных конструкциях и частоте их появления. Кроме этого, на типичных конструкциях отрабатывалась и совершенствовалась методология анализа структуры программ. Вот некоторые из результатов.

□ Структура вхождений DO-циклов. Фиксировались все формы вложенности операторов DO (DO-циклов). Сложные конструкции дополнительно разбивались на составные части по их вложенности, которые также включались в общую статистику. Выяснилось, что тесно вложенных гнезд циклов всего около 7%, причем такие гнезда с вложенностью 3 и более не встречались ни разу. Учитывая популярность тесно вложенных гнезд в исследовательских работах, была дополнительно определена доля программ, в которых хотя бы просто содержались подобные гнезда. Результат оказался еще хуже. Это говорит о том, что методы, ориентированные только на тесно вложенные циклы, не будут иметь большой перспективы. Интересным оказалось то, что около 40% всех конструкций представляют собой циклы, в тело которых линейно входит большое число других циклических конструкций. В среднем около 5, а максимальная последовательность состояла из 19 конструкций. Примерно в 20% случаев отдельные срабатывания тел одиночных циклов оказались независимыми друг от друга только за счет несовпадения идентификаторов входов и выходов операторов.

□ Мощность и внешняя вложенность DO-циклов. Рассматривались все операторы цикла DO и для каждого определялись две характеристики, позволяющие хотя бы приблизительно оценить вклад фрагмента в общее время счета. Первая — внешняя вложенность. Она определяется глуби-

Глава 6. Тонкая информационная структура программ

339

ной погружения в другие циклы и равна числу циклов, охватывающих данный оператор. Вторая — мощность. Она равна максимальной глубине вложенности входящих в цикл операторов относительно рассматриваемого оператора DO. Мощность любого цикла не меньше единицы, в то время как внешняя вложенность может быть равной нулю. Проведенное исследование говорит о том, что реальные циклические конструкции не являются даже правильными гнездами и содержат по несколько других операторов цикла на каждом уровне. Например, в анализируемом материале имелось 119 циклов внешней вложенности 0 и мощности 2, но 280 циклов внешней вложенности 1 и мощности 1. Это значит, что для проведения эффективного анализа необходимо разрабатывать и использовать методы, умеющие исследовать совместное функционирование линейно расположенных циклических конструкций.

□ Количество максимально вложенных циклов. Была сделана попытка определить число наиболее критичных по времени счета мест в программе. Для этого сначала определялась мощность программы как наибольшая мощность ее циклических конструкций. Затем по каждой мощности определялась доля программ, имеющих 1, 2, 3 и более максимально вложенных циклов. Обнаружен довольно интересный факт — доля программ, содержащих более одного критического фрагмента, достаточно велика. В частности, среди программ мощности 3 свыше 20% имеют 6 и более циклических конструкций максимальной вложенности.

□ Структура тел внутренних циклов. Исследовалось, какие типы операторов входят в самые внутренние циклы, т. е. циклы мощности 1. Статистика собиралась раздельно по циклам с различной внешней вложенностью, чтобы выявить структуру наиболее значимых по времени счета фрагментов. Обнаружено, что с ростом глубины вложенности заметно растет доля циклов, тела которых содержат только операторы присваивания. Например, для циклов глубины вложенности 1 эта доля составляет 73%, для циклов глубины вложенности 3 — 93%. Следовательно, циклическим конструкциям с телами циклов, состоящими только из операторов присваивания, необходимо уделять особое внимание.

П Структура вхождения альтернативных операторов. Альтернативные операторы осуществляют выбор дальнейшего действия в зависимости от выполнения некоторого условия. В статистике учитывались условные операторы, вычисляемый переход и переход по предписанию. Проверялось, задают ли альтернативные операторы ветвления в рамках тела данного цикла или же возможен побочный выход из цикла и соответственно прекращение его выполнения. Одновременно определялось, насколько часто в программах встречались безусловные фрагменты. Важным выводом является то, что относительно немного циклов имеют побочный выход. Это дает уверенность в их хорошей исследуемости.

340

Часть II. Параллельное программирование

Выбирая класс анализируемых программ, приходится решать две противоречивые задачи. С одной стороны, хотелось бы его взять как можно более широким, с тем чтобы он покрывал значительную часть, а в идеале даже все практически встречающиеся программы или их наиболее значимые фрагменты. С другой стороны, чем шире класс программ, тем меньше надежды на то, что для любой его программы удастся провести одинаково глубокий анализ. Умение, граничащее с искусством и удачей, состоит в нахождении "золотой середины". Проведение только что описанного статистического анализа как раз и было направлено на ее поиск. После некоторых как удачных, так и неудачных попыток было решено класс анализируемых программ сделать двухуровневым. Первый или базовый уровень образует строго описанный так называемый линейный класс. Для любой его программы проводится самый тщательный анализ информационной структуры. Второй уровень открытый. В него входят все программы, которые каким-либо способом сводятся к программам базового уровня.

Всюду в дальнейшем, если не сделано специальных оговорок, будем считать, что алгоритм записан с помощью следующих средств языка:

□ в программе может использоваться любое число простых переменных и переменных с индексами;

□ единственным типом исполнительного оператора может быть оператор присваивания, правая часть которого есть арифметическое выражение; допускается любое число таких операторов;

□ все повторяющиеся операции описываются только с помощью циклов DO; структура вложенности циклов может быть произвольной; шаги изменения параметров циклов всегда равны +1; если у цикла нижняя граница больше верхней, то цикл не выполняется;

□ допускается использование любого числа условных и безусловных операторов перехода, передающих управление "вниз" по тексту; не допускается использование побочных выходов из циклов;

□ все индексные выражения переменных, границы изменения параметров циклов и условия передачи управления задаются, в общем случае, неоднородными формами, линейными как по параметрам циклов, так и по внешним переменным программы; все коэффициенты линейных форм являются целыми числами;

□ внешние переменные программы всегда целочисленные, и вектора их значений принадлежат некоторым целочисленным многогранникам; конкретные значения внешних переменных известны только перед началом работы программы и неизвестны в момент ее исследования.

Программы, удовлетворяющие описанным условиям, будем называть линейными или принадлежащими линейному классу. Они и будут предметом

Глава 6. Тонкая информационная структура программ

341

всех наших исследований. Особая специфика записи операторов не нужна. Если требуется приблизить форму записи алгоритмов к математической, то будем писать индексы переменных так же, как в математических соотношениях, т. е. справа от переменной снизу и/или сверху. Если же нужно анализировать фрагменты конкретных реальных программ, то будем брать их такими, какие они есть. При этом, возможно, придется использовать прямые заглавные буквы, писать индексы рядом в скобках и т. д.

Здесь уместно сделать одно замечание относительно терминологии. Обычно под переменной с индексами понимается весь массив простых переменных, объединенных общим идентификатором. При изучении тонкой структуры программы такая "групповая" переменная очень неудобна. Гораздо удобнее рассматривать массив как группу простых переменных, идентификаторы которых составлены из идентификатора массива и индексов. Всюду в дальнейшем мы будем понимать под переменной с индексами отдельный элемент массива, а не весь массив.

Как показывает статистика, многие значимые фрагменты практически используемых программ непосредственно принадлежат линейному классу. По своему выбору линейный класс не претендует на особую широту, хотя даже он намного перекрывает все типы программ, которые изучаются в рамках аналогичных подходов. Далее будет показано, что линейный класс может быть исследован полностью. Кроме этого, в главе 8 мы установим, что существуют многочисленные приемы, позволяющие сводить к линейным фрагменты программ, формально не принадлежащие к линейному классу. Согласно статистике, учитывая все такие приемы, удается привести к линейному классу более 90—95% текста практически используемых программ. В целом среди программ на последовательных языках линейный класс играет примерно такую же роль, как линейная алгебра в численных методах, линейное программирование в экстремальных задачах, линейные задачи математической физики в нелинейных процессах и т. п.

Наша ближайшая цель будет состоять в изучении информационной структуры программ из линейного класса, опираясь только на анализ текста программ, без привлечения каких-либо дополнительных сведений как о самих программах, так и об описанных ими алгоритмах. Такой подход к изучению программ называется статическим. Его основное достоинство заключается в том, что вся информация о структуре программы получается до ее реализации и, следовательно, может быть использована наиболее эффективно. Главная трудность проведения статического анализа связана с тем, что тексты программ почти всегда зависят от внешних переменных, значения которых не известны. Поэтому все исследования приходится проводить для параметризованных объектов.

342

Часть II. Параллельное программирование

Вопросы и задания

1. Рассмотрите любой известный вам язык программирования. Как на этом языке описывается линейный класс программ?

2. Приведите различные примеры программ, которые формально не являются линейными, но становятся таковыми после каких-то эквивалентных преобразований.

3. 'Пусть программа содержит вызовы процедур. Предложите различные способы замены этих вызовов программными фрагментами, при которых исходная программа становится линейной и сохраняет все прежние информационные зависимости.

4. Приведите различные примеры программ, которые формально не являются линейными и которые вы не можете привести к линейным с помощью эквивалентных преобразований.

5. Как выглядят графы алгоритмов для примеров п. 4?

6. Насколько различны графы алгоритмов для примеров п. 4?

7. Как часто примеры п. 4 встречались в вашей практике?

§ 6.3. Графы зависимостей и минимальные графы

Прежде всего необходимо точно описать множество вершин. Пусть задана произвольная линейная программа. Перенумеруем подряд сверху вниз все операторы циклов do, точнее, все параметры циклов. Обозначим параметры через /], ..., 1_П. Будем считать, что из двух параметров младшим (старшим) является тот, у которого номер меньше (больше). Перенумеруем также сверху вниз все операторы присваивания и обозначим их через F]_, ..., F_m.

С каждым оператором присваивания свяжем тесно вложенное гнездо циклов. Его можно получить, оставляя в программе только те циклы do, в тела которых входит рассматриваемый оператор. Будем называть такое гнездо циклов опорным для данного оператора. Пусть опорное гнездо оператора F_tописывается параметрами /,- , ...,/,- . Рассмотрим арифметическое простран-

1 .V/

ство, координаты точек которого совпадают со значениями этих параметров. Его размерность равна Sj. Назовем такое пространство опорным. Если оператор не входит ни в какое гнездо, то размерность опорного пространства будем считать равной 0. Не ограничивая существенно общности, можно предполагать, что отдельный оператор описывается гнездом циклов, у которых нижние и верхние границы изменения каждого из параметров совпадают. Такое предположение позволяет приписать какие-то параметры даже отдельным операторам.

Границы изменения параметров циклов опорного гнезда определяют в опорном пространстве линейный многогранник. Будем называть его опорным для

Глава 6. Тонкая информационная структура программ

343

оператора /} и обозначать V_t. Ветвления, определяющие условия срабатывания оператора F_h вырезают из опорного многогранника некоторую область. Принимая во внимание целочисленность параметров циклов, эту область можно описать конечным числом замкнутых линейных многогранников. Будем ее

также называть опорной и обозначать V',•. По определению V, с V и Совокупность опорных областей V',• для / = 1, 2, ..., m назовем линейным пространством итераций. Это есть многосвязная область, состоящая из линейных многогранников, принадлежащих разным арифметическим пространствам. Факт, что некоторые или даже все многогранники могут порождаться одними и теми же параметрами циклов, не имеет сейчас никакого значения. Это будет отражаться лишь в том, что такие многогранники будут в чем-то похожи по расположению в своих пространствах и иметь какие-то размеры одинаковыми. По определению линейной программы каждый из параметров пробегает некоторое множество целочисленных значений с шагом +1. Назовем точку линейного пространства итераций целочисленной, если все ее координаты являются целыми числами. Совокупность всех целочисленных точек линейного пространства итераций назовем просто пространством итераций.

Подчеркнем, что границы изменения параметров циклов и условия ветвления могут зависеть от внешних переменных. Поэтому размеры всех многогранников и их конфигурации могут зависеть от значений этих переменных. Как правило, с ростом значений переменных размеры многогранников неограниченно увеличиваются. Это является характерной чертой пространства итераций.

Будем называть реализацию оператора F_t при конкретных значениях параметров циклов / ,•,...,/,• срабатыванием или итерацией. Для линейных

программ сложность оператора F_t не зависит от значений внешних переменных. Обычно она невелика. Поэтому множество операций, реализуемых программой, однозначно определяется множеством всех срабатываний всех операторов /}. Совокупность всех реализаций всех операторов, относящихся к одному значению параметра какого-то цикла, будем называть итерацией цикла.

Каждому срабатыванию оператора F_t при конкретных значениях параметров циклов I/ , ..., Ij поставим в соответствие точку пространства итераций из

области Vi с теми же значениями координат /₍- , ..., /₍- . Тем самым уста-

навливается взаимно однозначное соответствие между пространством итераций и множеством всех срабатываний всех операторов программы. Принимая во внимание структуру отдельных срабатываний, мы получаем отображение на пространство итераций множества всех исполняемых операций. Заметим, что все точки одной области V',• и только они соответствуют срабатываниям одного оператора /}.

344

Часть II. Параллельное программирование

Строя в дальнейшем какие-то графы на множестве операций программы, мы будем всегда в качестве множества вершин брать пространство итераций. Вершины будем называть точками или векторами.

Каждая линейная программа задает множество исполняемых операций. При реализации программы операции выполняются в строго определенном порядке, который диктуется самой программой. Этот порядок называется лексикографическим. Будем его обозначать символом -<. Нестрогий лексикографический порядок будем обозначать символом < .

Утверждение 6.1

Пусть точка J пространства итераций относится к /-ому оператору программы и описывается параметрами / . ,..., / . , точка I относится к /-ому оператору и

описывается параметрами /,-,..., /₍- . Пусть, например, /< i. Тогда:

• если пересечение совокупностей номеров у'_ь ...,j_s. и /_ь ..., i_s пусто, то любой параметр У. младше любого параметра 1- ;

• если пересечение совокупностей номеров /_ь ...,j_s. и /_ь ..., i_s не пусто, то

любой параметр, номер которого входит в пересечение, младше любого параметра, номер которого не входит в пересечение; любой параметр У,,

номер которого не входит в пересечение, младше любого параметра /,-,

'к

номер которого также не входит в пересечение.

Согласно свойствам операторов do, области действия любых двух таких операторов могут быть или вложенными одна в другую, или следующими одна за другой. Поэтому, если в пересечении есть хотя бы один общий параметр, то это означает, что у обоих опорных гнезд есть общий оператор цикла. В этом случае любой оператор цикла, содержащий в своем теле рассматриваемый общий оператор и присутствующий в одном из опорных гнезд, должен присутствовать и в другом опорном гнезде. Новому общему оператору цикла соответствует младший параметр.

Это утверждение позволяет ввести отношение порядка в линейном пространстве итераций. Будем также называть его лексикографическим и обозначать тем же символом -<. Рассмотрим любую пару различных точек У, /. Пусть точка У описывается параметрами У,- , ..., У,- , точка / описывается

параметрами У •,..., У- . Будем считать, что J < I, если:

П либо пересечение совокупностей номеров пусто и у < /;

□ либо пересечение совокупностей номеров не пусто, значения всех одинаковых параметров попарно совпадают и у < /;

□ либо пересечение совокупностей номеров не пусто, значения каких-то младших одинаковых параметров могут попарно совпадать, но среди

Глава 6. Тонкая информационная структура программ

345

одинаковых параметров, значения которых попарно не совпадают, самый младший параметр точки / имеет меньшее значение, чем тот же параметр точки /.

Если рассматривать точки пространства итераций как точки линейного пространства итераций, то лексикографический порядок в линейном пространстве итераций автоматически порождает лексикографический порядок в пространстве итераций. По построению он таков, что J < I тогда и только тогда, когда при последовательной реализации программы срабатывание оператора, соответствующее точке /, будет осуществляться раньше срабатывания оператора, соответствующего точке /.

Сказанное означает, что порядок выполнения операций в программе естественным образом порождает порядок в обоих пространствах итераций. Этот порядок проверяется конструктивно.

Теперь будем строить ориентированные графы. Две точки пространства итераций называются зависимыми, если при срабатываниях соответствующих им операторов имеют место обращения к одной и той же переменной. Соединим все или какие-то пары зависимых точек дугами, направляя их от лексикографически младших точек к лексикографически старшим. Тем самым получим ориентированный граф. Все графы такого вида называются графами зависимостей. Они отличаются друг от друга как типом обращения к переменной (использование ее значения или пересчет ее значения), так и числом дуг. Не каждая пара зависимых точек обязательно будет соединяться дугой. Но если пара зависимых точек соединяется дугой, то с данной дугой однозначно связывается некоторая переменная. С ней сначала что-то делается в операции, соответствующей начальной точке дуги, а затем с ней же что-то делается в операции, соответствующей конечной точке дуги. Это "что-то" в обеих точках может быть как одним и тем же, так и различным.

Заметим, что дуги связывают пары точек пространства итераций, хотя в действительности они относятся к конкретным входам или выходам операций, задаваемых этими точками. У любой операции выход всегда один, но входов может быть несколько. Если начальная и/или конечная точка дуги связана с каким-либо входом, то для полноты сведений о графе зависимостей такую точку и инцидентные с ней дуги надо бы пометить номером входа. Без дополнительных оговорок мы будем всюду предполагать, что такая разметка вершин и дуг имеется.

Различают четыре типа зависимостей. Для всех начальных (конечных) точек дуг одного типа имеет место один и тот же тип обращения к переменной, определяющей зависимость. Именно, либо всюду значение переменной используется в качестве аргумента при срабатывании оператора, либо всюду результат срабатывания оператора используется для замены значения переменной. Будем обозначать использование значения переменной в качестве аргумента символом "in", использование результата для замены значения

346

Часть II. Параллельное программирование

символом "out". Парой in-out (in-in, out-out, out-in) будем обозначать тип зависимости. Левый (правый) символ в паре относится к начальной (конечной) точке дуги зависимости. Традиционно для типов зависимости используются следующие названия:

□ out-in — истинная или dataflow-зависимость;

П in-out — антизависимость;

П out-out — зависимость по выходу;

П in-in — зависимость по входу.

Соответственно этому различают четыре типа графов зависимостей. Все дуги любого графа имеют один и тот же тип зависимости.

Каждая точка пространства итераций однозначно определяет переменные, значения которых используются как аргументы при срабатывании соответствующего ей оператора, и переменную, значение которой изменяется. Зависимость может определяться по любой из этих переменных. Число аргументов может быть более одного. Поэтому зависимости типа *-in могут определяться в каждой точке более чем одной переменной независимо от того, какой смысл имеет символ *. Зависимости типа *-out определяются только одной переменной.

Понятия зависимостей и графов зависимостей являются традиционными и используются достаточно давно. Однако долгое время на их основе не удавалось получить существенные результаты в изучении параллельной структуры программ из какого-нибудь представительного класса. Это связано с тем, что само по себе понятие зависимости является достаточно широким, как и понятие влияния. В частности, при большом числе вершин почти всегда будут существовать вершины, в которые будет входить много дуг зависимостей. Кроме этого, изучению и применению графов зависимостей в значительной мере мешает нетранзитивность отношения зависимости. Успех в использовании графов зависимостей пришел лишь тогда, когда среди всего их многообразия стали применяться в определенном смысле минимальные графы.

Для каждого типа зависимостей существует граф, содержащий максимальное число дуг. Он получается в том случае, когда дугой соединяется каждая пара точек, зависимых хотя бы по одной переменной. Будем называть этот граф максимальным. Зафиксируем какую-нибудь вершину. Разобьем все множество дуг максимального графа, входящих в данную вершину, на группы. Отнесем к одной группе дуги зависимостей по одной и той же переменной. В каждой группе выберем дугу, у которой начальная вершина ближе всего лексикографически к зафиксированной вершине. Построим ориентированный граф, в котором множество вершин совпадает с множеством точек пространства итераций, а множество дуг — с выбранным множеством. Будем называть такой граф минимальным снизу.

Глава 6. Тонкая информационная структура программ

347

В соответствии с введенными типами зависимостей всего имеется четыре минимальных графа. В каждую вершину минимального снизу графа типа *-in может входить несколько дуг, но не больше, чем число аргументов, которые имеет соответствующая вершине операция. В каждую вершину минимального графа типа *-out может входить не более одной дуги. Минимальный граф типа out-out (граф зависимостей по выходу) представляет совокупность попарно непересекающихся путей. Каждый из путей объединяет множество вершин, в которых пересчитывается одна и та же переменная. На разных путях этого графа пересчитываются разные переменные.

Кроме минимальных снизу можно построить и другие графы, минимальные в каком-то смысле. Снова рассмотрим максимальный граф. Разобьем все множество дуг максимального графа, выходящих из данной вершины, на группы. Отнесем к одной группе дуги зависимости по одной и той же переменной. В каждой группе выберем дугу, у которой конечная вершина ближе всего лексикографически к зафиксированной вершине. Построим ориентированный граф, в котором множество вершин совпадает с множеством точек пространства итераций, а множество дуг — с выбранным множеством. Будем называть такой граф минимальным сверху. Снова имеется четыре типа таких графов.

Легко проверить, что для зависимостей по выходу минимальные сверху и снизу графы совпадают. Совпадают между собой и оба графа для зависимостей по входу. Для двух остальных типов зависимостей минимальные сверху и снизу графы различаются. Минимальный сверху граф антизависимостей будем называть графом обратных зависимостей. Его не следует путать с минимальным снизу графом антизависимостей. Это разные графы, хотя во многом они похожи.

В графах, минимальных снизу, конечная вершина дуги однозначно (с точностью до фиксации номера аргумента в зависимостях типа *-in) определяет начальную вершину. В графах, минимальных сверху, наоборот: начальная вершина дуги (с точностью до фиксации номера аргумента в зависимостях типа in-*) однозначно определяет конечную. Из каждой вершины минимального сверху графа типа in-* может выходить несколько дуг, но не больше, чем число аргументов, которые имеет соответствующая вершине операция. Из каждой вершины минимального сверху графа типа out-* может выходить не более одной дуги.

Как мы увидим в дальнейшем, между различными типами графов зависимостей нет принципиального различия ни по устройству, ни по способам построения. Для каждого типа зависимостей наибольший интерес представляет минимальный снизу или сверху граф. Именно эти графы будут предметом наших дальнейших исследований. Говоря далее о графе зависимостей, мы будем иметь в виду минимальный граф любого типа. Ни в каком другом смысле название "граф зависимостей" использоваться не будет. Минимальный снизу

348

Часть II. Параллельное программирование

граф истинных зависимостей, очевидно, есть ничто иное, как граф алгоритма, имея в виду алгоритм, описанный исследуемой программой.

Итак, пусть задана произвольная линейная программа. Количество входных и выходных вхождений переменных в каждом операторе конечно. Поэтому формально минимальный снизу (сверху) граф зависимостей можно описать некоторой конечнозначной функцией Ф, заданной в пространстве итераций. Для любой точки / пространства итераций множество значений функции Ф(7) есть множество тех точек пространства итераций, из которых (в которые) идут дуги графа в точку (из точки) /. В общем случае число значений функции Ф может быть различным в разных точках. Всегда существуют точки, в которых функция Ф не определена.

Принципиальный вопрос состоит в выяснении того, как устроена функция Ф. Пусть в пространстве итераций задана система однозначных функций Ф^. Будем говорить, что граф, описываемый функцией Ф, покрывается системой функций Ф^, если при любых значениях внешних переменных для каждой точки / из пространства итераций, в которой определена функция Ф, найдется такая подсистема функций Ф^ , что множество значений

функции Ф(7) совпадает с множеством значений функций Ф^ (Г) с точностью до кратности отдельных значений. Покрывающие функции Ф^ могут обладать каким-нибудь характерным свойством, которое нельзя проверить на дискретном множестве значений аргументов. Например, таким свойством является свойство линейности. В этом случае без дополнительных пояснений будем считать, что покрывающие функции определены в линейном пространстве итераций.

Для всех исследований, проводимых в дальнейшем с графами зависимостей, фундаментальное значение имеет следующая теорема.

Теорема 1

Для любой линейной программы любой минимальный снизу или сверху граф зависимостей покрывается конечной системой функций, линейных как по пространству итераций, так и по пространству внешних переменных программы. Число этих функций не зависит от значений внешних переменных. В линейном пространстве итераций функции определены на линейных многогранниках. Грани многогранников описываются уравнениями, также линейными как по пространству итераций, так и по пространству внешних переменных.

Мы не будем сейчас заниматься доказательством этой теоремы из-за ее сложности. Желающих познакомиться с ней мы отсылаем к статье [63]. Здесь же дадим краткий комментарий.

Утверждение теоремы кажется удивительным, хотя оно и ожидалось в какой-то мере. В самом деле, если программа зависит от внешних переменных, то от их значений будут зависеть и графы зависимостей. Из определения графов не видно, как влияют на их структуру внешние переменные.

Глава 6. Тонкая информационная структура программ

349

Однако совершенно очевидно, что при увеличении значений внешних переменных графы могут увеличиваться неограниченно. Согласно утверждению теоремы вся зависимость покрывающих функций от внешних переменных сосредоточена в их свободных членах и в свободных членах уравнений гиперплоскостей, описывающих грани многогранников. Все свободные члены являются функциями, линейно зависящими от внешних переменных.

Число покрывающих функций зависит от многих факторов. В частности, оно зависит от арифметической природы коэффициентов линейных выражений и числа исполняемых операторов программы. На практике число покрывающих функций оказывается не очень большим. Исследование реальных программ показало наличие двух особенностей. Во-первых, общее число линейных покрывающих функций пропорционально числу операторов присваивания в программе. Коэффициент пропорциональности не превосходит нескольких единиц. На меньшее число функций рассчитывать не приходится, если операторы связаны друг с другом. Во-вторых, в подавляющем большинстве случаев система покрывающих функций описывает граф зависимостей абсолютно точно. Именно, почти всегда для любой покрывающей функции Ф^- и любой целочисленной точки / из ее области определения пара точек Ф^(^) и / определяет дугу графа зависимостей. Нам известно лишь несколько реальных примеров, в которых системы покрывающих функций задают не граф зависимостей, а какое-то его расширение.

В силу фундаментального значения теоремы 1 для изучения структуры последовательных программ мы дадим ей специальное название "теорема об информационном покрытии ".

Если программа принадлежит линейному классу, то согласно теореме 1, граф описываемого программой алгоритма покрывается системой линейных функций, заданных на линейных многогранниках. Программа может формально не принадлежать линейному классу, но граф алгоритма может, тем не менее, покрываться таким же образом. Как мы увидим в дальнейшем, информационная структура соответствующих алгоритмов исследуется достаточно полно. По аналогии с программами подобные алгоритмы будем называть линейными или принадлежащими линейному классу. Один из фундаментальных вопросов связан с тем, как распознавать линейные алгоритмы по их записям.

Изучение информационной структуры алгоритмов и программ есть, в первую очередь, изучение структуры всех максимальных графов зависимостей. Значение минимальных графов зависимостей для решения данной задачи определяется двумя фактами. Согласно теореме 1 все минимальные графы могут быть явно описаны конечным числом линейных функций и, следовательно, могут быть эффективно исследованы. Кроме этого, любая дуга любого максимального графа может быть представлена одним или двумя путями минимальных графов. Точнее, справедливо

350

Часть II. Параллельное программирование

Утверждение 6.2

Если две зависимые точки пространства итераций не связаны дугой минимального графа, то они связаны:

• путем минимального графа зависимостей по входу для зависимых по входу точек;

• путем минимального графа зависимостей по выходу для зависимых по выходу точек;

• путем, составленным из пути минимального графа зависимостей по выходу и дуги минимального снизу графа истинных зависимостей, для истинно зависимых точек;

• путем, составленным из пути минимального графа зависимостей по входу и дуги минимального снизу графа антизависимостей, для антизависимых точек.

Доказательства всех фактов проводятся аналогично. Рассмотрим его, например, для случая истинно зависимых точек. Пусть точки х, у истинно зависимы. Допустим, что операция, соответствующая точке х, перевычисляет значение переменной а, а операция, соответствующая точке у, использует значение переменной а в качестве одного из своих аргументов. По предположению х < у. Рассмотрим множество всех точек jq, ..., х_р таких, которые лексикографически находятся между х и у и в которых перевычисляются значения переменной а. Не ограничивая общности можно считать, что х -< х\ -< Х2 ■<...-< х_р -< у. Если множество точек х\, ..., х_р пустое, то точки х, у должны быть связаны дугой истинной зависимости. Если же оно не пустое, то точки х, jq, ..., х_р связаны путем минимального графа по выходу, а точки х_р, у дугой истинной зависимости.

Возможность представления графов зависимостей линейными функциями делает актуальной задачу разработки эффективных алгоритмов вычисления по тексту программы коэффициентов этих функций и коэффициентов линейных неравенств, описывающих области определения линейных функций. Данной задаче будут посвящены ближайшие исследования. Для всех типов графов зависимостей они проводятся одинаково с точностью до небольших терминологических различий. Для определенности мы будем исследовать граф алгоритма. В отношении других графов ограничимся минимальными комментариями.

Вопросы и задания

1. Рассмотрим линейное тесно вложенное гнездо циклов с телом, состоящим из одного оператора-преобразователя. Покажите, что в этом случае понятия опорного многогранника, опорной области и линейного пространства итераций совпадают и представляют один линейный многогранник.

2. Верно ли утверждение п. 1, если тело гнезда циклов состоит из нескольких операторов-преобразователей?

Глава 6. Тонкая информационная структура программ

351

3. Укажите характерный признак линейного пространства итераций для линейного тесно вложенного гнезда циклов с несколькими операторами.

4. Пусть в линейном замкнутом многограннике V задан лексикографический порядок. Постройте какую-нибудь функцию f[x), для которой при любых точках х, у е К выполняются соотношения

> 0, если х >- у;

Ах) - f(y) - = 0, если х = у;

< 0, если х -< у.

5. Является ли функция Дх) из п. 4 непрерывной в многограннике V.

6. Будет ли функция Дх) из п. 4 задавать лексикографический порядок во всем пространстве?

7. Как изменяется функция Дх) из п. 4, если размеры многогранника V неограниченно увеличиваются?

8. Обратите внимание на то, что все дуги графа алгоритма, выходящие из одной вершины, связаны с одной и той же переменной.

9. Что означает пустота одного или нескольких типов графов зависимостей с точки зрения параллельных вычислений?

10. *Линейные многогранники, на которых заданы покрывающие функции в теореме 1, зависят от внешних переменных. Как меняется взаимное расположение многогранников при изменении значений внешних переменных?

11. "Попробуйте построить необходимый и достаточный критерий, позволяющий по виду программы устанавливать принадлежность описываемого ею алгоритма линейному классу, или докажите невозможность существования такого критерия.

12. Докажите, что для графа зависимостей по выходу любые две покрывающие функции целочисленно не пересекаются, как по областям определений, так и по областям значений.

§ 6.4. Простые и элементарные графы

Рассмотрим произвольную программу из линейного класса. Выберем какую-нибудь дугу графа алгоритма и зададимся следующим вопросом: "Все ли элементы программы определяют выбранную дугу?". Цель этого вопроса состоит в попытке расщепить программу на такие фрагменты, чтобы каждый из них определял какое-то подмножество дуг. Если ответ на вопрос будет отрицательным, то задачу построения дуг графа алгоритма для исходной программы можно будет свести к последовательности аналогичных задач для меньших программ. Можно надеяться, что эта процедура упростит построение графа.

Выберем в программе любой исполняемый оператор F_t, и пусть точка / пространства итераций принадлежит опорной области V_i. Каждая дуга графа алгоритма связана с вполне конкретной переменной. Если дуга входит в

352

Часть II. Параллельное программирование

точку /, то соответствующая дуге переменная однозначно определяется этой точкой и каким-то входом оператора /}. Вообще говоря, разные входы определяют в точке / разные переменные, но в частных случаях переменные могут совпадать. Чтобы найти начальную точку дуги, нужно, согласно определению минимального снизу графа, рассмотреть те точки, в которых пере-считывается значение переменной, и среди них выбрать точку, ближайшую к / лексикографически снизу.

Таким образом, любая выбранная дуга графа алгоритма исходной программы будет входить в множество дуг графа алгоритма любой другой программы, если для нее:

□ пространство итераций является подмножеством пространства итераций исходной программы;

□ лексикографический порядок в пространстве итераций совпадает с исходным порядком;

□ пространство итераций содержит конечную точку дуги, и в этой точке используется соответствующая выбранной дуге переменная;

□ пространство итераций содержит все точки, в которых эта переменная пересчитывается, и которые лексикографически младше конечной точки дуги.

Для определения множества дуг графа алгоритма не нужны сведения о функциональном содержании вершин. Значение имеет только то, какие переменные используются на входах и выходах соответствующих вершинам операторов присваивания. Построим, исходя из данной программы, семейство формальных программ по следующим правилам. Зафиксируем какой-нибудь вход какого-нибудь оператора. Он определяет имя переменной, простой или с индексами. Вычеркнем все правые части всех исполняемых операторов. Оставим только в правой части выбранного оператора переменную, описывающую фиксированный вход. Вычеркнем в левых частях исполняемых операторов все вхождения всех переменных, имеющих имя, отличное от имени переменной в фиксированном входе. Теперь вычеркнем все операторы, у которых оказались пустыми левые и правые части, все ветвления, которые охватывают только пустые операторы, и все циклы с пустыми телами и телами, содержащими только условные операторы. Если окажется, что после всех вычеркиваний какой-нибудь условный оператор осуществляет передачу управления на несуществующий оператор, то заменим ее передачей управления на ближайший снизу из оставшихся операторов.

С формальной точки зрения оставшаяся часть программы не является "фор-транной" программой, т. к. левые и правые части некоторых операторов могут быть пустыми. Мы можем сделать ее "фортранной" программой, если пустые части заменим любыми переменными. Единственное требование состоит в том, чтобы никакая переменная справа не совпадала с переменной слева.

Глава 6. Тонкая информационная структура программ

353

Любая программа такого типа называется простой, а ее граф — простым графом. Каждая программа из линейного класса порождает множество простых программ. Их ровно столько, сколько вхождений всех переменных в правые части операторов присваивания.

Чтобы сравнить графы алгоритмов исходной программы и порожденной ею простой программы, полезно сначала сравнить их пространства итераций. Линейное пространство итераций исходной программы есть объединение всех опорных областей V',•. Если у программы вычеркивается 5-ый оператор, то из пространства итераций исключается опорная область Vs. Поэтому без ограничения общности можно считать, что линейное пространство итераций простой программы есть объединение опорных областей тех операторов, следы от которых остались в программе. Пространство итераций простой программы снова есть множество всех целочисленных точек ее линейного пространства. Очевидно также, что лексикографический порядок в линейном или дискретном пространстве итераций простой программы, порожденный самой простой программой, совпадает с лексикографическим порядком исходной программы, рассматриваемым лишь в этих пространствах. Заметим еще, что пространство итераций каждой простой программы содержит все точки, в которых пересчитываются переменные с зафиксированным ранее именем и не пересчитываются никакие другие переменные.

Теперь сравним процесс построения графа алгоритма исходной программы и графов алгоритмов простых программ. Зафиксируем какой-нибудь вход какого-нибудь оператора присваивания. Это однозначно фиксирует какую-нибудь простую программу. Множества точек пространств итераций обеих программ, в которых определен фиксированный вход, совпадают. Более того, в каждой точке обе программы определяют одну и ту же переменную. Множества точек пространств итераций обеих программ, в которых пере-считывается любая общая переменная, также совпадают. Никаких других переменных, кроме переменных с выбранным именем, простые программы не пересчитывают. Поэтому имеет место общее

Утверждение 6.3

Для любой программы из линейного класса минимальный граф зависимостей любого типа есть объединение графов того же типа всех простых программ.

Определение простой программы немного меняется, смотря по тому, какой рассматривается тип зависимостей. Для истинных зависимостей простая программа имеет один фиксированный вход и все выходы, в которых пересчитываются переменные с именем, фиксированным на входе. Именно этот вариант мы только что обсуждали. Для антизависимостей простая программа имеет один фиксированный выход и все входы, в которых используются переменные с именем, фиксированным на выходе. Для зависимостей по выходу простая программа имеет один фиксированный выход и содержит все

354

Часть II. Параллельное программирование

остальные выходы, в которых пересчитывается переменная с фиксированным именем. Для зависимостей по входу простая программа имеет один фиксированный вход и содержит все остальные входы, в которых используется переменная с фиксированным именем. С точностью до этих различий все остальные рассуждения о расщеплении минимальных графов на простые остаются без изменений.

Процесс расщепления линейных программ и соответствующих им минимальных графов зависимостей можно продолжить. Снова рассмотрим его на примере графа алгоритма. Вычеркнем в простой программе все операторы присваивания, кроме оператора, имеющего фиксированный вход, и какого-нибудь оператора, пересчитывающего переменную с фиксированным именем. В частности, второй оператор может совпадать с первым. Теперь вычеркнем все циклы с пустыми телами и телами, содержащими только условные операторы. Если окажется, что после всех вычеркиваний какой-либо условный оператор осуществляет передачу управления на несуществующий оператор, то заменим ее передачей управления на ближайший снизу из оставшихся операторов.

Любая программа такого типа называется элементарной, а ее граф — элементарным графом. Элементарная программа содержит не более двух операторов присваивания, имеющих в совокупности одну и ту же переменную на единственном входе и единственном выходе. Кроме этого, она может содержать какое-то число условных операторов перехода, в том числе, даже в случае одного исполняемого оператора. Каждая простая программа порождает столько элементарных программ, сколько в ней операторов, пересчитывающих переменные с фиксированным именем. Легко видеть, что любая дуга графа алгоритма исходной программы является дугой графа алгоритма одной из элементарных программ. Следовательно, справедливо

Утверждение 6.4

Для любой программы из линейного класса минимальный граф зависимостей любого типа есть остовный подграф объединения минимальных графов того же типа всех элементарных программ.

Напомним, что подграф называется остовным, если множество его вершин совпадает с множеством вершин графа.

Итак, отыскание минимального графа зависимостей для программы из линейного класса сводится к отысканию аналогичных графов для элементарных программ. Эти программы содержат не более двух операторов и также принадлежат линейному классу. Они очень просто устроены. Поэтому появляется уверенность в возможности построения для них минимальных графов.

Подчеркнем еще раз, что рассмотренные в данном параграфе расщепления линейных программ на простые и элементарные носят формальный характер. Компоненты расщепления могут даже не быть программами в строгом

Глава 6. Тонкая информационная структура программ

355

смысле этого слова, т. к. некоторые части каких-то операторов могут просто отсутствовать. Такие расщепления формально не связаны с расщеплениями исходного алгоритма на более простые алгоритмы. Они связаны лишь с расщеплениями различных графов, относящихся к исходному алгоритму, на более простые графы. Расщепление графов сопровождается расщеплением вершин, если соответствующие операции имеют более одного аргумента. При объединении графов расщепленные вершины сливаются.

Вопросы и задания

1. Внимательно проанализируйте примеры 6.1—6.3 из § 6.8 с точки зрения процедуры расщепления программ и графов на простые и элементарные.

2. Как зависит расщепление в этих примерах от типа определяемого графа зависимостей?

§ 6.5. Лексикографический порядок и /.-свойство матриц

В общем случае линейное пространство итераций представляет собой сложное множество, в котором введен лексикографический порядок. Рассмотрим этот порядок более внимательно в одном арифметическом пространстве размерности п. Будем считать, что для точек х = (х\, , х_п), у = (у\, , у„) выполняется отношение х -< у, если для некоторого s, 1 < s < п, имеют место соотношения

Х{ = У\, ...,X_S- i= y_s- i,x_s< y_s.

Это определение лексикографического порядка полностью согласовано с определением, данным в §6.3.

Утверждение 6.5

Пусть в вещественном арифметическом пространстве в двух системах координат введены отношения лексикографического порядка. Для того чтобы эти отношения совпадали на всем пространстве, необходимо и достаточно, чтобы матрица перехода от одной системы координат к другой была левой треугольной с положительными диагональными элементами.

Обозначим через S~^l матрицу перехода от старой системы координат к новой. Пусть х, у — любые различные векторы пространства. В новой системе координат они будут задаваться векторами Sx и Sy. Заметим, что условия х -< у и Sx -< Sy эквивалентны условиям (х — у) -< 0 и S(x — у) -< 0. В свою очередь, последние условия эквивалентны отрицательности первых ненулевых координат векторов х — у и S(x — у). Рассмотрим множество Zвекторов, имеющих первую ненулевую координату отрицательной. Теперь надо показать, что для того чтобы множество Z было инвариантно к умножению на

356

Часть II. Параллельное программирование

матрицу S, необходимо и достаточно, чтобы матрица S была левой треугольной с положительными диагональными элементами.

Достаточность очевидна. Предположим, что из z е Z следует Sz е Z. Допустим, что для некоторого у > 1 элемент sy первой строки матрицы S отличен от нуля. Возьмем подмножество векторов, у которых первая координата равна — 1, у'-я координата произвольная, а все остальные равны нулю. Это подмножество принадлежит Z. Однако при умножении векторов подмножества на матрицу S первая координата образов не может оставаться неположительной в силу неравенства нулю элемента sy. Следовательно, множество Z не является инвариантным к умножению на матрицу S. Матрица S невырожденная. Поэтому диагональный элемент первой строки матрицы S будет положительным, а все ее элементы справа от диагонали — нулевыми. Пусть для / > 1 первые / строк матрицы S обладают нужным свойством. Допустим, что для некоторого у > / + 1 элемент s,+ \_t j матрицы S отличен от нуля. Возьмем подмножество векторов, у которых (/ + 1)-я координата равна — 1, у'-я координата произвольная, а все остальные равны нулю. При умножении векторов подмножества на матрицу S первые / координат образов будут всегда нулевыми. Далее, повторяя почти дословно рассуждения, касающиеся первой строки, показываем, что (/ + 1)-я строка матрицы S также имеет нужный вид. Аналогичный вид будет иметь матрица S~^l.

Таким образом, если при сохранении лексикографического порядка на всем пространстве мы хотим найти систему координат, обладающую каким-либо дополнительным свойством, то выбор систем, вообще говоря, не очень широк. Именно, мы можем гарантированно осуществлять поиск только среди тех систем координат, которые связаны друг с другом преобразованиями с левыми треугольными матрицами, имеющими положительные диагональные элементы.

Среди разных задач, связанных с лексикографическим порядком, довольно часто мы будем иметь дело с задачей поиска в замкнутой области точки, старшей в лексикографическом отношении. Будем называть такую точку точкой лексикографического максимума. Пусть область D, в которой ищется точка лексикографического максимума, является ограниченным многогранником и задается системой линейных неравенств

(а,, х) < а,;

(6.3)

(а_т, х) < о_т.

Здесь а\, ..., а_т — векторы размерности п и т> п. Обозначим точку максимума через xq. Точка максимума единственная и должна быть одним из углов многогранника. В самом деле, если xq не является углом, то существует принадлежащий многограннику отрезок прямой, для которого точка xq будет внутренней. Но на любом отрезке лексикографический максимум дос-

Глава 6. Тонкая информационная структура программ

357

тигается на одном из концов. Следовательно, точка х₀ действительно единственная и должна быть одним из углов. Поэтому для отыскания точки лексикографического максимума многогранника в общем случае нужно перебрать лишь его углы. Угловые точки являются решениями систем линейных алгебраических уравнений вида

(а,- , х) = ст,- ;

(6.4)

с невырожденной матрицей. Кроме этого, они должны удовлетворять системе неравенств (6.3).

В наших задачах системы неравенств типа (6.3) никогда не будут иметь большие размеры. Поэтому поиск точки лексикографического максимума в многограннике вроде бы можно осуществлять на основе прямого исследования всех его углов. Для этого нужно лишь перебрать все возможные системы линейных алгебраических уравнений вида (6.4) и среди принадлежащих многограннику их решений выбрать лексикографически старшее. Однако прямое решение данной задачи возможно только тогда, когда можно осуществить сравнение двух решений. В наших задачах правые части а, будут зависеть от внешних переменных, значения которых неизвестны. В этом случае сравнение решений приводит к появлению большого числа новых неравенств относительно этих переменных. Поэтому мы постараемся найти критерий отбора систем (6.4), основанный на проверке подходящих свойств их матриц.

Не ограничивая общности, можно считать, что точка х₀ является решением системы линейных алгебраических уравнений

(а_ь х) = сть

(6.5)

\G_n, X) — O_n

с невырожденной матрицей. Вычитая из первых п неравенств (6.3) соответствующие равенства (6.5) и вводя обозначение у = х — х₀, получим систему неравенств

(«ь У) < 0;

(6.6)

(««, У) < о. Покажем сначала, что если в угловой точке xq многогранника (6.3) достигается лексикографический максимум, то в этой точке существует система из п линейных алгебраических уравнений вида (6.5) такая, что все решения соответствующей системы неравенств (6.6) будут лексикографически меньше нуля.

358

Часть II. Параллельное программирование

Пусть угловая точка х₀ является решением системы линейных алгебраических уравнений

(а_ь х) = сть

(flp, х) = и_р, где р > п. Система неравенств, аналогичная (6.6), такова:

(«ь У) < 0;

(а_р, у) < 0.

Если в точке xq достигается лексикографический максимум, то в этом и только в этом случае все решения системы неравенств будут лексикографически меньше нуля. Но в общем случае р > п и не ясно, всегда ли найдется подсистема из п неравенств, обладающая аналогичным свойством.

Возьмем любую левую треугольную матрицу S с единичными диагональными элементами и сделаем замены

Z=Sy, b,= (S-^a,

для 1 < / < р. Система неравенств

(buz)<0;

{Ъ_Р, Z) < о

с векторами b_t лексикографически эквивалентна системе с векторами щ. Именно, если у -< 0, то z -< 0 и наоборот. Это следует из утверждения 6.5. Подберем матрицу S и перенумеруем векторы a_t так, что векторы b_t будут иметь специальный вид.

Подстановка в систему неравенств любого вектора, который лексикографически больше нуля, должна привести хотя бы в одном неравенстве к замене знака < на знак > . Возьмем в качестве у вектор, у которого все координаты нулевые, кроме последней, которая равна 1. Лексикографически он больше нуля. Результат его подстановки говорит о том, что среди последних координат векторов щ есть хотя бы одна положительная. Не ограничивая общности, можно считать, что / = п. Выполнение этого условия можно обеспечить перенумерацией векторов щ. Пусть в матрице S среди внедиагональных элементов ненулевыми могут быть лишь элементы последней строки. Очевидно, что матрицу S можно подобрать так, чтобы все координаты вектора Ъ_п, кроме последней, стали нулевыми. Последняя координата вектора Ь_п совпадает с последней координатой вектора а„ и, следовательно, является поло-

Глава 6. Тонкая информационная структура программ

359

жительной. Предположим, что вектор а„ уже имеет такой же вид, как и полученный вектор Ъ_п.

Возьмем далее в качестве у вектор, у которого все координаты нулевые, кроме предпоследней, которая равна 1. Лексикографически он также больше нуля. Результат его подстановки в систему неравенств говорит о том, что среди предпоследних координат векторов a_h в предположении, что вектор а„ имеет указанный выше вид, есть хотя бы одна положительная. Согласно договоренности, предпоследняя координата вектора а„ нулевая. Поэтому можно считать, что i = п — 1. Выполнения этого условия можно добиться перенумерацией векторов a_h не затрагивая вектор а„. Пусть в матрице S среди внедиагональных элементов ненулевыми могут быть лишь элементы предпоследней строки. Вектор а„ при умножении на такую матрицу S не изменится. Предпоследнюю строку матрицы S можно подобрать так, что все координаты вектора Ь„ - \, кроме двух последних, станут нулевыми. Последние две координаты вектора b„ - \ будут совпадать с последними двумя координатами вектора а_п - \ и, следовательно, предпоследняя координата будет положительной.

Продолжая описанный процесс, заключаем, что с помощью перенумерации векторов-столбцов щ и выбора матрицы S можно получить эквивалентную систему неравенств, в которой векторы-столбцы Ь\, ..., Ь„ образуют левую треугольную матрицу с положительными диагональными элементами. Векторы Ь\, ..., Ь„ линейно независимы, их число равно п и система неравенств с такими векторами имеет только такие решения, которые лексикографически меньше нуля. Что и требовалось показать.

Теперь мы хотим найти некоторое характерное свойство векторов щ, ..., а„, если система неравенств (6.6) имеет лишь такие решения, которые лексикографически меньше нуля.

Для дальнейшего нам потребуется утверждение, называемое леммой Фарка-ша—Минковского [48]. Мы приведем ее без доказательства, изменив формулировку применительно к нашим исследованиям.

Утверждение 6.6 (лемма Фаркаша—Минковского)

Пусть задана система векторов Ь_ь ..., Ь_р. Рассмотрим множество ^решений q системы неравенств (b_h q) < 0, 1 < / < р. Тогда множество всех векторов Ь, для которых выполняются неравенства (b, q) < 0 при всех q е К и только оно пред-ставимо в виде

7 = 1

где X, > 0, !</</>.

360

Часть II. Параллельное программирование

Пусть е_к есть к-й координатный вектор, т. е. все его координаты нулевые, кроме к-&, которая равна 1. Обозначим а„ + ₂к- \ ⁼ ^еь ^ап + 2к ⁼ ~ ^ек ^и Р^ас~ смотрим системы неравенств

(я,, и) <0;

(а„, и) < 0;

(6.7) К + ь и) <0;

К + гь ") ^ 0. Для каждого к = 0, 1, ..., л — 1 добавление 2& последних неравенств выделяет из множества решений системы (6.6) подмножество, для которого первые к координат решений являются нулевыми. По построению все решения системы первых п неравенств из (6.7) лексикографически меньше нуля. Поэтому при каждом к = 0, 1, ..., л — 1 любое решение системы (6.7) имеет неположительными первые к + 1 координат. Это означает, в частности, что для каждого к = 0, 1, ..., я — 1 выполняется неравенство (е^ + \, и) < 0 для всех решений системы неравенств (6.7). В соответствии с утверждением 6.6 заключаем, что

п + 2к

^ек ₊ 1 - 2^^к1 ^а'' (6.8)

где 7i'^c ⁺¹⁾ > 0 для всех /, к.

Пусть А есть матрица, столбцами которой являются векторы щ, ..., а_п. По построению матрица А невырожденная. Обозначим через д/^-1) столбец матрицы А~^] с номером /. Будем считать, что по определению а</^_1^ ⁼ 0. Умножая равенство (6.8) слева на матрицу А^-1, находим, что

^ХьГ'Ч + Х^ч¹'- (6-9)

/ = 1 / = 0

Здесь vf^k ⁺ !) — какие-то числа.

Если любое решение системы неравенств (6.6) лексикографически меньше нуля, то для столбцов матрицы А~^] имеет место представление (6.9). В частности, все элементы первого столбца матрицы А~¹ неотрицательные. Любой столбец, кроме первого, получается как сумма линейных комбинаций предыдущих столбцов и некоторого вектора с неотрицательными координатами. Отсюда следует, что в каждой строке матрицы А~¹ первый ненулевой элемент является положительным. Пусть теперь столбцы матрицы А~¹ имеют представление (6.9). Покажем, что любое ненулевое решение системы неравенств (6.6) лексикографически меньше нуля.

Глава 6. Тонкая информационная структура программ

361

Предположим, что ненулевой вектор у является решением системы неравенств (6.6). Тогда

(щ,у) = 5,;

(<*„, У) = 5„,

где все 5_г < 0. Представим эту систему в матрично-векторной форме А'у = 5, где 5 = (5ь ..., 5_Й). Так как векторы щ линейно независимы, то вектор 5 не равен нулю. Имеем у = (А')~^]5 = (А~^])'д. Пусть у = {у\, ..., у„). Представляя координаты вектора у через элементы матрицы А~^] и вектор 5, находим, что

(о,(-1), 5)=_У];

(о_и<^-1), 5) = у„.

Умножая соотношение (6.9) справа скалярно на 5 и обозначая у$ =

= (ci()(~^]\ 5), имеем

y_k ₊ _l=^ ₊ i + J_Jvf ⁺ ^[)y_J (6.10)

7 = 0

для к = 0, 1, ..., я — 1. Ясно, что у$ = 0 и число

?A ₊ i = I>f ⁺ ¹⁾8^0. (6.11)

i = 1

Вектор у ненулевой по предположению. Следовательно, не все его координаты нулевые. Согласно (6.10), (6.11) первая ненулевая координата вектора у отрицательная, т. е. у -< 0.

Покажем теперь, что столбцы любой матрицы А~^] имеют представление (6.9), если только в каждой ее строке первый ненулевой элемент положительный. Рассмотрим столбец «["/. В предыдущих столбцах с номерами

1, 2, ..., к, вообще говоря, могут находиться первые ненулевые элементы каких-то строк. Пусть они находятся в столбцах с номерами k < h < ••• < h_k- к ^и' соответственно, в строках с номерами ly, lj, ..., /_s .

Все координаты, кроме координат с номерами 1\, ..., I , для всех векторов a\(~^l\ ..., a_k(~^l\ в том числе, векторов яН\ ..., аН-¹ являются нулевыми.

'l ^ls_k

Напомним, что все первые ненулевые элементы в строках матрицы положительные. Поэтому всегда можно подобрать такие числа

v^ ⁺ ^[),..., v^ ⁺^!), начиная с v⁽:^k ⁺ ^[\ что в векторе

h h_k h_k

-дИ) +v<* + ¹⁾oH) +_v(* + ¹⁾fl<-¹⁾ +... + v^{k + ⁱ⁾a^{r^l) (6-¹²)

362

Часть II. Параллельное программирование

все координаты будут неположительными. Действительно, в векторе — aj~₊(, кроме возможных ненулевых координат с номерами 1\, /₂, ..., /_? могут быть

ненулевыми те координаты, которые соответствуют первым ненулевым элементам строк, находящимся в (к + 1)-м столбце матрицы А~\ если, конечно, они там есть. Но эти элементы отрицательные по условию. Они не меняются при прибавлении к вектору — а[~/ любой линейной комбинации векторов a_i ,...,a_t. За счет выбора коэффициента v^ ⁺ ¹⁾b векто-

ре - я£~+\ + v\^k ⁺ ^а,-^-1^ можно дополнительно сделать неположительными те

^sk ^sk

координаты, номера которых совпадают с номерами строк, чьи первые ненулевые элементы находятся в г -м столбце. Подбираем аналогичным способом коэффициенты v,- __b...,v, делая в сумме (6.12) неположительными

^sk

координаты с номерами /], /₂, ..., /_?; и, следовательно, все координаты. За

счет подбора неотрицательных коэффициентов \[^к ⁺ *) равенство (6.9) теперь удовлетворяется тривиально.

Будем говорить, что невырожденная матрица А обладает L-свойсшвом, если в каждой строке матрицы А~^] первый ненулевой элемент положительный. Очевидно, что любая правая треугольная матрица с положительными диагональными элементами обладает Z-свойством. Перестановка столбцов матрицы и умножение слева на любую правую треугольную матрицу с положительными диагональными элементами сохраняет Z-свойство. Несмотря на простоту этих фактов, они оказываются полярными при исследовании конкретных матриц относительно Z-свойства. Проведенные исследования показывают, что справедливо

Утверждение 6.7

Точка лексикографического максимума в многограннике (6.3) совпадает с тем из его углов, в котором описывающая его матрица А имеет обратную и обладает /.-свойством.

Заметим, что критерий отбора систем (6.4), основанный на проверке Z-свойства их матриц, может выделить более одной системы. Чтобы определить среди них нужную, необходимо решить все выделенные системы и среди их решений взять то, которое принадлежит многограннику. Если правые части неравенств (6.3) зависят от внешних переменных, то проверка принадлежности решения многограннику снова приводит к появлению новых неравенств относительно этих переменных. Однако таких неравенств уже немного, т. к. лишь немного матриц среди проверяемых обладает Z-свойством.

Глава 6. Тонкая информационная структура программ

363

Вопросы и задания

1. Среди углов многогранника (6.3) может существовать несколько углов, которые описываются матрицами с Х-свойством. Как это согласуется с единственностью точки лексикографического максимума в многограннике?

2. Докажите, что при изменении правых частей неравенств (6.3) любое ребро многогранника не меняет своего векторного направления до тех пор, пока оно не стягивается в точку.

3. Пусть правые части неравенств (6.3) являются линейными функциями параметра /. Докажите, что при изменении / любое ребро многогранника может стягиваться в точку не более одного раза.

4. Докажите, что в условиях п. 3 существует такое t₀, что для t > t₀ длина любого ребра многогранника либо остается постоянной, либо асимптотически является линейной функцией от t.

5. *С учетом полученных сведений о многогранниках снова вернитесь к вопросу п. 10 из § 6.3.

6. Пусть правые части неравенств (6.3) являются линейными функциями координат вектора /. Обратите внимание, что любой угол многогранника есть также линейная вектор-функция от этих координат.

7. В условиях п. 6 постройте модель изменения многогранника (6.3) при изменении координат вектора t, если, например, сами координаты принадлежат некоторому усеченному конусу.

§ 6.6. Построение минимальных графов зависимостей

При построении минимальных графов зависимостей будем руководствоваться теоремой 1. Будем считать, что мы умеем строить минимальные графы, если удастся разработать алгоритм вычисления коэффициентов линейных покрывающих функций и коэффициентов, определяющих области их задания. Снова ограничимся рассмотрением графа алгоритма.

Поставим сначала математически задачу нахождения минимального графа зависимостей для элементарной программы. Линейное пространство итераций элементарной программы в общем случае состоит из двух опорных областей: области V/, которая связана со входом одного оператора, и области Vj, которая связана с выходом другого оператора. Если элементарная программа содержит только один оператор, то опорные области V; и Vj совпадают. Пусть дуга идет из вершины / е Vj в вершину I е V-_t. Это означает, что в вершине / вычисляется значение некоторой переменной, а в вершине I это же значение этой же переменной используется. Более того,

364

Часть II. Параллельное программирование

эта переменная не перевычисляется ни в одной вершине, которая лексикографически старше /, но младше I.

Пусть элементарная программа описывается переменной с индексами. Переменные на выходе и входе имеют одно и то же имя, но по форме выражений могут различаться индексами. Обозначим через p(J, N) вектор, координатами которого являются индексы выходной переменной, через q(J, N) — вектор индексов входной переменной. В общем случае для программы из линейного класса векторные функции p(J, N) и q(J, N) являются неоднородными и линейными как по векторам параметров циклов I, /, так и по вектору N внешних переменных программы. Если в действительности переменная является простой, то без ограничения общности можно считать p(J, N) = q(J, TV) = 0. Обозначим через Q/, Qy множества целочисленных точек /, / соответственно в опорных областях V-_t, Vj.

Зафиксируем входную вершину I. Это однозначно определяет вектор индексов q(J, N). Чтобы из вершины / выходила дуга в вершину I, необходимо, чтобы вектор q(J, N) совпадал с вектором индексов p(J, TV). Поэтому первое, что мы должны сделать, — это потребовать выполнение равенства

p(J, N) = q(J, N). (6.13)

В действительности задача значительно сложнее. Нужно не только найти какие-то решения уравнения (6.13) относительно /, но и добиться выполнения условий

J < I, J е Q.j, I е Q₇. (6.14)

Задача (6.13) при условии (6.14) может иметь неединственное решение. Однако на самом деле нужно найти на множестве всевозможных решений / из (6.13), (6.14) то решение J₀, которое является лексикографически самым старшим. Такое решение

/о = lex.max/ (6.15)

уже единственное.

Решение Jq = Jq(I, N) задачи (6.13)—(6.15) зависит как от вектора параметров циклов У", так и от вектора N внешних переменных программы. Напомним, что по определению линейной программы множество допустимых векторов N принадлежит некоторой совокупности многогранников, конкретных для каждой определенной программы. Для реальных программ многогранники часто оказываются неограниченными. Множество допустимых векторов I также принадлежит некоторой совокупности многогранников. Эти многогранники всегда ограниченные и, как правило, зависят от вектора внешних переменных N, значения которых неизвестны.

В целом задача (6.13)—(6.15) является целочисленной, т. к. целочисленными являются векторы I, J, N, коэффициенты линейной системы (6.13) и ко-

Глава 6. Тонкая информационная структура программ

365

эффициенты линейных многогранников из V_h К,-. Пусть вектор ^фиксирован. Если при каком-то I функция Jq(I, TV) определена, то ее значение задает начальную точку дуги, идущей в точку I. Если в точке / функция Jo(I, N) не определена, то в точку / не идет дуга. Именно целочисленность делает решение задачи (6.13)—(6.15) особенно трудным.

Теперь снова вернемся к задаче (6.13)—(6.15). Заменим эту задачу ее непрерывным аналогом, руководствуясь следующими идеями. Если решение Jq(I, N) непрерывной задачи при допустимых целочисленных векторах I, N окажется целочисленным, то оно будет совпадать с решением дискретной задачи (6.13)—(6.15). По форме непрерывная задача почти совпадает с рассмотренной в §6.5 задачей отыскания лексикографического максимума. Нужно лишь заменить каждое равенство из (6.13) системой противоположных неравенств и аккуратно свести к системе неравенств условие J < I. Кроме этого, нужно принять во внимание, что многогранников может быть несколько. После этого для решения непрерывной задачи можно использовать аппарат матриц с Х-свойством.

Пусть вершина I соответствует оператору присваивания с номером /, вершина / — оператору с номером j. Обозначим через У, , ..., У,- и /•,...,/

1 qi J\ Jpj

координаты этих вершин. Предположим для определенности, что первые s параметров циклов, соответствующих опорным гнездам вершин I, J, являются общими. Если общих параметров нет, то проверка условия J < I становится тривиальной и сводится к сравнению i,j. Пусть, например, i>j. Построим систему альтернативных многогранников. Первый из них описывается плоскостью:

J\ h

(6.16)

^JL

и рассматривается только в случае / > j. Все остальные альтернативные многогранники рассматриваются во всех случаях. Второй многогранник будет таким:

J\ h

(6.17)

7.V-1 <v-l '

В каждом последующем многограннике число описывающих его равенств будет уменьшаться. Неравенство всегда будет одно.

366

Часть II. Параллельное программирование

Третий многогранник описывается следующим образом:

Jj'" = i, ; ^(6Л8)

Js-2 h-2 '

J: </,- -1.

И, наконец, последний альтернативный многогранник будет таким:

/у, </,•,-!. (6.19)

По построению любая точка любого альтернативного многогранника удовлетворяет условию J < I. Более того, лексикографически ближе к / будет та точка, которая находится в альтернативном многограннике с меньшим номером. Это обстоятельство позволяет решать непрерывную задачу, заменяя условие J < I условием принадлежности / сначала первому альтернативному многограннику, затем второму и т. д. В общем случае опорные области Vj и Vj могут состоять из нескольких многогранников. Допустим, что

мы умеем строить элементарный граф для случая, когда эти области содержат только по одному многограннику. Решим все такие задачи, выбирая из Vj и Vj по одному многограннику. Чтобы по их решениям построить истинный элементарный граф, надо для каждого многогранника из V_t взять решения, соответствующие всем многогранникам из Vj, и найти их лексикографический максимум. Эта задача относительно простая, и мы рассмотрим ее несколько позднее. А пока будем считать, что каждая из опорных областей К,- и Vj описывается только одним многогранником.

Рассмотрим первый альтернативный многогранник. Теперь непрерывная задача становится такой: в многограннике, заданном равенствами (6.13), условием J е Vj а соотношениями (6.16), найти точку /, обеспечивающую

лексикографический максимум. Процесс ее решения состоит из следующих шагов:

□ выписываются в форме (6.3) все линейные ограничения на координаты искомой точки /; в левых частях ограничений указывается зависимость от координат /; в правых частях ограничений указывается зависимость от координат I к N;

П по выписанной системе ограничений находятся все системы линейных алгебраических уравнений типа (6.4), матрицы которых обладают Z-свойством;

□ решаются все найденные системы линейных алгебраических уравнений относительно координат точки /; тем самым определяются точки /' —

Глава 6. Тонкая информационная структура программ

367

претенденты на решение задачи; координаты всех точек-претендентов являются линейными функциями координат точек / и вектора N неизвестных переменных;

□ координаты каждой точки-претендента /' подставляются во все линейные ограничения на координаты искомой точки /; совокупность полученных равенств и неравенств порождает линейный многогранник V_i',

которому должна принадлежать точка /. Конфигурация и размеры многогранника могут зависеть от внешних переменных;

□ рассматривается пересечение многогранников Vj и V_t '; если оно не пусто, то в точках / этого пересечения точка /' дает искомое решение /₀ непрерывной задачи; если пересечение пусто, то точка /' как претендент на решение задачи не рассматривается;

□ строится объединение пересечений многогранников V_{ и V_i ', полученных для всех претендентов /'.

Повторяются все шаги с заменой первого альтернативного многогранника вторым и многогранника Vj его неисчерпанной пересечениями частью.

Процесс перебора альтернативных многогранников продолжается до тех пор, пока не будут исчерпаны все из них. После окончания перебора какая-то часть Vj должна остаться неисчерпанной. Эта и только эта часть соответствует тем целочисленным точкам /, в которых элементарная программа использует на входе входные данные элементарной задачи. Индексы переменных, определяющих входные данные, задаются вектором q(I, N). Только в эти точки / не входят дуги элементарного графа.

Сделаем несколько замечаний. Проверка пересечения многогранников Vj, Vj ' на непустоту порождает ограничения на неизвестные переменные, определяющие размеры многогранников. Довольно часто эти переменные являются плохо описанными, и их значения не могут быть определены из текста программы. Поэтому проверка непустоты пересечения может быть связана с получением дополнительной информации, касающейся области изменения внешних переменных. Вообще говоря, при одних и тех же значениях переменных пересечения многогранников Vj и V_t ' могут иметь непустые пересечения между собой для разных точек-претендентов /'. Однако напомним, что точка лексикографического максимума в многограннике единственная. Поэтому на пересечении пересечений точки-претенденты должны совпадать.

Итак, решение непрерывной задачи для любой элементарной программы из линейного класса в случае, когда каждая из опорных областей V_t и Vj описывается только одним многогранником, представимо в виде конечной сие-

368

Часть II. Параллельное программирование

темы функций, линейных как по пространству итераций, так и по пространству внешних переменных программы. Число этих функций не зависит от значений внешних переменных. Как следует из процесса построения, каждая из функций задана в какой-то области, принадлежащей V_h Граница

области составлена из линейных кусков гиперплоскостей. Число этих кусков и их конфигурация также не зависят от значений внешних переменных. Такую область всегда можно представить как объединение конечного числа линейных многогранников, у которых какие-то грани могут быть открытыми. Эти грани мы можем сделать замкнутыми, изменив на единицу свободный член в описании соответствующей гиперплоскости. При этом в каждом из многогранников не будет потеряна ни одна из целочисленных точек. Напомним, что только такие точки представляют для нас истинный интерес. По построению все полученные замкнутые линейные многогранники будут непересекающимися попарно.

Решение /₀(7, N) непрерывной задачи обладает двумя особенностями. Во-первых, оно получено в форме, соответствующей теореме 1. И, во-вторых, если в целочисленной точке / значение функции J₀(I, N) оказывается целочисленным, то пара точек Jq(I, N) а I задает дугу элементарного графа.

Если подматрица системы уравнений (6.13), относящаяся к вектору /, имеет полный столбцовый ранг, то граф алгоритма элементарной программы определяется в основном этой системой. Именно, если при заданных целочисленных векторах /, N система (6.13) имеет целочисленное решение /о е Qy, то это решение будет единственным, и пара точек Jq, I определяет дугу графа. Если же система (6.13) не имеет ни одного целочисленного решения, то в точку / не входит дуга графа. В этих условиях решение Jq(I, N) непрерывной задачи совпадает с решением системы (6.13) и поэтому описывает элементарный граф абсолютно точно.

Утверждение 6.8

Пусть подматрица системы (6.13), относящаяся к вектору /, имеет полный столбцовый ранг. Если в целочисленной точке / решение J₀(I, TV) непрерывной задачи оказывается целочисленным и принадлежит пространству итераций, то пара точек /₀.1 определяет дугу элементарного графа. Если же в целочисленной точке /решение J₀(I, N) непрерывной задачи не является целочисленным, то в точку /не входит дуга графа.

Если система (6.13) не удовлетворяет условию утверждения 6.8, то решение Jo(I, N) непрерывной задачи не всегда описывает элементарный граф точно. По-прежнему, в случае целочисленных векторов /₀, / эта пара определяет дугу графа. Но если для целочисленного вектора / вектор Jq оказывается нецелочисленным, то это не означает отсутствие дуги. В случае, когда дуга существует, разность между начальной точкой дуги и непрерывным решением представляет вектор, который лексикографически максимальный, но не больше нуля, и принадлежит ядру подматрицы системы (6.13), относящейся

Глава 6. Тонкая информационная структура программ

369

к вектору /. Поэтому решение дискретной целочисленной задачи (6.13)— (6.15) можно представить как решение /₀(7, N) непрерывной задачи, к которому в точках, соответствующих целочисленным /, внесены поправки. Все коэффициенты, описывающие кусочно-линейную функцию Jq(I, TV), являются рациональными. Поэтому поправки оказываются периодическими, за исключением участков вблизи границы многогранника Vj. Относительно

легко поправки строятся в том случае, когда ядро подматрицы системы (6.13), относящейся к вектору /, имеет размерность 1. В общем же случае алгоритм построения поправок оказывается очень запутанным.

Для того чтобы понять, насколько необходимы на практике более сложные алгоритмы решения дискретной задачи (6.13)—(6.15) в условиях, выходящих за рамки утверждения 6.8, был поставлен эксперимент. Были найдены решения непрерывных задач, возникающих в самых различных реальных прикладных программах. Оказалось, что подавляющее большинство решений является целочисленным. И лишь в нескольких случаях они не были такими. Но каждый раз, когда решение не было целочисленным, не выполнялось условие утверждения 6.8.

Даже если предположить, что могут появляться отдельные примеры, для которых решение непрерывной задачи не будет целочисленным, но будет целочисленным решение дискретной задачи, — это еще не является веским аргументом в пользу применения существенно более тяжелых методов решения задачи (6.13)—(6.15). Заметим, что не представляет особого труда написать абстрактную элементарную программу, для которой указанные условия действительно имеют место. Возможно, что сказанное означает только то, что множество реальных программ из линейного класса устроено существенно проще, чем класс в целом. Напомним, что структура любых линейных программ описывается теоремой 1.

Всюду в дальнейшем мы будем считать, что любой элементарный граф может быть точно представлен решением непрерывной задачи.

Согласно утверждению 6.3, для любой программы из линейного класса ее минимальный граф зависимостей есть объединение минимальных графов всех простых программ. Процесс нахождения минимальных графов зависимостей для элементарных программ определен с точностью до сделанных выше оговорок. Поэтому для построения минимального графа линейной программы достаточно уметь строить простой граф из элементарных. Если будут построены расширения простых графов, то их объединение даст расширение минимального графа исходной программы. Для дальнейшего нам потребуется почти очевидное

Утверждение 6.9

Пусть в вещественном линейном пространстве заданы два замкнутых линейных в общем случае пересекающихся многогранника А_{ и А₂. Существует сие-

370

Часть II. Параллельное программирование

тема замкнутых линейных не пересекающихся многогранников А'_ь ..., А'_р таких, что множество целочисленных точек пространства, попавших как в многогранник Д_ь так и в многогранник Д₂, совпадает с множеством целочисленных точек, попавших в какие-то многогранники из А'_ь ..., А'_р.

Рассмотрим у любую простую программу и все порожденные ею элементарные программы. Пусть каждый элементарный граф представлен системой линейных функций, заданных на замкнутых линейных непересекающихся многогранниках. Возьмем объединение этих систем. Все многогранники из объединения принадлежат одной и той же опорной области V_t Многогранники из объединения могут попарно пересекаться, но лишь в том случае, когда они относятся к разным элементарным графам. Принимая во внимание утверждение 6.9, можно считать без ограничения общности, что многогранники в объединении не пересекаются. Такое предположение приводит к некоторому увеличению числа линейных функций, которыми представляется каждый элементарный граф. Однако сейчас это не имеет какого-либо значения.

Итак, пусть объединение элементарных графов описывается системой непересекающихся многогранников, заданных в опорной области V_i. На каждом

из многогранников определено несколько линейных функций со значениями в разных опорных областях. Из этого описания легко получить описание простого графа. Рассмотрим ту же систему многогранников и пусть А один из них. Предположим, что на А определены линейные функции Ф], ..., Ф^. В каждую целочисленную точку У из А входит одна и только одна дуга простого графа. Начальная точка этой дуги есть целочисленный лексикографический максимум из точек Ф^У), ..., Ф^(У).

Возьмем любые две функции Ф_г, Фу. Возможны две принципиально различные ситуации. В одной из них в многограннике А существуют две точки У, L такие, что, например, Ф/(У) -< Ф/(У), но ФДХ) -^ФДХ). Подобные функции будем называть лексикографически не упорядоченными на многограннике А. В другой ситуации для любых точек У из А имеем, например Ф_г(У) < ФД-0-Эти функции будем называть лексикографически упорядоченными. В частности, функции Ф/, Фу будут строго лексикографически упорядоченными,

если их значения относятся к опорным гнездам циклов, не имеющих общих параметров.

Пусть функции Ф/, Фу не являются лексикографически упорядоченными. Рассмотрим гиперплоскость, полученную приравниванием самых младших из общих координат Ф, и Фу. Она разделит многогранник А на три многогранника. На одном из них А/ ~< Ау, на другом А,- >- Ау и на третьем у функций Ф/, Фу совпадают младшие общие координаты. Первые два многогранника являются полуоткрытыми, т. к. в них не входят грани, соответствующие ги-

Глава 6. Тонкая информационная структура программ

371

перплоскости. Мы можем сделать эти многогранники замкнутыми, если изменим на ± 1 свободные члены уравнений гиперплоскостей этих граней. При этом в каждом многограннике сохранится множество целочисленных точек. Теперь рассмотрим функции Ф_г, Фу на третьем многограннике и повторим для него процедуру расщепления, приравняв следующие по старшинству общие координаты. Будем повторять процедуру расщепления до тех пор, пока не будут приравнены все общие координаты. В результате многогранник А будет расщеплен на многогранники A'_l5 ..., A'_q. Они линейные замкнутые непересекающиеся и в совокупности содержат те и только те целочисленные точки, в которые входят дуги простого графа. На этих многогранниках функции Ф_г и Фу лексикографически упорядочены. Если Ф/ < Фу на каком-то из многогранников и Ау целочисленная, то целочисленный лексикографический максимум из точек Ф_г-(/) и Фу (Г) всегда равен Фу(7) независимо от того, какова функция Ф/.

Процесс расщепления многогранника А можно продолжить, сравнивая поочередно все пары функций из Ф_ь ..., Ф^. Это позволяет привести описание простого графа к некоторому каноническому виду. В каноническом виде простой граф описывается системой линейных замкнутых непересекающихся многогранников Aj, ..., А/, расположенных в опорной области V-_t. На каждом из многогранников А,- заданы линейные функции Ф,-,..., Ф,-. Их значения

принадлежат разным опорным областям. Функции лексикографически упорядочены, т.е. Ф, -< Ф, -<-<Q>i для всех точек из многогранника А,.

Пусть / есть произвольная целочисленная точка из многогранника А/. Начальная точка дуги простого графа, входящей в точку /, есть последняя целочисленная точка в ряду точек Ф, (/),..., Ф, (/). Если в этом ряду нет целочисленных точек, то в точку / дуга простого графа не входит.

Заметим, что аналогичный канонический вид имеет место для элементарных и простых графов во всех случаях. Даже тогда, когда не выполняется условие утверждения 6.8. Единственное отличие будет состоять в том, что в общем случае значения разных функций Ф,-,..., Ф_л необязательно принадлежат разным опорным областям. Конечно, не ограничивая общности, можно считать, что среди функций, значения которых принадлежат одной и той же опорной области, нет совпадающих. Во всем остальном канонический вид сохраняется.

Выше мы предполагали при построении элементарного графа, что каждая из опорных областей описывается только одним многогранником. Теперь ясно, что отказ от этого предположения приводит к двухступенчатому процессу построения элементарного графа. Сначала строится семейство графов путем выбора всевозможных пар многогранников из V_} и V_t, а затем лексикографический максимум из них находится по только что описанной процедуре.

372

Часть II. Параллельное программирование

Всюду в дальнейшем мы будем считать, что любой минимальный граф программы из линейного класса представлен как объединение простых графов, описанных в каноническом виде. Как показывает анализ большого числа реальных программ, почти всегда набор Ф, ,..., Ф, состоит из одной

целочисленной функции. И лишь очень редко некоторые из наборов состоят из нескольких функций.

С формальной точки зрения предшествующие исследования относятся к минимальным снизу графам. Для минимальных сверху графов исследования и результаты отличаются незначительно. Прокомментируем эти различия на примере графа обратных зависимостей.

Понятия простой и элементарной программы остаются такими же, как для графа алгоритма. Утверждения 6.3 и 6.4 снова имеют место. Основная задача (6.13)—(6.15) заменяется на следующую: найти целочисленную функцию Jq = = /₀(Л Ю, где

/₀ = lex.min /, p(J, N) = q(J, N) J у I, Je Qj, I £ Q/.

Естественно, что в тексте начальная и конечная вершины дуги меняются местами. Опять сначала решаем непрерывную задачу. Справедлив аналог утверждения 6.7. Нужно лишь в определении Z-свойства слово "положительный" заменить словом "отрицательный", а в тексте утверждения слово "максимума" заменить словом "минимума". При построении альтернативных многогранников неравенства меняются на противоположные и —1 в них заменяется на +1. При построении простых и им подобных графов из функций Ф_;],...,Ф, надо выбирать не лексикографически старшую, а лексикографически младшую. Во всем остальном построение элементарного и простого графов остается без изменения.

Сложность построения минимальных графов зависимостей во многом определяется возможной неединственностью решений уравнения (6.13). Среди всех его решений / необходимо найти лексикографически ближайшее к точке / снизу. Именно это обстоятельство вносит в процесс наибольшие трудности. Неединственность решений уравнения (6.13) имеет место тогда и только тогда, когда значения переменных пересчитываются более одного раза. Однако пересчет полностью отсутствует в программах на языках однократного присваивания и в любых математических соотношениях. Ничто не мешает математические соотношения оформлять как программы без пересчета значений переменных. В этом случае уравнение (6.13) либо не будет иметь ни одного решения, либо будет иметь только одно. Процесс построения минимальных графов значительно упрощается, а некоторые графы просто пропадают. Например, графы зависимостей по выходу и графы антизависимостей всегда будут пустыми.

Глава 6. Тонкая информационная структура программ

373

Вопросы и задания

1. Внимательно проанализируйте примеры 6.1—6.4 из § 6.8 с точки зрения процесса построения минимальных графов зависимостей.

2. В чем меняется процесс, если строятся минимальные графы зависимостей других типов?

3. Опишите процесс построения минимальных графов зависимостей для случая, когда ни одна переменная в программе не пересчитывается.

§ 6.7. Циклы ParDO

и избыточные вычисления

Отметим, что покрывающие функции не могут быть произвольными линейными функциями. Все графы зависимостей обладают общим свойством. Именно, для каждой дуги конечная вершина лексикографически старше начальной. Такие графы называются лексикографически правильными. Любой лексикографически правильный граф является ациклическим.

Изучение параллельной структуры программ связано с изучением множеств операций, которые можно выполнять независимо друг от друга. Дадим определения соответствующих понятий. Пусть в пространстве итераций задан ориентированный лексикографически правильный граф G. Это может быть какой-нибудь из минимальных графов зависимостей или некоторый подграф любого из объединений минимальных графов или какой-либо другой граф. Если программа зависит от внешних переменных, то от них будет зависеть и граф G Рассмотрим непересекающиеся множества М\, ..., М_р вершин пространства итераций. Назовем эти множества параллельными по графу G или просто параллельными, если при любых фиксированных значениях внешних переменных:

□ любой путь графа G, связывающий две вершины одного множества, целиком лежит в этом множестве;

□ никакие две вершины из разных множеств не связаны путем графа G.

Понятие параллельных множеств имеет очень прозрачный смысл. Допустим, что граф G является объединением всех четырех минимальных графов. Предположим, что выполнены все операции, которые соответствуют начальным вершинам дуг, идущих в точки одного множества. Тогда можно начинать выполнение операций этого множества независимо от того, выполняются или не выполняются какие-либо другие операции, в том числе, операции из других множеств. При этом гарантируется, что получаемые результаты будут правильными.

Под параллельной структурой программы мы будем понимать совокупность сведений о параллельных множествах в пространстве итераций. Сюда же

374

Часть II. Параллельное программирование

будем относить и сведения о тех преобразованиях, целью которых является либо выявление, либо изменение параллельных множеств. Говоря о параллелизме в программах, обычно обсуждают два его вида: макропараллелизм и микропараллелизм. Макропараллелизм связан с ситуацией, когда все или хотя бы часть из параллельных множеств содержат много точек. Микропараллелизм имеет дело с теми случаями, при которых в каждом из параллельных множеств находится всего лишь несколько точек. Типичным для микропараллелизма является ситуация, когда множества содержат только по одной точке. В частности, параллельными будут те множества-точки пространства итераций, которые не связаны дугой графа G.

Рассмотрим какой-нибудь цикл do произвольной программы из линейного класса. Его также можно считать программой из линейного класса. Параметры циклов, внешних по отношению к данному циклу do, играют в нем такую же роль, как и внешние переменные программы. Их значения хотя и фиксированы к началу выполнения цикла, но на момент исследования неизвестны. Можно лишь утверждать, что вектор параметров внешних циклов является целочисленным и принадлежит совокупности линейных многогранников. Рассмотрим далее пространство итераций цикла do. Все его точки можно разбить на непересекающиеся множества, если отнести к каждому множеству те из них, которые соответствуют одной и той же итерации цикла. Обозначим эти множества через М\, ..., М_р. Пусть в пространстве итераций цикла введен ориентированный лексикографически правильный граф G. Будем говорить, что цикл имеет тип ParDO по графу G, если множества М\, ..., М_р параллельны по этому графу при любых допустимых, но фиксированных значениях внешних переменных.

Заметим, что при любых значениях внешних переменных группы операций, соответствующие множествам М\, ..., М_р, могут выполняться последовательно друг за другом без выполнения каких-либо других операций. Это означает, что если множества М\, ..., М_р параллельны по графу G, то несвязанность путем любой пары точек, принадлежащих различным множествам M_h эквивалентна их несвязанности дугами. Поэтому имеет место

Утверждение 6.10

Пусть в пространстве итераций цикла do задан ориентированный лексикографически правильный граф G. Для того чтобы цикл do был циклом ParDO по графу С, необходимо и достаточно, чтобы никакая пара точек пространства итераций, соответствующих одним и тем же значениям параметров внешних циклов, но различным значениям параметра рассматриваемого цикла, не была бы связана дугой графа G.

Теперь рассмотрим для цикла do его минимальные графы зависимостей или какие-нибудь объединения этих графов.

Если цикл do имеет тип ParDO по графу алгоритма, то никакие пары точек пространства итераций, соответствующие разным итерациям цикла, не могут быть связаны дугами графа алгоритма. Это означает, что при последова-

Глава 6. Тонкая информационная структура программ

375

тельном исполнении цикла результаты реализации операций, относящихся к разным итерациям цикла, не влияют друг на друга. Потенциально итерации цикла ParDO по графу алгоритма можно выполнять независимо друг от друга. Однако для осуществления такой возможности нужно быть уверенным в правильности порядка пересчета значений одних и тех же переменных на разных итерациях цикла.

Пусть цикл do имеет тип ParDO по объединению графов алгоритма, антизависимостей и зависимостей по выходу. В этом случае в цикле не существует ни одной пары операций, относящихся к разным итерациям, в которых одна и та же переменная или пересчитывается, или пересчитывается и используется. Однако могут существовать пары операций, в которых используется одна и та же переменная. Итерации такого цикла можно выполнять в любом порядке. При этом гарантируется правильность получаемых результатов. Циклы подобного типа можно реализовывать на любых многопроцессорных вычислительных системах. Но наиболее эффективно они реализуются на системах с общей памятью. На системах с распределенной памятью возможны большие временные потери из-за межпроцессорных обменов.

Предположим, наконец, что цикл do имеет тип ParDO по объединению всех четырех минимальных графов зависимостей. Теперь любые пары операций из разных итераций циклов всегда имеют дело с разными переменными. Поэтому такие циклы эффективно реализуются на любых вычислительных системах, в том числе и на многопроцессорных системах с распределенной памятью.

Таким образом, графы зависимостей цикла do играют исключительно важную роль в распознавании параллельных свойств цикла. В силу этого необходимо иметь эффективные критерии установления свойства ParDO по таким графам. Пусть граф G представлен покрывающими функциями вида х = Jy + ф. Здесь / числовая матрица, вектор ср линейно зависит от внешних переменных цикла, векторы х и у задают точки пространства итераций цикла. Заметим, что параметру цикла соответствуют первые координаты векторов х, у. Один из критериев таков.

Утверждение 6.11

Пусть граф С задан покрывающими функциями вида х = Jy + ср. Для того чтобы цикл имел тип ParDO по графу С, достаточно, чтобы граф G был пустым или для всех покрывающих функций первое равенство в выражениях х = Jy + ср имело вид xi = у\.

Почти всегда это условие на практике оказывается и необходимым. Например, оно заведомо будет таким, если граф описывается покрывающими функциями точно и покрывающие функции являются целочисленными.

В заключение отметим следующее. Мы описали критерий принадлежности цикла типу ParDO на основе графов, построенных для цикла. Критерий оказался очень простым. Но если мы хотим исследовать много циклов, то придется строить и много графов, например, графов зависимостей. Вообще говоря, можно было бы поступить иначе. Именно, ввести графы в пространстве

376

Часть II. Параллельное программирование

итераций программы в целом и построить критерий принадлежности цикла типу ParDO на основе анализа свойств этих графов. Такая идея реализуется конструктивно. Однако мы не будем ее развивать здесь по следующим причинам. Во-первых, критерий становится несколько сложнее. Он связан с установлением целочисленной совместности некоторых целочисленных систем относительно небольших размеров. Во-вторых, графы нужного вида не всегда можно построить для программы в целом из-за каких-то особенностей, не относящихся к исследуемому циклу. И, наконец, алгоритм построения графов зависимостей оказался столь эффективным, что его многократное применение не приводит к большим дополнительным временным затратам.

Конечно, определение циклов ParDo далеко не исчерпывает сферу применения графов зависимостей. В качестве еще одного, вообще говоря, нетривиального примера их прямого использования укажем на возможность отыскания так называемых избыточных вычислений. Предположим, что некоторая переменная получила значение а, а затем значение р. Если значение а нигде не было использовано, то соответствующее ему вычисление и называется избыточным.

Причин появления в программе избыточных вычислений может быть достаточно много. Во-первых, это желание написать компактную программу. Следующий фрагмент

DO / = 1, П DO j = 1, П

END DO

a„ = 1

END DO

представляет типичную программу получения единичной матрицы. Каждый диагональный элемент во внутреннем цикле сначала определяется нулем, а затем заменяется на единицу без использования нулевого значения.

Во-вторых, распространенной причиной избыточных вычислений являются обычные ошибки программирования. Допустим, что программист захотел найти сумму элементов каждой строки матрицы А, но сделал ошибку и в последнем операторе присваивания вместо переменной s написал ss. В итоге получилась такая программа

DO / = 1, П

s = 0

DO j = 1, П

s = s + a,j

END DO

bj=ss

END DO

Глава 6. Тонкая информационная структура программ

377

Данная ошибка приведет к появлению избыточных вычислений: значение переменной s, вычисленное на последней итерации внутреннего цикла, нигде не использовано, а затем на следующей, кроме последней, итерации внешнего цикла переменная s примет значение 0. И, наконец, источником многочисленных избыточных вычислений оказываются постоянные переделки программ, когда вычеркиваются группы операторов, вставляются "заплатки" и при этом нередко что-то остается в программах лишнее.

Умение находить избыточные вычисления — важная задача. Очевидно, что избыточные вычисления будут генерировать те и только те точки пространства итераций, из которых выходит дуга графа зависимостей по выходу, но не выходит ни одна дуга графа алгоритма. Зная покрывающие функции указанных графов, обнаружить избыточные вычисления совсем не трудно.

Вопросы и задания

1. Пусть пространство итераций линейной программы разбито на непересекающиеся множества My, ..., М_р и на этом пространстве задан лексикографически правильный граф G. Докажите, что для того, чтобы множества My, ..., М_р были попарно параллельны по графу, необходимо и достаточно, чтобы они не были связаны дугами графа G.

2. В чем различие и общность утверждения п. 1 и утверждения 6.10?

3. Какими свойствами дополнительно обладают множества My, ..., M_pva п. 1, если в качестве графа С взять минимальный граф зависимостей определенного типа или объединение всех четырех минимальных снизу графов?

4. В чем различие и общность утверждения п. 3 и исследования, проведенного ранее для цикла do?

5. Пусть My, ..., М_р представляют множества точек отдельных итераций цикла DO, упорядоченные по параметру цикла. Покажите, что My, ..., М_р образуют ярусы обобщенной параллельной формы любого лексикографически правильного графа.

6. Укажите условия, при которых множества My, ..., М_р образуют ярусы строгой параллельной формы лексикографически правильного графа.

7. Рассмотрим линейное тесно вложенное гнездо циклов. Предположим, что все циклы этого гнезда имеют тип ParDO по лексикографически правильному графу С. Докажите, что никакие точки пространства итераций гнезда циклов не связаны дугами графа С.

8. Сохранятся ли полученные выше результаты, если отказаться от требования, чтобы граф С был лексикографически правильным?

9. Как за конечное число действий проверить лексикографическую правильность графа, если он задан линейными функциями на линейных многогранниках?

10. Насколько упрощается процесс реализации циклов ParDO, если в исходной программе не пересчитывались никакие переменные?

378

Часть II. Параллельное программирование

§ 6.8. Примеры

Во всех приводимых здесь примерах мы снова ограничимся рассмотрением графов алгоритмов. Основная цель заключается в иллюстрации различных теоретических понятий и действий из §§6.3—6.7. Начнем с тех примеров, которые уже исследовались в §4.4.

Пример 6.1. Запись основной части алгоритма (4.5) вычисления произведения двух матриц такова:

DO i=l,n DO j=\,n DO k=\,n

a,j = a,j+b„fi_kj

END DO END DO END DO

Эта программа есть тесно вложенное гнездо циклов с параметрами /, j, к. Параметр / самый младший, параметр к самый старший. Опорное пространство единственного оператора имеет размерность 3. Опорный многогранник V совпадает с опорной областью, т. к. отсутствуют альтернативные операторы.

Линейное пространство итераций совпадает с опорным многогранником К и представляет трехмерный куб 1 < /,_/', к < п. Пространство итераций Q описывается множеством точек в этом кубе, имеющих целочисленные координаты /, у, к. Согласно утверждению 6.3, граф алгоритма есть объединение графов алгоритмов всех простых программ. Всего существует три простые программы и они имеют вид:

□ DO / = 1, П П DO / = 1, П П DO / = 1, П


DO j	= 1,	Я
	DO	*к=У,*	Я
		*^aij =*	ay
	END	DO
END	DO
) DO

DO j = 1, Я DO j = 1, Я

DO к = 1, Я DO к = 1, Я

0 = Ъ_1к 0 = c_kj

END DO

END DO END DO

END DO

где символ 0 означает пустую часть оператора. Ясно, что в данном случае все простые графы зависимостей совпадают с элементарными. Переменные с именами b и с не пересчитываются. Поэтому графы алгоритмов для двух последних простых программ будут пустыми, т. е. не имеющими ни одной дуги. Следовательно, граф алгоритма для примера 6.1 совпадает с графом алгоритма первой простой программы.

Глава 6. Тонкая информационная структура программ

379

Рассмотрим для нее задачу (6.13)—(6.15). Вектор N одномерный и его единственная координата равна п > 1. В обозначениях задачи точка / имеет координаты /= (i,j, к). Предположим, что искомая точка / обладает координатами J~ (i',J^:'> к'). Соответственно q(I, N) = (i,j), p(J, N) = (i',j). Векторное равенство (6.13) превращается в систему линейных алгебраических уравнений

'' = '. j'=j относительно неизвестных i',j', к'. Ясно, что /' = /, / = j, и остается определить неизвестное к' из условий, что точка / обеспечивает лексикографический максимум при J < I, J е Q. Согласно общему процессу для этого нужно найти лексикографический максимум во втором альтернативном многограннике (6.17). Он описывается соотношениями

' ' = i,j'=j,k'<k-l, 1 < /', /, к', /, j, к<п.

Даже не используя Z-свойство, очевидно, что к' = к — 1, если п > 2 и 2 < к < п — 1. Появившееся ограничение п > 2 вместо допустимого ограничения п > 1 отражает тот факт, что при п = 1 граф алгоритма будет содержать только одну вершину и, следовательно, не будет иметь ни одной дуги. Покрывающая функция Ф графа алгоритма одна. Она имеет вид

flOO^ 010 001

(

о 1

определена на многограннике 1 < / < я, l<j<n, 2<k<nu описывает граф точно. Как и следовало ожидать, граф алгоритма, определенный по формальным правилам, полностью совпадает с графом на рис. 4.3, а, который был угадан интуитивно. Принимая во внимание вид покрывающей функции Ф, заключаем согласно утверждению 6.11, что два внешних цикла рассматриваемой программы перемножения матриц имеют тип ParDO.

Пример 6.2. Исследуем теперь формальным образом алгоритм (4.7). Его запись выглядит следующим образом:

1 X\ = bi

DO Х = 2,П

2 X; = bi

DOj=l,i-l (6.20)

END DO END DO

В программе имеется два параметра /, j. Параметр / младше параметра j. Оператору F_k соответствует оператор с меткой, равной к. С этими операто-

380

Часть II. Параллельное программирование

рами связаны следующие опорные пространства: с оператором F\ пространство нулевой размерности, с оператором Fi пространство размерности 1 с координатой /, с оператором Ft, пространство размерности 2 с координатами /,_/'. Опорное гнездо, например, для оператора с меткой з таково:

DO 7 = 2, «

DO 7= 1,/-1

о X/ X/ ciipvj

END DO END DO

Опорный многогранник V\ для оператора F\ есть точка, опорный многогранник Кг для оператора Fj есть отрезок 2 < i < п, опорный многогранник Vj для оператора Fj есть треугольник, заданный неравенствами 2 < / < «, 1 <_/'< / — 1. Будем считать, что единственная точка из V\ имеет координату z ⁼ 0. Опорные многогранники совпадают с опорными областями, т. к. отсутствуют альтернативные операторы. Линейное пространство итераций есть объединение отрезка V₂, треугольника К₃ и точки, соответствующей оператору F\. Операционное содержание вершин из многогранника Vj иное, чем у вершин из многогранников V\ и К₂.

Программа (6.20) расщепляется на 5 простых программ по общему числу всех входов всех ее операторов. Так как не все входные переменные пере-считываются в программе, то нужно рассмотреть только две простые программы. Это

❒ 1


xi = 0 ❒	1	XX =0
DO i = 2,n		DO i = 2,n
_Xi = 0	2	_Xi=0
DOj= 1, i- 1		DOj= 1, i- 1
Xi — Xi	3	Xi — Xj
END DO		END DO
END DO		END DO
простая программа из (6.21) расще
*i = 0		❒ DO / = 2, n
do *i = 2,n*		2 Xi = 0
D0J= 1,/-1		D0j= 1, /-1
*0=_Xi*		3 0=Xi
END DO		END DO

(6.21)

❒ 1

X\ = 0 ❒ do / = 2, n ❒ do / = 2, n

D0j= 1, /-1

X;=X; (6.22)

END DO END DO

Глава 6. Тонкая информационная структура программ

381

END DO END DO

Вторая простая программа из (6.21) также расщепляется на 3 элементарные:

❒ 1


*1 = 0	❒	do *i = 2,n*	❒	do *i =* *2,n*
DO Х = 2,П	2	*x, = 0*		D0j= \,i-	-1
DOy'= \,i-\		D0j= 1, 7-1	3	*X, = Xj*
<Z>=Xj	3	0=JCy		END DO
END DO		END DO		END DO
END DO		END DO

(6.23)

Первый элементарный граф из (6.22) пустой, т. к. пересчитанное значение переменной х\ в операторе с меткой 1 нигде не используется в операторе с меткой з в силу ограничения 2 < i < п. Остальные элементарные графы непустые. Покрывающие функции элементарных графов будем помечать двумя или тремя индексами. Первый индекс снизу означает номер по метке опорного пространства, в котором расположена область определения функции. Второй индекс снизу означает номер по метке опорного пространства, в котором расположена область значений функции. Если функций с одинаковыми нижними индексами несколько, то они различаются верхними индексами. Стрелка в обозначениях вида V_t -> Vj относится не к дугам графа, а лишь показывает, где у покрывающей функции находится область определения и куда она отображается. Дуги графов всегда имеют обратное направление. Итак, покрывающие функции для элементарных графов таковы:

Ф₁₃ = 0;

(1,0)

2 < i< n, 1 <j < i ( (П

1, V₃ -> V₂;

П<П

■1

, 3</</j, 2<y</-l, K₃-> V₃;

Ф₁₃ = (0, 0)

2<i<n, /=1, K₃-> Vi,

, 3<i<n, 2<y< 1, V₃^ V₂;

Ф23 = (0, 1)

fOlV/^

( (П

3 <i<n, 2<j<i- 1, V₃ -^V₃

382

Часть II. Параллельное программирование

Напомним, что в концевых точках каждой дуги пересчитывается и используется одна и та же переменная. В каждой точке всех элементарных графов, относящихся к одной и той же простой программе, также используется одна и та же переменная. Именно эти обстоятельства дают возможность убирать лишние дуги при объединении элементарных графов в простой граф. В частности, по данной причине при построении простого графа для первой простой программы из (6.21) от второй элементарной программы из (6.22) остаются только дуги, входящие в вершины приу= 1. Все остальные дуги "перекрываются" дугами из третьей элементарной программы. По этой же причине при построении простого графа для второй простой программы из (6.21) не входит ни одна дуга от второй элементарной программы из (6.23). Все они "перекрываются" дугами из третьей элементарной программы в (6.23).

Рис. 6.11. Опорные многогранники

Вообще говоря, опорные многогранники могут располагаться относительно друг друга как угодно. Однако в целях наглядности или в каких-либо иных целях бывает удобно располагать их рядом в одном пространстве. Такое размещение опорных многогранников для примера 6.2 приведено на рис. 6.11 для п = 5. Здесь вершина в верхнем левом углу находится в точке с координатами /= 1, j= 0. Координаты соседних точек различаются на 1. Сейчас выбор расположения опорных многогранников определяется желанием сравнить граф алгоритма (4.7), представленный на рис. 4.4, а, и граф алгоритма (6.20), построенный формальным образом. Суммируя сказанное о покрывающих функциях простых графов для простых программ из (6.21) и принимая во внимание выбранное размещение для опорных многогранников, заключаем, что покрывающие функции для графа алгоритма, описанного программой (6.20), будут иметь следующий вид:

Глава 6. Тонкая информационная структура программ

383

Ф,

Гооул

ГП

1, K,-> Vu

чЛ

о,

,2<i<n, j

Ф,

ПоУЛ

( 0\

2</<л, y=l, K₃-> K₂;

-1

Ф,

roiV/^

3</</j, 2<y</-l, K₃^ K₃:

По

kJj

Ф₄

3</<л, 2 <y</-l, K₃^ K₃.

Легко проверить, что описываемый этими функциями граф полностью совпадает при п = 5 с графом на рис. 4.4, а. Покрывающие функции описывают граф алгоритма точно. Из утверждения 6.11 не следует, что хотя бы один цикл имеет тип ParDO. И это действительно так, что видно из рис.4.4, а. Но из этого же рисунка видно, что параллелизм имеется на множествах точек пространства итераций, параллельных оси / или, что в данном случае одно и то же, перпендикулярных оси у. Этот параллелизм не описывается циклами типа ParDO непосредственно. Опять же из рисунка видно, что циклы по / и/ можно переставить и тогда отмеченный параллелизм уже будет описываться циклом ParDO. К этим вопросам мы вернемся в главе 7.

Пример 6.3. Таким же образом исследуем алгоритм (4.8). Его запись выглядит следующим образом:

1 Ху = Ьу

DO / = 2, П

2 x,= b, _(6J4)DO /=/"1, 1,-1

END DO END DO

Формально эта программа не принадлежит к линейному классу, т. к. шаг изменения параметра у во втором цикле равен — 1, а не +1. Сделав замену переменных у = i — z, приведем ее к линейной:

Ху = Ьу

DO / = 2, я

ж,- = Ь,

(6.25)

DO Z = 1, / - 1

384

Часть II. Параллельное программирование

END DO END DO

В целом анализ программы (6.25) осуществляется по той же схеме, что и для программы (6.20). Программа (6.25) тоже расщепляется на 5 простых программ, из которых 3 простые программы имеют пустые графы алгоритмов. Каждая из двух оставшихся простых программ расщепляется на три элементарные. Мы не будем проводить детальный анализ программы (6.25), а ограничимся тем, что приведем покрывающие функции для графа алгоритма, описанного программой (6.24). Чтобы иметь возможность сравнить полученный граф с графом на рис. 4.4, б, расположим опорные многогранники V\, Vj, V₃ программы (6.24) так, как они показаны на рис. 6.12. Здесь верхняя угловая вершина находится в точке с координатами / = 1, j = 1. Покрывающие функции имеют следующий вид:

Ф =

+ . , 2 < / < n, j = 1, К₃ -> V_x;

v j

ф,

АОУП (

< (П i

2</<л, у=1, К₃-> К₂;

vJ/

Ф,

foiyn

3 < /<«, 2<j<i- 2, V₃ -> V₃;

Ф₄

3 <j + 1 < i<n, V₃^ V₃.

Рис.6.12. Опорные многогранники

Глава 6. Тонкая информационная структура программ

385

Снова они описывают граф алгоритма точно. По всем критериям и рис. 4.4, б видно, что никакого параллелизма в алгоритме примера 6.3 нет.

Пример 6.4. Пусть элементы и^ одномерного массива переставляются по такому алгоритму

DO / = 1, П DO j = 1, П

^ui+j⁼ ^u2n + l-i-j

END DO

Эта программа интересна, с одной стороны, своей предельной простотой и, с другой стороны, зависимостью индексных выражений от внешних переменных. Посмотрим еще раз, как для данного примера строится формально граф алгоритма. В программе имеется одна входная переменная и₂и + i - /-у ^и одна выходная переменная щ+j. Поэтому существует только один элементарный граф и он совпадает с графом алгоритма в целом. Линейное пространство итераций V представляет квадрат 1 < /, j < п. Приравнивая индексы переменных, заключаем, что при построении графа всегда придется решать уравнение

/' +/ = 2п+ 1 - i-j (6.26)

относительно неизвестных /', /, где

1</', /, U ]<п. (6.27)

На множестве решений уравнения (6.26) при ограничениях (6.27) необходимо найти точку с координатами /', /, которая лексикографически ближе всего снизу к точке с координатами /, j.

Согласно (6.17), второй альтернативный многогранник, определяющий условия лексикографического предшествования, описывается следующим образом

/' = /,/< у-1. (6.28)

Из равенства (6.26) и равенства в (6.28) получаем систему линейных алгебраических уравнений

»'+/ = 2л+ I- i-j;

V = i.

Отсюда находим, что

'' ⁼ '' (6.29)

/ = -2i-j+ 2п+ 1.

Подставляя эти выражения для /', / в неравенства (6.27) и в неравенство из (6.28), заключаем, что должны выполняться такие неравенства:

1 < / < л;

l<j<n;

386

Часть II. Параллельное программирование

1 <2п+ 1 -2i-j<n; (6.30)

п+ 1 < i+j. При тех значениях /, j, которые удовлетворяют этой системе неравенств, граф будет задаваться функцией (6.29). Перепишем систему (6.30) в таком виде

2i+j<2n; (⁶-³¹>

п + 1 < / + у.

Ее совместность теперь очевидна.

Рассмотрим третий альтернативный многогранник (6.19). Он описывается так:

/' < / - 1.

Из уравнения (6.26) находим, что

f = 2n+l-i-j- /'. (6.32)

Подставим это выражения для j' в (6.27). Соберем вместе все неравенства для /', представив их в виде (6.3). Имеем

/' < л;

~'" * ~ ^1; (6-33)

— i' < i + j — п — 1;

/' < — i — j + 2n;

V < / - 1

и, кроме этого,

i < i< n, 1 <j< n. (6.34)

Из системы неравенств (6.33) необходимо выбрать такие подсистемы, матрицы которых относительно определяемых параметров обладают Z-свойством. Так как неизвестный параметр только один, то порядок матриц будет равен 1. Такие матрицы обладают Z-свойством тогда и только тогда, когда их единственный элемент положительный. Следовательно, для определения параметра /' из системы (6.33) необходимо рассмотреть лишь первое, четвертое и пятое неравенства.

Первое неравенство /' < п дает /' = п. При этом условии последнее неравенство из (6.33) всегда оказывается невыполненным, если принять во внимание (6.34).

Четвертое неравенство /' < — / — j + 2п дает /' = — / —j + 2п. Из (6.32) находим, что у' = 1. В этих условиях неравенства (6.27), (6.33) становятся такими

1 < / < п; (6.35)

l<j<n;

Глава 6. Тонкая информационная структура программ

387

я < i + у <2n — 1; 2я + 1 < 2/ + у. Множество решений системы (6.35) не пересекается с множеством решений системы (6.31). Оно описывается также неравенствами

/< я;

j ^ п;

(6.36) i + j<2n-l;

In + 1 <2i+j.

На этом множестве граф задается функцией

i' = -i-j+2n; ₍₆₃₇₎

Г = 1-Пятое неравенство i < / — 1 дает /' = / — 1. Из (6.32) находим, что у' = — 2/ — — у + 2я + 2. В этих условиях неравенства (6.27), (6.33) становятся такими:

2 < / < я;

1<у<я; (б-³⁸)

n + 2<2i + j<2n + 1.

Множество решений системы (6.37), не принадлежащих системе (6.31), описывается неравенствами

/+у<я; (6-39)

я + 2 < 2/ + у. На этом множестве граф алгоритма будет задаваться функцией

^l' ⁼ ^l~^l'> (6.40)

У = - 2i-j+ 2п + 2.

Множества (6.31), (6.36), (6.39) не покрывают все целочисленные точки квадрата 1 < / < я, 1 <у < я. Остается область, описываемая неравенствами

1 < /; (б-⁴¹)

2/ + у<я + 1,

а также целочисленная точка с координатами (я, я). Во всех этих точках в качестве аргумента операции берется одно из входных данных.

Итак, для примера (6.4) множество функций, покрывающих граф алгоритма,

388

Часть II. Параллельное программирование

выглядит следующим образом:

( 1 ovn ( -П

на многограннике (6.39);

-2-1

^ 1

2-1

In + 2

О ^Л2л+ 1

Фо =

на многограннике (6.31);

(6.42)

yJy

(2п\ 1

на многограннике (6.36).

l-i vn

Ф4

О О

Все эти функции действуют из V в V. На многограннике (6.41) и в точке с координатами (п, п) покрывающие функции не определены. Будем считать условно, что здесь заданы пустые функции соответственно Ф] и Ф₅. Их введение удобно для последующих иллюстраций. На рис. 6.13 представлены области определения функций Ф]—Ф₅. Здесь на области с номером /задана функция Ф/. Область с номером / расположена между сплошной линией слева от цифры / и пунктирной линией справа от той же цифры. На рисунке приведены уравнения сплошных линий. Уравнения соседних пунктирных линий получаются из них уменьшением свободных членов на 1. Совокупность (6.42) покрывающих функций представляет граф алгоритма точно.

Рис. 6.13. Области определения покрывающих функций

Рассмотренный пример показывает неожиданную ситуацию. Оказывается, что даже в простейших по форме записи алгоритмах поведение дуг их графов может описываться довольно сложно, но в то же время точно. Следовательно, простота записей алгоритмов не является гарантией простоты информацион-

Глава 6. Тонкая информационная структура программ

389

ных связей. Не в этом ли факте скрывается причина многочисленных трудностей изучения тонкой структуры алгоритмов и программ?

Теперь рассмотрим процесс построения графа алгоритма для внутреннего цикла примера 6.4. Условие совпадения значений параметра внешнего цикла для концевых вершин дуг графа дает равенство /' = /. Поэтому из равенства (6.26) заключаем, что

'' ⁼ '' (6.43)

j' = 2n+ 1-2/ -j.

Снова должны выполнятся неравенства (6.27). Кроме этого, должно быть справедливо неравенство предшествования/ <j— 1. Собирая все неравенства и подставляя в них значения /',_/' из (6.43), находим, что покрывающая граф функция только одна и ее можно, например, записать в следующем виде:

ф"

( 1 ovn ( о ^

(6.44)

2-1

yJy

2n + l

Она задана на многограннике

2i+j<2n;

(6.45)

n+ 1 < / + j;

V = i.

Мы специально записали функцию Ф" и область ее определения в таком виде, чтобы обратить внимание на совпадение Ф" с функцией Ф₃ из (6.42). Дело в том, что граф алгоритма для внутреннего цикла примера 6.4 можно было бы находить из представления (6.42) графа целиком. Для этого из всех дуг (6.42) надо оставить только те, для концевых точек которых значения первых координат совпадают. Такие дуги в данном конкретном случае описываются лишь функцией Ф3.

Из представления (6.44), (6.45) легко находим вид покрывающей функции (6.44), соответствующий теореме 1. Именно,

Ф"С/) = 2л+ 1-2/ -j. Задана она на отрезке

п + 1 - / < j < п,

если 1 < / < я/2, если я/2 < / < п -

(6.46)

п + 1 — / < j < 2п — 2/,

На дополнительных отрезках

1 <j < п - i и 2п - 2/ + 1 <j < п, если [я/2] + 1 < / < п - 1, (6.47)

покрывающая функция Ф" не определена. В этих точках в качестве аргумента операции берется либо одно из входных данных, либо какое-то зна-

390

Часть II. Параллельное программирование

чение функции, вычисленное при меньших значения параметра /. Снова будем считать, что на дополнительных отрезках заданы соответственно пустые функции Ф' и Ф'".

В примере 6.4 ни один из циклов не является циклом ParDO. Тем не менее, параллелизм в этом примере имеется, и он значителен. Интересно отметить, что пример 6.4 пропускался на многих зарубежных параллелизующих компиляторах и автономных системах выявления параллелизма, но всюду безуспешно. Это что-то говорит об уровне используемых технологий анализа структуры программ.

Пример 6.5. Рассмотрим программу решения системы линейных алгебраических уравнений Ах = b методом Жордана без выбора ведущего элемента.

DO к = 1, п

1 k = 1М*

DO р = 2, П

2 lp⁼~ ^apk

END DO

DO j = к + 1, n + 1

3 Uj = «i/i do i=2, n

END DO

5 a_nj = Uj

END DO END DO

Здесь в массиве А элементов ay размеров n(n + 1) в первых п столбцах задаются столбцы матрицы А системы, в последнем столбце — правая часть Ь. На месте матрицы системы получается обратная к ней матрица А~¹, на месте правой части — решение х. Этот пример более сложный. Рассмотрим его с точки зрения принадлежности циклов типу ParDo по графу алгоритма. Покрывающие функции Ф^ будем помечать тремя индексами снизу и одним

сверху. Первый индекс снизу означает номер по метке опорного пространства, в котором расположена область определения функции. Второй индекс снизу означает номер по метке опорного пространства, в котором расположена область значений функции. Третий индекс снизу означает номер входа оператора, к которому относится функция. Если функций с одинаковыми нижними индексами несколько, то они различаются верхними индексами. Мы не будем разбирать процесс построения графа, а воспользуемся V-Ray System для его получения. Будем считать, что п > 3.

Глава 6. Тонкая информационная структура программ

391

Имеем

Ф|41


Г¹]		Г-П
1	к +	0
0 V )		2

, 2<к<п;

(Ю\(к\

, 2 < к < n, р = п;

, 2<к<п, 2 < р<п-1;

251

v /

уР;

V /


Ю" 10	V	+	0
01 V /	W		1

241


КГ 01	'Г	+	'-Г 0
00 V /	UJ		2

, 2<k<n, k + l<j<n + l;

341

Ф₃12 = (1 0)

(к\

, 1<к<п, к + l< j <п + \;

yJj


Г¹⁰⁰!	*(кЛ*		(-\\
010	j	+	0
001 V /	i V )		1

, 2<k<n, k + l<j<n + l, 2 < / < я - 1;

441


Г¹⁰⁰!			f^_1l
010 V /	J i V )	+	0

, 2< к < n, к + l< j <n + l,i = n;

451

Ф₄22

10 0"

001

V /

ГАЛ

, 1 < к < n, k + l<j<n + l, 2<i<n;

v j


	f¹⁰⁰l	V
	010 V /	J i V /

, 1 < к < n, k + l<j<n + l, 2 < i < n;

432

10"

V /

(k\

, l<k<n, k + \<j<n + \.

531

yJ;

Цикл по параметру к не имеет тип ParDO. Это следует из того, что существуют покрывающие функции, например, Ф[₄₁, Ф'₂51 и др., у которых аргументы и значения имеют разные координаты, соответствующие параметру к.

392

Часть II. Параллельное программирование

Цикл по параметру р имеет тип ParDO, что вытекает хотя бы из отсутствия покрывающих функций вида Ф^* • Граф алгоритма для него пустой. В пространстве итераций цикла по параметру j действуют функции Ф₃₄1, Ф441»

Ф451 > Ф432 ^и ^ki • Для ^всех ^них аргументы и значения имеют одни и те же координаты, соответствующие параметру j. Поэтому данный цикл заведомо имеет тип ParDO. В пространстве итераций цикла по параметру / действует

только одна функция Ф₄₄1 • Для нее аргументы и значения имеют разные координаты, соответствующие параметру /. Но аргумент всегда лексикографически старше значения. А т. к. для функции Ф₄₄1 координата аргумента,

соответствующая параметру /, меньше аналогичной координаты значения, то граф алгоритма для цикла по параметру / пустой, а цикл имеет тип ParDO.

Заметим, что тип ParDO по графу алгоритма означает лишь потенциальную возможность выполнять итерации цикла параллельно. Чтобы она была реальной, нужно чтобы на разных итерациях не использовались одни и те же переменные. Этому условию удовлетворяют циклы по параметрам р и j. Однако цикл по параметру / ему не удовлетворяет, хотя граф алгоритма для данного цикла пустой. Формально это обстоятельство иллюстрируется тем, что для цикла по параметру / не является пустым минимальный граф антизависимостей.

Обратим также внимание на то, что в данном цикле непустота графа антизависимостей связана с глобальными переменными. Поэтому вводить новые переменные для устранения антизависимостей следует аккуратно.

Глава 7

Эквивалентные преобразования программ

Если бы строители возводили здания

так же, как программисты пишут

программы, первый залетевший дятел

разрушил бы цивилизацию.

Из законов Мерфи

В предыдущей главе мы познакомились с фундаментальными основами изучения тонкой информационной структуры алгоритмов и программ. Они были связаны с введением и построением минимальных графов зависимостей. Даже первые исследования показали, что эти графы несут много полезных сведений. Одной из целей обращения к тонкой структуре является поиск новых способов описания алгоритмов, более приспособленных к использованию на различных вычислительных системах, чем традиционные записи на последовательных, расширенных или параллельных языках программирования. Собственно говоря, данный поиск идет постоянно на протяжении всей истории развития программирования. Просто сейчас становится ясно, что каким-то образом в нем должна более полно учитываться информация о структуре алгоритмов. В конце концов, не так важно, в какую конкретную форму будут облечены новые способы. Важно лишь, чтобы они были приемлемы для пользователей и не требовали от него предоставления сведений о компьютерно-зависимых свойствах алгоритмов. Вся необходимая информация должна автоматически получаться только из описания алгоритмов в процессе либо компиляции, либо предварительной их обработки с помощью автономных систем.

О некоторых возможностях получения такой информации пойдет речь в настоящей главе. Более детально будут рассмотрены две идеи. Одна из них связана с представлением минимальных графов зависимостей в виде векторных полей в линейном пространстве итераций. Такие поля в математическом анализе часто исследуются с помощью параметризованных семейств гладких многообразий, покрывающих в совокупности все пространство. Основной момент исследований состоит в изучении пересечения отдельных векторов с отдельными многообразиями при изменении параметра. В качестве семейства многообразий мы будем брать поверхности уровней скалярных функций. Другая идея связана с преобразованиями программ, которые приходится выполнять после получения необходимых сведений. Мы будем разбираться, какие преобразования можно делать, какие нельзя и почему.

394

Часть II. Параллельное программирование

§ 7.1. Развертки графа

Параллелизм вычислений, задаваемый циклами ParDO, не всегда представляет весь параллелизм в программе. Более общий аппарат выявления массового параллелизма связан с использованием специальных функций на графах.

Пусть в пространстве итераций задан ориентированный лексикографически правильный граф G. Рассмотрим вещественный функционал / определенный на его вершинах. Предположим, что дуга графа идет из точки и в точку v. Будем говорить, что функционал/возрастает (не убывает) вдоль дуг графа G, если/fv) >/(w) (A^v) ^Л^и)) Для ^всех ^паР точек и, v, связанных дугами графа G. Назовем функционал / строгой (обобщенной) разверткой графа G, если он строго возрастает (не убывает) вдоль дуг графа.

Степень важности разверток для исследования графов определяется их свойствами. Пусть известна какая-нибудь строгая развертка. Тогда на любой ее поверхности уровня никакие точки пространства итераций не могут быть связаны дугами графа G. Более того, никакие из этих точек не могут быть связаны даже путями графа. Поэтому любые непересекающиеся множества точек любой поверхности уровня любой строгой развертки являются параллельными по графу G.

Рассмотрим теперь любую обобщенную развертку / Разобьем точки пространства итераций на группы. Будем относить к одной группе только те из них, которые принадлежат одной и той же поверхности уровня функционала/ Перенумеруем группы по возрастанию значений функционала. Это позволяет расщепить описанный программой алгоритм на фрагменты. Каждый из фрагментов соответствует одной группе точек пространства итераций. Фрагменты могут выполняться последовательно друг за другом в порядке возрастания номеров групп. Если в действительности развертка является строгой, то каждый из фрагментов можно расщепить на параллельные множества операций. Одно множество соответствует тем операциям, которые определяют одну точку пространства итераций.

Множество обобщенных разверток не пусто для любого графа G Например, обобщенной разверткой будет любой функционал / который принимает одинаковые значения во всех точках пространства итераций, т. е. является константой. Нетривиальным примером является следующая развертка.

Не ограничивая общности, будем считать, что программа представляет последовательность гнезд циклов с какими-то телами. Возможно, что для некоторых циклов верхние и нижние границы изменения значений параметров будут совпадать. Перенумеруем подряд в порядке лексикографического роста все значения параметров самых внешних циклов. Тем самым каждой точке пространства итераций будет присвоен некоторый номер. Естественно, могут существовать точки с одинаковыми номерами. Введем в пространстве итераций

Глава 7. Эквивалентные преобразования программ

395

вещественный функционал, положив его значение в точке, равное номеру точки. Не трудно проверить, что этот функционал является обобщенной разверткой. Обобщенной разверткой будет и любая неубывающая функция от номеров значений параметров циклов. Все такие развертки называются основными. Подчеркнем, что основные развертки не зависят от графа.

Множество обобщенных разверток замкнуто в отношении некоторых операций над ними. Из определения разверток следует, что справедливо

Утверждение 7.1

Обобщенной разверткой является:

• сумма двух обобщенных разверток;

• произведение обобщенной развертки на неотрицательное число;

• максимум из двух обобщенных разверток;

• минимум из двух обобщенных разверток.

С нетривиальными свойствами разверток можно познакомиться в [10, 64].

Любая развертка позволяет расщепить пространство итераций на группы. Однако от развертки зависит число групп и число точек в группах, характер связей между группами и между точками в группе. Среди разверток можно выделить два особых типа. Один тип составляют развертки, которые обеспечивают отсутствие связей внутри групп. Это строгие развертки. Второй тип составляют развертки, которые обеспечивают отсутствие связей между группами. Такие развертки будем назвать расщепляющими. Они позволяют расщепить описанный программой алгоритм на фрагменты, не связанные между собой по графу G. Это означает, что поверхности уровней расщепляющей развертки представляют множества, параллельные по тому же графу G. К расщепляющим отнесем и развертки, являющиеся константами. Такие развертки не имеют практического значения, но полезны при проведении теоретических исследований. Очевидно, что если цикл имеет тип ParDO по графу G, то основная развертка в пространстве итераций цикла является расщепляющей для графа G.

Пусть для графа G построены обобщенные развертки /j и fa. Функционал f~ А ⁺ fi также будет разверткой. Допустим, что в пространстве итераций имеются точки х\ и х₂ такие, что f(x\) = ]\x-i), но f\(x{) ^/lfe). Предположим, например, что f\(xi) >fi(x₂). Отсюда сразу же вытекает, что fi(^xi) <fi(^x2)- Если точки связаны путем графа G, то путь может идти лишь из точки с меньшим значением развертки в точку с большим ее значением. Поэтому мы заключаем, что точки х\ и х₂ не могут быть связаны путем графа G. Аналогичный вывод имеет место и в случае предположения

/l(*l)</l(*2)-

396

Часть II. Параллельное программирование

Следовательно, справедливо

Утверждение 7.2

Пусть для графа С известны обобщенные развертки /J v\f₂. Возьмем любые положительные числа а, р и построим развертку/= a/J + $f₂. Если в пространстве итераций существуют точки jq и х₂ такие, что

Лх₁)=Лх₂),Л(х₁)*Л(х₂), (7.1)

то они не могут быть связаны путем графа G.

Это утверждение позволяет выделять многоярусные параллельные множества в пространстве итераций с помощью обобщенных разверток. Предположим, что найдено не менее двух независимых разверток. Возьмем их сумму. Она является обобщенной разверткой. По этой развертке в соответствии с ее поверхностями уровней расщепим пространство итераций на последовательно связанные между собой группы. Для всех точек одной группы выполняется равенство из (7.1). Теперь возьмем любую из разверток и в соответствии с ее поверхностями уровней расщепим каждую из групп на множества. Каждое из множеств соответствует пересечению поверхностей уровней суммы разверток и выбранной развертки. Для точек одной группы, но принадлежащих разным множествам, выполняется неравенство из (7.1). Поэтому множества в каждой группе оказываются параллельными по графу G. Выберем далее любую развертку, отличную от первой и в соответствии с ее поверхностями уровней расщепим каждое из множеств на подмножества. Подмножества, порожденные каждым множеством, также оказываются параллельными по графу G. Следовательно, параллельными будут все подмножества, порожденные одной группой. Более дробное расщепление может осуществляться до тех пор, пока не останется неиспользованной одна из тех разверток, которые образовали исходную сумму разверток. Параллелизм в пространстве итераций, определяемый поверхностями уровней разверток, называется скошенным. Частный случай этого параллелизма, определяемый циклами ParDO, называется координатным.

Большое значение, которое играют развертки при изучении структуры последовательных программ, вынуждает искать эффективные методы их построения. В первую очередь они нужны для разверток минимальных графов зависимостей. Однако даже в этом случае множество разверток в целом устроено очень сложно. Тем не менее, для минимальных графов программ из линейного класса существуют и достаточно простые, но представительные развертки, которые, к тому же, можно конструктивно построить.

Рассмотрим в линейном пространстве итераций вещественный функционал, обладающий следующими свойствами:

□ его область определения есть линейный замкнутый многогранник в опорном многограннике;

□ он линеен как по точкам пространства итераций, так и по внешним переменным.

Глава 7. Эквивалентные преобразования программ

397

Естественно, возникает вопрос о возможности представления разверток системой линейных функционалов. Если такие развертки существуют, то будем их называть кусочно-линейными.

Имеется определенное сходство между системой покрывающих функций из теоремы 1 и рассматриваемыми линейными функционалами. Но между ними существует и принципиальное различие. Пусть граф зависимостей представлен системой покрывающих функций. Многогранники, на которых они определены, могут пересекаться по дискретному пространству итераций и никогда в совокупности не покрывают его полностью. Допустим, что развертку можно представить системой линейных функционалов. В этом случае многогранники, на которых заданы функционалы, не могут пересекаться по дискретному пространству итераций, но в совокупности должны покрывать его полностью.

Мы уже отмечали, что в наших исследованиях граф, для которого должны находиться развертки, будет на самом деле либо одним из минимальных графов зависимостей, либо каким-нибудь подграфом объединения минимальных графов. Теорема 1 играет решающую роль в том, что процесс построения кусочно-линейных разверток можно сделать конструктивным.

Рассмотрим векторы N= (N\, ..., N_s) внешних переменных программы. Предположим, что они принадлежат некоторой совокупности многогранников, в общем случае, неограниченных. Допустим, что в линейном пространстве итераций задана система замкнутых линейных многогранников V]_, ..., V_m, которые не пересекаются по дискретному пространству итераций, но в совокупности покрывают его полностью. В частности, многогранники Vj могут совпадать с опорными многогранниками, но могут и отличаться от них. Пусть в линейном пространстве итераций задана другая система замкнутых линейных многогранников Vy, которые могут пересекаться и иметь различные размерности. Будем считать, что обе системы многогранников связаны между собой следующим образом: если многогранник Vy имеет непустое пересечение с многогранником Vj, то он входит в V_t целиком. Выполнения этого условия можно всегда добиться либо за счет укрупнения многогранников Vj, либо за счет дробления многогранников Vy, либо за счет обеих операций вместе. Если каждый из многогранников Vy входит в какую-нибудь опорную область, а в качестве Vj взяты опорные многогранники, то данное условие также выполняется. Предположим, что вершины всех многогранников являются линейными неоднородными функциями переменных N_h ..., N_s.

Допустим, что граф G в пространстве итераций задан системой покрывающих функций. Пусть каждая из них является линейной как по точкам пространства итераций, так и по переменным TV], ..., N_s. Предположим, что областью определения отдельной покрывающей функции является один из многогранников Vy, а область ее значений входит в один из многогранников

398

Часть II. Параллельное программирование

V\, ..., V_m. Выполнения последнего условия снова можно добиться за счет подходящего выбора многогранников. И снова оно выполняется, если в качестве Vj взяты опорные многогранники, а граф G является одним из графов зависимостей.

Допустим, что заданная на многограннике Vy покрывающая функция имеет вид х = Jy + ф и ее значения принадлежат V^. Здесь / числовая матрица, вектор ф линейно зависит от внешних переменных. Любой граф зависимостей для линейной программы удовлетворяет этим требованиям. Пусть обобщенная развертка на Vj имеет вид (Ь, у) + 5, а на V^ вид (а, х) + у. Направляющие векторы a, b и свободные члены у, 5 неизвестны и подлежат нахождению. Будем искать векторы a, b как не зависящие от переменных N], ..., N_s, а свободные члены у, 5 как линейные неоднородные функции от этих переменных.

Так как из функционалов (а, х) + у и (Ь, у) + 5 должна составляться обобщенная развертка, то для всех у е Vy обязано выполняться неравенство

(а, х) + у<(Ь,у) + 5

или, другими словами,

(J^Ta - Ъ, у) < ~ (а, _Ф) + 5 - у. (7.2)

Обозначим через у¹ вершины многогранника Vy. Известно [4], что каждая точка ограниченного линейного многогранника может быть представлена как выпуклая линейная комбинация его вершин, т. е.

У = ^^а'^у1' ^а' -⁰' Х^а' =¹" (7-3)

Искомые функционалы удовлетворяют неравенству (7.2) для всех у е Vy. Представление (7.3) показывает, что неравенство (7.2) эквивалентно следующей системе неравенств

(J^Ta - b, У) < - (а, _Ф) + 5 - у. (7.4)

Согласно предположениям, у¹ и ф являются линейными неоднородными функциями от N\, ..., N_s. Пусть

у = уо + yiTVi + ... + y_sN_s,

5 = 5₀ + Si^! + ... + d_sN_s.

Перепишем неравенство (7.4) следующим образом:

(/о +У о" §o)+(//+Ti- ONi +••• + (//+ У,- h)N_s <0, (7-5)

где все fj являются какими-то конкретными линейными однородными

функциями неизвестных координат направляющих векторов а, Ь.

По предположению, вектор N внешних переменных принадлежит некоторой системе многогранников, в общем случае, неограниченных. Для каждого из

Глава 7. Эквивалентные преобразования программ

399

многогранников существует конечное число точек N^k = \N\ , ..., N^k) и конечное число векторов M^q = \М\ , ..., M^q_s) таких, что

^=2^* +Хм^> (7.6)

k q

где

а, >0, £а, =1, Р^°- ⁽⁷'⁷⁾

Неравенства (7.5) имеют место для всех N из (7.6), (7.7). В частности, неравенства

(/"о +Yo-§o)+(/,^/+Y,-§,к +... + (/"/ +y,-5>.f<0;

(/i'+_Yl -5,)м/ +... + (// +у,-5,)д/«<0

выполняются для всех к, q. Они могут быть получены из (7.5), если положить сначала а^ = 1 для фиксированного км fi_q = 0 для всех q и затем а^ = 1 для фиксированного к и р_? = + со для фиксированного #. Значения остальных Р_? в последнем случае можно считать равными 0. Неравенства (7.8) не зависят от Ni, ..., N_s. Если мы каким-нибудь способом определим направляющие векторы a, b и свободные члены у, 5 из (7.8), то с учетом (7.6)—(7.8) заключаем, что неравенства (7.5) будут выполняться для всех допустимых векторов N из выбранного многогранника при тех же a, b и у, 5.

Обозначим через t вектор, составленный для всех многогранников V_t из координат векторов а и коэффициентов разложения свободных членов у по параметрам 1, Ni, ..., N_s. Будем называть его направляющим вектором кусочно-линейной развертки. Зафиксируем какой-нибудь многогранник, в котором определен вектор внешних переменных N. Соберем далее вместе неравенства типа (7.8) для всех покрывающих функций графа. Левую их часть можно представить в виде произведения At, где А есть числовая матрица. Проведенные исследования показывают, что имеет место

Теорема 2

Для любой линейной программы и любого линейного многогранника, задающего область изменения внешних переменных, существует не зависящая от значений внешних переменных матрица А такая, что любой ненулевой вектор t, удовлетворяющий векторному неравенству

At < 0, (7.9)

является направляющим вектором кусочно-линейной развертки.

Эта теорема совместно с утверждением 7.2 дает мощный инструмент для исследования структуры графов. Находить развертки из системы неравенств (7.9) можно с помощью симплекс-метода [4].

400

Часть II. Параллельное программирование

Ответ на вопрос, существуют ли кусочно-линейные развертки, не связанные с решением неравенства (7.9), определятся тем, насколько избыточно набор покрывающих функций описывает граф G. Если набор описывает граф точно, то никаких других кусочно-линейных разверток не существует. Как уже отмечалось, минимальные графы зависимостей для реальных программ почти всегда описываются точно.

Матрица А из теоремы 2 зависит от выбора многогранников V_t и Vy. Как правило, в качестве V_t берутся опорные многогранники, а в качестве Vy многогранники, на которых задаются покрывающие функции. Другой выбор имеет смысл делать лишь в тех случаях, когда нужно принять во внимание какие-то частные особенности покрывающих функций и их областей определения. Если многогранники V/ и Vy фиксированы, то остается зависимость матрицы А от многогранника, в котором заданы внешние параметры. В том случае, когда область определения внешних переменных состоит из нескольких многогранников, направляющие векторы кусочно-линейных разверток для каждого из многогранников будут удовлетворять своей системе неравенств.

Утверждение 7.3

Пусть /есть любая развертка графа G. Граф С всегда можно расщепить на такие графы G_{ и С₂, что развертка /будет строгой для графа G_{ и расщепляющей для графа С₂.

Рассмотрим поверхности уровней развертки/ Будем считать, что у графа G и получаемых из него графов G\ и G₂ одно и то же множество вершин. Отнесем к графу (jj (G₂) те дуги графа G, концевые вершины которых лежат на разных (одних и тех же) поверхностях уровней функции / По построению функция/является строгой разверткой для графа G\, и расщепляющей для графа G₂.

Само по себе это утверждение, конечно, тривиально. Нетривиальным, однако, может быть осуществление разбиения графа G. Для кусочно-линейных разверток и графов, заданных кусочно-линейными функциями, это разбиение можно выполнить конструктивно.

Предположим, что внешние переменные заданы одним многогранником. Рассмотрим поведение кусочно-линейной развертки на семействе дуг, определяемом одной покрывающей функцией х = Jy + ср. Чтобы неравенство (7.2) было строгим для всех у и всех N, необходимо и достаточно, чтобы неравенство (7.4) было строгим для всех / и всех N. Для этого, в свою очередь, необходимо и достаточно, чтобы для всех / и всех к было строгим первое неравенство из (7.8). Поэтому для того чтобы развертка с направляющим вектором t, удовлетворяющим неравенству (7.9), была строгой при всех у £ Vy и всех N для покрывающей функции х = Jy + ср, необходимо и достаточно, чтобы среди координат вектора At, соответствующих этой покры-

Глава 7. Эквивалентные преобразования программ

401

вающей функции, отрицательными были все те, которые определяются первым неравенством из (7.8).

Если при каком-то у и некотором N неравенство (7.2) в действительности оказывается равенством, то при этом же N и каких-то / должны быть равенствами неравенства (7.4). Но тогда при этом N неравенство (7.2) будет равенством для всех тех и только тех у, которые принадлежат выпуклой линейной оболочке вершин у¹, обращающих неравенство (7.4) в равенство. Естественно, что этой же линейной оболочке принадлежит и рассматриваемая точка у. Для того чтобы при фиксированном / и том же самом N неравенство (7.4) становилось равенством, необходимо и достаточно, чтобы для данного / какие-то из первых неравенств (7.8) были в действительности равенствами. Наличие реальных равенств во вторых неравенствах (7.8) не имеет в данном случае какого-либо значения. Но все это означает, что неравенство (7.4) для рассматриваемого / будет равенством при всех N, принадлежащих некоторому многограннику А/. На его формирование уже влияют равенства из вторых соотношений (7.8). Этот многогранник описывается выпуклой оболочкой типа (7.6). Суммирование ведется по тем k, q, которые соответствуют равенствам в обоих соотношениях (7.8). Теоретически, по-видимому, возможно (на практике такая ситуация не встречалась), когда для разных / многогранники А/ различны. В этом случае область задания внешних переменных можно разбить на такие многогранники, в каждом из которых при каждом / неравенство (7.4) всегда является либо строгим неравенством, либо равенством. Структуру графа по отношению к данной развертке можно исследовать отдельно на каждом многограннике. Не ограничивая существенно общность, будем считать, что это условие выполняется для всех покрывающих функций на всей области задания внешних переменных.

Условия легко контролировать. Упорядочим строки матрицы А и, соответственно, координаты вектора At следующим образом. Разобьем строки матрицы А на блоки, отразив в одном блоке все неравенства (7.8), относящиеся к одной покрывающей функции. Разобьем блоки на группы, отразив в одной группе все неравенства (7.8), относящиеся к одному /. Каждую из групп разобьем на две подгруппы. В первой отразим первые неравенства (7.8), во второй — вторые. В каждой подгруппе строки расположим соответственно одной и той же нумерации индексов к, q. Типичную ситуацию определяет

Утверждение 7.4

Для того чтобы неравенство (7.4) для фиксированного / при всех допустимых N было строгим неравенством (равенством), необходимо и достаточно, чтобы в каждой группе координат вектора At для того же / все координаты первой подгруппы были отрицательными (все координаты группы были ненулевыми).

Таким образом, в областях определения линейных покрывающих функций всегда можно выделить такие подобласти, в общем случае представляющие

402

Часть II. Параллельное программирование

зависящие от внешних переменных многогранники, что соответствующие им дуги графа будут лежать в поверхностях уровней развертки, полученной из неравенства (7.9).

Представление лексикографически правильных графов линейными функциями позволяет обнаруживать ряд свойств разверток непосредственно из системы (7.9). Если развертка является расщепляющей, то на концах любой дуги она принимает одно и то же значение. Поэтому соотношение (7.2) должно быть равенством. Отсюда следует, что направляющие векторы расщепляющих разверток и только они удовлетворяют системе уравнений At = 0. Для любой строгой развертки соотношение (7.2) должно быть строгим неравенством. Легко проверить, что строгость неравенств (7.2) эквивалентна строгости первых неравенств из (7.8). Нетрудно также установить, что развертка с векторами а вида а = (1, 0, ..., 0) является основной. Подобные исследования мы будем проводить по мере необходимости.

Введенные совершенно формально как функционалы на графах развертки имеют очень прозрачный смысл. Обозначим через t(v) момент окончания выполнения операции, соответствующей вершине v пространства итераций. Если в вершину v идет дуга из вершины и, например, графа алгоритма, то очевидно, что t(v) > т(и). Равенство здесь может быть только в том случае, когда операция, соответствующая вершине v, реализуется мгновенно. Поэтому любая развертка графа алгоритма в действительности описывает временной режим некоторого способа выполнения самого алгоритма, реального или гипотетического. Реальным режимам соответствуют строгие развертки. В математических исследованиях удобнее считать, что все операции выполняются мгновенно. Если же необходимо учесть время их реализации, то это можно учитывать через времена передачи информации "по дугам графа".

Вопросы и задания

1. Рассмотрим следующие операции над развертками, определенными на точках v одного и того же пространства итераций и соответствующими одному и тому же графу С:

• Ф) = /i(v) ©/₂(v) = max \f_y{v), f₂(v)};

• ¥(v) = /i(v) ®fi(v) = min {/[(v), /₂(v)};

. 9(v) = XV/₁(v)=/₁(v)VX=/₁(v) + X.

Будем называть эти операции "сложением", "умножением" и "умножением на число". Докажите, что функции (p(v), ^i(v), 0(v) являются развертками графа G.

2. Покажите, что операции Ф, <8>, V не выводят из множества неотрицательных разверток, если X > 0.

3. Докажите, что на множестве разверток выполняются следующие соотношения:

• f®f=f,

Глава 7. Эквивалентные преобразования программ

403

• /i©/₂=/₂©/i;

• /i®/2=/2®/i;

• (Л®/₂)®/з=/1®(£®/з);

• (/1®/₂)®/з=/1®(/2®/з);

• /1®(Л®/₂)=/ь

• /i®(/l®/₂)=/i;

• (ЛФ/₂)®/з = (Л®/з)Ф(/₂®/з).

Любое множество, в котором относительно пары операций выполняются такие соотношения, называется дистрибутивной решеткой.

4. Функционал 0(v) = 0 для всех точек v называется "нулевой разверткой" и обозначается символом 0. Докажите, что на множестве неотрицательных разверток/это есть единственная развертка, обладающая, свойствами

/©0=0©/=/ 0®/=/®0=0

для всех/

5. Существует ли такая развертка l(v), что для всех неотрицательных разверток / выполняются соотношения:

1®/=/®1=/?

6. Рассмотрим множество неотрицательных разверток и для любой пары разверток введем вещественный функционал

(/,/)= max(/l(v)+/₂(v)).

Будем называть его "скалярным произведением". Докажите, что выполняются следующие соотношения

. О>0, если/* 0, ДО, 0) = 0;

• (A/₂) = (/₂,/i);

• (^V/,/₂) = XV(/₁,/₂);

• (Л®/2,/з) = (/ь/з)®(4/з).

7. На множестве неотрицательных разверток/введем вещественный функционал

||/||= max Av).

Будем называть его "нормой". Докажите, что выполняются следующие соотношения: . H/II > 0, если/* 0, || 0 || = 0;

• ll/i©/₂|| = ll/ill®ll/₂||;

• II/i®/₂II ^11/1II® II/₂II;

. || X V/|| = XV||/||.

8. Является ли множество всех разверток или неотрицательных разверток линейным векторным пространством с операциями V, ©?

9. Докажите, что операции ©, <8> на множестве разверток не имеют обратные операции.

404

Часть II. Параллельное программирование

10. Рассмотрим множество неотрицательных разверток с ограничениями. Именно, если из вершины и идет дуга в вершину v, то будем считать, что выполняются неравенства

/у) -Дм) > w_uv,

где w_uv — любые заданные неотрицательные числа, одни и те же для всех разверток /

Докажите, что множество разверток с ограничениями замкнуто относительно операций Ф, <8>, V.

11. Пусть в каждой вершине, не имеющей входные дуги, все развертки принимают одни и те же неотрицательные значения. В общем случае они разные в разных вершинах. Назовем их граничными значениями. Докажите, что множество неотрицательных разверток с заданными ограничениями и граничными значениями замкнуто относительно операций Ф, <8>.

12. Докажите, что в условиях п. 11 существует развертка Opt, принадлежащая рассматриваемому классу и такая, что

Opt®/=/® Opt=/ Opt<g>/=/<8> Opt = Opt

для любой развертки из этого же класса.

13. Предложите интерпретацию развертки Opt, связанную с временными характеристиками процесса реализации алгоритма на каком-то компьютере.

14. Докажите, что если все ограничения w_uv положительные, то любая развертка с такими ограничениями является строгой.

15. Для каких типов графов зависимостей реализации алгоритмов на реальных компьютерах автоматически приводят к положительным ограничениям в развертках?

§ 7.2. Макрографы зависимостей

Представление графов зависимостей линейными функциями открывает большие возможности в изучении параллелизма в программах как на микро-, так и на макроуровне. Исследования на микроуровне дают много детальной информации, но они достаточно трудоемки. Исследования на макроуровне менее сложные. Однако и сведения они дают менее подробные. При изучении структуры реальных программ приходится сочетать оба типа исследований. На макроуровне выделяются фрагменты программы (или, другими словами, множества точек в пространстве итераций), которые не связаны между собой по графу. На микроуровне детальному исследованию подвергаются только эти фрагменты (только эти множества). Опишем один из подходов проведения исследований на макроуровне. Он связан с построением макрографов.

Пусть в пространстве итераций программы задан ориентированный лексикографически правильный граф G. Выберем в линейном пространстве итераций систему замкнутых областей. Будем считать, что эти области попарно не пересекаются, в совокупности включают в себя все начальные вершины

Глава 7. Эквивалентные преобразования программ

405

дуг графа Си их число не зависит от значений внешних переменных. Области могут быть многосвязными и каждая из них может принадлежать разным опорным многогранникам.

Будем называть выбранные области макровершинами. Назовем макродугой всю совокупность дуг графа G, начальные вершины которых принадлежат одной макровершине, а конечные другой. Будем считать, что направление макродуги совпадает с направлением образующих ее дуг графа G. Множество макровершин и макродуг задает ориентированный макрограф, порожденный графом G.

Напомним, что ориентированный граф (подграф) называется сильно связанным, если в нем существует замкнутый путь, проходящий через все вершины. Сильно связанный подграф назовем изолированным, если никаким добавлением к нему новых вершин и новых дуг из графа его нельзя оставить сильно связанным. Очевидно, что любой ориентированный граф можно разбить по множеству вершин на изолированные сильно связанные подграфы. В частных случаях подграф может содержать и одну вершину, и все вершины графа.

Теперь разобьем макрограф на изолированные сильно связанные подмак-рографы. Множество макровершин каждого подмакрографа объявим новой макровершиной. Две новые макровершины свяжем новой макродугой, если были связаны старой макродугой какие-нибудь две старые макровершины, принадлежащие новым макровершинам. Тем самым будет построен новый макрограф. Он не имеет изолированных сильно связанных подмакрографов, содержащих более одной макровершины. Построим для него параллельную форму. Тогда множество точек пространства итераций, которые входят в один ярус и принадлежат отдельным макровершинам, являются параллельными по графу G. Если какая-то из макровершин не имеет петли, то ее вершины также могут образовывать параллельные множества. Проводить детальный анализ нужно только для тех фрагментов программ, которые определяют новые макровершины.

Пусть граф G представлен линейными функциями, заданными на замкнутых линейных многогранниках. Рассмотрим два наиболее простых способа построения макрографа. В первом в качестве областей возьмем опорные многогранники. Установление макродуг здесь осуществляется тривиально. Во втором в качестве областей возьмем многогранники, на которых заданы линейные функции. Для установления макродуг теперь нужно проверять непустоту пересечения пар многогранников. В каждой паре один из многогранников представляет область определения одной из линейных функций. Другой многогранник является областью значений какой-то другой функции.

Каждый из рассмотренных макрографов имеет конечное число макровершин, не зависящее от значений внешних переменных. Поэтому отыскание

406

Часть II. Параллельное программирование

изолированных сильно связанных подмакрографов можно осуществить любым подходящим методом, в том числе, основанным на переборе. Проводя детальный анализ отдельных макровершин, можно получать более подробные макрографы. В том числе можно строить макрографы, число вершин которых зависит от значений внешних переменных, но которые, тем не менее, устроены достаточно регулярно. Такая ситуация возникает, например, в том случае, когда какая-то макровершина описывается циклом ParDO.

Один из самых эффективных и многообещающих способов построения макрографов осуществляется с помощью разверток. Отвлечемся на время от линейного класса программ и будем считать, что граф алгоритма задан кусочно-непрерывными функциями в произвольной односвязной области D. В соответствии с интерпретацией, данной в § 7.1, рассмотрим строгую развертку т = t(v), определенную в точках v е D, и исследуем ее поверхности уровней. Они могут иметь сложное строение, в том числе, могут быть многосвязными. Однако, если с изменением х поверхности уровней меняются непрерывно, то по одну их сторону всегда будут находиться вершины, для которых выполнение соответствующих операций происходит до момента т, а по другую сторону — вершины, для которых выполнение операций происходит после момента т. Вершины, лежащие на самой поверхности, можно отнести к одной из этих групп вершин. Тогда перенос информации от вершин одной группы к вершинам другой группы осуществляется лишь теми дугами графа алгоритма, которые пересекают поверхности уровней развертки x(v). Поверхности уровней показывают в области D распределение потоков информации, перенос которой осуществляется в процессе реализации алгоритма.

Предположим, что граф алгоритма имеет хотя бы одну подходящую развертку. Она определяет систему поверхностей уровней или, что то же самое, систему ориентированных разрезов. Эти поверхности могут быть односвяз-ными, как на рис. 7.1, а, или не быть таковыми, как на рис. 7.1, б. Здесь цифрами отмечены поверхности уровней, соответствующие последовательным значениям т. Так как х есть время, то систему поверхностей уровня можно трактовать как систему фиксированных состояний некоторой перемещающейся во времени поверхности. Внешне движение этой поверхности напоминает движение волны в области D. По этой причине аналогичным объектам дают такие названия, как волновой фронт, фронт вычислений и т. п.

Система поверхностей уровней одной строгой развертки определяет некоторую параллельную форму алгоритма, с точки зрения решения задачи отображения алгоритмов на архитектуру вычислительных систем поверхности уровня одной развертки дают не очень много информации. Можно лишь сказать, что эти поверхности позволяют расщепить все операции алгоритма на подмножества. Вершины графа алгоритма, соответствующие операциям одного подмножества, и только они лежат на одной поверхности уровня. Все подмноже-

Глава 7. Эквивалентные преобразования программ

407

ства операций могут быть выполнены последовательно друг за другом, а операции одного подмножества могут быть выполнены параллельно.

Рис. 7.1. Поверхности уровней одной развертки

Положение существенно меняется, если число имеющихся независимых разверток совпадает с размерностью области D, как это показано на рис. 7.2. Выбирая из системы поверхностей уровней любые подсистемы, легко свести граф алгоритма к макрографу. Для этого нужно в качестве макровершин взять подграфы, ограниченные соседними поверхностями уровней из выбранных подсистем. Параллельная структура макрографа очевидна. В качестве примера на рис. 7.2 разной штриховкой отмечены для него несколько ярусов параллельной формы. Выбирая подходящие подсистемы поверхностей, можно при некоторых условиях добиться малости отношения числа дуг, связанных в среднем с одной макровершиной, к числу вершин графа алгоритма, приходящихся в среднем на одну макровершину. Это означает, что алгоритм эффективно реализуется на вычислительной системе с многоуровневой памятью.

Рис. 7.2. Поверхности уровней двух разверток

408

Часть II. Параллельное программирование

Заметим, что в обсуждаемых вопросах построения макрографов строгие развертки вполне можно заменить обобщенными. В рассуждениях почти ничего не меняется. Просто в этом случае допускается, что некоторые из дуг могут лежать на самих поверхностях уровней.

Вопросы и задания

1. Пусть задан ориентированный ациклический граф высоты я и ширины т. Докажите, что для любых натуральных чисел щ < п, т§ < т граф можно разбить на подграфы, образующие ориентированный ациклический макрограф высоты я₀ и ширины от₀-

2. Можно ли гарантировать, что все макровершины макрографа из п. 1 будут содержать примерно одинаковое число вершин исходного графа?

3. Рассмотрим управляющий и информационный графы, в которых вершины суть операторы. С точки зрения отдельных срабатываний операторов эти графы можно считать макрографами. Теперь рассмотрим граф алгоритма и построим для него макрограф в соответствии с п. 1. Каково принципиальное различие между данными макрографами в отношении реализации алгоритма по макровершинам?

4. Предположим для простоты, что алгоритм записан в виде тесно вложенного гнезда циклов и граф алгоритма имеет s > 2 независимых разверток. Постройте для графа алгоритма макрограф с использованием всех s разверток и предложите на его основе параллельную реализацию алгоритма.

5. Как зависит от s число процессоров, которые можно в п. 4 использовать параллельно?

6. Как зависит от s интенсивность обмена информацией между процессорами, если алгоритм реализуется согласно п. 4?

§ 7.3. Эквивалентные программы

Чтобы использовать обнаруженный в программе параллелизм, его нужно прежде всего каким-то образом записать. Обычно параллелизм описывают с помощью специальных циклов. Мы уже отмечали это на примере циклов ParDO. Чтобы параллелизм в программе описать циклами, программу приходится преобразовывать. Остановимся сначала на общих принципах выполнения таких преобразований.

Будем называть два арифметических выражения эквивалентными, если их записи совпадают с точностью до обозначения переменных. Перенумеруем одинаковым образом входные переменные эквивалентных выражений. Рассмотрим две линейные программы. Предположим, что между их пространствами итераций установлено такое взаимно однозначное соответствие, при котором соответствующие точки задают срабатывания операторов с эквивалентными выражениями в правых частях. Подобные пространства итераций будем называть эквивалентными, а указанное соответствие — соответствием эквивалент-

Глава 7. Эквивалентные преобразования программ

409

ности. Пусть фиксировано правило, по которому для линейной программы однозначно строится какой-нибудь граф зависимостей. Возьмем две программы с эквивалентными пространствами итераций и предположим, что соответствие эквивалентности является изоморфным для графов. Кроме того, будем считать, что сопоставляемые при изоморфизме дуги графов зависимостей относятся к входным переменным с одними и теми же номерами. Такие программы будем называть эквивалентными по графам зависимостей, а сами графы — графами эквивалентности. Любое преобразование программы в эквивалентную ей программу будем называть эквивалентным.

Введенное понятие эквивалентности программ зависит от того, какие графы мы хотим принять во внимание при преобразовании программ. Все эквивалентные программы выполняют одно и то же множество операций, описанных арифметическими выражениями. Однако при последовательной реализации программ порядки выполнения операций могут различаться. В общем случае разные порядки могут приводить к разным результатам. При специальном выборе графов эквивалентности эквивалентные программы дают в одинаковых условиях реализации одни и те же результаты, включая всю совокупность ошибок округления. Одинаковые условия предполагают, в частности, что ошибка округления при выполнении любой операции на конкретном компьютере определяется только входными данными операции. Этому требованию удовлетворяют все используемые на практике компьютеры. Множества используемых переменных в эквивалентных программах могут быть организованы в массивы по-разному и могут различаться по их числу. В частности, по-разному могут быть организованы переменные, через которые задаются входные данные и которые формируют результаты.

В реальных условиях приходится выполнять также неэквивалентные преобразования. Типичным примером является замена одного оператора последовательностью операторов, реализующих в точных вычислениях ту же самую операцию. С формальной точки зрения преобразование не является эквивалентным, т. к. меняется пространство итераций. В практическом отношении такая замена из-за влияния ошибок округления чаще всего приводит к изменению результатов вычислений, что также не дает основание считать подобное преобразование эквивалентным.

Программы могут быть неэквивалентными даже в случае эквивалентности их пространств итераций. Рассмотрим, например, суммирование элементов массива. Пусть в одной из программ осуществляется последовательное суммирование, в другой — принцип сдваивания. Допустим далее, что графами эквивалентности являются графы алгоритма. Пространства итераций совпадают как по числу точек, так и по содержанию соответствующих им операций. Тем не менее, программы не эквивалентны, т. к. их графы алгоритмов не изоморфны. Заметим, что и в этом случае при точных вычислениях программы будут давать одинаковые результаты, если суммируются элементы

410

Часть II. Параллельное программирование

одного и того же массива. Но в условиях влияния ошибок округления результаты будут различными.

Сохранение результатов вычислений имеет безусловный приоритет при преобразовании программ. Поэтому очень важно иметь критерий такого сохранения. Мы уже отмечали особую роль графа алгоритма среди минимальных графов. Посмотрим, что объединяет программы, эквивалентные по этим графам.

Построим каноническую параллельную форму графа алгоритма одной из программ. По построению начальная вершина любой дуги будет всегда находиться в ярусе с меньшим номером, чем конечная вершина. В силу изоморфизма графов эквивалентности каноническую параллельную форму другого графа можно взять такой же, включая такое же расположение соответствующих вершин в ярусах. При этом одинаково расположенным вершинам параллельных форм будут соответствовать одни и те же операции. Одинаково расположенные дуги будут относиться к входным переменным с одними и теми же номерами. Тогда все различия в последовательных реализациях программ сводятся к различиям в переборах вершин параллельных форм графов, определяемых лексикографическими порядками в пространствах итераций.

При любом порядке перебора вершин результаты выполнения операций, соответствующих первым ярусам, зависят только от входных данных программ. Поэтому для обеих программ они будут одинаковыми при одних и тех же входных данных в операциях, соответствующих одинаково расположенным вершинам. Предположим, что для обеих программ одинаковыми будут результаты выполнения всех соответствующих операций из всех ярусов от 1-го до к-го, к > 1. Рассмотрим любую вершину /из (к + 1)-го яруса. Если в вершину / входит дуга из вершины /, то для каждой из программ / -< J по определению графа алгоритма. Вершина / обязательно находится в ярусе, номер которого не превосходит к. Следовательно, при любом допустимом переборе вершин наборы значений аргументов для операции, соответствующей вершине /, будут одними и теми же. Это означает, что и для {к + 1)-го яруса результаты выполнения соответствующих операций будут для обеих программ одинаковыми. Заканчивая перебор всех ярусов, заключаем, что справедливо

Утверждение 7.5

Пусть программы эквивалентны по графам алгоритма. Тогда при последовательной реализации на одном и том же компьютере при одних и тех же входных данных они будут давать одни и те же результаты, включая всю совокупность ошибок округления.

По существу программы, эквивалентные по графам алгоритма, представляют различные записи одного и того же алгоритма. Единственное, чем они могут

Глава 7. Эквивалентные преобразования программ

411

принципиально отличаться друг от друга, — это объемом памяти, необходимым для хранения результатов промежуточных вычислений, а также формой организации переменных в массивы. Кроме этого, входные и выходные данные таких программ могут отличаться друг от друга какой-либо их пересортировкой. Мы будем предполагать, что при реализации эквивалентных программ необходимая пересортировка делается. Эквивалентные программы обладают одним и тем же параллелизмом. Однако записан он может быть по-разному. Например, в одной программе какой-то параллелизм может быть описан явно в форме циклов ParDO. В другой программе этот же параллелизм может оказаться неявно описанным в форме скошенного.

Основная цель преобразования программы заключается в приведении ее к такому виду, в котором весь ее массовый параллелизм представлен явно в форме циклов ParDO. Обязательным условием любого преобразования является сохранение уровня точности получаемых результатов. Запись преобразованной программы на алгоритмическом языке имеет большое значение. Но в ближайших исследованиях мы не будем заниматься этим вопросом. Будем понимать сейчас под преобразованием программы преобразование ее пространства итераций с одновременным изменением используемых переменных. В этих условиях реализация программы означает выполнение операций, соответствующих точкам пространства итераций, в той последовательности, которая диктуется лексикографическим порядком в данном пространстве.

Пусть выполняется преобразование программы. Чтобы показать, что исходная и преобразованная программы дают одни и те же результаты, вроде бы нужно построить для них графы алгоритмов и сравнить эти графы на изоморфизм. Однако этот способ проверки эквивалентности программ не всегда возможно осуществить на практике. Сравнение графов на изоморфизм является довольно трудоемкой задачей. Кроме этого, очень часто принимать решение о том, какое преобразование нужно делать, приходится по ходу построения самого преобразования. В этом случае мы просто не можем получить граф алгоритма преобразованной программы. Поэтому мы поступим иначе. Будем выполнять специальное преобразование. Оно гарантирует в ряде случаев эквивалентность по графам алгоритма и позволяет осуществлять промежуточный контроль. Это преобразование охватывает большую группу конкретных преобразований, объединенных общим названием переупорядочивание пространства итераций. Пусть для исходной программы построен граф зависимостей. Специальное преобразование таково:

□ выполняется эквивалентное преобразование пространства итераций;

□ для новой программы выбираются такие переменные, чтобы при преобразовании пространства итераций разные переменные переходили в разные, одинаковые — в одинаковые;

□ в новом пространстве итераций устанавливается лексикографический порядок, при котором образ графа зависимостей будет лексикографически правильным.

412

Часть II. Параллельное программирование

Рассмотрим сначала случай, когда в специальном преобразовании используется граф зависимостей, являющийся объединением всех четырех минимальных снизу графов. Будем помечать образы точек пространства итераций штрихами. Пусть Г, /' являются начальной и конечной вершинами дуги графа алгоритма новой программы. Точка / на выходе и точка / на соответствующем входе имеют одинаковые переменные. Предположим сначала, что I < J. Эти точки истинно зависимы. Поэтому, согласно утверждению 6.2, существует точка Р такая, что I < Р < J, пара точек /, Р или связана путем

графа зависимостей по выходу или I = Р, а пара точек Р, / связана дугой графа алгоритма исходной программы. В силу третьего свойства специального преобразования заключаем, что Г < Р' < /'. В силу второго свойства в

точках /' и Р' пересчитывается одна и та же переменная. Следовательно должно быть /' = Р', I = Р, т. к. в противном случае пара точек Г, /' не может задавать дугу графа алгоритма. Итак, в этом случае дуга графа алгоритма новой программы есть образ дуги графа алгоритма исходной программы.

Пусть теперь I >- J. Аналогично заключаем, что существует точка Р такая, что I у Р у J, пара точек /, Р связана дугой графа антизависимостей, а пара точек Р, / или связана путем графа зависимостей по входу или Р = J. Это означает, что Г >- Р' у /'. Однако на самом деле /' -< /'. Поэтому случай

/ у /невозможен.

Рассмотрим далее пару вершин /, / исходной программы, связанную дугой графа алгоритма. Пусть I < J. Согласно свойствам специального преобразования, точка /' на выходе и точка У на соответствующем входе имеют одинаковые переменные. Кроме этого, Г < /'. Существует точка Q' такая, что Г < Q' < /', пара точек /', Q' связана путем графа зависимостей по выходу,

а пара точек Q', /'связана дугой графа алгоритма. Согласно сказанному выше, пара точек Q, / задает дугу графа алгоритма исходной программы и Q < J. Но по заданной конечной вершине / и заданному ее входу начальная вершина дуги графа алгоритма определяется однозначно. По предположению это есть /. Поэтому 1= Q, Г= Q'. Это означает, что образ дуги графа алгоритма исходной программы есть дуга графа алгоритма новой программы.

Суммируя сказанное, заключаем, что при выполнении специального преобразования образ графа алгоритма исходной программы является графом алгоритма преобразованной программы. Аналогичные утверждения справедливы и в отношении всех остальных минимальных графов зависимостей. Следовательно, справедливо общее

Утверждение 7.6

Пусть над любой программой выполняется специальное преобразование, в котором в качестве графа зависимостей используется объединение всех четырех минимальных снизу графов. Тогда образ любого из минимальных снизу графов

Глава 7. Эквивалентные преобразования программ

413

зависимостей исходной программы есть минимальный снизу граф зависимостей того же типа преобразованной программы.

Чтобы обеспечить эквивалентность по графу алгоритма, наблюдая лишь за лексикографической направленностью образов, нам пришлось учитывать все четыре минимальных снизу графа зависимостей. К сожалению, число наблюдаемых таких графов нельзя уменьшить. Можно лишь уменьшить число наблюдаемых дуг.

Утверждение 7.7

Пусть граф задан линейной функцией Ф на многограннике А. Для того чтобы граф был лексикографически правильным, необходимо и достаточно, чтобы лексикографически правильными были дуги, относящиеся лишь к угловым точкам многогранника А.

Рассмотрим для определенности случай, когда функция Ф задает входящие дуги. Случай исходящих дуг рассматривается аналогично. Необходимость очевидна. Для доказательства достаточности обозначим через у произвольную точку многогранника А, через у¹ — его угловые точки и воспользуемся известным соотношением [4], что

y = Yj^a'^yl' ^а/-°> Х^а/=¹' ^уеА-i i

Если функция Ф задает входящие (исходящие) дуги, то Ф(у¹) -< 0 (>- 0) для всех /. Поэтому

Ф(^) = £_а/Ф(У)^0(^0)

для всех у е А в силу того, что а/ > 0 для всех /.

В наших случаях все графы будут задаваться линейными функциями на линейных многогранниках, и будем мы совершать, как правило, линейные преобразования. Из утверждения 7.7 следует, что образ такого графа при линейном преобразовании будет лексикографически правильным тогда и только тогда, когда лексикографически правильными будут образы дуг, входящих в вершины многогранников. Специальное преобразование сохраняет объем используемых входных, выходных и промежуточных переменных. Если увеличить объем используемых переменных, то все графы, кроме графа алгоритма, можно существенно упростить.

Рассмотрим следующее элементарное преобразование, не обсуждая сейчас возможность его записи. Возьмем любую точку пространства итераций и весь пучок дуг графа алгоритма, выходящих из этой точки. Заменим связанную с данными дугами переменную на любую другую, не совпадающую ни с одной из используемых в программе переменных. Очевидно, что полученная программа будет эквивалентна исходной по графу алгоритма. Однако в гра-

414

Часть II. Параллельное программирование

фе зависимостей по выходу пропадет дуга, входящая в выбранную точку, и дуга, выходящая из нее. В графе антизависимостей пропадет дуга, входящая в эту точку. В нем также пропадут все дуги, которые были связаны со старой переменной и выходили из конечных вершин рассматриваемого пучка дуг графа алгоритма. Могут пропасть и некоторые дуги графа зависимостей по входу. В общем случае возможно появление новых дуг. Но если выполнять элементарные преобразования, например, последовательно, начиная с лексикографически самой младшей точки, то новых дуг не будет. Поэтому заключаем, что имеет место

Утверждение 7.8

Для любой программы существует эквивалентная по графу алгоритма программа, у которой графы зависимостей по выходу, антизависимостей и обратных зависимостей пустые. Дуги графа зависимостей по входу эквивалентной программы связывают только те точки пространства итераций, которые являются конечными для дуг графа алгоритма, выходящих из одной точки.

Мы уже отмечали в § 6.7важность факта, когда итерации цикла, имеющего тип ParDO по графу алгоритма, не связаны дугами других минимальных графов. Обеспечить это может выполнение рассмотренных элементарных преобразований. Конечно, совсем не обязательно исключать все возможные дуги. Обычно достаточно исключить лишь те из них, которые связаны с временными переменными.

Математические записи алгоритмов не допускают пересчета значений используемых переменных. В программах такой пересчет допускается. Если граф зависимостей по выходу пустой, то это означает, что в программе нет пересчета переменных. Поэтому получение эквивалентной программы из утверждения 7.8 можно трактовать как восстановление по программе математического описания алгоритма.

В заключение обратим внимание на одно важное обстоятельство. Рассмотрим специальное преобразование для программы, у которой все минимальные снизу графы являются максимально пустыми. Совершенно очевидно, что требование лексикографической правильности образа графа зависимостей по входу является для данного случая излишним при доказательстве эквивалентности по графу алгоритма исходной и преобразованной программ. Это объясняется тем, что четыре минимальных снизу графа дают в совокупности избыточную информацию о структуре алгоритма, описанного программой. На данном конкретном случае указанная избыточность и проявляется. Напомним, что минимальные снизу графы являются отражением традиционно используемых графов зависимостей. Минимальные сверху графы не градиционны. Точная структура описанного программой алгоритма задается некоторой комбинацией минимальных снизу и сверху графов.

Рассмотрим теперь случай, когда в качестве наблюдаемого графа зависимостей используется объединение графа алгоритма, графа зависимостей по вы-

Глава 7. Эквивалентные преобразования программ

415

ходу и графа обратных зависимостей. В полной аналогии с утверждением 7.6 устанавливается

Утверждение 7.9

Пусть над любой программой выполняется специальное преобразование, в котором в качестве графа зависимостей используется объединение графов алгоритма, зависимостей по выходу и обратных зависимостей. Тогда образ любого из этих графов является аналогичным графом преобразованной программы.

Вопросы и задания

1. Докажите, что каким бы образом не менять местами координаты /, j, к в пространстве итераций примера 6.1, получаются эквивалентные пространства.

2. Докажите, что в условиях п. 1 получаются программы, эквивалентные по графу алгоритма.

3. Докажите, что если поменять местами координаты /, j пространства итераций примера 6.2, представленного на рис. 6.11, получается эквивалентное пространство.

4. Докажите, что в условиях п. 3 получается программа, эквивалентная исходной по графу алгоритма.

5. Докажите, что если поменять местами координаты /, j пространства итераций примера 6.3, представленного на рис. 6.12, получается эквивалентное пространство.

6. Получается ли в условиях п. 5 программа, эквивалентная исходной по графу алгоритма?

§ 7.4. Наиболее распространенные преобразования программ

Рассмотрим кратко некоторые преобразования, получившие наиболее широкое применение на практике. Проведенные выше исследования позволяют значительно упростить изучение возможности их использования. Если для преобразуемой программы известны нужные графы зависимостей, то в большинстве случаев удается точно ответить на вопрос, можно или нельзя выполнять то или иное преобразование. Здесь мы коснемся лишь математических особенностей преобразований и не будем обсуждать особенности, связанные с учетом деталей архитектуры параллельного компьютера.

Прежде чем переходить к рассмотрению конкретных преобразований, сделаем одно уточнение. Общие исследования, проведенные в § 7.3, не связывали преобразование пространства итераций и установление в новом пространстве лексикографического порядка перебора точек. Это определялось тем, что в общих исследованиях не фиксировалась форма записи преобразованной программы. При рассмотрении конкретных преобразований ситуация иная. Теперь форма записи преобразованной программы фиксируется.

416

Часть II. Параллельное программирование

Она определяет лексикографический порядок в новом пространстве итераций. Поэтому при обсуждении эквивалентности преобразований мы будем принимать во внимание только одно соответствие между пространствами итераций преобразуемой и преобразованной программ. Именно то, которое определяется конкретным рассматриваемым преобразованием. На преобразованном пространстве итераций мы будем считать заданным вполне определенный лексикографический порядок. Именно тот, который диктуется формой записи преобразованной программы.

Перестановка циклов

Преобразование состоит в перестановке местами каких-либо двух циклов в тесно вложенном гнезде циклов. Не ограничивая существенно общность, можно считать, что первый (самый внешний) цикл переставляется с к-ым. Для установления эквивалентности преобразования по графу алгоритма можно воспользоваться критериями, сформулированными в утверждениях 7.6, 7.9. Чтобы применить эти критерии, нужно быть уверенным в том, что перестановка 1-ой и к-ок координат точек пространства итераций переводит лексикографически правильную дугу в лексикографически правильную. Легко проверить, что для выполнения данного условия достаточно, чтобы к-ая координата конечной вершины дуги была больше к-ок координаты начальной вершины. Если графы зависимостей для гнезда циклов представлены линейными функциями на линейных многогранниках, то соотношение между координатами устанавливается весьма просто.

В частности, всегда можно переставлять рядом стоящие циклы, имеющие по всем зависимостям тип ParDO. После перестановки свойство ParDO сохраняется у обоих циклов. Если возможна перестановка 1-го цикла с к-ым и 1-ый цикл имеет тип ParDO, то после перестановки тип ParDO будет иметь к-ъш цикл. Пусть самый внешний цикл имеет тип ParDO по всем зависимостям. Его всегда можно переставить со вторым циклом. Новый второй цикл будет также иметь тип ParDO по всем зависимостям. Поэтому его можно переставить с третьим циклом и т. д. Это означает, что любой цикл ParDO всегда можно поставить в тесно вложенном гнезде на любое более глубокое место. При этом свойство ParDO сохраняется. В противоположность этому, в общем случае переставлять внутренний цикл ParDO "наружу" нельзя.

Область изменения параметров циклов в гнезде описывается треугольными соотношениями. В случае перестановки 1-го и к -го циклов новая область, вообще говоря, будет иметь более сложное описание. Единственным исключением является ситуация, когда границы изменения к-го параметра не зависят от других параметров. Тогда новая область также описывается треугольными соотношениями.

Слияние циклов

Рассмотрим две подряд идущие циклические конструкции с одинаковыми (с точностью до обозначения параметров) самыми внешними циклами. Преоб-

Глава 7. Эквивалентные преобразования программ

417

разование заключается в слиянии этих конструкций в одну. Она представляет прежний внешний цикл, тело которого образовано из подряд идущих тел внешних циклов исходных конструкций. Для эквивалентности преобразования снова потребуем, чтобы лексикографически правильная дуга графа зависимостей преобразовывалась в лексикографически правильную. Очевидно, что нужно рассмотреть только те дуги, которые идут из точек пространства итераций первой циклической конструкции в точки пространства итераций второй циклической конструкции. Для всех остальных дуг это требование выполняется при преобразовании автоматически. Для того чтобы оно выполнялось и для рассматриваемых дуг, достаточно, чтобы первые координаты начальных вершин не превосходили первые координаты конечных вершин. Имея явные формулы для дуг, это проверить несложно.

Допустим, что внешние циклы сливаемых конструкций имеют тип ParDO. Если для дуг, которые идут из точек пространства итераций первой циклической конструкции в точки пространства итераций второй циклической конструкции, первые координаты начальных и конечных вершин совпадают, то внешний цикл преобразованной конструкции будет иметь тип ParDO.

Переупорядочивание операторов

Преобразование состоит в выполнении последовательности перестановок местами пар операторов или циклов в пределах ближайшего объемлющего их цикла. Допустим, что построен граф зависимостей для тела объемлющего цикла. Зафиксируем любую пару переставляемых объектов и рассмотрим все дуги, у которых хотя бы один из концов принадлежит опорным пространствам (или опорному пространству, если в объекте имеется только один оператор) одного из объектов. Для того чтобы перестановка объектов была преобразованием, эквивалентным по графу алгоритма, достаточно, чтобы при ее выполнении не менялось соотношение между номерами опорных пространств, содержащих концевые вершины дуг. Другими словами, если дуга шла, например, из пространства с большим номером в пространство с меньшим номером, это соотношение должно сохраняться и после перестановки, и т. п. Данное преобразование сохраняет циклы ParDO.

Распределение цикла

Это преобразование является обратным по отношению к преобразованию слияния циклов. Пусть задан некоторый цикл. Построим для него граф зависимостей. Допустим, что после переупорядочивания в теле цикла его можно представить в виде двух подряд идущих фрагментов, и нет ни одной дуги, идущей из опорных пространств второго фрагмента в опорные пространства первого фрагмента. Тогда цикл можно представить в виде двух подряд идущих циклических конструкций. Самые внешние циклы у них совпадают. Телом первого цикла является первый фрагмент, телом второго — второй фрагмент. Если преобразуемый цикл имел тип ParDO, то тип

418

Часть II. Параллельное программирование

ParDO будут иметь оба внешних цикла преобразованной программы. Оба внешних цикла или один из них могут иметь тип ParDO и в том случае, когда таковым не является преобразуемый цикл.

Скашивание цикла

Это преобразование направлено на выявление и использование параллелизма, отличного от задаваемого циклами типа ParDO. Как правило, оно связывается с параллельными множествами, расположенными в линейных многообразиях пространства итераций. В специальной литературе можно найти много различных предложений по реализации таких преобразований. Однако все они ориентированы на какие-то частные случаи.

Расщепление пространства итераций

Преобразование заключается в представлении цикла в виде двух подряд идущих циклов. Тела обоих циклов совпадают с телом преобразуемого цикла. Нижняя (верхняя) граница изменения параметра первого (второго) цикла также совпадает с соответствующей границей исходного цикла. Поэтому нужно найти лишь верхнюю (нижнюю) границу первого (второго) цикла. Эти границы должны удовлетворять следующим условиям: нижняя граница второго цикла должна быть строго больше верхней границы первого цикла и обе границы должны находиться между границами преобразуемого цикла. Во всем остальном выбор границ произволен. Очевидно, что достаточно найти только верхнюю границу первого цикла. Если исходный цикл имел тип ParDO, то при любом способе нахождения границы оба получаемых цикла будут иметь тип ParDO. Оба получаемых цикла или один из них могут иметь тип ParDO и в том случае, когда таковым не является преобразуемый цикл.

Выполнение итераций цикла в обратном порядке

Формально преобразование заключается в перемене местами верхних и нижних границ изменения параметра какого-нибудь цикла программы и замене шага изменения параметра этого цикла с +1 на —1. Снова воспользуемся критериями утверждений 7.6, 7.9. Допустим, что существует хотя бы одна дуга истинных зависимостей, антизависимостей или зависимостей по выходу, связывающая две итерации преобразуемого цикла исходной программы. При рассматриваемом преобразовании образы этих дуг не будут лексикографически правильными. Поэтому все такие дуги должны отсутствовать. Это означает, что преобразуемый цикл должен иметь тип ParDO по объединению графов алгоритма, антизависимостей и зависимостей по выходу. Согласно исследованиям, проведенным в §6.7, итерации такого цикла вообще можно выполнять в любом порядке, а не только в обратном.

Глава 7. Эквивалентные преобразования программ

419

Выделение стандартных операций

Преобразование состоит в поиске в тексте программы одинаковых фрагментов и подстановки на их места обращений к оптимизированной процедуре. Основная трудность связана с установлением факта эквивалентности фрагментов. Для решения этого вопроса можно воспользоваться критериями утверждений 7.6, 7.9.

Среди преобразований программ, связанных с изменением координат точек пространства итераций, наиболее простыми являются те, которые не нарушают лексикографического отношения. Основой построения таких преобразований служит утверждение 6.5.

Треугольные преобразования

Будем считать, что каждое опорное пространство преобразуется само в себя. Пусть в /-ом пространстве преобразование имеет вид

Z = B_iX+bi. (7.10)

Здесь Bj есть левая треугольная целочисленная матрица с единичными диагональными элементами. Она не зависит от внешних переменных программы. Координаты вектора b_t могут быть линейными неоднородными функциями от внешних переменных, имеющими целочисленные коэффициенты. Вектор х задает координаты точки в старой системе координат, вектор z — в новой. Согласно утверждению 6.5, преобразование (7.10) сохраняет лексикографическое отношение между точками пространства. Дополнительные условия целочисленности гарантируют, что образы и прообразы целочисленных точек для преобразования (7.10) будут целочисленными.

Если /-ое и у'-ое опорные пространства не имеют общих параметров циклов, то матрицы и свободные члены в преобразованиях этих пространств могут быть не связаны между собой. Если же общие параметры имеются, то после преобразования программы одинаковые значения общих параметров должны перейти в одинаковые, разные — в разные. Пусть /-ое и у'-ое опорные пространства имеют г общих параметров. Будем считать, что первые г строк матриц Д и Bj попарно совпадают, так же как и первые г координат векторов bj и bj.

Построим для всех опорных пространств преобразования вида (7.10) с указанными особенностями матриц Bj и векторов bj. Назовем такие преобразования треугольными. Выразим из соотношений (7.10) старые параметры х_кчерез переменные Zj и подставим всюду в текст программы вместо старых параметров соответствующие выражения. Приведем границы изменения новых параметров цикла к стандартной форме. Очевидно, что новый текст представляет описание программы из линейного класса. Соответствие между пространствами итераций исходной и преобразованной программ сохраняет по построению лексикографическое отношение. Выполненное преобразование программы удовлетворяет всем условиям описанного выше специального преобразования. Поэтому новая программа будет эквивалент-

420

Часть II. Параллельное программирование

на исходной по графу алгоритма и, следовательно, будет сохранять результаты реализации программы при одних и тех же входных данных.

Формальная запись новой программы получается из старой с помощью замены всех вхождений параметров циклов их выражениями, полученными из соотношений (7.10). Однако лишь этого факта было бы недостаточно для обеспечения эквивалентности преобразования программы. Чтобы формальная замена параметров циклов привела к эквивалентной программе, нужно на преобразования (7.10) наложить какие-то ограничения. Они могут быть такими, какие имеют треугольные преобразования, но могут быть и другими.

Любое треугольное преобразование переводит независимые точки пространства итераций в независимые, зависимые — в зависимые того же типа. Отсюда, в частности, следует

Утверждение 7.10

Любое треугольное преобразование переводит цикл ParDO в цикл ParDO и сохраняет его тип. Никаких новых циклов ParDO при треугольном преобразовании появиться не может.

Само по себе треугольное преобразование не несет большой самостоятельной смысловой нагрузки. Однако оно имеет важное значение как предварительное преобразование перед выполнением каких-то других преобразований. С помощью треугольных преобразований можно сделать более явными некоторые структурные свойства программы. Например, в программе не виден параллелизм, задаваемый с помощью разверток. Не видно даже, какие точки пространства итераций относятся к одной поверхности уровня развертки, а какие к разным. Выполняя специальным образом подобранное треугольное преобразование, можно сделать подобную информацию более явной.

Множество используемых на практике преобразований постоянно расширяется. Этому процессу в немалой степени способствует появление компьютеров новой архитектуры. Многие преобразования не требуют для своей реализации серьезного математического обоснования. К ним относятся, например, следующие: вынесение за пределы цикла нескольких первых или последних итераций, объединение нескольких циклов тесно вложенного гнезда в один, дублирование тела цикла несколько раз с одновременным уменьшением во столько же раз числа повторений цикла, полная раскрутка цикла по всем итерациям, преобразование одномерного цикла в двумерную циклическую конструкцию, генерация нескольких вариантов для какого-то фрагмента с выбором конкретного варианта во время исполнения программы и многие другие.

С некоторыми другими преобразованиями программ, в особенности с теми, которые требуют математического обоснования, можно познакомиться в книге [6].

Глава 7. Эквивалентные преобразования программ

421

Вопросы и задания

1. Для различных программ или их фрагментов постройте графы зависимостей и выполните эквивалентные преобразования. Не правда ли, после нескольких успешных и, тем более, безуспешных примеров захотелось иметь автоматизированную систему, помогающую осуществлять такую работу?

§ 7.5. Две сопутствующие задачи

Проведенные исследования являются основой для решения самых различных задач, так или иначе связанных с алгоритмами и их структурами, формами записи, использованием и т. п. Рассмотрим кратко две из них.

Графы зависимостей и развертки позволяют выявлять параллелизм вычислений в алгоритмах. Всегда полезно знать, весь ли параллелизм обнаружен или нет. Ответ на этот вопрос дают нижние и верхние оценки длины критического пути графа алгоритма. Особенно важно иметь оценки величины массового параллелизма или, другими словами, параллелизма, определяемого значениями внешних переменных. Следовательно, в первую очередь, хотелось бы иметь оценки длины критического пути, в которых точно отражен порядок зависимости именно от этих переменных. Допустим, что в результате проведенных исследований получена программа, в которой какие-то циклы отмечены типом ParDO. Для этой программы легко оценить порядок длины критического пути графа алгоритма, считая остальные циклы последовательными. Вообще говоря, такую оценку следует считать оценкой сверху, т. к. какой-то массовый параллелизм может оказаться не выявленным. Оценить уровень параллелизма в тех фрагментах, где он еще не обнаружен, можно с помощью разверток.

Пусть задан граф алгоритма G. Если для него известна строгая развертка, то число различных поверхностей уровня, уменьшенное на 1, дает оценку сверху длины критического пути графа G. При соответствующей нормировке развертки эта оценка равна разности между максимальным и минимальным ее значением на точках пространства итераций. Всегда существует развертка, для которой эта разность равна длине критического пути. Под именем максимальной параллельной формы она описана в § 4.2. Находить строгие развертки достаточно трудно. Гораздо проще находить обобщенные развертки. Поэтому мы поступим следующим образом. Выберем подходящий класс разверток и найдем в нем развертку, которая строго возрастает вдоль максимально возможного числа дуг. Вообще говоря, она необязательно будет строгой. Но в выбранном классе она будет "самой строгой". Можно надеяться, что с ее помощью также удастся получить нужные оценки.

Процесс нахождения "самой строгой" развертки будем осуществлять рекурсивно. Допустим, что для выбранного класса разверток мы умеем решать следующую задачу: для заданного графа найти развертку, которая строго возрастает хотя бы вдоль одной дуги, или установить, что такая развертка не

422

Часть II. Параллельное программирование

существует. Сначала решаем эту задачу для графа G Предположим, что найдена нужная развертка g. Пусть она строго возрастает вдоль дуг из множества Е, необязательно строго возрастает вдоль дуг из множества Е' и множества Е и Е' не пересекаются. Пространство итераций и множество дуг Е' образуют граф G'. Теперь для него решаем основную задачу. Предположим, что найдена нужная развертка g'. Пусть она строго возрастает вдоль дуг из множества Е\ с Е\ необязательно строго возрастает вдоль дуг из множества Е\ с Е' и множества Е\ и Е\ не пересекаются. Число дуг в графе G конечно, хотя оно может зависеть от внешних параметров. Поэтому минимальное приращение функции g' вдоль дуг из множества Е может быть отрицательным, но обязательно ограниченным снизу. Минимальное приращение функции g вдоль дуг из множества Е положительно по ее выбору. Следовательно, существует такое число а > 0, возможно зависящее от значений внешних переменных, что функция

g\=a.g + g' (7.11)

будет иметь положительные приращения вдоль всех дуг из объединения Е и Е\ и не будет иметь отрицательные приращения вдоль всех дуг из множества Е\. Это означает, что функция gi из (7.11) является разверткой для графа G и строго возрастает вдоль большего числа дуг, чем исходная развертка g. Продолжая этот процесс, мы приходим к развертке, которая строго возрастает вдоль максимально возможного числа дуг графа G Конечно, мы надеемся, что общее число шагов в рекурсивном процессе не будет большим.

В качестве подходящего класса возьмем кусочно-линейные развертки, описанные в § 7.1. Пусть куски линейности совпадают с опорными многогранниками Vj. Все такие развертки определяются решениями неравенства (7.9). Будем считать, что это неравенство одно и соответствует оно одному многограннику, задающему значения внешних переменных. В данном классе разверток легко найти "самую строгую". Допустим, что мы умеем решать следующую задачу: для заданной матрицы А найти какое-нибудь решение неравенства At < 0, не являющееся решением равенства At = О, или доказать, что такое решение не существует. Это можно осуществить, например, с помощью методов линейного программирования [4]. Пусть мы нашли такое решение для неравенства (7.9). Представим матрицу А, руководствуясь утверждением 7.4, в виде суммы двух матриц

А = В+ С, (7.12)

составленных из нулевых строк и строк матрицы А. Именно, в матрице В оставим только те строки матрицы А, для которых координаты вектора At отрицательные; остальные строки возьмем нулевыми. В матрице С оставим только те строки матрицы А, для которых координаты вектора At нулевые; остальные строки возьмем нулевыми. Далее решаем аналогичную задачу для матрицы С. Она проще, чем для матрицы А, т. к. матрица С содержит меньше ненулевых строк. Пусть мы нашли решение t'. Согласно (7.11), составим вектор Ц = at + t', где а > 0. Очевидно, что множитель а всегда мож-

Глава 7. Эквивалентные преобразования программ

423

но подобрать так, что вектор At\ будет неположительным и будет иметь больше отрицательных координат, чем вектор At. В отличие от общего случая множитель а не зависит явно от значений внешних переменных и определяется лишь векторами At и Bt'. Продолжая этот процесс, мы найдем такое решение t неравенства (7.9), что вектор At будет иметь максимально возможное число отрицательных координат. Соответствующую развертку будем называть самой строгой обобщенной кусочно-линейной разверткой.

В разложении (7.12) для подобной развертки матрица С либо нулевая, либо обладает следующим свойством: любое ненулевое решение неравенства Ct < 0 удовлетворяет равенству Ct = 0. Самая строгая кусочно-линейная развертка не единственная. Однако для всех таких разверток разложение (7.12) для матрицы А будет одним и тем же. Если матрица С нулевая, то самая строгая развертка будет просто строгой разверткой. Матрица А целочисленная. Если ограничиться нахождением целочисленных векторов t, то при соответствующей нормировке разверток длину критического пути графа можно оценить разностью между максимальным и минимальным значениями развертки на линейном пространстве итераций. Так как это пространство состоит из опорных многогранников, то вычисление разности сводится к вычислению значений развертки в вершинах многогранников. Поэтому оценка длины критического пути как функция внешних переменных в данном случае будет линейной, в крайнем случае, кусочно-линейной.

Если матрица С в разложении (7.12) для самой строгой развертки с направляющим вектором t не нулевая, то сначала поступим следующим образом. Руководствуясь утверждением 7.4, пересортируем в матрицах В и С строки матрицы А согласно их упорядочиванию, описанному в конце § 7.1. Оставим в матрице В максимальное число строк, которые, во-первых, содержат все строки отдельных блоков и, во-вторых, имеют в каждом блоке отрицательными все координаты вектора At, относящиеся к первым подгруппам. Если после этого матрица С окажется нулевой, то самая строгая развертка снова будет просто строгой. Если же и теперь матрица С ненулевая, то построенная самая строгая развертка по существу является обобщенной. В этом случае исследование графа надо продолжить. Оно осуществляется рекурсивно по такой же схеме. Но покрывающие функции берутся не на всех многогранниках Vy, а только на тех многогранниках типа А/, о которых говорилось в § 7.1. Конечно, рекурсию необязательно доводить до конца. Оценивание можно остановить тогда, когда многогранники А/ по объему станут меньше, чем длина критического пути строгой части развертки, определяемой матрицей С.

Этот способ может дать оценку длины критического пути графа алгоритма, достаточно хорошо отражающую уровень "массового" параллелизма в алгоритме. Сравнивая полученную оценку с прямой оценкой на основе анализа циклов ParDO, можно сделать выводы относительно истинного уровня параллелизма.

При решении задач на массивно-параллельных компьютерах или распределенных вычислительных системах время доступа к памяти чужого процессо-

424

Часть II. Параллельное программирование

ра значительно превосходит время доступа к своей памяти. Поэтому перед решением задачи нужно так распределить данные по модулям памяти, чтобы по возможности минимизировать общее время доступа к ним. Успешно решать задачу на массивно-параллельном компьютере можно лишь в том случае, когда в программе имеются циклы ParDO. Более того, эти циклы должны быть как можно более внешними и охватывать основную часть выполняемых операций. Итерации каждого из них не должны использовать общие переменные. Следовательно, с практической точки зрения наиболее важно рассмотреть распределение данных именно в этих условиях.

Исследуем сначала случай использования одного массива в самом внешнем цикле. Будем считать, что массив А есть множество элементов, отождествляемых с точками /--мерного арифметического пространства, где г — размерность массива. Выделим в пространстве элементов какой-нибудь ненулевой вектор у. Назовем секцией множество элементов массива, лежащих в гиперплоскости с направляющим вектором у. Все пространство элементов разбивается на непересекающиеся секции. Номером секции, которой принадлежит элемент и, можно считать значение скалярного произведения (у, и). Основная задача состоит в нахождении такого вектора у, чтобы при реализации одной итерации цикла все ссылки на массив А обращались к одной и той же секции. При реализации разных итераций цикла ссылки должны обращаться к разным секциям. Если вектор у существует, то распределение массива А по модулям памяти осуществляется следующим образом: в память процессора, выполняющего какую-то итерацию цикла, помещается именно та секция массива А, к которой происходят обращения при реализации этой итерации.

Рассмотрим какое-нибудь вхождение массива. Предположим, что индексы имеют вид и = B_kl^k + р^. Здесь I^k — точка пространства итераций, соответствующая данному вхождению, и — элемент массива, В_к — числовая матрица, р^ — вектор, линейно зависящий от внешних переменных. Обозначим через р значение параметра цикла. Гиперплоскость (a_k, I^k) = р, где а_к = (1, 0, ..., 0), содержит все точки пространства итераций, соответствующие итерации цикла со значением параметра, равным р. Параллельные несовпадающие гиперплоскости относятся к разным итерациям цикла. Пространство точек I^k с помощью линейного преобразования и = B_kI^k + р^ отображается на пространство элементов и. Согласно поставленной задаче, мы хотим найти такой вектор у, чтобы при данном преобразовании параллельные несовпадающие гиперплоскости с направляющим вектором а_к либо отображались на параллельные несовпадающие гиперплоскости с направляющим вектором у в целом, либо отображались на какие-то части таких гиперплоскостей. Как показано в [6], для этого необходимо и достаточно, чтобы была совместной система линейных алгебраических уравнений

в£у = а_к. (7.13)

Глава 7. Эквивалентные преобразования программ

425

Если система (7.13) несовместна, то искомое распределение массива не существует.

Теперь рассмотрим всю совокупность вхождений массива. Вектор у должен удовлетворять системам (7.13) для всех к. Кроме этого, при всех преобразованиях и = Вф + р^ гиперплоскости (а^,1^к) = р для каждого р должны отображаться на одну и ту же гиперплоскость. Также в [6] установлено, что существует матрица Bq, которая вычисляется по всем вхождениям массива и такая, что выполняется равенство

% = 0. (7.14)

Соберем вместе все системы (7.13) и систему (7.14). Тем самым мы получаем для определения вектора у систему линейных алгебраических уравнений. Если эта система совместна, то любое из ее решений дает искомое распределение массива А по модулям памяти. Если же система несовместна, то, вообще говоря, нужного распределения нет. В этом случае можно попытаться ослабить требования на распределение массивов по модулям памяти.

Во-первых, можно попытаться решить лишь системы (7.13). Если это удалось, то при реализации отдельной итерации процессор будет обращаться в "чужие" секции. Однако таких секций будет немного, и они находятся от "своей" секции на одних и тех же "расстояниях" для всех процессоров. Такая ситуация представляет интерес и может быть использована.

Во-вторых, можно попытаться уменьшить число принимаемых во внимание вхождений массива. Рассмотрим какое-нибудь из неучтенных вхождений. Вполне возможно, что для него система (7.13) имеет решение для какого-то другого вектора у. В этом случае секции массива, соответствующие этому вектору у, можно продублировать. Чтобы уменьшить число дублирований секций, новый вектор у нужно выбирать так, чтобы он был общим для наибольшего числа неучтенных ссылок.

Допустим, что хотя бы для одного к система (7.13) несовместна и матрица Bj_{ имеет полный столбцовый ранг. Тогда чаще всего это означает, что на

каждой итерации цикла к-ое вхождение обращается ко всем или почти ко всем элементам массива. Обеспечение независимой работы процессоров для реализации данной программы на массивно-параллельном компьютере требует дублирования всего массива в каждом модуле памяти. Если цикл имеет тип ParDO по всем четырем минимальным графам, то независимая работа процессоров снова возможна.

Если система (7.13) или несовместна, или имеет полный столбцовый ранг, то никакая линейная замена переменных в опорном пространстве не может изменить ситуацию. Поэтому, если дублирование массива в каждом модуле памяти неприемлемо по каким-либо причинам, приходится радикально изменять программу.

426

Часть II. Параллельное программирование

Необходимость дублирования какой-то части массива не означает, что в каждом модуле обязательно нужно отводить столько же памяти. Как правило, один и тот же элемент массива на разных итерациях используется в разное время. Довольно часто дублирование почти полностью можно заменить пересылками информации между процессорами, осуществляемыми в специальным образом выбранные моменты времени, например, так, как это делается в систолических массивах [9]. Переход к блочным вариантам алгоритмов значительно снижает временные затраты на пересылки. К сожалению, использование пересылок несколько уменьшает параллельные свойства вычислительных процессов, т. к. приходится учитывать их синхронизацию во времени. К тому же, в этих случаях нередко приходится изменять порядок выполнения операций, что, строго говоря, приводит к неэквивалентным по вычислениям преобразованиям программ.

Проведенные исследования показывают, что распределение данных по модулям памяти осуществляется независимо для каждого массива. Следовательно, использование в программе нескольких массивов не усложняет принципиально рассматриваемую задачу. Не усложняет принципиально ее и одновременное рассмотрение нескольких внешних циклов.

Формально мы почти нигде не использовали тот факт, что цикл может иметь тип ParDO. Однако он самым тесным образом связан со свойствами систем линейных алгебраических уравнений для определения вектора у. Если описанную технику применить для циклов, тип которых неизвестен, то, скорее всего, соответствующие системы (7.13), (7.14) для какого-нибудь массива будут несовместны. Если же совокупность систем (7.13), (7.14) окажется совместной для какого-то массива, то цикл будет иметь тип Pa г do по всем четырем минимальным графам, построенным именно для этого массива.

Итак, для существования нужного распределения любого массива по итерациям цикла необходимо, чтобы цикл имел тип ParDO по всем графам зависимостей, связанным только с этим массивом. Какой тип имеет цикл по графам зависимостей для других переменных, не имеет никакого значения. Наличие типа ParDO у цикла не гарантирует существование нужного распределения.

§ 7.6. Примеры

Пример 7.1. Поясним процесс построения разверток на примере 6.2. Будем считать, что пространство итераций представлено на рис. 6.11. Обозначим через V линейное пространство итераций. Это есть треугольник с вершина-

Глава 7. Эквивалентные преобразования программ

427

ми в точках (1,0), (я, 0), (я, п — 1). Четыре покрывающие функции из примера 6.2 могут быть объединены в две

Ф,

лл

0^Л■1

-1

2 < / < я, 1 < у < / - 1; 2 < / < я, 1 < у < / - 1.

01 01

Г/Л

ф₀

v^/

В треугольнике К будем искать обобщенные развертки вида (а, х) + у, где a = (a\, a₂), у = уо + у\ п. В нашем случае функции Ф] и Ф₂ действуют из V в К Поэтому в соответствии с обозначениями § 7.1 в соотношениях (7.2) и др. будем иметь a = b, у = 5. Очевидно, что представление (7.6), (7.7) для внешней переменной п имеет вид

я = 2 + р, р>0. (7.15)

С учетом сказанного соотношение (7.2) для функции Ф] становится таким

а₂ > 0. (7.16)

Функция Ф₂ определена на треугольнике, вершинами которого являются точки (2, 1), (я, 1), (я, п — 1). Подставляя координаты этих вершин в неравенства (7.4), получаем неравенства (7.5):

— ai — a₂ < 0, (ai — a₂) — na\ < 0.

Теперь, принимая во внимание (7.15), находим, что неравенства (7.8) будут выглядеть следующим образом:

— а\ — «2 < 0, — а\ < 0.

Присоединяя к ним неравенство (7.16), заключаем, что для координат а\, а₂направляющего вектора а развертки {а, х) + у должны иметь место неравенства

а, > 0, а₂ > 0 . (7.17)

Легко проверить по рис. 4.4, а, что никаких других линейных на многограннике Кразверток граф алгоритма из примера 6.2 не имеет.

Если проделать аналогичные вычисления для графа алгоритма примера 6.3, то можно установить, что в этом случае соотношения для координат а\, а₂будут такими:

«1 > 0, а₂ = 0. (7.18)

Формальное сравнение соотношений (7.17), (7.18) также показывает различие между примерами 6.2 и 6.3. Неравенства (7.17) имеют два независимых решения. Например, щ = I, а₂ = 0 и а\ = 0, а₂= 1. Соотношения (7.18) имеют только коллинеарные решения. Поэтому граф на рис. 4.4, а имеет две независимых развертки, граф на рис. 4.4, б только одну, как и должно быть,

428

Часть II. Параллельное программирование

основную. Оба графа не имеют расщепляющих разверток. Для графа на рис. 4.4, а любая развертка с положительными координатами направляющего вектора будет строгой. Отсюда, в частности, следует, что операции алгоритма, соответствующие вершинам, лежащим на прямой вида / + j = const, можно выполнять параллельно.

Пример 7.2. Посмотрим на примере 6.4, что дает построение макрографов зависимостей для анализа макроструктуры, например, графа алгоритма.

Будем считать области на рис. 6.13 макровершинами. Чтобы установить, из каких макровершин выходят макродуги, входящие в макровершину с номером /, нужно определить каким областям принадлежат значения функции Ф/ в угловых точках /-ой области. Такая проверка показывает, что макрограф имеет следующий вид (рис. 7.3).

13 2 4 5

Рис. 7.3. Общий макрограф

Макровершины с номерами 1, 4, 5 не имеют петли, поэтому операции, соответствующие их вершинам, можно выполнять параллельно. Макровершины с номерами 2, 3 принадлежат сильно связанному подмакрографу. Поэтому их параллельную структуру надо исследовать совместно и более тщательно. Прямой анализ программы примера 6.4 в целом не позволил обнаружить параллелизм, который давал бы возможность существенно сократить время ее реализации.

Теперь построим макрограф для внутреннего цикла программы примера 6.4. Имеются три покрывающие функции Ф', Ф" и Ф'". Снова в качестве макровершин возьмем их области определения. Аналогичная проверка показывает, что макрограф внутреннего цикла имеет вид, приведенный на рис. 7.4.

*^ И

Рис. 7.4. Макрограф внутреннего цикла

Глава 7. Эквивалентные преобразования программ

429

Все макровершины не имеют петли. Поэтому операции, соответствующие их вершинам, можно выполнять параллельно. Это означает, что программу примера 6.4 можно записать следующим образом

DO i = 1, n

DO j = 1, n- i

^ui+j~ U2n+l-i-j END DO (7.19)

DO j = n - i + 1, и

Uj+j = Ii2n+l-l-j

END DO END DO

Очевидно, что оба внутренних цикла имеют тип ParDO. Заметим, что с помощью традиционно используемых методов программу примера 6.4 не удается привести к виду (7.19), в котором параллелизм имеется в циклах.

Пример 7.3. Покажем, как строится макрограф с помощью разверток. Рассмотрим решение краевой задачи для уравнения теплопроводности. Пусть требуется найти функцию u(t, х), где

э7=э^' ' °-'-^г' (⁷-²°)

и(0, х) = ф(х), u(t,0) = «о(0, ^М(^?Д) ⁼ ^Mi(0-Построим равномерную сетку с шагом h по х и шагом ? по t. Предположим, что по тем или иным причинам выбрана явная схема

u'j - u'j~^l u'j~_\ - 2u'j~^l + u'j~₊\

h²где u'j = u(h, jh). Пусть алгоритм реализуется в соответствии с формулой

^"Г+^я+^^м)- ⁽⁷'²¹⁾

Для построения графа алгоритма введем прямоугольную систему координат с осями /, j. Переменные t, х связаны с переменными /, j соотношениями

t=h,x = jh.

2т т ® = a(l-—) + —{b + c),

h h

430

Часть II. Параллельное программирование

выполняемой для разных значений аргументов а, Ь, с. Предположим, что переменные /, j изменяются в пределах

О < /< т, 0 </'< п.


i 1 ,	1 -ч У	ЧУ	ЧУ!	Ч У	\/	^\/^	^\/^	pt-—«	>-
и	►/'


/ У *i '/* 1 -./ .		ЧУ	ЧУ	\/	^\/^	/С 4,/У
L	►У

Рис. 7.5. Поверхности уровней разверток

Непосредственно из (7.21) следует, что покрывающие функции для графа алгоритма будут такими:

fi\

Ф,

По}

v /

(-1Л

, \<i<m, 1 < j < n - 1;

V /

(-Л

, 0,

, 1 < / < /и, 1 < j < n - 1;

(7.22)

Ф,

,01,

V /

, 1 < / < m, 1 < j < n - 1.

Для случая x = 2/6, /г = 1/8 граф алгоритма представлен на рис. 7.5, а. Пунктирными линиями показаны вершины, относящиеся к одному временному слою.

Теперь опишем множество обобщенных разверток этого графа. Будем искать их в следующем виде:

/= ш + (3/ + у.

Не привлекая общего метода их нахождения, заключаем из рис. 7.5, а, что в соответствии с покрывающими функциями (7.22) коэффициенты а, р должны удовлетворять системе неравенств

а + р > 0, а > 0, а-р>0.

Глава 7. Эквивалентные преобразования программ

431

Эта система заведомо имеет два независимых решения. Например,

Л = >+J,f2 = i-j-Некоторые из их поверхностей уровней показаны на рис. 7.5,6.

Поверхности уровней обобщенных разверток разбивают линейное пространство итераций на прямоугольники. В качестве макровершин берутся вершины, попадающие в отдельные прямоугольники. Кроме граничных, любая макровершина получает информацию от двух соседних, находящихся под ней макровершин и передает информацию двум соседним, находящимся над ней макровершинам. Количество получаемой и передаваемой по макродуге информации пропорционально числу вершин, лежащих на соответствующей "стороне макровершины" и непосредственно примыкающих к этой "стороне".

В связи с этим примером заметим следующее. При решении нестационарных задач явными методами почти всегда расчеты ведутся по временным слоям, последовательно слой за слоем. В нашем случае — по пунктирным линиям на рис. 7.5, а. Если вся информация о соседнем слое помещается в оперативную память, то особых проблем не возникает. Кстати, на каждом временном слое операции не связаны между собой и могут выполняться параллельно. Поэтому счет по временным слоям особенно эффективен на параллельных вычислительных системах с общей памятью.

Если задача настолько большая, что информация о соседнем слое не помещается в оперативную память, то приходится пользоваться меленной памятью и тогда возникают проблемы. Время переноса информации о слое из медленной памяти в оперативную пропорционально числу точек в слое. Время нахождения решения задачи на очередном слое также пропорционально числу точек в слое. Но время выполнения одной операции значительно меньше среднего времени пересылки единицы информации из медленной памяти в оперативную. Поэтому при счете по временным слоям большая часть времени будет уходить на организацию пересылок, т. е. будет тратиться непроизводительно.

Теперь представим, что алгоритм реализуется по макровершинам. В этом случае время на пересылки информации для каждой макровершины будет пропорционально длине (в общем случае, площади) границы содержащего ее прямоугольника. Время выполнения макровершины будет пропорционально площади (в общем случае, объему) прямоугольника. При увеличении прямоугольников длины границ растут медленнее площадей. Следовательно, разбиение линейного пространства на прямоугольники всегда можно выбрать таким, что время пересылок информации из медленной памяти в оперативную будет составлять сколь угодно малую долю.

Как показывают исследования, проведенные в § 7.2, возможность реализации по макровершинам оказывается реальной для широкого круга алгоритмов. В частности, эта возможность широко использовалась при решении

432

Часть II. Параллельное программирование

задач линейной алгебры блочными методами [5]. Общий случай впервые рассмотрен в [11].

Пример 7.4. Рассмотрим снова пример 6.5. Среди циклов ParDO в нем наибольшим по объему вычислений является цикл с параметром j. Выясним, можно ли распределить массив А таким образом, чтобы на разных итерациях этого цикла не было обращений к одним и тем же секциям массива. Ответ очевиден: секции массива должны совпадать с его столбцами. Но мы получим этот ответ формальным способом.

В цикле с параметром j примера 6.5 вхождения элементов массива А имеют следующий вид

(0\ (Л

'0"

V /

J +

V J

j +

V J

\ j

v j

В соответствии с ними системы линейных алгебраических уравнений (7.13) для вектора у = (уь Уг) будут такими:

0 у, + 1 у₂ = 1, 0 у, + 1 у₂ = 1, 0 yi + 1 у₂ = 1, 1 У1 + 0 у₂ = 0, 1 у! + 0 у₂ = 0, 0 _У1 + 1 уз = 1.

Отсюда находим, что если исходное распределение существует, то оно единственно и определяется вектором у = (0,1).

Пример 7.5. Теперь рассмотрим пример 6.1 вычисления матричного произведения А = ВС, где все матрицы плотные квадратные порядка п. Два внешних цикла программы имеют тип ParDO по всем графам зависимостей. Поэтому потенциального параллелизма в программе вполне достаточно.

Исследуем возможность распределения массивов А, В, С. Ограничимся сначала параллелизмом самого внешнего цикла. Вхождение элементов массива А единственное и имеет вид

(10 0"! 010

(i\

Система (7.13) будет такой:

1 Yi + 0 у₂ = 1;

0 yi + 1 у₂ = 0;

0 у, + 0 у₂ = 0.

Она имеет единственное решение у = (1,0). Вектор у = (1,0) соответствует распределению массива А по строкам. Вхождение массива В также единственное и имеет вид

(10 0"! 001

(i\

Глава 7. Эквивалентные преобразования программ

433

Ему соответствует следующая система (7.13)

1 Yi + О Y2 = 1;

О у, + 0 уз = 0;

0 Yi + 1 Y2 = 0. Эта система имеет единственное решение у = (1,0), что означает распределение массива В по строкам. Единственное вхождение массива С таково:

(0 0 1\ 010

Г[\

Ему соответствует система (7.13) вида

0 у, + 0 у₂ = 1;

0 у, + 1 у₂ = 0;

1 Yi + 0 у₂ = 0.

Она несовместна. Так как матрица системы имеет полный столбцовый ранг, то отсюда вытекает, что на каждой итерации внешнего цикла будет использоваться весь массив С. Факт, который легко проверить по тексту программы.

Дублирование массива С целиком в каждом модуле памяти может быть нецелесообразным из практических соображений. Поэтому посмотрим, как используется массив С на итерациях второго цикла. Для этого цикла вхождение массива С имеет вид

fOlVy^

10 U

и ему соответствует такая система (7.13)

0 Yi + 1 Y2 = 1;

1 Yi + 0 Y2 = 0.

Она уже совместна и имеет единственное решение у = (0,1). Это означает распределение массива С по столбцам.

Если используется параллелизм вычислений лишь самого внешнего цикла, то при каждом значении параметра / оба внутренних цикла будут выполняться на одном и том же процессоре. Проведенные исследования показывают, что без ограничения общности можно считать, что каждый процессор для вычисления одной строки массива А требует того же номера строку массива В и весь набор столбцов массива С. Теперь вспомним, что второй цикл по параметру j также имеет тип ParDo. И хотя мы не будем использовать этот факт для распараллеливания вычислений, его можно принять во внимание для выбора нужного порядка использования столбцов массива С.

434

Часть II. Параллельное программирование

Пусть в собственной памяти /-го процессора отведено место для четырех векторов размерности п: вектор a_h где вычисляется /-ая строка массива А, вектор bj, где хранится /-ая строка вектора В и вектор q, где первоначально хранится /-ый столбец массива С, а также рабочий вектор dj. Для процессоров, связанных, например, в кольцо, программу вычисления матричного произведения А = ВС можно переписать следующим образом:

DOj=l,n

Par DO i=\,n

с, -> d, (723)

d;_\ —> Cj

a_y =a,j + (b_h dj)

END DO END DO

Здесь do = d„. Порядок вычислений в этой программе иной по сравнению с исходной. Поэтому, строго говоря, она не эквивалентна ей по вычислениям. Тем не менее, в условиях точных вычислений обе программы будут давать одни и те же результаты. Существует много программ типа (7.23). Каждая их них приспособлена к какому-то одному типу связей процессоров между собой.

Заметим, что весь анализ программы примера 6.1 был выполнен формально. Простота программы сказалась лишь на объеме вычислений, необходимых для проведения этого анализа.

Пример 7.6. Следующий пример особенно интересен с точки зрения иллюстрации применения описанной в этой книге теории исследования информационной структуры алгоритмов и программ. В 1992 г. нам представилась возможность провести ряд экспериментов на крупнейших компьютерах фирмы Cray Research Inc., USA. В арсенале у нас была уже упоминавшаяся система V-Ray [65], предназначенная для изучения параллельной структуры последовательных программ. Применение этой системы не требует никакой предварительной информации ни о структуре программы, ни о ее математическом содержании. Не привязана V-Ray System и к какой-либо архитектуре вычислительной системы. Поэтому было очень интересно понять, чего же можно достичь с помощью данной системы на самых современных компьютерах.

В качестве тестовых примеров были выбраны программы из пакета Perfect Club Benchmarks [46]. Мы остановились на этом пакете, главным образом, из-за его широкой известности. Программы пакета Perfect Club Benchmarks тестировались и оптимизировались практически на всех крупных компьютерах, причем самыми разными людьми. Нам было важно не только удовлетворить собственное любопытство, но и увидеть в сравнении, что можем мы и что могут другие.

Глава 7. Эквивалентные преобразования программ

435

В табл. 7.1 приведены значения реальной производительности компьютеров Cray М90 и Cray С90 на программе TRFD из пакета Perfect Club Benchmarks, полученные в различных режимах. Заметим, что пиковая производительность одного процессора Cray М90 составляет 333 Мфлопс, одного процессора Cray С90 — 960 Мфлопс.

Таблица 7.1. Результаты оптимизации для компьютеров Cray М90 и С90


Cray М90, CPUs	Базовая произв., Мфлопс	Ручная опт., Мфлопс	V-Ray опт., Мфлопс
1 4 8	56.19* 54.86 54.34	81.72¹261.84 481.03	247+ 822 954^+t
Cray С90, CPUs	Базовая произв., Мфлопс	Ручная опт., Мфлопс	V-Ray опт., Мфлопс
1 8	89.5* 89.6	139.71^!962.68	579.7^f2440.5*

Здесь графа "Базовая производительность" означает производительность на программе TRFD, полученную с помощью штатного компилятора без какой-либо предварительной оптимизации. Графа "Ручная оптимизация" означает наибольшую производительность, полученную специалистами США с помощью ручной оптимизации программы. Графа "V-Ray оптимизация" означает производительность, полученную с помощью оптимизации, выполненной на основе информации о структуре программы, которая была выявлена V-Ray System. Дополнительные символы означают следующее:

□ (+) — значение производительности получено не в монопольном режиме и может быть улучшено;

□ (*) — результат занимает седьмое место среди значений производительности на всех тринадцати программах пакета Perfect Club Benchmarks;

□ (!) — результат занимает девятое место;

□ (у) — результат занимает первое место среди значений производительности на всех программах из пакета Perfect Club Benchmarks, оптимизированных вручную;

□ (ф) — результат занимает второе место среди значений производительности на всех программах из пакета Perfect Club Benchmarks, оптимизированных вручную, уступая лишь хорошо распараллеливаемой программе MG3D.

436

Часть II. Параллельное программирование

Приведенные в таблице результаты говорят сами за себя. Тем не менее, мы дадим к ним небольшой комментарий. Программа TRFD относительно простая. Тем интереснее результаты, приведенные в первых двух графах. Первая графа говорит о том, что нет никакой надежды на то, что штатный компилятор параллельной вычислительной системы сможет обеспечить эффективную реализацию прикладной программы без дополнительной информации о ее структуре. Получение этой информации целиком возложено на пользователя. Так же как и ответственность за результаты ее применения. Вторая графа показывает, что получить и эффективно использовать нужную информацию трудно даже для специалистов высокой квалификации, знающих практически все о компьютере и компиляторе, и даже в том случае, когда программа относительно проста и о ней вроде бы все известно.

Искушенный читатель может возразить, что программа TRFD записана на последовательном языке, а использованные компьютеры параллельные, что для эффективного применения параллельных компьютеров специально разработаны параллельные языки программирования и т. п. Все это верно. Однако заметим, что все параллельные языки помогают только записать в нужном виде дополнительную информацию о структуре реализуемого программой алгоритма и не имеют никакого отношения к способам ее получения. К тому же компиляторы с параллельных языков не дают гарантий о степени эффективности реализации тех или иных конструкций параллельных языков. Поэтому независимо от того, написана ли программа на последовательном или параллельном языке, пользователю приходится многократно пропускать разные варианты программы на компьютере, чтобы обнаружить ее узкие места и понять, как их устранить. Этот процесс очень плохо формализован и именно он вызывает наибольшие трудности при ручной оптимизации программ.

Третья графа таблицы говорит о том, что, по-видимому, с помощью V-Ray System удается выявить такую информацию о структуре программы, которую трудно получить каким-либо другим способом.

Так оно и есть. С самого начала V-Ray System задумывалась как автономная инструментальная система для автоматизации процесса исследования программ и их преобразования к виду, удобному для целевого параллельного компьютера. Поводом для ее создания послужили фундаментальные результаты, полученные авторами книги в области изучения структуры алгоритмов, записанных в виде программ на последовательных языках. Однако по мере развития системы возникло большое число специфических проблем, связанных с повышением эффективности ее функционирования, обеспечением наглядности получаемых результатов, представлением различных сервисных услуг и многими другими сторонами процесса взаимодействия с параллельными вычислительными системами. Поэтому спустя какое-то время V-Ray System стала совершенствоваться, главным образом, под влиянием интересов потенциальных пользователей системы. Тем не менее, в нее по-

Глава 7. Эквивалентные преобразования программ

437

стоянно вводились и вводятся сейчас новые методы исследования программ. В свою очередь, опыт анализа реальных программ с помощью V-Ray System привел к появлению ряда новых задач, интересных в математическом отношении.

Но вернемся к программе TRFD и рассмотрим в общих чертах те ее преобразования, которые привели к результатам в третьей графе табл. 7.1.

В программе TRFD большая часть вычислений и основной временной выигрыш от преобразований приходится на подпрограмму OLDA. Структуру данной подпрограммы можно представить в виде циклического профиля на рис. 7.6, в котором каждая скобка соответствует циклу do.

jj .iiyj&uib^ij^

Рис. 7.6. Циклический профиль

После первого анализа подпрограммы OLDA были выявлены следующие факты:

□ все самые внутренние циклы имеют тип ParDO по всем графам зависимостей и этот факт может быть обнаружен с помощью самых простых традиционных методов анализа;

□ все самые внешние циклы имеют тип ParDO по графу алгоритма; этот факт трудно обнаружить с помощью формального применения традиционных методов анализа, но легко обнаружить визуально;

□ никакие традиционно используемые методы анализа структуры программ не позволяют установить принадлежность или непринадлежность типу ParDO хотя бы какого-нибудь из внутренних циклов, не являющегося самым внутренним;

□ число итераций в каждом цикле относительно невелико;

□ в целях экономии памяти основной многомерный массив хранится компактно в виде одномерного, в силу чего индексные выражения вычисляются по сложным нелинейным (относительно параметров цикла) выражениям;

□ вторая циклическая конструкция описывает только пересылку данных и не содержит арифметические операции.

Ручная оптимизация основана на использовании первых двух фактов. Однако четвертый факт говорит о том, что этого недостаточно. Принимая во внимание третий факт, становится понятно, почему результаты второй графы таблицы в предисловии невысоки.

438

Часть II. Параллельное программирование

Первое, что нужно установить, — это принадлежность или непринадлежность типу ParDO внутренних циклов подпрограммы OLDA. Для этого нужно построить для них минимальные графы зависимостей. Сложная циклическая конструкция программы и большая глубина вложенности отдельных циклов не являются препятствием для применения V-Ray System. Но пятый факт не дает возможность ее использовать, т. к. подпрограмма OLDA не принадлежит линейному классу.

Чтобы обойти это препятствие, была построена другая программа. Она отличается от OLDA только тем, что в ней основной одномерный массив снова представлен как многомерный с линейными индексными выражениями. На рис. 7.7 представлен циклический профиль новой программы. Он несколько отличается от циклического профиля программы OLDA, показанной на рис. 7.6.

--------------------------------------•--------------------------------------1 i-------------------------•-----------------' i-----------------------------------------------•------------------------------------------------------

Рис. 7.7. ParDO-циклический профиль

Восстановление полноразмерного массива привело к появлению нескольких новых циклов. Для хранения полноразмерного массива требуется несколько больше памяти, чем для одномерного. Однако увеличение памяти не столь существенно, чтобы отказаться от использования построенной программы. Тем более, что ее параллельные свойства превосходны. С помощью V-Ray System были построены все графы зависимостей и определены все циклы ParDO. На рис. 7.7 они отмечены точками. Из рис. 7.7, в частности, видно, что если в программе использовать параллелизм лишь самых внутренних и самых внешних циклов исходной программы, то большая часть параллелизма не будет принята во внимание.

Из рис. 7.7 следует общая стратегия преобразований, которые необходимо выполнить с новой программой:

□ объединить в один два самых внешних цикла в первой и третьей циклических конструкциях, тем самым значительно увеличив длину внешних циклов;

□ переместить эти длинные циклы внутрь и использовать их для векторизации;

□ самые внутренние циклы переместить наружу и использовать их для параллельного выполнения независимых ветвей вычислений процессорами компьютера;

□ последовательные циклы, определяющие перевычисление одних и тех же элементов массивов, использовать для повышения локальности обращения к данным.

Глава 7. Эквивалентные преобразования программ

439

JJ 1Й

Jj 11--------^

iJi____ii

распределение цикла 1

UI____h

ijj _LLi

перестановка циклов 2,1

перестановка циклов 2,3

^] ^

iJI____l|

У Ilk

слияние циклов 2

^] ^

^J * h

^ _LL

i ' ^L

перестановка циклов 2,1

4$ ^

^J * h

^ _LL

i * ^L

распределение цикла 1

i] ^

±JI_____Ii

Й1 Ilk

перестановка _v циклов 3,1

i] 1Ш

iJI____h

^JJ] Ilk

Рис. 7.8. Преобразования циклов

Цепочка последовательных преобразований для первой циклической конструкции на рис. 7.7 представлена на рис. 7.8. Меткой 1 в исходном виде конструкции отмечен цикл, объединяющий два самых внешних цикла той же конструкции на рис. 7.7.

Все эти и подобные им преобразования позволили достичь тех впечатляющих результатов, которые представлены в третьей графе табл. 7.1. Важно отметить, что вся оптимизация программы TRFD была выполнена на уровне языка Fortran без использования ассемблерных вставок и обращений к высокоэффективным библиотечным подпрограммам.

ЧАСТЬ III

Смежные проблемы и применение

Глава 8

Вычислительные системы и алгоритмы

Неизбежным результатом расширяющихся

связей между различными уровнями иерархии

является возрастающая область непонимания.

Из законов Мерфи

Бурное развитие микроэлектроники позволило достичь к концу 70-х годов прошлого столетия невиданного ранее скачка в развитии вычислительной техники. Стали функционировать вычислительные системы с производительностью в несколько сотен миллионов операций в секунду, мощность проектируемых систем определялась миллиардами операций. Появились многочисленные устройства, позволяющие очень быстро решать различные простые задачи, такие как матричные и векторные преобразования, быстрое преобразование Фурье, обработка сигналов, распознавание простейших изображений и т. п. Основной целью создания этих устройств было ускорение и упрощение процесса решения конкретных задач. Каждое из них имело свою собственную архитектуру, и не было почти ничего общего между различными устройствами. Тем не менее, эти очень скромные по современным понятиям успехи уже тогда привели к появлению весьма дерзкой мысли о возможности в будущем построения заказных специализированных вычислительных систем, ориентированных на эффективное решение конкретных задач.

Кроме впечатляющих результатов и радужных надежд успехи микроэлектроники принесли немало серьезных проблем в деле освоения вычислительной техники, в особенности больших параллельных систем. Очень скоро стало ясно, что построение для таких систем эффективных численных методов является делом и трудным, и малоизученным. Трудности определялись, главным образом, значительным разнообразием архитектур самих систем и, как следствие, таким же разнообразием способов организации вычислений. Различные способы организации вычислений влекли за собой различные организации данных, требовали создания различных численных методов и алгоритмов, различного программного обеспечения, новых средств и языков общения с вычислительной техникой.

Глубокое понимание перспектив развития, а также проблем использования вычислительной техники привело академика Г. И. Марчука к формированию в те годы нового фундаментального научного направления, названного "отображение задач вычислительной математики на архитектуру вычисли-

444

Часть III. Смежные проблемы и применение

тельных систем". Его стержнем должно было стать совместное исследование численных методов и структур вычислительных систем. Тогда это направление, кратко называемое "проблемой отображения", оказалось на острие многих вопросов, связанных с вычислениями. Таким оно остается и сейчас. Наверное, оно будет таким же и в будущем, по крайней мере, ближайшем.

Основные трудности развития нового направления связаны с отсутствием строгих математических постановок нужных задач. Обсуждения, проведенные в главах 2, 3 этой книги, говорят об огромном числе различных факторов, влияющих на выбор структуры компьютеров. В свою очередь, данное обстоятельство приводит к большому разнообразию самих компьютеров. Только число названий классов вычислительной техники измеряется десятками: векторные, конвейерные, многопроцессорные, систолические, программируемые и т. п. В каждом классе имеется немало существенно различных представителей. Поэтому нельзя надеяться на разработку в ближайшее время математической модели, сколько-нибудь адекватно отражающей процессы функционирования хотя бы основного множества компьютеров. Тем не менее, во всех представителях из всех классов можно увидеть применение нескольких идей, решающим образом влияющих на производительность. Это, в первую очередь, — параллелизм и конвейерность вычислений, иерархическая структура памяти, использование коммутаторов и коммуникационных сетей для связи функциональных устройств между собой. Ясно, что как минимум, эти идеи должны находить свое отражение в структуре численных методов.

Вычислительная техника и алгоритмы — это две опоры, на которых строится проблема отображения. Но как бы не велики были достижения в области развития вычислительной техники, она является всего лишь инструментом для решения прикладных задач. Инструментом, который создается и совершенствуется по своим законам, определяемым успехами микроэлектроники, авторскими идеями, чьими-то амбициями и много чем другим, не всегда даже полезным при проведении практических расчетов. Инструментом, который почти всегда претендует на универсальность своего использования и поэтому почти всегда используется с трудом при решении конкретных задач. Как уже отмечалось, создание общей математической модели процессов функционирования компьютеров кажется делом маловероятным. Поэтому представляется вполне естественным, что продвижение в проблеме отображения должно начинаться с разработки фундаментального математического аппарата, позволяющего описывать и исследовать детальную структуру алгоритмов. Структуру, показывающую, как в процессе реализации алгоритма отдельные его операции связаны между собой и с памятью компьютера.

Об этом аппарате мы уже говорили в главах 6 к 7. Однако изучение проблемы отображения начиналось не с него. По мере ее осмысления большое беспокойство вызывало отсутствие базового математического формализма, помогающего оценивать качество работы многих функциональных устройств

Глава 8. Вычислительные системы и алгоритмы

445

и соответственно этому предлагать те или иные схемы реализации алгоритмов. Дело в том, что одновременное использование многих функциональных устройств является одной из центральных идей, позволяющих получить дополнительное ускорение процесса решения задач. Для оценки их работы были введены различные характеристики, такие как пиковая производительность, реальная производительность, ускорение, эффективность, загруженность и т. п. Работа [43] и подобные ей говорят о том, что в понимании этих характеристик существует большой произвол, а это, в свою очередь, делает невозможным проведение строгих исследований. Поэтому всем таким характеристикам необходимо было придать четкий математический смысл. Точные определения и аккуратные выводы в базовом формализме даны в § 2.3. Они позволили заложить математическую основу в изучение процессов функционирования сложных вычислительных систем. Точное определение основ делает возможным получение точных выводов. Мы показали это в § 2.3 на примере сравнения оценок Амдала и Густавсона— Барсиса для ускорения.

Была и другая веская причина для аккуратного рассмотрения процесса функционирования многих функциональных устройств. На рубеже 70—80-х годов прошлого столетия в США, а под их влиянием и в Европе, начались активные исследования в области так называемых систолических массивов. Систолические массивы представляют простейшие вычислительные системы с многими функциональными устройствами. Они не имеют памяти и коммуникационной сети, реализуются на одном кристалле и, как утверждалось, исключительно дешевы в изготовлении. Более детально с истинными причинами проявления особого интереса к этим устройствам можно познакомиться в работе [54]. Систолические массивы заинтересовали нас как возможный элемент проблемы отображения. К этому времени уже стала вырисовываться следующая схема ее решения: раскладываем задачу на простейшие, простейшие реализуем с помощью спецпроцессоров, а вычислительная система в целом получалась как объединение этих спецпроцессоров с помощью подходящей коммуникационной сети. Казалось, что на роль спецпроцессоров вполне могут подойти систолические массивы. Однако определенные сомнения оставались. Каждый отдельный систолический массив мог реализовывать только один алгоритм, причем относительно простой. Набор алгоритмов, подлежащих реализации, был совершенно не ясен. Его мы надеялись установить, анализируя программы пользователей с помощью системы V-Ray, которая к тому времени уже начинала создаваться. Но отсутствовала конструктивная методология построения систолических массивов, соответствующих заданному алгоритму. По существу, ее еще предстояло создать. Для решения всех этих вопросов также необходимо было изучать работу большого числа устройств.

Таким образом, ключевым моментом в решении проблемы отображения оказался анализ структуры алгоритмов. Ответ на вопрос, какие алгоритмы

446

Часть III. Смежные проблемы и применение

необходимо изучать в первую очередь, дан в §§ 4.3, 4.4. Это алгоритмы, записанные на языках программирования. Аппарат исследования программ, описанный в главах 6, 7 а система V-Ray, реализующая данный аппарат, являются основным инструментом выделения в прикладных программах тех структур, которые должны будут реализовываться специальным образом. Остается только решить, какие именно структуры надо выделять.

Практика написания прикладных программ говорит о том, что наибольший объем вычислений почти всегда концентрируется в подпрограммах. Поэтому подпрограммы вроде бы вполне могли быть кандидатами на быструю реализацию. Для их выделения не нужно привлекать сложный аппарат исследований, а достаточно всего лишь просматривать тексты программ. По первоначальной идее именно подпрограммы должны были реализовываться в виде систолических массивов. Однако заметим, что различных подпрограмм очень много. К тому же сами подпрограммы могут содержать в своих телах вызовы других подпрограмм. Все это, в конечном счете, приводило к тому, что с помощью систолических массивов оказывалось возможным реализо-вывать только отдельные алгоритмы из библиотек стандартных подпрограмм. Более того, по самой сути конструирования систолических массивов эти алгоритмы обязаны были иметь фиксированный размер (размерность, число шагов и т. п.), что вносило определенные трудности в решение задач переменного размера. Несмотря на высказанные замечания, введение спецпроцессоров типа систолических массивов в состав высокопроизводительных вычислительных систем безусловно было бы полезным. Об этом мы будем еще говорить.

При разработке методологии построения математических моделей систолических массивов [14] было установлено, что на подобных вычислительных системах успешно реализуются алгоритмы, графы которых устроены регулярно. С другой стороны, анализ информационной структуры большого числа алгоритмов с помощью системы V-Ray показал, что в очень многих случаях их графы сводятся именно к регулярным. При этом важно отметить, что часто разные алгоритмы имеют либо одни и те же, либо очень похожие графы. Это наблюдение позволило нам выдвинуть гипотезу, что в реально используемых программах основные вычислительные ядра имеют информационные связи, принадлежащие небольшому по численности набору типовых структур. Пока эта гипотеза не опровергнута. Более того, она постоянно находит новые подтверждения, особенно при анализе сходных задач. Любые свойства типовых информационных структур, в том числе параллельные, возможно исследовать заранее. Поэтому, зная состав типовых информационных структур в конкретных программах и их связь между собой, можно заранее сказать, какова наиболее подходящая архитектура вычислительной системы в данном случае и насколько эффективно данные программы будут реализованы на конкретном компьютере. Перспектива стоит того, чтобы подобными исследованиями заниматься серьезно.

Глава 8. Вычислительные системы и алгоритмы

447

Помимо достижения очевидной цели, направленной на повышение эффективности использования вычислительной техники, исследование информационной структуры алгоритмов постепенно стало формировать и другую цель, значительно более фундаментальную. Хотелось понять, какое место занимают параллельные вычисления среди тех наук, которые так или иначе определяют процессы функционирования сложных компьютерных систем. Конечно, в первую очередь мы интересовались математическими науками. Выяснилось любопытное обстоятельство [10]. Оказалось, что некоторые задачи, связанные с алгоритмами, но внешне не имеющие никакого отношения к параллельным вычислениям, могут быть, тем не менее, точно описаны таким образом, что информационная структура алгоритмов становится определяющим элементом описания. Например, задачи восстановления линейного функционала, вычисления значений градиента, оценивания величины ошибок округления результатов промежуточных вычислений и многие другие могут быть сформулированы в терминах нахождения решения системы линейных алгебраических уравнений. По структуре ненулевых элементов матрицы этих систем очень похожи на матрицу смежностей графа алгоритма. Так как граф алгоритма не имеет петель, то перестановкой строк и столбцов матрицы систем можно привести к треугольному виду. Исследовать такие системы очень просто. Но из них получаются и нетривиальные выводы. В случае задачи вычисления градиента решение системы "очевидным" способом приводит к методу, сложность которого линейно зависит от размерности пространства. Если ту же систему решать другим способом, то появляется метод быстрого вычисления градиента, сложность которого не зависит от размерности пространства. Многие задачи изучения процессов работы функциональных устройств, в том числе оптимальных процессов, описываются системой линейных неравенств, матрицы которых совпадают с матрицей инциденций графа алгоритма. Это также открывает путь к новым исследованиям.

Параллельные вычисления стали сейчас не только нужной, но и модной областью исследований. По необходимости или ради любопытства ими занимаются многие специалисты. Большое число вроде бы полезных результатов и фактов здесь лежит на поверхности. Для их получения довольно часто не требуется глубоких познаний. Достаточно более или менее "войти в предмет" и уже можно делать содержательные выводы, возможно, даже никем не опубликованные. Такого рода результаты мало помогают в деле решения действительно серьезных проблем. К тому же они создают впечатление, что в параллельных вычислениях нет ничего другого, кроме каких-то околонаучных манипуляций с простыми понятиями. В конечном счете, это связано с тем, что как раздел науки параллельные вычисления до сих пор находятся в стадии своего становления.

448

Часть III. Смежные проблемы и применение

Мы надеемся, что проводимое исследование информационной структуры алгоритмов и проблемы отображения убедят читателя в том, что он имеет дело с весьма сложным междисциплинарным предметом, обладающим разветвленными связями с самыми различными областями знаний. А параллельные вычисления являются всего лишь одним из акцентов в изучении этого предмета.

§ 8.1. Расширение и уточнение линейного класса

Любая программа на стадии предварительного анализа с помощью автономных систем типа V-Ray может быть приведена к некоторому каноническому виду, в котором все ее фрагменты размечены по принадлежности или непринадлежности к линейному классу. Нелинейность фрагментов может быть либо устранимой, либо принципиальной. Устранимая нелинейность означает, что с помощью каких-то эквивалентных преобразований фрагмент может быть приведен к линейному виду. Как показывает практика, большая часть нелинейностей оказывается устранимой. Довольно часто она возникает от стиля программирования и желания сэкономить ресурсы памяти компьютера. Но может возникать и по существу как, например, при использовании стандартных функций и подпрограмм, циклов типа go to, ветвлений и т. п. Обнаружить принципиально нелинейные фрагменты и сделать программу максимально линейной — сложная задача. Ее решение целиком определяется уровнем интеллектуальности процесса канонизации. Исследуя проблему отображения, мы будем, как правило, считать программы и алгоритмы линейными. В подтверждение обоснованности такого решения рассмотрим сначала некоторые типичные случаи преобразования нелинейных или трудно анализируемых фрагментов в линейные и, возможно, более простые.

Прямая подстановка

Не так уж и редко индексы используемых переменных вычисляются подобно тому, как в следующем фрагменте:

р = 0

DO / = 1, Я

... = ... а_р ...

------------ (8.1)

а_р+1 = ... р=р + \

END DO

Формально этот фрагмент не является линейным, т. к. значения индексов р и р + 1 переменной а вычисляются. Однако прямая подстановка вместо р

Глава 8. Вычислительные системы и алгоритмы

449

эквивалентного ему выражения / — 1 и вычеркивание оператора р — р + 1 делают фрагмент (8.1) линейным:

DO / = 1, Я

... = ... а,-_!...

в,- = ...

END DO

Вычисляемый цикл до to

Допустим, что программа реализует итерационный метод. Пусть на каждой итерации пересчитывается некоторая величина t и процесс заканчивается, когда t < е, где е — заданная внешняя переменная, символизирующая, например, точность. Вполне возможно, что программа будет иметь такой вид:

1 тело цикла

if (t>e) go to 1 (⁸-²)

Даже если тело цикла представляет линейный фрагмент, программа в целом не является линейной, т. к. цикл не имеет тип цикла do. Обычно из каких-то соображений известно, что количество итераций не превосходит некоторого целого числа ш. Выберем параметр, не используемый в теле цикла. Предположим, что это есть /. Тогда программа (8.2) будет эквивалентна программе

do i= 1, m

Тело цикла

if (t<s) go to 2 '

END DO

2 CONTINUE

Предположим теперь, что программа, реализующая тело цикла, выполняется на разных итерациях совершенно одинаково. В этом случае любой граф зависимостей тела цикла программы (8.3) не будет зависеть от параметра /. Следовательно, граф программы (8.3) будет представлять многослойную конструкцию. Все слои одинаковы и являются графами зависимостей тела цикла. Число слоев равно числу итераций и не превосходит числа т. Ясно, что в данном случае выбор числа т никак не сказывается на особенностях графов зависимостей программы (8.3) в целом.

Вычисляемые ветвления

Предположим, что некоторая функция / вычисляется по разным формулам в зависимости от полученного в программе значения переменной q.

450

Часть III. Смежные проблемы и применение

Рассмотрим, например, следующий фрагмент

±f(q>r) go to 1

/= ф(сс, Р)

go to 2 ₍₈_₄₎

1 /=v|/(y)

2 CONTINUE

Здесь q — вычисляемая переменная, г — внешняя переменная, ср(а, Р) и ц/(у) представляют какие-то функции, определяющие значение/в зависимости от значения переменной q. Этот фрагмент не может быть линейным хотя бы потому, что условие q > г является вычисляемым. Пусть мы изучаем граф алгоритма. При одних значениях переменной q в вершины, соответствующие функции f, будут входить дуги, определяемые переменными а, р, при других — переменной у. Какими бы ни были q а г, фрагмент (8.4) всегда перевычисляет значение переменной / Ничто не мешает рассматривать фрагмент (8.4) как способ вычисления некоторой функции Q(q, г, а, р, у), зависящей от всей совокупности входящих в (8.4) переменных. Поэтому фрагмент (8.4) можно заменить одним оператором присваивания

/= 9(<7, г, а, р, у). (8.5)

Если все аргументы в правой части представляют простые переменные или переменные с линейными индексными выражениями, фрагмент (8.5) будет принадлежать линейному классу.

Допустим снова, что для программы в целом строится граф алгоритма. При наличии в программе фрагмента (8.4) этот граф будет заведомо зависеть от значений переменной q, по крайней мере, в части тех дуг, которые связаны с вычислением / После замены фрагмента (8.4) фрагментом (8.5) зависимость графа алгоритма от значений переменной q пропадает. Однако теперь в графе будет несколько больше дуг. Некоторые из них будут соответствовать фиктивным связям, относящимся к тем функциям ср(а, Р) или у (у), которые не срабатывают при конкретных значениях переменной q.

Подчеркнем, что данный пример является типичным образцом введения и использования расширенного графа. Расширенный граф будет часто появляться в тех ситуациях, когда исходный граф имеет какие-то плохо исследуемые особенности, но существует другой граф, не имеющий такие особенности и содержащий исходный граф в качестве своего подграфа. Этот другой граф и называется расширенным. При выборе расширенного графа важно не потерять слишком много из нужных свойств исходного графа.

Нелинейные индексные выражения

На практике нередко встречаются программы, в которых какая-то часть индексных выражений оказывается нелинейной.

Глава 8. Вычислительные системы и алгоритмы

451

Пусть фрагмент имеет вид

DO j = 1, Я - 1

^Ю/=У'""¹ (8.6)

^anj-ii- 11//2 ~ ^anj-(j- iy/2 + Щ +{/- 1)(я-y/2)

END DO

Все опорные многогранники в нем линейные и нелинейность имеется только в индексах используемых переменных. Методика построения графов зависимостей в любых нелинейных случаях остается такой же, как в линейных. В частности, для всех элементарных графов нужно решать уравнение (6.13) и на множестве его решений находить лексикографически максимальное при выполнении условий (6.14). Будем строить граф алгоритма. Для первого элементарного графа из (8.6) уравнение (6.13) относительно у', /' таково

nj'-0'-l)J'/2 = nj-(/-iy/2.

Но функция nj — (/'^— 1)у/2 на множестве 1 <у < п — 1, у < i < п — 1 не зависит от / и монотонно возрастает по/ Поэтому решение задачи (6.13), (6.14) имеет вид

j'=j,i' = i-l, (8.7)

если 1 < j < п — 1, j < i < п — 1. В вершины, для которых / = у, дуги элементарного графа не входят. Для второго элементарного графа из (8.6) уравнение (6.13) относительно у', /' имеет вид

nj' ~ О - 1)У'/2 = /+(/- 1)(л -у/2). (8.8)

Из (6.14) следует, что j'<j. Как уже отмечалось, левая часть равенства монотонно возрастает по у'. Легко проверить, что приу' =j разность между левой и правой частями (8.8) равна п — /, что на множестве 1 <у < п — 1, у < / < п — 1 больше или равно 1. Приу' = j — 1 та же разность равна у— /— 1, что на том же множестве 1 <у < п — 1,у < /< п не превосходит — 1. Следовательно, на допустимом множестве изменения параметров у', i',j, i уравнение (8.8) не имеет ни одного решения.

Таким образом, граф алгоритма нелинейной программы (8.6) определяется только соотношениями (8.7), т. е. является линейным. Для случая п = 6 он представлен на рис. 8.1.

Теоретически ясно, что любой линейный алгоритм можно описать программой из линейного класса. Тогда возникает вопрос о том, почему же автор программы (8.6) захотел использовать нелинейную форму записи. Интересно докопаться до ответа на данный вопрос еще и потому, что из выбранной формы записи совсем не видны многие свойства программы. Например, из соотношений (8.7) или рис. 8.1 очевидно, что внешний цикл програм-

452

Часть III. Смежные проблемы и применение

мы (8.6) имеет тип ParDO. Но это почти невозможно понять непосредственно из текста (8.6).

:: :: :: :: •

:: :: :: ^

:: :: ^ ::

¹-------•}

Рис. 8.1. Граф алгоритма нелинейной программы

Из программы (8.6) вытекает, что алгоритм заключается в многократном пересчете некоторых элементов одномерного массива. Назовем эти элементы опорными. Они имеют индексы, равные nj — (/' — 1)у/2. Согласно только что проведенным исследованиям, разным значениям параметра j соответствуют разные опорные элементы. Конкретное же содержание алгоритма состоит в последовательном прибавлении к опорным элементам других элементов, находящихся между выбранными опорными элементами и опорными элементами, предшествующими выбранным. Преобразовать нелинейную программу к линейной можно многими способами. Одна из линейных программ, эквивалентная (8.6), такова


DO j	= 1, n -	-1
DO	i=j,n	-1
*^anj*	= a_nJ +	*a,j*
END	DO
END	DO

(8.9)

если считать, что a

i + (j - \)(n - j/2)

для всех допустимых i,j. Теперь по-

нятно, что участвующие в процессе вычислении элементы одномерного массива могут быть представлены как элементы нижнего левого треугольника квадратной матрицы порядка п. В этой трактовке алгоритм (8.6) сводится к суммированию элементов столбцов матрицы, за исключением наддиаго-нальных элементов. Результат помещается на месте элементов последней строки. Все свойства алгоритма и реализующей его программы (8.9) становятся прозрачными.

Так все же зачем вместо ясной программы (8.9) была написана трудно анализируемая программа (8.6)? Дело в том, что почти все языки программиро-

Глава 8. Вычислительные системы и алгоритмы

453

вания допускают оформление данных только в виде прямоугольных или квадратных матриц. В этом случае в программе (8.9) не будет использоваться верхняя половина массива и, следовательно, для реализации программы (8.9) потребуется примерно вдвое больше памяти, чем необходимо на самом деле. Чтобы избежать этого и была написана программа (8.6).

Рассмотренный пример очень типичен. При решении многомерных задач в сложных областях трудно эффективно использовать память компьютера, применяя лишь многомерные матричные массивы данных. В этих случаях довольно часто данные оформляют как одномерные массивы. Но тогда неизбежно появляются нелинейные индексные выражения. Они затрудняют анализ структуры программ. Поэтому, в частности, для обнаружения свойств параллельности полезно восстановить линейный вид программ. В случае использования стандартных "упаковок" многомерных массивов в одномерные это восстановление осуществить достаточно просто. Однако в общем случае работа с нелинейными индексными выражениями оказывается сложной. Некоторые аспекты восстановления линейных программ рассмотрены в работе [40].

Уточнение описания внешних переменных

Следует отметить, что в некоторых случаях без дополнительной информации о значениях внешних переменных успешный анализ информационной структуры программы может оказаться крайне затрудненным. Допустим, что составляется программа для реализации разложения ленточной матрицы порядка п и ширины m на две треугольные с помощью компактной схемы метода Гаусса [5]. При малых по сравнению с п значениях m ненулевые элементы ленточной матрицы занимают лишь незначительную часть всех элементов квадратной матрицы или, другими словами, массива размера п. Поэтому в этом случае ленточную матрицу часто представляют в виде одномерного массива. Естественно, появляются нелинейные индексные выражения. Однако за счет специального расположения элементов ленточной матрицы в прямоугольном массиве программу можно сделать линейной и при этом не потерять существенно память. Рассмотрим следующий ее фрагмент

DOi = n-k + l, n-m

t = -1/A(i, k + 1)

DO j = i + 1, n

A(j, k+l+i-j) = A(j, k+l+i-j) xt

DO 1 = 1, m

(8.10)

A(j, k+l+i-j+l)= A(j, k+l + i-j+l) +

+ A(j, k+l+i-j) x A(i, k + 1 + 1) END DO END DO

END DO

454

Часть III. Смежные проблемы и применение

По отношению к данному фрагменту переменные n, m, к являются внешними. Если для него строить графы зависимостей без использования какой-либо априорной информации о значениях этих переменных, то возникнут две дополнительные трудности. Во-первых, пространство переменных i, j, l будет разбито на очень большое число областей, т. к. формально нужно принять во внимание все возможные соотношения между значениями внешних параметров. Во-вторых, истинная информационная структура фрагмента будет сильно искажена из-за появления "ложных" связей, возникающих при "нереальных" соотношениях между внешними переменными. В то же время известно, что п есть порядок матрицы. Следовательно, п > 1. Ширина m ленты матрицы не может превышать ее порядка п. Поэтому п > m > 1. Переменная к, как видно из программы в целом, означает номер основного шага вычислительного алгоритма, т. е. к > т. Если при построении графов зависимостей фрагмента (8.10) принять во внимание, что n>k > m > 1, то весь процесс уже никаких затруднений не вызовет.

Вот почему при проведении анализа тонкой информационной структуры фрагментов программ необходимо максимально учитывать возможные соотношения между внешними переменными. Заметим, кстати, что далеко не всегда все соотношения можно найти из текста программ. Нередко какие-то из них используются по умолчанию. Тем не менее, следует помнить, что чем полнее описана область определения внешних переменных, тем точнее будет выполнен анализ структуры.

Подпрограммы, функции

и неанализируемые фрагменты

В процессе анализа структуры программ нередко встречаются ситуации, когда какие-то фрагменты, состоящие из отдельного оператора или группы операторов, выводят программы из линейного класса. Но в то же время по тем или иным причинам детальное исследование таких фрагментов может или оказаться невозможным, или просто не представлять интереса. Например, наличие обращения к подпрограмме заведомо выводит из линейного класса. Однако почти всегда текст подпрограммы бывает недоступен и, следовательно, с ним нельзя что-либо сделать. Аналогичное положение имеет место в отношении вызовов функций. Может встретиться фрагмент, который устроен очень сложно. Но из каких-то соображений, прямых или косвенных, становится понятно, что параллельная его структура не играет заметную роль в организации вычислительного процесса и поэтому ее можно не изучать.

Перечислять подобные примеры можно довольно долго. Для всех них характерно то, что знание подробной структуры фрагментов не требуется. А раз так, то сами фрагменты можно заменить фиктивными линейными программами и изучать строение исходной программы с этими фиктивными вставками. Для получения правильных сведений о структуре необходимо иметь сведения о входных и выходных данных заменяемых фрагментов.

Глава 8. Вычислительные системы и алгоритмы

455

Предположим, что в программе происходит вызов подпрограммы gauss, осуществляемый оператором

CALL GAUSS (А, В, N) (8.11)

Пусть известно, что в массиве а размером n х n и массиве в размером n х 1 задаются входные данные, а в массиве в, к тому же, получаются результаты. Выберем любую простую переменную, которая не используется в анализируемой программе. Допустим, что это есть переменная с идентификатором fiction. Теперь рассмотрим такую программу

DO i = 1, N DO j = 1, N fiction = A(i, j) END DO

fiction = B(i) (⁸-ⁱ²)

END DO DO k = 1, N B(k) = fiction END DO

Программа gauss могла решать систему линейных алгебраических уравнений порядка n с матрицей и правой частью, расположенными, соответственно, в массивах айв. Программа (8.12) никакого отношения к решению системы линейных алгебраических уравнений не имеет. Более того, она почти целиком состоит из избыточных вычислений. Тем не менее, обе программы имеют одинаковые входные и выходные данные. Теперь предположим, что с исходной программой выполнены следующие действия: вместо оператора (8.11) подставлено тело подпрограммы gauss и вместо того же оператора (8.11) подставлена подпрограмма (8.12). Пусть для обеих полученных программ построены графы зависимостей одного и того же типа. Далее в графах каждой из программ при всех значениях внешних по отношению к оператору (8.11) параметров циклов сольем в одну вершину пространства итераций соответственно тела подпрограммы gauss и подпрограммы (8.12), сохранив при этом все дуги. Легко проверить, что с точностью до числа дуг, представляющих петли, оба построенных таким образом графа полностью совпадают. Подпрограмма (8.12) линейная. Если исходная программа была во всем остальном, кроме оператора (8.11), линейной, то будет линейной программа, полученная после подстановки программы (8.12) вместо оператора (8.11).

Аналогично заменяются вызовы функций, не анализируемые или трудно анализируемые фрагменты, а также фрагменты, структурой которых мы не интересуемся.

456

Часть III. Смежные проблемы и применение

Использование функций min и max

Среди многочисленных функций функции min и max заслуживают особого внимания. Во-первых, по данным статистики данные функции встречаются наиболее часто. А, во-вторых, при преобразовании программ, основанных на знании скошенного параллелизма, пределы изменения параметров циклов почти всегда выражаются именно через них. Рассмотрим функцию min. Функция max исследуется аналогично. Пусть она имеет какое-то вхождение

- min (f_bf₂) ... .

Заменим это вхождение таким фрагментом

if (Л>£) go to 1

-Л -

до to 2 (_8ЛЗ)

1 CONTINUE

2 CONTINUE

где выражения f\ nf₂ находятся в программе точно в том же положении, как и функция mia(fi,f2). Если/j и f₂ были линейными функциями параметров циклов, что является типичной ситуацией, и линейность исходной программы нарушалась только из-за функции min, то замена этой функции согласно (8.13) делает программу линейной.

Прямое вычисление графов зависимостей

Существует немало других способов сведения программ к линейным. Но если уж ничто не помогает, можно построить граф зависимостей непосредственно по программе для какого-то частного случая и проанализировать его вручную с целью обнаружить общую закономерность. Основанием к выбору такого подхода исследований являются свойства графов зависимостей, описанные в вопросах и заданиях к § 6.5.

Рассмотрим снова пример 6.4. Мы уже отмечали, что с анализом его структуры не справился ни один из параллелизирующих компиляторов. На рис. 8.2 представлен граф алгоритма для п = 10.

На первый взгляд — в дугах сплошная путаница. Однако более внимательное рассмотрение рис. 8.2 позволяет обнаружить нечто интересное. Именно, при каждом значении / существует только одна дуга, которая связывает вершины с тем же значением координаты /. Более того, эти вершины являются соседними по координате у. Поэтому внутренний цикл программы примера 6.4 заведомо можно представить как последовательность двух циклов типа ParDO. Сначала идет цикл, в котором параметр j меняется от 1 до

Глава 8. Вычислительные системы и алгоритмы

457

координаты j начальной точки указанной дуги включительно. Затем идет цикл, в котором параметр j меняется от координаты j конечной точки дуги до п. Легко установить, что начальные точки дуг лежат на прямой / + j = п, и мы сразу получаем преобразование (7.19). На рис. 8.2 также видно, что обсуждаемые параллельные оси у дуги лежат на критическом пути графа алгоритма. Его длина равна 2п — 2. Следовательно, преобразование (7.19) передает уровень параллелизма, имеющегося в исходной программе примера 6.4, абсолютно точно.

Рис. 8.2. Граф алгоритма "простейшей" программы

Анализ графа на рис. 8.2 позволяет понять причины, по которым исследование примера 6.4 вызывает большие трудности. Рис. 8.3 демонстрирует ярусы канонической параллельной формы графа. Видно, что они устроены достаточно сложно. При изменении номеров ярусов изменяются не только местоположение и размеры самих ярусов, но даже их "размерность" и конфигурация.

458

Часть III. Смежные проблемы и применение

1 о

О 3

2 5

4 7

6 9

8 11

10 13

12 15

14 17

Рис. 8.3. Ярусы канонической параллельной формы

Вопросы и задания

1. Пусть параметр р, входящий в индексное выражение, многократно пересчитыва-ется в программе по линейному закону. В каком случае прямая подстановка всех результатов пересчета параметра р даст линейное индексное выражение?

2. Что меняется в прямой подстановке, если какие-то операторы пересчета параметра р охватываются условными передачами управления?

3. Пусть программа имеет перекрывающиеся до to-циклы. Как исключить такое перекрытие?

4. Пусть тело цикла не меняется при повторных срабатываниях. Как построить развертку цикла, если известна развертка его тела?

5. *Рассмотрите решение общей задачи (6.13), (6.14) для случая, когда индексные выражения являются многочленами (выпуклыми, возрастающими по каждой переменной, лексикографически возрастающими, представленными в виде суммы одномерных возрастающих многочленов).

6. Пусть для программы со вставкой (8.12) вместо (8.11) известна строгая развертка. Приведите примеры зависимости операций, не относящихся к вставке (8.12), но лежащих на одном ярусе развертки.

7. Как надо видоизменить процесс построения разверток для программ со вставками типа (8.12), чтобы результат был гарантированно правильным?

Глава 8. Вычислительные системы и алгоритмы

459

8. Покажите, что длина критического пути графа линейного алгоритма оценивается сверху полиномом от внешних переменных.

9. *Докажите или опровергните гипотезу, что для достаточно больших значений внешних переменных длина критического пути графа линейного алгоритма есть полиномиальная функция от внешних переменных.

10. *Если гипотеза п. 9 верна, то как определять коэффициенты полинома, используя прямое вычисление графа алгоритма?

§ 8.2. Граф-машина

Рассмотрим произвольный ациклический ориентированный граф G. Поместим в каждую его вершину простое функциональное устройство, имеющее столько входов, сколько дуг входит в вершину. Будем считать дуги графа направленными линиями связи, обеспечивающими передачу информации от устройства к устройству. Предположим, что ФУ, помещенные в вершины без входящих дуг, являются устройствами ввода, помещенные в вершины без выходящих дуг, — устройствами вывода. Заставим работать построенную систему по правилам, описанным в § 2.3. Будем называть такую модельную вычислительную систему граф-машиной. Граф G будет графом этой системы. На граф-машину распространяются все полученные в § 2.3 результаты. Граф-машина не имеет собственной памяти и может сохранять результаты промежуточных вычислений только в самих ФУ до следующих срабатываний.

В процессе своего функционирования граф-машина будет реализовывать какой-то алгоритм. Естественно, он будет зависеть как от графа G, так и от состава ФУ, помещенных в его вершины. В рамках зафиксированных ограничений граф G может быть любым. Но поскольку наше внимание сейчас направлено на решение проблемы отображения, интерес представляют вычислительные системы, реализующие заданный алгоритм. Поэтому в качестве графа G мы возьмем граф анализируемого алгоритма, а в каждую его вершину поместим такое ФУ, которое может выполнять операцию, соответствующую именно этой вершине.

Возможны два типа функционирования граф-машины: режим однократного срабатывания устройств и режим многократного срабатывания. При однократном срабатывании каждое ФУ включается только один раз, в том числе, один раз включаются все входные и выходные устройства. Поэтому входных и выходных устройств должно быть ровно столько, сколько входных данных и результатов связано с алгоритмом. Естественно, включение осуществляется лишь после того, как готовы все входные данные устройства. В режиме однократного присваивания хорошо видно одно из важнейших достоинств граф-машины — возможность локального управления работой отдельных ФУ. В самом деле, источники получения входных данных для каждого ФУ известны. Поэтому само ФУ может следить за их появлением и, следователь-

460

Часть III. Смежные проблемы и применение

но, само ФУ может определять момент начала своего срабатывания. Поэтому для граф-машины внешнее глобальное управление работой всей совокупности ФУ не является необходимым. В какие бы из допустимых моментов не начали срабатывать ФУ, результат работы граф-машины будет одним и тем же и будет соответствовать рассматриваемому алгоритму.

При многократном срабатывании каждое ФУ включается столько раз, сколько раз будут готовы для него новые входные данные. Очередное включение может осуществляться только в те моменты, когда результат предыдущего срабатывания либо уже был использован, либо уже начал использоваться. При однократном срабатывании на выходных устройствах граф-машины будут находиться результаты реализации того алгоритма, граф которого взят в качестве графа вычислительной системы. При многократном срабатывании на выходных устройствах будут последовательно появляться результаты реализации этого же алгоритма, но соответствующие последовательно вводимым входным данным. Так как граф алгоритма ациклический, то при соблюдении правил работы ФУ, описанных только что, а также в §2.3, никакое "перемешивание" процессов вычислений, соответствующих разным по порядку ввода входным данным, невозможно. Это означает, что при изучении граф-машины можно ограничиться изучением лишь режима однократного срабатывания. Ему и будут посвящены наши ближайшие исследования.

Одной из важнейших характеристик, определяющих эффективность алгоритма, является время его реализации на вычислительной системе. Конечно, время реализации зависит не только от алгоритма. В немалой степени оно определяется также структурой и временными характеристиками вычислительной системы.

Совместное влияние параметров вычислительной системы и структуры алгоритма на время реализации алгоритма является довольно сложным и неоднозначным. Об этом убедительно свидетельствует вся история развития вычислительной математики и вычислительной техники. Алгоритмы, считавшиеся эффективными на однопроцессорных ЭВМ, нередко становятся очень неэффективными на существующих сегодня параллельных вычислительных системах. Однако эти же алгоритмы могут снова оказаться эффективными в будущем, если вычислительная техника начнет развиваться в благоприятном для них направлении.

Как же оценивать время реализации алгоритма? Очевидно, что прямое его измерение на конкретном компьютере дает возможность сравнивать временные характеристики различных алгоритмов только по отношению к данному компьютеру. По отношению к другому компьютеру аналогичное сравнение, вообще говоря, дает другие результаты. Поэтому необходимо ввести некоторое абстрактное сравнение времени реализации алгоритмов или, другими словами, необходимо сравнивать времена реализации алгоритмов

Глава 8. Вычислительные системы и алгоритмы

461

на некоторой абстрактной вычислительной системе. Эта вычислительная система не должна зависеть от особенностей развития технологии на текущий момент, но должна, тем не менее, отражать общие тенденции в принципах построения вычислительных систем.

Последовательная реализация алгоритмов как при ручном счете, так и при использовании однопроцессорных компьютеров давно привела к созданию вполне определенной процедуры сравнения алгоритмов по времени реализации. Эта процедура хорошо известна и состоит в сравнении числа операций, выполнение которых необходимо для получения решения задачи с заданной точностью. Она достаточно хорошо отражает основные особенности последовательной реализации алгоритмов и почти не зависит от технологических изменений в самом процессе реализации. Именно эти обстоятельства сделали число операций тем критерием эффективности алгоритмов, который оказался приемлемым для широкого круга вычислительных средств от человека до однопроцессорных компьютеров различных типов. Формально можно считать, что число операций есть время реализации алгоритма на абстрактном однопроцессорном компьютере, у которого время выполнения любой операции равно 1, а время выполнения всех других процедур (ввод/ вывод данных, взаимодействие с памятью, передача данных по каналам связи и т. п.) равно 0. При этом предполагается, что операции выполняются подряд без какого-либо простоя в работе компьютера.

Как было показано раньше, сравнение времен реализации алгоритмов по числу операций становится совершенно неприемлемым ни для практики, ни для теории, если реализацию самих алгоритмов осуществлять на параллельных вычислительных системах. Поэтому и абстрактный последовательный компьютер, используемый для сравнения времен реализации алгоритмов, также оказывается неприемлемым для этой цели. Теперь в качестве подходящей модельной вычислительной системы выступает граф-машина.

Есть одно принципиальное различие между абстрактной последовательной ЭВМ и граф-машиной. Именно, на первой реализуются все алгоритмы, на второй — только один. Конечно, не представляет никакого труда сразу ввести абстрактную параллельную вычислительную систему. Предположим, что она имеет бесконечно много процессоров, время выполнения любой операции на любом процессоре равно 1, а время выполнения всех других процедур, включая установление нужных связей между процессорами, равно 0. Тогда сравнение алгоритмов по скорости реализации на параллельных системах можно заменить сравнением времен реализации алгоритмов на построенной абстрактной параллельной вычислительной системе. Однако с введением подобной системы не стоит торопиться.

Прежде чем изучать, чем различаются различные реализации различных алгоритмов, необходимо понять, чем различаются различные реализации одного и того же алгоритма. Граф-машина вполне подходит для решения

462

Часть III. Смежные проблемы и применение

последней задачи. Более того, на ней решать эту задачу значительно проще, чем на абстрактной параллельной системе, т. к. теперь фиксирована коммуникационная сеть, а также номенклатура и число процессоров. После изучения множества реализаций одного и того же алгоритма нетрудно перейти к сравнению реализаций различных алгоритмов, т. е. перейти к использованию абстрактной параллельной вычислительной системы в качестве инструмента моделирования вычислительных процессов.

Если алгоритм реализуется на граф-машине, то каждая его операция выполняется в какое-то определенное время. Обозначим через t(v) момент окончания срабатывания операции, соответствующей вершине v графа. Перенумеруем подряд цифрами 1, ..., N все вершины. Нумерация пока может быть произвольной и никак не связанной со строением пространства итераций. Рассмотрим вектор t = (Ц, ..., ty). Если в вершину v идет дуга из вершины и, то очевидно, что t(v) > t(u). Поэтому вектор t есть не что иное, как векторное представление развертки. Таким образом, множество режимов однократного срабатывания устройств граф-машины или, что то же самое, множество реализаций заданного алгоритма на любых реальных или гипотетических вычислительных системах полностью описывается множеством разверток графа алгоритма. Следовательно, при изучении граф-машины можно использовать любые свойства разверток, описанные в главе 7. В частности, обнаружив какие-то новые свойства, мы можем на их основе попытаться построить и новые типы вычислительных устройств или систем.

Принимая во внимание реалии действительности, с вершинами и дугами графа необходимо связать дополнительные характеристики. Каждая операция выполняется за какое-то время. Обозначим его через hj > 0 для у'-й вершины. Вектор h = (hi, ..., /z/v) назовем вектором реализации. Если из вершины / идет дуга в вершину j, то передача информации вдоль этой дуги также требует времени wy > 0. Вектор w, составленный из чисел wy, назовем вектором задержек. Среди всех вершин граф-машины особую роль играют входные вершины. Там находятся устройства, поставляющие входные данные. На практике именно они определяют момент начала вычислительного процесса. Поэтому полезно рассмотреть те реализации алгоритма, которые связаны с фиксированными моментами подачи входных данных. Обозначим через gj множество номеров вершин, из которых идут дуги в вершину с номером j. Пустое множество будем обозначать стандартным символом 0. Ясно, что gj= 0 только для входных вершин. Будем считать, что если gj= 0, то для времен tj заданы значения sj. Вектор s с координатами Sj, gj= 0 будем называть вектором граничных значений. По смыслу этот же вектор можно было назвать вектором начальных условий или вектором начальных значений. Название выбрано с учетом геометрической интерпретации фактов. Как показывает практика, входные вершины чаще всего размещаются на границе пространства итераций. Развертки, при определении

Глава 8. Вычислительные системы и алгоритмы

463

которых принимаются во внимание все векторы s, w, h или только какие-нибудь из них, будем называть развертками с ограничениями.

Обозначим через R = R(s, w, И) класс разверток с одними и теми же векторами s, w, h. Имеет место очевидное

Утверждение 8.1

Развертки с фиксированными ограничениями s, w, h описываются следующими соотношениями

t- > max(?! + W//) + h:, если g,- * 0;

leg,-

(8.14) tj = sj, если gj = 0.

Как и над любыми другими, над развертками с ограничениями из класса R, можно выполнять все ранее введенные операции. Результат всегда будет разверткой, но он может не принадлежать R. Так, например, операции сложения разверток и прибавления к развертке неотрицательного числа X всегда выводят из класса R, если только вектор s и число X не являются нулевыми. Это подтверждается тем, что уравнения s + s = s и s + X = s, X >0 имеют решения лишь когда s = О, X = 0. Операция умножения развертки на положительное число X остается в классе R только в случае X = 1. Это подтверждается тем, что уравнения s = Xs, h = Xh, h ф 0, имеют решения лишь при X = 1.

Утверждение 8.2

Класс R(s, w, К) замкнут относительно операций Ф, <8>.

Рассмотрим любые две развертки t', t" из класса R и исследуем сначала развертку t = t' ® t". На множестве вершин, для которых gj = 0, развертки ? и t" принимают одни и те же значения. По смыслу операции Ф на том же множестве вершин развертка t будет иметь такие же значения. Теперь возьмем какую-то вершину у с условием gj ф 0. Находим, учитывая (8.14), что

t₃ ={t' ® t"}j =max(tptj)>

> max maxU/ + w_n) + h,-, maxU/ + w_n) + h,-= max(max((// + и>/,-) + h_h (tj + vc_//) + /*,)) = = maxUmax^/, t") + w_lt) + h,) = max(?/ + w_lt) + h,.

legj legj

Следовательно, развертка t'@ t" принадлежит классу R в силу того, что она описывается теми же векторами ограничений s, w, h. Теперь рассмотрим

464

Часть III. Смежные проблемы и применение

развертку t = t' ® t". Она имеет тот же вектор s граничных значений, что и развертки t'и t". Для вершину с условием gj^ 0 заключаем, что

t_j={t'®f}_j=mm{t'_j,f_j)>

> min maxU/ + w'n) + h,-, maxUf + w_n) + h,-

> max(min((?; + w_tj ) + hj, (tj + w_e) + hj)) =

= max(min(?/', t") + w_/;) + h, = max!/, + vc_//-) + h,. legj legj

Это означает, что развертка t'<2> t" описывается теми же векторами ограничений s, w, h, как и развертки t\ t", т. е. она принадлежит классу R.

Утверждение 8.3

В любом классе R(s, w, h) существует развертка 0 = Q(s, w, /г), которая описывается соотношениями

е =max(e_/ +w,i) +h■ если gj *0; ...

leg/ [р. \0)

Qj = Sj, если gj= 0. Она удовлетворяет равенствам

Q®t=t@Q = t, 0® ?=/<S>0 = 0 (8.16)

для любой развертки t из R.

Развертку 9 построим конструктивно. Рассмотрим каноническую параллельную форму графа алгоритма. На первом ярусе и только на нем находятся вершины, для которых gj = 0. Никаких других вершин на данном ярусе нет. В этих вершинах развертке 9 припишем значения, соответствующие координатам вектора s. Далее, во всех вершинах второго яруса развертке 9 припишем значения, вычисленные согласно первому равенству из (8.15). После прохождения аналогичным образом всех ярусов канонической параллельной формы графа алгоритма развертка 9 будет построена. Очевидно, что по способу ее нахождения она принадлежит классу R(s, w, И) и для нее выполняются равенства (8.16).

Развертка 9 является наименьшей разверткой в классе R. Более того, значение развертки 9 в любой вершине не превосходит значения любой развертки из класса R в той же вершине. По этой причине развертку 9 будем называть минимальной в классе R. Сказанное означает, что в классе R(s,w, И) минимальная развертка соответствует реализации алгоритма за минимальное время.

Итак, R(s, w, И) представляет множество разверток с фиксированными ограничениями s, w, h. На этом множестве действуют две операции <8>, Ф. Обе

Глава 8. Вычислительные системы и алгоритмы

465

операции коммутативные и ассоциативные, причем операция "умножения" <8> дистрибутивна относительно операции "сложения" ©. На множестве R(s, w, И) существует минимальная развертка Q(s, w, К), которая, согласно (8.16), по отношению к операциям <8>, © играет роль нулевого элемента. Если бы операция Ф имела на множестве R(s, w, И) обратную, то само множество было бы кольцом. Но операция Ф обратную не имеет. Поэтому класс разверток с фиксированными ограничениями и операциями <8>, Ф представляет полукольцо с нулевым элементом.

Среди ограничений s, w, h ограничения w, h описывают "техническую" сторону граф-машины, ограничение s — математическую. Обозначим через R(w, И) класс разверток с одними и теми же векторами w, h. Он представляет объединение классов R(s, w, И) для всех возможных векторов s.

Утверждение 8.4

Класс R(w, К) замкнут относительно операций Ф, <8>, V.

Доказательство замкнутости класса R(w,h) относительно операций Ф, <8> почти дословно повторяет доказательство утверждения 8.2. Замкнутость относительно операции V очевидна.

В классе R(w, И) для каждого вектора начальных значений s существует минимальная развертка 9. Ее можно считать результатом воздействия на вектор s оператора Q(s), определяемого соотношениями (8.15). Для нас интересно отметить, что этот оператор является "линейным" по отношению к паре операций Ф, V.

Утверждение 8.5

Для любых векторов s^ s₂, и любых чисел а_ь а₂ выполняется соотношение

9 (cXiV^) Ф (a₂Vj₂)) = (cciVG (sj) Ф (a₂V0 (s₂)). (8-17)

Обозначим через 9', 9 " и 9 минимальные развертки, соответствующие векторам граничных значений s\, Sj и (ai V s\) Ф (осг V si)- Векторное соотношение (8.17) эквивалентно координатным равенствам

9/ = тах(ои + 9} , сс₂ + 9' )

для всех j = 1, ..., N. Снова построим каноническую параллельную форму графа алгоритма. Для вершин первого яруса равенства (8.18), очевидно, выполняются, т.к. Q'_t- =s'_t-,Q"j =s", а 0у = max(ai + s'-,a.2+ s"). Здесь s'-,s"

суть у'-ые координаты векторов s\, Sj- Предположим, что равенства имеют место для всех вершин, находящихся в ярусах с номерами 1, ..., к, к> 1.

466

Часть III. Смежные проблемы и применение

Для вершин из яруса с номером к + 1 находим, что

9/ = max (9] + wy) + hj = max(max(a, + 9/, a₂ + Q") + wy) + hj =

= max(max(a] + 6/ + w_tj + h •, a₂ + 0' + % + h •)) = = max(max(a] + 6/ + W/- + /z ■), max(a₂ + 0" + w_lf + h ■)) =

= max(a! + (max(0^ + w_tj) + h,),a₂ + (max(0" + w_lf) + h •)) =

= max(oc, + 0'-, a₂ + 0').

Перебрав все ярусы, заключаем, что равенства справедливы для всех j = 1, ..., N к, следовательно, справедливо соотношение (8.17).

В завершение общих исследований отметим монотонность оператора 9(s). Для двух векторов a, b будем писать а > b (>, <, <), если это соотношение выполняется для всех соответствующих координат векторов а, Ъ.

Утверждение 8.5*

Пусть рассматриваются минимальные развертки из любого класса R{w, h). Если _Sl > s₂ (>, <, <), то 9(_Sl) > Q(s₂) (>, <, <).

Для всех видов неравенств доказательства проводятся одинаково. Поэтому ограничимся рассмотрением знака >. Опять построим каноническую параллельную форму графа алгоритма. На первом ярусе и только на нем находятся вершины, на которых заданы начальные значения. Следовательно, неравенство 9(^i) > 9(^2) на вершинах первого яруса выполняется просто потому, что ^i > S2 по условию. Предположим, что неравенство Q(si) > 9(52) имеет место для всех вершин, находящихся в ярусах с номерами 1, ..., к, к> 1. Для вершин из яруса с номером к + 1 неравенство Q(s\) > 9(^) выполняется в соответствии с (8.15), т. к. все вершины с номерами / расположены в первых к ярусах.

Итак, описано множество режимов функционирования граф-машины, обеспечивающих минимальное время реализации алгоритма при заданных временах ввода входных данных. Заметим, что хотя множество минимальных разверток линейно по операциям Ф, V, оно не является по ним линейным пространством. В первую очередь, из-за того, что операция © не имеет обратную. Операция V также может не иметь обратную. Это будет, например, в том случае, когда допустимыми оказываются только неотрицательные развертки. Для нахождения минимальных разверток необходимо решать относительно величин 0J, ..., 9ту уравнения (8.15). Они называются дискретными уравнениями Беллмана. Неравенства (8.14) называются дискретными неравенствами Беллмана.

Глава 8. Вычислительные системы и алгоритмы

467

Граф-машина как модельная вычислительная система имеет немало достоинств, среди которых, пожалуй, самое главное — возможность любых временных реализаций алгоритма, в том числе за минимальное время. Но сразу же видны ее серьезные недостатки. Число используемых ФУ и число линий связи зависят в целом от числа выполняемых операций алгоритма. Как уже неоднократно отмечалось, в реальных задачах это число очень велико. В режиме однократного срабатывания каждое ФУ граф-машины выполняет только одну операцию за время реализации алгоритма. Следовательно, загруженность ФУ будет недопустимо малой. К тому же граф-машина не позволяет эффективно использовать конвейерные ФУ. Тем не менее, именно из граф-машины можно построить математические модели многих типов вычислительных систем. Среди них имеются и такие, которые также реализуют алгоритм за минимально возможное время, но обладают лучшими "техническими" характеристиками. В основе преобразования граф-машины лежит гомоморфная свертка графа [36].

Рассмотрим произвольный ориентированный граф G с множеством вершин V и множеством дуг Е. Сейчас граф может не быть ациклическим и может содержать петли. Выберем в К любые две вершины u, v и сольем их в одну вершину z- Новое множество вершин обозначим V. Перенесем на V без изменения те дуги из G, для которых концевые вершины не совпадают ни с и, ни с v. Если же какая-то из концевых вершин совпадает с и или v, то такие дуги перенесем с заменой этих вершин на z- И, наконец, в новом графе все петли, относящиеся к одной вершине, заменим одной петлей. Также заменим одной дугой все кратные дуги. Множество дуг на V обозначим £'. Граф с множеством вершин V и множеством дуг is" обозначим G'. Преобразование графа G в граф G' называется простым гомоморфизмом, а многократное преобразование простого гомоморфизма называется гомоморфной сверткой графа. При гомоморфной свертке графа G множество его вершин распадается на непересекающиеся подмножества. Каждое из подмножеств состоит из тех и только тех вершин, которые в конечном счете сливаются в одну вершину. Вершины подмножества называются гомоморфными прообразами полученной вершины, а сама эта вершина — гомоморфным образом своих прообразов. Ясно, что любой ориентированный граф всегда можно гомоморфно свернуть в граф, состоящий из одной вершины и одной петли. Пример операций простого гомоморфизма приведен на рис. 8.4. Сливаемые вершины обозначены на нем "звездочками".

Рис. 8.4. Операции простого гомоморфизма

468

Часть III. Смежные проблемы и применение

Простым и конструктивным приемом осуществления гомоморфной свертки является операция проектирования. Предположим, что граф G расположен в конечномерном пространстве, т. е. его вершины являются точками пространства, дуги — векторами. Спроектируем граф вдоль любой прямой на перпендикулярную ей гиперплоскость. Пусть при этом какие-то вершины спроекти-руются в одну точку. Если в ту же точку спроектируются некоторые вектор-дуги, то поставим около точки петлю. Очевидно, что подобная операция есть гомоморфная свертка графа G. Чем больше точек-вершин графа расположено по направлению проектирования, тем больше вершин спроектируются в одну точку. Ничто не мешает повторять операцию проектирования многократно, пока не получится граф нужного строения. После числа шагов, равного размерности пространства, всегда в проекции получится одна точка. Если в графе G была хотя бы одна дуга, то около точки будет петля.

Гомоморфная свертка имеет очень прозрачный смысл. Пусть граф G представляет граф-машину. Совершим операцию простого гомоморфизма. Выбирая вершины и, v, мы определяем две операции алгоритма и два ФУ, которые эти операции реализуют. Сливая вершины и, v, мы связываем с вершиной z не одну, а пару операций. ФУ, отвечающее вершине z, должно иметь возможность выполнить обе операции последовательно. После многократного применения операции простого гомоморфизма полученный граф можно рассматривать как граф новой модели вычислительной системы. ФУ, связанное с любой его вершиной, обязано последовательно выполнять все операции алгоритма, связанные со всеми вершинами-прообразами. Дуги по-прежнему символизируют направленные передачи информации. Наличие петли около вершины говорит о том, что соответствующее ФУ будет срабатывать многократно.

Имеется одно принципиальное отличие граф-машины от вычислительной системы, полученной при гомоморфной свертке. Граф-машина не имеет память. Роль ее ячеек успешно выполняют сами ФУ в силу того, что каждое из них срабатывает только один раз. При многократном срабатывании ФУ результаты предшествующих срабатываний могут оказаться не использованными полностью. Для их сохранения уже нужна память. Зная граф алгоритма и временной режим срабатываний ФУ новой системы, можно подсчитать величину требуемой памяти и даже изучить процесс ее использования. Но мы не будем сейчас заниматься подобными подсчетами и исследованиями. Наша ближайшая задача связана с изучением возможностей осуществления наискорейших реализаций алгоритма.

В общем случае на вычислительной системе, полученной после гомоморфной свертки, нельзя реализовать все временные режимы, допустимые для граф-машины. Например, при слиянии всех вершин в одну мы получаем образ однопроцессорного компьютера. На нем можно реализовать только последовательные режимы. Пусть режим реализации алгоритма на граф-машине описывается разверткой / Если при этом режиме какие-то опера-

Глава 8. Вычислительные системы и алгоритмы

469

ции выполняются одновременно, то сливая соответствующие вершины в одну, мы будем вынуждены выполнять такие операции последовательно. Следовательно, на полученной после свертки системе нельзя будет реализовать данный режим. Отсюда, в частности, вытекает, что слияние любых вершин граф-машины, не связаных путем графа алгоритма, заведомо сужает множество возможных временных реализаций. Тем интереснее выделить такие свертки, при которых сохраняется все множество допустимых режимов.

На время реализации алгоритма влияют как времена выполнения операций, так и времена задержек при передаче информации. Во многих ситуациях предполагатся, что все задержки являются нулевыми. В этом случае почти очевидно

Утверждение 8.6

Пусть все задержки являются нулевыми и при гомоморфной свертке сливаются лишь вершины, находящиеся на одном пути графа алгоритма. Тогда на построенной системе реализуется весь спектр временных режимов граф-машины, в том числе наискорейшие.

Достаточная разнесенность во времени моментов включения ФУ построенной системы гарантируется здесь тем, что сливаемые вершины находятся на одном пути. Поэтому соответствующие им операции как обязаны были раньше, так и имеют возможность теперь выполняться последовательно друг за другом. Подчеркнем также, что совсем не обязательно, чтобы образ сливаемых вершин имел в качестве своих прообразов все вершины, находящиеся на одном пути. Важно лишь, чтобы прообразы были связаны одним путем. Это обстоятельство имеет существенное значение, т. к. чаще всего объединяются вершины, соответствующие однотипным операциям, а они обычно в вычислениях перемешиваются с операциями других типов. Что же касается установления соответствия между вершинами графа алгоритма и срабатываниями ФУ, помещенными в вершины графа вычислительной системы, полученной после гомоморфной свертки, то теперь оно очень простое. Именно, если из двух вершин графа алгоритма одна достижима из другой, то из двух соответствующих срабатываний ФУ ей соответствует более позднее.

Таким образом, разбивая вершины графа алгоритма на подмножества, лежащие на одном пути, и объединяя их с помощью операций простого гомоморфизма, мы получаем конструктивный способ построения математических моделей вычислительных систем. Естественно, что таких систем может быть много, и они, вообще говоря, неодинаковы с точки зрения состава ФУ, их загруженности, размера присоединенной памяти, сложности коммуникационной сети и т. п. Но все эти системы по своим основным параметрам, кроме размера памяти, лучше, чем граф-машина. Они содержат меньшее число ФУ, загруженность каждого ФУ больше, число линий связи между ФУ меньше и при этом часто реализуется весь спектр временных режимов, включая наискорейшие. Снова можно ставить задачу оптимизации, пытаясь

470

Часть III. Смежные проблемы и применение

разбить вершины графа алгоритма на наименьшее число подмножеств, лежащих на одном пути. И снова возникает противоречивая ситуация: уменьшение числа ФУ может привести к усложнению коммуникационной сети и увеличению объема памяти.

Вопросы и задания

1. Рассмотрим режим многократного срабатывания граф-машины. Пусть каждый раз все ФУ, включая входные и выходные, срабатывают за одно и то же время и максимально быстро после предыдущего срабатывания. Будет ли для всех наборов входных данных реализован наискорейший режим?

2. Пусть в условиях п. 1 граф-машина работает достаточно долго. Можно ли утверждать, что асимптотическая загруженность каждого ФУ равна 1?

3. Пусть граф-машина работает в режиме однократного присваивания. Чему равно минимальное время между моментом ввода первого входного данного и моментом получения последнего результата?

4. Докажите, что класс разверток R(s, w, h) является множеством, ограниченным снизу и замкнутым покоординатно.

5. Докажите, что класс разверток R(s, w, К) является множеством, выпуклым относительно обычных векторных операций сложения и умножения на число.

6. Докажите, что среди всех классов R(s, w, h) только класс R(0, w, h) замкнут относительно обычных векторных операций сложения и умножения на число.

7. Пусть множество векторов граничных значений содержит "нулевой" относительно операции © вектор л°. Докажите, что, во-первых, любую развертку из класса R(s, w, К) можно представить в виде "суммы" по операции © развертки 0(,s, w, h) и некоторой развертки из класса Дл°, w, К). И, во-вторых, "сумма" по операции © развертки 0(,s, w, h) и любой развертки из R(sP, w, К) дает развертку из R(s, w, К). Символически это выражается так:

R(s, w, И) = Q(s, w, И) Ф Д/», w, И).

8. Пусть а_ь а₂, ..., а_и и |3_Ь |3₂, ..., Р„ — любые две последовательности вещественных чисел. Докажите, что всегда справедливы соотношения:

max max a_{, max /3_; = max (max(a_i, Д))

I 1< i < n l<i<n I l<i<n

min max a_{, max /3_; > max (min^, /3_;))

^l<i<ll l<i<n J l<i<_n

9. Рассмотрите алгоритмы последовательного и попарного суммирования чисел. Графы этих алгоритмов представлены на рис. 4.2. С помощью операции гомоморфной свертки получите графы вычислительных систем, сохраняющих наискорейшие режимы и содержащие минимальное число вершин. Не правда ли, полученные графы различаются очень сильно?

Глава 8. Вычислительные системы и алгоритмы

471

10. **Для заданного графа алгоритма предложите метод осуществления гомоморфной свертки, обеспечивающий на модельной вычислительной системе сохранение наискорейших режимов и гарантирующий минимальность числа ФУ (минимальность числа связей, минимальность объема требуемой памяти, максимальность загруженности системы ФУ и т. п.).

§ 8.3. Регулярные и направленные графы

Возможность построения эффективных моделей вычислительных систем на основе объединения вершин графа алгоритма, лежащих на одном пути, стимулирует выделение класса алгоритмов, где такие пути устроены наиболее просто.

Пожалуй, чаще всего в вычислительной математике используются алгоритмы, записываемые в виде рекуррентных соотношений с линейными индексами. Рассмотрим конечномерное пространство целочисленных вектор-индексов. Будем считать, что в этом пространстве введены естественный базис, обычное понятие ортогональности и лексикографический порядок. Пусть дана область В, содержащая непустое множество вектор-индексов. Соотношения вида

u_f= Fj(u_f-_fi , ..., u_f-_fr), fe В (8.18)

называются рекуррентными соотношениями с линейными индексами, если вектор-индексы/, ...,f_r фиксированы, целочисленные и не зависят от/ Функции Ff могут быть произвольными, в том числе как линейными, так и нелинейными. Выполняются соотношения (8.18) в порядке лексикографического роста вектор-индекса / Чтобы данный процесс был возможен, необходимо, чтобы при всех / каждый из векторов/—/!, •••■>f~fr либо не принадлежал области В, либо был лексикографически меньше / При этом предполагается, что если какой-либо из векторов/—/ не принадлежит области В, соответствующая переменная и у - _f считается заданной и представляет одно из входных данных алгоритма. Известно, что для осуществимости процесса (8.18) достаточно, чтобы первая по лексикографическому старшинству ненулевая координата каждого из векторов/, ...,/ была положительной. Мы не будем сейчас обсуждать детали использования лексикографического порядка на множестве векторов.

Будем размещать вершины графа алгоритма в точках области В с целочисленными координатами. Вершине, задаваемой вектором/ поставим в соответствие функцию Ff. Если/е D, то из (8.18) вытекает, что в вершину/будут входить дуги из вершин /— /, ...,/—/ и только из этих вершин. В случае, когда какой-то из векторов /—/ не принадлежит области Д вектор/—/ будет символизировать функцию ввода переменной «/- / •

Построенный таким образом граф имеет очень простую структуру. Если

472

Часть III. Смежные проблемы и применение

дуги задавать векторами, то в каждую вершину из области В будет входить один и тот же пучок дуг, который переносится параллельно от одной вершины к другой. Заметим, что при других размещениях вершин графа алгоритма регулярная структура дуг может нарушаться. Данный пример наглядно подтверждает важность согласования формы записи алгоритма с формой представления его графа.

Специфические особенности графа алгоритма должны привести к появлению специфических свойств разверток. Специфические свойства будет иметь и граф алгоритма. Свойства графа и разверток мы будем изучать одновременно.

Граф алгоритма (8.18) полностью определяется областью В и набором векторов f\....,f_r. В некоторых задачах, не описываемых формально рекуррентными соотношениями, также появляются аналогичные графы или графы, отличающиеся от подобных не слишком сильно. Однако относительно них не всегда бывает известно, что они могут рассматриваться как графы каких-нибудь алгоритмов, т. к. априори не ясно, имеют ли графы контуры. Такая ситуация возникает, например, тогда, когда мы пытаемся "аппроксимировать" граф алгоритма некоторым другим графом. Относительно графов, определяемых фиксированным набором векторов f_h...,f_r, приходится решать немало задач, не связанных непосредственно с отысканием разверток. Поэтому мы начнем с того, что опишем класс исследуемых графов, не привязывая его к каким-то конкретным алгоритмам. К рекуррентным соотношениям (8.18) будем обращаться только с целью иллюстрации получаемых результатов.

Пусть задано «-мерное арифметическое пространство. Зафиксируем векторы /ь ...,f_r с целочисленными координатами и будем называть их базовыми. Построим бесконечный граф, возьмем в качестве множества вершин множество всех точек с целочисленными координатами. Будем считать, что в каждую вершину входит один и тот же пучок дуг, совпадающий с векторами /ь ...,f_r Назовем такой граф бесконечным регулярным графом степени г. Любой его конечный подграф будем называть регулярным графом степени г. Если регулярный граф является графом некоторого алгоритма, то соответствующий алгоритм также будем называть регулярным.

Очевидно, что граф алгоритма (8.18) является регулярным. Он будет оставаться регулярным и в том случае, если каждая из функций Ff зависит не от всего множества переменных и _f ■_ у■,..., и /■ _ / , а лишь от какого-то его подмножества.

Основной смысл введения понятия регулярности состоит не только в том, чтобы выделить графы, которые устроены так же красиво, как граф алгоритма (8.18). Нужно также описать графы, которые могут быть расширены до подобных графов. Реальные графы нередко имеют локальные нерегулярности, особенно вблизи границы области задания вершин. В целом эти нерегулярности могут значительно портить структуру графа. Однако очень

Глава 8. Вычислительные системы и алгоритмы

473

часто они слабо влияют на изучаемые объекты, в частности, на множество подходящих разверток. Заметим, что при расширении графа множество разверток сужается. Структура же графа после расширения может стать вполне хорошей. Более того, может появиться возможность легко найти нужные развертки. С точностью до различий в области задания эти развертки будут также развертками для исходного графа. Желание не изучать влияние локальных нерегулярностей и привело нас к введению бесконечного регулярного графа. Его использование особенно оправдано в тех случаях, когда мы ничего не можем заранее сказать о структуре нерегулярностей. Основные свойства регулярных графов являются отражением соответствующих свойств бесконечных регулярных графов. Если бесконечный граф расщепляется на не связанные между собой подграфы, то аналогичное расщепление имеет место и для любых подграфов бесконечного графа. Если бесконечный граф не имеет контуров, то не имеет контуров и любой его подграф. Если для бесконечного графа можно найти развертку, то она порождает развертку для каждого подграфа, и т. п. Все эти обстоятельства побуждают начать детальное исследование бесконечных регулярных графов.

Бесконечный регулярный граф может содержать бесконечные подграфы, также устроенные регулярно. Вершинами одного из них являются линейные комбинации базовых векторов со всевозможными целочисленными коэффициентами линейных комбинаций. Назовем такой подграф главным регулярным подграфом. В общем случае главный подграф не совпадает со всем бесконечным регулярным графом.

Утверждение 8.7

Рассмотрим два подграфа бесконечного регулярного графа, каждый из которых получен путем параллельного переноса главного подграфа. Имеет место альтернатива: или эти подграфы совпадают, или они не связаны.

Пусть G\ и С?2 — два указанных подграфа. Предположим, что они имеют общую вершину g. Рассмотрим произвольную вершину и из G\. Так как G\ получен из главного подграфа путем параллельного переноса, то вектор и — g может быть представлен в виде линейной комбинации базовых векторов с целочисленными коэффициентами. Но Gi также получен из главного подграфа путем параллельного переноса. Поэтому, прибавляя к вектору g эту линейную комбинацию, мы должны получить некоторую вершину из G^. Это означает, что вершина и принадлежит G^, т. е. подграфы G\ и Gj совпадают. Пусть подграфы соединены хотя бы одной дугой. Так как вершины главного подграфа определяются всевозможными комбинациями базовых векторов с целочисленными коэффициентами, то подграфы, связанные дугой, обязаны иметь общие вершины. Следовательно, они должны совпадать.

474

Часть III. Смежные проблемы и применение

Утверждение 8.8

Любой бесконечный регулярный граф можно представить как объединение подграфов, полученных из главного подграфа путем параллельного переноса на векторы с целочисленными координатами.

Если бесконечный регулярный граф не совпадает со своим главным подграфом, то в графе есть хотя бы одна вершина g, не принадлежащая подграфу. Перенесем главный подграф параллельно, совместив его нулевую вершину с вершиной g. Если два подграфа не покрывают полностью бесконечный регулярный граф, то в нем есть хотя бы одна вершина и, не принадлежащая ни одному из подграфов. Снова перенесем главный подграф параллельно, совместив его нулевую вершину с вершиной и. Продолжая этот процесс, убеждаемся в справедливости утверждения.

Заметим, что подграфы, указанные в утверждении 8.8, не могут быть связаны между собой дугами.

Рассмотрим линейные комбинации базовых векторов, имеющие следующий

вид:

Здесь все числа а, удовлетворяют соотношениям 0 < а_г < 1. Это множество векторов образует полуоткрытый многогранник, который назовем базовым. В базовый многогранник попадает некоторое число вершин регулярного графа. Назовем их опорными.

Утверждение 8.9

Пусть размерность линейной оболочки базовых векторов совпадает с размерностью пространства. Тогда бесконечный регулярный граф расщепляется на не связанные между собой подграфы, полученные путем параллельного переноса главного подграфа в некоторые опорные вершины.

Согласно утверждению 8.7, подграфы, полученные путем параллельного переноса главного подграфа в любые две опорные вершины, или совпадают, или не связаны. Рассмотрим объединение всех подграфов, полученных путем параллельного переноса главного подграфа в опорные вершины. Предположим, что этому объединению не принадлежит какая-то вершина g бесконечного регулярного графа. Вектор g имеет целочисленные координаты и лежит в линейной оболочке базовых векторов. Очевидно, что всегда можно прибавить к нему такую линейную комбинацию базовых векторов с целочисленными коэффициентами, при которой результирующий вектор обязательно попадет в базовый многогранник. Это означает, что наряду с вершиной g в построенное объединение не входит одна из опорных вершин, что невозможно по построению.

Глава 8. Вычислительные системы и алгоритмы

475

Если базовые векторы линейно независимы, то никакие две различные опорные вершины не могут принадлежать одному и тому же подграфу, полученному из главного путем параллельного переноса. Если же базовые векторы линейно зависимы, то такие пары опорных вершин могут существовать.

Таким образом, любой бесконечный регулярный граф всегда расщепляется на не связанные между собой подграфы, изоморфные главному подграфу. Этот изоморфизм описывается параллельным переносом. Поэтому при изучении параллельной структуры бесконечного регулярного графа почти всегда можно ограничиться изучением параллельной структуры его главного подграфа.

В общем случае базовые векторы могут быть такими, что регулярный граф будет иметь контуры. Подобные графы не могут быть графами каких-либо алгоритмов. Поэтому важно иметь критерий, показывающий отсутствие контуров в регулярном графе.

Утверждение 8.10

Бесконечный регулярный граф не имеет контуры тогда и только тогда, когда существует целочисленный вектор, образующий острые углы со всеми базовыми векторами.

Пусть/], ...,f_r— базовые векторы. Предположим, что указанный вектор q существует, но регулярный граф имеет контур. Проходя этот контур в положительном направлении дуг, заключаем, что имеет место равенство

1 = 1

где все числа a_t целые, неотрицательные и не все равны нулю. Умножая это равенство скалярно на вектор q и принимая во внимание, что (f_t, q) > 0 для всех /, приходим к противоречию. Следовательно, существование вектора, образующего острые углы со всеми базовыми векторами, исключает существование у любого регулярного графа, в том числе бесконечного, хотя бы одного контура.

Предположим теперь, что для заданных базовых векторов /j, ..., f_r не существует ни одного вектора q с указанными свойствами. Выберем среди базовых векторов максимальную подсистему, для которой такой вектор существует. Не ограничивая общности, можно считать, что это будут векторы f\, ..., У/, где Кг. Пусть К есть открытый конус векторов q, определяемый системой неравенств (/J, q) > О для 1 < / < /. По построению при j > I выполняется неравенство (//, q) < 0 для всех q е К. Следовательно, (— Jj, q) > 0 для всех q, принадлежащих не только открытому конусу К, но и его замыканию К. Согласно утверждению 6.6, каждый из векторов f/ + i, ...,f_r представляется в виде линейной комбинации с отрицательными коэффициентами некото-

476

Часть III. Смежные проблемы и применение

рых из векторов/], ...,/. Пусть, например, / + j = p_lt/j + ... +$_sf_s, где s < I u все числа (З_г- отрицательные. Это означает, что вектор и = (— (Зь ..., — р_Л 1), все координаты которого строго положительны, является решением однородной системы линейных алгебраических уравнений Фи = О, где столбцы матрицы Ф составлены из координат векторов/], ...,/,/+ ].

Рассмотрим систему Фи = О более детально. Матрица Ф имеет целочисленные коэффициенты. Воспользовавшись формулами Крамера для нахождения фундаментальной системы решений, заключаем, что все векторы фундаментальной системы можно выбрать с рациональными и, следовательно, с целыми координатами. Как было установлено, система Фи = 0 имеет решение с положительными значениями неизвестных. Это решение есть линейная комбинация векторов фундаментальной системы решений. В силу непрерывной зависимости линейной комбинации от коэффициентов и целочисленное™ векторов фундаментальной системы следует, что сколь угодно малыми изменениями коэффициентов линейной комбинации можно получить решение системы Фи = О с рациональными положительными значениями неизвестных. Поэтому система Фи = 0 обязательно будет иметь положительное целочисленное решение.

Если у], ..., y_s, у/+ 1 — значения соответствующих неизвестных, то векторы Yi/ъ ■■■> Isfsi li+ ifi+ 1 образуют контур. Следовательно, отсутствие вектора q, образующего острые углы со всеми базовыми векторами, неизбежно влечет существование контуров в бесконечном регулярном графе. Отсутствие контуров гарантирует, что указанный вектор существует.

Вектор q является внутренней точкой конуса, определенного системой неравенств (fj, q) > О для 1 < / < г. Из соображений непрерывности его всегда можно выбрать рациональным, а в силу однородности скалярных произведений и целочисленным.

Зафиксируем базовые векторы/, ...,/. Предположим, что никакая их линейная комбинация с неотрицательными целочисленными координатами не равна нулю. Согласно утверждению 8.10, существует вектор q, образующий острые углы со всеми базовыми векторами, т. е. выполняются неравенства (fi, q) > 0 для 1 < / < г. Обозначим через х вектор пространства, в котором находятся вершины графа, и рассмотрим линейные функции вида t(x) = (х, q) + у, где у — любая константа. Поверхности уровня t(x) = а для этих функций являются гиперплоскостями.

Пусть G— произвольный регулярный граф с базовыми векторами/, ...,/•. Предположим, что какие-то вершины и, v связаны дугой /, вершина и является для дуги начальной, вершина v — конечной.

Тогда имеем

t(v) ~ t(u) = (v, q) ~ (и, q) = (v- и, q) = (f_h q) > 0.

Глава 8. Вычислительные системы и алгоритмы

477

Это означает, что функция t(x) является линейной разверткой для графа G. Более того, если положить задержку для дуги f_t равной (f_h q), то функция t(x) будет минимальной разверткой. Следовательно, справедливо

Утверждение 8.11

Пусть регулярный граф имеет в качестве базовых векторы /_ь ...,f_r Выберем любой вектор q , образующий острые углы с базовыми векторами, и каждой дуге, задаваемой вектором f_h установим задержку (/•, q). Тогда функция вида t{x) = (х, q) + у будет для графа минимальной разверткой при q = q .

Отметим, что в данном утверждении ничего не говорится о начальных условиях для развертки. Они легко восстанавливаются по самой развертке.

Развертка t(x) определяет параллельную форму графа. Ее ярусы задаются теми поверхностями уровня, которые содержат хотя бы одну вершину. Но поверхность уровня функции t(x) = (х, q) + у есть гиперплоскость с направляющим вектором q. Поэтому вся совокупность ярусов параллельной формы описывается совокупностью различных гиперплоскостей, имеющих в качестве направляющего один и тот же вектор q и содержащих в себе все вершины графа. Если граф является графом алгоритма, то число покрывающих его различных гиперплоскостей определяет время реализации алгоритма. Так как все гиперплоскости имеют один и тот же направляющий вектор, то они параллельны. Поэтому число гиперплоскостей определяется расстояниями между ними. Чтобы не рассматривать частные особенности регулярных графов, снова обратимся к бесконечному регулярному графу. Проведем через каждую целочисленную точку пространства гиперплоскость с направляющим вектором q и рассмотрим расстояние между соседними гиперплоскостями.

Утверждение 8.12

Гиперплоскости с целочисленным направляющим вектором q, проходящие через целочисленные точки пространства, образуют семейство равноотстоящих гиперплоскостей. Расстояние между соседними гиперплоскостями равно

d ML¹, где d— наибольший общий делитель модулей ненулевых координат вектора q, | ■ | —евклидова норма вектора.

Рассмотрим гиперплоскость (х, q) = 5. Вектор q = (q\, ..., q_n) имеет целочисленные координаты. Так как гиперплоскость проходит хотя бы через одну целочисленную точку, то число 5 — целое. Пусть z ⁼ (Z\, ..., Z_n) — целочисленный вектор. Известно, что уравнение q\Z\ + ... + q_nz_n ⁼ § имеет решение в целых числах тогда и только тогда, когда 5 делится на наибольший общий делитель d модулей координат q\, ..., q_n. При этом число решений всегда бесконечно.

478

Часть III. Смежные проблемы и применение

Обозначим q_t = dq', где q\ — целое, и рассмотрим невязку

r = d(q'_lZi+...+q'„Z„)-S. (8.19)

Числа q\, ..., q'_n взаимно простые, поэтому уравнение

q\l\ + ... + q'_nz_n = 1 обязательно имеет решение в целых числах. Следовательно, выражение в круглых скобках в (8.19) может принимать всевозможные целочисленные значения. Это означает, что на множестве целочисленных векторов с координатами Z\, ..., Z_n модуль минимального ненулевого значения невязки г в (8.19) равен d, а расстояние между соседними гиперплоско-

j и и-¹стями равно d щ .

Желание минимизировать время реализации алгоритма приводит к минимизации числа гиперплоскостей, покрывающих граф. Если не принимать во внимание частные особенности графов, то вектор q следует выбрать так,

чтобы величина d jqj была максимальной.

Таким образом, параллельная структура любого регулярного графа определяется, причем конструктивно. Конечно, для конкретного графа найденные таким образом развертки могут оказаться неминимальными. Однако почти всегда из них можно получить либо минимальные развертки, либо развертки, близкие к минимальным.

Собственно говоря, есть две причины, мешающие получить минимальные развертки. Во-первых, пока не было учтено, что регулярный граф может расщепляться на не связанные между собой подграфы из-за расщепления бесконечного регулярного графа. В этом случае и вся система гиперплоскостей может расщепляться на несвязанные подсистемы гиперплоскостей согласно расщеплению бесконечного регулярного графа. Во-вторых, регулярный граф может иметь какие-то конкретные особенности. Они, вообще говоря, могут изменить строение минимальных разверток. Однако чаще всего подобное изменение приводит к разверткам, близким к минимальным.

Обратим внимание на следующее обстоятельство. Выбор вектора q, образующего острые углы с базовыми векторами регулярного графа, означает выбор вектора, образующего острые углы со всеми дугами графа. Если граф не является регулярным, то он все же может иметь вектор, образующий острые углы со всеми дугами. В этом случае исследование параллельной структуры графа осуществляется по той же самой схеме, что и для регулярного графа. Особенности графа сказываются на определении вектора q, но не на способе построения разверток. В общем случае нельзя только доказать близость разверток к минимальным. Графы, у которых существуют векторы, образующие острые углы со всеми дугами, оказываются существенно более простыми с точки зрения изучения их параллельных свойств. Такие графы называются строго направленными, а соответствующие векторы q — направляющими.

Глава 8. Вычислительные системы и алгоритмы

479

Рассмотрим любой строго направленный граф, вершины которого находятся в целочисленных точках. С помощью специальных преобразований его можно свести не только к регулярному графу, но даже к координатному регулярному графу, дуги которого совпадают с координатными векторами. В частности, к координатному графу можно свести любой регулярный граф без контуров, т. к. он является строго направленным.

Пусть векторы s\, ..., s_p описывают все множество дуг графа. Предположим, что для некоторого вектора q выполняются условия (sj, q) > О для всех /. Эти условия позволяют выбрать различные целочисленные системы векторов g\, ..., g_n такие, что будут справедливы неравенства (лу, gj) > О для всех i,j. Подобных систем существует много, и среди них можно выбрать наиболее подходящую. Например, систему векторов g\, ...,g„ всегда можно выбрать как базис пространства.

Для каждого / построим систему параллельных гиперплоскостей с направляющим вектором gj. Согласно утверждению 8.12, расстояние между различными гиперплоскостями, проходящими через целочисленные точки, не может быть сколь угодно малым. Поэтому, не ограничивая общности, можно считать, что ни одна из гиперплоскостей не проходит ни через одну целочисленную точку пространства. Построенная система гиперплоскостей рассекает пространство на полуоткрытые параллелепипеды, грани которых перпендикулярны g\, ..., g_n. Теперь построим новый граф. В качестве его вершин возьмем параллелепипеды вместе с попавшими в них вершинами исходного графа и частями его дуг. Отождествим вершины нового графа с узлами прямоугольной регулярной решетки. Будем считать, что две соседние вершины нового графа связаны дугой, если через грань, разделяющую два соответствующих параллелепипеда, проходит хотя бы одна дуга исходного графа. Все дуги исходного графа, пересекающие одну грань, образуют с ее направляющим вектором острые углы. Поэтому дуга нового графа определяется корректно. Ее направление возьмем в соответствии с направлением направляющего вектора грани. Построенный граф будет координатным регулярным графом.

Заметим, что аналогичные преобразования графа алгоритма мы рассматривали в § 7.2 в связи с исследованием возможности реализации алгоритма на вычислительной системе с многоуровневой памятью. Регулярные координатные графы устроены настолько просто, что о них известно практически все. Рассмотрим, например, вопрос о выборе максимальной параллельной формы. Если не принимать во внимание частные особенности графов, то это сводится согласно утверждению 8.12, к следующей задаче. Пусть fy, ...,f_rявляются координатными векторами единичной длины. Тогда в конусе (/J, q) > О, 1 < / < г нужно найти вектор q, максимизирующий величину

rf|q|_E . Почти очевидно, что решением данной задачи является вектор

q = (1, ..., 1). Так же просто решаются и многие другие задачи.

480

Часть III. Смежные проблемы и применение

Исследуя графы алгоритмов, мы почти нигде не делали различия между отдельными вершинами и дугами. Однако в действительности разным вершинам могут соответствовать разные операции, а разные дуги могут означать передачу информации разной природы. Это обстоятельство отчетливо видно на рассмотренном преобразовании графа. Объявляя параллелепипеды новыми вершинами, мы по существу вводим новые операции. Размеры параллелепипедов могут быть разными, что влечет за собой разную мощность как операций, так и передаваемой между ними информации. В некоторых случаях приходится учитывать различие содержаний, вкладываемых в вершины и дуги.

В интересах практического применения утверждения 8.6 необходимо для регулярных графов найти какие-нибудь простые множества вершин, гарантированно лежащие на одном пути. Естественно, возникает мысль о вершинах, находящихся на прямой линии. Оказывается, что далеко не каждая прямая обладает нужным свойством.

Рассмотрим главный регулярный подграф бесконечного регулярного графа. Предположим, что базовые векторы /j, ..., f_r линейно независимы. Возьмем любую прямую линию, лежащую в линейной оболочке базовых векторов. Обозначим через / направляющий вектор прямой. Без ограничения общности можно считать, что / >- 0. Если / -< 0, то вместо / берем вектор —/. Допустим, что на прямой имеются две вершины u, v. Пусть для определенности и < v. Так как мы хотим, чтобы эти вершины лежали на одном пути, то должно выполняться равенство

v - и = оц/i + ... + a_rf_r,

где все числа oq, ..., a_r целые неотрицательные. С другой стороны, справедливо соотношение

v - и = а/,

где а > 0 в силу условий и -< v, I >- 0. Вектор /, как вектор линейной оболочки векторов f]_, ...,f_r, раскладывается по этим векторам как по базису, т. е.

/=Pl/l + ... + Рг/л

Следовательно, всегда должно выполняться равенство

оц/i + ... + a_rf_r= a(Pi/i + ... + p_r/_r).

Из независимости векторов /j, ..., f_r следует, что

cci = aPi, ..., a_r = ap_r.

Поэтому числа oq, ..., a_r и p_l5 ..., p_r могут быть неотрицательными только одновременно. Таким образом, имеет место

Утверждение 8.13

Пусть в линейной оболочке базовых векторов /_ь ...,f_r главного регулярного подграфа задана прямая линия с направляющим вектором /. Предположим, что

Глава 8. Вычислительные системы и алгоритмы

481

базовые векторы линейно независимы и на прямой находится хотя бы одна вершина. Если в разложении вектора /по векторам/_ь ...,f_r все ненулевые коэффициенты разложения имеют одинаковые знаки, то на такой прямой все вершины подграфа связаны одним путем.

Отметим в заключение, что графы на рис. 4.3, 4.6, 7.5 регулярные. Граф на рис. 4.4, а не регулярный, но направленный. В качестве направляющего можно взять вектор, например, с координатами 1,1.

Вопросы и задания

1. Приведите примеры алгоритмов, графы которых регулярные.

2. Пусть все дуги графа, рассматриваемые как векторы, имеют неотрицательные координаты. Докажите, что граф является направленным и в качестве направляющего может быть взят любой вектор с положительными координатами.

3. Предположим, что вершины графов расположены в точках я-мерного арифметического пространства с целочисленными координатами и все дуги имеют неотрицательные координаты. Рассмотрим для графов линейные развертки. Докажите, что гиперплоскости с направляющим вектором q= (1, 1, ..., 1) являются поверхностями уровней строгой развертки для любого из рассматриваемых графов и обеспечивают максимальное расстояние между соседними поверхностями уровней линейных разверток.

4. Приведите пример, когда для графа из п. 3 существует строгая линейная развертка с направляющим вектором, имеющим как минимум одну отрицательную координату.

5. Обозначим через е_ь ..., е_п координатные векторы я-мерного арифметического пространства. Выберем любой граф из п. 3 и добавим к нему любые дуги, направленные так же, как векторы е_ь ..., е_п. Докажите, что любая линейная обобщенная (строгая) развертка исходного графа с неотрицательным (положительным) направляющим вектором остается обобщенной (строгой) разверткой нового графа.

6. Остается ли справедливым утверждение п. 5, если не требовать неотрицательности (положительности) направляющего вектора развертки?

7. Рассмотрите любой граф из п. 3. Любую его дугу можно представить в виде линейной комбинации векторов е_ь ..., е_п с неотрицательными целочисленными коэффициентами. Эти разложения называются укладкой графа по координатному базису. Предложите геометрическую интерпретацию укладки, позволяющую свести граф к координатному.

8. *Попробуйте решить задание 10 из § 8.2 для координатного графа.

9. Докажите, что проекция регулярного графа вдоль любой прямой на любую гиперплоскость есть граф, изоморфный регулярному.

10. Приведите примеры, когда проекция регулярного графа, не имеющего контуры, будет иметь контуры.

11. Приведите условия, гарантирующие отсутствие контуров в проекции.

482

Часть III. Смежные проблемы и применение

12. Пусть базовые векторы/_ь ...,f_r линейно независимы. Докажите, что с точностью до умножения на —1 любое ненулевое решение q системы линейных алгебраических уравнений

SiOb 4) = 8₂(4 q)= ...= 8,(/n q) является направляющим вектором графа, если только все числа 5_Ь 8₂, ..., 5_Г вещественные, ненулевые и имеют одинаковые знаки.

13. Докажите, что вектор q из п. 12 образует одинаковые углы со всеми базовыми векторами, если

_II г ц~1 е _у г ц~1 е _|| г \\~l

i ~ IkiIIe ' ² ~ 1к2Не ' •••' °r ~ ||//-|1е •

§ 8.4. Математические модели систолических массивов

Уровень технологических возможностей микроэлектроники во многом определяет уровень развития вычислительной техники. Повышение плотности расположения элементов на кристалле, увеличение скорости их переключения приводят не только к повышению быстродействия компьютеров и уменьшению их размеров, но и позволяют разрабатывать вычислительные системы с принципиально новыми архитектурными решениями. Достижения микроэлектроники дают возможность уже в настоящее время создавать достаточно сложные сверхминиатюрные вычислительные устройства, расположенные на одном кристалле. При массовом производстве такие устройства оказываются, к тому же, относительно дешевыми. Все эти обстоятельства не только открывают новые перспективы конструирования вычислительных систем, но и порождают многочисленные новые проблемы, в том числе математические.

Одной из самых трудных является проблема создания коммуникационных сетей, обеспечивающих быстрые необходимые связи между отдельными функциональными устройствами. Пока скорости срабатывания устройств были не очень большими, основными факторами, препятствующими созданию нужных коммуникационных сетей, являлись число линий связи и сложность коммутаторов. Однако с ростом скорости срабатывания устройств наряду с этими факторами стали иметь большое значение также и длины линий связи.

В определенном отношении самой простой и эффективной является коммуникационная сеть, в которой нет коммутаторов, все устройства соединены непосредственно друг с другом и длины всех линий связи, а потому и времена задержек при передаче по ним информации минимальные, в некотором смысле, нулевые. С конца семидесятых годов прошлого столетия стали появляться работы, активно призывающие строить специализированные вычислительные системы, получившие название систолические массивы. Эти

Глава 8. Вычислительные системы и алгоритмы

483

системы устроены предельно просто и в то же время имеют предельно простую коммуникационную сеть. Поэтому они являются исключительно эффективными по быстродействию, но каждая из них ориентирована на решение весьма узкого класса задач [54].

Общий подход к конструированию математических моделей систолических массивов основан на следующей идее. Пусть в нашем распоряжении имеется достаточно большое число функциональных устройств. Все ФУ являются простыми и срабатывают за одно и то же время. Математическое содержание и техническая конструкция ФУ сейчас не имеют особого значения. Важно, чтобы выходная и входная информация устройств соответствовали друг другу. Если по каким-либо причинам информация не подается на входы ФУ, ничто не мешает считать, что она в этих случаях вырабатывается самими ФУ. Допустим, что конструктивно каждое ФУ выполнено в виде некоторого плоского правильного четырех- или шестиугольника. Пусть входы и выходы ФУ выведены на границу многогранников. Будем называть эти ФУ систолическими ячейками (процессорными элементами, элементарными процессорами, чипами и т. п.).

Теперь начнем складывать из ФУ-многоугольников различные фигуры, присоединяя без наложения последовательно многоугольник за многоугольником и предполагая, что соседние многоугольники соприкасаются друг с другом. В местах соприкосновения соединим входы и выходы соседних ФУ. В результате такого построения получится некоторая фигура, у которой останутся свободными какие-то входы и какие-то выходы. Мы получим модель специализированной вычислительной системы, если заставим всю совокупность собранных ФУ работать по правилам, описанным в §2.3, например, в синхронном режиме с одинаковым временным тактом. Подавая на свободные входы в том же синхронном режиме входные данные, будем получать какие-то результаты, начиная с некоторого момента, на свободных выходах. Созданная подобным образом модельная вычислительная система называется систолической системой.

Весьма заманчиво хотя бы теоретически рассмотреть общий случай систолической системы. Однако мы не будем это делать просто в силу того, что практическая необходимость пока не требует таких исследований. Будем считать, что при построении систолических систем используются только плоские ФУ-многоугольники. Они имеют одинаковые конфигурации и размеры, пристыковываются друг к другу без зазоров и все вместе находятся в одной плоскости, образуя некоторый плоский массив. Подобные систолические системы и называются систолическими массивами.

Прежде чем обсуждать различные аспекты конструирования и функционирования систолических массивов, рассмотрим простой пример. Это один из первых систолических массивов, построенных с момента возникновения самой идеи создания вычислительных систем такого типа. Предположим,

484

Часть III. Смежные проблемы и применение

что необходимо построить специализированную вычислительную систему, на которой достаточно быстро реализуется операция вычисления матрицы D = С + АВ, где

a_n a_n


	п ^Ъп Ъ\ъ*	0"
в =	Ь₂\ ъ_г1... ... Ъ_Ъ1...
	0	-

^a2\ ^a2l

^аЪ\ ^аЪ2

л 42

'11 42 Ч;

'14

'21 "-22

'31 "-32

^с41

Здесь все матрицы — ленточные порядка п. Матрица А имеет одну диагональ выше и две диагонали ниже главной. Матрица В имеет одну диагональ ниже и две диагонали выше главной. Матрица С имеет по три диагонали выше и ниже главной.

Пусть в нашем распоряжении имеется достаточно большое число функциональных устройств, выполняющих скалярную операцию с + ab и осуществляющих одновременно передачу данных. Такие операции как раз и реализуются либо на четырех-, либо на шестиугольных систолических ячейках. Они представлены на рис. 8.5.


b а 1Д		^aN	с	*S^b*
с —►	—► с		У ч
W b а		ъ"	У с	^

Рис. 8.5. Систолические ячейки с операцией с + ab

Здесь каждое ФУ имеет три входа a, Ь, с и три выхода а, Ь, с. Входные (in) и выходные (out) данные в общем случае связаны соотношениями

^Lout

С|д "Г C

^гиАш ^out ⁼ b-_m, а_оЫ = a_in. (8.20)

Глава 8. Вычислительные системы и алгоритмы

485

Если в момент выполнения операции какие-то данные не поступают, то будем считать, что они заменяются нулями. Точка указывает ориентацию систолической ячейки на плоскости.

На рис. 8.6 представлен систолический массив, реализующий указанную выше матричную операцию С + АВ. Здесь же указаны расположение и схема подачи входных данных.

Рис. 8.6. Систолический массив для перемножения ленточных матриц

При построении систолического массива использованы шестиугольные систолические ячейки. Сделаем по этому рисунку некоторые пояснения.

Вся плоскость покрыта регулярной косоугольной решеткой, образованной двумя семействами равноотстоящих параллельных прямых, пересекающихся под углами соответственно 60° и 120°. В узлах этой решетки размещены ФУ и входные данные. Система работает по тактам. За каждый такт все данные перемещаются в соседние узлы по направлениям, указанным стрелками.

486

Часть III. Смежные проблемы и применение

На рисунке показано состояние в некоторый момент времени. В следующий такт все данные переместятся на один узел и элементы a\\, Ь\\, с\\ окажутся в одном ФУ, находящемся на пересечении штриховых линий. Следовательно, будет вычислено выражение сц + a\\b\\. В этот же такт, в частности, данные д_]2 и Ь₂\ приблизятся вплотную к ФУ, находящемуся в вершине систолического массива. В следующий такт все данные снова переместятся на один узел в направлении стрелок и в верхнем ФУ окажутся элементы «12, #21 ^и результат срабатывания ФУ, находящегося снизу, т. е. сц + оцйц. Следовательно, будет вычислено выражение сц + оц^п ⁺ ^an^2\- Это есть элемент d\ \ матрицы D.

Продолжая потактовое рассмотрение процесса, можно убедиться, что на выходах ФУ, соответствующих верхней границе систолического массива, периодически через три такта будут выдаваться элементы матрицы D. На каждом выходе будут появляться элементы одной и той же диагонали. Примерно через Ъп тактов будет закончено вычисление всей матрицы D. Загруженность каждой систолической ячейки асимптотически равна 1/3.

Трудно предположить, что после рассмотрения данного примера у читателя сложилось четкое представление в отношении возможностей систолических массивов как специализированных вычислительных систем. Скорее возникло много вопросов. В самом деле, этот пример показывает, что для данной задачи систолический массив может быть построен. Но почему он выглядит именно так? Существуют ли другие систолические массивы, позволяющие решать ту же задачу? С чем связана относительно низкая загруженность ФУ? Как разработать общую методологию отображения алгоритмов на систолические массивы? Такие вопросы можно задавать долго.

К настоящему времени построено много других систолических массивов для решения различных задач, в основном матрично-векторных. Тем не менее, мы не будем сейчас рассматривать новые примеры. Это связано с тем, что анализ конкретных систолических массивов не дает ответы на многие вопросы, касающиеся потенциальных возможностей вычислительных систем данного типа. На конкретных примерах легко объяснить, как заданный систолический массив решает заданную задачу, но почти невозможно понять, как построить систолический массив, чтобы на нем можно было решать нужную задачу.

Для разработки методологии построения систолических массивов исследуем сначала вид графов алгоритмов, реализуемых подобными вычислительными системами. Не будем пока принимать во внимание, что некоторые или даже все выходные данные ФУ могут совпадать с какими-то входными данными. Не важно и то, что теперь каждое ФУ имеет более одного выхода, а не один, как чаще всего предполагалось до сих пор. Вообще говоря, сейчас важнее не то, какие операции выполняют ФУ, а то, как они будут управляться и в каком временном режиме смогут работать. Разрабатывая методологию по-

Глава 8. Вычислительные системы и алгоритмы

487

строения систолических массивов, мы будем стремиться как можно полнее перенести на эти вычислительные системы две важнейшие особенности граф-машины. Во-первых, возможность локального управления работой системы ФУ и, во-вторых, возможность реализации всего спектра временных режимов, включая наискорейшие. Первую особенность мы сохраним безусловно и будем строить лишь такие систолические массивы, в которых систолические ячейки сами управляют своей работой и моментами срабатывания. Принимая во внимание вторую особенность, мы будем строить систолические массивы, реализующие алгоритм по возможности максимально быстро. Кроме этого, мы сохраним еще одну особенность, подмеченную в реально созданных систолических массивах. Именно, любая систолическая ячейка, начав работать в какой-то момент времени, продолжает срабатывать каждый такт или с постоянным периодом, пока не закончится весь процесс ее функционирования. Другими словами, в работе систолических ячеек не бывает как больших, так и неконтролируемых перерывов.

Очевидно, что плоскость можно покрыть без зазоров как четырех-, так и шестиугольниками одного размера. Если задан какой-то лежащий в плоскости систолический массив, то он вырезает из покрытия плоскости соответствующую ему односвязную фигуру. Выберем в плоскости массива два семейства параллельных равноотстоящих прямых линий таким образом, чтобы центр любой систолической ячейки находился в точке пересечения двух прямых. Эти семейства выбираются однозначно в случае четырехугольников и неоднозначно в случае шестиугольников. На основе выбранных семейств построим аффинную систему координат. Пусть она такова, что центры всех систолических ячеек описываются двумерными векторами с целочисленными координатами. Соседние ячейки всегда имеют равными одну из координат и различающуюся на 1 другую координату. Обозначим оси координат х, у. Теперь возьмем любую ось t, не лежащую в плоскости х, у, и установим на ней направление. При t=0, 1, 2, ... проведем плоскости, параллельные плоскости х, у. Предположим, что t = 0 соответствует плоскости систолического массива.

Будем считать t осью времени. Пусть систолический массив начинает работать при / = 0и продолжает функционировать с тактом, равным 1. Построим ориентированный граф. Вершинами являются точки трехмерного пространства, в которых координаты х, у соответствуют систолической ячейке, срабатывающей в момент t. Дуги символизируют передачу информации от ячейки, которая произвела ее в момент t, к ячейке, которая получит ее в момент t + 1. Очевидно, что число различных дуг, рассматриваемых как векторы в трехмерном пространстве, не превосходит числа различных по направлению передач информации от одной систолической ячейки к другой соседней в самом систолическом массиве. При сделанных предположениях координаты векторов-дуг по осям х, у равны 0, 1 или —1, а по оси t коорди-

488

Часть III. Смежные проблемы и применение

ната всегда равна 1. Вспоминая исследования, проведенные в § 8.3, заключаем, что справедливо

Утверждение 8.14

Если ячейки систолического массива работают в синхронном режиме, то систолический массив реализует алгоритм, граф которого изоморфен подграфу бесконечного регулярного графа.

Таким образом, систолические массивы как специализированные вычислительные системы могут реализовывать лишь вполне определенный класс алгоритмов. Это — регулярные алгоритмы. Реально используемые алгоритмы часто являются регулярными изначально. Многие алгоритмы легко сводятся к регулярным. Иногда процесс сведения оказывается достаточно трудным. Конечно, имеются алгоритмы, не сводимые к регулярным без значительного ухудшения временных характеристик. Обо всем этом мы еще будем говорить позднее. Сейчас же только отметим одну особенность.

По-видимому, самой характерной чертой систолических массивов является отсутствие каких-либо дополнительных линий связи при соединении входов и выходов систолических ячеек. Соединение отдельных ячеек между собой лишь в местах соприкосновения приводит к тому, что в систолических массивах все связи имеют минимально возможные длины и, следовательно, оказываются минимальными временные затраты на передачу информации от одних функциональных устройств к другим. Подразумевая именно эту особенность, говорят, что в систолических массивах реализуется принцип близкодейспгвия. Это, в свою очередь, приводит к тому, то в графах связей систолических массивов дуги никогда не пересекаются. Точнее, дуги могут иметь общими только концевые вершины. Такие графы называются плоскими.

Как видно из рис. 8.5 и формул (8.20), систолические ячейки могут выполнять функции переносчика информации. Это очень важная их черта. Она помогает в вычислительных системах организовывать транспортные связи. Если некоторое данное должно использоваться во многих устройствах, то необходимо применение специальных способов его рассылки. Один из способов реализует шинную связь. Рассылаемое данное поступает на шину и одновременно принимается несколькими устройствами. Для систолических массивов такой способ неприемлем. В подобных вычислительных системах транспортные связи оказываются более подходящими. В этом случае данное поступает в ФУ, используется в нем как операнд и, не изменяясь, пересылается по транспортной магистрали в соседнее ФУ, где используется, пересылается дальше и т. д.

При преобразовании графов алгоритмов многократная передача информации через систолические ячейки означает замену "длинных" дуг графа путем, составленным из "коротких" дуг. Данный путь не обязан быть прямолинейным. Обратим особое внимание на то, что такая замена может

Глава 8. Вычислительные системы и алгоритмы

489

увеличить длину критического пути графа алгоритма и, следовательно, увеличишь время наискорейшей реализации. Вводя транспортные связи, об этом следует помнить.

Теперь ключевыми моментами методологии создания систолических массивов становятся умение строить и исследовать графы алгоритмов, а также утверждения 8.6, 8.13, 8.14 [14]. Для регулярных графов операция гомоморфной свертки может быть выполнена как операция однократного или даже многократного ортогонального проектирования. Выбор направления проектирования ограничен лишь требованием, чтобы последняя проекция представляла собой плоский граф. В целом при увеличении числа вершин, лежащих на прямых с выбранным направлением, повышается загруженность систолических ячеек. Если на каждой такой прямой все вершины связаны одним путем, то сохраняется весь спектр временных реализаций алгоритма. Во всех остальных случаях возможность наискорейших реализаций не гарантируется.

с,

л »,

¹ *!

') »'

Рис. 8.7. Одномерные систолические массивы

Рассмотрим следующий пример. Предположим, что граф алгоритма имеет вид, показанный на рис. 8.7. Подобные графы свойственны многим вычислительным методам линейной алгебры и математической физики. С одним из них мы встречались, например, в § 4.4 при рассмотрении алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиа-гональной матрицей. Этот граф регулярный. На горизонтальных или вертикальных прямых, а также на прямых, параллельных прямой, проходящей через вершины с кружками, либо нет ни одной вершины, либо все вершины связаны одним путем. Проектируя граф вдоль таких прямых на перпендикулярные им прямые линии, получаем различные схемы одномерных систолических массивов. Они тоже показаны на рис. 8.7. Согласно утверждению 8.6, все систолические массивы имеют возможность реализовать весь

490

Часть III. Смежные проблемы и применение

спектр временных режимов, в том числе, наискорейшие. Тем не менее, они имеют разное число устройств и, следовательно, разную их загруженность. Схемы передач информации также различные. В двух из них осуществляется односторонняя передача, в одной — двухсторонняя. Наиболее простой представляется схема систолического массива, расположенная на рис. 8.7 справа. Однако учет дополнительных факторов, таких как подача к систолическим ячейкам входных данных алгоритма, может в некоторых случаях сделать более предпочтительными другие схемы.

В каждый такт работы систолического массива срабатывают какие-то его ячейки. Исходя из принципов построения подобных вычислительных систем, можно утверждать, что соответствующие этим ячейкам операции не могут быть связаны между собой информационно. Следовательно, процесс функционирования систолического массива в действительности реализует некоторую строгую параллельную форму графа алгоритма. Ярусы параллельной формы описываются работающими одновременно систолическими ячейками, номера ярусов — временами срабатывания ячеек.

Напомним, что граф систолического массива мы получаем путем ортогонального проектирования графа алгоритма вдоль прямой линии. Обозначим ее направляющий вектор через р. Если граф алгоритма регулярный, то, согласно утверждению 8.10, существует вектор q, который образует острые углы со всеми базовыми векторами. Поэтому на любой гиперплоскости с направляющим вектором q не могут находиться вершины, связанные дугами. Другими словами, совокупность гиперплоскостей, проходящих через вершины графа алгоритма и имеющих в качестве направляющего вектор q, разбивает все вершины на ярусы строгой параллельной формы. Если существует хотя бы одна дуга, параллельная вектору р, то векторы р и q не могут быть ортогональными.

Выберем подходящий вектор q и будем реализовывать на систолическом массиве соответствующую параллельную форму. Проведем через вершины графа алгоритма гиперплоскости с направляющим вектором q. Перенумеруем их подряд в направлении этого вектора. Пусть наименьший номер гиперплоскости, содержащий хотя бы одну вершину, равен 1. Эти и только эти вершины определяют систолические ячейки, которые будут срабатывать в 1-й такт. Гиперплоскость с номером 2 определяет те и только те ячейки систолического массива, которые будут срабатывать во 2-й такт, и т. д. Тем самым фиксируется программа работы каждой систолической ячейки. В процессе работы систолического массива в его плоскости в соответствии с номерами гиперплоскостей распространяется фронт вычислений, показывая, как систолические ячейки вступают в процесс функционирования и как они его заканчивают. Каждая систолическая ячейка будет срабатывать не обязательно каждый такт, но обязательно периодически. Период для всех ячеек один и тот же. Он на 1 больше числа гиперплоскостей, помещающихся между соседними точками на прямой с направляющим вектором р.

Глава 8. Вычислительные системы и алгоритмы

491

Мы уже рассматривали в §4.4 задачу вычисления произведения А = ВС двух квадратных матриц порядка п. На рис. 4.3, а для я = 2 показан граф алгоритма без учета ввода входных данных, т. е. элементов матриц В и С. На рис. 4.3, б эти данные показаны рядом с графом алгоритма. Видна их множественная рассылка. Это означает, что при построении систолического массива обязательно появится транспортная связь.

Построим модель систолического массива для более часто встречающейся задачи вычисления матрицы А + ВС, где А, В, С — заданные матрицы порядка п. Если элементы матрицы А + ВС находятся по обычным формулам, то для п = 3 граф алгоритма будет таким, как показано более жирными стрелками на рис. 8.8. Легко проверить, что один и тот же элемент матрицы В или С требуется для выполнения операций, соответствующих вершинам, лежащим на прямой, параллельной оси j или /. Элементы матрицы А требуются для выполнения лишь операций, соответствующих начальным вершинам путей графа алгоритма. На рис. 8.8 линиями без стрелок обозначены будущие транспортные связи. Направление передачи информации определяется выбором порядка выполнения операций.

Рис. 8.8. Граф алгоритма и транспортные связи

Если спроектировать граф алгоритма на плоскость, перпендикулярную оси к, то проекция будет состоять только из изолированных вершин. В этом случае реализовать алгоритм за минимально возможное время можно лишь при рассылке начальных данных В, С с помощью шинных связей, параллельных осям у, /. Если для реализации операции А + ВС мы хотим построить систолический массив, то должны фигуру на рис. 8.8 превратить в регулярный граф или, другими словами, установить направления передач информации. Пусть эти направления совпадают с направлениями осей i,j. Тем самым фигура на рис. 8.8 становится регулярным координатным графом. Заметим, что при этом длина критического пути графа сразу увеличивается в три раза.

Спроектируем полученный граф на плоскости, перпендикулярные оси /, вектору с координатами (1, 1, 1) и оси у. Соответствующие схемы систолических массивов представлены на рис. 8.9, а—е. Сразу видны различия

492

Часть III. Смежные проблемы и применение

множеств систолических ячеек и конфигураций связи. Кроме этого, нетрудно заметить общность схем на рис. 8.9, б и 8.6. Более жирными линиями на рис. 8.9 указаны проекции ребер куба, содержащего вершины графа. Будем считать, что реализуется параллельная форма, определяемая гиперплоскостями с направляющим вектором q = (1, 1, 1). В систолических массивах на рис. 8.9, а, 8.9, в любая систолическая ячейка, начиная с некоторого момента, срабатывает каждый такт, на рис. 8.9, б — один раз в три такта. Штриховыми линиями отмечено распространение фронта вычислений. На рис. 8.9, а и 8.9, в фронт распространяется по диагонали квадрата от угла, ближайшего к началу координат, к наиболее удаленному углу, на рис. 8.9, б от центра к границе. Во всех трех случаях функции систолических ячеек описываются, в основном, соотношениями (8.20) с переменой местами букв а и с.

Рис. 8.9. Систолические массивы для операции А + ВС

Разные проекции приводят не только к различиям в числе вершин и конфигураций связей, но и к различиям в организации процессов. Так, в проекции на рис. 8.9, б имеется достаточное число связей для выполнения операций (8.20) без использования какой-либо памяти. В проекциях на рис. 8.9, а, 8.9, в связей меньше. Поэтому здесь каждая систолическая ячейка должна иметь по одной ячейке памяти для хранения соответственно элементов ^скр btk матриц С, В. Это приводит, в свою очередь, к различиям в процессах загрузки и разгрузки систолических массивов.

Заметим, что ни один из систолических массивов не позволяет реализовать операцию А + ВС за минимально возможное для нее время. Данный факт является платой за использование транспортных связей и он не противоречит, например, утверждению 8.6. Справедливость утверждения 8.6 связана с предположением, что любое ФУ, осуществляющее все необходимые операции после слияния вершин, может работать в тех же условиях передачи ин-

Глава 8. Вычислительные системы и алгоритмы

493

формации, что и в граф-машине. Но введение транспортных связей как раз и нарушает данные условия, что диктуется, в конечном счете, потребностью организации множественных рассылок.

Рассмотрим более содержательный пример 6.5 из § 6.8, описывающий процесс решения системы линейных алгебраических уравнений методом Жордана без выбора ведущего элемента. Ясно, что граф алгоритма должен состоять из графов опорных гнезд с метками 1—5 и связующих графов. Анализируя покрывающие функции, видим, что графы гнезд 1—3, 5 пустые. В опорном гнезде 4 дуги имеются. В этом гнезде заведомо есть путь длиной я — 1. Следовательно, нельзя рассчитывать на то, что алгоритм можно реализовать быстрее, чем за п параллельных шагов. Связи между гнездами таковы:

□ для гнезда 1 дуги заходят из гнезда 4 и выходят в гнездо 3;

□ для гнезда 2 дуги заходят из гнезда 4 и выходят в гнездо 4;

□ для гнезда 3 дуги заходят из гнезд 1,4 и выходят в гнездо 4;

□ для гнезда 4 дуги заходят из гнезд 2—5 и выходят в гнезда 1—4;

□ для гнезда 5 дуги заходят из гнезда 3 и выходят в гнездо 4.

Связи из гнезда 1 в гнездо 3, из гнезда 2 в гнездо 4, а также из гнезда 3 в гнездо 4 — множественные. Поэтому здесь придется организовывать транспортные магистрали. Все это хорошо видно из явного представления покрывающих функций графа алгоритма.

Суммируя сказанное, разместим вершины опорных гнезд 1—3, 5 вокруг опорного гнезда 4. Область, занимаемая вершинами графа алгоритма, изображена на рис. 8.10. Она представляет усеченную пирамиду, из которой исключено ребро 6. Вершины опорного гнезда 1 размещены на ребре 1, гнезда 2 — на грани 2, гнезда 3 — на грани 3, гнезда 5 — на грани 5, вершины опорного гнезда 4 размещены в остальной части пирамиды.

(п, л+1, п+1) (п, п, п+1)

-5

(1, п+1, п+1) (1, 1, 1) -------770. 1,4+1)

Рис. 8.10. Расположение вершин метода Жордана

Основной объем вычислений приходится на оператор 4, который является телом тройного цикла. Неоднородности вычислений, связанные с операто-

494

Часть III. Смежные проблемы и применение

рами 1—3, 5 локализованы на границе. Структура связей в графе алгоритма вместе с транспортными связями показана на рис. 8.11. В каждую вершину графа входят и выходят дуги, определяемые векторами (1, 0, — 1), (О, 1, 0), (0, 0, 1) в системе координат (k,j, i). В вершинах, лежащих на границе пирамиды рис. 8.10 отсутствуют дуги, связанные с внешним пространством. Транспортные магистрали для рассылки элементов Uj расположены на прямых, параллельных оси /. Они начинаются на грани 3 и заканчиваются на грани 5, проходя через соответствующие точки пирамиды. Транспортные магистрали для рассылки элементов 1_р начинаются на грани 2 и ребре 1 и проходят через соответствующие точки пирамиды на прямых, параллельных оси j. При этом мы полагаем, что р совпадает с /. Входные данные, т. е. элементы матрицы А, поступают через нижнюю грань.

(/с+1,у+1,/-2)

(/с+1,у+1, /+1)

(/с+1,у-1,/-2)

(Аг, у-1, /-2)

(/с,у-1,/+1)

Рис. 8.11. Граф метода Жордана

Граф алгоритма с учетом введенных транспортных связей легко сводится к координатному с помощью линейного преобразования

k'=k,j' = j, i'= i + к- 1.

Область, занимаемая графом в пространстве (k',j", /') изображена на рис. 8.12. Соответствие между операторами и вершинами координатного графа остается аналогичным рассмотренному выше. Все неоднородности вычислений в новом графе также локализованы на границе. Параллельная форма минимальной высоты снова задается вектором q = (1, 1, 1).


ч. 1	S	(п. п+1. 2п) /7 (л, п, 2л) ^(1, п+1, п+1) п+1)
(1, 1, 1)	(1,1,	(п. п+1. 2п) /7 (л, п, 2л) ^(1, п+1, п+1) п+1)

Рис. 8.12. Новое расположение вершин

Глава 8. Вычислительные системы и алгоритмы

495

Рассмотрим две проекции координатного графа для л = 4. Ортогональная проекция по направлению (1, 1, 1) представлена на рис. 8.13. Введем в плоскости проектирования новые координаты £ = / — к, ц = j — к. В этих координатах ребро 1 перешло в точку (0, 0), грань 2 — в линию (1, 0)— (п - 1, 0), грань 3 — в линию (0, 1)—(0, п), грань 5 — в линию (л, 1)—(я, л). При таком проектировании все неоднородности снова остались на границе.

Рис. 8.13. Схема систолического массива

Функции систолических ячеек определяются содержанием операций, которым они соответствуют, а также необходимостью пересылки элементов uj, I, и входных данных. Ячейки осуществляют полностью или частично операции типа (8.20). Именно,

□ ячейка (0, 0): /_out = l/a-_m, o_OHt = a_in;

□ ячейки (1, 0)—(л — 1, 0): /_out = — «i_n;

□ ячейки (0, l)-(0, n): u_ont = a_in/_in, /_out = /_in;

□ ячейки (n, 1)—(л, n): a_oul = % + u_m;

П остальные ячейки: a_oul = a_in + w_in/_in, w_out = w_in, /_out = /_in.

Всю совокупность ячеек можно свести к устройствам двух типов. Функции ячейки (0, 0) таковы:

^out ^— ^in> "out ^— V^in> '-out ^— Qm Qn ^— !■•

Остальные ячейки можно взять с функциями

Q>ut ^— С'ш ^in"in> "out ^— "im ^out ^— ^in-

Предполагается, что недостающие операнды всегда доопределяются нулями, а на вход Ь_ш ячейки (л, 1) всегда подается — 1.

496

Часть III. Смежные проблемы и применение

Схема систолического массива и порядок подачи данных и выдачи результатов для п = 4 приведены на рис. 8.14. Общее время решения системы порядка п приблизительно равно 5п. Каждая ячейка срабатывает один раз в три такта. При этом средняя загруженность ячеек систолического массива будет около 0,1.

Рис. 8.14. Ввод данных и получение результатов

Глава 8. Вычислительные системы и алгоритмы

497

Рассмотрим теперь ортогональную проекцию координатного графа алгоритма для п = 4 по направлению (0, 0, 1). Она представлена на рис. 8.15. В новых координатах Z, = j, г\ = к ребро 1 и грань 2 перешли в линию (1, 1)— (я, п), грани 3, 5 и внутренность пирамиды перешли на всю область, за исключением этой линии. Каждая ячейка систолического массива теперь будет срабатывать каждый такт после начала функционирования. Схема систолического массива, порядок подачи данных и выдачи результатов приведены на рис. 8.16. Результаты вычислений будут выдаваться из ячейки (п + 1, п) в последовательные такты, начиная с (Зя + 2)-го. Все ячейки массива меняют выполняемые ими функции во время счета, хотя в целом они делают примерно то же, что и в случае первой проекции. Загруженность ячеек систолического массива приблизительно равна 0,25.

Рис. 8.15. Схема другого систолического массива

Эти примеры показывают, что на одиночной задаче загруженность систолических массивов может оказаться не очень высокой. Особенно заметно она уменьшается из-за достаточно длинных этапов загрузки и разгрузки массивов. На загруженность влияет также выбор прямой, вдоль которой осуществляется проектирование графа алгоритма. Чем больше длина пути, связывающего соседние сливаемые вершины, тем реже срабатывает соответствующая систолическая ячейка и, следовательно, тем ниже ее загруженность. Определенную помощь в выборе прямой при проектировании оказывает утверждение 8.12. Максимизируя величину djqj , мы в общем случае минимизируем

время реализации алгоритма. В частности, для проекции графа на рис. 8.12 вдоль вектора (1, 1, 1) эта величина равна У¹/², а вдоль вектора (0, 0, 1) она равна 1. Кроме этого, загруженность уменьшается из-за введения транспортных связей. Загруженность можно повысить, решая одновременно несколько одинаковых задач, отличающихся только входными данными. Возможность такого режима гарантируется тем, что все систолические ячейки срабатывают с одним и тем же периодом. Систолические массивы без суще-

498

Часть III. Смежные проблемы и применение

ственной потери своих качеств могут успешно работать не только в общем синхронном, но и в асинхронном режиме. Управление процессом легко осуществить, например, с помощью тегирования, т. е. переноса от ячейки к ячейке управляющей информации.

^х1

х₂

^хз

^Х4

•I

—>

•I

—>

•I

-►

•I

—►

—>

•I

т т т т т

^а11 ............

^Э21 ^Э12 .........

а₃₁ а₂₂ а₁₃

а₄₁ а₃₂ а₂₃ а₁₄

^Э42 ^Э33 ^Э24 ^1

^а43 ^а34 ^2

^Э44 ^Й3

ь₄

Рис. 8.16. Другое перемещение информации

Вопросы и задания

1. Почему систолические ячейки делают в форме правильных четырех- или шестиугольников, а не, скажем, трех- или пятиугольников?

2. Рассмотрим бесконечный регулярный граф и семейство прямых с направляющим вектором, принадлежащим линейной оболочке базовых векторов. Докажите, что на всех прямых, на которых имеется хотя бы одна вершина, находится бесконеч-

Глава 8. Вычислительные системы и алгоритмы

499

но много вершин, расстояние между соседними вершинами постоянно и не зависит от расположения прямых.

3. Докажите, что любой плоский граф делит плоскость на односвязные области, ограниченные дугами. Если граф конечный, то среди этих областей одна будет неограниченной, остальные — ограниченными.

4. Пусть плоский односвязный граф имеет п вершин, m дуг и делит плоскость на / односвязных областей. Докажите формулу Эйлера, определяемую равенством п — - т + 1=2.

5. Покажите, что трехмерный регулярный граф с базовыми векторами (1, 0, 0), (0, 1, 0), (1, 1, 1), (1, —1, 1) при ортогональном проектировании вдоль вектора (0, 0, 1) дает не плоский граф.

6. Докажите, что для трехмерного координатного графа существует только 13 направлений, ортогональное проектирование вдоль которых дает плоские графы.

7. "Попробуйте получить по возможности конструктивно проверяемое необходимое, достаточное или, лучше всего, необходимое и достаточное условие изоморфное™ ориентированного ациклического графа регулярному графу.

8. "Попробуйте получить то же самое для графов линейных алгоритмов.

9. "Попробуйте разработать конструктивную методологию сведения графов линейных алгоритмов к регулярным.

§ 8.5. Математическая модель алгебраического вычислителя

Проведенные исследования позволяют высказать некоторые соображения о построении моделей вычислительных систем, специализированных для решения классов задач. Мы рассмотрим в качестве примера одну из возможных моделей для решения задач линейной алгебры с плотными матрицами.

Для задач данного класса характерным является исключительно большая их трудоемкость. В общем случае решение практически любой из них требует выполнения порядка я³ арифметических операций, где п есть параметр, определяющий порядок используемых матриц или размерность векторов. В настоящее время нередко возникает необходимость в решении задач линейной алгебры с плотными матрицами порядка 10³—10⁵. По существу единственный путь быстрого их решения связан с применением специализированных систем с большим числом одновременно работающих функциональных устройств.

Чтобы вычислительная система могла работать наиболее эффективно, недостаточно лишь наличия в ней большого числа ФУ. Столь же важно иметь подходящие алгоритмы, которые позволили бы обеспечить необходимый уровень загруженности всех или, по крайней мере, большей части ФУ системы. Для повышения общего быстродействия существенно так же, чтобы

500

Часть III. Смежные проблемы и применение

структура алгоритмов не требовала от вычислительной системы сложной коммуникационной сети.

Одним из самых эффективных типов вычислительных систем с многими ФУ являются систолические массивы. Весьма заманчиво сконструировать один или несколько массивов, с помощью которых можно решать различные задачи линейной алгебры с плотными матрицами. На первый взгляд, эта задача не кажется такой уж нереальной, т. к. опыт создания систолических массивов, реализующих различные алгоритмы решения задач линейной алгебры, говорит о том, что в подобных массивах есть много общего. Более того, иногда один и тот же массив может решать различные задачи всего лишь после незначительного изменения функций систолических ячеек или способа подачи данных. Тем не менее, по-видимому нецелесообразно идти непосредственно по этому пути.

Число ячеек систолического массива, предназначенного для решения конкретной задачи линейной алгебры с матрицей порядка п, обычно имеет порядок п². Хотя в теоретическом плане систолические массивы легко наращиваются, зависимость числа ячеек от п не дает возможности эффективно использовать все функциональные устройства при фиксированном п. К тому же, при больших п общее число систолических ячеек оказывается настолько значительным, что начинают возникать серьезные технические трудности. В частности, требуется очень большое число каналов связи с памятью для обеспечения режима максимального быстродействия. К сожалению, невозможно построить систолические массивы с фиксированными числами ячеек, обеспечивающие решение сколько-нибудь сложной задачи линейной алгебры с матрицами произвольного порядка без многократного обращения к памяти для записи и считывания результатов промежуточных вычислений. Созданию унифицированных систолических массивов мешает и то обстоятельство, что массивы для разных задач все-таки отличаются друг от друга. Суммарный объем этих различий весьма велик и затрагивает не только функции систолических ячеек, но и коммуникационную сеть.

Модель специализированной вычислительной системы для решения задач линейной алгебры с плотными матрицами может быть предложена, если ориентироваться на использование клеточных или блочных методов [5, 13]. Основанием к этому предложению служат следующие факты:

□ разработаны клеточные аналоги для всех основных численных методов линейной алгебры;

□ основная часть вычислений в клеточных методах приходится на выполнение операций сложения и умножения матриц небольшого фиксированного размера;

□ клеточные методы являются экономичными с точки зрения числа и времени обменов с памятью;

Глава 8. Вычислительные системы и алгоритмы

501

П для реализации матричных операций с матрицами небольшого фиксированного размера можно построить систолические массивы.

Детальный анализ различных клеточных методов показывает, что основная часть вычислений приходится в действительности на выполнение матричных операций вида

D = A + Y_JB_lC_h (8.21)

/ = /

где s либо равно 1, либо является достаточно большим числом. При этом в обоих случаях имеется много независимых операций вида (8.21). Во всех методах матрицы А, В/, Q квадратные и имеют такой же порядок, как клетки, на которые разбиваются входные, выходные и промежуточные данные. Остальные матричные операции, необходимые для реализации клеточных методов, так же разнообразны, как разнообразна вся совокупность численных методов линейной алгебры. Однако общий объем приходящихся на них вычислений относительно невелик и все нестандартные операции, как правило, относятся к матрицам размера одной клетки.

Если 5=1, то мы имеем уже рассмотренную задачу вычисления матрицы А + ВС. Наличие потока независимых задач этого типа позволяет загрузить систолический массив почти полностью. Если s является достаточно большим числом, то ситуация новая и мы рассмотрим ее более подробно.

Пусть порядок всех матриц из (8.21) равен ш. Обозначим В= (В\, ..., B_s) и С = (C[,...,C'_S). Матрицы В, С имеют размеры m х ms и очевидно, что

D = А + ВС. Поэтому в данном случае систолический массив должен реали-зовывать матричную операцию А + ВС для прямоугольных матриц В, С и квадратной матрицы А. При этом число столбцов (строк) матрицы В (С) кратно числу ее строк (столбцов). Коэффициент кратности может быть произвольным, в том числе достаточно большим.

Предположим, что матричная функция А + ВС вычисляется стандартным способом, и пусть s фиксировано. В этом случае граф алгоритма аналогичен представленному на рис. 8.8, но увеличенному по оси к в s раз. Вершины графа заполняют прямоугольный параллелепипед, содержащий по m вершин вдоль осей /, j и ms вершин вдоль оси к. После введения транспортных связей граф оказывается координатным. Конечно, мы хотим построить систолический массив, размеры которого не зависит от числа s. Единственная проекция, которая удовлетворяет данному условию, есть проекция вдоль оси к. Граф систолического массива будет выглядеть так же, как на рис. 8.9, а и 8.9, е.

В качестве направляющего вектора, определяющего реализуемую параллельную форму, опять можно взять q = (1, 1, 1). В целом новый систолический

502

Часть III. Смежные проблемы и применение

массив будет работать так же, как рассмотренный ранее для случая квадратных матриц А, В, С, только примерно в s раз дольше.

Универсальный не очень быстрый

процессор ------------?------------

Небольшая быстрая память

-----------?-----------

Массовая память

Систолический массив А+ВС

Рис. 8.17. Схема алгебраического вычислителя

Общая схема вычислительной системы для решения задач линейной алгебры с плотными матрицами блочными методами показана на рис. 8.17. Систолический массив предназначен для быстрого выполнения потока операций вида (8.21) при фиксированном размере блоков. Быстрая память необходима, в основном, для подачи данных на систолический массив и считывания результатов его работы. Универсальный процессор предназначен для выполнения всех остальных операций, кроме операций (8.21). Он необязательно должен обладать большим быстродействием. Вся его работа может осуществляться параллельно с работой систолического массива. Общий объем выполняемой им работы относительно невелик. Нетрудно вывести различные соотношения, связывающие общее время решения задачи со скоростью выполнения операций универсальным процессором, числом ячеек систолического массива, скоростью их срабатывания, размером быстрой памяти и числом каналов связи с массовой памятью.

Мы не будем подробно обсуждать модель данной вычислительной системы, т. к. это обсуждение зависит от многих конкретных деталей. Заметим только, что при подходящем согласовании всех ее узлов на ней можно решать задачи со скоростью, пропорциональной скорости реализации матричной операции А + ВС на систолическом массиве. Если по каким-либо причинам сдерживающим фактором является время выполнения нестандартных операций на универсальном процессоре, то для повышения общего быстродействия в его состав также можно ввести систолические массивы, но уже существенно меньших размеров. Конечно, для быстрого выполнения мат-

Глава 8. Вычислительные системы и алгоритмы

503

ричной операции А + ВС можно использовать и другие систолические массивы, а также принципиально другие устройства, если таковые будут предложены.

Вопросы и задания

1. Промоделируйте на рассмотренном алгебраическом вычислителе процессы решения различных алгебраических задач блочными методами.

2. Постройте модель алгебраического вычислителя для реализации "блочных" аналогов методов, использующих преобразования вращения или отражения.

3. Постройте модель вычислителя для решения нестационарных линейных уравнений математической физики с постоянными коэффициентами явными разностными методами.

4. Какие различия между систолическими массивами, используемыми в вычислителях пп. 1—3?

5. Выведите соотношения, связывающие число ячеек систолического массива, скорость выполнения операций универсальным процессором, скорость выполнения операций систолическими ячейками и скорость обмена информацией с массовой памятью в вычислителях пп. 1—3.

6. *Болыпинство методов, подходящих для реализации на рассматриваемых вычислителях, имеют достаточно регулярную структуру. Нельзя ли использовать этот факт для разработки специальной структуры массовой памяти, в том числе, на уровнях иерархии?

7. *Каковы узкие места в рассматриваемых вычислителях, мешающие достижению максимально возможной скорости решения задач?

§ 8.6. Матрицы и структура алгоритмов

Для достижения различных целей в изучении алгоритмов используются различные формы их описания. Записи в форме программ удобны для осуществления процесса реализации. Общие графовые формы предпочтительны для выбора подходящей архитектуры вычислительной системы. Функциональная форма представления графов позволяет эффективно проводить исследование информационной структуры. Мы уже неоднократно убеждались в том, что все эти формы тесно связаны между собой, выгодно оттеняя отдельные стороны либо самих алгоритмов, либо процесса их изучения. Матричные формы также находят свою сферу применения.

Рассмотрим любой алгоритм, граф которого не меняется при изменении входных данных. Как уже неоднократно отмечалось, большинство вычислительных алгоритмов или их основных фрагментов обладает подобным свойством. Поэтому все реализации такого алгоритма можно описать последовательностями операций, порядок выполнения которых также не меняется

504

Часть III. Смежные проблемы и применение

при изменении входных данных. При подходящем соответствии между операциями и вершинами графа алгоритма все последовательности будут определять исходный граф. Следовательно, не уменьшая существенно общности, можно на каком-то этапе исследований ограничиться рассмотрением лишь одной последовательности операций.

Будем считать, что алгоритм описывается последовательностью операций над числами. Обозначим через иу, ..., u_p его входные данные. Пусть процесс реализации алгоритма заключается в выполнении действий

^uk = ^Fki^uk^ ■■■■> ^uk_sl), Р <k<n; к_{, ...,k_St < к, (8-22)

где все F_k являются достаточно гладкими функциями своих аргументов. В качестве результатов реализации алгоритма не может рассматриваться что-либо иное, кроме какой-то совокупности величин %. Не накладывая серьезных ограничений, можно предполагать, что результат состоит только из величины и„. Это означает, что рассматриваются лишь алгоритмы, которые описывают процессы вычисления значений числовых функций в точках. Значительная широта такого класса алгоритмов очевидна.

Итак, будем предполагать, что рекуррентные соотношения (8.22) задают процесс вычисления значений некоторой функции

v = F(u_h ..., u_p), (8.23)

зависящей от р переменных u\, ..., u_p. В различных теоретических исследованиях и практической деятельности кроме вычисления значений функций F в точках требуются многие другие сведения, касающиеся функции F. характеристики процесса распространения ошибок округления, значения отдельных производных и градиента в точках и т. п. Все эти сведения легко получаются лишь в случаях, когда имеется явное представление функции F через переменные щ, ..., Up, и само представление является достаточно простым. Если процесс вычисления функции (8.23) задан алгоритмом (8.22), то при больших п получить явное представление самой функции через входные данные удается очень редко. В этом случае не остается ничего другого, кроме исследования функции через определяющие ее рекуррентные соотношения.

Соотношения (8.22) можно рассматривать как систему уравнений для определения величин %. Запишем эту систему в следующем виде:

^Fk(^uk_l>--->^uk_Sk)-^uk=⁰' P<k<n; k_{,...,k_s<k. (8.24)

В общем случае она является нелинейной. При исследовании процесса (8.22) или, что то же самое, множества решений системы (8.24) приходится исследовать близкие решения. Они удовлетворяют такой системе:

F_k{u_k + Au_k ,..., и_к + Аи_к ) - {ц_к + Au_k) = О,

, , (⁸-²⁵)

р < к < n; k_l,...,k_s < к,

Глава 8. Вычислительные системы и алгоритмы

505

где все вариации Аи_к малые в каком-то смысле. Вычитая из уравнений (8.25) уравнения (8.24), получаем с точностью до малых второго порядка линейную систему для вариаций Аи_к:

&dF_k(u_k,...,u_k )

> -------------------'-*— Au/, - Au_t = О,

1 "^uki

p < к < n; ky,..., k_s < k.

(8.26)

Матрица *F линейной системы (8.26) есть функциональная матрица Якоби функций F_k(u_k,...,u_k ) — u_k по переменным и\, ..., u_n. Так как число

1 ^sk

функциональных соотношений в (8.24), (8.25) равно п — р, а число переменных равно п, то матрица системы (8.26) имеет размеры (п — р) х п. Она, как правило, сильно разреженная в силу того, что каждая из функций F_kзависит обычно лишь от небольшого числа переменных. Матрица *Р имеет полный ранг. Это видно хотя бы из того, что она является левой треугольной относительно диагонали, проходящей через правый нижний угол матрицы. При этом на диагонали стоят элементы, равные — 1. Будем называть матрицу ¥ вариационной матрицей алгоритма (8.22). Естественно, что ее элементы в общем случае зависят от переменных и\, ..., и_п- \. В целом они таковы:

■1.

если j = i + р; , если j есть одно из чисел (/ + р)у,...,(/ + p)_s

(8.27)

i + р

¥»

dUj

О — в остальных случаях.

Как мы увидим в дальнейшем, именно вариационная матрица будет возникать в различных задачах, связанных с изучением алгоритма (8.22).

Вариационная матрица алгоритма тесно связана с графом алгоритма. Сопоставим к-к вершине графа получение величины и_к. Ясно, что первые р вершин будут символизировать ввод начальных данных щ, ..., и_р, а остальные вершины — вычисление величин и_к как значений функций F_k из (8.22). Будем считать, что дуга идет из /-Й вершины ву'-ю в том и только в том случае, когда при вычислении величины uj величина щ используется в качестве аргумента. В соответствии с записью (8.22) дуги не будут входить в к-ю вершину, если к < р. Если же к > р, то в к-ю вершину будут входить дуги из вершин с номерами к\, ..., k_s.

Теперь опишем полученный граф некоторой матрицей Ф размеров (п с элементами фу.

■ р) х п

506

Часть III. Смежные проблемы и применение

Положим

— 1, если j = i + р; <?ц=\ 1, если j есть одно из чисел (/+ р)_{,...,(/ + p)_s ', (о.la)

О — в остальных случаях.

Легко видеть, что к-& столбец матрицы Ф соответствует величине %, а к-я строка — величине и_к ₊ _р. В к-к строке элемент —1 стоит в том столбце, номер которого соответствует номеру вычисляемой величины и^ + _р. Элементы + 1 стоят в тех столбцах, номера которых соответствуют номерам аргументов вычисляемой величины и^ + _р. Матрица Ф описывает информационную связь величин и_к между собой. По этой причине будем называть ее матрицей информационной связности алгоритма (8.22). Очевидна связь матрицы информационной связности с вариационной матрицей. Первая получается из второй путем замены всех элементов, равных частным производным функции F_k, единицами. Поэтому структуры ненулевых элементов обеих матриц полностью совпадают.

Из матрицы информационной связности алгоритма можно получить целое семейство матриц, относящихся по существу к тому же графу алгоритма. Для этого заменим все ее ненулевые элементы какими-нибудь числами. Любую такую матрицу будем называть взвешенной матрицей информационной связности алгоритма. Вариационная матрица алгоритма есть одна из подобных матриц. Здесь мы будем иметь дело лишь с этой матрицей. Все подобные матрицы позволяют однозначно восстановить граф алгоритма. Поэтому структура расположения их нетривиальных элементов отражает в действительности структуру алгоритма.

Мы уже неоднократно встречались с таким фактом, что с помощью подходящей перенумерации вершин графа алгоритма можно упростить описание самого графа. Следовательно, можно попытаться за счет перенумерации операций в алгоритме (8.22) привести матрицу информационной связности алгоритма и, соответственно, его вариационную матрицу к какому-нибудь более удобному виду. Рассмотрим любую параллельную форму алгоритма (8.22). Перенумеруем все его операции по ярусам: сначала операции первого яруса, затем второго и т. п. В этой нумерации любая взвешенная матрица информационной связности будет блочной левой почти треугольной. Все блоки над главной диагональю суть единичные матрицы со знаком минус. Их порядки равны ширине соответствующих ярусов параллельной формы. Первый блочный столбец и только он относится к операциям, символизирующим ввод начальных данных.

Матрицы традиционно используются для описания графов. Пусть задан ориентированный граф G= (V, Е) без петель и кратных дуг. Предположим,

Глава 8. Вычислительные системы и алгоритмы

507

что он имеет п вершин и m дуг. Квадратная матрица В порядка п с элементами by называется матрицей смежностей графа, если

[1, если из /-и вершины в у-ю идет дуга;

Ь„= ,

[О — в остальных случаях.

Отметим, что в матрице смежностей главная диагональ нулевая. Нулевыми являются также строки, соответствующие выходным вершинам, и столбцы, соответствующие входным вершинам. Матрица смежностей графа алгоритма тесно связана с его матрицей информационной связности. Именно, в нумерации вершин, согласованной с записью (8.22), матрица информационной связности Ф есть подматрица, состоящая из последних п — р строк матрицы В'— Е. Здесь В— матрица смежностей графа алгоритма, Е— единичная матрица, знак "штрих" означает транспонирование.

Прямоугольная матрица D размеров п х т с элементами dy называется матрицей инциденций графа, если

4»

1, если у-я дуга выходит из /-и вершин; — 1, если /-я дуга заходит в i-ю вершин; О — в остальных случаях.

В каждом столбце матрицы инциденций графа лишь два элемента отличны от нуля. Отсутствие петель говорит о том, что они равны —1 и 1. Так как граф по предположению не имеет кратных дуг, то матрица инциденций не имеет одинаковых столбцов.

Некоторые факты очень легко формулируются в матричных терминах. Например, почти очевидно следующее

Утверждение 8.15

Для того чтобы ориентированный граф без петель и кратных дуг не имел контуры, необходимо и достаточно, чтобы с помощью перенумерации вершин графа матрицу смежностей можно было сделать правой треугольной.

Предположим теперь, что алгоритм с матрицей D его графа реализуется на некоторой вычислительной системе. Будем считать, что относительно условий реализаций выполняются требования, высказанные в §§ 2.3, 8.2. Снова рассмотрим вектор t= (Ц, ..., t„) развертки. Рассмотрим также вектор задержек w. Поскольку времена выполнения операций всегда можно включить во времена задержек, то без ограничения общности допустим, что вектор реализации нулевой.

Имеет место

Утверждение 8.16

Пусть задан вектор задержек w, вектор реализации является нулевым и D есть матрица инциденций графа алгоритма. Для того чтобы вектор t был вектором

508

Часть III. Смежные проблемы и применение

развертки, соответствующей вектору задержек w, необходимо и достаточно выполнение неравенства

-D' t > w.

Пусть задан вектор задержек w. Выберем какую-нибудь последовательность вершин графа, образующую цикл. В такой последовательности связаны дугой любые две соседние вершины, а также первая и последняя вершины. Установим в цикле направление обхода вершин. Будем считать, что дуга проходится в положительном направлении, если сначала встречается ее начальная вершина, а затем конечная. В противном случае будем считать, что дуга проходится в отрицательном направлении. Пусть при обходе цикла ij-я дуга проходится Гу раз в положительном направлении и by раз в отрицательном. Сумму величин (гу — by)wy по всем /, j, соответствующим дугам цикла, будем называть ориентированной задержкой цикла. Цикл, у которого ориентированная задержка равна нулю, будем называть уравновешенным.

Утверждение 8.17

Все циклы графа алгоритма уравновешены или граф не имеет циклы тогда и только тогда, когда совместна система линейных алгебраических уравнений

-D' t > w. (8.29)

Предположим, что система (8.29) совместна и вектор t задает ее решение. Выберем в графе алгоритма любой цикл, если он имеется, и установим направление обхода вершин. Каждому проходу у-й дуги в положительном направлении поставим в соответствие равенство tj — Ц = wy, каждому проходу той же дуги в отрицательном направлении поставим в соответствие равенство Ц — tj= —wy. Просуммируем все равенства согласно обходу дуг цикла. В правой части суммы будет стоять ориентированная задержка цикла. Левая же часть суммы будет равна нулю. Действительно, при каждом проходе соседних дуг цикла инцидентная им вершина учитывается дважды. Соответствующая этой вершине величина tj всегда будет встречаться в двух соседних или последнем и первом уравнениях также дважды: сначала со знаком "плюс", а затем со знаком "минус". Следовательно, при суммировании каждая из величин t'j сократится.

Допустим теперь, что граф алгоритма либо не имеет циклы, либо все его циклы уравновешены. Не ограничивая общности, можно считать граф алгоритма односвязным. Возьмем, например, первую вершину и припишем t\ какое-нибудь значение. Предположим, что построен односвязный подграф, и его вершинам приписаны такие значения t_h что уравнения (8.29) выполняются для всех дуг подграфа. Добавим новую дугу, у которой хотя бы одна вершина принадлежит построенному подграфу. Если вторая вершина не принадлежит подграфу, то соответствующее ей значение ц однозначно определяется из того уравнения (8.29), которое можно написать для добавленной дуги.

Глава 8. Вычислительные системы и алгоритмы

509

Пусть вторая вершина тоже принадлежит подграфу. В силу сделанного предположения об односвязности подграфа это означает, что добавленная дуга образует с некоторыми дугами подграфа какие-то циклы. Выберем любой из таких циклов и установим в нем направление обхода, при котором добавленная дуга проходится в положительном направлении. Пусть начальная вершина добавленной дуги имеет номер г, конечная — номер /. Соответствующие значения t_r и t/ определены раньше. Обойдем все дуги цикла, начиная с 1-й вершины и кончая r-й вершиной. Снова поставим в соответствие каждому проходу ij-й дуги в положительном направлении равенство tj — tj = Wy, в отрицательном направлении — равенство Ц — tj = —Wy. Просуммируем эти равенства. Согласно сделанному выше замечанию, сумма левых частей даст выражение t_r — Ц. Сумма правых частей, принимая во внимание уравновешенность цикла, даст — w_rt. Следовательно, уравнение (8.29) для г/-й дуги уже выполняется.

Продолжая процесс присоединения новых дуг, припишем в конце концов всем вершинам графа алгоритма такие значения ц, что будут выполняться все уравнения (8.29). Тем самым получено какое-то решение системы (8.29), т. е. установлена совместность этой системы.

Следствие

Если граф алгоритма односвязный и система (8.29) совместна, то множество ее решений представляет прямую линию с направляющим вектором

(1, 1, ...,!)■

Данное следствие вытекает из того, что решение системы (8.29) в случае односвязности графа однозначно определяется при фиксации значения любой из его координат ц и остается решением при добавлении вектора (1, 1, ..., 1). Довольно часто граф алгоритма является уравновешенным с вектором задержек w = е, где все координаты вектора е равны 1.

Утверждение 8.18

Ациклический ориентированный граф без петель и кратных дуг с матрицей смежностей В не имеет не уравновешенные по вектору е циклы тогда и только тогда, когда существует матрица перестановок Р такая, что матрица Р'ВР является блочной правой двухдиагональной с нулевыми квадратными диагональными блоками.

Будем считать граф графом некоторого алгоритма. Рассмотрим решение системы (8.29). Вектор t можно трактовать как вектор развертки при h = 0. Сопоставим ему параллельную форму графа, объединяя в ярус те вершины, у которых совпадают времена выполнения соответствующих операций. Каждая дуга связывает вершины, расположенные только на соседних ярусах, т. к. соответствующие им времена различаются на 1. Выбор матрицы Р определяется только нумерацией вершин. Если вершины графа занумеровать

510 Часть III. Смежные проблемы и применение

по ярусам, то матрица смежностей будет иметь указанный в утверждении вид. Но уж если матрица смежностей имеет такой вид, то у графа не могут существовать не уравновешенные по вектору е циклы.

Утверждения, касающиеся матрицы смежностей и матрицы инциденций, могут быть полезными при изучении матрицы информационной связности алгоритма и его вариационной матрицы. Они показывают, как нужно нумеровать операции алгоритма (8.22), чтобы исследование его структуры осуществлялось более просто.

Вопросы и задания

1. Может ли вариационная матрица алгоритма быть нулевой?

2. Предположим, что все элементы вариационной матрицы алгоритма нулевые, кроме равных —1 элементов на диагонали. Что представляет собой алгоритм?

3. Могут ли быть нулевыми вне диагональные элементы какой-либо одной строки вариационной матрицы алгоритма?

4. Что представляет собой алгоритм, если его вариационная матрица не зависит от входных данных?

5. Пусть алгоритм представляет последовательность операций сложения/вычитания двух чисел, умножения двух чисел и вычисления обратной величины числа. Докажите, что дополнительные операции, которые нужно выполнить при одновременной реализации алгоритма и нахождении его вариационной матрицы по сравнению с только реализацией алгоритма, составляют такое количество умножений, сколько имеется в алгоритме операций вычисления обратной величины.

6. Пусть для граф-машины все координаты вектора задержек равны 1, вектор реализаций — нулевой, т. е. w = е, h = 0. Докажите, что для того, чтобы в режиме многократного срабатывания каждое ФУ могло быть асимптотически загружено полностью, необходимо и достаточно, чтобы граф был уравновешенным по данным векторам задержек.

7. Предположим, что в граф-машине имеется цикл, при обходе которого число дуг, проходимых в положительном направлении, не совпадает с числом дуг, проходимых в отрицательном направлении. Может ли в такой граф-машине быть достигнута асимптотически полная загруженность всех ФУ в режиме многократного срабатывания?

8. Докажите, что координатный граф является уравновешенным по векторам

w = е, h = 0.

9. Приведите пример регулярного графа, не уравновешенного по векторам

w = е, h = 0.

10. Что означают пп. 8, 9 в свете того, что любой регулярный граф можно свести к координатному?

Глава 8. Вычислительные системы и алгоритмы

511

§ 8.7. Новое применение сведений о структуре

Использование матриц в предыдущем параграфе связано с фактами, относящимися к структуре алгоритмов. Раньше мы уже получили достаточно много подобных фактов с помощью других средств. Матричный аппарат не очень удобен для изучения собственно структуры алгоритмов, главным образом, из-за необходимости представлять любую информацию в "плоском" виде. Однако он оказался исключительно полезным инструментом для установления связи структурных свойств алгоритмов с различными их математическими свойствами. Покажем эту связь на нескольких примерах.

Восстановление линейного функционала

Рассмотрим более подробно частный случай алгоритма (8.22), где все функции Fk линейные. Это значит, что процесс реализации алгоритма заключается в выполнении действий

^uk =Х^а**^и**> Р<^к^^п'> к_ь...,к_!к<к. (8.30)

; = 1

Будем считать, что все числа <х_к известны к моменту начала осуществления

процесса (8.30). Очевидно, что данный процесс определяет некоторый способ вычисления значений какой-то числовой функции (8.23), которая должна быть линейной относительно совокупности переменных иу, ..., u_p. Следовательно, она имеет вид:

р v = F(u_x,...,u_p) = Y$jUj. (8-31)

Конечно, непосредственное вычисление значений функции F по формуле (8.31) значительно эффективнее, чем реализация процесса (8.30). Однако коэффициенты Ру могут быть неизвестны. Именно поэтому может возникнуть необходимость осуществлять вычисление значений функции /"из (8.31) косвенным образом через процесс (8.30). Естественно, возникает вопрос о том, как это сделать наиболее эффективно.

Однократная реализация процесса (8.30) требует выполнения операций умножения и сложения/вычитания чисел, общее число которых равно

N = 2 ^._ч-(п-р). (8.32)

к = р + 1

Однократное вычисление значений функции из (8.31) непосредственно через коэффициенты ру требует выполнения операции умножения и сложения/вычитания чисел, общее число которых равно

М=2р-1. (8.33)

512

Часть III. Смежные проблемы и применение

Ясно, что при больших п имеем N » М. Если процесс (8.30) приходится осуществлять многократно при одних и тех же коэффициентах а_к и разных

входных данных и\, ..., u_p, то с точки зрения уменьшения общего объема вычислительной работы может оказаться выгоднее сначала вычислить коэффициенты Ру, а затем уже многократно вычислять значение функции (8.31) непосредственно через коэффициенты Ру. И снова возникает вопрос о том, как наиболее эффективно вычислить коэффициенты Ру.

Казалось бы ответ очевиден. Действительно, обратимся к процессу (8.30). Величина u_p + \ уже представлена в виде линейной комбинации величин щ, ..., Up. Предположим, что мы имеем аналогичные представления для всех величин Up + 1, ..., u_k- \. Подставляя в (8.30) вместо всех и_к их представления в виде линейных комбинаций величин и\, ..., и_р и приводя подобные члены, получим необходимое представление (8.31) как линейное представление величины u_n. Если величины s^ ограничены, то для больших п отыскание явного представления (8.31) потребует выполнения порядка

К = 2р 5%, (8.34)

k = p + l

операций умножения и сложения/вычитания чисел. Это примерно в р раз больше, чем требуется для однократной реализации процесса (8.30). Сравнивая (8.32)—(8.34), можно сделать вывод, что если при одних и тех же коэффициентах а_к процесс (8.30) необходимо осуществлять более р раз, то

выгоднее сначала получить коэффициенты Ру, а затем вычислять значения линейной функции (8.31) непосредственно.

Однако оказывается, что этот очевидный вывод далеко не лучший. В действительности коэффициенты р_у- можно вычислить с существенно меньшими затратами по числу операций.

Рекуррентные соотношения (8.30) можно рассматривать как систему линейных алгебраических уравнений

2^cc_ku_k —u_k=Q, p<k<n; k\,...,k_s <к (8.35)

относительно переменных и_р ₊ \, ..., u_n. Более того, в действительности необходимо найти лишь одно переменное u_n. При этом переменные щ, ..., и_рможно считать свободными. Отметим, что матрица системы (8.35) есть вариационная матрица *¥ алгоритма (8.30). В данном случае она имеет такой вид:

— 1, если j = i + р; \|/_;/ = -j oij, если j есть одно из чисел (/ + р\,...,(/ + р\. ', (о.Jo)

0 — в остальных случая.

Глава 8. Вычислительные системы и алгоритмы

513

Теперь запишем систему (8.35) следующим образом:

Рх + Qy = 0. (8.37)

Здесь Р — прямоугольная матрица размеров (п — р) х р, составленная из первых р столбцов матрицы *F; Q — квадратная матрица порядка п — р, составленная из последних п — р столбцов матрицы *Р; х — вектор-столбец размерностир из элементов щ, ..., и_р; у — вектор-столбец размерности п — р из элементов u_p + _h ..., u_n. Из (8.37) находим, что

y=-Q~^xPx. (8.38)

Согласно (8.36), матрица Q левая треугольная с диагональными элементами, равными —1. Поэтому она невырожденная, и представление (8.38) возможно. По условию задачи необходимо найти лишь последний элемент вектора-столбца у. Коэффициенты Ру из (8.31) составляют последнюю строку матрицы — Q~^lP. Следовательно, сложность вычисления коэффициентов Ру есть сложность вычисления последней строки матрицы — Q~^]P.

Матрица Q левая треугольная. Известно, что для матрицы, обратной к левой треугольной, существует специальное мультипликативное представление [5]. Получить его можно, например, на основе применения к матрице Q метода исключения Гаусса с целью приведения самой матрицы к единичной. С учетом конкретного вида матрицы Q представление матрицы — Q ^_1 будет таким:

-Q-i = R„-_p-₁R_n-_p-₂...R_i. (8.39)

Здесь матрица R_t отличается от единичной матрицы только i-ш столбцом. Его наддиагональные элементы равны нулю, диагональный элемент равен + 1, поддиагональные элементы равны соответствующим поддиагональ-ным элементам /-го столбца матрицы Q.

Будем получать последнюю строку матрицы — Q~^], используя представление (8.39). Последняя строка матрицы R_n-_p-\ известна. Пусть известна последняя строка произведения R_n-_р- ₁ ... R_t. Тогда последняя строка произведения R_n -_р - i ... RjRj- х будет равна произведению последней строки матрицы R„ -_р- i ... Rj на матрицу Ri- \. Принимая во внимание специальный вид матрицы Rj- j, в последней строке нужно пересчитать только (/— 1)-й элемент. Если в матрице Rj- i имеется 5_г- i ненулевых поддиаго-нальных элементов, то для этого пересчета нужно выполнить 25_г -1 ^— 1 операций умножения и сложения/вычитания чисел. При подсчете числа операций учтен тот факт, что при любом / в последней строке матрицы R_n _ _р _ j ... Rj первые / — 1 элементов обязательно будут равны нулю. Используя данный алгоритм, можно определить последнюю строку матрицы — Q~^] за число операций умножения и сложения/вычитания, равное

п — р — 2

L' = 2 £б,-(и-/7-2) (8.40)

r = i

514

Часть III. Смежные проблемы и применение

Предположим, что в 1-м столбце матрицы Р находится а/ ненулевых элементов. Не ограничивая общности, можно считать, что а/ > 0 для всех /, т. к. в противном случае результат реализации алгоритма (8.30) не будет зависеть от какого-то входного данного. Ясно, что для получения последней строки матрицы — Q ~^]Р необходимо выполнить дополнительно

р L" = 2^a,-p (8.41)

операций умножения и сложения-вычитания чисел.

Суммируя затраты (8.40), (8.41), заключаем, что вычисление последней строки матрицы — Q ~^]Р или, что то же самое, вычисление коэффициентов ру из представления (8.31) можно осуществить за

п - р - 2 р

X ⁵<- + Х°1

L = L' + L'

(п-2)

операций умножения и сложения/вычитания. Но

и - р - 2 р п

ъ_п__р__х+ х ⁵/+ Х^о/= X^s*'

/ = 1 1 = 1 к = р + 1

так как выражения в левой и правой частях равенства означают число всех коэффициентов а_к, участвующих в процессе (8.30) или, что то же самое, число всех нетривиальных элементов вариационной матрицы алгоритма. Так как 5„ - р - j равно либо 0, либо 1, то в действительности с учетом (8.32) имеем:

N-p<L<N-p + 2. (8.42)

Таким образом, вычисление коэффициентов Ру по описанному алгоритму практически требует таких же вычислительных затрат, как и однократная реализация процесса (8.30). Этот алгоритм примерно в р раз более экономичен, чем очевидный алгоритм, соответствующий оценке (8.34). Поэтому, если при одних и тех же коэффициентах а_к процесс (8.30) необходимо реализовать более одного раза, то вместо многократной реализации данного процесса значительно выгоднее вычислить коэффициенты ру по описанному алгоритму и затем многократно вычислять значение линейной функции, используя представление (8.31). Если число р и число требуемых реализаций процесса (8.30) невелики по сравнению с п, то суммарные вычислительные затраты по числу операций будут незначительно отличаться от затрат однократной реализации процесса (8.30).

Проведенным исследованиям можно дать следующую формулировку. Функция (8.31) есть линейный функционал. Пусть он неизвестен. Допустим однако, что имеется возможность вычислять значения функционала с помо-

Глава 8. Вычислительные системы и алгоритмы 515

щью некоторого линейного процесса. Этот процесс имеет вид (8.30). Спрашивается, можно ли восстановить линейный функционал, и, если можно, то ценой каких вычислительных затрат? Традиционный способ восстановления линейного функционала имеет сложность /7-кратного вычисления значения функционала. Рассмотренный здесь способ говорит о том, что справедливо

Утверждение 8.19

Пусть значения линейного функционала вычисляются с помощью некоторого скалярного линейного алгоритма. Тогда линейный функционал может быть восстановлен со сложностью, не превосходящей сложность однократного вычисления значения функционала по заданному алгоритму.

Подчеркнем, что при построении эффективного способа восстановления линейного функционала в значительной мере была учтена структура графа алгоритма, реализующего вычисления значений самого функционала, или, что то же самое, структура вариационной матрицы.

Вычисление градиента

Снова рассмотрим алгоритм (8.22) в общем виде. Одной из важнейших задач, связанных с исследованием функции F из (8.23), является вычисление ее градиента. Традиционный подход к решению этой задачи состоит в следующем. Все величины и_к являются неявными функциями входных данных. Продифференцировав рекуррентные соотношения (8.22) как неявные функции, получим:

Ё д F_k(u_ki,...,u_k ) ---------^---------— grad_Myt;

, = i ^дик< (8.43)

р <к <п; к_ь ..., k_s <к;

gradu_k =е_к, к = 1,2, ...,р.

Здесь е^ есть к-к единичный координатный вектор. Если процессы (8.22), (8.43) проводить параллельно, то вместе с вычислением функций Fk можно одновременно вычислять и все их частные производные. Вся информация для этого имеется.

Градиенты величин и_к являются векторами размерности р. Не обсуждая сейчас сложность реализации процесса (8.43) подробно, заметим лишь, что общее число операций над числами, которое необходимо выполнить для вычисления градиента величины и_п непосредственно по формулам (8.43), будет пропорционально р.

На первый взгляд в этом выводе нет ничего неожиданного. Вычисляемый объект есть вектор размерности р. Поэтому вполне естественно, что он определяется через рекуррентный процесс над векторами размерности р. Отсюда вроде бы очевидно, что общие затраты на вычисление градиента вели-

516

Часть III. Смежные проблемы и применение

чины u_n также должны быть пропорциональны р. В действительности делать этот вывод преждевременно.

Сложность вычисления величин и^ и частных производных функций F^ при больших п практически не зависит от р. Зависимость от р появилась лишь потому, что процесс (8.43) описан и рассмотрен как процесс над векторами размерности р. Однако процесс вычисления градиента величины и„ можно осуществлять иначе.

Будем считать, что процесс (8.22) проведен. Это означает, что вычислены все величины и_к, и, следовательно, можно вычислить все частные производные всех функций F_k, которые не зависят от градиентов величин и_к. Обозначим

dF_k(u_k,...,u_k )

a_k =------------------^к—, v_k=gradu_k (8.44)

о "*,

для всех возможных к, и к. Теперь процесс (8.43) будет выглядеть следующим образом:

ч v_k =X⁰4^TV Р<^кйп; к_{,...,к_ч<к, (8.45)

r = i

где vi, ..., v_p заданы. В нашем случае vi, ..., v_p равны соответственно

в\, ..., вр.

С учетом обозначений (8.44) процесс (8.45) по существу совпадает с процессом (8.30). Если считать v\, ..., v_p свободными переменными, то при заданных ocj. переменная v_n есть линейная комбинация переменных vi, ..., v„, т. е.

'_Л=£РЛ- (8.46)

./=1

Коэффициенты р_у- неизвестны и их необходимо определить. Так как правую часть равенства нужно вычислить при единичных координатных векторах Vj, то коэффициенты Ру будут координатами искомого градиента величины и_п.

Таким образом, задача вычисления градиента функции по существу совпадает с рассмотренной ранее задачей восстановления линейного функционала. Поэтому сложность вычисления градиента функции должна быть сравнимой со сложностью реализации скалярного процесса типа (8.45).

Снова будем рассматривать рекуррентные соотношения (8.45) как систему линейных алгебраических уравнений

^oc^v*. -v_k =0, p<k<n; к_и...,к_ч, (8.47)

Глава 8. Вычислительные системы и алгоритмы

517

но теперь относительно векторных переменных v_p + \, ..., v„ размерности р. И снова нужно найти лишь одно переменное v„. Векторные переменные V], ..., v_p будем считать свободными. Матрица системы (8.47) есть кронеке-рово произведение *¥ х Е_р. Здесь *Р есть вариационная матрица алгоритма (8.22). С учетом обозначений (8.44) она имеет вид (8.36). Е_р — единичная матрица порядка р. Запишем систему (8.47) следующим образом:

(PxE_p)X+(QxE_p)Y=0, (8.48)

где Р и Q с точностью до обозначений (8.44) являются теми же матрицами, что и в равенстве (8.37); X— вектор-столбец размерности р², составленный из элементов векторов v\, ..., v_p; Y — вектор-столбец размерности (п — р)р, составленный из элементов векторов v_p+ \, ..., v„. Принимая во внимание свойства кронекерова произведения матриц, находим из (8.48), что

Y=((-Q-^] Р)хЕ_р)Х (8.49)

В векторе /необходимо найти лишь последние р его координат. Как следует из формулы (8.49), для этого достаточно знать последнюю строку матрицы — Q ~^]Р. Ее элементы и являются коэффициентами Ру из (8.48) или, что то же самое, координатами искомого градиента величины и_п. Задача вычисления последней строки матрицы — Q~^] Р была подробно рассмотрена выше. Там же было показано, что эту задачу можно решить за число операций, по существу не зависящее от р.

Рассмотрим более подробно случай, когда функции Е^ реализуют одну из следующих операций: сложение/вычитание двух чисел, умножение двух чисел и вычисление обратной величины. Будем считать для простоты все эти операции эквивалентными по сложности реализации. Вычисление величины и„ требует выполнения п — р таких операций. Вычисление градиента этой величины согласно описанному алгоритму требует дополнительных затрат на вычисление нетривиальных элементов вариационной матрицы алгоритма и вычисление последней строки матрицы — Q ~¹ Р.

Пусть Ек = щ + щ. В соответствии с обозначениями (8.44), (8.45) имеем

«*, =Ь %₂ =±1, s_k=2. Никаких затрат на вычисление коэффициентов <х_к не требуется. Пусть

Е_к = и_К х u_h . Тогда

^ak_t = ^ик₂ 5 ^ак₂ = ^ик_х 7 ^sk = 2-

Если процесс (8.22) реализован, то величины u_k , и_к известны, и никаких дополнительных затрат на вычисление коэффициентов а_к не требуется.

Пусть теперь Е_к = и~^[.

518

Часть III. Смежные проблемы и применение

Имеем

f' т .

си- , s_k - [.

Если процесс (8.22) реализован, то для вычисления коэффициента <х_к. в данном случае нужно выполнить только одну операцию умножения.

Итак, для всех рассмотренных операций при каждом к сумма числа коэффициентов <х_к. и числа дополнительных операций, требуемых на вычисление

этих коэффициентов, равна 2. Если функции F_k реализуют операции сложения/вычитания с константой или умножения на константу, то можно поступать по-разному: либо считать константы входными данными, либо рассмотреть отдельно эти частные случаи. Однако во всех случаях, в том числе и в этих частных, сумма числа коэффициентов <х_к и числа дополнительных

операций, требуемых на вычисление коэффициентов, при каждом к не превосходит 2.

Из соотношений (8.32), (8.42) вытекает, что для вычисления последней строки матрицы — Q ^_1 Р требуется выполнить L операций, где

L<2 5>,-(„-2).

к = р + 1

Кроме этого, согласно сделанному выше замечанию для вычисления элементов вариационной матрицы алгоритма требуется дополнительно выполнить Sопераций,где

п к = р + 1

Следовательно, для вычисления градиента величины u_n требуется выполнить дополнительно не более, чем

п п п

L + S<2- £ _Sk-(n-2)+ Y, (2-s_k)= ^_к+п-2р + 2

k=p+\ k=p+\ k=p+\

операций. И, наконец, если учесть, что для рассматриваемого множества операций s_k < 2 для всех к, то будем иметь

L + S<3(n~ р) - р + 2.

Заметим, что для вычисления градиента во всех случаях предварительно нужно реализовать процесс (8.22), т. е. выполнить п — р операций.

Глава 8. Вычислительные системы и алгоритмы

519

Поэтому проведенные исследования говорят о том, что справедливо

Утверждение 8.20

Пусть значение функции в ^-мерной точке вычисляется как последовательность операций сложения/вычитания двух чисел, умножения двух чисел и взятия обратной величины числа. Тогда независимо от величины р одновременное вычисление значения функции и ее градиента в одной и той же точке может быть осуществлено с затратами по числу операций, не превосходящими четырехкратного вычисления значений функции.

Основной примечательностью полученного результата является независимость затрат на вычисление градиента от его размерности. К сожалению, рассмотренный алгоритм требует памяти довольно большого объема. В целом она пропорциональна числу операций, затрачиваемых на вычисление функции. Хотя требуемая память велика, используется она в очень простом режиме. С точностью до не очень существенных деталей в нее один раз в каком-то порядке записывается некоторый массив данных и он же списывается один раз в противоположном порядке. Поэтому при решении не очень сложных задач большой размерности описанный алгоритм вычисления градиента может оказаться весьма эффективным.

Утверждение 8.20 доказано в условиях, когда в качестве базовых взяты операции сложения/вычитания, умножения и взятия обратной величины. Можно было бы вместо операции обратной величины взять операцию деления. В этом случае общая схема ускоренного вычисления градиента остается без изменения. Нужна лишь определенная аккуратность при вычислении последней строки матрицы — Q~^] Р. При этом будет иметь место утверждение, аналогичное утверждению 8.20. Лишь слова "взятие обратной величины числа" и "четырехкратного" заменяются словами "деления двух чисел" и "пятикратного". Это совпадает с известным результатом [44]. Заметим, что операция деления отсутствует почти на всех вычислительных машинах.

Если р = 1, то вычисление градиента превращается в вычисление производной. Теперь нет необходимости использовать описанный выше алгоритм, а можно сразу применять рекуррентные соотношения (8.43). Заметим, что для вычисления правой части в (8.43) нужны производные от тех же самых величин u_k , которые используются для вычисления частных производных

функций F_k. Следовательно, при вычислении производной по формулам (8.43) необходимо иметь память для хранения величин и_к точно такого

же объема, как и для хранения %. При этом не учитывается память, требуемая для вычисления самих правых частей в (8.43). Режимы записи величин % и и'_к в память и их считывание из памяти с точностью до незначительных

деталей совпадают по времени. Если алгоритм состоит из последовательности операций сложения/вычитания, умножения и взятия обратной величины, то дополнительные затраты по числу операций на вычисление произ-

520

Часть III. Смежные проблемы и применение

водной согласно формулам (8.43) не будут превосходить трехкратного вычисления значений функции. Мало что изменяется, если нужно вычислить не первую производную, а производную более высокого порядка. Пропорционально увеличенному на единицу порядку вычисляемой производной растет объем требуемой памяти.

Анализ ошибок округления

Одним из наиболее трудных вопросов, связанных с изучением и конструированием численных методов, является оценивание влияния на вычислительный процесс ошибок округления. Несмотря на значительные успехи в этой области, исследование ошибок округления в каждом конкретном алгоритме остается до сих пор тяжелой и скучной работой, требующей к тому же большой изобретательности и виртуозности в проведении самого исследования.

Причина подобного положения кроется в отсутствии общей теории оценивания влияния ошибок округления. В настоящее время нет даже отдельных теоретических положений, объясняющих, например, в чем заключается похожесть процессов оценивания ошибок для разных алгоритмов, где находятся узкие места этих процессов, когда возможно или невозможно их осуществление и т. п. Идеи прямого и обратного анализа не конструктивны и не дают никакого указания на то, как лучше проводить процессы оценивания. Не очень даже ясно, какая математическая задача решается в процессе оценивания ошибок, и как эта задача связана с той задачей, решение которой обеспечивает вычислительный процесс. Если с этих позиций взглянуть на все достижения в изучении ошибок округления, то нетрудно видеть, что отдельные результаты объединены не столько общностью способов получения тех или иных фактов, сколько общностью формы их представления [5, 38].

Предположим, что оператор F, в общем случае нелинейный, действует из пространства размерности р в пространство размерности г. Пусть для некоторого элемента и вычисляется его образ v = F(u). В реальных условиях элемент v редко будет получен. Основной причиной этого факта являются ошибки округления. Вместо элемента v мы будем, как правило, иметь некоторый другой элемент v. Именно его естественно считать приближенным образом элемента и.

Конечно, возникает вопрос: "Как оценить, насколько хорошо элемент v приближает элемент v?" Ответ кажется очевидным. Нужно оценить какую-нибудь норму ошибки v — v и на основе ее величины сделать тот или иной вывод. Точный элемент v неизвестен. Поэтому не остается ничего другого, кроме как оценивать ошибку v — v рекуррентно, следуя вычислительному процессу. Проводя рекуррентное оценивание шаг за шагом, в конце концов, можно получить оценку нормы ошибки v — v. Это и есть основная идея прямого анализа ошибок. Ничего более глубокого в этой идее нет.

Глава 8. Вычислительные системы и алгоритмы

521

Интуитивно ясно, что прямой анализ можно осуществить всегда. Другое дело, какая получится при этом оценка нормы ошибки v — v. Если она достаточно мала, то прямой анализ ошибок можно считать удачным. Если же она окажется большой, то это еще не означает, что прямой анализ ошибок проведен плохо. Большая оценка может появиться просто из-за того, что оператор /'является неустойчивым в окрестности элемента и. В этом случае никакое изменение вычислительного процесса не улучшит ситуацию. Более того, становится ясно, что нужно обратить внимание на оператор F.

Желание выделить описанную ситуацию и привело, собственно говоря, к обратному анализу ошибок. Его идея так же очень проста. Она заключается в попытке представить реально полученный элемент v как точный образ при преобразовании F некоторого элемента и . Если это удается сделать, то влияние ошибок округления можно оценить нормой разности и — и . Разность и — и стали называть эквивалентным возмущением. Ничего более глубокого в идее обратного анализа тоже нет.

Несмотря на простоту общей идеи, обратный анализ дал удивительные результаты. Оказалось, что для большого числа алгоритмов он позволяет получить оценки эквивалентных возмущений, не зависящие от меры устойчивости или неустойчивости оператора F. Выделение таких алгоритмов имеет огромное значение для вычислительной математики. Оно дает уверенность, что по сравнению с ними никакие другие алгоритмы не могут дать принципиально лучшие по точности результаты.

С формальных позиций кажется, что вопрос существования обратного анализа достаточно ясен. В самом деле, пусть оператор F отображает некоторую /7-мерную окрестность элемента и в r-мерную окрестность элемента v = F(u). Такая окрестность заведомо существует если якобиан оператора F на элементе и имеет ранг, равный г. Если в этих условиях элемент v попадает в окрестность элемента v, то в окрестности элемента и обязательно существует хотя бы один прообраз элемента v. Вроде бы можно сделать вывод об условиях существования обратного анализа ошибок, по крайней мере, в малом. В действительности высказанные соображения говорят только о теоретических условиях возможности осуществления обратного анализа. На практике условиях его выполнения обрастают многими деталями, связанными с конкретным способом вычисления значений оператора F. Более того, именно эти детали нередко создают узкие места в процессах получения оценок эквивалентных возмущений. Поэтому заранее не ясно, можно ли предложить такой процесс осуществления обратного анализа ошибок, чтобы практические условия его существования совпали с теоретическими.

Для того чтобы получить ответы на возникающие вопросы, нужно понять, решением каких задач являются ошибка v — v и эквивалентное возмущение и — и , как эти задачи связаны с алгоритмом вычисления значений оператора F, как они связаны со свойствами самого оператора Fa многое другое.

522

Часть III. Смежные проблемы и применение

Рассмотрим процесс распространения ошибок округления в алгоритме (8.22) вычисления функции (8.23). Формулы (8.22) отражают точные вычисления. При реальных вычислениях имеют место равенства

u_k=^Fk(u_k^...,u_k ), p<k<n; к_х ,...,к <к, (8.50)

или эквивалентные им равенства

"/с = ^Fd%,—,\) + Ц_к, р<к<п;к_х,...,к_ц <к.

Здесь F_k — "близкая" к F_k функция, реальное вычисление которой осуществляется в процессе реализации алгоритма вместо вычисления F^, u_k —

реально заданная или вычисленная величина и_к; г\_к — эквивалентная абсолютная ошибка, которая вносится в результат вычисления F_k. Будем пока считать, что ошибки г\_к известны. В общем случае они могут каким-то образом зависеть от и_к ,..., щ , но могут и не зависеть от них.

Попытаемся представить вычислительный процесс (8.50) в следующем виде: Щ +4 =^Fk(\ +е_к1,...,и_кч +£_кч), р<к<п; к_ь...,к_ч <к, (8.51)

где 8£ — некоторые числа. Если представление (8.51) возможно, то оно имеет очень простой смысл. Возмущения е^ вводятся во все величины и_к , в том числе и во входные данные. Возьмем возмущенные входные данные щ + S], ..., Up + ъ_р и будем в соответствии с ними проводить точный вычислительный процесс (8.22). Тогда на каждом шаге этого процесса в качестве точного результата будем получать величину й_к + е^.

Таким образом, имеем три последовательности: последовательность и_к, соответствующая точным вычислениям по точным входным данным U]_, ..., Up, реально вычисленная последовательность й_к, соответствующая

точным входным данным и\, ..., u_p, и, наконец, последовательность и_к + е^, соответствующая точным вычислениям по входным данным щ + б£ , ..., Up + ъ_к. Эти последовательности определяются рекуррентными соотношениями (8.22), (8.50), (8.51). Последовательности и_к, и_к, е^ существуют, т. к. предполагаем, что существуют как реализация алгоритма в условиях точных вычислений, так и реализация алгоритма в условиях появления ошибок округления.

Возмущения е^ величин и_к делают величины й_к + е^ результатами точной

реализации процесса (8.22), но лишь при возмущенных входных данных. В этом процессе уже нет никаких ошибок округления. Поэтому величины е^ можно рассматривать как возмущения реально вычисленных величин й_к, компенсирующие влияние ошибок округления, или, другими словами, эк-

Глава 8. Вычислительные системы и алгоритмы

523

Бивалентные ошибкам округления. По установившейся традиции величины 8£ будем называть эквивалентными возмущениями.

Заметим, что в отличие от общепринятого понятия эквивалентных возмущений, здесь рассматриваются эквивалентные возмущения не только входных данных, но и всех промежуточных данных, а также окончательных результатов. Это — принципиальное отличие, позволяющее понять особенности процессов распространения ошибок в реальных вычислительных процессах.

По крайней мере одна последовательность е^ из (8.51) всегда существует. В самом деле, положим S] = ... = ъ_р = 0. Сравнивая (8.22) и (8.51), заключаем, что для всех остальных е^ имеется однозначное решение е^ = и_к — u_t

Следовательно, в данном случае е^ есть не что иное, как абсолютная ошибка вычисленной величины и_к. Такая последовательность е^ определяет прямой анализ ошибок.

Если е„ велико, то нужно выяснить причины появления большой ошибки и искать способы ее устранения. Большая ошибка может появиться либо из-за плохих свойств алгоритма (8.22) вычисления значений функции (8.23), либо из-за неустойчивости самой задачи вычисления функции (8.23), либо из-за обеих причин вместе. Задача изучения влияния ошибок округления в алгоритмах исключительно сложна. Следовательно, очень важно иметь гарантии, что большая ошибка в результате не появится из-за каких-то особенностей алгоритма.

Предположим, что удалось найти такую последовательность е'_к из (8.51), что е'„ =0. Процесс (8.51) является точным для возмущенных входных данных. Поэтому реально вычисленную в условиях влияния ошибок округления (8.50) величину и„ можно представить так:

и„ = Д«1 + e'i, ..., u_p + е'_р). (8.52)

Если эквивалентные возмущения ej, ..., е'_р малы, то независимо от величины ошибки в и_п эта величина является результатом точного вычисления

функции (8.23) со слабо возмущенными входными данными. Теперь большая ошибка в и„ однозначно свидетельствует о неустойчивости задачи вычисления функции (8.23). Появляется возможность сравнить эквивалентные возмущения е\, ..., е'_р в (8.52) с ошибками задания входных данных

в (8.23). Если возмущения не очень сильно превосходят эти ошибки, то данный факт означает, что никакой другой алгоритм вычисления функции (8.23) не может привести к существенно лучшим по точности результатам. Такой подход к изучению влияния ошибок округления, как уже отмечалось, получил название обратного анализа ошибок. Отметим, в частности,

524

Часть III. Смежные проблемы и применение

что именно обратный анализ ошибок дал возможность построить исключительно эффективные по точности алгоритмы для решения самых различных задач линейной алгебры [5, 38].

Итак, последовательность е^ из (8.51), у которой эквивалентные возмущения входных данных равны нулю, описывает прямой анализ ошибок. Все последовательности е/с, У которых эквивалентные возмущения выходных результатов равны нулю, описывают обратный анализ ошибок. Другие последовательности 8£ описывают смешанный анализ ошибок. В этих случаях влияние ошибок округления в вычислительных алгоритмах оценивается одновременно через эквивалентные возмущения входных данных и ошибки результатов, полученных на основе возмущения данных.

Для получения соотношений, позволяющих определять эквивалентные возмущения, исключим величину и_к из (8.50), (8.51). Тогда будем иметь следующую систему уравнений:

£а =^Fk@k_l +e_il,...,M_i + е_к )-F_k(u_k ,u_k )-r\_k,

,,. ■ . ,:' * * (8.53)

р <k<n; k_l7..., k_s < к. ^v '

Величины u_k и ошибки г\_к определяются вычислительным процессом (8.50).

Поэтому, задавая любым способом эквивалентные возмущения еь ..., е_р для входных данных, можно однозначно определить, по крайней мере, в теоретическом плане, все остальные эквивалентные возмущения е^ последовательно для к> р. При заданных и_к, Л/t система уравнений (8.53) является в

общем случае нелинейной относительно величин е^. Чтобы описать множество решений системы (8.53), необходимо сделать какие-то предположения. Таких предположений будет два.

Первое из них основано на том, что локальные ошибки щ, как правило, являются малыми. Это дает основание к тому, чтобы рассматривать лишь малые эквивалентные возмущения е#. Второе предположение связано с тем, что функции Ffr являются достаточно гладкими в малой окрестности величин u_k ,...,и_к , получаемых при точном вычислительном процессе. На практике

в качестве F^ выступают функции, реализующие операции сложения, умножения, деления и т. п., которые, очевидно, обладают нужной гладкостью.

Принимая во внимание сделанные предположения, заменим нелинейную систему (8.53) линейной системой

АЭ^(м^,...,М4 ) г_к=2_,--------=:---------^l—-e^-r\_k, p<k<n; к_и...,к <к.

Эта система всегда совместна, т. к. ранг ее матрицы равен п — р, т. е. равен числу уравнений в системе. Поэтому при малых Л/t все е^ действительно

Глава 8. Вычислительные системы и алгоритмы

525

можно выбрать малыми. Следовательно, мы сделаем ошибку высшего порядка малости, если реально вычисленные величины u_k ,...,и_к заменим на

точные величины щ, ..., и_к . Теперь будем рассматривать такую систему:

lLdF_k(u_k,...,u_k )

2j--------д--------- ^£^< -^£к = ^rU' Р<к<п; k_u...,k_Sk <к. (8.54)

, = \ ^биК

Если величины r|,t являются малыми по сравнению с единицей, то все малые решения е^ линейной системы (8.54) с точностью до малых второго порядка описывают все малые решения нелинейной системы (8.53), т. е. с точностью до малых второго порядка описывают все множество малых эквивалентных возмущений из (8.51). Конечно, при малых ц^ могут существовать большие эквивалентные возмущения е^. Однако такие возмущения не представляют особого интереса для исследования. Отметим, что матрица системы (8.54) есть вариационная матрица именно того алгоритма (8.22), в котором изучаются процессы распространения ошибок округления.

Выполняя тот или иной вид анализа ошибок, мы будем вынуждены накладывать какие-то ограничения на эквивалентные возмущения. Это приводит, в свою очередь, к появлению ограничений на возможность проведения анализа, т. е. ограничений на условия совместности системы. Рассмотрим более подробно обратный анализ ошибок.

Утверждение 8.21

Чтобы при любых малых локальных ошибках ц_к существовал обратный анализ ошибок с малыми эквивалентными возмущениями для величин и_ь ..., и_п алгоритма (8.22), необходимо и достаточно, чтобы градиент вычисляемой функции (8.23) в точке и_ь ..., и_р был отличен от нуля.

Чтобы при малых локальных ошибках г\_к существовал обратный анализ ошибок с малыми эквивалентными возмущениями, необходимо и достаточно, чтобы линейная система (8.54) имела решение, в котором е„ = 0. Причем такое решение должно существовать при любых малых локальных ошибках. Это эквивалентно условию, что ранг подматрицы, составленной из первых п — 1 столбцов вариационной матрицы алгоритма, равен п — р. Данное условие корректно, т. к. всегда р > 1, и, следовательно, всегда п — р < п — I, т.е. всегда число строк подматрицы не больше числа ее столбцов. Обозначим указанную подматрицу через Ф.

Установить ранг матрицы Ф можно по матрице BW, где D любая невырожденная матрица. Матрицу D можно подобрать так, чтобы матрица BW была наиболее простого вида. В частности, можно взять D= Q~^l, где матрица Q та же, что и в системе (8.48). В этом случае последние я — р — 1 столбцов матрицы Q ^_1 Ф будут совпадать с первыми п — р — 1 столбцами единичной

526

Часть III. Смежные проблемы и применение

матрицы порядка п — р. Последние п — р — 1 элементов последней строки матрицы Q ~' Ц> равны нулю. Если равны нулю и первые р элементов последней строки матрицы Q ^_1 Ч>, то эта матрица и, следовательно, матрица Ф не могут иметь ранг п — р. Поэтому для того, чтобы матрица *Р имела ранг, равный п — р, необходимо, чтобы среди первых р элементов последней строки матрицы Q ~' Ф был хотя бы один ненулевой элемент. Легко видеть, что это условие является и достаточным. Если, например, /-и из указанных элементов отличен от нуля, то будет отличен от нуля минор матрицы Q ~¹ Ф , составленный из /-го ее столбца и последних п — р — 1 ее столбцов. Остается заметить следующее. Как было показано выше, первые р элементов последней строки матрицы Q ^_1 Ч> совпадают с координатами градиента вычисляемой функции (8.23) в точке щ, ..., и_р, взятыми с противоположными знаками.

Таким образом, вопрос о возможности выполнения обратного анализа ошибок в случае алгоритма, вычисляющего значение функции, полностью решен. Важно подчеркнуть, что возможность или невозможность выполнения обратного анализа никак не зависит от алгоритма. От алгоритма будет зависеть лишь сложность выполнения обратного анализа. Конечно, это связано с тем, что процесс выполнения обратного анализа мы трактуем здесь как процесс решения системы (8.54).

Как в теоретических исследованиях, так и на практике результат реализации алгоритма (8.22) редко состоит лишь из одной величины u_n. Как правило, результатом является некоторый набор величин u_q ,...,u_q, где р < q\, ..., q_r< п.

Конечно, среди чисел q\, ..., ^.должно быть число п, т. к. в противном случае нет смысла проводить процесс (8.22) до конца. Однако сейчас это обстоятельство не будет нас интересовать. Естественно, что в этом случае прямой анализ ошибок осуществляется точно так же, как прежде, и вопрос об условиях его выполнения не возникает. Что же касается обратного анализа ошибок, то условия возможности его осуществления формулируются иначе.

Утверждение 8.22

Пусть результатом реализации алгоритма (8.22) является набор величин u_q ,..., u_q. Чтобы при любых малых локальных ошибках \\_к существовал обратный анализ ошибок с малыми эквивалентными возмущениями для величин и_ь ..., и„ алгоритма (8.22), необходимо и достаточно, чтобы функциональная матрица Якоби величин u_q ,...,u_q в точке «_ь ..., и_р имела ранг, равный г.

Доказательство почти аналогично тому, что было проведено в утверждении 8.21. Поэтому мы остановимся на нем очень кратко. Чтобы при малых локальных ошибках \\_к существовал обратный анализ ошибок с малыми эк-

Глава 8. Вычислительные системы и алгоритмы

527

Бивалентными возмущениями, необходимо и достаточно, чтобы линейная система (8.54) имела решение, в котором г = ... =^_Чг =0. Причем такое

решение должно существовать при любых малых локальных ошибках. Это эквивалентно условию, что ранг подматрицы, полученной из вариационной матрицы алгоритма путем вычеркивания ее столбцов с номерами q\, ..., q_r, равен п — р. Обозначим указанную подматрицу через Ч> и рассмотрим матрицу Q ^_1 Ц>. Первые р элементов строк матрицы Q ~' Ч>, имеющих номера qi, ..., q_r, совпадают с координатами градиентов величин и ,...,и , взятыми

с противоположными знаками. В совокупности эти элементы с точностью до знака образуют функциональную матрицу Якоби величин u_q ,...,u_q в

точке щ, ..., Up. Последние п — р — г элементов указанных строк равны нулю. Отсюда и вытекает справедливость высказанного утверждения.

Следствие

Если число результатов алгоритма больше числа его входных данных, то обратный анализ ошибок может быть осуществим не при всех даже малых локальных ошибках г\_к или неосуществим вообще.

Действительно, в этих условиях число строк матрицы Якоби больше числа столбцов. Поэтому ранг матрицы Якоби не может равняться числу ее строк.

До недавнего времени вопрос существования обратного анализа прямо связывался с его конструктивностью. На пути выполнения анализа ошибок встречалось немало "подводных камней". Одни из них были связаны с неоднозначностью локального обратного анализа, другие — с размножением информации, имелись и другие "подводные камни", затрудняющие процесс анализа.

Утверждения 8.21, 8.22 полностью решают вопрос об осуществимости обратного анализа ошибок, если сам анализ рассматривать как процесс решения систем (8.54). В этом случае практические условия осуществимости совпадают с теоретическими. Они никак не связаны с алгоритмом, хотя анализ ошибок выполняется именно для алгоритма. Все это согласуется с установленной связью между процессом оценивания ошибок и той задачей, решение которой реализует исследуемый алгоритм. От алгоритма зависят лишь величины эквивалентных возмущений и сложность процесса их определения. Эти вопросы связаны со свойствами систем типа (8.54), т. е. со свойствами вариационной матрицы алгоритма.

Использование систем (8.54) для определения эквивалентных возмущений имеет особенности. Первая из них связана с тем, что значения элементов матрицы системы в общем случае будут известны только после выполнения алгоритма. Это означает, что системы (8.54) более подходят для апостериорного оценивания эквивалентных возмущений, хотя они полезны и в прове-

528

Часть III. Смежные проблемы и применение

дении априорного анализа. Вторая особенность связана с тем, что правые части систем неизвестны, а известны лишь верхние оценки для их модулей. Более того, даже эти оценки чаще всего известны апостериорно. Все это говорит о том, что для анализа ошибок округления в целом, по-видимому, более естественным является апостериорный, а не априорный процесс его проведения.

Вопросы и задания

1. Обратите внимание, что одновременное вычисление функции и ее градиента в точках необходимо для реализации многих численных методов: различные варианты метода Ньютона для решения систем нелинейных уравнений, различные варианты метода скорейшего спуска для отыскания минимумов функций и т. п.

2. *Попробуйте предложить более эффективный метод вычисления градиента функции в точках, если сама функция выписывается на нескольких страницах.

3. *Предположим, что имеется программа вычисления значения функции в точке. Разработайте автоматизированный алгоритм написания программы вычисления градиента в точке для той же функции.

§ 8.8. Примеры

Пример 8.1. Рассмотрим пример, демонстрирующий технику ускоренного вычисления градиента функции. Пусть в сделанных ранее обозначениях алгоритм выглядит так:

u_k = au_k-_p+ft, р < к < п, (8.55)

где а, р — некоторые фиксированные числа. Легко найти точное представление функции и„:

u_n = а^аи₈ + (а^а " ! + а^а " ² + ... + 1)р. (8.56)

Здесь а есть целая часть от деления п на р, 5 — остаток. Предположим, что мы не догадались, как выглядит точное представление, и стали вычислять градиент и„, исходя из прямого дифференцирования соотношения (8.55). Тогда будем иметь:

gradw^ = a gradw^ _ _р.

Если не принимать во внимание специфику данного соотношения, то для вычисления градиента u_n придется выполнить (п — р)р операций. Как и должно быть, сложность вычисления градиента и„ по порядку в р раз больше сложности вычисления функции.

Теперь рассмотрим алгоритм вычисления градиента и„, описанный выше. Составим вариационную матрицу *Р алгоритма (8.55).

Глава 8. Вычислительные системы и алгоритмы

529

Она будет такой:

ц<

a :-1 а

1 I

Первые р и последние п — р столбцов матрицы *Р образуют соответственно матрицы Р и Q из представления (8.37). В матрице *¥ лишь элементы двух диагоналей отличны от нуля. Именно, ф,-,-=а, если /— у = О, и ф,_; = — 1,

если / — у' = — /?.

Согласно алгоритму необходимо далее вычислить последнюю строку матрицы — Q~^l. Для этого воспользуемся представлением (8.39). Все матрицы R_tквадратные порядка п — р. Принимая во внимание вид матрицы Q, заключаем, что среди поддиагональных элементов /-го столбца матрицы R_t только один элемент может быть отличен от нуля. При / < п — 2 р он находится в строке с номером р + i и равен а. Матрицы R_t при п — 2р < i < п — р — 1 в данном алгоритме совпадают с единичными, если р > 1. Поэтому при р > 1 последняя строка произведения матриц R_n -_р - \ ... R_n-_2p + \ будет последней строкой единичной матрицы порядка п — р. При умножении этой строки справа на матрицу R_n - 2_Р в ней изменится только один элемент в позиции с номером п — 2р, который станет равным а. Далее, при умножении вновь полученной строки справа на матрицы R_n-_2p -\ ... R_n - з_р + \ в ней не будут меняться элементы. И лишь при умножении строки справа на матрицу R_n - т,_р в ней снова изменится один элемент в позиции с номером п — Зр, который станет равным а². Окончательно заключаем, что ненулевые элементы в последней строке матрицы — Q~^l будут находиться только в позициях с номерами п — pi, где /= 1, 2, ..., а, и они равны a^l~ ¹. Если не обращать внимания на то, что при последовательном умножении на матрицы R_t элементы строки изменяются не всегда, то нетрудно подсчитать, что для получения последней строки матрицы — Q ^_1 нужно выполнить не более п — р операций.

Для получения координат градиента и_п остается вычислить произведение последней строки матрицы — Q ^_1 на матрицу Р. Принимая во внимание вид обоих сомножителей, заключаем, что все координаты градиента и„ равны нулю кроме одной в позиции с номером 5, которая равна сс^а. Непосредственное сравнение полученного результата с (8.56) показывает его правильность. Если снова не учитывать специфику элементов последней строки

530

Часть III. Смежные проблемы и применение

матрицы — Q ^], то для вычисления координат градиента как элементов указанного произведения необходимо выполнить не более р операций.

Суммируя все затраты, видим, что на вычисление градиента и„ было затрачено не более п операций. На реализацию вычисления и„ согласно (8.55) должно быть затрачено 2(я — р) операций. Справедливость утверждения 8.20 на рассмотренном примере подтверждена. Одновременно подтверждена справедливость утверждения 8.19.

Пример 8.2. Пусть вычисляется сумма s чисел щ, ..., и_р. Градиент s есть вектор, все координаты которого равны 1. Согласно утверждению 8.21, это означает, что обратный анализ ошибок для любого алгоритма суммирования чисел будет возможен при всех значениях чисел U]_, ..., u_p, если только сам алгоритм основан на использовании операций, описываемых достаточно гладкими функциями. Рассмотрим традиционный алгоритм накопления:

«р + 1 = «1 + «2, ^up + i = ^U_P + i - l + "/ + ь 2 < / < р - 1. (8.57)

Здесь s = и_2р - 1.

Согласно исследованиям, проведенным выше, эквивалентные возмущения е_г величин щ удовлетворяют системе (8.54) при дополнительном условии 82^ - 1 = 0. Вариационная матрица *Р алгоритма (8.57) имеет вид

<- р -> <- р-\ ->

1 1

-1 1 -1

т р-\

Дополнительное условие г_2р - \ — 0 означает, что эквивалентные возмущения s\,...,S2_P-2 удовлетворяют системе, матрица Фкоторой получается из матрицы ^Р вычеркиванием последнего столбца. Матрица Ф имеет ранг р — 1. Следовательно, система (8.54) будет всегда совместна даже при условии S2_P - 1 = 0. Это подтверждает уже сделанный вывод о том, что обратный анализ ошибок всегда возможен. Решая систему (8.54) с вычеркнутым последним столбцом, находим

Ч2р-^:Ц2р-

Z2p-' S2/>-

^2р-

S3 - Цр + 2 ~ S/> +1

si + г₂ = r\_p+ i + Sp+i.

+ e„ + ъ

Глава 8. Вычислительные системы и алгоритмы

531

Для оценивания точности операции суммирования нужно знать лишь сумму эквивалентных возмущений входных данных. Поэтому из полученных соотношений имеем

р р -1

X^Si = Х^-И-/ = 1 / = I

Это хорошо известный результат [5]. Если вычисления осуществляются с плавающей запятой, то | ц_р + _t \ < е | щ + и₂ + ... + щ + \\ . Здесь е — некоторая малая величина, определяющая точность выполнения арифметических операций на вычислительной системе. Связана она с параметрами представления чисел. Отсюда, в частности, видно следующее. Если в режиме с плавающей запятой суммируются неотрицательные числа, то для получения наименьшей погрешности в сумме необходимо складывать числа в порядке их неубывания. Это тоже известный результат [1]. В данном примере мы хотели обратить внимание только на тот факт, что анализ ошибок может быть выполнен по формальным правилам.

Пример 8.3. Пусть вычисляются значения функции (wi + и^щ. Градиент этой функции есть вектор с координатами 2(щ + и^щ, 2(щ + 1*2)113, (ui + U2)². Согласно утверждению 8.21, обратный анализ ошибок будет возможен, если U] + U2 * 0. Предположим, что алгоритм вычисления значений функции выглядит следующим образом:

щ = И] + и₂, и₅ = щщ, щ = щи₅. (8.58)

Вычисления функций и^ и щ требуют одного и того же аргумента щ. Следовательно, в алгоритме есть размножение информации. Вариационная матрица *Р алгоритма (8.58) будет такой:

"11 -1

ц<

1л -1

Эквивалентные возмущения еь ..., еь удовлетворяют системе (8.54) при дополнительном условии 86 = 0. Матрица Фсистемы для возмущений еь ..., 55 получается из матрицы *Р вычеркиванием последнего столбца. Условием совместности этой системы при произвольных правых частях является равенство ранга матрицы Ф числу 3. Это же является условием выполнимости обратного анализа. Не равные тождественно нулю миноры третьего порядка

матрицы ¥ принимают одно из значений U4U5, и₄ , W3W4 + ^и5- В этом можно убедиться непосредственной проверкой. Принимая во внимание (8.58), заключаем, что ранг матрицы *Р равен 3, если щ + и₂ *■ 0. Этот результат подтверждает уже сделанный вывод об условии выполнимости обратного анализа ошибок.

532

Часть III. Смежные проблемы и применение

Если вычисления осуществляются с плавающей запятой, то при выполнении условий И] + и₂ ф О, щ ф О локальные ошибки л,- можно представить в виде произведений г\ и,-. При этом модули всех величин е' будут ограничены сверху малой величиной е, зависящей только от параметров представления чисел в вычислительной системе и способа выполнения операции округления. Будем искать эквивалентные возмущения е, в виде аналогичных произведений е" щ для / > 3. Ясно, что S] + е₂ можно так же искать в виде

произведения е"₂ щ. Принимая во внимание (8.58), находим

// __ № __ t ,

£₂ £₄ ~~ £ 4->

е₃ т е₄ е₅ - s 5>

е₄ + е₅ -е₆.

Эквивалентные возмущения определяются неоднозначно. В качестве одного из решений этой системы можно взять

£₂-е₄ + е₆, £₃-е₅-е₅, е₄-еб, е₅ - 0.

В данном примере мы хотели обратить внимание на тот факт, что в некоторых случаях можно находить малые относительные, а не только абсолютные эквивалентные возмущения.

Глава 9

Пользователь

в среде параллелизма

Если ничто не помогает, прочтите, наконец, инструкцию.

Из законов Мерфи

Параллельные вычисления универсальны. Они могут использоваться в любой области науки, где традиционного последовательного способа обработки данных недостаточно и необходимо существенно ускорить процесс вычислений. Астрофизика, аэро- и гидродинамика, вычислительная механика, квантовая химия, геофизика и экология, криптография и статистика — эти, как и многие другие области науки нуждаются в высокопроизводительных параллельных компьютерах. Однако практически все ученые, работающие в той или иной среде параллельных вычислений, сталкиваются с общей проблемой: как эффективно использовать параллельные компьютеры? Это и неудивительно. Параллельная вычислительная среда обладает своими особенностями, для работы в ней во многих случаях нужно знать технологии параллельного программирования, параллельные методы решения задач, архитектуру параллельных компьютеров, методы анализа структуры программ и алгоритмов и другие смежные дисциплины, нехарактерные для предметной области ученого: химика, биолога, физика, медика. Понятно, что в такой ситуации успешно "прорваться" через круг возникающих сопутствующих проблем удается далеко не всегда — отсутствие помощи, дополнительных сведений, доступа к ресурсам, полигонов для тестовых испытаний и других сервисных служб среды параллелизма значительно усложняет работу прикладных специалистов.

Эффективное использование параллельных вычислительных систем — это главная проблема параллельных вычислений. Сейчас нет технологических трудностей построить компьютер из тысячи процессоров, но по-настоящему серьезная проблема — сделать его эффективно используемым многими исследователями.

Параллельные вычисления начались с потребностей пользователей в решении больших задач. Развиваясь, они дали жизнь многим направлениям, которые сейчас пытаются быть самостоятельными и независимыми друг от друга. Архитектура параллельных компьютеров, технологии параллельного программирования, параллельные методы решения задач — все это примеры подобных направлений. Конечно, по каждому их них нужно проводить свои

534

Часть III. Смежные проблемы и применение

собственные исследования. Нельзя только забывать, для чего все это делается. Создали оригинальный язык программирования, а им никто не пользуется. Почему? Разработали новый метод, а для решения практических задач он непригоден. Почему? Установили уникальный компьютер, а на нем никто не считает. Почему? Чаще всего ответы на подобные вопросы следует искать у пользователей.

К сожалению, на практике часто забывают, что параллельные вычисления — это не цель, а лишь средство для решения наиболее трудоемких и сложных задач. По этой причине мы решили последние три параграфа данной книги посвятить описанию различных сторон работы пользователя в среде параллелизма.

Для анализа структуры исследуемых фрагментов мы будем часто пользоваться возможностями, предоставляемыми системой V-Ray. Эта система разработана на основе теории, изложенной в данной книге {главы 6 и 7), и прошла апробацию в ходе выполнения большого числа реальных проектов и экспериментов с использованием параллельных вычислительных систем.

§ 9.1. Типичные ситуации в вопросах и ответах

В данном параграфе мы обсудим целый ряд типичных проблем, с которыми в той или иной степени сталкивается каждый пользователь параллельных вычислительных систем. Изложение построено так, что каждая проблема формулируется в виде отдельного вопроса, иллюстрируется примерами реальных программ, и затем предлагается способ ее решения. В качестве объектов исследования мы рассматриваем различные компьютеры: Cray С90, Cray T3D, IBM SP2. Во многих случаях более пристальное внимание мы уделяем многопроцессорному векторно-конвейерному компьютеру Cray С90. Интерес к данному компьютеру объясняется просто. Помимо традиционных проблем, связанных с распараллеливанием программ между несколькими процессорами, Cray С90 одновременно заставляет думать и о векторизации. Мало провести локальный анализ того или иного фрагмента. Для полного использования потенциала компьютера нужен анализ свойств всей программы целиком. В такой постановке задача анализа и отображения программ на архитектуру компьютера становится намного сложнее.

Безусловно, все проблемы мы обсудить не сможем. Это не реально, да и не нужно. Намного важнее понять общий подход к анализу структуры программ. Различных задач на практике возникает очень много, однако большая их часть может быть успешно решена схожими методами. Важно осознать общую идею, научиться пользоваться ключевыми понятиями и методами, после чего применить эти знания на практике для вас уже не составит большого труда.

Глава 9. Пользователь в среде параллелизма

535

На программе очень плохая производительность. В чем причина? Итак, самая типичная ситуация, с которой сталкиваются все программисты на параллельных вычислительных системах, состоит в том, что есть правильно работающая программа, но используемый компьютер выполняет ее с крайне низкой производительностью. С одной стороны, пользователь знает о пиковой производительности данного компьютера. С другой стороны, он видит реальные цифры, полученные на конкретной программе и отличающиеся от желаемых значений иногда на несколько порядков. Сразу же возникает вопрос: "Почему?"

Возьмем фрагмент (9.1) и предположим, что мы его выполняем на вектор-но-конвейерном компьютере Cray С90. Несмотря на то, что пиковая производительность одного процессора С90 равна почти 1 Гфлопс, на данном фрагменте он показывает лишь 118 Мфлопс. В чем причина?

DO 111 NUM = 10, 40, 5 (9.1)

DO 100 MS = 1, NUM DO 100 MR = 1, MS

DO 10 MQ = 1, NUM

DO 10 MI = 1, NUM 10 XI(MI,MQ,MR,MS) = 0.0D + 00

DO 4 0 MP = 1, NUM

DO 30 MQ = 1, MP

DO 20 MI = 1, NUM

XI(MI,MQ,MR,MS) = XI(MI,MQ,MR,MS)+XNEW(MQ,MP,MR,MS)*V(MP,MI)

XI(MI,MP,MR,MS) = XI(MI,MP,MR,MS)+XNEW(MQ,MP,MR,MS)*(MQ,MI) 20 CONTINUE 30 CONTINUE 40 CONTINUE

DO 90 MI = 1, NUM

DO 50 MJ = 1, MI 50 XIJ(MJ,MI,MR,MS) = 0.0D + 00

DO 7 0 MQ = 1, NUM

DO 60 MJ = 1, MI 60 XIJ(MJ,MI,MR,MS) = XIJ(MJ,MI,MR,MS)+XI(MI,MQ,MR,MS)*V(MQ,MJ) 70 CONTINUE

DO 80 MJ = 1, MI 80 XNEW(MJ,MI,MR,MS) = XIJ(MJ,MI,MR,MS) 90 CONTINUE

100 CONTINUE

111 CONTINUE

536

Часть III. Смежные проблемы и применение

Обратимся к структуре данного фрагмента и особенностям целевого компьютера. С помощью системы V-Ray легко определить, что все самые внутренние циклы фрагмента имеют тип ParDO (по графу алгоритма), и, следовательно, все они могут быть векторизованы. Другими словами, 100% арифметических операций будут выполняться в векторном режиме. Векторизация осуществляется по ведущему измерению основных массивов, поэтому выборка данных для векторных операций идет с шагом 1 и конфликтов при обращении к памяти не происходит. Массив v описан как v (41, 41), поэтому выборка по его второму измерению идет с нечетным шагом 41, т. е. тоже без конфликтов. Устройства сложения и умножения загружены равномерно и всегда используются в режиме с зацеплением. Все векторные операции фрагмента требуют только два входных векторных аргумента, что опять же хорошо согласуется с особенностями архитектуры Cray С90.

Остается лишь один фактор, сильно снижающий производительность векторно-конвейерных компьютеров — это очень короткие внутренние циклы. Не сложно заметить, что во время исполнения данного фрагмента их длина не превышает значения num, меняющегося от 10 до 40, поэтому говорить о сколько-нибудь значительной производительности, конечно же, не приходится.

Итак, причина найдена, но этим решена только часть задачи. Мы знаем, что именно нам мешает, но не знаем, во-первых, можно ли это препятствие преодолеть, и, во-вторых, если можно, то как. Обратимся к следующему разделу.

Причина известна. Как ее устранить? Если мы хотим отказаться от векторизации самых внутренних циклов фрагмента (9.1) и найти для этого более подходящие операции, то первое, что необходимо понять, а из чего же можно выбирать. Для выполнения любой векторной операции необходим, прежде всего, набор независимых операций и самый простой способ их нахождения — это выделение циклов с независимыми итерациями или, другими СЛОВаМИ, ЦИКЛОВ ParDO.

На рис. 9.1 показан размеченный циклический профиль фрагмента (9.1) без учета самого внешнего цикла (с параметром num), в котором каждая горизонтальная скобка соответствует своему циклу. Структура вложенности скобок на профиле полностью повторяет структуру вложенности циклов, поэтому его можно рассматривать как своего рода "боковой срез" фрагмента. Все циклы с независимыми итерациями (циклы ParDO по графу алгоритма) помечены точками.

^_1 ■ ■ I'—-—' I ■ ■ U^l I'—-—' I U^l

■«---------1 I-----------------------------1 I------------------------«---------------------

Рис. 9.1. Циклический профиль фрагмента (9.1) с разметкой циклов ParDO

Глава 9. Пользователь в среде параллелизма

537

Сразу бросается в глаза большое число параллельных циклов. Это значит, что независимых операций в данном фрагменте много. Однако просто использовать какой-либо другой цикл данного фрагмента для векторизации не имеет смысла, т. к. все циклы имеют длину того же порядка, что и внутренние. Естественный выход из данной ситуации состоит в замене нескольких параллельных циклов одним. В частности, для данного примера это могут быть два внешних цикла с параметрами ms и mr и суммарным числом операций NUM * (NUM + 1)/2.

Пока не обговаривая детали, предположим, что циклы ms и mr мы каким-то образом будем использовать для векторизации. Но наш целевой компьютер — это Cray С90, объединяющий в максимальной конфигурации до 16-ти вектор-но-конвейерных процессоров. Если мы хотим, чтобы программа выполнялась с максимальной скоростью, то надо использовать все процессоры, для чего в программе нужно найти дополнительный ресурс параллелизма.

Обратимся снова к фрагменту (9.1). Легко определить, что все циклы с параметром mi, присутствующие во всех гнездах циклов, являются циклами ParDO, и именно этот ресурс параллелизма мы будем использовать для параллельной работы отдельных процессоров. Теперь ясно, что мы хотим сделать, и осталось лишь выполнить само преобразование программы.

Главная проблема, которая довольно часто возникает при объединении циклов для увеличения длины векторных операций, заключается в необходимости изменения используемых структур данных. Чтобы минимизировать вносимые изменения, перед выполнением анализируемого фрагмента вставим дополнительную часть кода, заполняющую новые структуры, а после него — часть для восстановления прежних структур. Для фрагмента (9.1) массивы xnew и v являются входными, но от переменных ms и mr зависят только индексные выражения элементов массива xnew, поэтому заполнение и восстановление связано только с этим массивом.

С Заполнение нового массива YNEW (9.2)

ICOUNT = 1

DO 1 MS = 1, NUM

DO 1 MR = 1, MS

DO 2 MP = 1, NUM

DO 2 MQ = 1, MP 2 YNEW(MQ,MP,ICOUNT) = XNEW(MQ,MP,MR,MS) 1 ICOUNT = ICOUNT + 1

С-----------

DO 100 MI = 1, NUM DO 100 MQ = 1, NUM DO 100 MSR = 1, NUM * (NUM + l)/2 100 XI(MI,MQ,MSR) = 0.0D + 00

538

Часть III. Смежные проблемы и применение

DO 20 MI = 1, NUM

DO 4 0 MP = 1, NUM

DO 30 MQ = 1, MP

DO 101 MSR = 1, NUM * (NUM + 1) / 2

XI(MI,MQ,MSR) = XI(MI,MQ,MSR) + YNEW(MQ,MP,MSR) *V(MP,MI)

XI(MI,MP,MSR) = XI(MI,MP,MSR) + YNEW(MQ,MP,MSR) *V(MQ,MI)

101 CONTINUE 30 CONTINUE 40 CONTINUE 20 CONTINUE

С-----------

DO 90 MI = 1, NUM

DO 50 MJ = 1, MI

DO 102 MSR = 1, NUM * (NUM + 1) / 2

102 XIJ(MJ,MI,MSR) = 0.0D + 00 50 CONTINUE

DO 7 0 MQ = 1, NUM

DO 60 MJ = 1, MI

DO 103 MSR = 1, NUM * (NUM + 1) / 2

103 XIJ(MJ,MI,MSR) = XIJ(MJ,MI,MSR) + XI(MI,MQ,MSR) * V(MQ,MJ) 60 CONTINUE

70 CONTINUE

DO 80 MJ = 1, MI

DO 104 MSR = 1, NUM * (NUM + 1) / 2

104 YNEW(MJ,MI,MSR) = XIJ(MJ,MI,MSR) 80 CONTINUE

90 CONTINUE С Восстановление массива XNEW ICOUNT = 1 DO 3 MS = 1, NUM DO 3 MR = 1, MS DO 4 MP = 1, NUM

DO 4 MQ = 1, MP 4 XNEW(MQ,MP,MR,MS) = YNEW(MQ,MP,ICOUNT) 3 ICOUNT = ICOUNT + 1

Фрагмент (9.2) получен из фрагмента (9.1) с помощью указанного преобразования, но в отличие от него выполняется с производительностью

Глава 9. Пользователь в среде параллелизма

539

322 Мфлопс. Несмотря на то, что выполненное преобразование относительно нетривиально, оба фрагмента эквивалентны с точностью до ошибок округления и в конце получают один и тот же массив xnew. Следует специально отметить, что для данного примера увеличение длины векторных операций (а значит увеличение производительности компьютера и уменьшение времени выполнения фрагмента) полностью компенсировало накладные расходы, связанные с поддержкой новых структур данных.

Какой же вывод можно сделать? Перед тем как смириться с низкой производительностью или же вообще отказаться от существующего варианта программы, надо определить ее потенциальные свойства и найти способ их использования. Перед тем как заменять один алгоритм другим, надо убедиться в том, что старый действительно плох и на самом деле не позволяет эффективно использовать особенности данного параллельного компьютера. Для этого и создаются инструментальные средства для исследования структуры программ, позволяющие ответить на вопрос, можно ли использовать какие-либо резервы данной программы или же принципиальных улучшений добиться в принципе невозможно.

Можно ли еще улучшить программу? Итак, увеличив длину векторных операций, мы получили намного более эффективный вариант программы. Можно ли его еще улучшить за счет каких-либо других преобразований? Вопрос на самом деле очень важный. Обоснованный ответ позволяет понять, насколько далеко в настоящий момент мы находимся от оптимального варианта, можно ли вообще с помощью эквивалентных преобразований существенно улучшить программу или же подобная оптимизация в принципе не может дать большого выигрыша.

Вернемся к особенностям архитектуры векторно-конвейерного компьютера Cray С90 (см. § 3.2). Перед выполнением векторной операции необходимо данные занести в векторные регистры, а после завершения снова записать их в память. На перемещение данных между основной памятью и векторными регистрами, т. е. на операции чтения/записи, требуется дополнительное время, что неизбежно снижает общую производительность. Выход из такой ситуации может быть только один — повторное использование данных, уже хранящихся на векторных регистрах. В отличие от описанного выше преобразования, для этого надо исследовать не ресурс параллелизма программы, а свойства использования памяти, чтобы ответить на вопрос, на каких итерациях идет обращение к одним и тем же элементам массивов.

Рассмотрим цикл 70 фрагмента (9.2). Выражение xij(mj,mi,msr) , стоящее как в левой, так и правой частях оператора присваивания, не зависит от параметра этого цикла. На каждой итерации mq происходит обращение к одной и той же части массива хи, поэтому, как указывалось в § 7.4, имеет смысл выполнить раскрутку данного цикла. Фрагмент (9.3) содержит раскрученный вариант цикла 7 о с глубиной раскрутки 5. В отличие от преды-

540

Часть III. Смежные проблемы и применение

дущего тестового фрагмента нам потребовалось добавить еще одну циклическую конструкцию (с меткой 7 01), т. к. значение num может не быть кратно 5.

NUNROLL = 5 (9.3)

NZ = MOD(NUM,NUNROLL)

DO 7 0 MQ = 1, NUM - NZ, NUNROLL

DO 60 MJ = 1, MI

DO 103 MSR = 1, NUM * (NUM + 1) / 2

T = XIJ(MJ,MI,MSR)

T = T + XI(MI,MQ, MSR) * V(MQ, MJ)

T = T + XI(MI,MQ + 1,MSR) * V(MQ + 1,MJ)

T = T + XI(MI,MQ + 2,MSR) * V(MQ + 2,MJ)

T = T + XI(MI,MQ + 3,MSR) * V(MQ + 3,MJ)

T = T + XI(MI,MQ + 4,MSR) * V(MQ + 4,MJ) 103 XIJ(MJ,MI,MSR) = T 60 CONTINUE 70 CONTINUE С Выполнить остаток цикла 70

DO 701 MQ = NUM - NZ + 1, NUM

DO 601 MJ = 1, MI

DO 1031 MSR = 1, NUM * (NUM + 1) / 2 1031 XIJ(MJ,MI,MSR) = XIJ(MJ,MI,MSR) + XI(MI,MQ,MSR) * V(MQ,MJ) 601 CONTINUE 701 CONTINUE

Почти точно так же можно преобразовать цикл 20 фрагмента (9.2), однако, в отличие от цикла 7 о, для данного цикла есть одна проблема. Дело в том, что выражение xi (mi,mq,msr) первого оператора не зависит от параметра мр цикла 40, а выражение xi (mi,mp,msr) второго оператора не зависит от параметра mq цикла зо. Раскручивать одновременно оба цикла, сохраняя в теле цикла два оператора, не выгодно, т. к. резко возрастает число входных векторов. Возникает естественное желание разбить данный цикл на два, содержащих по одному оператору присваивания, и в каждом выполнить раскрутку по своему циклу. Можно ли это сделать и если можно, то как? Вопрос нетривиальный, учитывая, что в данном фрагменте есть зависимость между итерациями циклов 4 0 и 30.

Забегая немного вперед, скажем сразу: да, можно, но для этого нам понадобится исследовать тонкую информационную структуру данного фрагмента и выполнить специальное преобразование (данное преобразование будет описано немного ниже). В результате, используя указанные свойства циклов зо, 40 и 70 фрагмента (9.2), удается поднять значения производительности до

Глава 9. Пользователь в среде параллелизма

541

511 Мфлопс. В дальнейшем дополнительный ресурс параллелизма внешних циклов с параметром mi может быть эффективно использован для распараллеливания, что еще больше поднимет производительность в случае многопроцессорных конфигураций Cray С90.

В итоге проведенного исследования получаем следующее. Отталкиваясь от 118 Мфлопс исходного варианта (9.1), мы сначала определили точную информационную структуру фрагмента и выделили полный ресурс параллелизма (рис. 9.1). На основе этого мы приняли стратегическое решение для преобразования с учетом как векторизации, так и распараллеливания, и увеличили производительность до 322 Мфлопс (9.2). На последнем этапе мы использовали один из возможных подходов к тонкой настройке полученного фрагмента и подняли производительность до 511 Мфлопс. Как и всегда, следуем основной идее нашего подхода: сначала определяем потенциальные свойства программы, а затем принимаем решение о целевом преобразовании.

Можно ли распределить данные так, чтобы не было пересылок? Теперь предположим, что целевая вычислительная система совершенно другая — это массивно-параллельный компьютер с распределенной памятью, например, Cray T3D/T3E, IBM SP2, МВС-ЮООМ или обычный вычислительный кластер. В этом случае на каждом процессоре исполняется своя часть одной и той же программы, используя данные, расположенные в локальной памяти своего процессора. Если на каком-либо процессоре потребовались данные, расположенные в памяти другого процессора, то на передачу этих данных необходимо время, как правило, значительно превосходящее время обращения к своей локальной памяти.

Основное интуитивно понятное правило получения эффективных программ для подобного рода компьютеров состоит в том, чтобы выделить побольше примерно одинаковых по вычислительной сложности независимых фрагментов, которые бы поменьше обменивались данными во время исполнения. С точки зрения анализа и преобразования структуры программ это правило можно разделить на две задачи:

□ определение потенциального параллелизма фрагмента — эта часть в какой-то степени нам уже знакома;

□ нахождение множества возможных распределений данных по процессорам, согласованных с найденным ресурсом параллелизма.

Вторая задача предполагает поиск таких способов распределения данных по процессорам вычислительной системы, при которых обмены данными между процессорами были бы минимальными. Самая благоприятная ситуация возникает в том случае, когда удается распределить массивы так, что обмены данными отсутствуют вовсе.

Обратимся опять к внешнему циклу юо фрагмента (9.1). Его ресурс параллелизма мы уже определили в процессе оптимизации под архитектуру

542

Часть III. Смежные проблемы и применение

Cray С90. Однако мы пока ничего не знаем относительно множества возможных распределений массивов. Детальное исследование позволяет обнаружить следующие свойства фрагмента:

□ существуют такие распределения массивов xi, xnew, xij и v, при которых передачи данных во время исполнения программы отсутствуют;

□ если распределение данных согласовывать с ресурсом параллелизма циклов ms и mr, то массивы xi, xnew и xij, требующие больше всего памяти, можно распределить по процессорам без дублирования;

□ если распределение данных согласовывать с ресурсом параллелизма циклов mi, то распределить массив xnew без его дублирования нельзя;

□ любое распределение массивов, при котором отсутствуют пересылки данных, требует дублирования массива v на каждом процессоре;

□ использование ресурса параллелизма какого-либо одного цикла не позволит получить хорошо масштабируемой программы, т. к. число итераций каждого из них не превышает 40.

На основе этой информации не трудно найти способ относительно легкого получения параллельного варианта данного фрагмента без взаимодействия процессоров между собой. Использование параллелизма циклов ms и mr позволит легко распределить основные массивы xi, xnew и xij по процессорам без дублирования. Входными данными для каждого процессора будут массив v и соответствующая часть массива xnew, а массивы xi и xij, используя технику приватизации (array privatization), можно объявить локальными на каждом процессоре. Суммарное число итераций циклов ms и mr меняется от 55 (шм=ю) до 820 (num=4 0), что позволит получить хорошо масштабируемую программу для упомянутых выше параллельных компьютеров с распределенной памятью.

JLO = JL (9.4)

DO 100 MS = IL, IH

JHI = MS

IF( MS .NE .IL ) JLO = 1

IF( MS .EQ. IH ) JHI = JH

DO 100 MR = JLO, JHI

... (прежний вариант программы) 100 CONTINUE

Фрагмент (9.4) содержит один из возможных параллельных вариантов данного кода. Каждый процессор получает какое-то число лексикографически последовательных итераций, расположенных в подпространстве (ms,mr) между точками (il,jl) и (ih,jh). Предполагается, что в данном случае используется модель программирования SPMD, поэтому на каждом процессоре значения

Глава 9. Пользователь в среде параллелизма

543

переменных il, jl, ih, jh различны. В табл. 9.1 показаны времена выполнения данного фрагмента на различных конфигурациях компьютеров Cray T3D и IBM SP2, полностью подтверждающие хорошую масштабируемость параллельной программы (большие конфигурации компьютера IBM SP2 на момент проведения экспериментов не были доступны).

Таблица 9.1. Время выполнения фрагмента (9.4) (с) на массивно-параллельных компьютерах Cray T3D и IBM SP2.


Компьютер	Число процессоров
	2	4	8 16	32	64
Cray T3D IBM SP2	6,48 5,83	3,24 2,55	1,63 0,82 1,81	0,41	0,21

Можно ли применить данное преобразование к программе? Подобного рода вопросы довольно часто возникают во время оптимизации программ. Практически все программисты слышали о том, что бывают полезными перестановки циклов местами, распределение циклов или, наоборот, их слияние, раскрутка циклов и т. п. Но для того чтобы получить корректный преобразованный вариант программы, надо не только выполнить собственно преобразование, но и убедиться в его эквивалентности исходному варианту. Хорошо если преобразуемый фрагмент относительно прост или вы являетесь автором данной программы и понимаете "физический" смысл преобразования. А если это не так?

Рассмотрим возможность распределения цикла 20 фрагмента (9.5). Данный цикл является частью фрагмента (9.2), во время оптимизации которого мы обещали обосновать возможность распределения циклов для последующей раскрутки. Можно ли разбить данное гнездо циклов на одну или несколько циклических конструкций так, чтобы каждая содержала только один оператор присваивания? Заметим, что для этого фрагмента данное преобразование может быть полезно не только перед выполнением раскрутки (что мы и сделали ранее), но и для лучшего использования кэш-памяти команд и данных, и для получения большего числа циклов ParDO.

DO 20 MI = 1, NUM (9.5)

DO 20 MP = 1, NUM DO 20 MQ = 1, MP

DO 20 MSR = 1, NUM * (NUM + 1) / 2

XI(MI,MQ,MSR) = XI(MI,MQ,MSR) + YNEW(MQ,MP,MSR) *V(MP,MI) XI(MI,MP,MSR) = XI(MI,MP,MSR) + YNEW(MQ,MP,MSR) *V(MQ,MI) 20 CONTINUE

544

Часть III. Смежные проблемы и применение

Можно ли просто взять и разбить данный цикл на два, где каждый цикл будет содержать по одному оператору присваивания? Нет, так делать нельзя, поскольку эквивалентность фрагментов будет нарушена! Обратимся к пространству итераций исходного фрагмента. На рис. 9.2 показана передача информации от одного оператора присваивания к другому при изменении параметров циклов мр и mq.

Рис. 9.2. Передача информации между операторами

присваивания фрагмента (9.5) при изменении

параметров циклов МР и MQ

На данном рисунке вершины нижнего треугольника (нижняя плоскость) соответствуют первому оператору присваивания, а вершины верхнего — второму. Совершенно ясно, что простое деление цикла на два нарушает информационную зависимость: операция А (второй оператор), вычисляющая аргумент для операции В (первый оператор) еще не выполнена, а мы уже хотим выполнить В.

Вместе с тем, из этой же картинки не сложно найти такой способ преобразования данного фрагмента, при котором были бы выполнены и условия преобразования, и соблюдена эквивалентность. В самом деле, если "отрезать" диагональные итерации (мр = mq), то выполнение второго оператора уже не зависит от выполнения первого. Следовательно, сначала можно выполнить всю преддиагональную часть второго оператора (в эту часть входят те операции, для которых мр > mq), затем диагональные итерации в прежнем виде, а в самом конце преддиагональную часть первого оператора. Фрагмент (9.6) содержит преобразованный текст фрагмента (9.5).

Глава 9. Пользователь в среде параллелизма

545

С Преддиагональная часть второго оператора (9.6)

DO 20 MI = 1, NUM DO 20 MP = 1, NUM DO 20 MQ = 1, MP - 1 DO 20 MSR = 1, NUM * (NUM + 1) / 2 XI(MI,MP,MSR) = XI(MI,MP,MSR) + YNEW(MQ,MP,MSR) *V(MQ,MI)

20 CONTINUE

С Диагональная часть, MQ = MP DO 21 MI = 1, NUM DO 21 MP = 1, NUM MQ = MP

DO 21 MSR = 1, NUM * (NUM + 1) / 2

XI(MI,MQ,MSR) = XI(MI,MQ,MSR) + YNEW(MQ,MP,MSR) *V(MP,MI) XI(MI,MP,MSR) = XI(MI,MP,MSR) + YNEW(MQ,MP,MSR) *V(MQ,MI)

21 CONTINUE

С Преддиагональная часть первого оператора DO 22 MI = 1, NUM DO 22 MP = 1, NUM DO 22 MQ = 1, MP - 1 DO 22 MSR = 1, NUM * (NUM + 1) / 2 XI(MI,MQ,MSR) = XI(MI,MQ,MSR) + YNEW(MQ,MP,MSR) *V(MP,MI)

22 CONTINUE

В данном примере мы говорили только о распределении циклов. Однако практически для всех наиболее известных преобразований можно привести подобные нетривиальные примеры, когда корректность выполнения конкретного преобразования не очевидна и требует дополнительного анализа — аналитического (автоматического, автоматизированного) или визуального.

Опять подчеркнем, что, как и прежде, мы сначала определили точную информационную структуру программы, и лишь затем приняли решение о возможности выполнения целевого преобразования. Ответ на поставленный вопрос: "Можно ли выполнить распределение циклов в исходном фрагменте?" — был отрицательный, но, как мы видели, это совсем не значит, что для данного фрагмента указанное преобразование в принципе не применимо.

Нужно ли попробовать какой-либо другой препроцессор или метод оптимизации? Этот вопрос возникает особенно часто у начинающих программистов, когда используемые ими методы или средства оптимизации не дают ожидаемого эффекта. Почему нет эффекта и что делать дальше? Надо ли попробовать какой-либо другой подход или данную программу существенно улучшить невозможно? Точно такие же вопросы возникают даже в том случае, когда оптимизация программы уже позволила значительно увеличить

546

Часть III. Смежные проблемы и применение

производительность: может быть если попробовать что-то еще, то результат будет еще лучше?

Основная причина неуверенности и сомнений, явно выраженных в подобного рода вопросах, кроется в том, что практически все используемые в настоящее время препроцессоры, оптимизаторы, анализаторы и т. п. имеют два больших недостатка:

□ они ничего не говорят о структуре программы или фрагмента целиком, о потенциальных свойствах. Пользователь не знает, может ли оптимизация еще что-либо дать или же он уже использовал весь заложенный в программу потенциал и получил показатели производительности, близкие к предельно возможным;

□ они, как правило, ничего не говорят о том, что же можно ожидать в том случае, когда используемый ими метод анализа структуры программ не дает положительного результата. Почему цикл не векторизуем: метод слабый или данный цикл не может быть векторизован в принципе? Кэшпамять используется неэффективно из-за того, что оптимизатор не знает, как ее использовать эффективно, или для данного фрагмента использование кэш-памяти вообще не может дать никакого эффекта?

Недомолвки оптимизаторов естественно выливаются в неуверенность и недоверие пользователей: раз нет полной информации, то возникает естественное желание попробовать что-то еще.

Следует специально подчеркнуть, что говоря об оптимизации и полной информации о структуре программы, мы имеем в виду описание и использование двух основных характеристик программы: потенциала параллелизма (какие операции можно выполнять независимо друг от друга, а какие нет) и свойств работы с памятью (по какому закону происходит обращение к различным областям памяти). Сейчас мы не обсуждаем, например, как повышать производительность компьютера за счет использования более оптимальных алгоритмов генерации кода или за счет поиска общих подвыражений в тексте программ. Наша основная задача — сконцентрироваться на тех общих машинно-независимых свойствах программ, которые, с одной стороны, принципиально важны для эффективной реализации на параллельных компьютерах, а с другой, характеризуют реализованный в программе алгоритмический подход. Только в этом случае мы сможем определить, насколько полно используется потенциал программы, есть ли резерв для увеличения производительности или же надо сменить используемый алгоритм.

Тысячи строк исходного текста программ — можно ли в них разобраться?

Нужно использовать старую программу на данном параллельном компьютере... Нужно понять и устранить причины низкой производительности уже существующей чужой программы... Требуется перенести программу на другую параллельную платформу с сохранением разумной производительности...

Глава 9. Пользователь в среде параллелизма

547

Всякий, кто сталкивался хотя бы с одной из подобных задач, согласится с тем, насколько важно понять общую структуру той бездны строк, с которой приходится иметь дело. Основная проблема опять же идет от специфики параллельных компьютеров — надо добиться не только того, чтобы программа выдавала правильные результаты, но и работала с разумной производительностью .

С одной стороны, можно взять профилировщик, на обычном последовательном компьютере найти те фрагменты программы, на которые приходится 90% общего времени выполнения (а это, как правило, около 5—10% текста), и заняться их оптимизацией. Разумно? В некоторых случаях, безусловно, да.

Однако вспомним закон Амдала: если 9/10 программы исполняется параллельно, а 1/10 по-прежнему последовательно, то ускорения более, чем в 10 раз получить в принципе невозможно вне зависимости от качества реализации параллельной части кода. Если подобное ускорение устраивает пользователя или же ускорение его вообще не интересует, то с таким подходом вполне можно согласиться. Однако в жизни, как правило, ситуация иная: никто не станет использовать 2048 процессоров для ускорения программы в 10 раз.

Посмотрим на проблему с другой стороны. Какую же часть кода надо ускорить (а значит и предварительно исследовать), чтобы получить заданное ускорение? Ответ можно найти в следствии из закона Амдала (см. § 2.3): для того чтобы ускорить выполнение программы в q раз, необходимо ускорить не менее, чем в q раз не менее, чем (1 — 1/#)-ю часть программы. Следовательно, если нужно ускорить программу в 100 раз по сравнению с ее последовательным вариантом, то необходимо получить не меньшее ускорение не менее, чем на 99,99% кода, что почти всегда составляет существенную часть программы.

Вернемся опять к фрагменту (9.1). 99% времени занимает исполнение самых внутренних циклов, однако для того, чтобы найти способ его преобразования и получить 511 Мфлопс, нам потребовалось исследовать структуру всего фрагмента целиком. Если бы мы этого не сделали, то производительность так бы и осталась на прежнем уровне.

А что значит "понять структуру программы"? Каждый исследователь вкладывает в эти слова свой смысл в зависимости от стоящей перед ним задачи, сложности и размера кода, своей квалификации и многих других факторов. В разных ситуациях может понадобиться граф вызовов подпрограмм и функций, структура вхождения операторов CALL в отдельных процедурах, детальная информационная структура выбранных процедур или фрагментов, исследование потенциала параллелизма и локальности использования данных, структура взаимодействия подпрограмм через COMMON-блоки и многое другое. Более детально мы поговорим об этих структурах в § 9.2.

548

Часть III. Смежные проблемы и применение

Соответствует ли структура программы особенностям параллельного компьютера? Если нет, то какой компьютер следует использовать для решения задачи? Довольно часто в одной сети бывают доступными параллельные компьютеры с совершенно разной архитектурой, среди которых наиболее типичными являются массивно-параллельные и SMP-компьютеры, кластеры рабочих станций. Какой компьютер разумнее использовать для данной программы? Если решается вопрос о новом параллельном компьютере, то не понятно, какому классу отдать предпочтение. Можно ли определить, насколько хорошо структура программы или алгоритма соответствует особенностям архитектуры? Нет ли в данной программе фрагментов, которые заведомо будут узким местом при ее выполнении на данном компьютере?

Ясно, что можно сэкономить много усилий и времени, если перед разработкой программы или ее переносом на другую машину знать ответы на поставленные вопросы. Можно ли их найти? Рассмотрим фрагмент (9.7).

А = ABS(SMOOPI) (9.7)

R = А / (А +0.5+ SQRT(A + 0.25)) Т = 1. / (1.0 + R) DO 42 N = 1, 4 DO 10 J = 2, JL DW(1,J,N) = 0. 10 CONTINUE

DO 21 I = 2, IL DO 20 J = 2, JL DW(I,J,N) = DW(I,J,N) - R * (DW(I,J,N) - DW(I - 1,J,N))

20 CONTINUE

21 CONTINUE

DO 30 J = 2, JL DW(IL,J,N) = T * DW(IL,J,N) 30 CONTINUE

DO 41 I = IL - 1 , 2, -1

DO 4 0 J = 2, JL

DW(I,J,N) = DW(I,J,N) - R * (DW(I,J,N) - DW(I + 1,J,N))

40 CONTINUE

41 CONTINUE

42 CONTINUE

A = ABS(SMOOPJ)

R = A / (A +0.5+ SQRT(A + 0.25))

T = 1. / (1.0 + R)

DO 82 N = 1, 4

Глава 9. Пользователь в среде параллелизма

549


DO 50 I =	2, IL
DW(I,1,N)	= 0.
50 CONTINUE
DO 60 I =	2, IL
DO 61 J =	2, JL
DW(I, J,N)	= DW(I	J,N) - R * (DW(I,J,N)	- DW(I,J - 1,N
61 CONTINUE
60 CONTINUE
DO 7 0 I =	2, IL
DW(I, JL,N	= т *	DW(I, JL,N)
70 CONTINUE
DO 80 I =	2, IL
DO 81 J =	JL - 1	2, -1
DW(I, J,N)	= DW(I	J,N) - R * (DW(I,J,N)	- DW(I,J + 1,N
81 CONTINUE
80 CONTINUE
82 CONTINUE

Определим структуру данного фрагмента. Циклы 21, 41, 61, 81— последовательные, поскольку каждая итерация зависит от предыдущей из-за использования рекурсии первого порядка. Остальные циклы являются параллельными: два самых внешних цикла имеют по четыре итерации, число итераций других циклов порядка il или jl. Циклический профиль данного фрагмента, на котором точками отмечены все циклы ParDO, показан на рис. 9.3.

.—11 ~~' •~~ UI . IL=. ~~-----■~~ I | | I—.—11 ~~■ . J~~JI . IL^^

Рис. 9.3. Циклический профиль фрагмента (9.7)

Самые внешние циклы очень хорошо подходят для параллельного исполнения, т. к. их итерации независимы друг от друга. Единственная проблема — это малое число самих итераций (их всего четыре), поэтому данный вариант приемлем, если речь идет о распараллеливании лишь между 2—4 процессорами.

Если переставить местами циклы 60<->61и80<->81, то все внутренние циклы можно сделать параллельными и, следовательно, фрагмент можно полностью векторизовать. Производительность будет зависеть, прежде всего, от величин il и jl: чем они больше, тем производительность выше. Вместе с этим, следует иметь в виду два других фактора. Во-первых, на производи-

550

Часть III. Смежные проблемы и применение

тельности заведомо скажется дисбаланс операций сложения и умножения, т. к. число умножений в данном фрагменте меньше числа сложений. Во-вторых, векторизация будет проводиться как по первому измерению массива dw, так и по второму. Следовательно, чтобы избежать конфликтов при доступе в память, первая размерность этого массива должна быть выбрана, исходя из соответствующих требований архитектуры. В частности, для компьютера Cray С90 это может быть любое нечетное число.

Дополнительно, по всем последовательным циклам можно выполнить раскрутку, используя обращения к одним и тем же векторам на соседних итерациях. Например, для цикла 21 вектор dw(i, j,n) на итерации i есть то же самое, что вектор dw(i-i, j,n) на итерации i+i. В табл. 9.2 показана производительность компьютера Cray С90 на данном фрагменте в зависимости от значений il и jl и различной глубины раскрутки последовательных циклов.

Таблица 9.2. Производительность компьютера Cray С90

(и время выполнения в секундах) в зависимости

от значений пили различной глубины раскрутки

последовательных циклов фрагмента (9.7)


Значения переменных	Глубина раскрутки последовательных циклов
IL, JL	-	2	3	5
30,30	227(1,76-Ю"⁴)	251(1,59-10 "⁴)	259(1,54-Ю"⁴)	262(1,53-Ю"⁴)
150,150	364(2,92-10 ^_3)	414(2,57-10 ^_3)	437(2,44-10 ^_3)	453(2,35-10 ^_3)
1000,30	300(4,61 -10 -³)	341 (4,06-10-³)	362(3,82-10-³)	364(3,79-10 -³)
1000,150	413(1,73-10^-2)	445(1,60-10 ^_2)	459(1,55-10 ^_2)	468(1,52-10 ^_2)
1000,1000	463(1,03-10 "¹)	503(9,53-10 "²)	508(9,42-10 "²)	524(9,14-10 "²)

Рассмотрим многопроцессорные конфигурации векторно-конвейерных компьютеров с общей памятью. Если число процессоров не превышает четырех, то можно использовать параллелизм внешних циклов, что практически никак не повлияет на производительность каждого процессора в отдельности. Если процессоров больше четырех, то параллелизма внешних циклов недостаточно и единственная возможность загрузить все процессоры — это дополнительно разделить внутренние, предназначенные для векторизации, циклы на части: для 8-ми процессоров на две части, для 16-ти процессоров на четыре части и т. д. При этом надо иметь в виду, что деление внутренних циклов на части позволит загрузить все процессоры полезной работой, однако производительность каждого процессора неизбежно уменьшится, из-за уменьшения длины векторных операций. Окончательное решение, т. е. раз-

Глава 9. Пользователь в среде параллелизма

551

бивать ли внутренние циклы или нет, зависит только от конкретных значений IL И JL.

Наиболее сложен анализ данного фрагмента для параллельных компьютеров с распределенной памятью. Идеальный вариант заключается в использовании параллелизма внешних циклов, т. к. при использовании распределения массива dw по последнему измерению взаимодействий между процессорами во время работы фрагмента не будет совсем. Но точно так же ясно, что данный вариант, в силу своей ограниченности, не будет широко использоваться на практике.

Отойдем от использования параллелизма внешних циклов и рассмотрим общую структуру фрагмента. Его ресурс параллелизма мы уже знаем. Что можно сказать относительно возможных распределений единственного массива dw? Будем исходить из предположения, что весь фрагмент должен выполняться параллельно, т. к. параллельная реализация лишь одной половины не может ускорить его выполнение более, чем в два раза. Детальный анализ позволяет определить следующие свойства данного фрагмента:

□ не существует единого распределения массива dw, при котором параллельное выполнение данного фрагмента проходило бы без взаимодействия процессоров вообще;

□ координатное распределение массива dw по первому или второму измерению лучше, чем любое скошенное распределение;

□ если для всего фрагмента использовать координатное распределение по первому (второму) измерению, то первую (вторую) половину фрагмента процессоры будут вынуждены исполнять последовательно один за другим.

Отсюда следует, что для параллельного выполнения всего фрагмента потребуется, по крайней мере, одна точка перераспределения массива dw для перехода от одного координатного распределения к другому. Для массивно-параллельных компьютеров с распределенной памятью это очень неприятная операция, требующая больших накладных расходов. Однако на практике ситуация может быть еще хуже. Дело в том, что в приложениях, реализуемых на компьютерах подобного рода, стараются использовать одинаковое распределение данных в смежных фрагментах и подпрограммах. Если для приложения, содержащего данный фрагмент, это действительно так, то потребуется как минимум еще одна точка перераспределения, либо в начале фрагмента, либо в его конце. Если данный фрагмент составляет вычислительное ядро всего приложения, то на значительное ускорение работы по сравнению с выполнением на одном процессоре рассчитывать трудно, что полностью подтверждает табл. 9.3. Она содержит времена выполнения данного фрагмента (с двумя точками перераспределения) на массивно-параллельном компьютере Cray T3D с различным числом процессорных элементов и различными значениями il и jl.

552

Часть III. Смежные проблемы и применение

Таблица 9.3. Время выполнения фрагмента (9.7) на массивно-параллельном компьютере Cray T3D с двумя точками перераспределения


Значения	Число процессоров
переменных IL, л.	1	4	16	64	256
30,30	2,39-10 "³	1,56-Ю^-3	1,40- Ю^-3	2,15-Ю"³	2,47-10 ^_3
150,150	6,94-10 "²	3,11-10"²	1,05-10 ^_2	6,35-10 "³	1,04-10"²
1000,30	9,47-10 "²	4,28-10 "²	1,30-Ю"²	7,66-10 ^_3	1,22-Ю"²
1000,150	0,49	0,23	6,60-10 "²	2,33-10 "²	1,81-Ю"²
1000,1000	3,27	1,52	0,44	0,12	4,85-10 "²

Проведенное исследование показывает, насколько реальной и важной становится возможность априорного исследования качества отображения программ на различные типы архитектур. Мы опять использовали два ключевых объекта технологии: потенциальный параллелизм и локальность использования данных, позволивших определить все необходимые свойства программы.

Можно ли оценить потенциал параллелизма алгоритма, используемого в программе? Во многом на данный вопрос мы уже ответили в предыдущем разделе, когда исследовали свойства фрагмента (9.7). Для определения потенциального параллелизма мы использовали понятие циклов ParDO по графу алгоритма и показывали результат в виде размеченного циклического профиля. Однако не для всех программ этой информации достаточно. Координатный параллелизм (ParDo) действительно очень важен, но с его помощью нельзя описать весь потенциальный параллелизм программ. Для полной картины необходимо добавить информацию о конечном параллелизме на уровне фрагментов или отдельных операторов и информацию о скошенном параллелизме.

Для изучения конечного параллелизма лучше всего подходит параллельная форма: все множество фрагментов исследуемой программы разбивается на непересекающиеся группы (ярусы) так, что все группы должны выполняться в строгом порядке одна после другой, но все фрагменты, попадающие в одну группу, независимы и могут реализовываться параллельно.

Во время анализа одной программы нам встретилась подпрограмма ROT, состоящая из 86-ти одномерных циклов, расположенных подряд друг за другом. Исследование координатного параллелизма было явно недостаточно и нужно было понять, можно ли выполнять отдельные циклы независимо друг от друга или нельзя. Для этого мы воспользовались построенной сие-

Глава 9. Пользователь в среде параллелизма

553

темой V-Ray параллельной формой, показанной на рис. 9.4 (сама подпрограмма ROT весьма объемна, поэтому ее текст мы здесь не приводим).

К S) s> о iS S! о

о •

•

& iS О iS iS IS &

iS iS S> S>

Рис. 9.4. Параллельная форма подпрограммы ROT

Каждый цикл данной подпрограммы обозначен отдельной вершиной и все множество вершин расположено по ярусам, каждый ярус лежит на своей вертикальной линии. Все ярусы должны выполняться последовательно друг за другом слева направо, но все вершины, лежащие на одном ярусе, независимы и могут реализовываться параллельно.

Одновременно с построением параллельной формы мы пометили каждую вершину, являющуюся циклом ParDO, перечеркнув ее наклонной чертой. Для получения полной информации о параллельных свойствах данной подпрограммы осталось исследовать структуру тех циклов, которые не помечены как циклы ParDO. Детальный анализ средствами системы V-Ray показал, что все они очень похожи и устроены примерно так:

DO 3700 1 = 501, 2500

3700 F(l) = F(l) + F(l-500)

Каждая итерация по i от iooi до 2500 зависит от итерации с номером 1-500, поэтому данный цикл, конечно же, не обладает свойством ParDO. С другой стороны, данный цикл (как и остальные циклы, не помеченные как ParDo) может быть тривиально преобразован в последовательность из четырех циклов так, что все новые циклы должны исполняться последовательно друг за другом, однако каждый из них уже обладает свойством ParDo:

DO 3701 1 = 501,1000

3701 F(l) = F(l) + F(l-500) DO 3702 1 = 1001,1500

554

Часть III. Смежные проблемы и применение

3702 F(l) = F(l) + F(l-500) DO 3703 1 = 1501,2000

3703 F(l) = F(l) + F(l-500) DO 3704 1 = 2001,2500

3704 F(l) = F(l) + F(l-500)

После подобного исследования мы получили исчерпывающую информацию о параллельных свойствах исходной подпрограммы: конечный или макропараллелизм виден из параллельной формы, а параллелизм на уровне итераций циклов понятен как из разметки ParDO, так и из последнего детального исследования информационной структуры отдельных циклов. В итоге весь параллелизм, которым обладает подпрограмма, а значит и лежащий в ее основе алгоритм, нам известен.

Что следует из перечисленных примеров? Всем, кто хотя бы раз пытался написать действительно эффективную программу для параллельного компьютера, часть изложенных вопросов наверняка хорошо знакома. Подобные вопросы возникают в процессе его использования практически постоянно и находить на них ответы приходится всем. Это не проблемы конкретного пользователя, а общие проблемы, характерные для параллельных вычислений в целом. Попробуем критически проанализировать только что изложенный материал и выделить те основные положения и факты, на которых базировался проводимый в каждом случае анализ.

Отвечая на вопросы данного параграфа, мы практически всегда опирались на знание точной информационной структуры исследуемого фрагмента. С эффективностью выполнения фрагмента (9.1) было что-то не так, поэтому сначала мы определили его потенциальные свойства, поняли, какие резервы есть в нашем распоряжении, и лишь затем, согласуясь с особенностями целевого компьютера, приняли решение о преобразовании фрагмента. Только знание точной информационной структуры позволило нам оценить возможность реализации фрагмента (9.7) на параллельных компьютерах с совершенно разной архитектурой и описать весь ресурс параллелизма подпрограммы ROT, параллельная форма которой показана на рис. 9.4.

Чем точнее определяется информационная структура программы, тем лучше. Тезис абсолютно правильный, однако на практике сам по себе он мало что дает пользователям. Нужна математическая гарантия результатов исследования, без которой никогда не будет уверенности в качестве результатов оптимизации программ, да и сам процесс оптимизации скорее будет похож на "блуждание в потемках", чем на обоснованную последовательность действий.

Если на вопрос пользователя, обладает ли цикл, например, свойством ParDO, анализатор ответил "нет", что это значит? Возможны два варианта: данный цикл действительно не является циклом ParDO или же используемые анали-

Глава 9. Пользователь в среде параллелизма

555

затором методы не смогли определить истинной информационной структуры цикла, и для безопасности он дал отрицательный ответ. А что делать пользователю? Поверить или попробовать исследовать свою программу другими средствами? В любом случае пользователь должен точно знать, почему было сказано "нет".

Вспомним один из предыдущих вопросов — можно ли выполнить распределение циклов фрагмента (9.5) для их последующей раскрутки? Традиционный ответ "нет", объединяющий "нет" и "не знаю", абсолютно бесполезен для пользователя. Исследование фрагмента (9.7) показало, что для него не существует единого распределения данных, при котором отсутствовали бы пересылки данных между процессорами. Это "нет" может быть доказано, является неотъемлемым свойством данной программы, и поэтому никакой другой анализатор не даст иного ответа. Увидев отрицательный ответ, можно пойти дальше, чтобы определить и ликвидировать причину. В обсуждаемом примере после выполнения анализа и дополнительного преобразования этот ответ, по существу, был сведен к "да".

Другой обязательной составной частью технологии, без которой немыслима оптимизация программ для параллельных компьютеров с распределенной памятью, является согласование потенциального параллелизма с распределением данных. Несмотря на простоту формулировки, данное положение предполагает решение целого ряда сложных задач: определение потенциального параллелизма, деление массивов на распределяемые, дублируемые и локальные, нахождение распределений без пересылок данных, определение возможных точек перераспределения данных и т. п.

Со многими из перечисленных задач, но в достаточно простой форме, мы уже встречались, когда обсуждали возможность реализации фрагмента (9.7) на различных параллельных архитектурах. Единственный массив dw должен быть распределен. Распределение, согласованное с параллелизмом внешних циклов, при котором нет пересылок между процессорами, существует, однако более четырех процессоров эффективно использовать нельзя. Любое скошенное распределение приведет, во-первых, к очень неравномерной загрузке процессоров и, во-вторых, к взаимодействию процессоров на каждой итерации. Для использования координатного распределения потребуется по крайней мере одна точка перераспределения массива dw и т. д.

Следует отметить, что исследование множества возможных распределений данных программы необходимо не только для компьютеров с распределенной памятью, но и для эффективного использования кэш-памяти. В самом деле, для распределения массивов по процессорам мы делим массивы на блоки так, что основная масса ссылок на каждом процессоре является локальными ссылками к данным своего блока. Следовательно, данные каждого блока будут автоматически попадать в кэш, если порции вычислений,

556

Часть III. Смежные проблемы и применение

предназначенные отдельным процессорам, выполнять последовательно друг за другом.

Очень часто из программы приходиться буквально выжимать все резервы параллелизма. В этом случае уже нельзя ориентироваться на исследование какого-либо одного типа параллелизма, например, выделение только циклов ParDO. Необходим более сложный анализ структуры программы, показывающий весь ресурс параллелизма программы в терминах параллелизма по данным и параллелизма по вычислениям. Параллелизм по данным чаще всего соответствует параллелизму итераций циклов, а параллелизм по вычислениям — макропараллелизму на уровне отдельных фрагментов.

Оба вида параллелизма тесно связаны между собой. Полная картина потенциала параллелизма всей программы образует иерархию: на самом внешнем уровне есть несколько независимых ветвей вычислений (параллелизм по вычислениям), каждая ветвь содержит циклы, часть из которых параллельные (параллелизм по данным), в теле каждого цикла можно опять выделить независимые ветви вычислений, в которых опять содержатся циклы, и т. д. Примерно по такой схеме мы исследовали структуру подпрограммы ROT, для которой параллелизм по вычислениям описывали с помощью параллельной формы, а параллелизм по данным разметкой циклов ParDO.

Какой вид параллелизма, на каком уровне и в каком виде будет использоваться, зависит от особенностей архитектуры целевого параллельного компьютера и размера исходной задачи. Отдать предпочтение тому или иному виду параллелизма априори достаточно сложно, однако, располагая полной информацией о параллельной структуре фрагмента, можно всегда принять правильное решение в каждом конкретном случае.

Говоря об иерархии в описании потенциального параллелизма программы, становится очевидной необходимость единого подхода к анализу как простых, так и сложных фрагментов. Технология не должна ориентироваться на какой-либо фиксированный набор структур циклов или графов управления, например, только на тесновложенные гнезда циклов или на ациклические графы. В разных ситуациях бывает необходимо исследовать либо всю программную единицу целиком, либо самые внешние циклы, либо только их тела, либо структуру самых внутренних циклов.

Идея иерархичности пронизывает технологию анализа и преобразования программ практически на всех этапах. Анализ фрагментов программы на любом уровне вложенности циклов, иерархическое описание параллелизма в терминах параллелизма по вычислениям и параллелизма по данным, анализ в терминах фрагментов различной сложности (оператор, линейный участок, одиночный цикл, совокупность циклов), преобразование или описание потенциала параллелизма отдельного фрагмента на любом уровне

Глава 9. Пользователь в среде параллелизма

557

вложенности — эти и многие другие действия должны применяться к максимально широкому классу фрагментов, вне зависимости от их расположения в тексте программы.

Даже поверхностное знакомство с задачами, появляющимися в процессе оптимизации программ для параллельных вычислительных систем, показывает насколько они сложны и разнообразны. В одном случае нужно исследовать структуру графа управления, в другом информационную зависимость между операторами или отдельными фрагментами, в третьем проводить анализ локальности данных, в четвертом определять возможность выполнения того или иного преобразования и т. д., и т. д. Трудно рассчитывать на то, что можно создать полностью автоматическое средство анализа и преобразования одинаково эффективное для всего комплекса потенциальных задач и всего класса программ, написанных просто в соответствии с правилами входного языка. Естественный выход из данной ситуации заключается в том, что в технологии и построенных на ее основе инструментальных средствах должна быть предусмотрена возможность организации исследования в любом режиме — от полностью автоматического преобразования "текст—текст" до интерактивного режима с получением максимально детальной информации. В зависимости от задачи исследования (оценить потенциал параллелизма, выбрать целевой компьютер, перенести программу на новую платформу и т. п.), сложности программы и уровня своей подготовки пользователь должен иметь возможность выбрать подходящий для него режим.

Включение интерактивного режима накладывает серьезные требования на организацию программных средств, поддерживающих этот режим. Чаще всего этот режим будет использоваться тогда, когда в программе пользователя что-то не так. Например, он не может понять, почему нельзя выполнить некоторое преобразование или почему система говорит о наличии информационной зависимости, хотя с его точки зрения ее быть не должно. Для этого необходимы мощные средства визуализации структуры программы, поддерживающие все этапы анализа и помогающие пользователю лучше разобраться с особенностями его же программы. В частности, если он не может понять, почему нельзя выполнить явное распределение циклов фрагмента (9.5), то он должен иметь возможность простыми средствами получить изображение структуры данной циклической конструкции, например, так, как показано на рис. 9.2.

Похоже, что сложность предстоящего пути мы обрисовали. Однако не стоит пугаться всего того обилия проблем, которое обсуждалось в данном параграфе. Во-первых, далеко не со всеми из них вам сразу придется столкнуться. А, во-вторых, если и придется, то теперь вы знаете, как нужно действовать.

558

Часть III. Смежные проблемы и применение

Вопросы и задания

1. Как в программе найти те фрагменты, на которые приходится основное время вычислений?

2. По каким признакам можно выделить наиболее значимые (с точки зрения времени выполнения) фрагменты на основе только статического анализа?

3. Приведите пример фрагмента программы, для которого формальное применение перестановки циклов невозможно, однако выделение небольшой порции итераций в отдельную конструкцию приводит к искомому результату.

4. Какие графовые конструкции могут помочь при анализе структуры больших программных комплексов?

5. Возьмите любую работающую параллельную программу, на которой реальная производительность компьютера сильно отличается от пиковой. Попробуйте спланировать ее исследование, чтобы максимально быстро найти причину низкой эффективности. Какие программные средства могут помочь в этой работе? Какие характеристики и свойства программы нужно уметь определять?

6. Определите зависимость времени работы фрагмента (9.7) от способа распределения массива DW и значений переменных IL и JL.

7. *Разработайте методику исследования структуры программы, состоящей из десятков и сотен тысяч строк кода. Какие программные системы могут помочь решить эту задачу?

§ 9.2. Программный сервис в параллельных вычислениях

Сложных вопросов при использовании параллельных вычислительных систем в самом деле возникает много. Нам приходилось работать в рамках многих проектов на большом числе параллельных компьютеров, и практически всегда перед нами стояла задача — помощь в создании действительно эффективных параллельных программ. Конечно же, помощь нужна только тогда, когда есть какие-то проблемы: если нет проблем, то нет и вопросов. Однако интересно то, что сама проблема каждый раз формулировалась пользователями практически одинаково: "Что-то не так с эффективностью моей программы".

Иногда проблема снималась легко — достаточно было, например, разобраться в документации по работе с системой или компилятором (вспомните эпиграф к данной главе). Иногда приходилось довольно глубоко вникать в суть решаемой задачи. Чем дольше мы работали в этой области, тем отчетливей проявлялась многогранность исходной проблемы. Стало ясно, что мы уже не можем ограничиваться решением одной конкретной задачи, скорее речь должна идти о создании целой инфраструктуры, сопровождающей большинство прикладных работ на суперкомпьютерах.

Глава 9. Пользователь в среде параллелизма

559

В самом деле, давайте посмотрим, на какие составные части может разбиваться исходная задача, и почему нужен комплексный подход к анализу ситуации в каждом конкретном случае. Если "с программой что-то не так", то, как показала практика, проблемы могут возникать на самых разных уровнях:

АНАЛИЗ КОНФИГУРАЦИИ КОМПЬЮТЕРА

АНАЛИЗ ЭФФЕКТИВНОСТИ СИСТЕМНОГО И ПРИКЛАДНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

АНАЛИЗ ПРИКЛАДНОЙ ПРОГРАММЫ

АНАЛИЗ АЛГОРИТМИЧЕСКОГО ПОДХОДА

Начинать исследование, чаще всего, приходилось с анализа конфигурации конкретного компьютера: тип и число процессоров, уровни и объем памяти, параметры и топология коммуникационной среды, особенности ввода/ вывода и т. п. Даже эти, казалось бы, простые и очевидные вещи, на практике могут оказаться причиной вопросов пользователей. В свое время мы разрабатывали программу для векторно-конвейерного компьютера Cray С90. Когда программа была закончена и передана пользователю, он после нескольких запусков на своем компьютере стал утверждать, что "с программой что-то не так", т. к. время ее работы было где-то на 30% больше заявленного нами. Детальный анализ показал, что истинная причина крылась вовсе не в программе: процессор второго компьютера, в отличие от первого, имел лишь три канала, а не четыре, как предписано стандартной конфигурацией. С программой было "все так" и в рамках той конфигурации она работала идеально.

Следующий большой срез — это анализ эффективности системного и прикладного программного обеспечения. У многих когда-либо были нарекания на работу штатных компиляторов, поэтому проблемы данного пункта хорошо знакомы. Однако далеко не всегда удается столь легко найти виновника бед пользователей и тогда приходится проводить детальный анализ характеристик программного окружения. Когда в середине 90-х годов мы писали программу для компьютера Cray T3D, то обнаружили крайне низкую эффективность ряда коммуникационных процедур текущей реализации системы PVM, включенной в состав штатного программного обеспечения. Проблема с программой? Да нет, опять-таки далеко не в самой программе дело...

Для облегчения исследования эффективности программного окружения конкретного компьютера разработано целое множество тестов и бенчмарков. Многие вопросы, связанные с данной проблемой, мы уже обсуждали в § 3.6.

560

Часть III. Смежные проблемы и применение

Основная задача в рамках анализа прикладной программы состоит в поиске ответа на вопрос: "Можно ли не меняя алгоритма улучшить эффективность программы?" Занимаясь исследованиями в данном направлении в течение двух десятков лет, мы разработали и используем на практике комбинацию методов статического и динамического анализа. На основе проведенных исследований создана и успешно апробирована многоцелевая экспериментальная система — V-Ray, предназначенная для изучения структуры больших программных комплексов и адаптации этих комплексов к требованиям целевых компьютеров с параллельной архитектурой. Ее особенность заключается в том, что впервые система анализа и адаптации программ под архитектуру параллельных компьютеров базируется на использовании истории реализации программ. В отличие от существующих методов, предлагаемый подход опирается на компактное параметрическое описание информационной истории реализации программы, прогнозируя динамику поведения программ по их статической форме — исходному тексту. Несмотря на кажущийся недостаток информации, разработанные методы, в большом числе случаев, не только дают максимально точный ответ, но и позволяют гарантировать неулучшаемость полученных результатов. Эта проблематика обсуждалась во многих параграфах данной книги.

И, наконец, если анализ приложения показал, что структура программы не соответствует особенностям архитектуры компьютера, то проблемы эффективности исходной программы кроются в свойствах используемых алгоритмов. Единственное, что остается — это перейти к алгоритмическому анализу. Возможно, что в результате исследований этого этапа придется поменять алгоритм и полностью переписать некоторые части программы. В ряде случаев другого пути просто нет.

Как мы видим, проблема анализа и повышения эффективности параллельных программ — комплексная. Именно поэтому мы и говорили не о каком-то одном средстве, системе или методе для ее решения, а о целой инфраструктуре. В полной мере это касается и программного обеспечения. Понимая сложность проблемы и острую необходимость в разного рода средствах, к настоящему моменту разработано немало вспомогательных систем, входящих в состав штатного программного обеспечения компьютеров. Компиляторы, отладчики, анализаторы, конверторы, профилировщики — всем этим богатством нужно пользоваться, если есть желание грамотно использовать уникальные возможности параллельных вычислительных систем. Насколько это реально для вас, насколько развит программный сервис на доступном вам компьютере — это вопрос к сервисной службе и администраторам вашей системы.

Как же помочь пользователю максимально быстро разобраться со структурой исследуемой программы и локализовать фрагменты, требующие аккуратного детального анализа? Мы попробуем рассказать об общих подходах к решению данной задачи, иллюстрируя конкретные шаги на примере системы V-Ray.

Этот материал можно рассматривать и как руководство при анализе конкретных программ, и как описание необходимой функциональности проек-

Глава 9. Пользователь в среде параллелизма

561

тируемых систем для анализа структуры программных комплексов. Обсуждаемые структуры не являются чем-то сугубо теоретическим. Скорее наоборот, они продиктованы практикой и возникли в процессе работы с реальными программами. Большая часть этого материала реализована в системе V-Ray и прошла апробацию во многих проектах.

Изложение будет вестись в соответствии с общей стратегией анализа: от обсуждения общих структур будем постепенно переходить к все более и более детальным. Сначала рассмотрим формы представления структуры программы на межпроцедурном уровне, затем перейдем к макроструктуре отдельных процедур, и затем — к микроструктуре на уровне отдельных срабатываний операторов.

Граф вызовов процедур

Удачно организованный процесс исследования общей структуры программы во многом помогает проведению качественного детального анализа информационной структуры. Пользователь сразу видит состав процедур, распределение циклов в процедуре, все особенности ее графа управления, повторяющиеся фрагменты с одинаковой структурой и многое другое, что в дальнейшем может оказаться очень полезным для ее преобразования.

Простейшая форма графа вызовов процедур является традиционным объектом, помогающим получить первое представление о структуре программы. Каждой программной единице в графе вызовов соответствует отдельная вершина, причем вершины А к В соединяются направленной дугой А -> В только в том случае, если процедура А содержит вызов процедуры В.

Первую информацию о структуре программы можно получить из формы графа вызовов. В самом деле, если в некоторую вершину X входит много дуг, то данная процедура вызывается из многих мест программы. Если, кроме этого, вершина X является листовой, то от эффективности реализации данной процедуры может во многом зависеть и эффективность всей программы. Если вершина содержит много исходящих дуг, то в теле такой процедуры есть много обращений к другим программным единицам, поэтому для анализа параллелизма на верхнем уровне нужен более детальный анализ именно этой процедуры.

Изменение способа изображения графа вызовов

Практика показала, что все программные проекты обладают своими специфическими особенностями, отражающимися в структуре графа вызовов. В одних проектах есть вершины с большим числом входных или выходных дуг, а в других подобных явно выраженных "центров" нет. В одних граф вызовов имеет вид дерева, а в других часть путей многократно пересекается.

Указанную специфику проектов нужно хоть каким-то образом отразить в изображении графа. Трудно рассчитывать на то, что существует один уни-

562

Часть III. Смежные проблемы и применение

версальный способ изображения подобного рода объектов, позволяющий в каждом случае получить наглядное и понятное изображение. По этой причине нужно поддерживать целый набор методов изображения графов вызовов, чтобы в каждом конкретном случае пользователь мог выбрать тот из них, который с его точки зрения наиболее пригоден для анализа.

На рис. 9.5 показаны три варианта изображения одного и того же графа вызова программы ARC2D из пакета Perfect Club Benchmarks. Даже для столь небольшого примера заметна разница в восприятии структуры проекта.

Рис. 9.5. Три варианта изображения одного и того же графа вызовов процедур (начало)

Глава 9. Пользователь в среде параллелизма

563

(scaldt)

( tkinv )

( specf

(ypenta (ypent2

(xpenta (xpent2>* (xpentp (xpenp?

( verify )

(elapse)

calcps)

( filery

calcme) xidif ) etadif)

( filerx

(cputim)

Рис. 9.5. Три варианта изображения одного и того же графа вызовов процедур (окончание)

Расширенный граф вызовов процедур

Основной недостаток графа вызовов заключается в том, что по выходящим дугам нельзя определить ни общего числа вызовов каждой конкретной процедуры (между любыми двумя вершинами в классическом графе вызовов не может быть кратных дуг), ни порядка, в котором вызовы следуют по тексту программы. Чтобы решить эту проблему, система поддерживает построение расширенного графа вызовов. Данный объект сложнее обычного графа вызовов, но он свободен от указанных недостатков. На рис. 9.6 показан пример расширенного графа вызовов одной из анализируемых программ.

Разметка вершин графа вызовов

Для быстрого определения многих особенностей программы можно использовать разметку вершин графа. В частности, система сразу отмечает начальные вершины, т. е. те программные единицы, которые сами ниоткуда не вызываются. Обычно такая вершина в анализируемом проекте только одна, что соответствует единственной главной части программы. Однако, если анализируется, например, структура вызовов некоторой библиотеки, то число начальных вершин будет больше.

564

Часть III. Смежные проблемы и применение

С помощью этой же разметки можно сразу найти те процедуры, которые когда-то были включены в проект, но по какой-либо причине сейчас не используются — они также будут помечены как начальные. В одном из проектов, содержащем около 490 процедур, таким образом было обнаружено более 80 (!) "забытых" и, следовательно, неиспользуемых подпрограмм.

semsumsemsum

А А

Ш II Ш |Г

symd

symq

cabs2

test

semsum

energ2

nonlin energy curlbl аМ

vb1 sumal curlb2

Ж Ж Ж

i_t

I I С

timest

OOOOOOOOOOOOOOOOOOOOO

right

iterat error new

ж ж Ж

00000

step

mhd2

Рис. 9.6. Расширенный граф вызовов процедур

По разметке вершин графа вызовов можно получить первую информацию о возможных наиболее значимых подпрограммах. В самом деле, разметим все вершины согласно максимальной глубине вложенности содержащихся в каждой из них циклических конструкциях. Для многих программ выполняется правило: чем больше глубина вложенности, тем больше времени приходится на соответствующий фрагмент. Ясно, что это ни в коей мере не является законом, однако позволяет лучше понять структуру анализируемой программы. На рис. 9.7 показан размеченный подобным образом граф вызовов программы FL052Q, также входящей в состав пакета Perfect Club Benchmarks. Кстати, для нее на подпрограммы с максимальной глу-

Глава 9. Пользователь в среде параллелизма

565

биной вложенности циклических конструкций действительно приходится основное время.

Рис. 9.7. Размеченный граф вызовов

Разметку вершин графа можно применять в самых разных целях. В частности, не всегда исходный текст всех процедур, показанных на графе вызовов, доступен для анализа. Типичный пример — это использование внешних библиотек. Но действительно ли они используются, можно легко выяснить с помощью соответствующей разметки графа. На основе этого станет понятно, останутся ли после анализа в программе "темные" места или же программу можно будет исследовать целиком.

Исключительно важной характеристикой многих программ является организация операций ввода/вывода, которые имеют две отличительные особенности:

□ операции ввода/вывода намного медленнее арифметических;

□ операции ввода/вывода во многих случаях препятствуют оптимизации процесса вычислений.

566

Часть III. Смежные проблемы и применение

Поскольку ввод/вывод может сильно повлиять на скорость выполнения анализируемой программы, нужно уметь определять, каким образом операторы ввода/вывода распределены среди программных единиц проекта, для чего опять можно использовать механизм разметки вершин графа.

Циклический профиль путей

Для более точного анализа важно знать не только глубину вложенности циклических конструкций в процедурах, но и уметь оценивать общее число объемлющих циклов, в телах которых вызывалась каждая процедура. Для этого V-Ray строит циклический профиль путей, в котором отражена вся последовательность циклов для каждого пути графа вызовов. По существу строится, исследуется и описывается все множество путей графа вызовов. Ниже показаны фрагменты циклического профиля путей некоторого проекта:

10 : (GCMA³ —?—> DYNIMP¹ —^l-^HHSOLV³ —^l-^GAUSPH² —^l-^SINGL⁵), (9.8) 8 : (GCMA³ —?—> RADFL2⁴ —!—> RADFSW³ —!—> VARP8⁴)—^—> DELED3¹, 7 : (GCMA³ —?—> DYNIMP¹ —!—> DYNADD¹ —5—> MMATR2⁴).

Конструкция вида X^a —*—» 7^P, используемая в качестве основного элемента каждого пути, означает следующее: процедура X вызывает процедуру Y в у-мерном цикле, причем максимальная глубина вложенности циклов в самих процедурах X и Y равна аир соответственно. Если X содержит несколько вызовов Y, то на месте у будет указано максимальное значение.

Ясно, что интерес представляет как значение а, так и у + р. Самая левая колонка циклического профиля (9.8) показывает максимальную суммарную вложенность циклов по каждому пути, а скобками отмечена та цепочка пути, на которой достигается указанное значение. Поскольку все пути отсортированы по убыванию данного суммарного показателя, среди всех путей можно сразу выделить наиболее "тяжелые" в качестве кандидатов для детального анализа.

Граф использования общей памяти

Чтобы оценить возможное взаимодействие процедур проекта через объекты общей памяти (для языка Fortran — это COMMON-блоки, для С — глобальные переменные), можно построить граф использования общей памяти. Для языка Fortran этот граф можно представлять двудольным графом, в котором одно множество вершин составляют процедуры, а другое — COMMON-блоки. Вершины разных множеств соединяются дугой тогда и только тогда, когда соответствующая процедура содержит в своем теле соответствующий COMMON-блок. Можно расширить функциональность данной формы представления, позволяя детализировать состав каждого блока и анализировать способ работы с каждым объектом COMMON-блока, т. е. отмечать использование и/или изменение составляющих его переменных.

Глава 9. Пользователь в среде параллелизма

567

Граф управления и комбинированные структуры

Основной используемый на практике метод представления структуры процедуры использует структуру вложенности циклов. Для того чтобы упростить процесс анализа и не опускаться сразу на уровень отдельных операторов, каждой процедуре ставится в соответствие иерархическая система графов. Граф верхнего уровня показывает структуру процедуры в целом и состоит из вершин двух типов: вершины одного типа соответствуют самым внешним циклам процедуры, а вершины другого — линейным участкам между ними. Линейным участком будем называть такую последовательность операторов, в которой только первый оператор может иметь метку и только последний оператор может нарушать последовательный характер выполнения операторов. В любом из этих графов две вершины А а В связываются направленной дугой А -> В тогда и только тогда, когда фрагмент В может быть выполнен сразу после фрагмента А, т. е. данный вид графа является модификацией классического графа управления.

Каждый из циклов может представлять интерес для самостоятельного анализа, поэтому нужно поддерживать построение аналогичных графов на всех последующих уровнях, детализируя структуру составных вершин вплоть до отдельных линейных участков. Данный способ представления структуры программы назовем иерархическим или L-деревом.

На рис. 9.8 сверху показан пример графа первого уровня. Каждая вершина с петлей представляет один внешний цикл процедуры. Число внутри показывает глубину вложенности циклов данной конструкции, что помогает в первом приближении оценить значимость каждого фрагмента. Ниже показана структура тела цикла той же процедуры (граф второго уровня), помеченного цифрой 3 в верхней части рисунка. Совершенно аналогично можно построить граф для любого цикла процедуры.

Для проведения более детального анализа можно использовать две аналогичные формы представления структуры программы. В первой все макровершины текущего фрагмента раскрываются вплоть до отдельных линейных участков, а во второй — до отдельных операторов. Эти способы представления активно используются во время исследования тонкой информационной структуры отдельных фрагментов программ.

Циклический профиль процедуры

С одной стороны, иерархический способ представления структуры программы позволяет скрыть массу излишних подробностей. Однако с другой, для того чтобы понять внутреннюю структуру макровершины, надо последовательно просмотреть графы на всех подуровнях. На внешнем уровне мы видим только максимальную глубину вложенности циклов данного фрагмента, но не знаем ни сколько всего циклов он содержит, ни каким образом они распределены внутри него.

568

Часть III. Смежные проблемы и применение

ш.

U CD

00 О)

о.

Глава 9. Пользователь в среде параллелизма

569

Для того чтобы облегчить восприятие циклической структуры фрагмента, система поддерживает построение циклического профиля. Каждый цикл текущего фрагмента на циклическом профиле условно изображен в виде горизонтальной скобки. Для каждого графа в нижней части рис. 9.8 показаны циклические профили исследуемых фрагментов. Заметим, что если иерархический способ рассматривать как взгляд на программу сверху, то циклический профиль можно интерпретировать как боковой срез.

Разметка графа и циклического профиля

Как и для графов вызовов процедур, самым простым способом определения свойств фрагментов программы является разметка вершин графа процедуры. Система выполняет анализ и помечает все вершины графа разными цветами в зависимости от того, выполняется ли заданное свойство для вершины или нет.

Предположим, что мы хотим проверить, есть ли до to-циклы в исследуемой процедуре. Известно, что до to-циклы, обладая нерегулярной структурой, часто являются серьезным препятствием для детального анализа свойств фрагмента. Если пользователь сделал такой цикл самым внутренним циклом, то трудно будет анализировать и все объемлющие циклы. Если go to-цикл внешний, то на первом этапе его анализ можно не выполнять, сосредоточившись на хорошей реализации его тела. В любом случае первый шаг — это определение положения всех до to-циклов в данной процедуре, и проще всего это сделать с помощью разметки.

Аналогично можно разметить и циклический профиль процедуры. В этом случае, чтобы разметить весь профиль, кроме вершин текущего графа, система проверит, выполняется ли выбранное свойство у вершин всех последующих уровней. Наиболее активно разметка вершин и профиля используется при отображении свойства ParDO циклов программы.

Процедурный граф управления

Если в графе управления некоторого фрагмента оставить только те вершины, которые содержат обращения к другим подпрограммам и функциям, то получим редуцированную форму графа управления, называемую процедурным графом управления. В отличие как от графа вызовов, так и от расширенного графа вызовов, данная форма представления содержит информацию о том, зависят ли срабатывания каждого вызова от срабатывания альтернативных операторов или нет.

Пример такой конструкции показан на рис. 9.9. По данному графу легко определить, что подпрограмма DFLUXC вызывается в зависимости от выполнения условного оператора, а вызов подпрограммы EFLUX происходит всегда.

570

Часть III. Смежные проблемы и применение


	щ<------ *г "*	-J
	Hi .а 4t	il
	*—и** Щ— X	-\
	q= ■ ■о ¹— га —' б* £1	-\
	Го"	н -JJ
	1г m
	X	-1
	CO §---------*
	т ]

■&

СП Q.

■&

CO Q.

3 о

CO Q.

Глава 9. Пользователь в среде параллелизма

571

Расширенный граф вызовов с циклическим профилем

Практически полная картина как о структуре вызовов, так и о циклической структуре анализируемого программного комплекса может быть получена с помощью комбинации расширенного графа вызовов с циклическим профилем каждой процедуры. В этом случае, за основу берется расширенный граф вызовов и в каждую вершину "вписывается" ее циклический профиль. Подобная структура показана на рис. 9.10.

Циклические профили, использованные в данной форме представления, могут быть дополнительно размечены в соответствии с некоторым свойством. В частности, на рис. 9.10 помечены все циклы ParDO.

Локализация наиболее значимых частей кода

Итак, каким же образом можно локализовать наиболее значимые части анализируемой программы? Под "наиболее значимыми" будем понимать те фрагменты программы, на которые приходится значительная часть общего времени выполнения. Понятно, что именно эти части программы надо анализировать в первую очередь.

Методы решения данной задачи можно разделить на две большие группы: методы статического и динамического анализа. Все структуры и действия, поддерживающие статическое определение наиболее значимых частей кода, мы уже обсуждали, поэтому сейчас лишь соберем полученную информацию вместе. Совместный анализ

□ размеченного графа вызовов процедур,

□ циклического профиля путей,

□ циклического профиля процедур,

□ процедурного графа управления,

□ расширенного графа вызовов с циклическим профилем

позволяет выделить наиболее значимые части программ с достаточно высокой точностью. Без подобных методов не обойтись, т. к. далеко не всегда есть возможность выполнить программу на целевом компьютере. Не всегда в распоряжении исследователя есть программа целиком и возможно для анализа ему предоставлен лишь какой-то фрагмент. В конце концов для программы может не быть реальных входных данных, без чего ее выполнение часто либо невозможно в принципе, либо бессмысленно.

Динамическое профилирование программ

Если все же есть возможность выполнить программу, то полученную на этапе статического анализа информацию о наиболее значимых частях програм-

572

Часть III. Смежные проблемы и применение

мы можно уточнить данными профилирования. Система поддерживает все основные этапы профилирования, начиная с разметки исходного текста и заканчивая визуализацией результатов.

Конкретный способ разметки исходного текста зависит от двух параметров. Первый — в каких терминах проводить профилирование. Поддерживается несколько стандартных режимов: профилирование процедур, самых внешних циклов, циклов с заданной глубиной вложенности, операторов вызовов процедур и функций и некоторые другие.

Второй параметр управляет тем, какую информацию собирать: интегральную, когда не имеет значения, каким образом мы дошли до данного фрагмента или подробную, когда информация собирается отдельно по каждому возможному пути от начальной точки программы до данного фрагмента. Например, подпрограммы А к В вызывают подпрограмму С. В первом случае вся собираемая по С информация ассоциируется только с С, а во втором она распределяется между путями А -> С и В -> С.

В процессе профилирования система по умолчанию определяет пять величин: общее, среднее, минимальное и максимальное времена работы фрагмента и общее число обращений к данному фрагменту.

Для отображения результатов профилирования можно использовать либо специальные средства (разного рода диаграммы и гистограммы), либо соответствующую разметку обсуждавшихся выше структур. Использование расширенного графа вызовов позволяет отображать результаты профилирования отдельно по каждому пути.

Информационный граф и макроструктура программ

Следуя общей методике анализа программ, исследование информационной структуры процедуры можно разделить на два этапа: макро- и микроанализ. На первом этапе определяется зависимость между частями исходного текста процедуры, т. е. циклами, линейными участками либо операторами. Второй этап предполагает детальное исследование зависимостей фрагмента на уровне отдельных итераций циклов. На этапе макроанализа мы определяем взаимосвязь элементов процедуры на макроуровне и одновременно локализуем фрагменты, требующие детального исследования на уровне пространства итераций, т. е. микроанализа.

Основной инструмент для исследования информационной структуры процедуры на макроуровне — это информационный граф. Вершинам графа соответствуют фрагменты текста, которые связываются направленной дугой тогда и только тогда, когда одна вершина (фрагмент) вычисляет данные для другой. Дуга направлена от вершины, производящей данные, к вершине их использующей. Ясно, что построенный таким образом граф содержит толь-

Глава 9. Пользователь в среде параллелизма

573

ко истинные зависимости и, следовательно, позволяет определить потенциальный параллелизм процедуры на макроуровне.

Независимые фрагменты программ и компоненты сильной связности

Построение информационного графа преследует две цели. Во-первых, мы имеем возможность сразу определить те вершины (то есть фрагменты текста), которые в принципе являются информационно независимыми. В дальнейшем такие вершины можно будет исполнять в любом порядке. Во-вторых, информационный граф, показывая общую последовательность вычислений, часто позволяет сильно упростить последующий процесс анализа. Предположим, что в графе вершина А связана с вершиной В: А -> В. Ясно, что раздельный анализ таких фрагментов и проще, и позволяет выделить практически весь потенциальный параллелизм части АВ исходной программы. Если же связь между данными фрагментами циклическая: А <± В, то

ситуация принципиально иная, поскольку только совместный анализ фрагментов А к В позволит выделить скрытый скошенный параллелизм, приносящий во многих случаях существенное ускорение.

Из данного примера становится ясно, что за основу проведения последующего микроанализа надо брать компоненты сильной связности информационного графа. Для графа А -> В это как А, так и В, а для графа А <± В это фрагмент АВ целиком. Рассмотрим следующий пример:

DO 141 i = 1, 200

ABCl(i-l) = ABC2(i-l) + 1 BCDl(i-l) = ABCl(i-l)**2 A(i) = BCD1 (i-1) + D(i) ABC2(i) = B(i+1) + B(i-l) B(i) = C(i) + 1

141 C(i+1) = B(i) + 1 С-------

DO 142 i = 1, 100

142 A(i) = A(i) + B(i) + C(i) DO 143 i = 101, 200

143 A(i) = A(i) - B(i) - C(i)

На рис. 9.11 показан информационный граф этого примера. Мы видим, что первый цикл вычисляет данные, которые затем используются вторым и третьим циклами, причем последние два цикла оказались независимыми между собой. Кандидатами для проведения микроанализа являются все цик-

574

Часть III. Смежные проблемы и применение

лы фрагмента как наиболее существенные компоненты сильной связности. Заметим, что второй и третий циклы обладают свойством ParDO по графу алгоритма и потому не требуют дополнительного детального анализа (все итерации этих циклов независимы, поэтому у этих вершин нет петель).

-ИИ D №п Ш D Ш D о

Рис. 9.11. Информационный граф

Для исследования первого цикла повторим еще раз данную процедуру, приняв за вершины отдельные операторы тела цикла (рис. 9.12). Данное изображение исключительно информативно. Во-первых, структура связи компонентов сильной связности сразу показывает, что фрагмент можно преобразовать в последовательность из пяти циклов, содержащих пятый и шестой, четвертый, первый, второй, третий операторы исходного цикла соответственно. Во-вторых, только один компонент имеет контур, а значит лишь срабатывания двух последних операторов будут связаны между собой в процессе выполнения. Следовательно, остальные четыре цикла заведомо будут обладать свойством Pa г do и микроанализ для них опять-таки не нужен.

->а doa t>Q?D D о

Рис. 9.12. Информационный граф тела цикла

Если мы хотим оценить не только ресурс параллельности фрагмента, но и найти путь его реального преобразования, надо построить единый граф с указанием истинной зависимости, зависимости по выходу и антизависимости (рис. 9.13). Если мы не хотим вводить новых переменных, то для соблюдения эквивалентности преобразований последние не два, а три оператора надо объединить в один цикл. В противном случае старые значения массива в надо запомнить в новом массиве. Если нужно понять влияние какой-либо конкретной переменной на структуру всего фрагмента, то по точно такой же схеме можно построить информационный граф для любой переменной или для любого набора переменных.

Глава 9. Пользователь в среде параллелизма

575

-мз dod сьтао □ о

Рис. 9.13. Информационный граф тела цикла с указанием трех типов зависимостей

Параллельная форма

Для описания и визуализации макропараллельной структуры процедуры используется параллельная форма. По существу данная форма является объединением информационного графа и графа управления. Она показывает, какие части процедуры можно выполнять в любом порядке, а какие последовательно одну за другой. Параллельная форма разбивает все вершины графа на непересекающиеся множества (ярусы) так, что все множества должны выполняться строго один за другим, но все вершины одного и того же множества информационно независимы и могут исполняться в произвольном порядке. В § 9.1 был показан пример построения и использования параллельной формы.

Параллельная форма определена неоднозначно. Любую вершину можно переместить на ярус с большим номером вместе с перемещением зависящих от нее вершин. Среди всего множества форм система V-Ray выбирает каноническую параллельную форму, в которой любая вершина зависит от какой-либо вершины предыдущего яруса. Этот факт гарантирует нахождение теоретически наискорейшего способа выполнения анализируемого фрагмента при неограниченном числе процессоров. Перемещая избыточные вершины на ярусы с большими номерами, можно дополнительно учесть ограничения конфигурации целевого компьютера.

Микроструктура программ

Исследование тонкой информационной структуры программ опирается на построение графа алгоритма либо аналогичного графа по какому-либо другому виду зависимости. Фрагмент приводится к каноническому виду и для каждого входа каждого оператора строится граф в полном соответствии с изложенной в главе 6 теорией. Рассмотрим следующий фрагмент:

DO 10 i = 1, 2*n DO 10 j = 1, n+1 10 s = s + A(i,j)

с----------

DO 20 i = 1, n+1

576

Часть III. Смежные проблемы и применение

DO 20 j = 1, 2*n DO 20 к = 1, n

IF( i.EQ.l ) THEN

D(i,j,k) = B(i,j,k)*s ELSE

D(i,j,k) = D(i-l,j,k)*t + B(i,j,k) ENDIF 20 CONTINUE

Полное описание информационной структуры данного фрагмента в терминах графа алгоритма выглядит следующим образом (Nj описывает ограничение на значения внешних переменных, А, задает множество вершин (многогранник) в пространстве итераций, a F_t показывает вид покрывающих функций, описывающих дуги графа, / = 15):

N_l=in>l; N₂=\n> 1;

[1 < / < 2л;

J⁷!

i = i;

f = y'-i;

/' = / - 1; j" = n + 1;

2 < j < n + 1; 2 < / < 2л;

/ = i;

/ = 1;

1 < j < 1n\

\<k<n;

i = 2;

1 < j < In;

\<k<n;

3 < / < n + 1;

1 < j < 2л; 1 < к < n;

n>\;

/' = In; j' = n + 1;

/' = / - 1;

У = У

К — /с,

'/' = / - 1;

У = У к' = к.

N₄

n>\;

F_A

n>2;

Исследование этого описания позволяет определить всю необходимую информацию о структуре фрагмента и, в частности, выделить весь потенциальный параллелизм. Это же описание используется для визуализации различных аспектов тонкой структуры программ. Например, на рисунке 9.14, который может быть построен автоматически, показана структура данного фрагмента при п = 3.

Глава 9. Пользователь в среде параллелизма

577

Рис. 9.14. Визуализация информационной структуры фрагмента

Циклы ParDO

Начинать исследование микроструктуры процедуры можно с нахождения самого простого для последующего использования типа параллелизма — циклов ParDO по графу алгоритма. Если мы обнаружили, что некоторый цикл обладает свойством ParDO, то для того, чтобы этот факт использовать, как правило, не требуется серьезных дополнительных преобразований программы.

Вспомним, что цикл обладает свойством ParDO, если все его итерации независимы. Из данного определения сразу следует, что итерации ParDO-цикла могут быть выполнены в любом порядке, например, одновременно. Поскольку данное свойство относится к уже написанным циклам программы, то прямо в исходном тексте все циклы могут быть размечены в зависимости от того, обладают они этим свойством или нет.

В реальных программах циклы с данным свойством обладают одной особенностью. Если цикл помечен как ParDO по графу алгоритма, то это означает следующее: цикл в принципе обладает этим свойством, но для того, чтобы все итерации выполнять независимо, может потребоваться введение дополнительных переменных (что связано с возможной антизависимостью и зависимостью по выходу между различными итерациями этого цикла). Поэтому имеет смысл уточнить разметку программы и выделить циклы, которые не требуют никакого изменения. Рассмотрим следующий пример:

DO к = 2, nz - 1 DO i = 2, nx - 1

578 Часть III. Смежные проблемы и применение

DO j = 2, ny - 1

с-----------

tmpl = B(i,j,k)/C(i-l,j,k) tmp2 = A(i + l,j,k)/C(i-l,j,k)

с-----------

C(i,j,k) = C(i,j,k) - tmpl*D(i-l,j,k) D(i,j,k) = D(i,j,k) - tmpl*E(i-l,j,k) F(i,j,k,m) = F(i,j,k,m) - tmpl*F(i-l,j,k,m)

с-----------

B(i+l,j,k) = B(i+l,j,k) - tmp2*D(i-l,j,k) C(i+l,j,k) = C(i+l,j,k) - tmp2*E(i-l,j,k) F(i+l,j,k,m) = F(i+l,j,k,m) - tmp2*F(i-l,j,k,m) END DO END DO DO j = 2, ny - 1

F(nx,j,k,m) = F(nx,j,k,m)/C(nx,j,k)

F(nx-1, j , k,m) = (F(nx-1, j , k,m) - D (nx-1, j , k) *F (nx, j , k,m) ) + /C(nx-l,j,k)

END DO END DO

Система размечает входной текст с помощью директив ParDO и TrueParDO, показывая, какой цикл обладает данным свойством лишь в принципе, а какой можно сразу выполнять параллельно без какого-либо изменения. Каждая из этих директив относится только к ближайшему последующему циклу. Предыдущий пример система разметит следующим образом:

с ParDO

DO k = 2, nz - 1 DO i = 2, nx - 1 с ParDO

DO j = 2, ny - 1

с-----------

tmpl = B(i,j,k)/C(i-l,j,k) tmp2 = A(i+l,j,k)/C(i-l,j,k)

с-----------

C(i,j,k) = C(i,j,k) - tmpl*D(i-l,j,k) D(i,j,k) = D(i,j,k) - tmpl*E(i-l,j,k) F(i,j,k,m) = F(i,j,k,m) - tmpl*F(i-l,j,k,m)

с-----------

B(i+l,j,k) = B(i+l,j,k) - tmp2*D(i-l,j,k)

Глава 9. Пользователь в среде параллелизма

579

C(i+l,j,k) = C(i+l,j,k) - tmp2*E(i-l,j,k) F(i+l,j,k,m) = F(i+l,j,k,m) - tmp2*F(i-l,j,k,m) END DO END DO с TrueParDO

DO j = 2, ny - 1

F(nx,j,k,m) = F(nx,j,k,m)/C(nx,j,k)

F(nx-1, j , k,m) = (F(nx-1, j , k,m) - D (nx-1, j , k) *F (nx, j , k,m) ) + /C(nx-l,j,k)

END DO END DO

После такой разметки параллельная структура данного фрагмента во многом становится понятной. Более того, практически для всех существующих типов параллельных компьютеров этой информации о структуре фрагмента оказывается достаточно. Конкретный способ использования найденного ресурса параллельности зависит от архитектуры конкретного компьютера. Например, внешний цикл можно распараллелить, а самые внутренние циклы векторизовать. Причина того, что два цикла помечены как ParDO связана с использованием одних и тех же переменных tmpi и tmp2 на разных итерациях. Если их заменить на двумерные массивы, то оба цикла станут TrueParDO. В данном случае этого можно и не делать, поскольку такие простые действия и проверки должен выполнять компилятор.

Скошенный параллелизм

К сожалению, не всегда параллелизм программы можно полностью описать, отмечая только свойство ParDO у циклов исходного текста. Рассмотрим фрагмент программы:

DO j = 1, m

U(j,0) = О END DO DO k = 1, n

U(0,k) = 0

DO i = 1, m

U(i,k) = (F(i,k) - E(i-l,k)*U(i-l,k) - D (i, k-1) *U (i, k-1) ) + /B(i,k)

END DO END DO

580

Часть III. Смежные проблемы и применение

Только первый цикл этого примера обладает свойством ParDO, однако большого практического значения этот факт не имеет. Важно знать, существует ли какой-либо другой вид параллелизма и если да, то как его показать и использовать.

Если воспользоваться теорией, изложенной в главе 7, то можно легко определить, что данный фрагмент обладает скошенным параллелизмом. К сожалению, реальность такова, что скошенный параллелизм нельзя использовать так же просто, как координатный. Основная сложность заключается в том, что границы изменения параметров циклов в новом фрагменте описываются лишь кусочно-линейными функциями. А это значит, что либо преобразованная программа будет содержать большее число циклов, либо в границах циклов будут использованы функции min и мах, а моменты срабатывания некоторых операторов присваивания будут определять условные операторы, стоящие перед ними. Тем не менее, очень часто все это влечет лишь небольшие накладные расходы, которые полностью покрываются найденным параллелизмом. Одна из возможных форм записи предыдущего фрагмента показана ниже:

с \TrueParDO

DO j = 1, m U(j,0) = О END DO DO t = 1, n + m

IF( t.LE.n ) U(0,t) = 0 с \TrueParDO

DO k = MAX(1, t-m), MIN(t-l, n)

U(t-k,k) = (F(t-k,k) - E(t-k-l,k)*U(t-k l,k) -+ D(t-k,k-l)*U(t-k,k-l))/B(t-k,k) END DO END DO

Внутренний цикл фрагмента в такой записи обладает искомым свойством и может быть, например, векторизован. Если перед данным преобразованием выделить компоненты сильной связности, то оператор u(0,t) = 0 будет вынесен за пределы двойного гнезда, и условный оператор исчезнет.

Итак, надеемся, что все те сложности, которые были обозначены на пути освоения и использования параллельных вычислительных систем, постепенно исчезают. Если и не исчезают совсем, то, во всяком случае, появляется ощущение уверенности в их преодолении. Так и должно быть. Все эти проблемы появились не сегодня, накоплен опыт, произошло их осмысление, созданы многочисленные вспомогательные средства, появились высококлассные специалисты в данной области. Во многих центрах, имеющих вы-

Глава 9. Пользователь в среде параллелизма

581

сокопроизводительную вычислительную технику, уже создана инфраструктура поддержки пользователей. Если это не так, то обратитесь к заключительному параграфу данной книги.

Вопросы и задания

1. Возьмите достаточно большую программу и постройте для нее:

1.1. Граф вызовов.

1.2. Циклический профиль путей.

1.3. Графы управления для ключевых подпрограмм и функций.

1.4. Граф использования общей памяти.

1.5. Гистограмму времени исполнения отдельных процедур.

1.6. Информационный граф в терминах отдельных итераций для наиболее важных фрагментов.

2. Какие инструментальные средства были (или были бы) вам полезны для выполнения данной работы?

3. Какие функции для работы с графом вызовов были бы вам полезны, если граф для всей программы состоит из 1000 вершин?

4. Как определить свойство ParDO для цикла, содержащего обращение к процедуре?

5. "Разработайте систему, которая находит и показывает тонкую информационную структуру фрагмента.

§ 9.3. Организационная поддержка пользователя

Реальность сегодняшнего дня заключается в том, что исчезли принципиальные проблемы в потенциально бесконечном увеличении пиковой производительности компьютеров. Действительно серьезная проблема состоит в том, как этот колоссальный потенциал использовать. Очевидно, что недостаточно купить параллельный компьютер или объявить о создании суперкомпьютерного центра. Для того чтобы "дело пошло", для успешного решения всего множества смежных проблем необходим комплексный подход, рассматривающий в совокупности вопросы теории и практики, развития науки и образования, интегрирующий знания из различных предметных областей.

Конечно же, многое определяется тем, какие цели ставятся перед тем или иным центром. Однако даже в самых различных центрах имеется немало общего. Мы хотим поделиться своим опытом организации работ в Учебно-научном центре по высокопроизводительным вычислениям Московского государственного университета им. М. В. Ломоносова. Надеемся, что выска-

582

Часть III. Смежные проблемы и применение

занные соображения помогут вам правильно сориентироваться в практической деятельности. Многие подробности организации и технические детали нашего Центра можно найти на сайте http://www.Parallel.ru.

Учебно-научный центр по высокопроизводительным вычислениям создан на базе Научно-исследовательского вычислительного центра МГУ. Спектр деятельности Центра широк, что определяется как спецификой самой области высокопроизводительных вычислений, так и разнообразием стоящих перед ним задач. Среди приоритетных направлений можно назвать следующие:

□ поддержка фундаментальных научных исследований;

□ поддержка учебного процесса, подготовка и переподготовка специалистов;

□ создание инфраструктуры поддержки пользователей;

□ формирование сообщества ученых, работающих в данной области, и ряд других направлений.

Вычислительные ресурсы. Развитие вычислительной базы Учебно-научного центра проходит по двум направлениям, отражающим два основных направления развития суперкомпьютерной техники в мире. Это многопроцессорные вычислительные системы с общей и распределенной памятью. Каждый из этих классов компьютеров имеет свои достоинства и недостатки. Для компьютеров с общей памятью, в частности, для SMP-серверов, гораздо проще создавать эффективные программы, однако подобные системы, во-первых, достаточно дороги, а во-вторых, содержат лишь относительно небольшое число процессоров. Компьютеры с распределенной памятью, в частности, кластерные системы, могут содержать практически неограниченное число процессоров, но писать программное обеспечение для подобных систем, безусловно, сложнее.

В Центре должны присутствовать оба класса. Это определяется как требованиями со стороны прикладных задач, так и потребностью учебного процесса. Большая вычислительная мощность предоставляется кластерными системами. Вместе с тем, целый ряд алгоритмов накладывает исключительно жесткие требования к скорости межпроцессорного взаимодействия, чего можно достичь только на системах с общей памятью.

Перспективное направление, активно развиваемое в Центре в последнее время, — это метакомпьютинг. Он позволяет объединить воедино колоссальные вычислительные ресурсы компьютеров в сети, в частности, компьютеров в Интернете, или же объединить вычислительные ресурсы подразделений университета для решения отдельных задач. Приоритетная задача на ближайшее время состоит в создании унифицированной высокопроизводительной вычислительной среды.

С развитием собственно вычислительных ресурсов необходимо одновременное совершенствование материальной базы Центра в трех смежных направ-

Глава 9. Пользователь в среде параллелизма

583

лениях. Это создание высокоскоростной сетевой инфраструктуры, систем визуализации результатов численных экспериментов, а также средств хранения и обработки больших объемов данных. Как и любой хорошо сбалансированный организм, Центр по высокопроизводительным вычислениям не может развиваться только в направлении увеличения вычислительной мощности — необходимо согласованное развитие всей инфраструктуры.

Поддержка фундаментальных научных исследований. В том, что во многих областях науки необходимо использовать высокопроизводительную вычислительную технику, никого убеждать уже не надо. Однако заметим, что среди задач, решаемых на высокопроизводительных вычислительных системах, особое место занимают задачи, по существу отражающие интересы целых отраслей или областей знаний. На таких крупных областях исследований отрабатываются основные элементы технологии постановки и решения больших задач. Чтобы постоянно поддерживать их программное обеспечение на должном уровне, необходимо решить ряд трудных задач междисциплинарного характера. Одна из них состоит в разработке универсальной автоматизированной технологии адаптации программного обеспечения под требования архитектуры параллельных компьютеров. Другая задача определяется тем, что это, в свою очередь, требует привлечения высококвалифицированных специалистов очень широкого профиля. От них потребуются не только дополнительные знания по физике, механике, математике, химии и другим областям, но и хорошее владение как современной параллельной вычислительной техникой, так и технологиями параллельного программирования.

Поддержка учебного процесса, подготовка и переподготовка специалистов. Задача сложная, но необходимая. Без ее решения просто немыслимо какое-либо существенное продвижение вперед в будущем. Параллельные и высокопроизводительные вычислительные технологии уже стали неотъемлемой частью общей информационной культуры. Поэтому крайне необходимо создание соответствующей инфраструктуры учебного процесса: базовые и специализированные курсы, вычислительные практикумы, учебные материалы, поддержка выполнения курсовых и дипломных работ, спецсеминары, методическая и организационная деятельность и многие другие элементы. Объект особого внимания — подготовка и переподготовка преподавателей вузов.

Мировой опыт развития параллельных вычислений показывает исключительную важность развитой инфраструктуры поддержки пользователей. Деятельность по ее созданию составляет существенную часть работы Центра. Сюда входят как традиционные формы: консультационный центр, специальные представители Центра в подразделениях, hot-line, совместное выполнение проектов и т. п., так и новые способы работы с пользователями: электронная рассылка новостей Центра, разработка, внедрение и обучение инструментальным средствам исследования параллельных свойств программ, online-консультации, консультационный Интернет-Совет, Web-конференции и др.

584

Часть III. Смежные проблемы и применение

Важным фактором на пути реализации этих целей является объединение Учебно-научного центра с Информационно-аналитическим центром по параллельным вычислениям в сети Интернет http://www.Parallel.ru. Данный интернет-центр создан сотрудниками НИВЦ МГУ и уже признан научным сообществом в качестве центра общения специалистов данной области.

Сформулированные выше задачи мы не рассматриваем как локальные задачи для Московского университета. У многих коллективов есть уникальный опыт и интересные разработки — делитесь опытом, объединяйтесь, ставьте новые задачи, интересуйтесь проблемами других. В данной области, находящейся на стыке многих наук, нужно продвигаться вместе, интегрировать знания и усилия как на уровне отдельных ученых и научных групп, так и на уровне институтов и вузов. Только на этом пути можно получить качественно новые результаты и реальную отдачу от вложенных усилий, сохранить научные кадры и серьезно продвинуться вперед в решении многих задач.

Вопросы и задания

1. Предположим, что перед вами поставили задачу активизировать использование параллельных вычислений в научных исследованиях и учебном процессе вуза. Сильно ли изменится содержательная сторона вашей деятельности, если ориентироваться на собственные вычислительные ресурсы или на работу в удаленном режиме на суперкомпьютерных ресурсах другой организации?

2. Какие изменения, по вашему мнению, нужно внести в базовые учебные курсы на естественнонаучных факультетах, чтобы дать студентам представление о параллельных вычислительных технологиях? Что изменится, если не "дать представление", а научить студентов владению параллельными вычислительными технологиями? Рассмотрите варианты математических, физических, химических, биологических факультетов. Результаты опубликуйте на страницах http://www.ParalIel.ru.

3. Приведите примеры задач с каждого естественнонаучного факультета, которым для своего решения необходимы суперкомпьютерные вычислительные ресурсы.

4. Нужны ли суперкомпьютеры в гуманитарных исследованиях?

5. Как с вашей точки зрения должен быть устроен идеальный суперкомпьютерный центр? Какова должна быть программно-аппаратная инфраструктура? Какие элементы должны обязательно присутствовать в его организационной структуре?

Заключение

Параллельные вычисления: интеграция от А до Я

Вселенная не только необычнее,

чем мы воображаем. Она необычнее,

чем мы можем вообразить.

Из законов Мерфи

Итак, книга закончена. Мы назвали ее "Параллельные вычисления", безусловно поставив акцент на первом слове. Так чем же все-таки параллельные вычисления принципиально отличаются от просто вычислений? И в чем же, собственно говоря, состоит новизна книги? Ведь в наше время любые вычисления всегда имеют дело с компьютерами, программным обеспечением, численными методами, различными способами нечисловой обработки данных и т. п.

Ответ очень простой. Параллельные вычисления ничего не отрицают из того, что было, есть и будет использоваться в традиционных последовательных вычислениях.

Однако новейшие вычислительные средства, называемые суперкомпьютерами, параллельными вычислительными системами или как-нибудь иначе, настолько сильно отличаются по своему устройству от привычных персональных компьютеров и рабочих станций, что требуют для своего эффективного использования принципиально новой программной, математической и даже организационной среды. Вот об этих вычислительных средствах и окружающей их среде и шла речь в нашей книге.

В ней мы обсуждали в основном научные проблемы решения больших задач и лишь в конце слегка коснулись проблем организационных. В параллельных вычислениях оба типа проблем одинаково важны, поскольку конечной целью все же является реальное решение реальных задач. Понимание этого позволяет правильно оценить как то, что еще не сделано в параллельных вычислениях, так и то, что предстоит сделать.

Параллельные вычисления долгое время не были на острие внимания научной и, в том числе, вычислительной общественности. Мощности индивидуальных однопроцессорных компьютеров росли достаточно быстро, обеспечивая основные потребности большинства областей в решении текущих задач и поспевая в какой-то мере за ростом их сложности. Интерес к параллельным вычислениям сохранялся там, где большие задачи возникли давно. Но, в конце концов, случилось то, что должно было случиться — начался

586

Заключение

резкий подъем интереса к большим задачам едва ли не всюду. И тут стали обнаруживаться настораживающие обстоятельства: специалистов в области параллельных вычислений катастрофически не хватает; в основной своей массе вузы не готовят кадры, необходимые для постановки и решения больших задач; в области параллельных вычислений нет учебников, учебных пособий и т. д.

Причин возникновения создавшегося положения много. Но, возможно, главная из них связана с тем, что своевременно не был замечен и правильно оценен назревающий революционный с точки зрения технологии решения задач переход к использованию больших распределенных вычислительных систем. И это несмотря на то, что совершенно очевидные сигналы надвигавшихся трудностей появились уже давно. По мере развития вычислительной техники пользователю приходилось предоставлять все больший объем нетрадиционных сведений о параллельной структуре алгоритмов, распределении массивов данных и т. п. При этом ему самому было необходимо все в большей степени заботиться об использовании подобных сведений и нести ответственность за эффективность их применения. Теперь, с приходом кластеров и больших распределенных систем, пользователь почти весь процесс решения задач должен организовывать сам. Научиться этому, прочитав несколько страниц или даже томов инструкций, практически невозможно. Чтобы быть хорошим специалистом в области параллельных вычислений, необходимо иметь за плечами и опыт, и обширную фундаментальную подготовку.

Параллельные вычисления по сути своей являются интегрированной наукой. Они объединяют в единое целое сведения из таких разных областей, как архитектура компьютеров и вычислительных систем, системное программирование и языки программирования, различные методы обработки информации и т. п., фокусируя все это на построение процессов решения больших задач. Подобное объединение настолько глубоко и иерархично, что в каждой из областей, в свою очередь, также можно указать центры интеграции. Вспомните, например, сколько смежных знаний приходится привлекать для изучения математических моделей вычислительных процессов или информационной структуры алгоритмов и программ. Таких примеров можно привести очень много. По-видимому, эта особенность параллельных вычислений должна учитываться при составлении учебных программ, формировании учебных курсов и проведении научных исследований.

Отмеченная особенность параллельных вычислений связана с их интегрирующей ролью среди самих наук. Но у них проявляется и другая особенность — параллельные вычисления начинают стимулировать интеграцию научного сообщества.

Сейчас наступило время, когда большие задачи будут появляться часто и в разных областях. Там, где еще недавно достаточно было использования персонального компьютера, стремление либо получить большую точность, либо

Параллельные вычисления: интеграция от А до Я

587

усложнить модель изучаемого явления, либо просто ускорить счет естественным образом приводит к желанию использовать более мощную вычислительную технику. Но если эта техника имеет параллельную архитектуру, одного желания будет мало. Как мы уже знаем, программы с персонального компьютера в общем случае не переносятся эффективно на параллельные системы. Поэтому потребуется коренная их переделка, сопровождаемая дополнительным анализом задачи и, возможно, полной заменой методов обработки информации. Если на месте не у кого получить рекомендации, как это сделать, придется обращаться за помощью туда, где есть намеченная к использованию или похожая на нее вычислительная система.

Большие параллельные системы устанавливаются пока только в крупных организациях. Обычно здесь уже имеется достаточное количество техники меньшей мощности, накоплен опыт ее эксплуатации и подготовлен ряд больших задач. Как правило, вся техника связана локальной сетью, из которой возможен выход как на большую систему, так и в глобальную сеть. Эксплуатация систем параллельной архитектуры является делом исключительно сложным. Поэтому всегда создается группа сопровождения, состоящая из квалифицированных специалистов разного профиля, объединенных общей идеей — научиться и научить эффективно эксплуатировать новейшую технику, решать на ней большие задачи.

Такого рода группы оказываются теми звеньями, с которых начинается интеграция научного сообщества в области параллельных вычислений. К ним обращаются за консультациями. У них скапливается информация о том, какие пользователи и как осваивают новую технику. Они знают многое об узких местах вычислительных процессов и нередко имеют готовые рецепты по их преодолению. В силу накопленного опыта именно эти группы часто становятся инициаторами организации междисциплинарных семинаров по методам решения больших задач, технологиям программирования, повышению эффективности использования больших вычислительных систем. На них ложится составление всякого рода методических пособий и других материалов, ориентированных на применение в учебном процессе. В конце концов, эти группы оказываются в центре жизни научного общества, связанного с вычислениями. Все подготовлено для развертывания серьезного междисциплинарного сотрудничества.

Конечно, мы нарисовали несколько идеализированную картину. Для организации подобных групп сопровождения нужны не просто квалифицированные, но и очень активные кадры. Найти или воспитать их не легко. Но усилия на формирование инициативных групп сопровождения затратить стоит. Отдача не заставит себя ждать.

Мы уверены, что параллельные вычисления и все, что их окружает, еще не раз порадуют научное сообщество своими достижениями. Дерзайте, дорогу осилит идущий!

Список литературы

1. Андреев А. Н., Воеводин Вл. В., Жуматий С. А. Кластеры и суперкомпьютеры — близнецы или братья? // Открытые системы. — 2000. — № 5-6. - С. 9-14.

2. Андрианов А. Н., Бугеря А. Б., Ефимкин К. Н., Задыхайло И. Б. Норма. Описание языка. Рабочий стандарт / Препринт ИПМ им. М. В. Келдыша РАН. 1995. - № 120. - 50 с.

3. Антонов А. С, Воеводин Вл. В. Эффективная адаптация последовательных программ для современных векторно-конвейерных и массивно-параллельных супер-ЭВМ // Программирование. — 1996. — № 4. — С. 37-51.

4. Васильев Ф. П. Численные методы решения экстремальных задач. — М.: Наука, 1988. - 430 с.

5. Воеводин В. В. Вычислительные основы линейной алгебры. — М.: Наука, 1977. - 304 с.

6. Воеводин В. В. Информационная структура алгоритмов. — М.: МГУ, 1997. - 139 с.

7. Воеводин В. В. Компьютерная революция и вычислительная математика // Математика и кибернетика. — М.: Знание. — 1988. — Вып. 3. — 47 с.

8. Воеводин В. В. Массивный параллелизм и декомпозиция алгоритмов // ЖВМ и МФ. - 1995. - Т. 35. № 6. - С. 988-996.

9. Воеводин В. В. Математические модели и методы в параллельных процессах. — М.: Наука, 1986. — 296 с.

10. Воеводин В. В. Математические основы параллельных вычислений. — М.: МГУ, 1991. - 345 с.

11. Воеводин В. В. Параллельные структуры алгоритмов и программ. — М.: ОВМ АН СССР. 1987. - 148 с.

12. Воеводин В. В. Полиномиальное оценивание сложности алгоритмов // ЖВМ и МФ. - 1999. - Т. 39, № 6. - С. 1032-1040.

13. Воеводин В. В. Численные методы алгебры (теория и алгоритмы). — М.: Наука, 1966. - 248 с.

14. Воеводин В. В., Краснов С. А. Математические вопросы проектирования систолических массивов / Препринт ОВМ АН СССР. 1985. — № 80. — 26 с.

Список литературы

589

15. Воеводин В. В., Пакулев В. В. Определение дуг графа алгоритма / Препринт ОВМ АН СССР. 1989. - № 228. - 22 с.

16. Воеводин Вл. В. Статистический анализ и вопросы эффективной реализации программ // Вычислительные процессы и системы. — 1993. — № 9. - С. 249-301.

17. Воеводин Вл. В. Статистические оценки возможности выявления параллельной структуры последовательных программ // Программирование. — 1990. - № 4. - С. 44-54.

18. Воеводин Вл. В. Легко ли получить обещанный гигафлоп? // Программирование. - 1995. - № 4. - С. 13-23.

19. Воеводин Вл. В. Проект профессионального центра в сети Интернет // Тезисы докладов научной конференции "Интернет и современное общество" (30 ноября — 3 декабря. — 1999 г., г. Санкт-Петербург). СПб. — 1999. - 55 с.

20. Воеводин Вл. В. Суперкомпьютеры: вчера, сегодня, завтра // Наука и жизнь. - 2000. - № 5. - С. 76-83.

21. Воеводин Вл. В. Теория и практика исследования параллелизма последовательных программ // Программирование. — 1992. — № 3. — С. 38—53.

22. Воеводин Вл. В. Точное описание входных и выходных данных программ // Вестн. Моск. ун-та. Сер. 15, Вычислительная математика и кибернетика. — 1997. — № 1. — С. 41—44.

23. Воеводин Вл. В., Капитонова А. П. Методы описания и классификации архитектур вычислительных систем. — М.: МГУ. 1994. — 79 с.

24. Головкин Б. А. Параллельные вычислительные системы. — М.: Наука, 1980. - 520 с.

25. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. — М.: Мир. 1982. — 416 с.

26. Дымников В. П. Современные проблемы моделирования отклика климатической системы на малые внешние воздействия // Труды межд. теор. конф. "Проблемы гидрометеорологии и окружающей среды на пороге XXI века". — М.: Гидрометеоиздат, 2000. — С. 14—34.

27. Ершов А. П. Современное состояние теории схем программ // Проблемы кибернетики. — 1973. — № 27. — С. 87—110.

28. Забродин А. В., Луцкий А. Е., Марбашев К. X., Чернов Л. Г. Численное исследование обтекания летательных аппаратов и их элементов в реальных полетных режимах // Общероссийский науч.-техн. журнал "Полет". - 2001. - № 7. - С. 21-29.

29. Задыхайло И. Б. Организация циклического процесса счета по параметрической записи специального вида // ЖВМ и МФ. — 1963. — Т. 3.

№ 2. - С. 337-357.

590

Список литературы

30. Коновалов Н. А., Крюков В. А., Погребцов А. А., Сазанов Ю. Л. С-DVM — язык разработки мобильных параллельных программ // Программирование. — 1999. — № 1. — С. 20—28.

31. Крюков В. А., Удовиченко Р. В. Отладка DVM-программ // Программирование. - 2001. - № 3. - С. 19-29.

32. Арапов Д. М., Калинов А. Я., Ластовецкий А. Л., Ледовских И. Н., По-сыпкин Н. А. Язык и система программирования для высокопроизводительных параллельных вычислений на неоднородных сетях // Программирование. - 2000. - № 4. - С. 55-80.

33. Лебедев С. А. Электронно-вычислительные машины // Сессия АН СССР по научным проблемам автоматизации производства. Пленарные заседания. - М.: АН СССР. - 1957. - Т. 1. - С. 162-180.

34. Котов В. Е., Марчук Г. И. Проблемы вычислительной техники и фундаментальные исследования // Автомат, и вычисл. техн. — 1979. — № 2. — С. 3-14.

35. Мультипроцессорные системы и параллельные вычисления / Под ред. Ф. Г. Энслоу. - М.: Мир, 1976. - 384 с.

36. Оре О. Теория графов. — М.: Наука, 1980. — 336 с.

37. Михайлов А. П., Самарский А. А. Компьютеры и жизнь. — М.: Педагогика, 1987. - 128 с.

38. Уилкинсон Дж. X. Алгебраическая проблема собственных значений. — М.: Физматгиз, 1963. — 564 с.

39. Фаддеева В. Н., Фаддеев Д. К. Параллельные вычисления в линейной алгебре // Кибернетика. - 1977. - № 6. С. 28-40; 1982. - № 3. -С. 18-31, 44.

40. Хмелев Д. В. Восстановление линейных индексных выражений для сведения программ к линейному классу // ЖВМ и МФ. — 1998. — Т. 38. № 3. - С. 532-544.

41. Частиков А. П. От калькулятора до супер-ЭВМ // Вычислительная техника и ее применение. — М.: Знание. — 1988. — 96 с.

42. Abramov S. М., Adamowitch А. 1., Nesterov 1. A., Pimenov S. P., Shevchuck Yu. V. Autotransformation of evaluation network as a basis for automatic dynamic parallelizing // NATUG'1993 Spring Meeting "Transputer: Research and Application", May 10—11, 1993.

43. Bailey D. H. Twelve ways to fool the masses when giving performance results on parallel computers / RNR Technical Report RNR-91-20, NASA Ames Research Center, Moffett Field CA 94035, June 11, 1991.

44. Baur W., Strassen V. The complexity of partial derivatives // Theor. Comput. Sci., - 1983. - 22. - P. 317-330.

Список литературы

591

45. Berry М. et al. The Perfect Club Benchmarks: effective performance evaluation of supercomputers // Int. J. of Supercomputer Applications. — 1989. - 3(3) - P. 5-40.

46. Cybenko G., Kipp L., Pointer L., Kuck D. Supercomputer performance evaluation and the Perfect Benchmarks / Tech. Rep. 965, CSRD, Univ. of Illinois, 1990.

47. Davies J. et al. The KAP/S-1: An advanced source-to-source vectoriser for the S-l Mark 11 Supercomputer // IEEE Proc. of 1CPP. - 1986. - P. 833-835.

48. Fiacco A. V., McCormick J. P. Nonlinear programming: sequential unconstrained minimization techniques. — N. Y.; Research Analyses Corp., 1968. — 326 p.

49. Kesselman C, Foster 1. Eds. The Grid: blueprint for a new computing infrastructure. Morgan Kaufmann, 1999.

50. Gelernter D. Parallel programming in Linda / Technical Report 359, Yale University Department of Computer Science, Jan., 1985.

51. Gustafson J. L., Todi R. Conventional benchmarks as a sample of the performance spectrum // The Journal of Supercomputing. — 1999. — V. 13. — P. 321-342.

52. Huson C. et al. The KAP/205: An advanced source-to-source vectoriser for the Cyber 205 supercomputers // IEEE Proc. of 1CPP. - 1986. - P. 827-832.

53. Konovalov N. A., Krukov V. A., Mihailov S. N. and Pogrebtsov A. A. Fortran DVM — a language for portable parallel program development // Proceedings of Software For Multiprocessors & Supercomputers: Theory, Practice, Experience. Institute for System Programming, RAS, Moscow, 1994.

54. Kung H. T. Why systolic architecture? // Computer. — 1982. — 15. № 1. — P. 37-46.

55. Lamport L. The coordinate method for parallel execution of DO loops // Proc. 1973 Samagore Comput. Conf. Parallel Process., N. Y., IEEE. — 1973. - P. 1-12.

56. Lamport L. The hyperplane method for an array computer // Proc. 1974 Samagore Comput. Conf. Parallel Process., Lect. Notes Comput. Sci., 24. Berlin: Springer-Verlag. — 1975. - P. 113—131.

57. Lewis T. G. Foundation of parallel programming: machine-independent approach. IEEE Computer Society Press, 1994. — 282 p.

58. Maske T. et al. The KAP/ST-100: A Fortran translator for the ST-100 attached processor // IEEE Proc. of 1CPP. - 1986. - P. 171-175.

59. McMahon F. H., The Livermore Fortran Kernels: a computer test of the numerical performance range / Technical Report UCRL-53745, Lawrence Livermore National Laboratory, Livermore, Calif. — Dec, 1986.

592

Список литературы

60. Polychronopoulos С. D. Compiler optimizations for enhancing parallelism and their impact on architecture design // IEEE Trans, on Computers. — 1988. — V. 37. № 8. - P. 991-1004.

61. Borck W.C., McReynolds R.C., Slotnik D.L. The SOLOMON computer // AF1PS Conf. Proa, 22. - 1962. - P. 97-107.

62. "The FORGE Product Set", Applied Parallel Research, Inc.

63. Voevodin V. V. Information structure of sequential programs // Russ. J. of Num. An. and Math. Modelling. - 1995. - V. 10. № 3. - P. 279-286.

64. Voevodin V. V. Mathematical foundations of parallel computing. World Scientific Publishing Co., Series in computer science. 1992. V. 33. — 343 p.

65. Voevodin V. V., Voevodin VI. V. V-Ray technology: a new approach to the old problems. Optimization of the TRFD Perfect Club Benchmark to CRAY Y-MP and CRAY T3D supercomputers // Proc. Of the High Performance Computing Symposium'95, Phoenix, Arizona, USA. — 1995. — P. 380—385.

66. Arpaci-Dusseau R., Wong F., Culler D., Martin R. Architectural requirements and scalability of the NAS Parallel Benchmarks // Proc. of SC99 Conference on High Performance Networking and Computing. — Nov. 1999.

67. Zhiyu Shen, Zhiyan Li, Pen-Chung Yew. An empirical study of Fortran programs for parallelizing compilers // IEEE Trans, on Parallel and Distributed Systems. — July 1990. - P. 350—364.

Интернет-ресурсы

1. http://www.citforum.ru — сервер информационных технологий.

2. http://www.parallel.ru — Информационно-аналитический центр по параллельным вычислениям в сети Интернет.

Предметный указатель

L-свойство матрицы 362

Автокод 31

Автоматическое распараллеливание

программ 222 Автономная программная система 323

V-Ray 436 Адрес слова 15

физический 27 Алгоритм:

детерминированный 193

линейный 349

недетерминированный 193

параллельный 199

Штрассена 206 Альтернативные многогранники 365 Анализ ошибок:

обратный 521

прямой 520 Арифметика:

разрядно-параллельная 51

разрядно-последовательная 51 Арифметико-логическое устройство 16 Архитектура:

ccNUMA 73

NUMA71

UMA71

Байт 15

Барьерная синхронизация 144

Бенчмарк 166

Банк памяти 53 Бит 14

Вектор:

данных 124

граничных значений 462

задержек 462

реализации 462 Величина, заданная на области 313 Вершина:

входная 192

выходная 192 Взаимодействие процессов:

Put/Get 299

Send/Receive 299 Внутренний код 16 Волновой фронт 406 Время разгона конвейера 125 Выделение стандартных операций 419 Выражение индексное нелинейное 450 Вычисления избыточные 376 Вычислительное ядро 36 Вычислительный кластер 146 Вычисляемые ветвления 449

Гиперкуб 69

Гомоморфизм простой 467 Гомоморфная свертка 467 Гомоморфный:

образ 467

прообраз 467

594

Предметный указатель

Граф:

алгоритма 192

влияния 334

вызовов процедур 561

вызовов процедур расширенный 563

зависимостей 333

максимальный 346

минимальный сверху 347

минимальный снизу 346

обратный 347

простой 353

элементарный 354

покрытие 348 информационный 329 использования общей памяти 566 лексикографически правильный 373 направленный 478

направляющий вектор 478 параллельная форма 194

каноническая 194

линейная 195

максимальная 194

обобщенная 195

строгая 194 параметризованный 193 передач управления 327 плоский 488 программы 327

простой канонический вид 371 расширенный 450 регулярный 472

бесконечный 472

базовые векторы 472

базовый многогранник 474

главный регулярный подграф 473

опорные вершины 474 решетчатый 336 сильно связанный 405 системы 84 управления 327

процедурный 569 управляющий 327 эквивалентности 409 элементарный канонический

вид 371 Граф-машина 459 Графовая модель программы 326

Денотационный подход 325 Динамическое порождение

процессов 298 Дискретное неравенство Беллмана 466 Дискретное уравнение Беллмана 466 Дистрибутивная решетка 403 Доля последовательных вычислений 87

Зависимость 345

data-flow 346

анти 346

истинная 346

по входу 346

по выходу 346 Зависимые точки графа 345 Загруженность:

системы 82

устройства 80 Закон:

Амдала 1-й 86

Амдала 2-й 87

Густавсона—Барсиса 89

Мура 43 Запятая:

плавающая 21

фиксированная 21 Значение неготовое 302

Иерархия памяти 58 Иллюстративная модель компьютера 38 Информационная структура программы 324 тонкая 324 Информационное ядро 197 Информационные типовые структуры 446 гипотеза 446 История реализации программы 329 Итерация 343 цикла 343

Предметный указатель

595

Каскадный переключатель 66 Классификация:

В. Хендлера 103

Д. Скилликорна ПО

Л. Шнайдера 107

М. Флинна 97

М. Флинна MIMD 98

М. Флинна MISD 98

М. Флинна S1MD 98

М. Флинна S1SD 97

Р. Хокни 100

Т. Фенга 101 Когерентность кэш-памяти 72 Код:

внутренний 16

машинный 16 Команда:

векторная 48

машинная 16

скалярная 48 Коммуникационный профиль

приложений 175 Коммутатор матричный 66 Компилятор 16 Компьютер:

ATLAS 53

BBN Butterfly 72

Beowulf-кластеры 147

CDC-6600 53

CDC-7600 53

Cm* 71

Connection Machine 70

Cray C90 116

Cray T3D/T3E 142

Cray-1 57

Hewlett-Packard Superdome 135

IBM 701 51

IBM 704 51

IBM 709 51

ILLIAC IV 54

STRETCH 52

БЭСМ-6 29

M-20 29

MBC-1000M 150

Сетунь 24

Стрела 56

SMP64

с архитектурой ccN UMA 73

с архитектурой NUMA 71

с архитектурой UMA 71

с общей памятью 63

с распределенной памятью 64 Конвейер:

длина 47

команд 53

ступень 47 Концепция неограниченного

параллелизма 199 Кортеж система Linda 268 Критическая секция программы 233

Лексикографически:

неупорядоченные функции 370

упорядоченные функции 370 Лексикографический порядок:

в линейном пространстве итераций 344

в программе 344

в пространстве итераций 345 Линейные фрагменты 341 Линейный класс алгоритмов 349 Локальность:

вычислений 57

использования данных 57

Макровершина 405 Макрограф 405 Макродуга 405 Макропараллелизм 374 Массивов:

выравнивание 239

распределение 238 Матрица:

алгоритма вариационная 505

информационной связности 506 взвешенная 506

инциденций 507

смежностей 507

596

Предметный указатель

Машинный нуль 22 Метакомпьютинг 155

Condor 155

GIMPS 156

Globus 156

РАСХ-МР1 155

SETI@home 156 Микропараллелизм 374 Модель программирования:

master/slaves 274

SPMD 275

Норма 403

Область 311 Обработка:

конвейерная 46

параллельная 44 Обратное выполнение цикла 418 Общая шина 65 Общие данные DVM 242 Операнд 15

Операционная система 17 Операционно-логическая история 328 Операционный подход 325 Операция 15

коллективная 293

произведения областей 311 Опорная область 343 Опорное:

гнездо циклов 342

пространство 342 Опорный многогранник 342 Отношение:

влияния 335

зависимости 333

Память 15

адресуемая 26 быстрая 26

виртуальная 28

время доступа 25

конфликты 117

кэш 26

медленная 26

неадресуемая 26

оперативная 26

постоянная 26

проблема когерентности кэш 72

разрядно-параллельная 51

разрядно-последовательная 51

регистровая 26

сверхбыстрая 26 Параллелизм:

внутренний 207

координатный 396

массовый 421

скошенный 396 Параллельная форма графа 194

высота 194

каноническая 194

линейная 195

обобщенная 195

строгая 194

ширина 194

ширина яруса 194

ярус 194 Параллельные множества 373 Параллельный алгоритм 199 Передача сообщений:

асинхронная 285

синхронная 280 Переменная:

координатная 252

локальная 226

неготовая 303

общая 226

размазанная 251

распределенная по сети 250 Перестановка циклов 416 Переупорядочивание операторов 417 Покрытие графа 348 Полукольцо разверток 465 Портабельность программ 33 Порядок:

линейный 195

частичный 192

Предметный указатель

597

Правило собственных вычислений 237 Принцип близкодействия 488 Проблема отображения 444 Программа 31

иерархическое представление

структуры 567 история операционно-

логическая 328 история реализации 329 канонизация 448 линейный участок 567 нелинейность устранимая 448 преобразование:

специальное 411

треугольное 419

элементарное 413 L-дерево 567 векторизация 123 графовая модель 326 детерминированная 193 исследование:

динамическое 571

статическое 341 линейная 340 линейный класс 340 недетерминированная 193 параллельная структура 373 параметр:

младший 342

старший 342 портабельность 33 преобразователь 326 простая 353 распознаватель 326 элементарная 354 Производительность: Flops 165 MIPS 164

асимптотическая 86 пиковая 80 реальная 80 Пространство: кортежей 268 итераций 343 переупорядочивание 411 расщепление 418

линейное 343 Процесс сдваивания 200 рекуррентный 203

Процессор 17

матричный 54

с архитектурой VLIW 62

суперскалярный 62

центральный 17 Процессы параллельные

FORK/JOIN 226 Прямая подстановка 448

Развертка 394 вектор: граничных значений 462 задержек 462 реализации 462 кусочно-линейная 397

направляющий вектор 399 минимальная 464 нулевая 403 обобщенная 394 обобщенная самая строгая 423 основная 395 расщепляющая 395 с ограничениями 463 строгая 394 Раскрутка цикла 131 Распределение цикла 417 Расслоение памяти 52 Рекуррентные соотношения 471

Свойства метакомпьютера 157 Связи фиктивные 450 Связь:

информационная 327

операционная 327

по управлению 327

транспортная 488

шинная 488 Сдваивания рекуррентного процесса 203 Сеть:

каскадная перестраиваемая 41

латентность 151

пропускная способность 151

598

Предметный указатель

Синхронизация барьерная 144 Система коммутации 65 Система программирования:

DVM 235

Linda 268

mpC 248

MPI 275

MPI-2 298

OpenMP 225

НОРМА 309

Т-система 301 Систолическая:

система 483

ячейка 483 Систолический массив 482 Скалярное произведение 403 Скашивание цикла 418 Слияние циклов 416 Слово 15

адрес 15

длина 15

содержимое 15 Спецпроцессор 61 Список Тор500 167 Срабатывание оператора 343 Стоимость:

операции 80

работы 80 Сумматор 24

Теневые грани массива 242 Теорема об информационном

покрытии 348 Тестирование компьютеров:

HINT 176

UNPACK 166

NPB 172

PERFECT Club Benchmarks 171

SPEC 175

STREAM 168

Top500 167

бенчмарк 166

Ливерморские циклы 170 Технологии параллельного программирования 220

Топология:

гиперкуба 69

связи процессоров 68 Точка лексикографического максимума 356

Укладка графа 481 Умножитель 24 Ускорение 83 Устройство 16

ввода/вывода 16

арифметико-логическое 16

загруженность 80

конвейерное 79 время разгона 125 длина 79 ступень 79

оперативное запоминающее 26

простое 79

управления 17 Уточнение внешних переменных 453

Формула Эйлера 499 Фронт:

волновой 406

вычислений 406 Функции:

базовые 249

лексикографически неупорядоченные 370

лексикографически упорядоченные 370

покрывающие 348

сетевые 254

узловые 249

чистые 302

Центральный процессор 17 Цикл:

ParDo 374

TrueParDo 578



	В. В. Воеводин, Вл. В. Воеводин

	Параллельные ычислення

	Рекомендовано Министерством образования Российской Федерации в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению 510200 "Прикладная математика и информатика"

	Санкт-Петербург «БХВ-Петербург» 2002



	УДК 681.3.06+519.68 ББК 32.973 В63

	Воеводин В. В., Воеводин Вл. В. В63 Параллельные вычисления. — СПб.: БХВ-Петербург, 2002. — 608 с: ил. ISBN 5-94157-160-7 Книга известных российских ученых посвящена обсуждению ключевых проблем современных параллельных вычислений. С единых позиций рассматриваются архитектуры параллельных вычислительных систем, технологии параллельного программирования, численные методы решения задач. Вместе со строгим описанием основных положений теории информационной структуры программ и алгоритмов, книга содержит богатый справочный материал, необходимый для организации эффективного решения больших задач на компьютерах с параллельной архитектурой. Для научных работников, инженеров, преподавателей, аспирантов и студентов естественнонаучных специальностей

	УДК 681.3.06+519.68 ББК 32.973

	Группа подготовки издания: Главный редактор Екатерина Кондукова Зам. главного редактора Анатолий Адаменко Зав. редакцией Анна Кузьмина Редактор Петр Науменко Компьютерная верстка Натальи Смирновой Корректор Наталия Першакова Дизайн обложки Игоря Цырульникова Зав. производством Николай Тверских

	Лицензия ИД № 02429 от 24.07.00. Подписано в печать 23.09.02. Формат 70x100¹/i6- Печать офсетная. Усл. печ. л. 49,02. Тираж 3000 экз. Заказ № "БХВ-Петербург", 198005, Санкт-Петербург, Измайловский пр., 29. Гигиеническое заключение на продукцию, товар № 77.99.02.953.Д.001537.03.02 от 13.03.2002 г. выдано Департаментом ГСЭН Минздрава России. Отпечатано с готовых диапозитивов в Академической типографии "Наука" РАН 199034, Санкт-Петербург, 9 линия, 12.

	ISBN 5-94157-160-7 © Воеводин В. В., Воеводин Вл. В., 2002 © Оформление, издателвство "БХВ-Петербург", 2002



	Предисловие Много ли надо знать о параллельных вычислениях? Ничего нельзя сказать о глубине лужи, если не попасть в нее. Из законов Мерфи В активе человечества имеется не так много изобретений, которые, едва возникнув, быстро распространяются по всему миру. Одним из них является компьютер. Появившись в середине двадцатого столетия, он через несколько десятков лет повсеместно стал незаменимым инструментом и надежным помощником в обработке самой разнообразной информации: цифровой, текстовой, визуальной, звуковой и др. Известно, что первопричиной создания компьютеров была настоятельная необходимость быстрого проведения вычислительных работ, связанных с решением больших научно-технических задач в атомной физике, авиастроении, климатологии и т. п. Решение таких задач и сейчас остается главным стимулом совершенствования компьютеров. Однако в настоящее время основная сфера их применения связана с совсем иной деятельностью, в которой вычислительная составляющая либо отсутствует совсем, либо занимает небольшую часть. Работа биржи, управление производством, офисные приложения, корпоративные информационные системы, процессы образования, игры, ведение домашнего хозяйства — это всего лишь отдельные примеры областей невычислительного использования компьютеров. В подобных областях вполне приемлемо применение персональных компьютеров и рабочих станций для достижения необходимых целей. Относительная простота процесса использования и комфортная программная среда формируют здесь устойчивое впечатление о компьютере как о весьма дружественном помощнике. И мало кто из пользователей такой техники догадывается и, тем более, знает, что все радикально меняется с переходом к решению больших и очень больших задач. Компьютеры становятся весьма сложными, куда-то пропадает дружественность интерфейса, программная среда переходит на жесткий командный язык и начинает требовать от пользователей предоставления такой информации, которая не всегда известна, и т. п. Эта книга о больших и супербольших компьютерах и особенностях их использования. О тех проблемах, с которыми неизбежно приходится сталки-



	Глава 1 Что скрывают "обыкновенные" компьютеры Внутри каждой большой задачи сидит маленькая, пытающаяся пробиться наружу. Из законов Мерфи В своем развитии персональные компьютеры достигли высокого уровня совершенства. Они компактны, обладают большой скоростью выполнения заданий и, что особенно важно, достаточно просты в обращении. Все эти качества привели к их широкому использованию, в том числе среди лиц, не имеющих специальной компьютерной подготовки. По существу персональный компьютер становится таким же привычным устройством, как пылесос, кухонный комбайн и телевизор. Он остается удобным инструментом до тех пор, пока не приходится решать очень большие задачи. Конечно, в этом случае можно попытаться использовать самый быстрый персональный компьютер с максимально большой памятью. Можно также перейти к использованию рабочей станции. Однако увеличение возможностей на этом пути все же ограничено. И тогда приходится обращаться к суперкомпьютерам. Согласно распространенному мнению, суперкомпьютер — это такой компьютер, у которого все самое-самое: супербольшая скорость, супербольшая память, супербольшая цена. Это действительно так. Но, переходя от персонального компьютера к суперкомпьютеру, пользователю приходится также сталкиваться с очень большими трудностями в их использовании. Главное, на суперкомпьютерах отсутствует характерная для персональных компьютеров пользовательская среда. Оказывается, что использовать суперкомпьютер гораздо сложнее, чем персональный компьютер, а некоторые суперкомпьютеры даже очень сложно. Кроме этого, выясняется, что разных типов суперкомпьютеров довольно много, они не совместимы друг с другом, и на разных суперкомпьютерах совсем разные пользовательские среды. Взвесив предстоящие трудности, пользователи нередко отказываются от использования суперкомпьютеров вообще или переходят к более простым суперкомпьютерам. Если же пользователь все же решается использовать суперкомпьютер, ему важно понимать причины появления новых трудностей и пути их преодоления. Современные суперкомпьютеры возникли не вдруг. Они являются продуктом длительного развития "обыкновенных" компьютеров, к которым, кстати, относится и типовой персональный компьютер. Эти "обыкновенные" компью-



	22	Часть I. Параллельные вычислительные системы

	Тогда будем иметь, что 1/2 < \|я\| < 1. (1.4) Число а называется мантиссой числа х, число b — его двоичным порядком. Если х = О, то считается, что а = 0, а число b не определено. Пусть на изображение порядка без знака отводится г битов, на изображение мантиссы без знака % — г битов. Представив порядок и мантиссу как числа с фиксированной запятой, мы получаем представление числа х с плавающей запятой. При изображении мантиссы и порядка нет отмеченной выше потери относительной точности, т. к. в обоих случаях положение запятой строго определено. Порядок всегда является целым числом, а первый после запятой двоичный разряд мантиссы всегда равен 1. Порядок представляется точно. Мантисса будет точно представлена только для чисел, которые в двоичном разложении имеют не более % — г ненулевых разрядов. Все числа, которые могут быть представлены с плавающей запятой, всегда представляются с высокой относительной точностью. Это числа из диапазона T^r <\х\<2^г~¹. Минимальное положительное число со, которое можно представить с плавающей запятой, называется машинным нулем. Ясно, что в нашей трактовке представления чисел ю = 2-²\ Все числа из диапазона -Т¹' <х< Т¹' изображаются нулем. В разных компьютерах под порядок и мантиссу отводятся разные числа разрядов. В частности, в упоминавшемся уже компьютере Сгау-1 на мантиссу со знаком выделено 49 разрядов, на двоичный порядок — 15 разрядов. Огромный диапазон представляемых чисел и большая их относительная точность, безусловно, определены ориентацией компьютера Cray-1 на научно-технические расчеты. В современных компьютерах используются оба способа представления чисел. Операции над числами с фиксированной запятой выполняются быстрее, чем над числами с плавающей запятой. Это связано с тем, что при реализации операций с плавающей запятой по существу приходится выполнять все действия с парами чисел с фиксированной запятой. Рассмотрим два числа х = а2^ь, у = c2^d с плавающей запятой. Имеем ху = {ас)Ъ^ь+<1).



	Глава 1. Что скрывают "обыкновенные" компьютеры	41

	Вопросы и задания 1. Предположим, что один землекоп может за час вырыть яму размером 1x1x1 м³и способен работать в таком режиме достаточно долго. За какое время бригада из 5, 10, 20 землекопов выроет яму размером 2x2 м² и глубиной 1 м? 2. Постройте график времени выполнения работы в зависимости от числа землекопов в бригаде. 3. Повторите задания пп. 1, 2 для ямы размером 10x10 м², глубиной 1 м и бригады из 10, 100 землекопов. 4. Чем принципиально различаются эти варианты? 5. Пусть предпринимается попытка увеличить реальную мощность производственного отдела из иллюстративной модели компьютера путем наращивания однотипного оборудования. Не кажется ли вам, что возникнет ситуация, аналогичная рассмотренной в пп. 1—4? 6. Для создания очень мощного компьютера часто объединяют вместе большое число персональных компьютеров. Пусть их будет п. Для обмена информацией между компьютерами необходимо создать коммуникационную сеть. Теоретически самый простой способ — соединить каждый компьютер с каждым прямыми связями, т. к. в этом случае информация вроде бы должна передаваться наиболее быстро. Всего потребуется п(п — 1) таких связей. Рассмотрите подобные коммуникационные сети для п = 3, 5, 8. 7. В реальных компьютерах величина п может достигать 10⁴—10⁵. Можете ли вы представить всю совокупность связей в этом случае, если они организованы согласно п. 6? 8. Пусть снова сверхмощный компьютер создается как объединение п персональных компьютеров. Построим неориентированный граф, в котором вершины символизируют персональные компьютеры, а ребра — прямые связи. Будем считать, что граф связный, т. е. для каждой пары вершин существует связывающая их цепь ребер. Такой граф называется коммуникационным. Исследуйте коммуникационный граф из п. 6. 9. Пусть в коммуникационном графе существуют не все ребра. Будем считать, что передача информации между персональными компьютерами может осуществляться вдоль любой цепи коммуникационного графа, связывающей соответствующие вершины. Постройте различные коммуникационные графы, уменьшая общее число ребер. 10. Если вам удалось построить коммуникационный граф, имеющий п вершин, п ребер и такой, что между любыми двумя вершинами существует цепь, состоящая не более чем из 21og₂« ребер, то вы на правильном пути. Соответствующие коммуникационные сети называются каскадными перестраиваемыми сетями.



	Глава 2 Как повышают производительность компьютеров Независимо от того, куда вы идете, это в гору и против ветра. Из законов Мерфи Замечено, что эмоциональное состояние человека, впервые сталкивающегося с суперкомпьютером, проходит несколько стадий. Сначала он испытывает что-то вроде эйфории, начитавшись рекламных данных о компьютере и находясь в предвкушении быстрого разрешения всех своих вычислительных проблем. После первого запуска своей программы у него возникает недоумение и подозрение, что что-то он сделал не так, поскольку реально достигнутая производительность слишком сильно отличается от ожидаемой. Он запускает программу повторно, но результат, если и меняется в лучшую сторону, то очень и очень слабо. Он идет к местному компьютерному гуру, и тут-то его поджидает настоящий удар. Сначала ему говорят, что полученные им 5% от пиковой производительности компьютера являются не таким уж и плохим результатом. А затем добавляют, что если он хочет "выжать" из такой вычислительной системы максимум, то для него вся работа только начинается. Нужно обойти возможные конфликты в памяти и постараться сбалансировать вычислительную нагрузку между процессорами. Необходимо подумать об оптимальном распределении данных, помочь компилятору разобраться со структурой программы, заменить последовательные части алгоритма на параллельные. Надо сделать еще много чего, что, вообще-то говоря, раньше совершенно не было свойственно работе прикладного программиста. И все прежние проблемы, характерные для последовательных компьютеров и традиционного последовательного программирования, разумеется, остаются... Эту ситуацию заметили давно и предлагали различные способы ее решения. Изменялась архитектура компьютеров, развивалась среда программирования, но оставалось постоянным одно — "головная боль" прикладных программистов, решивших серьезно встать на путь параллельных вычислений. Оговоримся сразу, мы далеки от мысли кого-либо обвинять в такой ситуации. Инженерами и программистами проделана колоссальная работа, без которой и предмет нашего обсуждения не существовал бы. Просто область сложна сама по себе, да и жизнь постоянно вносит свои коррективы. Создавая кэш-память, которая прекрасно работает в одном микропроцессоре, никто и не подозревал, какие проблемы она принесет в многопроцессорных



Глава 2. Как повышают производительность компьютеров			43

системах. Только научились анализировать структуру исходного текста программ на Fortran, как появились языки С и C++, привнесшие значительные трудности в статический анализ параллельной структуры программ. Чуть ли не единственным достижением, постоянное развитие которого никак не задевает программиста, является увеличение тактовой частоты: программа работает быстрее, а он для этого ничего дополнительного не делает. В той области, которая является предметом нашего исследования, всегда было и всегда будет очень много нового, непривычного, часто даже парадоксального. Во все времена для компьютеров, работающих на предельных скоростях, будут требоваться технологии, отличающиеся от "массовых", они всегда будут "на передовом крае", и, следовательно, они всегда будут вызывать трудности в использовании. Но для того и создана данная книга, чтобы показать возможные проблемы и пути их решения. Но это немного позже. В данной главе мы остановимся на базовых понятиях и посмотрим, как проходило развитие и каковы основные особенности современных компьютеров. § 2.1. Усложнение и наращивание аппаратных средств Бесспорно, успехи микроэлектроники впечатляют. Согласно закону Мура, не имеющего строгого доказательства, но подтверждающегося уже не один десяток лет, производительность "обычных" компьютеров удваивается каждые полтора года. Однако попытаемся разобраться, только ли этими причинами определяются те рекордные показатели производительности, которыми обладают современные компьютеры. Обратимся к известным историческим фактам и проведем простое сравнение (рис. 2.1). На одном из первых компьютеров мира — EDSAC, появившемся в 1949 году и имевшем время такта 2 микросекунды, можно было выполнить 2« арифметических операций за 18« миллисекунд, т. е. в среднем 100 арифметических операций в секунду. Сравним эти данные, например, с характеристиками одного вычислительного узла современного суперкомпьютера Hewlett-Packard Superdome: время такта приблизительно 1,3 не (процессор РА-8700, 750 МГц), а пиковая производительность около 192 миллиардов арифметических операций в секунду.

EDS АС 1949 год тактовая частота 0,5 МГц	1,5x10	>	HP Superdome 2001 год 770 МГц

производительность 10²оп/с 1,9х10⁹ ^> 1,9х10¹¹оп/с

Рис. 2.1. Увеличение производительности ЭВМ — за счет чего?



	Глава 2. Как повышают производительность компьютеров	91

	Поэтому всегда имеем: Ргб > Рл при s > 1 Ргб ~ Фа ^пР^и больших N₂/N\, /?гб ~ Рл ^ПР^И малых N₂/N\. Кроме этого, из (2.10) вытекает, что во всех случаях о Фа 1 + С$ - 1)р^ Подставляя это выражение для р_ГБ в (2.9), получаем, что l + (s-l)P_A ф_А+(1-р_А) Таким образом, если учесть связь между р^ ^и Ргб> ^то оценки ускорения по Амдалу и по Густавсону—Барсису полностью совпадают. В частности, если взять p^ = 0,5, то эквивалентное значение р_ГБ должно быть равным не 0,5, как это берется в примере 1.6 из [57], a s/(s + 1). И тогда R-A ~ -^гб ⁼ 2s/(s + 1), что по обеим оценкам одинаково плохо. Кроме того, что в [57] неверно сравниваются формулы (2.8) и (2.9), там же имеются и другие неточности. Например, без всяких на то оснований противопоставляются сфера применения формулы Амдала (2.8) и алгоритм с параллелизмом по данным. На самом деле, никаких причин для такого противопоставления нет. Алгоритмы с параллелизмом по данным характерны тем, что в параллельной части они распадаются на одинаковые по выполняемым операциям ветви. Это обстоятельство обеспечивает возможность загрузить одинаковым образом и полностью все ФУ системы при выполнении параллельной части. Но уж если такая возможность имеется, то независимо от причин, приведших к ее появлению, можно с одинаковым успехом применять как формулу Амдала, так и формулу Густавсона—Барсиса. Это мы уже показали выше. При правильном использовании параметра (3 никаких различий между обеими формулами нет. Формулу Амдала следует применять для прогноза возможного ускорения. В данном случае величину р можно подсчитать, не пропуская программу на параллельной вычислительной системе. Формулу же Густавсона—Барсиса можно применять для оценивания достигнутого ускорения, не пропуская программу на однопроцессорном компьютере. Величина р при этом измеряется в процессе решения задачи. С другими понятиями дело обстоит не лучше. Особенно много всяких псевдонаучных изысканий вокруг понятий пиковой и реальной производитель-ностей. Можно понять стремление создателей вычислительной техники использовать такое определение пиковой производительности, при котором



	Глава 2. Как повышают производительность компьютеров	93

	Вопросы и задания 1. Почему в конвейерных функциональных устройствах длительности срабатываний отдельных ступеней делают одинаковыми? 2. Пусть граф вычислительной системы есть ориентированное кольцо, все дуги которого направлены в одну сторону, например, по часовой стрелке. Покажите, что существуют различные временные режимы, при которых система будет функционировать. 3. Докажите, что в условиях п. 2 при одних и тех же входных данных разные временные режимы приводят к одним и тем же результатам. 4. Докажите, что в условиях п. 2 алгоритм, реализуемый вычислительной системой, расщепляется на независимые между собой ветви вычислений. 5. На сколько ветвей расщепляется алгоритм в п. 2? 6. Что имеется общего между отдельными ветвями? 7. Что меняется в ответах на пп. 2—6, если граф вычислительной системы состоит из двух ориентированных колец разного размера, имеющих одну общую вершину? 8. Что меняется в ответах на пп. 2—6, если граф вычислительной системы состоит из одного пути?



	Глава 3 Архитектура параллельных вычислительных систем Внутренняя согласованность ценится больше эффективной работы. Из законов Мерфи В процессе решения любой задачи на параллельном компьютере можно выделить следующие этапы: формулировка задачи, выбор метода ее решения, фиксация алгоритма, выбор технологии программирования, создание программы и, наконец, выполнение ее на том или ином компьютере. Все эти этапы важны и для обычных компьютеров, но при использовании параллельных вычислительных систем они приобретают особую значимость. Любой параллельный компьютер — это тщательно сбалансированная система, которая может дать фантастический результат. Такие компьютеры специально проектируются для того, чтобы работать с огромной производительностью. Но параллельные компьютеры не могут работать одинаково производительно на любых программах. Если структура программы не соответствует особенностям их архитектуры, то производительность неизбежно падает. Указанное несоответствие может возникнуть на любом этапе решения задачи. Если на каком-либо одном шаге мы не учли особенностей целевого компьютера, то большой производительности на программе заведомо не будет. В самом деле, ориентация на векторно-конвейерный компьютер или вычислительный кластер с распределенной памятью во многом определит метод решения задачи. В одном случае в программе необходимо векторизовать внутренние циклы, а в другом надо думать о распараллеливании значительных фрагментов кода. И то, и другое свойство программ определяется свойствами заложенных в них методов. Не обладает выбранный метод такими свойствами, их не будет и в программе, а, значит, и не будет высокой производительности. Параллельный компьютер стоит в конце всей цепочки, и поэтому его влияние прослеживается везде. Чем аккуратнее мы проходим каждый этап, чем больше структура программы соответствует особенностями архитектуры компьютера, тем выше его производительность и тем ближе она к его пиковым показателям. Все понимают, что достичь пиковой производительности невозможно. Этот показатель в сравнении с реальной производительностью скорее играет роль ориентира, показывая, насколько полно использованы



	118	Часть I. Параллельные вычислительные системы

	Секция ввода/вывода Этой части компьютера не будем уделять много внимания. Скажем лишь, что он поддерживает три типа каналов для работы с внешними устройствами, которые различаются скоростью передачи данных: □ Low-speed (LOSP) channels — 6 Мбайт/с; □ High-speed (HISP) channels — 200 Мбайт/с; □ Very high-speed (VHISP) channels — 1800 Мбайт/с. Секция межпроцессорного взаимодействия Основное назначение данной секции заключается в передаче данных и управляющей информации между процессорами для синхронизации их совместной работы организации взаимодействия друг с другом. Секция межпроцессорного взаимодействия содержит разделяемые регистры и семафоры, объединенные в одинаковые группы — кластеры. Каждый кластер состоит из восьми 32-разрядных разделяемых адресных регистров (SB), восьми 64-разрядных разделяемых скалярных регистров (ST) и 32 однобитовых семафоров. Число кластеров в системе определяется конфигурацией компьютера. Теперь перейдем к описанию структуры отдельного процессора. Все процессоры имеют одинаковую вычислительную секцию, состоящую из регистров и функциональных устройств (ФУ). Различные регистры и функциональные устройства могут хранить и обрабатывать три класса данных: адреса, скаляры и векторы. Регистровая структура процессора Каждый процессор имеет набор основных и набор промежуточных регистров. К основным регистрам относятся адресные регистры А, скалярные регистры S и векторные регистры V. Промежуточные регистры В и Т, играющие роль промежуточного хранилища между памятью и основными регистрами, предусмотрены для регистров А и S соответственно. Все основные регистры связаны с памятью и функциональными устройствами, а регистры А и S имеют дополнительную связь с соответствующими промежуточными регистрами. Промежуточные регистры связаны только с памятью и основными регистрами, непосредственной связи с функциональными устройствами у них нет. Здесь же заметим, что и традиционной кэш-памяти в данном компьютере нет. В структуре компьютера предусмотрено 8 адресных регистров в основном наборе А, и 64 регистра в промежуточном наборе В. Адресные регистры предназначены для хранения и вычисления адресов, индексации, указания величины сдвигов, числа итераций циклов и т. д. Все регистры данной группы имеют по 32 разряда. Как и в случае адресных регистров, в основном наборе скалярных регистров S содержится 8 регистров, и еще 64 регистра в промежуточном наборе Т.



	*122*	Часть I. Параллельные вычислительные системы

	Секция управления процессора Команды выбираются из оперативной памяти блоками и заносятся в буфера команд, откуда затем они выбираются для исполнения. Если необходимой для исполнения команды нет в текущем буфере, она ищется в других буферах. Если требуемой команды в буферах не оказалось, то происходит выборка очередного блока. Такова основа архитектуры компьютера Cray С90. Нетрудно видеть, что идеи параллельной обработки пронизывают все ее составные части. Среди основных особенностей архитектуры, дающих заметный вклад в ускорение выполнения программ, можно назвать следующие. □ Конвейеризация выполнения команд. Все основные операции, выполняемые процессором, т. е. обращение в память, обработка команд и выполнение инструкций функциональными устройствами являются конвейерными. □ Независимость функциональных устройств. Функциональные устройства в Cray С90 являются независимыми, поэтому несколько операций могут выполняться одновременно. □ Векторная обработка. Векторная обработка увеличивает скорость и эффективность обработки за счет того, что обработка целого набора (вектора) данных выполняется одной командой. Скорость выполнения операций в векторном режиме может быть в 10—15 раз выше скорости скалярной обработки. □ Зацепление функциональных устройств. Возможность выполнения нескольких векторных операций в режиме "макроконвейера" дает дополнительный выигрыш в скорости их обработки. □ Многопроцессорная обработка. В максимальной конфигурации компьютер может содержать до 16 независимых процессоров. Эти процессоры могут быть использованы по-разному. В частности, они могут выполнять несколько независимых программ, но могут и все быть назначены на выполнение одной программы. Пиковая производительность Cray С90 Зная архитектуру компьютера, легко посчитать его пиковую производительность. Поскольку нас, прежде всего, интересует скорость выполнения операций над вещественными числами, то нужно максимально загрузить функциональные устройства для вещественной арифметики. Операция нахождения обратной величины сама по себе используется редко, а в операции деления ей дополнительно требуется операция умножения. Поэтому для определения пиковой производительности компьютера будем задействовать только устройства умножения и сложения. Для получения максимальной производительности их нужно использовать в режиме с зацеплением. Именно так



	Глава 3. Архитектура параллельных вычислительных систем	125

	Рассмотрим еще один пример: DO i = 1, n A(i) = Funct( A(i), B(i)) END DO В явном виде такой фрагмент также не может быть векторизован. Компилятор не знает, какая операция соответствует вызову пользовательской функции Funct, и, следовательно, он не знает, на какие векторные команды можно заменить данный фрагмент. В некоторых случаях компилятор может получить дополнительную информацию, если проведет межпроцедурный анализ, выяснит содержание функции Funct и выполнит in-line подстановку. На этом краткое введение в векторизацию программ мы закончим и перейдем к анализу узких мест в архитектуре компьютера Cray С90. Основное, что нам предстоит выяснить, какие особенности архитектуры необходимо учитывать при написании действительно эффективных программ для данного компьютера. Анализ факторов, снижающих реальную производительность компьютеров, начнем с обсуждения уже известного нам закона Амдала. Одна из его интерпретаций сводится к тому, что время работы программы определяется ее самой медленной частью. В самом деле, предположим, что одна половина некоторой программы — это сугубо последовательные вычисления, которые невозможно векторизовать. Тогда вне зависимости от свойств другой половины, которая может быть идеально векторизована и, скажем, выполнена мгновенно, ускорения работы всей программы более чем в два раза мы не получим. Влияние данного фактора надо оценивать с двух сторон. Во-первых, по природе самого алгоритма все множество операций программы Q разбивается на последовательные операции Qi и операции Q₂, исполняемые в векторном режиме. Если доля последовательных операций велика, то программист сразу должен быть готов к тому, что большого ускорения он никакими средствами не получит и, быть может, следует уже на этом этапе подумать об изменении алгоритма. Во-вторых, не следует сбрасывать со счетов и качество компилятора. Он вполне может не распознать векторизуемость отдельных конструкций, сгенерировать для них скалярный код и, тем самым, часть "потенциально хороших" операций из Q₂ перенести в Qj. Следующие два фактора, снижающие производительность компьютера на реальных программах, определяют принципиальную невозможность достижения пиковой производительности на векторно-конвейерных устройств. Это время разгона векторной команды и секционирование длинных векторов. Для инициализации векторной команды требуется несколько тактов, после чего начинается заполнение конвейера и лишь через некоторое время появ-



	Глава 3. Архитектура параллельных вычислительных систем 141

	Вопросы и задания 1. Назовите преимущества и недостатки двух систем: 16-процессорной системы с общей памятью и 16-процессорного вычислительного кластера, построенных на базе одних и тех же процессоров. 2. Чему равна пиковая производительность 16-процессорного компьютера с общей памятью HP Superdome и 16-процессорного вычислительного кластера, построенных на базе процессоров РА-8700 / 750 МГц? Попробуйте оценить стоимость каждого решения. Какие преимущества имеет более дорогое решение? 3. Проведите исследование методов организации доступа к общей памяти в современных SMP-серверах. 4. Выделите основные особенности и характерные черты архитектуры IA-64. Какие современные процессоры построены в соответствии с этой архитектурой? 5. Сколько процессоров содержат современные SMP-компьютеры, имеющие наилучшее соотношение цена/производительность? Проведите исследование по разным типам процессоров и систем. 6. Какое соотношение между объемами памяти на различных уровнях иерархии характерно для современных SMP-компьютеров? Для вычислительных систем с архитектурой ccNUMA? 7. Какое соотношение между скоростью выполнения арифметических операций и скоростью обмена с основной памятью характерно для современных SMP-компьютеров? 8. Напишите тестовую программу, которая автоматически определяет соотношение между скоростью выполнения арифметических операций и скоростью обмена с различными уровнями памяти. 9. Напишите тестовую программу, которая автоматически определяет разницу во времени обращения к локальной и удаленной памяти для вычислительных систем с архитектурой ccNUMA. 10. Напишите программу, работающую с максимальной производительностью на любой доступной вам вычислительной системе с общей памятью. Постройте зависимость производительности от числа процессоров. 11. Добавьте в вычислительное ядро программы из предыдущего вопроса использование массивов (если их там не было). Постройте зависимость производительности вычислительной системы с общей памятью от числа процессоров и размеров используемых массивов. 12. Исследуйте зависимость производительности вычислительной системы с общей памятью, показываемой на тестах из предыдущих двух вопросов, от нагрузки на других процессорах системы.





	ЧАСТЬ II Параллельное программирование



	Глава 4 Большие задачи и параллельные вычисления Если у веревки есть один конец, значит у нее должен быть и другой. Из законов Мерфи Если создают большие вычислительные системы, значит они для чего-то нужны. Это что-то — большие задачи, которые постоянно возникают в самых различных сферах деятельности. Практическая потребность или просто любознательность всегда ставили перед человеком трудные вопросы, на которые нужно было получать ответы. Строится высотное задание в опасной зоне. Выдержит ли оно сильные ветровые нагрузки и колебания почвы? Проектируется новый тип самолета. Как он будет вести себя при различных режимах полета? Уже сейчас зафиксировано потепление климата на нашей планете и отмечены негативные последствия этого явления. А каким будет климат через сто и более лет? Подобного рода вопросы сотнями и тысячами возникают в каждой области. Уже давно разработаны общие принципы поиска ответов. Первое, что пытаются сделать, — это построить математическую модель, адекватно отражающую изучаемое явление или объект. Как правило, математическая модель представляет собой некоторую совокупность дифференциальных, интегральных, алгебраических или каких-то других соотношений, определенных в области, так или иначе связанной с предметом исследований. Решения этих соотношений и должны давать ответы на поставленные вопросы. Как следует из предыдущих глав, существующие компьютеры сами по себе не могут решить ни одной содержательной задачи. Они способны выполнять лишь небольшое число очень простых действий. Вся их интеллектуальная сила определяется программами, составленными человеком. Программы также реализуют последовательности простых действий. Но эти действия целенаправленные. Поэтому искусство решать задачи на компьютере есть искусство превращения процесса поиска решения в процесс выполнения последовательности простых действий. Называется такое искусство разработкой алгоритмов. Если математическая модель построена, то следующее, что надо сделать, — это разработать алгоритм решения задачи, описывающей модель. Довольно часто в его основе лежит принцип дискретизации изучаемого объекта и, если необходимо, окружающей его среды. Исследуемый объект и среда разби-



	Глава 4. Большие задачи и параллельные вычисления	191

	Вопросы и задания 1. Допустим, что перемножаются две квадратные матрицы. Какие появятся особенности в организации вычислительных процессов, если взять матрицы максимального размера и стараться решить задачу по возможности быстрее? Рассмотрите варианты вычислительных систем: 1.1. С общей памятью и универсальными процессорами. 1.2. С общей памятью и конвейерными сумматорами, умножителями и делителями. 1.3. С распределенной памятью и универсальными процессорами. 1.4. С распределенной памятью и конвейерными сумматорами, умножителями и делителями. 2. Проделайте то же самое для решения системы линейных алгебраических уравнений методом Гаусса. 3. Что меняется во втором задании, если делители не будут конвейерными? § 4.2. Граф алгоритма и параллельные вычисления Любая программа для "обыкновенного" компьютера описывает некоторое семейство алгоритмов. Выбор конкретного алгоритма при ее реализации определяется тем, как срабатывают условные операторы. Состав и порядок выполнения остальных операторов строго задается самой программой. Если в программе отсутствуют условные операторы, то программа изначально описывает только один алгоритм. В свою очередь, срабатывания условных операторов зависят исключительно от входных данных. Поэтому "обыкновенный" компьютер всегда выполняет какую-то последовательность действий, которая однозначно определена программой и входными данными. Более того, для одной и той же программы эта последовательность будет одной и той же на любых моделях "обыкновенного" компьютера. Тем самым заведомо однозначно определяется результат. Все это является, в конечном счете, следствием того, что в любом "обыкновенном" компьютере в любой момент времени может реализоваться только одна операция. Любая другая операция в этот момент может лишь проходить стадию подготовки к реализации. Иначе обстоит дело на вычислительных системах параллельной архитектуры. Теперь в каждый момент времени может выполняться целый ансамбль операций, не зависящих друг от друга. На любой конкретной параллельной системе программа и входные данные однозначно определяют как состав ансамблей, так и их последовательность. Но на разных системах ансамбли и последовательности могут быть разными. Чтобы, тем не менее, гарантировать получение однозначного результата, порядок выполнения всей совокупности операций должен подчиняться некоторому условию.



	Глава 5 Технологии параллельного программирования Все, что начинается хорошо, кончается плохо. Все, что начинается плохо, кончается еще хуже. Из законов Мерфи Итак, вы приступаете к созданию параллельной программы. Желание есть, задача ясна, метод выбран, целевой компьютер, скорее всего, тоже определен. Осталось только все мысли выразить в той или иной форме, понятной для этого компьютера. Чем руководствоваться, если собственного опыта пока мало, а априорной информации о доступных технологиях параллельного программирования явно недостаточно? Наводящих соображений может быть много, но в результате вы все равно будете вынуждены пойти на компромисс, делая выбор между временем разработки программы, ее эффективностью и переносимостью, интенсивностью последующего использования программы, необходимостью ее дальнейшего развития. Не вдаваясь в детали выбора, попробуйте для начала оценить, насколько важны для вас следующие три характеристики. Основное назначение параллельных компьютеров — это быстро решать задачи. Если технология программирования по разным причинам не позволяет в полной мере использовать весь потенциал вычислительной системы, то нужно ли тратить усилия на ее освоение? Не будем сейчас обсуждать причины. Ясно то, что возможность создания эффективных программ является серьезным аргументом в выборе средств программирования. Технология может давать пользователю полный контроль над использованием ресурсов вычислительной системы и ходом выполнения его программы. Для этого ему предлагается набор из нескольких сотен конструкций и функций, предназначенных "на все случаи жизни". Он может создать действительно эффективную программу, если правильно воспользуется предложенными средствами. Но захочет ли он это делать? Не стоит забывать, что он должен решать свою задачу из своей предметной области, где и своих проблем хватает. Маловероятно, что физик, химик, геолог или эколог с большой радостью захочет осваивать новую специальность, связанную с параллельным программированием. Возможность быстрого создания параллельных программ должна приниматься в расчет наравне с другими факторами. Вычислительная техника меняется очень быстро. Предположим, что была найдена технология, позволяющая быстро создавать эффективные парал-



	232	Часть II. Параллельное программирование

	NTHREADS = OMP_GET_NUM_THREADS() PRINT , 'Number of threads = ', NTHREADS ENDIF С Завершение параллельной секции !$ОМР END PARALLEL END Каждая нить выполнит фрагмент кода, представляющий параллельную секцию, и напечатает приветствие вместе с номером нити. Дополнительно, нить-мастер напечатает общее число порожденных нитей. В объявлении параллельной секции явно указано, что переменные nthreads и tid являются локальными. Для определения общего числа нитей и их номеров использованы библиотечные функции omp_get_num_threads и omp_get_thread_num. Теперь рассмотрим программу сложения векторов. PROGRAM VEC_ADD_DO INTEGER N, CHUNK, I PARAMETER (N = 1000) PARAMETER (CHUNK =100) REAL A(N), B(N), C(N) ! Инициализация массивов DO I = 1, N A(I) = I 1.0 B(I) = A(I) END DO !$OMP PARALLEL SHARED(A,B,C,N) PRIVATE(I) !$OMP DO SCHEDULE(DYNAMIC,CHUNK) DO I = 1, N C(I) = A(I) + B(I) END DO !$OMP END DO NOWAIT !$OMP END PARALLEL END В данном примере массивы а, в, с и переменная n объявлены общими. Переменная i является локальной, каждый процесс будет иметь свою копию данной переменной. Итерации параллельного цикла будут распределяться между нитями динамически. Размер блоков фиксирован и равен chunk.



	242	Часть II. Параллельное программирование

	CDVM$ ON MB (2) CALL JACOBY(A2, B2, Ml + 1, N2 + 1) CDVM$ END ON CDVM$ ON MB(3) CALL JACOBY(A3, ВЗ, M2, N2) CDVM$ END ON CDVM$ END TASK_REGION В динамической форме итерация цикла отображается на задачу. Эта спецификация синтаксически похожа на обычную директиву параллельного цикла, но существует семантическое отличие. В параллельном цикле на каждом процессоре из решетки виртуальных процессоров выполняется непрерывный диапазон итераций цикла, а в цикле параллельных задач каждая итерация цикла выполняется на секции данной решетки. Пример динамической формы отображения блоков программы на задачи может быть таким: CDVM$ TASK_REGION MB CDVM$ PARALLEL (I) ON MB (I) DO I = 1, NT END DO CDVM$ END_TASK REGION Общие данные. Общими данными в системе DVM считаются те данные, которые вычисляются на одних процессорах, а используются на других. Все общие данные в DVM делятся на четыре группы: "соседние" общие данные, REMOTE-данные, "редукционные" данные и across-данные. "Соседние" общие данные. Рассмотрим следующий фрагмент программы CDVM$ PARALLEL (i) ON B(i), SHAD0W_RENEW (A(dl:d2)) DO i = 1 + dl, N - d2 B(i) = A(i - dl) + A(i + d2) END DO Необходимые каждому процессору общие данные размещены на соседних виртуальных процессорах. Спецификация shadow_renew указывает, что в данном цикле используются новые значения общих данных из массива а, значение dl указывает размер требуемых данных от левого соседа, a d2 — от правого. Для доступа к данным, размещенным на других процессорах, используются так называемые теневые грани массива. Теневую грань пользователь может представлять себе буфером, который является непрерывным продолжением локальной секции массива в памяти процессора. Перед выполнением цикла требуемые данные автоматически пересылаются с соседних процессоров в теневые грани массива а на каждом процессоре. Доступ к



	262	Часть II. Параллельное программирование

	parent [0]; scheme { int i ; par (i = 0; i < m; i++) 100%% [i]; par (i = 1; i < m; i++) 100%% [i] - > [0]; }; }; Первая строка вводит имя Galaxy этого сетевого типа и список формальных параметров — целые скалярные параметры m и к, а также векторный параметр п, состоящий из m целых чисел. Следующая строка объявляет координатную переменную i, изменяющуюся в пределах от о до m - 1. Далее виртуальные процессоры привязываются к этой системе координат, и описываются абсолютные объемы вычислений, которые должны быть выполнены этими виртуальными процессорами. В качестве единицы измерения используется объем вычислений, необходимый для расчета группы из к тел. Предполагается, что /-и элемент векторного параметра п равен числу тел в группе, обрабатываемой /-ым виртуальным процессором. Число операций, необходимое для обработки одной группы, пропорционально квадрату числа тел в этой группе. Поэтому, объем вычислений, выполняемый /-ым виртуальным процессором в (n[i]/k)² раз отличается от объема вычислений, принятого за единицу (это и записано в соответствующей строке). Следующая строка специфицирует объемы данных в байтах, передаваемые между виртуальными процессорами во время выполнения алгоритма. Она просто говорит, что /-Й виртуальный процессор посылает атрибуты всех своих тел виртуальному хост-процессору. Заметим, что данное определение описывает в точности одну итерацию основного цикла алгоритма. Это является достаточно хорошим приближением, поскольку практически все вычисления и обмены данными сосредоточены в этом цикле. Исходя из этого, общее время выполнения алгоритма приблизительно равно времени выполнения одной итерации, умноженному на общее число итераций. Наконец, блок scheme описывает, как именно виртуальные процессоры взаимодействуют во время выполнения алгоритма. Сначала все виртуальные процессоры параллельно выполняют все 100% вычислений. Затем все виртуальные процессоры, кроме хоста, параллельно посылают 100% тех данных, которые должны быть посланы виртуальному хост-процессору. Наиболее важными фрагментами остального кода этой mpC-программы являются следующие: void [] main(int [host]argc, char [host]argv) { TestGroup[] = (AllGroups[0]) [] ;



	266	Часть II. Параллельное программирование

	М : { double A[myN/r] [г] [N] , ВТ [myN/r] [г] [N] , C[myN/r] [г] [N] , Brow[r] [N] ; repl PivotProcessor, RelPivotRow, AbsPivotRow; for(AbsPivotRow = 0, RelPivotRow = 0, PivotProcessor = 0; AbsPivotRow < N; RelPivotRow + = r, AbsPivotRow + = r) { if(RelPivotRow >= d[PivotProcessor]) { PivotProcessor ++; RelPivotRow = 0; } Brow[] = [w:I == PivotProcessor]ВТ[RelPivotRow/r][]; for(i = 0; i < myN/r; i ++) SerialAxBT(A[i][0],Brow[0],C[j][0] + AbsPivotRow,r,N,r); } } } Оператор recon обновляет оценку производительности реальных процессоров, используя последовательное умножение тестовой матрицы г х п на тестовую матрицу п х t с помощью функции seriaiAxBT (вычисления, выполняемые каждым из виртуальных процессоров как раз, в основном, и приходятся на вызов функции SeriaiAxBT). Следующий блок, выполняемый виртуальным хост-процессором, вычисляет оптимальное число физических процессоров, вовлеченных в параллельное умножение матриц. Операция timeof оценивает время выполнения алгоритма, специфицируемого его операндом — некоторым конкретным типом сети, без его фактического выполнения. Вычисленное значение переменной р будет использовано в качестве числа процессоров. Определение сети w вызывает отображение ее виртуальных процессоров на физические процессоры таким образом, чтобы минимизировать время выполнения программы. Блок, следующий за определением сети w и выполняемый этой сетью, реализует алгоритм параллельного умножения матриц. Основные свойства этого алгоритма были описаны в определении сетевого типа ParallelAxBT.



	278	Часть II. Параллельное программирование

	int MPI_Init(int argc, char argv) Инициализация параллельной части программы. Все другие функции MPI могут быть вызваны только после вызова MPiinit. Необычный тип аргументов MPi_init предусмотрен для того, чтобы иметь возможность передать всем процессам аргументы функции main. Инициализация параллельной части для каждого приложения должна выполняться только один раз. Поскольку для сложных приложений, которые состоят из многих модулей и пишутся разными людьми, это отследить трудно, введена дополнительная функция MPi_initiaiized: MPI_Initialized (int flag)* Здесь out flag — признак инициализации параллельной части программы. Если функция MPi_init уже была вызвана, то через параметр flag возвращается значение 1, в противном случае 0. int MPI_Finalize(void) Завершение параллельной части приложения. Все последующие обращения к любым MPI-функциям, в том числе к MPiinit, запрещены. К моменту вызова MPi_Finaiize каждым процессом программы все действия, требующие его участия в обмене сообщениями, должны быть завершены. Общая схема MPI-программы выглядит так: main(int argc, char argv) { MPI_Init(Sargc, Sargv); MPI_Finalize(); } int MPI_Comm_size(MPI_Comm comm, int size)* □ comm — идентификатор коммуникатора; □ out size — число процессов в коммуникаторе comm. Определение общего числа параллельных процессов в коммуникаторе comm. Результат возвращается через параметр size, для чего функции передается адрес этой переменной. Поскольку коммуникатор является сложной структурой, перед ним стоит имя предопределенного типа MPi_comm, определенного в файле mpi.h. *int MPI_Comm_rank(MPI_Comm comm, int rank)** □ comm — идентификатор коммуникатора; □ out rank — номер процесса в коммуникаторе comm.



	292	Часть II. Параллельное программирование

	П comm — идентификатор коммуникатора; □ out request — идентификатор асинхронного приема. Формирование запроса на выполнение приема сообщения. Все параметры точно такие же, как и у функции MPi_irecv, однако, в отличие от нее, реальный прием не начинается до вызова функции MPi_startaii. MPI_Startall(int count, MPI_Request requests) □ count — число запросов на взаимодействие; □ out requests — массив идентификаторов приема/передачи. Запуск всех отложенных операций передачи и приема, ассоциированных с элементами массива запросов requests и инициированных функциями MPi_Recv_init, MPi_send_init или ее тремя модификациями. Все отложенные взаимодействия запускаются в режиме без блокировки, а их завершение можно определить обычным образом с помощью функций семейств MPI_Wait И MPI_Test. Совмещенные прием и передача сообщений.* Совмещение приема и передачи сообщений между процессами позволяет легко обходить множество подводных камней, связанных с возможными тупиковыми ситуациями. Предположим, что в линейке процессов необходимо организовать обмен данными между /-м и / + 1-м процессами. Если воспользоваться стандартными блокирующими функциями посылки сообщений, то возможен тупик, обсуждавшийся ранее. Один из способов обхода такой ситуации состоит в использовании функции совмещенного приема и передачи. int MPI_Sendrecv( void sbuf, int scount, MPI_Datatype stype, int dest, int stag, void rbuf, int rcount, MPI_Datatype rtype, int source, MPI_Datatype rtag, MPI_Comm comm, MPI_Status *status) □ sbuf — адрес начала буфера с посылаемым сообщением; □ scount — число передаваемых элементов в сообщении; □ stype — тип передаваемых элементов; □ dest — номер процесса-получателя; □ stag — идентификатор посылаемого сообщения; □ out rbuf — адрес начала буфера приема сообщения; □ rcount — число принимаемых элементов сообщения; □ rtype — тип принимаемых элементов; □ source — номер процесса-отправителя; □ rtag — идентификатор принимаемого сообщения; □ comm — идентификатор коммуникатора; □ out status — параметры принятого сообщения.



	Глава 5. Технологии параллельного программирования	301

	§ 5.3. Другие языки и системы программирования У ученых всегда было много идей, на основе чего можно было бы построить новые системы программирования. Одни идеи отражали особенности архитектуры компьютеров, другие опирались на различные разделы математики или теоретического программирования, третьи отталкивались от предметной области решаемых задач. В качестве примеров подобных систем можно назвать Sisal, Haskell, Cilk, Т-система, НОРМА и др. Систем много, но не надо забывать, что реальное распространение систем всегда определяли три фактора: простота программирования, эффективность программ, переносимость программ. Да, задача создания системы программирования, удовлетворяющей всем этим требованиям, пока не решена. Но потому мы и решили включить данный параграф в книгу, чтобы показать, насколько интересными и неожиданными могут оказаться идеи, на базе которых можно создавать новые системы. Если возникнет желание работать в данном направлении, то не нужно сразу отказываться от, казалось бы, безумных идей. Возможно, что именно на стыке различных областей и будет найден разумный вариант, удовлетворяющий всем необходимым условиям. В данном параграфе мы расскажем про две российские разработки: Т-сис-тему и язык НОРМА. Одна предлагает подход к автоматическому динамическому распараллеливанию программ, а другая позволяет программировать практически в терминах математических формул. Т-система В этом разделе мы рассмотрим ключевые аспекты технологии автоматического динамического распараллеливания программ, известной как Т-система [42]. Разработка Т-системы была начата в Институте программных систем РАН (г. Переславль-Залесский) в конце 80-х годов прошлого столетия. Наиболее характерной чертой Т-системы является использование парадигмы функционального программирования для обеспечения динамического распараллеливания программ. На этой основе удалось найти и реализовать в Т-системе интересные формы для организации параллельных вычислений, в частности, для синхронизации или распределения нагрузки. Вместе с тем, функциональный стиль Т-системы удалось удачно совместить с традиционными языками программирования с помощью расширений языков С, C++ или языка Fortran. Явные параллельные конструкции в языке отсутствуют, и программист в тексте явно не указывает, какие части программы следует выполнять параллельно. Базовые принципы Т-системы опираются на результаты общей теории функционального программирования. Для их пояснения можно не вдаваться



	Глава 5. Технологии параллельного программирования	305

	029 terrprint( 030 "Usage:\n" 031 "gr_fib <number>\n" 032 ) ; 033 return - 1; 034 } 035 n = (unsigned)atoi(argv[l]); 036 fib(n, &res); 037 (unsigned)res; 038 terrprint("fib(%u) = %u\n", n, res); 039 return 0; 040 } В программе с помощью ключевого слова tvai определены переменные resi, res2 и res, способные хранить как обычное, так и неготовое значение. В тот момент, когда их адреса передаются в Т-функцию fib, а это вызовы fib в строках 18, 19 и 36, выполнение вызывающей функции не останавливается, и она продолжает работать дальше. Поскольку второй формальный параметр Т-функции fib имеет описание tout, то в моменты вызовов соответствующая переменная resi, res2 и res становится "неготовой". Она будет содержать то самое специальное неготовое значение. Когда вызванная функция fib вычислит результат и вернет его в переменную (строка 15 или 20), это значение будет заменено обычным "готовым" значением. Обращение к неготовым переменным за их значением блокирует процесс вычисления функции. Например, такое может произойти в строке 20, где стоит обращение к переменным resi и res2. В строках 18 и 19 не требуется знания значения переменных resi и res2, поэтому оба вызова Т-функций fib будут выполнены без блокировки, и их вычисление может происходить параллельно. Порожденные в процессе работы программы вызовы Т-функций fib (строки 18, 19 и 36) формируют независимые порции работы (гранулы параллелизма), готовые к вычислению. Все порции помещаются в очередь, откуда вычислительные процессы-исполнители получают для себя работу. Т-функции в тексте программы указывают шаблоны потенциальных параллельных фрагментов кода. Реальные параллельные фрагменты появляются и обрабатываются Т-системой во время работы программы, как результат реальных вызовов Т-функций. Условный оператор, стоящий в строке 14, выполняет две задачи. С одной стороны, нужно в какой-то момент времени остановить образование новых порций работы и начать формировать окончательный результат. В этом смысле здесь полная аналогия с обычными рекурсивными функциями. С другой стороны, все формируемые порции работы должны быть достаточ-



	Глава 5. Технологии параллельного программирования	307

	023 return res; 024 } 025 tfun void tsum(const struct tree tptr _tree, 026 tout int _res) { 027 tval int left_sum, right_sum; 028 029 if (_tree->left != NULL) { 030 tsum(_tree->left, &left_sum); 031 } else { 032 left_sum = _tree->value; 033 } 034 if (_tree->right != NULL) { 035 tsum(_tree->right, &right_sum); 036 } else { 037 right_sum = _tree->value; 038 } 039 _res = left_sum + right_sum; 040 } 041 042 int tmain (int argc, char* argv[]) 043 { 044 struct tree tptr tree = create_tree(12); 045 tval int sum; 046 tsum(tree, &sum) ; 047 terrprint("sum = %u\n", sum); 04 8 return 0; 049 } В этой программе дерево структур с типом tree сначала порождается функцией create_tree, а затем обходится в рекурсивной функции tsum. Как и в предыдущем примере, происходит распараллеливание в каждом узле дерева: сначала порождаются вызовы для левой и правой ветви, и лишь затем происходит обращение к результатам обхода. Ключевое слово tptr служит для описания глобальных ссылок на неготовые переменные. При операции чтения данных по Т-указателю может происходить ожидание готовности значения и его подгрузка из узла вычислительной системы, в котором расположено значение, в узел, где произошло обращение по Т-указателю. При операции записи значение передается в нужный узел системы, и там значение записывается в соответствующую Т-пере-менную, делая ее готовой.



	Глава 5. Технологии параллельного программирования	317

	24 VARIABLE г DEFINED ON slo. 25 DOMAIN PARAMETERS n=4. 26 DISTRIBUTION INDEX i=2..8, j=l. 27 FOR so/t=0 ASSUME m=a. 28 FOR slo/t=0 ASSUME r=b. 29 sa,sb:s/i=t. sal,sbl:sl/i=t. 30 MACRO INDEX ti [t - l,i=t]. 31 MACRO INDEX tij [ti,j=t]. 32 FOR sa ASSUME m = m[ti] / m[tij]. 33 FOR sal ASSUME r = r[ti] / m[tij]. 34 FOR sb ASSUME m = m[t - 1] - m[t - 1,j=t] * m[i=t]. 35 FOR sbl ASSUME r = r[t - 1] - m[t - l,j=t] * r[i=t]. 36 FOR is ASSUME x = r[t=n]. 37 END PART Прокомментируем операторы программы. Используемые ниже номера совпадают с нумерацией строк программы. (1) Заголовок главного раздела программы Gauss. (2) Начало главного раздела. (3) Описание индексов областей. (4—6) Определение одномерных областей is, js и многомерной области ijs, на которых определены начальные данные задачи. (7—8) Описание переменных а, ь и х, где а — матрица коэффициентов системы, ь — столбец свободных членов, х — результат решения системы. (9—10) Ввод начальных данных из файла gauss.dat. (11) Задание параметра областей. (12) Вызов раздела calculate, осуществляющего расчет. (13) Вывод результата в файл gauss.out. (14) Конец главного раздела. (15) Заголовок простого раздела calculate. (16) Обозначение входных (а, Ь) и выходных (х) параметров раздела. (17) Начало простого раздела. (18) Описание индексов областей. (19) Определяется многомерная область so, состоящая из областей ts и ijs. Область ijs, в свою очередь, состоит из is и js.



	Глава 6 Тонкая информационная структура программ Всегда не хватает времени, чтобы выполнить работу как надо, но на то, чтобы ее переделать, время находится. Из законов Мерфи Данная глава является достаточно трудной для чтения. Тем не менее, мы посчитали необходимым включить ее в эту книгу. Несколько мотивов стали побудительными для такого решения. Как свидетельствует история, развитие и использование вычислительной техники постоянно сопровождается одним малоприятным явлением, держащим в напряжении пользователей компьютеров, в особенности наиболее активную их часть. Меняются языки программирования, совершенствуются пользовательские среды. Но каждый раз, как только появляются компьютеры нового типа, приходится модернизировать прикладное программное обеспечение. Иногда изменения незначительны, но чаще всего они оказываются радикальными. Несмотря на оптимистические заверения разработчиков новых языков программирования, в настоящее время нельзя быть уверенным, что программы, написанные на любом из них, будут широко востребованы хотя бы в течение ближайших 3—5 лет. Поэтому необходимо признать тот факт, что еще долгое время пользователи будут вынуждены видоизменять свои программы, подстраивая их под особенности компьютеров. Это обстоятельство заставляет думать о том, как облегчить такой труд. Но прежде всего нужно понять, в каком же направлении следует думать. Начиная с 60-х годов прошлого столетия увеличение быстродействия компьютеров определяется не столько уменьшением тактового периода элементной базы, сколько принятием новых решений в архитектуре вычислительных систем. При этом ускорение вычислений достигается за счет отображения характерных особенностей программ и алгоритмов в аппаратуре. Уже на раннем этапе были подмечены локальность счета и частое использование лишь небольшого числа данных, выделены основные элементы программ — циклы, ветвления, процедуры и т. п. Это сразу нашло отражение в буферах команд и регистрах, кэш-памяти, аппаратурной организации стека и во многом другом. Одновременно решалась и задача выравнивания скоростей работы различных узлов вычислительных систем (вспомните 1-й закон Амдала как одно из следствий утверждения 2.4. Одни аппаратур-



	342	Часть II. Параллельное программирование

	Вопросы и задания 1. Рассмотрите любой известный вам язык программирования. Как на этом языке описывается линейный класс программ? 2. Приведите различные примеры программ, которые формально не являются линейными, но становятся таковыми после каких-то эквивалентных преобразований. 3. 'Пусть программа содержит вызовы процедур. Предложите различные способы замены этих вызовов программными фрагментами, при которых исходная программа становится линейной и сохраняет все прежние информационные зависимости. 4. Приведите различные примеры программ, которые формально не являются линейными и которые вы не можете привести к линейным с помощью эквивалентных преобразований. 5. Как выглядят графы алгоритмов для примеров п. 4? 6. Насколько различны графы алгоритмов для примеров п. 4? 7. Как часто примеры п. 4 встречались в вашей практике? § 6.3. Графы зависимостей и минимальные графы Прежде всего необходимо точно описать множество вершин. Пусть задана произвольная линейная программа. Перенумеруем подряд сверху вниз все операторы циклов do, точнее, все параметры циклов. Обозначим параметры через /], ..., 1_П. Будем считать, что из двух параметров младшим (старшим) является тот, у которого номер меньше (больше). Перенумеруем также сверху вниз все операторы присваивания и обозначим их через F]_, ..., F_m. С каждым оператором присваивания свяжем тесно вложенное гнездо циклов. Его можно получить, оставляя в программе только те циклы do, в тела которых входит рассматриваемый оператор. Будем называть такое гнездо циклов опорным для данного оператора. Пусть опорное гнездо оператора F_tописывается параметрами /,- , ...,/,- . Рассмотрим арифметическое простран- 1 .V/ ство, координаты точек которого совпадают со значениями этих параметров. Его размерность равна Sj. Назовем такое пространство опорным. Если оператор не входит ни в какое гнездо, то размерность опорного пространства будем считать равной 0. Не ограничивая существенно общности, можно предполагать, что отдельный оператор описывается гнездом циклов, у которых нижние и верхние границы изменения каждого из параметров совпадают. Такое предположение позволяет приписать какие-то параметры даже отдельным операторам. Границы изменения параметров циклов опорного гнезда определяют в опорном пространстве линейный многогранник. Будем называть его опорным для