|
|
Close Help | ||||||||||||||
При написании этой статьи использовались материалы лекций по дискретной математики, прочитанных Валентином Борисовичем Алексеевым на факультете ВМиК МГУ в 1992 году.
Автор-составитель: А.Чернобаев.
Введение
Автор-составитель данной статьи не ставил перед собой задачу строго и формально изложить основы теории графов. Читатели, интересующиеся ее математической стороной, могут обратиться к [1-3, 6]. В этой статье понятия теории графов излагаются с прикладной, можно сказать - программистской точки зрения. Основное внимание уделяется алгоритмам решения типичных задач на графах. В то же время, наряду с неформальным изложением, используются относительно строгие определения, теоремы и доказательства. Надеюсь, что этот текст поможет читателю получить представление о полезности теории графов при решении практических задач.
Алгоритмы, о которых рассказывается в статье, были собраны из различных источников, в числе которых стоит отметить [4-5]. Многие алгоритмы реализованы составителем в объектно-ориентированной библиотеке AGraph, написанной на языке Object Pascal.
Содержание
1. Элементы
теории графов
Граф (graph) - пара G=(V,E), где V - множество объектов произвольной природы, называемых вершинами (vertices, nodes), а E - семейство пар ei=(vi1, vi2), vijОV, называемых ребрами (edges). В общем случае множество V и/или семейство E могут содержать бесконечное число элементов, но мы будем рассматривать только конечные графы, т.е. графы, у которых как V, так и E конечны.
В приведенном определении графа E не случайно названо семейством пар, а не множеством. Дело в том, что элементы E могут быть неуникальны, т.е. возможны кратные ребра. Существует другое, более корректное определение: граф определяется как тройка G=(V,E,j), где V - множество вершин, E - множество ребер, а j=j(v,u,e) - трехместный предикат (булевская функция от трех переменных), возвращающая True тогда и только тогда, когда ребро e инцидентно вершинам v и u. Однако такие "строгости" в нашем изложении являются чрезмерными.
Если порядок элементов, входящих в ei, имеет значение, то граф называется ориентированным (directed graph), сокращенно - орграф (digraph), иначе - неориентированным (undirected graph). Ребра орграфа называются дугами (arcs). В дальнейшем будем считать, что термин "граф", применяемый без уточнений "ориентированный" или "неориентированный", обозначает неориентированный граф.
Пример: G=(V,E); V={1,2,3,4}; E=<(1,1), (1,2), (1,3), (2,4), (2,4)>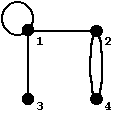 
G
Если e=(v,u), то вершины v и u называются
концами ребра. При этом говорят, что ребро e является смежным
(инцидентным) каждой из вершин v и u. Вершины v и u также называются
смежными (инцидентными). В общем случае, допускаются ребра вида e=(v,v); такие
ребра называются петлями.
Степень вершины графа - это число ребер, инцидентных данной вершине, причем петли учитываются дважды. Поскольку каждое ребро инцидентно двум вершинам, сумма степеней всех вершин графа равна удвоенному количеству ребер: Sum(deg(vi), i=1..|V|)=2Ч|E|.
Граф, не содержащий петель и кратных ребер, называется обыкновенным, или простым графом (simple graph). Во многих публикациях используется другая терминология: под графом понимается простой граф, граф с кратными ребрами называют мультиграфом, с петлями - псевдографом.
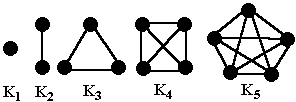
Некоторые классы графов получили особые наименования. Граф с любым количеством вершин, не содержащий ребер, называется пустым. Обыкновенный граф с n вершинами, любая пара вершин которого соединена ребром, называется полным и обозначается Kn (очевидно, что в полном графе n(n-1)/2 ребер).
Граф, вершины которого можно разбить на непересекающиеся подмножества V1 и V2 так, что никакие две вершины, принадлежащие одному и тому же подмножеству, не смежны, называется двудольным (или бихроматическим, или графом Кенига) и обозначается Bmn (m=|V1|, n=|V2|, m+n=|V|). Полный двудольный граф - такой двудольный граф, что каждая вершина множества V1 связана со всеми вершинами множества V2, и наоборот; обозначение - Kmn. Замечание: полный двудольный граф Bmn не является полным (за исключением B11=K2).
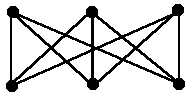B33
Подграфом, или частью графа G=(V,E) называется такой граф G'=(V',E'), что V'НV и две несмежные вершины в G не смежны в G'. Полным подграфом называется подграф, любая пара вершин которого смежна.
Остовным подграфом (суграфом) графа G называется любой его подграф, содержащий то же множество вершин, что и G.
Графы G1=(V1,E1) и G2=(V2,E2) называются изоморфными (обозначение: G1~G2), если между графами существует взаимно-однозначное отображение j: G1<G2 (V1<V2, E1<E2), которое сохраняет соответствие между ребрами (дугами) графов, т.е. для любого ребра (дуги) e=(v,u) верно: e'=j(v,u)=(j(v),j(u)) (eОE1, e'ОE2). Отображение j называется изоморфным отображением.
Иными словами, изоморфные графы различаются только обозначением вершин.
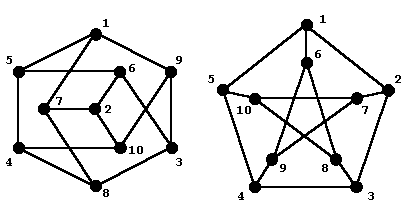
Изоморфные графы. Одно из изоморфных отображений: (0,0),
(1,3), (2,5), (3,6), (4,7), (5,2), (6,1), (7,4), (8,9), (9,8).
Характеристики графов, инвариантные относительно изоморфизмов графов (т.е. принимающие одинаковые значения на изоморфных графах), называются инвариантами графов.
Подразделением ребра (v1,v2) графа называется операция добавления в граф вершины v' и замены этого ребра на два смежных ребра (v1,v') и (v',v2): V'=V+{v'}, E'=E-{(v1,v2)}+{(v1,v')}+{(v',v2).
Граф G' называется подразделением графа G, если он может быть получен из G путем конечного числа подразделений ребер.
Два графа называются гомеоморфными, если для них существуют изоморфные подразделения.
Путем в графе (или маршрутом в орграфе) называется чередующаяся последовательность вершин и ребер (или дуг - в орграфе) вида v0, (v0,v1), v1, ... , (vn-1,vn), vn. Число n называется длиной пути. Путь без повторяющихся ребер называется цепью, без повторяющихся вершин - простой цепью. Путь может быть замкнутым (v0=vn). Замкнутый путь без повторяющихся ребер называется циклом (или контуром в орграфе); без повторяющихся вершин (кроме первой и последней) - простым циклом.
Утверждение 1. Если в графе существует путь, ведущий из вершины v0 в vn, то существует и простая цепь между этими вершинами.
Доказательство: такую простую цепь можно построить, "выкинув" из пути все циклы.
~
Граф называется связным, если существует путь между любыми двумя его вершинами, и несвязным - в противном случае. Несвязный граф состоит из нескольких связных компонент (связных подграфов).
Для орграфов понятие связности является более сложным: различают сильную связность, одностороннюю связность и слабую связность. Орграф называется сильно связным, если для любых двух его вершин v и u существует как маршрут из v в u (v->u), так и из u в v (u->v). Орграф называется односторонне связным, если для любых двух его вершин u и v существует по крайней один из маршрутов v->u или u->v. Наконец, орграф называется слабо связным, если связен неориентированный граф, получаемый из этого орграфа путем снятия ориентации с дуг. Очевидно, что любой сильно связный граф является односторонне связным, а односторонне связный - слабо связным, но не наоборот.
Деревом называется произвольный связный граф без циклов.
Лемма 1. Пусть G=(V,E) - связный граф, вершины v1 и v2 которого не смежны. Тогда в графе G'=(V,E+(v1,v2)) существует простой цикл, проходящий через ребро (v1,v2).
Доказательство: т.к. G - связный, в нем существует путь из v2 и v1, а значит (по утверждению 1), и простая цепь v2...v1. Следовательно, в графе G' существует путь v2...v1(v1,v2)v2, который является простым циклом (по определению).
~
Лемма 2. Пусть G=(V,E) - связный граф, ребро e=(v1,v2) которого входит в некоторый цикл. Тогда граф G'=(V,E-e) - также связен, т.е. при удалении кольцевого ребра (ребра, входящего в некоторый цикл) из связного графа этот граф остается связным.
Доказательство: т.к. G - связный, в нем существует путь S между любыми двумя вершинами vi и vj. Если e не входит в путь S=vi...vj, то этот путь существует и в графе G', а значит, G' остается связным. Иначе (e входит в этот путь): S=vi...v1(v1,v2)v2...vj. По условию e - входит в некоторый цикл, следовательно, существует замкнутый путь C=v2(v2,v1)v1Tv2 (началом замкнутого пути мы можем считать любую его вершину), причем ребро e=(v1,v2) не входит в T (если существует путь между вершинами, то существует и путь, который является простой цепью - см. утверждение 1). Но тогда существует путь S'=vi...v1Tv2...vj, в который не входит ребро e=(v1,v2) и, следовательно, этот путь существует в графе G'.
~
Лемма 3. Пусть G=(V,E), p=|V|, q=|E|.
1) число
связных компонент в G больше либо равно |V|-|E| (Nкомп._p-q);
2) если в G нет циклов, то число связных компонент
в G равно |V|-|E| (Nкомп.=p-q).
Доказательство: построим пустой граф с p вершинами (очевидно, в нем ровно p связных компонент) и будем добавлять ребра по одному.
При добавлении ребра возможны две ситуации: (а) новое ребро соединяет вершины, находившиеся до этого в разных компонентах (в этом случае количество компонент уменьшается на единицу) и (б) новое ребро соединяет вершины, принадлежащие одной компоненте (число компонент не изменяется). Следовательно, при добавлении q ребер число компонент уменьшится не более чем на q, и, следовательно, количество компонент в графе будет больше либо равно p-q. Это доказывает утверждение (1).
В соответствии с леммой 1, при добавлении ребра в связный граф в нем появляется цикл. Если в графе нет циклов, это означает, что при добавлении ребер всегда происходил вариант (а) - иначе появились бы циклы. Следовательно, число компонент при каждом добавлении ребра уменьшалось на единицу, и после добавления q ребер в графе будет ровно p-q компонент. Это доказывает утверждение (2).
~
Следствие 1 леммы 3: если |E|_|V|-2, то граф G=(V,E) несвязен (следует непосредственно из леммы 3).
Теорема 1. Любой связный граф содержит подграф, являющийся деревом.
Доказательство: если в связном графе нет циклов, то он уже является деревом по определению. Иначе находим любое кольцевое ребро и удаляем его; в соответствии с леммой 2 граф остается связным. Продолжаем процесс, пока в графе существуют циклы. В силу конечности графа этот алгоритм построит дерево за конечное число шагов.
Замечание: фактически доказано более сильное утверждение - что любой связный граф содержит остовный подграф (подграф с тем же количеством вершин, что и сам граф), являющийся деревом.
~
Теорема 2. Для любого дерева G=(V,E) верно: |V|-|E|=1.
Доказательство: по определению, в дереве нет циклов, следовательно, в соответствии с леммой 3 в нем ровно |V|-|E| связных компонент. Но по определению дерево связно, т.е. состоит из одной связной компоненты, поэтому |V|-|E|=1.
~
Теорема 3. Следующие свойства графов эквивалентны:
(1)=>(2): допустим, что некоторые две вершины v1 и v2 графа G соединены, по крайней мере, двумя различными простым цепями L1=u1....uk, где u1=v1 и uk=v2, и L2=w1....wm, где w1=v1 и wm=v2. Из того, что цепи являются простыми и различными, следует, что существует число j, 1<j<min(k,m), такое, что uj-1=wj-1, uj№wj, ... , uj+a-1№wj+b-1, uj+a=wj+b, где a_1, b_1. Следовательно, в G существует цикл С=uj-1(uj-1,uj)uj...uj+a(wj+b,wj+b-1)wj+b-1... wj(wj,wj-1)wj-1 (см. рисунок) - получили противоречие с (1).
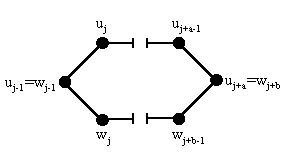
(2)=>(1):
(а) граф G является связным по
определению связности (любые две вершины графа соединены цепью);
(б)
допустим, что в графе G существует цикл, проходящий через некоторую вершину v:
C=v(v,u1)u1....uk(uk,v)v. Но это
означает, что между v и любой из вершин ui существуют, по крайней
мере, два различных пути
L1=v(v,u1)u1...ui-1(ui-1,ui)ui
и
L2=v(v,uk)uk...ui+1(ui+1,ui)ui
(пути различны, т.к. по определению в цикле отсутствуют повторяющиеся ребра). В
силу утверждения 1
из этих путей можно "выделить" простые цепи, которые также будут различны (в
L1и L2 нет совпадающих ребер), - получили противоречие с
(2).
Из (а), (б) и определения дерева следует, что G является деревом.
(2)=>(3): по теореме 2;
(3)=>(4): по лемме 3;
(4)=>(5): т.к. |E|=|V|-1, то после удаления ребра в новом графе
будет |V|-2 ребер, и по следствию 1
леммы 3 этот граф будет несвязным;
(5)=>(6):
(a) докажем
первую часть утверждения (G - граф без циклов): допустим, в G есть циклы; но
тогда при удалении любого кольцевого ребра он останется связным, что
противоречит (4);
(б) докажем вторую часть утверждения (при добавлении
любого ребра в G появляется ровно один простой цикл): из связности графа и леммы 1
следует, что при добавлении любого ребра в G появляется, как минимум, один
простой цикл; в силу (2) этот простой цикл единственен (обратное означало бы,
что в G существуют вершины, соединенные более чем одной простой цепью);
(6)=>(1): допустим, G - не дерево, т.е. граф не связен или
содержит циклы. Циклов не может быть в силу (5а), поэтому остается вариант: G -
несвязен и состоит минимум из двух компонент. Но тогда при добавлении ребра
между вершинами, принадлежащими разным компонентам, циклы не образуются, а это
противоречит (5б).
~
Остовным деревом (остовом) связного графа называется любой его остовный подграф, являющийся деревом.
Существование остовного подграфа для любого связного графа доказывается теоремой 1.
Общее число остовных деревьев связного графа может быть весьма велико. Так, для полного графа с n вершинами оно равно nn-2 (без доказательства).
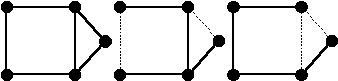
Для произвольного (возможно, несвязного) графа G остовное дерево определяется как любой его остовный подграф, не содержащий циклов и имеющий столько же компонент связности, что и G.
Цикломатическое число и фундаментальные циклы
Цикломатическим числом графа G=(V,E) называется с k связными компонентами называется число n(G)=|E|-|V|+k.
Фундаментальным циклом графа G=(V,E) с остовным деревом T=(V,E') называется простой цикл, получаемый в результате добавления в T одного из ребер G, не принадлежащего E'.
Утверждение 1. Количество фундаментальных циклов графа G=(V,E) при любом фиксированном остовном дереве T=(V,E') равно цикломатическому числу G.
Доказательство: согласно лемме 3 п.2, k=|V|-|E'|, следовательно, <количество ребер G, не принадлежащих E'> = |E|-|E'| = |E|-(|V|-k) = n(G). При добавлении любого из этих ребер в T появляется ровно один простой цикл в силу теоремы 3 п.6; все получаемые при этом простые циклы различны, т.к. каждый из них содержит по крайней мере одно уникальное ребро - то самое ребро G, не принадлежащее E', которое было добавлено в дерево.
~
Сопоставив вершинам графа точки на плоскости или в пространстве, а ребрам -
линии, соединяющие точки, соответствующие концам ребра, можно получить диаграмму
- визуальное представление данного графа.
Очевидно, что для любого графа
можно построить бесконечное количество таких диаграмм. Если на некоторой
диаграмме среди точек, соответствующих вершинам графа, нет совпадающих, а линии,
соответствующие ребрам графа, не имеют общих точек (за исключением концов), то
эта диаграмма называется геометрической реализацией графа.
Теорема 1. Для любого графа существует геометрическая реализация в трехмерном евклидовом пространстве.
Доказательство:
Возникает вопрос: любой ли граф можно реализовать на плоскости? Ответ - отрицательный. Геометрическую реализацию на плоскости допускают лишь некоторые графы; такие графы называются планарными.
Для последующего изложения нам понадобится понятие грани. Неформально определим грань как часть плоскости, на которые плоскость "разрезается" линиями геометрической реализации графа. Всегда существует неограниченная внешняя грань.
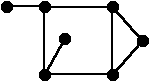- 7 вершин, 8 ребер, 3 грани
Формула Эйлера. Для любой геометрической реализации графа G=(V,E) на плоскости верно: p-q+r=2, где p=|V|, q=|E|, r - число граней (без доказательства).
Теорема 2. Если в связном планарном графе нет циклов длины меньше k и k_3, то q_k(p-2)/(k-2), где p=|V|, q=|E|.
Доказательство (не совсем формальное): пусть граф реализован на плоскости и
при этом получилось r граней. Пусть qi - число сторон в i-й грани
(см. рисунок). Каждое ребро является стороной двух граней, поэтому
2q=Sum(qi, i=1..r). По условия в графе нет циклов длины меньше k, но
тогда qi_k (т.к. стороны грани образуют
цикл) и 2q=Sum(qi, i=1..r)_kЧr. По формуле Эйлера r=2-p+q, следовательно, 2q_kЧ(2-p+q), из чего следует
доказываемое неравенство.
- 8 ребер, 3 грани, 3+6+7=16 сторон
~
Следствие 1 теоремы 2: для любого связного планарного графа без петель и кратных ребер выполняется неравенство: q_3(p-2), где p=|V|, q=|E|.
Доказательство: т.к. по условию в графе нет петель и кратных ребер, в нем нет и циклов длины меньше 3, поэтому, подставляя k=3 в неравенство теоремы 2, получаем: q_k(p-2)/(k-2)=3(p-2).
~
Теорема 3. Граф K5 не планарен.
Доказательство: K5 связен, в нем нет петель и кратных ребер, но следствие 1 теоремы 2 не выполняется - q=10>3(p-2)=9. Значит, K5 не планарен.
~
Теорема 4. Граф K33 не планарен.
Замечание: использование следствия 1 теоремы 2 здесь не поможет, т.к. q=9<3(p-2)=12.
Доказательство: в K33 нет циклов длины меньше 4, поэтому применим неравенство теоремы 2 непосредственно (при k=4): q=9>4(p-2)/2=8. Следовательно, K33 не планарен.
~
Теорема Понтрягина-Куратовского (критерий планарности графов). Граф G планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K5 или K33.
Доказательство: необходимость следует из утверждений 1-4 (см. ниже), а также из того факта, что графы K5 и K33 не планарны (в соответствии с теоремами 3 и 4).
Утверждение 1: если графы U1 и U2 изоморфны, то U1 планарен тогда и только тогда, когда U2 планарен.
Доказательство: любая геометрическая реализация U1 является геометрической реализацией U2, и наоборот.
Утверждение 2: любое подразделение U' графа U планарно тогда и только тогда, когда U планарен.
Доказательство:
(=>) граф U' планарен, следовательно, существует его
геометрическая реализация на плоскости R'. Построим по R' плоскую геометрическую
реализацию R графа U. Для этого объединим все линии R', соответствующие ребрам
U', полученным в результате выполнения операций подразделения ребер. В силу
существования R граф U является планарным.
<=) граф U планарен,
следовательно, существует его геометрическая реализация на плоскости R. Построим
по R плоскую геометрическую реализацию R' графа U'. Для этого повторим в любой
последовательности операции подразделения ребер, которые привели к построению
U'. После выполнения каждой из этих операций будем разбивать линию,
соответствующую подразделяемому ребру, на две линии (разбиение можно производить
в любой точке, не совпадающей с концами линии). В силу существования R' граф U'
является планарным.
Утверждение 3: если графы U1 и
U2 гомеоморфны, то U1 планарен тогда и только тогда, когда
U2 планарен.
Доказательство:
(=>) по условию U1 и U2
гомеоморфны R {по определению} R существуют их изоморфные подразделения U1' и
U2'. По условию граф U1 планарен R {по утв.2} R граф U1'
планарен R {по утв.1} R
изоморфный ему граф U2' планарен R {по
утв.2} R граф U2 планарен.
(<=)
аналогично.
Утверждение 4: если подграф U' графа U не планарен, то U также не планарен.
Доказательство: допустим, что граф U планарен. Следовательно, существует его плоская геометрическая реализация R. Но тогда можно построить плоскую геометрическую реализацию R' графа U': для этого достаточно удалить из R точки и линии, соответствующие тем вершинам и ребрам U, которых нет в U'. Из существования R' следует, что U' планарен - получили противоречие.
Достаточность теоремы доказывается гораздо сложнее (см., например, [3]).
~
Существуют и другие критерии планарности графов [3].
Вершинной раскраской (далее - просто раскраской) графа называется отображение множества вершин графа на конечное множество (множество цветов); n-раскраска графа - раскраска с использованием n цветов. Раскраска называется правильной, если никакие две вершины одного цвета не смежны. Очевидно, что для графа без петель всегда существует правильная раскраска в |V| цветов.
Хроматическим числом графа G называется минимальное число n=c(G), такое, что существует правильная n-раскраска.
Лемма 1. В любом планарном графе без петель и кратных ребер существует вершина степени не более пяти.
Доказательство: допустим, что степени всех вершин превосходят 5. Тогда 2q=Sum(deg(vi), i=1..|V|)_6p и q_3p. Но по следствию 1 теоремы 2 должно выполняться неравенство q_3(p-2)<3p - получили противоречие.
~
Теорема о пяти красках. Каждый планарный граф без петель и кратных ребер является не более чем 5-хроматическим.
Доказательство: (индукцией по числу вершин).
При p=1 утверждение теоремы верно. Допустим, что (*) утверждение верно для всех p<p0. Докажем, что тогда оно верно и для p0.
Рассмотрим планарный граф G без петель и кратных ребер с p0 вершинами; по лемме 1 в нем есть вершина v0 степени не более 5. По предположению индукции (*) граф G', получаемый удалением из G вершины v0 (очевидно, также планарный), может быть раскрашен не более, чем в 5 цветов. Пусть (**) v1...vk, k=deg(v0) - все вершины-соседи вершины v0, расположенные по часовой стрелке относительно v0. Если в раскраске вершин v1...vk используется не более 4-х цветов, то "покрасим" вершину v0 в оставшийся 5-й цвет и получим правильную раскраску.
Осталось рассмотреть случай, когда в раскраске вершин v1...vk в графе G' используется 5 цветов (k=5). Пусть ci - цвет вершины vi (i=1..5). Рассмотрим множество A, состоящее из вершины v1 и всех вершин графа G, исключая v0, в которые можно дойти из v1 только по вершинам цветов c1 и c3. Возможны два случая:
Остается второй случай. Из принадлежности вершины v3 множеству A следует, что существует путь из v1 в v3 (v1Sv3), проходящий только по вершинам цветов c1 и c3 (см. рисунок). Рассмотрим цикл L=v1Sv3(v3,v0)v0(v0,v1)v1 и замкнутую кривую, которая соответствует этому циклу в геометрической реализации графа. Вершина v2 находится внутри этой замкнутой кривой, а v4 - снаружи. Это следует, во-первых, из того, что линии, соответствующие ребрам графа в его геометрической реализации, не могут пересекаться (не считая концов), и, во-вторых, из (**). Определим множество B, состоящее из вершины v2 и всех вершин графа G, исключая v0, в которые можно дойти из v2 только по вершинам цветов c2 и c4. Вершина v4 не принадлежит B, поскольку любой путь из v2 в v4 должен проходить, по крайней мере, через одну вершину, принадлежащую циклу L - т.е. либо через вершину v0, либо через вершину, окрашенную в цвета c1 или c3. Следовательно, как и в первом случае, можно поменять цвета вершин множества B (c2<c4) и "покрасить" v0 в c2.
~
Теорема о четырех красках. Каждый планарный граф без петель и кратных ребер является не более чем 4-хроматическим.
Проблема четырех красок оставалась нерешенной в течение многих лет. Утверждается, что эта теорема была доказана с помощью хитроумных рассуждений и компьютерной программы в 1976 году (Kenneth Appel and Wolfgang Haken. Every Planar Map is Four Colorable. Contemporary Mathematics 98, American Mathematical Society, 1980). Краткое изложение идеи их доказательства имеется в [3].
Во многих случаях элементам (вершинам и ребрам) графа ставятся в соответствие различные данные - атрибуты (метки). Если в качестве атрибутов используются целые или вещественные числа, то такие графы называют взвешенными. Фактически, взвешенный граф - это функция, определенная на графе. В качестве атрибутов могут выступать и нечисловые данные, поэтому я буду называть графы с атрибутами помеченными, или атрибутированными (А-графами). Например, структурные формулы химических соединений представляются молекулярными графами - А-графами, вершины которых соответствуют атомам химической структуры, а ребра - валентным связям между атомами. Для вершин молекулярного графа определен, по крайней мере, атрибут "номер атома в периодической таблице элементов", для ребер - "тип валентной связи (одинарная, двойная, тройная и др.)"; могут использоваться дополнительные атрибуты, например, заряд атома.
Для графов с атрибутами можно ввести усиленное определение изоморфизма: будем считать два А-графа изоморфными, если они изоморфны в обычном смысле, и, кроме того, изоморфное отображение сохраняет атрибуты (т.е. атрибуты соответствующих вершин и ребер в обоих графах совпадают).
Независимые множества и покрытия
Независимое множество вершин (НМВ) - множество вершин графа, никакие две вершины которого не инцидентны.
Максимальное независимое множество вершин (МНМВ) - НМВ, которое не содержится ни в каком другом НМВ.
Замечание: в данном определении "максимальность" означает "нерасширяемость"; в общем случае граф может иметь несколько МНМВ различной мощности.
Наибольшее независимое множество вершин - НМВ максимальной мощности.
Мощность наибольшего НМВ (очевидно, это одно из МНМВ) называется вершинным числом независимости графа (а также неплотностью, числом внутренней устойчивости или числом вершинной упаковки графа); обозначение - a(G).
Независимое множество ребер (НМР), или паросочетание - множество ребер графа, никакие два ребра которого не инцидентны.
Мощность наибольшего паросочетания называется числом паросочетания графа; обозначение - n(G).
Доминирующее множество вершин (ДМВ) - такое множество вершин графа, что каждая вершина графа либо принадлежит ДМВ, либо инцидентна некоторой вершине, принадлежащей ДМВ.
Вершинное покрытие (ВП) - такое множество вершин графа, что каждое ребро графа инцидентно хотя бы одной вершине, принадлежащей ДМВ.
Мощность наименьшего вершинного покрытия называется числом вершинного покрытия графа; обозначение - t(G).
Доминирующее множество ребер (ДМР), или реберное покрытие - такое множество ребер связного графа, что каждая вершина графа инцидентна хотя бы одному ребру, входящему в ДМР.
Мощность наименьшего ДМР называется числом реберного покрытия графа; обозначение - r(G).
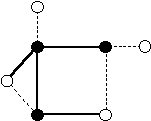
На рисунке обозначены реберное покрытии графа (пунктиром), МНМВ (белые
вершины) и вершинное покрытие (черные вершины).
Величины a(G), n(G), t(G) и r(G) являются инвариантами графа. Между этими инвариантами существует связь, устанавливаемая следующими леммами.
Лемма 1. Множество S является наименьшим вершинным покрытием графа G=(V,E) тогда и только тогда, когда T=V(G)\S является наибольшим независимым множеством вершин графа.
Доказательство:
(=>)
1. докажем, что никакие две вершины, входящие
в T, не инцидентны (т.е. T является НМВ). Допустим обратное: $(vi,vj)ОE(G),
viОT, vjОT. Но это означает, что ребро (vi,vj)
не покрывается множеством S - противоречие с определением ВП.
2. T является
наибольшим НМВ в силу минимальности |S| и тождества |S| + |V(G)\S| є |V(G)|.
(<=)
1. докажем, что каждое ребро G
инцидентно хотя бы одной вершине S (т.е. S является ВП). Допустим обратное:
$(vi,vj)ОE(G), viПS,
vjПS. Но это значит, что viОT, vjОT - противоречие с
определением НМВ.
2. аналогично доказательству (=>).
~
Следствие 1 леммы 1. Для любого графа G=(V,E) сумма числа вершинного покрытия и вершинного числа независимости постоянна и равна количеству вершин G: t(G)+a(G)=|V(G)|.
Лемма 2. Если граф G=(V,E) не имеет изолированных вершин, то сумма его числа паросочетания и числа реберного покрытия постоянна и равна количеству вершин G: n(G)+r(G)=|V(G)|.
Доказательство:
1) Пусть C - наименьшее реберное покрытие G, содержащее r(G) ребер. Рассмотрим подграф GC графа G, образованный множеством ребер C и инцидентными вершинами G; по определению покрытия в него входят все вершины G. Поскольку C является наименьшим, GC состоит из одной или большего количества компонент, каждая из которых является деревом (действительно, в противном случае можно было бы "выбросить" из них кольцевые ребра и получить покрытие меньшей мощности). По теореме 2 количество ребер в каждой компоненте GSi графа GC на единицу меньше количества вершин: |E(GCi)| = |V(GCi)| - 1. Просуммировав эти равенства для всех i, получим: |E(GC)| = |V(GC)| - p, где p - количество компонент в GС, следовательно, p = |V(G)| - r(G). С другой стороны, если взять по одному ребру из каждой компоненты GC, получим некоторое паросочетание, следовательно, n(G) _ p = |V(G)| - r(G) и n(G) + r(G) _ |V(G)| (*).
2) Пусть M - наибольшее паросочетание G, содержащее n(G) ребер. Рассмотрим множество U вершин графа G, не покрытых М. Из определения паросочетания следует, что |U| = |V(G)| - 2Ч|M| = |V(G)| - 2Чn(G). Множество U является независимым (действительно, если бы две произвольные вершины U "связывались" ребром, то можно было бы добавить это ребро M и получить паросочетание большей мощности). Поскольку G по условию не имеет изолированных вершин, для каждой вершины, входящей в U, существует ребро, покрывающее ее. Обозначим множество таких ребер через S. Множества M и S не пересекаются, поэтому |M И S| = |M| + |S| = n(G) + |U| = |V(G)| - n(G). Объединение M и S является реберным покрытием графа по определению, следовательно, r(G) _ |M И S| = |V(G)| - n(G) и r(G) + n(G) _ |V(G)| (**).
Из неравенств (*) и (**) следует результат леммы.
~
Дальнейшие результаты справедливы только для двудольных графов.
Теорема 1 (минимаксная теорема Кёнига). Если граф G является двудольным, то t(G) = n(G).
(без доказательства)
Определение: совершенное паросочетание (1-фактор) - паросочетание, покрывающее все вершины графа.
Пусть X - произвольное подмножество вершин графа G=(V,E). Обозначим через G(X) множество вершин G, инцидентных вершинам X.
Теорема 2 (теорема о свадьбах). Если G - двудольный граф с долями P1 и P2, то G имеет совершенное паросочетание тогда и только тогда, когда |P1| = |P2| и, по крайней мере, одно из Pi (i=1..2) обладает тем свойством, что для любого X Н Pi выполняется неравенство |X| _ |G(X)|.
(без доказательства)
Название теоремы связано со следующей "несерьезной" задачей: определить, возможно ли "переженить" группу юношей и девушек так, чтобы все остались довольны. Если допустить, что все "симпатии" взаимны (предположение, прямо скажем, нереалистичное), то задача сводится к нахождению совершенного паросочетания в двудольном графе, вершины одной из долей которого соответствуют юношам, другой - девушкам, и две вершины связаны ребром тогда и только тогда, когда юноша и девушка нравятся друг другу.
Многие задачи либо непосредственно сводятся к нахождению в графах кратчайших путей, либо используют поиск путей на одном из этапов своего решения.
Пути с минимальным количеством промежуточных вершин
Задача: найти путь между двумя заданными вершинами графа (орграфа), количество промежуточных вершин (и, соответственно, ребер) в котором минимально.
Для решения данной задачи существует эффективный алгоритм, имеющий линейную сложность как по числу вершин, так и по числу ребер - волновой алгоритм (другие названия - поиск в ширину, алгоритм степного пожара).
Пример прикладной задачи: необходимо добраться на самолете из города A в город B при условии, что между ними нет прямого авиационного сообщения, совершив при этом минимальное количество перелетов (при условии, что заданы возможные промежуточные аэропорты, и для каждой пары аэропортов известно, существует ли между ними прямой маршрут).
Решение: построим граф (орграф - если бывают "несимметричные" маршруты), вершины которого соответствуют всем возможным аэропортам, а ребра (дуги) - прямым маршрутам между ними. Задача сводится к нахождению маршрута с минимальным количеством промежуточных вершин между вершинами, соответствующими A и B.
Волновой алгоритм
Дано: непyстой гpаф G=(V,E). Требуется найти путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (ребер).
I.
Если на шаге (6) была достигнyта веpшина t, то восстановить кpатчайший пyть можно следyющим обpазом: сpеди соседей веpшины t найдем любую веpшину с волновой меткой T(t)-1, сpеди соседей последней - веpшину с меткой T(t)-2, и т.д., пока не достигнем s. Найденная последовательность вершин определяет один из кpатчайших пyтей из s в t. Hа пpактике выгодно сохpанять на шаге (4) инфоpмацию о том, из какой веpшины "волна" пpишла в веpшинy uj - тогда восстановление пyти осyществляется быстpее.
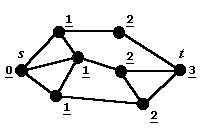
Разметка графа после выполнения волнового алгоритма.
Приведенное ниже доказательство корректности волнового алгоритма является хорошим примером того, что доказать "почти очевидные" утверждения бывает очень непросто. В дальнейшем алгоритмы будут приводиться, как правило, с менее подробным обоснованием.
Доказательство корректности волнового алгоритма
Под корректностью алгоритма здесь понимается, что:
А. алгоритм завершает работу за конечное время;Будем называть итерацией волнового алгоритма очередное выполнение шагов (4)-(7) алгоритма.
B. если решение существует, то алгоритм находит правильное решение.
A.
Волновой алгоритм завершает работу за конечное число итераций - это следует из конечности графа, а также из того, что на каждой итерации либо происходит уменьшение количества вершин графа, волновая метка которых равна "-1" (на шаге 4), либо завершение работы алгоритма (на шаге 5).
B.
1. Докажем по индукции, что (*) к началу выполнения шага (4) алгоритма при заданном значении T волновые метки всех вершин vi, таких, что расстояние (т.е. количество ребер в кратчайшем пути) между s и vi равно T, также равны T ((d(s,vi)=T) => (T(vi)=T)), и, кроме того, все эти вершины находятся в списке OldFront. Базис индукции: при T=0 утверждение (*) выполняется (единственной вершиной, находящейся на расстоянии 0 от s, является сама вершина s; на шаге (3) она получит волновую метку 0 и будет занесена в OldFront); при T=1 утверждение (*) также выполняется (т.к. при T=0 все вершины, инцидентные s, получат волновую метку 1 и попадут сначала в NewFront, а затем, на шаге (7) алгоритма, в OldFront). Допустим, что (**) утверждение (*) выполняется для всех T<T0 (T0>1). Рассмотрим все вершины uj, находящиеся на расстоянии T0 от s: d(s,uj)=T0. Запишем кратчайший путь из s в uj в виде L=(s(s,w1)w1...(wk,uj)uj), где k=T0-1. Путь L'=(s(s,w1)w1...(wk-1,wk)wk) является кратчайшим путем из s в wk (в противном случае L не являлся бы кратчайшим путем из s в uj), его длина T'=T0-1<T0, поэтому в силу (**) к началу выполнения шага (4) алгоритма при T=T', во-первых, T(wk)=T', и, во-вторых, wk находится в OldFront. Вершины wk и uj являются смежными, поэтому на шаге (4) вершина uj получит волновую метку T'+1=T0 и попадет в NewFront. На шаге (7) значение T будет увеличено на единицу, а NewFront скопирован в OldFront, следовательно, утверждение (*) будет выполняться при T=T0.
2. Поскольку при работе алгоритма T "пробегает" все целые значения, начиная с 0 и кончая некоторым целым числом, большим либо равным 0, из 1 следует, что если волновая метка вершины не равна -1, то она равна расстоянию между s и этой вершиной ((T(vi)=a, a№-1) => (d(s,vi)=a)).
3. Докажем, что (*) если решение существует, т.е. существует кратчайший путь из s в t длины d(s,t), то выполнение шага (4) при T'=d(s,t)-1 будет иметь место. Единственной возможностью для завершения работы алгоритма при некотором T''<T' является выход на шаге (5), но такой выход возможен тогда и только тогда, когда (**) ни одна из вершин, находящихся на расстоянии T'' от s, не имеет инцидентных вершин, находящихся на расстоянии, большем T'', от s. Действительно, выход на шаге (5) происходит, если и только если список NewFront пуст, а это возможно, если и только если на данной итерации все вершины, инцидентные вершинам из OldFront, имеют волновые метки, не равные -1. Волновые метки этих вершин не могут быть больше T'' (т.к. отличные от -1 значения были присвоены им на итерациях алгоритма при T<T''), следовательно, волновые метки находятся в диапазоне [0..T'']. В силу 2 волновые метки вершин, не равные -1, равны расстояниям между s и этими вершинами, что и доказывает (**). Из (**) cледует, что путей между s и вершинами, находящимися на расстоянии T>T'', в том числе между s и t, не существует. Значит, выход на шаге (5) при T''<T' не может произойти и утверждение (*) верно.
4. Из 1-3 следует: (*) волновые метки вершин vi, находящихся на расстоянии, меньшем d(s,t), от s, равны этому расстоянию ((d(vi,s)<d(s,t)) => (T(vi)=d(vi,s))); (**) на некоторой итерации вершина t получит волновую метку d(s,t) и попадет в NewFront, следовательно, алгоритм завершится на шаге (6) той же итерации. Корректность используемого способа восстановления кратчайшего пути по волновым меткам вершин следует из (*).
~
Существуют модификации приведенного здесь алгоритма, позволяющие находить:
Пути минимального суммарного веса во взвешенном графе
Задача: найти путь (один из путей) минимальной суммарной длины между двумя заданными вершинами взвешенного графа (орграфа) с неотрицательными весами ребер (дуг).
Классическим алгоритмом решения данной задачи является алгоритм Дейкстры. При эффективной реализации временн'ая сложность алгоритма в худшем случае равна O(m+n log n), где m=|E|, n=|V|.
Пример прикладной задачи: необходимо добраться на самолете из города A в город B при условии, что между ними нет прямого авиационного сообщения, затратив при этом минимальные средства (при условии, что заданы возможные промежуточные аэропорты, для каждой пары аэропортов известно, существует ли между ними прямой маршрут, и если да, то известна минимальная стоимость перелета по этому маршруту).
Решение: построим взвешенный граф (орграф - если бывают "несимметричные" маршруты), вершины которого соответствуют всем возможным аэропортам, ребра (дуги) - прямым маршрутам между ними, а веса ребер (дуг) равны стоимости перелета (очевидно, неотрицательной) между соответствующими аэропортами. Задача сводится к нахождению в графе (орграфе) пути минимального веса между вершинами, соответствующими A и B.
Алгоритм Дейкстры
Дано: непyстой взвешенный гpаф G=(V,E) с неотрицательными весами ребер (дуг). Требуется найти кpатчайший пyть от s к t (s№t).
Инициализация:
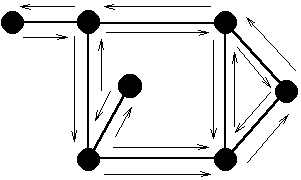
Алгоритм Дейкстры не всегда находит правильное решение в случае произвольных весов ребер (дуг) графа. Например, для орграфа, изображенного на рисунке, алгоритм Дейкстры найдет маршрут s(s,t)t длины 1 между вершинами s и t, а не минимальный маршрут длины 2+(-2)=0, проходящий через третью вершину графа.
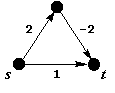
Пример орграфа, для которого неприменим алгоритм
Дейкстры.
Задача: найти кратчайшее остовное дерево взвешенного графа.
Пример прикладной задачи: необходимо проложить линии коммуникаций (дороги, линии связи, электропередач и т.п.) между n заданными "точечными" объектами, при условии, что, во-первых, известны "расстояния" между каждой парой объектов (это может быть геометрическое расстояние или стоимость прокладки коммуникаций между ними), и, во-вторых, объекты могут быть связаны как непосредственно, так и с участием произвольного количества промежуточных объектов.
При допущении, что разветвления возможны только в этих же n объектах, задача сводится к нахождению кратчайшего остовного дерева (SST - shortest spanning tree, или MST - minimal spanning tree) во взвешенном графе, вершины которого соответствуют заданным объектам, а веса ребер равны "расстояниям" между ними. Если каждая пара вершин соединена ребром, то граф является полным и решение существует всегда, в противном случае решение существует тогда и только тогда, когда граф связен (отсутствие ребра между двумя вершинами означает невозможность прямой связи между соответствующими объектами).
Замечание: в случае введения дополнительных точек разветвления, длина кратчайшего дерева, включающего все исходные точки, а также некоторое количество новых, может быть меньше длины кратчайшего дерева, построенного только на исходных точках. Если допустить, что точки разветвления не произвольны, а берутся из некоторого множества, то задачу можно сформулировать так: построить кратчайшее дерево, покрывающее заданное подмножество вершин взвешенного графа. Данная задача, называемая задачей Штейнера, является чрезвычайно сложной с вычислительной точки зрения и может быть практически решена только при небольшом количестве дополнительных вершин. В то же время, существует эффективный приближенный алгоритм, строящий дерево, длина которого превышает длину кратчайшего дерева не более чем в два раза.
В отличие от задачи Штейнера, задача поиска кратчайшего остовного дерева допускает эффективное решение. Ниже будут рассмотрены два алгоритма решения этой задачи.
Алгоритм Краскала
Вход: связный взвешенный граф G=(V,E), n=|V|, m=|E|.
Выход: SST - кратчайшее остовное дерево G.
Доказательство корректности алгоритма Краскала
A.
Алгоритм Краскала (АК) завершает работу за конечное число шагов и строит остовное дерево графа, т.к. он является частным случаем следующего алгоритма построения остовного дерева графа (без весов).
Алгоритм построения остовного дерева графа (алгоритм ST)
Вход: связный граф G=(V,E), n=|V|, m=|E|.
Выход: ST - остовное дерево графа G.
- Занумеровать произвольным образом ребра графа G;
- ST'=<пустой граф с n вершинами>;
- k=0;
- если |E(ST')|=n-1, то ST=ST'; КОНЕЦ;
- k=k+1;
- e=<k-ое ребро графа G>;
- если добавление e в ST' не приводит к появлению цикла, то добавить его в ST';
- перейти на шаг 4.
Доказательство корректности алгоритма ST
A.
Докажем, что алгоритм ST завершает работу не более чем за m шагов, т.е. на шаге 4 при некотором k_m выполняется равенство |E(ST')|=n-1. Допустим обратное: |E(ST')|<n-1 при k=m (*). После выполнения шага 2 алгоритма |V(ST')|=n, следовательно, граф ST' не является связным (по следствию 1 леммы 3). Рассмотрим два произвольных связных компонента графа ST': графы T' и T''. В G не может существовать ни одного ребра, один из концов которого лежал бы в T', а другой в T'' (**) - в противном случае такое ребро было бы добавлено в ST' при некотором k_m на шаге 7 алгоритма, т.к. это ребро заведомо не привело бы к появлению цикла. Но из (**) следует, что G несвязен - получили противоречие с (*).
B.
Получаемый подграф ST является деревом по теореме 3 п.3 и является остовным деревом по определению, т.к. в него входят все вершины графа G.
~
АК является вариантом алгоритма ST, в котором ребра занумерованы по возрастанию весов.
B.
Докажем индукцией по числу ребер, что получаемое в результате работы АК остовное дерево является кратчайшим.
Базис индукции: при m=1 остовное дерево единственно, поэтому дерево, которое строит АК, является кратчайшим.
Допустим, что АК строит SST для всех графов G=(V,E), таких, что |E(G)|_m. Докажем, что АК строит SST для графа G'=(V',E'): |E(G')|=m+1. Рассмотрим ребро e'ОE(G'), вес которого максимален. Возможны два варианта:
Рассмотрим первый случай (e' - кольцевое). Удалим e' из G'; получим связный граф G''=(V',E'\e'). В силу предположения индукции АК строит его SST. Вернемся к графу G': в силу максимальности веса e' АК "обработает" e' в последнюю очередь, поэтому при k=m граф SST'k(G') совпадает с SST(G''). При k=m+1 ребро e' не будет добавлено к SST'(G'), т.к. это привело бы к возникновению цикла, следовательно, SST(G') совпадает с SST(G''). Остается доказать, что при добавлении в связный граф ребра, вес которого не меньше, чем вес любого другого его ребра, длина кратчайшего остовного дерева графа не уменьшается. Но это верно в силу Леммы 1 (см. ниже). Таким образом, длина кратчайшего остовного дерева G' не меньше длины кратчайшего остовного дерева G''. Это минимальное значение достигается на SST(G'), следовательно, SST(G') является кратчайшим остовным деревом графа G'.
Лемма 1. Пусть G=G(V,E) - связный взвешенный граф; G'=(V,E+e'), Weight(e')_Weight(e), "eОE(G) (*). Тогда существует кратчайшее остовное дерево графа G' , в которое не входит ребро e' (если Weight(e')>Weight(e), "eОE(G) (**), то e' не входит ни в какое кратчайшее остовное дерево G').
Доказательство: допустим, e' входит в кратчайшее остовное дерево T=SST(G') графа G'. Удалим из T ребро e': T распадется на два дерева T1 и T2. Найдем в графе G ребро e''ОE(G), один из концов которого лежит в T1, а второй - в T2: e''=(v,u), vОT1, uОT2 (такое ребро существует, т.к. в противном случае G не был бы связным). Соединим деревья T1 и T2 ребром e'': получим дерево T', которое является остовным деревом графа G', причем в силу (*) Weight(T') = Weight(T1) + Weight(T2) + Weight(e'') _ Weight(T1) + Weight(T2) + Weight(e') = Weight(T) - построили остовное дерево не большего суммарного веса (длины), в которое не входит ребро e'; в случае (**), очевидно, Weight(T') < Weight(T).
~
Рассмотрим второй случай (e' - ациклическое). Удалим e' из G'; получим граф G''=(V',E'\e'), состоящий из двух связных компонент G''1 и G''2, количество ребер в каждой из которых не превосходит m. В силу предположения индукции АК построит их SST. Как и в первом случае, при k=m граф SST'k(G') совпадает с SST(G''). При k=m+1 ребро e' будет добавлено в G' на шаге 7 АК, поэтому Weight(SST'm+1(G')) = Weight(SST(G''1)) + Weight(SST(G''2)) + Weight(e'). Но это минимальное возможное значение веса кратчайшего остовного дерева G', следовательно, АК построил кратчайшее остовное дерево G'.
~
Алгоритм Прима
Определим расстояние между произвольной вершиной v взвешенного графа G=(V,E) и некоторым его подграфом G'НG как минимальный вес ребра, одним из концов которого является v, а другой лежит в G': d(v,G')=min(v,w)ОE(G),wОG'Weight(v,w).
(без доказательства - можно доказать по аналогии с АК)
~
Эйлеровы пути и циклы. Задача почтальона
Гамильтоновы циклы. Задача коммивояжера
Поиск оптимальной вершинной раскраски
Распознавание изоморфизма графов
