APR Jun Jul 18 2007 2008 2009 16 captures 28 Oct 04 - 18 Jun 08

Close Help

Исходный текст методички в формате DOC можно скачать ЗДЕСЬ

Введение

Данное пособие предназначено для поддержки двухсеместрового курса "Методы формальной спецификации программ". Курс состоит из двух частей. Первая часть рассматривает вопросы разработки программного обеспечения на основе подходов, предложенных RAISE методологий, и вопросы автоматизации тестирования на основе формальных спецификаций, где в качестве иллюстративного материала также используются RAISE спецификации. Вторая часть курса посвящена современным объектно- ориентированным методам разработки программного обеспечения. Основное внимание в этой части курса уделено анализу требований, системному анализу, переходу от системного проектирования к реализации. В качестве языка спецификаций во второй части используются языки SDL и MSC. Тем самым слушатели данного курса имеют возможность познакомиться с двумя в значительной степени разными подходами к использованию формальных методов в современных индустриальных технологиях разработки программного обеспечения.

Языки формальных спецификаций были разработаны для того, чтобы упростить и там, где это возможно, автоматизировать процессы создания и анализа программного обеспечения. Большая часть языков формальных спецификаций в качестве своих истоков имеет либо математическую нотацию, либо некоторый формализм, который в свою очередь имеет строгую математическую интерпретацию. Тяга к математическим построениям и формальным моделям была обусловлена тем, что неоднозначность и нечеткость в неформальных или полуформальных описаниях могла быть преодолена только заменой таких описаний на формальные, которыми и являются формальные спецификации.

Тем самым, использование формальных методов и соответствующих средств является необходимым условием для реализации технологий, нацеленных на создание программного обеспечения с заданными свойствами, и на анализ программ, позволяющих установить наличие или отсутствие таковых свойств. Однако формальные методы, в целом, и языки спецификации, в частности, не достаточны для того, чтобы решить задачу создания качественного программного обеспечения. Эта задача для своего решения требует систематического применения разнообразных инженерных методов, часть из которых может с успехом использовать и формальные методы.

Одной из важнейших целей данного курса была демонстрация современных достижений в области использования формальных методов при создании реального программного обеспечения. Для решения этой задачи, с одной стороны, необходимо было выбрать язык спецификаций, зарекомендовавший себя как инструмент практических программистов, и, с другой стороны, показать, как формальные методы могут использоваться в ходе всех фаз жизненного цикла программного обеспечения: от проектирования до тестирования.

В качестве такого языка был выбран RSL. Этот язык является языком методологии разработки программ RAISE - Rigorous Approach to Industrial Software Engineering. RAISE является результатом работы группы европейских ученых, которые в конце 80- х годов объединилась для создания метода разработки программного обеспечения, пригодного для использования не только в исследовательских целях, но и в индустрии.

RSL с одной стороны, вобрал в себя полезные возможности нескольких других широко известных языков, таких как VDM/Meta- IV, Z, LOTOS, CSP, с другой стороны, он оказался достаточно экономным и естественным, что упрощает его изучение и использование в программной индустрии. Одним из привлекательных свойств RSL является его близость к традиционным языкам программирования.

Данное руководство не заменяет ни описания языка, ни описания собственно RAISE методологии. Наиболее полным описанием языка является монография [1]. Руководство содержит краткие описания тем практических занятий и контрольных заданий, которые студенты выполняют при изучении данного курса лекций. По форме это упражнения для закрепления навыков использования RSL. Вместе с тем, обратим внимание читателя на то, что за этими упражнениями стоит целый спектр задач разработки промышленного программного обеспечения. Эти задачи должны не только помочь в овладении языком RSL, они должны научить видеть задачи системного анализа проектных материалов, реализации, форвард- и реверс- инженерии и научить решать их систематическим образом и, если это возможно, при помощи формальных методов.

Глава 1. Основные понятия языка RSL

Цель данного раздела - описать основные встроенные типы языка RSL, уделяя особое внимание специфике RSL логики. Раздел содержит упражнения по выработке навыков вычисления и оформления выражений языка RSL на базе встроенных типов.

1.1.1.     Встроенные типы языка RSL

В языке RSL предусмотрены следующие встроенные типы:

Bool - представляет булевские значения,

Int - целые числа,

Nat - натуральные числа,

Real - вещественные числа,

Char - символы,

Text - строки символов,

Unit - содержит единственное специальное значение ().

Тип Bool содержит два значения true и false, над значениями данного типа определены операции Ù, Ú, Þ, ~, =, ¹.

Для значений типа Int определены операции +, - , *, /, ­, \, abs, real, где ­ означает возведение в степень, \ - взятие остатка от деления, abs - префиксная операция для вычисления модуля числа и real - префиксная операция для преобразования из типа Int в тип Real. Кроме того значения данного типа можно сравнивать с помощью операций <, £, >, ³, =, ¹.

Тип Nat является подтипом типа Int и задается соотношением:

Nat = {| i : Int • i ³ 0 |}. К значениям этого типа применимы все операции, определенные для типа Int.

К значениям типа Real применимы операции +, - , *, /, ­, <, £, >, ³, =, ¹, abs, int, где int - префиксная операция для преобразования из типа Real в тип Int, возвращающая ближайшее по направлению к 0 целое число. Например:

int 4.6 = 4

int - 4.6 = - 4

Наличие десятичной точки в записи вещественных констант обязательно (1.0, 12.35 и т.д.).

Тип Char содержит символы, к значениям этого типа применимы операции = и ¹, константы типа Char заключаются в апострофы ( например: ¢f¢, ¢Z¢ и т.д. ).

Тип Text предназначен для описания строк символов, причем каждая строка должна начинаться и заканчиваться символом ². Например, ²ABC², ²²²² -пустая строка. К значениям этого типа применимы операции =, ¹.

Тип Unit используется в описаниях сигнатур функций для изображения отсутствующих входных или выходных параметров.

1.1.2.     Логика в языке RSL

Остановимся более подробно на вычислении логических выражений в языке RSL, поскольку принятая в языке логика имеет некоторую специфику по сравнению с классической логикой. Суть этой специфики связана с наличием в RSL специального выражения chaos, предназначенного для обозначения непредсказуемого (хаотичного) поведения программы во время выполнения, возникающего в результате какого- либо отказа в программе и приводящего к ситуации, когда вычисление значения какого- либо выражения может не завершиться. chaos не принадлежит ни к одному из типов RSL и в выражениях может появляться в позициях, предусмотренных для значений различных типов. Например, chaos может встречаться как вместо вхождения значений типа Bool, так и вместо типа Int. В RSL принята сокращенная схема вычисления логических выражений, т.е. если значение всего выражения полностью определяется значением его первого операнда, то вычисление второго операнда не производится.

Ниже приводятся таблицы истинности (с учетом chaos ) для основных логических операций. Левая колонка соответствует первому операнду, верхняя строка - второму операнду.

Ù	true	false	chaos
true	true	false	chaos
false	false	false	false
chaos	chaos	chaos	chaos

Ú	true	false	chaos
true	true	true	true
false	true	false	chaos
chaos	chaos	chaos	chaos

Þ	true	false	chaos
true	true	false	chaos
false	true	true	true
chaos	chaos	chaos	chaos

Определение операции ~ необходимо расширить соотношением:

~ chaos º chaos

В таблицах истинности для операций = и º символы a и b обозначают выражения, значения которых отличаются друг от друга.

º	a	b	chaos
a	true	false	false
b	false	true	false
chaos	false	false	true

=	a	b	chaos
a	true	false	chaos
b	false	true	chaos
chaos	chaos	chaos	chaos

На основании приведенных таблиц можно заметить, например, что в отличие от классической логики в RSL операции Ù и Ú не обладают свойством коммуникативности, т.е. выражения e₁ Ù e₂ º e₂ Ù e₁ и e₁ Ú e₂ º e₂ Ú e₁ уже не являются тавтологиями.

Для обеспечения возможности альтернативного выбора при вычислении выражений в RSL введены условные выражения, имеющие следующий вид:

if value_expr then value_expr₁ else value_expr₂ end,

где value_expr является логическим выражением, а выражения value_expr₁ и value_expr₂ имеют один и тот же тип, который является и типом всего условного выражения. При вычислении значений условных выражений необходимо иметь в виду следующие свойства:

if true then expr₁ else expr₂ end º expr₁ (1)

if false then expr₁ else expr₂ end º expr₂ (2)

if a then expr₁ else expr₂ end º

if a then expr₁[true/a] else expr₂[false/a ] end (3)

if chaos then expr₁ else expr₂ end º chaos (4)

Запись вида expr₁[true/a] обозначает подстановку в выражение expr₁ значения true вместо a.

Квантифицированные выражения языка RSL имеют традиционную форму и используются в основном для записи аксиом. Допускаются кванторы: ", $, $!.

Упражнения

1.       Ниже приведены равенства, которые верны в классической логике. Какие из них верны в RSL?

(a)   ~(~a) º a

(b) true Ú a º true

(c)   a Ú true º true

(d) a Þ true º true

(e)   a Þ b º ~a Ú b

(f)    a Ú ~a º true

(g)   (a Ù ~a) º false

(h)   (a Ù b) Ù c º a Ù (b Ù c)

(i)     (a Ú b) Ú c º a Ú (b Ú c)

(j)    (a = a) º true

(k) (a º a) º true

Указания:

·        воспользуйтесь приведенными в разделе 1.1.2 таблицами истинности для основных логических операций;

·        для проверки справедливости предложенных утверждений достаточно исследовать их значения на наборах данных, где хотя бы один операнд обращается в chaos.

Например, для пункта (c):

chaos Ú true º chaos,

(chaos º true) º false

Следовательно, утверждение (c) неверно в RSL.

2.     Упростить следующие выражения:

(a)   if true then false else chaos end º ?

(b) if a then ~( a º chaos) else false end º ?

Указание: воспользуйтесь свойствами (1) - (4) раздела 1.1.2.

3.       Какие из следующих выражений верны ?

(a)          " i : Int • $ j : Int • i+j = 0

(b)         " i : Int • $ j : Nat • i+j = 0

(c)          $ i : Int • " j : Int • i+j = 0

4.       Напишите RSL выражение, выражающее тот факт, что нет наибольшего целого числа.

Указание: воспользуйтесь квантифицированными выражениями RSL.

5.       Завершите определение функции, которая проверяет, является ли ее аргумент четным числом.

is_even : Nat ® Bool

is_even(n) º ...

Указания:

можно использовать операцию \ (остаток от деления) или квантифицированное выражение.

1.2.         Описание функций

Цель данного раздела - познакомить читателя с различными принятыми в RSL стилями описания констант и функций, а также дать методические рекомендации по выбору того или иного стиля описания в зависимости от решаемой задачи. Раздел содержит упражнения по выработке навыков описания констант и функций языка RSL в явном (explicit), неявном (implicit) и аксиоматическом (axiomatic) стилях.

1.2.1.     Декартовы произведения ( products )

Декартовым произведением называется упорядоченный конечный набор значений, возможно, различных типов, например:

(1,2)

(1,true,²John²).

В декартовом произведении существенен порядок следования элементов, т.е. (1,2) и (2,1) являются различными значениями.

Тип, представляющий собой декартово произведение других типов, задается выражением вида:

type_expr₁ ´ ... ´ type_expr_n, где n³2.

Значениями такого типа являются декартовы произведения длины n (v₁,...,v_n), где каждое v_i - некоторое значение типа type_expr_i.

Примеры записи значений декартовых произведений с указанием их типов:

(true,p Þ q) : Bool ´ Bool

(x + 1, 0, ²this is a text²) : Nat ´ Nat ´ Text

Над декартовыми произведениями разрешены операции = и ¹.

1.2.2.     Описание констант

В RSL константа рассматривается как частный случай функции, а именно как функция без параметров с постоянным значением, поэтому для описания констант и функций в языке предусмотрено единое понятие value.

Описание констант (value definition) в языке RSL может производиться в одном из трех стилей:

·        явном (explicit),

·        неявном (implicit),

·        аксиоматическом.

Явный стиль описания применяется, когда непосредственно указывается значение константы. Например, RSL- спецификация вида:

value x : Int = 1

определяет целочисленную константу x=1.

Неявный стиль описания следует использовать, если точное значение константы не указывается, а задаются лишь некоторые ограничения на это значение. Например:

value x : Int • x > 0

определяет целочисленную константу x, значением которой может являться любое целое положительное число. Спецификация при этом получается неполной и может быть уточнена в дальнейшем. Такой прием называется недоспецификацией (under- specification) и применяется в том случае, когда описываемое значение по каким- либо причинам не может быть определено полностью.

Аксиоматический стиль описания заключается в том, что наряду с типом определяемой константы задается также некоторый набор аксиом, накладывающих дополнительные ограничения на значение константы. Заметим, что как для явного, так и для неявного описаний можно построить эквивалентное описание в аксиоматическом стиле. Например, эквивалентная форма приведенных выше описаний константы x в аксиоматическом стиле выглядит следующим образом:

value x : Int

axiom x º 1 (для явного описания),

value x : Int

axiom x > 0 (для неявного описания).

1.2.3.     Описание функций

Описание функции в RSL начинается с определения её сигнатуры, т.е. имени функции и типов входных и выходных параметров, здесь же задается вид функции с точки зрения возможности её вычисления для всех значений, определяемых типом входных параметров.

1.2.3.1.          Всюду вычислимые и частично вычислимые функции

Функция f, отображающая значения типа T₁ в значения типа T₂, является всюду вычислимой (total function), если для любого значения из T₁ f возвращает некоторое единственное значение из T₂, т.е. f обладает следующим свойством:

" x : T₁ • $! y : T₂ • f(x) º y

Сигнатура функции f в этом случае имеет вид:

f : T₁ ® T₂

Всюду вычислимые функции всегда детерминированы и определены для всех значений входных параметров.

Функция f, отображающая значения типа T₁ в значения типа T₂, является частично вычислимой (partial function), если существует такое значение v типа T₁, для которого вычисление f(v) может либо вообще не завершиться (в этом случае f(v) º chaos), либо приводить к недетерминированному результату, когда разные обращения к функции f со значением v могут возвращать различные значения типа T₂.

Сигнатура частично вычислимой функции f имеет вид:

f : T₁ - ~® T₂

Частично вычислимые функции включают в себя всюду вычислимые функции.

Дальнейшее определение функции подобно рассмотренному ранее определению констант может производиться в различных стилях в зависимости от специфики решаемой задачи.

1.2.3.2.          Явный стиль описания функций

Описание функции в явном стиле (explicit function definition) ориентировано на описание конкретного алгоритма и используется в том случае, когда явно задаётся способ преобразования входных параметров в выходные. Примером явного описания всюду вычислимой функции может служить следующий фрагмент RSL спецификации:

value

f : Int ® Int

f(x) º x + 1

В качестве примера описания частично вычислимой функции в явном стиле рассмотрим функцию p(x), вычисляющую значение 1/x:

value

p : Real - ~® Real

p(x) º 1.0/x

pre x ¹ 0.0

Последняя строка данного описания содержит предусловие, накладывающее некоторое ограничение на значения входного параметра.

1.2.3.3.          Неявный стиль описания функций

Описание функции в неявном стиле (implicit function definition), абстрагируясь от конкретного алгоритма, во главу угла ставит формализацию отношений, связывающих между собой входные и выходные параметры, т.е. здесь описывается не сам алгоритм, а эффект его применения. Этот стиль описания является более общим в том смысле, что алгоритм преобразования не уточняется и, следовательно, для одной и той же неявной спецификации можно предложить разные алгоритмы, эффект применения которых удовлетворяет указанной спецификации. Ниже приведены примеры описания в неявном стиле всюду вычислимой функции f(x), возвращающей в качестве результата некоторое целое число, превосходящее входное значение:

value

f : Int ® Int

f(x) as r post r > x

и частично вычислимой функции square_root(x) для нахождения значения квадратного корня:

value

square_root : Real - ~® Real

square_root(x) as s

post s * s = x /\ s ³ 0.0

pre x ³ 0.0

Причем, как видно из примеров, конкретный алгоритм получения результата остается в обоих случаях за рамками рассмотрения.

1.2.3.4.          Аксиоматическое описание функций

При использовании аксиоматического стиля описания функции предлагается некоторый набор аксиом, определяющих свойства результата функции, а также, возможно, и ее входных параметров. Этот стиль описания может применяться с одинаковым успехом и для описания алгоритма, и для описания эффекта выполнения функции, поэтому как для явного , так и для неявного описаний всегда можно предложить эквивалентное описание в аксиоматическом стиле. Кроме того данный стиль является единственно возможным при описании алгебраических спецификаций, где аксиомы имеют специфический вид (например, f(g(x), x) º h(x)), т.е. в качестве аргумента функции допускается использование обращения к функции.

В качестве примеров приведем аксиоматическое описание всюду вычислимой функции f(x), эквивалентное рассмотренному выше явному описанию той же функции:

value

f : Int ® Int

axiom " x : Int • f(x) º x + 1

и частично вычислимой функции square_root(x), также рассмотренной ранее:

value

square_root : Real - ~® Real

axiom

     " x : Real • x ³ 0.0 Þ

         $ s : Real •

               square_root(x) = s /\

               s * s = x /\ s ³ 0.0

1.2.3.5.          Схема определения функции

Подводя итог вышесказанному, можно предложить следующую схему определения функции:

1.      выбрать имя функции;

2.      выбрать тип:

(a)   аргументов,

(b) результата,

(c)   отображения:

·          всюду вычислимая функция (может быть определена для всех значений входных параметров),

·          частично вычислимая функция (необходимо предусловие);

3.        выбрать стиль описания:

(a)     явный (можно задать формулу вычисления результата),

(b)    неявный (можно описать связь входа и выхода посредством предиката),

(c)     аксиоматический (может быть использован всегда, необходим в алгебраических спецификациях).

Упражнения

1.     Для обеспечения работы с комплексными числами описать:

(a)   тип 'Complex' для представления комплексных чисел,

(b) константу 'zero' для представления комплексного числа 0 + 0i,

(c)   константу 'c', представляющую любое комплексное число вида x + xi;

(d) функции 'add' и 'mult' для сложения и умножения комплексных чисел,

(e)   функцию 'f', возвращающую в качестве результата некоторое комплексное число, отличное от заданного.

Указания:

·               в пунктах (b) и (d) воспользуйтесь явным (explicit) стилем описания константы и функций, т.к. здесь явно указано значение константы и способ получения результатов функций по их входным значениям;

·               в пунктах (c) и (e) следует использовать неявное (implicit) описание константы и функции, поскольку в условии не оговаривается явно значение константы и способ получения результата по входному значению;

·               в пунктах (c) и (d) для упрощения записи удобно воспользоваться конструкцией let. С помощью этой конструкции, например, для пункта (c) факт равенства действительной и мнимой частей комплексного числа c можно записать так:

let (x, y) = c in x = y end

2. Пусть система координат описывается следующим образом:

SYSTEM_OF_COORDINATES=

class

     type

          Position = Real ´ Real

     value

          origin : Position = (0.0,0.0),

          distance : Position ´ Position ® Real

          distance((x₁, y₁),(x₂, y₂)) º

               ((x₂ - x₁)­2.0 + (y₂ - y₁)­2.0)­0.5

end

Здесь тип 'Position' предназначен для описания координат точек на плоскости, константа 'origin' задает начало координат, функция 'distance' определяет способ вычисления расстояния между двумя точками. Обратите внимание на то, что при описании константы 'origin' и функции 'distance' использован явный стиль описания (explicit definition), т.к. указано непосредственное значение константы и формула для вычисления расстояния.

Используя заданную спецификацию описать:

(a)     тип 'Circle' для описания окружности по ее центру и радиусу;

(b)    функцию 'on_circle', определяющую лежит ли точка с заданными координатами на заданной окружности;

(c)    окружность с радиусом 3.0 и центром в начале координат;

(d)    константу 'pos' для представления произвольной точки, лежащей на заданной окружности.

Указания:

·          в пункте (a) опишите вспомогательные типы 'Center' и 'Radius' для представления центра окружности и ее радиуса соответственно, для описания типа 'Center' используйте тип 'Position', для типа 'Radius' воспользуйтесь следующим описанием:

Radius = {| r : Real • r ³ 0.0 |}, задающим подтип действительных чисел с неотрицательными значениями;

·          в пунктах (b) и (c) следует воспользоваться явным стилем описания (explicit definition), можно также использовать конструкцию let для достижения большей наглядности записи;

·          в пункте (d) используйте неявный (implicit) стиль описания константы.

3.     Определить функцию 'max', возвращающую значение максимума из двух целых чисел, используя один из следующих стилей описания:

(a)     явный,

(b)    неявный,

(c)     аксиоматический.

Указания:

·           воспользуйтесь общей схемой определения функции, изложенной в пункте 1.2.3.5;

·           для удобства записи используйте условное выражение языка RSL вида if логическое_выражение then выражение else выражение end.

4.     Определить функцию 'approx_sqrt', которая с заданной точностью 'eps' (положительное вещественное число) находит приближённое значение корня квадратного из неотрицательного вещественного числа. Возвращаемый функцией результат должен быть таким, чтобы точное значение квадратного корня square_root(x) лежало в полуоткрытом интервале [approx_sqrt(x,eps),approx_sqrt(x,eps) + eps[.

Указания:

·        здесь следует использовать неявный стиль описания, т.к. в постановке задачи оговариваются только соотношения между входными и выходными параметрами и не уточняется алгоритм вычисления приближенного значения;

·        обратите внимание на то, что функция определена не для всех значений входных параметров, т.е. является частично вычислимой.

5.     Рассмотрим следующее описание функции:

value

f : Int - ~® Int

f(x) º f(x)

Какие из перечисленных ниже функций удовлетворяют данному описанию?

(a) value

f : Int - ~® Int

f(x) º chaos

(b) value

f : Int - ~® Int

f(x) º 1

(c) value

f : Int ® Int

f(x) º 1

Указания:

·          запишите исходное определение функции в аксиоматическом стиле и с помощью эквивалентных преобразований упростите полученный результат;

·          воспользуйтесь тем фактом, что частично вычислимые функции включают в себя всюду вычислимые функции.

1.3.         Множества

Цель данного раздела - познакомить читателя с принятыми в RSL способами описания множеств и основными операциями над множествами. Раздел содержит упражнения по использованию абстракции множеств в моделеориентированных спецификациях.

1.3.1.     Понятие множества

Множеством называется неупорядоченный набор различных значений одного и того же типа. Например:

{1,3,5}

{²Mary²,²John²,²Peter²}

При этом, как видно из определения множества, записи {1,3,5}, {5,3,1} и {3,5,1,1} определяют одно и то же множество.

Для описания типа множества в RSL предусмотрена конструкция type_expr‑set для конечных множеств и type_expr‑infset для бесконечных, при этом type_expr задает тип входящих в множество элементов. Так, значениями типа Bool‑set являются следующие конечные множества:

{}

{true}

{false}

{true, false},

причем сюда включается пустое множество {}.

Тип type_expr‑infset представляет как конечные, так и бесконечные множества, состоящие из элементов типа type_expr. Следовательно, для любого типа T тип T‑set является подтипом T‑infset. Например, тип Nat‑infset содержит все конечные (в том числе и пустое) и бесконечные множества натуральных чисел.

Для работы с множествами в RSL определены следующие операции: È,Ç,\,Î,Ï,Ì,Í,É,Ê и card, кроме того можно использовать отношения = и ¹.

Операция card вычисляет размер конечного множества, т.е. количество его элементов:

card : T‑infset - ~® Nat

При применении к бесконечному множеству card возвращает chaos. Например:

card {1,4,56} = 3

card {} = 0

card {n | n : Nat} º chaos

1.3.2.     Способы определения множеств

Конечное множество может быть задано путем непосредственного перечисления его элементов, как в приведенных выше примерах, в этом случае выражение, определяющее значение множества, имеет вид {v₁,...,v_n}, где n³0. Кроме того, для конечных множеств, образованных из целых чисел, возможно также использование диапазона для задания значения множества, причем левая граница диапазона не должна превышать его правую границу (в противном случае множество будет пусто). Например, выражение {3 .. 7} задает множество {3,4,5,6,7}, {3 .. 3} - множество из единственного элемента {3} и {3 .. 2} - пустое множество {}.

Более общей формой выражения, определяющего значение как конечного, так и бесконечного множества, является выражение вида:

{ value_expr | set_limitation },

называемое сокращенной (compehended) записью множества или сокращенным выражением, где value_expr задает формулу для вычисления значений элементов множества, set_limitation - некоторый предикат, определяющий элементы данного множества. Примером такой формы записи может служить следующее выражение:

{2*n | n : Nat • n £ 3},

с помощью которого задается множество {0,2,4,6}.

Упражнения

1.        Написать выражение, задающее значение множества, элементами которого являются нечетные числа в диапазоне от 0 до 10.

Указания:

используйте два способа задания значения множества: непосредственное перечисление его элементов и сокращенное выражение.

2.       Пусть база данных университета описана следующим образом (для простоты комментарии приведены на русском языке):

scheme

UNIVERSITY_SYSTEM =

     class

          type

               Student,

               Course,

               CourseInfo = Course ´ Student- set,

               University = Student- set ´ CourseInfo- set

          value

              /* allStudents возвращает множество всех студентов, обучающихся в данном университете */

               allStudents : University ® Student- set,

               /* hasCourse проверяет, читается ли данный курс в данном университете*/

               hasCourse : Course ´ University ® Bool,

               /* numberOK возвращает значение true, если любой читаемый в университете курс посещает не менее 5 и не более 100 студентов */

               numberOK : University ® Bool,

               /* studOf возвращает множество студентов заданного университета, посещающих заданный курс */

               studOf : Course ´ University - ~® Student- set,

               /* attending возвращает множество курсов, которые посещает заданный студент в указанном университете */

               attending : Student ´ University - ~® Course- set,

               /* newStud добавляет нового студента к числу студентов заданного университета */

               newStud : Student ´ University - ~® University,

               /* dropStud исключает указанного студента из числа студентов заданного университета */

               dropStud : Student ´ University - ~® University

end

Определите функции, сигнатура которых приведена в данном описании.

Указания:

воспользуйтесь явным стилем описания функций и операциями над множествами.

3.     Почему некоторые из перечисленных выше функций частично вычислимы?

1.4.         Списки

Цель данного раздела - познакомить читателя с принятыми в RSL способами описания списков и основными операциями над списками. Раздел содержит упражнения по использованию списков в спецификациях программ.

1.4.1.     Понятие списка

Списком называется последовательность значений одного и того же типа, например:

á1,3,3,1,5ñ

átrue,false,trueñ

Для списков допустимо использование отношений = и ¹. Порядок следования элементов в списке существенен, т.е. списки á1,3,5ñ и á5,3,1ñ являются различными (á1,3,5ñ ¹ á5,3,1ñ). Кроме того, допускается повторное вхождение элементов в список (как в рассмотренных выше примерах), причем á1,3,3,1,5ñ ¹ á1,3,5ñ.

Для описания конечных списков в RSL используется конструкция вида type_expr^*, где type_expr задает тип элементов списка. Например, тип Bool^* описывает любой конечный список (в том числе и пустой) из булевских значений. Конструкция type_expr^w задает тип как конечных, так и бесконечных списков из элементов типа type_expr. Таким образом, для любого типа T, T^* является подтипом T^w.

1.4.2.     Способы определения списков

Для списков применяются те же способы определения значений, что и для множеств. Так, значение конечного списка может быть задано путем непосредственного перечисления его элементов. В этом случае значение списка определяется выражением вида áv₁,...,v_nñ, где n³0 и все v_i являются выражениями одного и того же типа, в частности, áñ задает пустой список. Конечный список из последовательных целых чисел можно задать, указав диапазон изменения значений элементов списка, т.е. выражением вида áv₁..v₂ñ, где v₁ и v₂ задают соответственно нижнюю и верхнюю границы диапазона, причем при v₁ > v₂ список пуст.

Использование такого способа записи иллюстрируют следующие примеры:

á3..7ñ =á3,4,5,6,7ñ

á3..3ñ = á3ñ

á3..2ñ = áñ

Значение списка можно задать также по аналогии с множествами и с помощью так называемого сокращенного выражения (comprehended list expression), имеющего вид á value_expr | list_limitation ñ. Этот способ применяется в том случае, когда новый список строится на основе какого- то уже существующего. Здесь value_expr определяет общую формулу для вычисления значений элементов нового списка, list_limitation задает базовый список, на основе которого строится данный, с возможным указанием некоторого предиката для отбора элементов из базового списка.

Например, в выражении:

á2*n | n in á0 .. 3ññ

базовым является список á0 .. 3ñ, предикат отбора отсутствует и, следовательно, в результате вычисления получается список á0,2,4,6ñ, причем упорядоченность элементов нового списка полностью определяется порядком следования элементов в базовом списке. Примером использования предиката для отбора элементов базового списка может служить выражение:

án | n in á1 .. 100ñ • is_a_prime(n)ñ,

где предикат is_a_prime(n) позволяет определить, является ли n простым числом. С помощью данного выражения задается список, элементами которого являются в возрастающем порядке простые числа из диапазона 1 .. 100, т.е. á2,3,5,7,...,97ñ.

Для доступа к какому- либо отдельному элементу списка в RSL предусмотрено понятие индекса. В качестве индекса используются натуральные числа, причем индексация элементов списка начинается с 1 и для конечных списков заканчивается числом, равным длине списка. Например:

á2,5,3ñ(2) = 5

áá2,5,3ñ, á3ññ(1) = á2,5,3ñ

áá2,5,3ñ, á3ññ(1)(2) = á2,5,3ñ(2) = 5

Значение бесконечного списка может быть задано с помощью аксиом, определяющих правила формирования списка. Так, список, содержащий все натуральные числа в возрастающем порядке, может быть определен следующим образом:

value

     all_natural_numbers : Nat^w

axiom

     all_natural_numbers(1) = 0,

     " idx : Nat •

          idx ³ 2Þ

              all_natural_numbers(idx) = all_natural_numbers(idx - 1) + 1

На основе уже определенного бесконечного списка с помощью сокращенного выражения можно задавать новые бесконечные списки. Например, список, элементами которого являются все простые числа в возрастающем порядке, может быть определен посредством выражения:

án | n in all_natural_numbers • is_a_prime(n)ñ

1.4.3.     Операции над списками

Над списками в RSL определены следующие операции:

^ : T^* ´ T^w ® T^w

hd : T^w - ~® T

tl : T^w - ~® T^w

len : T^w - ~® Nat

elems : T^w ® T- infset

inds : T^w ® Nat- infset

Операция ^ означает конкатенацию двух списков, первый из которых обязательно должен быть конечным.

Результатом применения операций hd и tl являются соответственно головной элемент списка и оставшаяся после удаления головного элемента часть списка, причем обе эти операции определены только для непустого списка.

Операция len возвращает длину конечного списка, при применении к бесконечному списку результатом является chaos.

Операция elems выдает в качестве результата множество, состоящее из элементов заданного списка. Например, количество различных элементов списка L можно определить с помощью выражения card elems L.

Результатом применения операции inds является множество индексов заданного списка. Таким образом, для конечного списка fl:

inds fl = {1 .. len fl},

для бесконечного списка il:

inds il = {idx | idx : Nat • idx ³ 1}.

Упражнения

1.        Определить следующие функции:

(a)    'length' - вычисляет длину списка без использования встроенной операции len,

(b)   'rev' - переставляет элементы списка в обратном порядке.

Указания:

·          используйте рекурсивное определение функций с помощью операций hd и tl;

·          в рекурсивном определении воспользуйтесь условным выражением или конструкцией case.

2.       Определить функцию 'pascal', генерирующую треугольники Паскаля до порядка n включительно. Результатом функции является список из n списков, каждый из которых задает очередной ряд треугольника. Например, для n = 5 получим список:

á1ñ

á1 , 1ñ

á1 , 2 , 1ñ

á1 , 3 , 3 , 1ñ

á1 , 4 , 6 , 4 , 1ñ

Очередной k- ый ряд треугольника (k>1) начинается и заканчивается 1, i‑ый элемент ряда (1<i<k) вычисляется как сумма (i- 1)- го и i- го элементов (k‑1)- го ряда.

Указания:

·          определите тип N1 для описания элементов очередного ряда треугольника;

·          используйте рекурсивное определение функции через операцию ^;

·          в рекурсивном определении воспользуйтесь сокращенным выражением для конструирования списка.

3.       Предложить спецификацию следующей упрощенной модели системы обработки текстов: текст разделен на страницы, каждая страница состоит из строк каких- то слов. Определить модуль 'PAGE', обеспечивающий описание:

(a)     типов 'Page', 'Line', и 'Word' для описания соответственно страницы, строки и слова текста,

(b)    функции 'is_on', проверяющей, встречается ли указанное слово на заданной странице,

(c)     функции 'number_of', подсчитывающей количество вхождений указанного слова в текст заданной страницы.

Указания:

·          в пункте (a) воспользуйтесь конечными списками для описания типов 'Page' и 'Line',

·          в пункте (b) используйте квантифицированное выражение и операции inds и elems,

·          в пункте (c) опишите с помощью сокращенного выражения множество пар индексов (номер строки, номер слова в строке), определяющее все вхождения указанного слова в строки данной страницы, и воспользуйтесь операцией card.

1.5.         Отображения (maps)

Цель данного раздела - познакомить читателя с понятием отображения (map), принятыми в RSL способами описания отображений и основными операциями над ними. Раздел содержит упражнения по использованию абстракции отображений в спецификациях.

1.5.1.     Понятие отображения

Отображением называется неупорядоченный набор пар значений, который отображает значения одного типа в значения другого типа, при этом множество отображаемых значений называется областью определения или доменом (domain) отображения, а множество значений, в которые осуществляется отображение, называется его областью значений (range). Например:

[3 ↦ true, 5 ↦ false]

[²Klaus² ↦ 7, ²John² ↦ 2, ²Mary² ↦ 7]

Первый пример задает отображение из натуральных чисел в значения типа Bool, второй - из типа Text в тип Nat. Областью определения (доменом) для первого отображения является множество {3,5}, областью его значений - множество {true,false}, для второго отображения такими множествами являются {²Klaus²,²John²,²Mary²} и {2,7}.

Тип отображения задается следующей конструкцией:

type_expr₁ - m® type_expr₂

Отображение может быть конечным или бесконечным в зависимости от того, конечным или бесконечным является набор пар, определяющий это отображение. Конечное отображение имеет вид:

[v₁ ↦  w₁,...,v_n ↦  w_n],

бесконечное отображение имеет вид:

[v₁ ↦  w₁,...,v_n ↦  w_n,...],

где n ³ 0, v_i и w_i - некоторые выражения типа type_expr₁ и type_expr₂ соответственно.

Отображение может быть детерминированным или недетерминированным при применении к элементам из его домена. Для детерминированного отображения справедливо соотношение:

v_i = v_j Þ w_i = w_j ,

где v_i и v_j - любые элементы из домена этого отображения.

Примером конечного детерминированного отображения может служить любое из приведенных выше отображений, имеющих тип Nat - m® Bool и Text - m® Nat соответственно. В качестве примера конечного недетерминированного отображения можно привести отображение:

[3 ↦  true,3 ↦  false],

имеющее тип Nat - m® Bool.

1.5.2.     Способы определения отображений

Для определения отображений в RSL используются те же способы, что и для множеств и списков, а именно: явное перечисление элементов и сокращенное выражение. Первый способ применяется для конечных отображений, в этом случае отображение задается выражением вида:

[v₁ ↦  w₁,...,v_n ↦  w_n],

где n ³ 0. В частности, при n = 0 имеем пустое отображение []. Именно этот способ был использован во всех рассмотренных ранее примерах. Порядок следования пар в отображении несущественен, поэтому, например, следующие два выражения задают одно и то же отображение:

[3 ↦  true,5 ↦  false] = [5 ↦  false,3 ↦  true]

(для отображений определены отношения = и ¹).

Сокращенное выражение (comprehended map expression) используется для определения значений как конечных, так и бесконечных отображений и имеет вид:

[ value_expr_pair | set_limitation ],

где value_expr_pair задает общую формулу для определения входящих в отображение пар, set_limitation задает возможные ограничения на область определения (домен) отображения. Например, значением сокращенного выражения:

[ n ↦ 2*n | n : Nat • n £ 2 ]

является конечное отображение [0 ↦ 0,1 ↦ 2,2 ↦ 4].

Выражение [ n ↦ 2*n | n : Nat ] определяет бесконечное отображение [0 ↦ 0,1 ↦ 2,2 ↦ 4,...].

Значение отображения для какого- либо конкретного элемента из его домена задается с помощью выражения value_expr₁(value_expr₂), где value_expr₁ является выражением, определяющим данное отображение, value_expr₂ - выражение для вычисления значения некоторого элемента из домена отображения. Например:

[²Klaus² ↦ 7, ²John² ↦ 2, ²Mary² ↦ 7](²John²) = 2,

[1 ↦ [²Per² ↦ 5, ²Jan² ↦ 7], 2 ↦ []](1)(²Jan²) =

= [²Per² ↦ 5, ²Jan² ↦ 7] (²Jan²) = 7,

или для недетерминированного отображения:

[3 ↦ true,3 ↦ false](3) = true |^| false,

где символ |^| означает недетерминированный выбор из двух указанных значений.

1.5.3.     Операции над отображениями

Над отображениями определены следующие операции:

dom : (T₁ - m® T₂) ® T₁- infset

rng : (T₁ - m® T₂) ® T₂- infset

† : (T₁ - m® T₂) ´ (T₁ - m® T₂) ® (T₁ - m® T₂) 

∪ : (T₁ - m® T₂) ´ (T₁ - m® T₂) ® (T₁ - m® T₂)

\ : (T₁ - m® T₂) ´ T₁- infset ® (T₁ - m® T₂)

/ : (T₁ - m® T₂) ´ T₁- infset ® (T₁ - m® T₂)

° : (T₂ - m® T₃) ´ (T₁ - m® T₂) ® (T₁ - m® T₃)

Результатом операции dom является домен отображения, причем в зависимости от вида отображения это множество может быть конечным или бесконечным. Например:

dom [3 ↦ true, 5 ↦ false, 5 ↦ true] = {3,5}

dom [] = {}

dom [ n ↦ 2*n | n : Nat ] = { n | n : Nat }

Операция rng возвращает в качестве результата область значений отображения.

Результатом операции † является набор пар, полученный объединением наборов пар первого и второго отображений, причем в случае пересечения областей определения предпочтение отдается парам из второго отображения, т.е. для элементов, попавших в пересечение доменов отображений, второе отображение перекрывает первое. Эффект выполнения данной операции иллюстрируют следующие примеры:

[3 ↦ true, 5 ↦ false] † [5 ↦ true] = [3 ↦ true, 5 ↦ true]

[3 ↦ true] † [5 ↦ false] = [3 ↦ true, 5 ↦ false]

[3 ↦ true] † [] = [3 ↦ true]

Операция ∪ просто объединяет наборы пар двух заданных отображений, например:

[3 ↦ true, 5 ↦ false] ∪ [5 ↦ true] = [3 ↦ true, 5 ↦ false, 5 ↦ true]

Операции \ и / позволяют изменять область определения отображений, а именно: \ удаляет из домена отображения указанное множество, / , наоборот, оставляет в домене только те элементы, которые входят в указанное множество. Более точно определение этих операций выглядит следующим образом:

m \ s = [d ↦ m(d) | d : T₁ • d Î dom m Ù d Ï s]

m / s = [d ↦ m(d) | d : T₁ • d Î dom m Ù d Î s]

Некоторые примеры:

[3 ↦ true, 5 ↦ false] \ {5,7} = [3 ↦ true]

[3 ↦ true, 5 ↦ false] / {5,7} = [5 ↦ false]

[3 ↦ true, 5 ↦ false] \ {3,5,7} = []

[3 ↦ true, 5 ↦ false] / {3,5,7} = [3 ↦ true, 5 ↦ false]

Операция ° позволяет осуществлять композицию двух отображений, т.е. для отображений m₁ и m₂ она определяется так:

m₁ ° m₂ = [x ↦ m₁(m₂(x)) | x : T₁ • x Î dom m₂ Ù m₂(x) Î dom m₁]

Например:

[3 ↦ true, 5 ↦ false] ° [²Klaus² ↦ 3, ²John² ↦ 7] = [²Klaus² ↦ true]

[3 ↦ true] ° [²Klaus² ↦ 5] = []

Упражнения

1.      Пусть база данных университета описана следующим образом (для простоты комментарии приведены на русском языке):

scheme

MAP_UNIVERSITY_SYSTEM =

     class

          type

               Student,

               Course,

               CourseInfos = Course - m® Student- set,

               University = Student- set ´ CourseInfos

          value

               /* allStudents возвращает множество всех студентов, обучающихся в данном университете */

               allStudents : University ® Student- set,

               /* hasCourse проверяет, читается ли данный курс в данном университете*/

               hasCourse : Course ´ University ® Bool,

               /* numberOK возвращает значение true, если любой читаемый в университете курс посещает не менее 5 и не более 100 студентов */

               numberOK : University ® Bool,

               /* studOf возвращает множество студентов заданного университета, посещающих заданный курс */

               studOf : Course ´ University - ~® Student- set,

               /* attending возвращает множество курсов, которые посещает заданный студент в указанном университете */

               attending : Student ´ University - ~® Course- set,

               /* newStud добавляет нового студента к числу студентов заданного университета */

               newStud : Student ´ University - ~® University,

               /* dropStud исключает указанного студента из числа студентов заданного университета */

               dropStud : Student ´ University - ~® University

end

Определите функции, сигнатура которых приведена в данном описании.

Указания: воспользуйтесь явным стилем описания функций и операциями над отображениями.

Глава 2. Задание практикума

В данной главе формулируется задание практикума по составлению спецификаций на языке RSL для описания программных систем средней сложности. Здесь также приводятся конкретные варианты заданий и методические рекомендации по их выполнению.

2.1.         Постановка задачи

Для определяемой вариантом задания программной системы построить три вида спецификаций на языке RSL: моделеориентированные спецификации в явном и неявном стилях и алгебраическую спецификацию. При описании модели предложенной системы предусмотреть операции по формированию информационной базы системы, обеспечивающей возможность накапливать и использовать необходимую информацию. Способ представления такой информационной базы выбрать самостоятельно. В предложенных ниже вариантах заданий дается лишь краткое описание программных систем с указанием минимально необходимого набора операций, тем самым разработчику спецификаций предоставляется возможность расширить этот набор по своему усмотрению.

2.2.         Варианты заданий

1.      Система учета ²автомобили - владельцы - доверенности².

Система должна обеспечивать следующие возможности: добавлять/удалять нового владельца и соответственно новый автомобиль для заданного владельца, осуществлять аналогичные операции с доверенностями на автомобиль, выдавать необходимую справочную информацию (например, для указанного автомобиля определять его владельца и т.д.), при этом предполагается, что у каждого автомобиля может быть только один владелец, на один и тот же автомобиль может быть зафиксировано несколько доверенностей.

2.      Генеалогическое дерево.

Система поддержки генеалогического дерева должна предоставлять следующие возможности: добавлять в дерево нового члена семьи (ребенка, супруга, предка), вносить изменения в узлы дерева (например, фиксировать смену фамилии или дату смерти), осуществлять поиск полезной информации по дереву (например, для указанного члена семьи находить его детей и наоборот).

3.      Железнодорожное расписание станции.

На железнодорожной станции имеется набор платформ и путей, на которые могут прибывать поезда, известны номера прибывающих поездов, время их прибытия и отправления, а также станции отправления и назначения. Система поддержки железнодорожного расписания станции должна обеспечивать возможность формирования расписания, внесения в него изменений и выдачу полезной информации (например, список поездов до указанной станции назначения).

4.      Управление семафорами и стрелками на участке железной дороги.

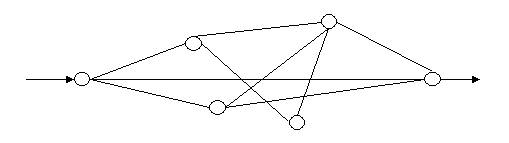
Задан участок железной дороги, конфигурация которого приведена ниже. В узлах участка установлены семафоры и стрелки, состояния которых определяют движение поезда по той или иной ветке участка. Считается, что на каждой ветке может находиться не более одного поезда и все поезда на участке движутся в одном направлении слева направо. Система поддержки управления семафорами и стрелками должна обеспечивать следующие операции: открыть/закрыть семафор, повернуть стрелку налево/направо (при этом необходимо учитывать текущее положение стрелки и конфигурацию участка железной дороги), а также обеспечивать выдачу полезной информации (например, о наличии в данный момент поезда на ветке).

5.      Система поддержки составления расписания занятий.

Система должна обеспечивать возможность составления расписания некоторого учебного заведения, внесения в расписание изменений и выдачу полезной информации (например, по итоговому расписанию получить расписание указанной группы на заданный день). В расписании должны фиксироваться время и место проведения занятия, предмет и преподаватель, проводящий занятие, а также номер группы, для которой это занятие проводится. Расписание не должно содержать коллизий (например, разные занятия не должны пересекаться друг с другом по месту и времени их проведения).

6.      Планирование автобусного движения в районе.

В районе имеется несколько автовокзалов, у каждого из которых есть ряд посадочных площадок. Между автовокзалами курсируют рейсовые автобусы, для каждого рейса фиксируется станция отправления и назначения, посадочная площадка, с которой происходит отправление, а также время посадки в автобус и время в пути. Система поддержки планирования автобусного движения должна обеспечивать возможность добавлять/удалять новые рейсы, вносить изменения в уже имеющиеся рейсы и выдавать полезную справочную информацию (например, для указанного автовокзала определять все рейсы, отправляющиеся с заданной посадочной площадки и т.д.).

7.      Заказ/учет товаров в ²бакалейной лавке².

В ²бакалейной лавке² для каждого товара фиксируется место хранения (определенная полка), количество и поставщик этого товара. Система поддержки заказа/учета товаров должна обеспечивать возможность добавления/удаления нового товара, изменения информации об имеющемся товаре (например, при изменении количества товара и т.д.) и выдачи необходимой справочной информации (например, список товаров, количество которых необходимо пополнить).

8.      Управление библиотекой.

В библиотеке осуществляется регистрация всех читателей и ведутся каталоги поступивших в библиотеку книг, кроме того фиксируется информация о том, какие книги у какого читателя находятся в данный момент. Система поддержки управления библиотекой должна обеспечивать возможность добавления/удаления читателей и соответственно книг в каталоги, регистрацию взятых и возвращенных читателем книг, а также выдавать полезную справочную информацию (например, о наличии в данный момент указанной книги).

9.        Управление памятью на диске. Система обслуживает запросы процессов. Процесс может запросить новую область памяти указанной длины, вернуть ее. При выделении области памяти по запросу процесса, процесс становится владельцем данной области. Различные процессы могут получать доступ к памяти на чтение и запись. Определение и изменение прав доступа осуществляется только владельцем. Неявная и алгебраическая спецификация должны описывать широкий спектр стратегий управления памятью.

10. Информационное табло по состоянию авиарейсов.

На табло отражается следующая информация о рейсе: номер рейса, пункт вылета, время прилета по расписанию, ожидаемое время прилета, статус (отложен, вылетел, прилетел). Система поддержки информационного табло должна обеспечивать добавление и удаление информации о рейсах, а также внесение изменений в состояние табло, если произошло некоторое событие (например, вылет какого- то рейса отложен на N минут, произошла посадка самолета указанного рейса и т.д.)

11. Управление версиями программного проекта.

Программный проект представляет собой некоторую совокупность программ, каждая программа в свою очередь состоит из файлов, файлы связаны друг с другом отношением ²использует². Для каждого файла может существовать несколько его вариантов и для каждой программы соответственно несколько ее версий. Конкретный вариант файла однозначно идентифицируется именем файла и номером варианта, аналогично версия программы идентифицируется именем программы, номером версии и списком вариантов файлов. Каждая версия программы должна быть замкнута по отношению ²использует². Система поддержки управления версиями должна обеспечивать возможность создавать новые варианты файлов и новые версии программ, добавлять и исключать варианты файлов из версий без нарушения указанной замкнутости, т.е. нельзя, например, удалить из версии какой- то вариант файла, если он используется оставшимися файлами.

12. Система поддержки составления расписания поездов на железной дороге.

Железная дорога представляет собой сеть станций, связанных между собой путями, (причем могут существовать как однопутные, так и двухпутные перегоны), на каждой станции имеется N путей, для каждого перегона известно время, необходимое для его прохождения. В расписании указывается список поездов данной железной дороги с указанием маршрутов их следования (маршрут следования задается списком станций, на которых останавливается поезд) и временем прибытия/отправления на станции маршрута. Расписание должно быть свободно от коллизий, т.е. на пути перегона так же, как и на пути станции не может находиться одновременно более одного поезда. Система поддержки составления расписания должна обеспечивать возможность добавления и удаления новых маршрутов, внесения изменений в уже составленное расписание, а также выдачу полезной информации (например, по расписанию всей железной дороги получить расписание для указанной станции).

13. Управление процессами.

Специфицируется набор операций, при помощи которых планировщик операционной системы поддерживает очереди процессов к ресурсам (например, к устройству ввода/вывода, памяти, процессору, порту ввода/вывода другого процесса), при этом внешние операции и/или прерывания, при помощи которых пользовательские процессы обращаются к планировщику (возбуждают требование на обслуживание планировщиком) не рассматриваются. Планировщик поддерживает следующие структуры данных: набор ресурсов, набор процессов, порты ввода/вывода процессов. Набор операций должен позволять строить и модифицировать перечисленные структуры данных, размещать процесс в очередях к ресурсам, изымать процесс из очереди.

14. Протокол для передачи пакетов.

Специфицируется два набора операций, при помощи которых одна сторона, получив запрос на передачу сообщения, передает пакеты в линию и получает подтверждения, а вторая сторона, принимая пакеты, передает подтверждения.

15. Утилита make.

Утилита получает на вход список файлов и функцию, которая для каждого файла выдает список файлов, от которого он зависит (например, по использованию типов данных). Кроме того утилита использует в качестве входных данных совокупность файлов. Все файлы, которые утилита получает как исходные данные (прямо или косвенно), должны принадлежать этой совокупности. Результатом утилиты должен стать список файлов - транзитивного замыкания исходного списка. Список- результат должен определять порядок обработки файлов: каждый "зависящий" файл не должен опережать в списке ни один из файлов, от которого он зависит.

2.3.         Методические рекомендации

При разработке спецификаций необходимо выбрать подходящую абстракцию данных и предложить набор операций (функций), обеспечивающих моделирование заданной программной системы. В качестве абстракции данных в зависимости от специфики решаемой задачи можно использовать множества, списки и отображения. Набор операций должен содержать операции, позволяющие накапливать в системе необходимую информацию, т.е. осуществлять наполнение некоторой информационной базы системы, способ представления которой определяется выбранным способом абстракции. Для этого обычно достаточно включить в состав операций следующие операции: инициализацию соответствующей информационной базы пустым значением, добавление в базу нового элемента и удаление указанного элемента из базы. При описании данных операций необходимо предусмотреть возможные ограничения на их выполнение, связанные с обеспечением непротиворечивости (консистентности) хранящейся в базе информации. Так, например, при формировании информационной базы системы поддержки составления расписания добавление нового занятия в расписание заданной группы может производиться только в том случае, если в указанное время у этой группы и преподавателя нет других занятий и свободна указанная аудитория. Одним из важных средств описания консистентного состояния являются инварианты, которые в RSL представляются либо в форме аксиом, либо в форме ограничений подтипов.

Кроме этих основных операций по наполнению информационной базы системы полезно предусмотреть операции, позволяющие изменять отдельные элементы базы, а также осуществлять в базе поиск полезной с точки зрения разработчика спецификаций информации. Некоторые примеры таких операций приводятся в описании заданий практикума, однако их набор может быть расширен по желанию разработчика спецификаций.

Глава 3. Сценарий работы с редактором eden

В данной главе описывается сценарий работы с основным инструментом поддержки RAISE технологии - синтаксически управляемым редактором eden (entity editor), обеспечивающим ввод и редактирование текстов на языке RSL. Этот инструмент разработан датской компанией Computer Resources International - CRI.

3.1.         Начало работы с редактором

Редактор eden является синтаксически управляемым редактором, т.е. он гарантирует синтаксическую правильность любого вводимого с помощью редактора текста спецификации на языке RSL и кроме того обеспечивает статическую проверку типов. Функционирование редактора осуществляется в среде операционной системы UNIX.

При синтаксически управляемом редактировании процесс построения текста программы заключается в следующем. В любой момент редактирования текст программы (спецификации) представляет собой текст на базовом языке программирования (в нашем случае на языке RSL), куда могут входит метапеременные языка (т.н. гнезда редактирования) для обозначения еще не конкретизированных фрагментов, подлежащих уточнению в дальнейшем. При выборе пользователем любой такой метапеременной (любого гнезда) в качестве объекта редактирования редактор предлагает список вариантов, показывающих на что может быть заменена данная метапеременная в соответствии с синтаксисом базового языка. Таким образом, отсекается возможность возникновения синтаксически неверных конструкций, поэтому на любом этапе редактирования текст является синтаксически правильным. В ходе синтаксически управляемого редактирования в памяти системы формируется абстрактное синтаксическое дерево, представляющее собой вывод текста в грамматике базового языка. Процесс построения текста завершается, когда все входящие в текст метапеременные будут заменены на соответствующие конструкции базового языка, т.е. в тексте не останется ни одного вхождения метапеременных (ни одного гнезда редактирования).

Сценарий работы с редактором рассмотрим на примере построения текста модуля QUEUE, содержащего следующую спецификацию очереди:

QUEUE =

     class

          type

               Element,

               Queue = Element^*

          value

               empty : Queue = áñ,

               enq : Element ´ Queue ® Queue

               enq(e,q) º q ^ áeñ,

               deq : Queue- ~® Queue ´ Element

               dec(q) º (tl q,hd q)

               pre q ¹ empty

     end

Для начала работы с редактором создайте средствами UNIX директорию для хранения своих файлов и объявите ее текущей. Вызов редактора осуществляется командой:

raise_eden QUEUE,

где QUEUE - имя модуля. Вид окна, полученного на экране в результате выполнения этой команды, показан на рисунке 1.
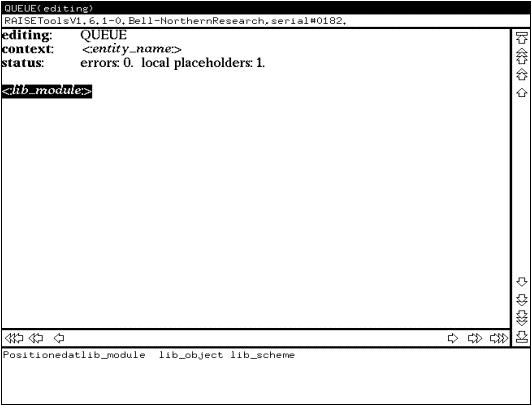
Рис. 1

В верхней части окна располагается поле, содержащее заголовок редактируемого модуля. Ниже следует командная строка, которая используется для вывода информационных сообщений и сообщений об ошибках (в данный момент там содержится информация о версии редактора). Под командной строкой располагается непосредственно окно редактирования, где и производятся основные операции по редактированию текста. Три верхние строчки этого окна содержат краткую информацию о редактируемом модуле: имя модуля, его контекст, т.е. список связанных с ним модулей, и статус (количество обнаруженных в модуле ошибок по несоответствию типов и количество гнезд редактирования). Ниже располагается текст самого модуля. В данный момент этот текст представляет собой вхождение единственной метапеременной lib_module, которая и является текущей метапеременной (текущим гнездом редактирования). Справа и снизу от окна редактирования находятся вертикальная и горизонтальная полосы прокрутки. В нижней части окна располагается поле, используемое для вывода подсказок при синтаксически управляемом редактировании. Здесь содержится информация о текущей метапеременной, подлежащей редактированию (гнезде редактирования), и список вариантов, определяющих замену текущей метапеременной на возможные конструкции языка RSL.

3.2.         Командное меню редактора

Вызов командного меню осуществляется по нажатию правой кнопки мыши. Вид окна редактора после выполнения этой операции приведен на рисунке 2.

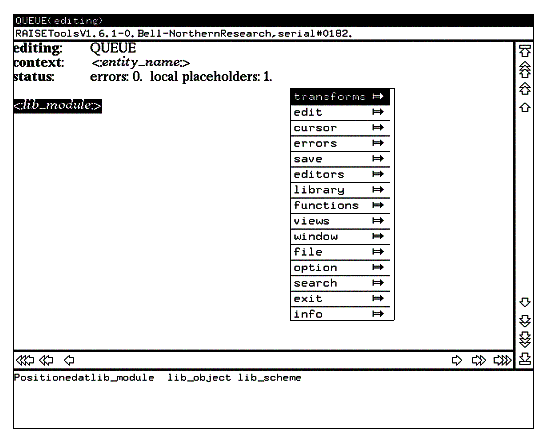
Рис. 2

Каждый пункт командного меню содержит, как правило, несколько команд, поэтому каждому пункту меню соответствует выпадающее подменю, откуда и выбираются команды редактора. При этом в подменю рядом с названием команды указывается комбинация управляющих клавиш для ее вызова, таким образом, вызов команды может производиться как с помощью меню, так и посредством набора соответствующей комбинации управляющих клавиш.

Кратко опишем назначение основных пунктов командного меню:

·        transforms - позволяет при синтаксически управляемом редактировании заменять текущее гнездо редактирования на некоторую конструкцию языка RSL, список которых указывается в качестве подменю данного пункта. Обратите внимание на то, что содержимое подменю полностью совпадает со списком альтернатив в поле подсказки, т.е. выбор очередной альтернативы может производиться как в подменю данного пункта, так и непосредственно в поле подсказки.

·        edit - содержит команды, позволяющие вносить изменения в редактируемый текст.

·        errors - позволяет изменять формат вывода сообщений об ошибках, т.е. выдавать эти сообщения в более развернутой или более краткой форме.

·        save - содержит команды, позволяющие сохранять отредактированный текст, причем сохранение производится в текущей директории (при выборе команд, начинающихся ключевым словом write) или текущей библиотеке (команды начинаются ключевым словом save).

·        file - позволяет замещать текущее гнездо редактирования содержимым указанного файла (при этом для успешной замены содержащийся в файле текст должен быть синтаксически правильным) и, наоборот, запоминать в файле с указанным именем выбранный фрагмент редактируемого текста в ASCII формате.

·        exit - команда выхода из редактора.

3.3.         Редактирование модуля

Начальный этап редактирования модуля показан на рисунке 1. Редактируемый текст представляет собой единственное гнездо редактирования lib_module, это же гнездо является текущим (на экране выделено на фоне остального текста).Выберите в поле подсказки или в пункте transforms командного меню альтернативу lib_scheme, т.к. спецификация разрабатываемого модуля представляет собой схему в терминологии RSL. Эффект выполнения команды иллюстрирует рисунок 3.

Как видно из рисунка, теперь текст модуля содержит описание схемы, причем имя схемы совпадает с именем модуля. Текущим гнездом редактирования является class_expr, соответствующее следующей в порядке обхода абстрактного синтаксического дерева метапеременной. Поле подсказки содержит уже новый список альтернатив, определяющий возможные варианты уточнения для метапеременной class_expr.

Редактор eden позволяет наряду с синтаксически управляемым редактированием осуществлять редактирование в текстовом режиме. Для этого в позиции текущего гнезда редактирования на клавиатуре набирается нужный фрагмент текста, причем данный фрагмент должен соответствовать синтаксической категории гнезда редактирования. Редактор производит разбор введенного фрагмента и в случае успеха добавляет полученное в ходе разбора дерево к общему дереву вывода конструируемого модуля.

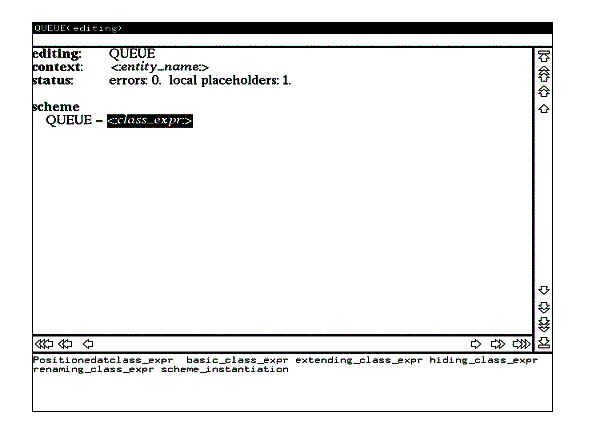
Рис. 3

В качестве следующего шага редактирования используйте текстовый режим, для чего наберите в выделенной позиции фрагмент class end . При этом на экране появляется указатель текущего вводимого символа, называемый кареткой, выделенная область ввода представляет собой текстовый буфер, куда и помещается вводимый текст. Передвижение каретки на тот или иной символ внутри области ввода осуществляется с помощью мыши или нажатием клавиш ^B (назад) и ^F (вперед), символы слева от каретки могут быть удалены нажатием клавиши Delete , символы справа от каретки удаляются нажатием ^D. Если введенный текст является синтаксически правильным значением для данного гнезда редактирования, выход из текстового режима осуществляется по выполнению любой команды, не относящейся к режиму текстового редактирования.

В нашем случае для выхода из текстового режима достаточно (не нажимая клавишу RETURN) переместить указатель мыши на любой фрагмент текста, лежащий вне области ввода, например, на имя схемы QUEUE и щелкнуть левой кнопкой мыши. После выхода из текстового режима для продолжения процесса редактирования щелкните левой кнопкой мыши на фрагменте class . Вид экрана после выполнения этих операций приведен на рисунке 4.

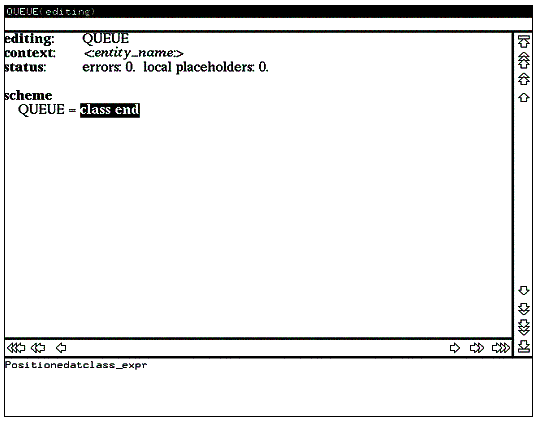
Рис. 4

Отображенное на данном рисунке состояние редактора показывает, что разбор введенного фрагмента текста произведен успешно (о чем свидетельствует нулевое количество ошибок в строке статуса) и данному фрагменту соответствует синтаксическое дерево категории class_expr . Заметим, что полностью аналогичный результат был бы получен в режиме синтаксически управляемого редактирования (см. рис. 3) при выборе альтернативы basic_class_expr в списке альтернатив.

Для продолжения процесса редактирования нажмите клавишу RETURN, по которой вызывается команда обхода соответствующего синтаксического дерева слева направо с отображением на экране всех встречающихся в порядке обхода гнезд редактирования. Полученный вид экрана иллюстрирует рисунок 5.

Еще раз нажмите клавишу RETURN (при этом в поле подсказки появится список альтернатив для гнезда decl_string) и выберите в поле подсказки альтернативу type_decl. Эффект выполнения данных действий показан на рисунке 6.

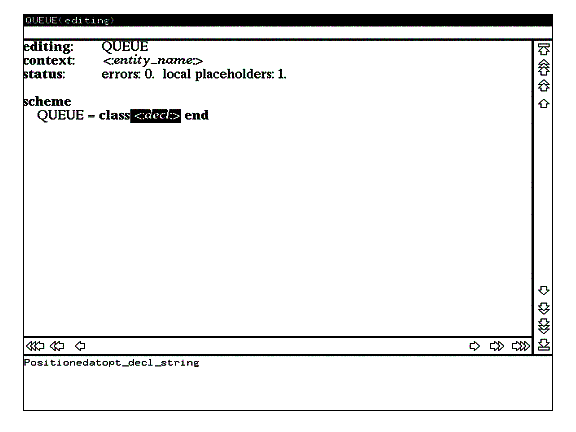
Рис. 5

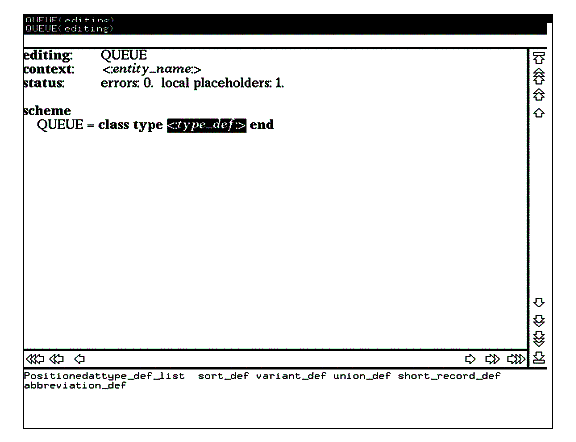
Рис. 6

Теперь в выделенной позиции наберите на клавиатуре имя типа Element (при этом редактор переходит в текстовый режим) и нажмите клавишу RETURN. По нажатию данной клавиши редактор возвращается в режим синтаксически управляемого редактирования (поскольку введенный фрагмент был синтаксически правильным) и на экране появляется следующее в порядке обхода дерева гнездо редактирования (см. рис. 7).

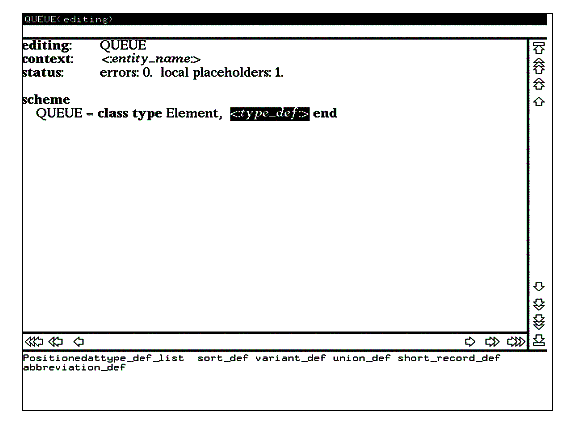
Рис. 7

3.4.         Обработка ошибок редактирования

Рассмотрим теперь обработку ошибок редактирования. Для этого введите в выделенной области некоторый текст, содержащий ошибку, например, синтаксически неверное определение типа в виде фрагмента Queue = и нажмите клавишу RETURN. Вид экрана после выполнения этих действий иллюстрирует рисунок 8.

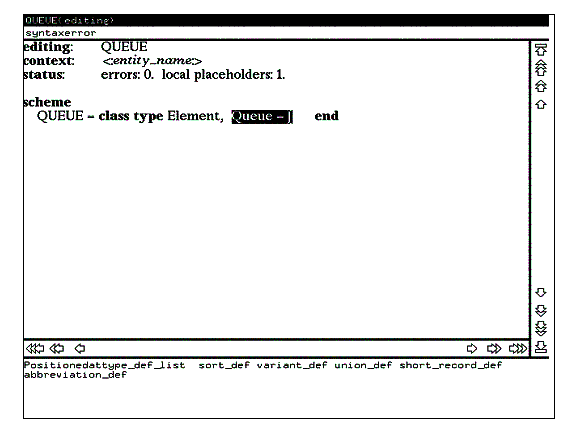
Рис. 8

Как видно из этого рисунка, в командной строке появляется сообщение о синтаксической ошибке, редактор продолжает оставаться в текстовом режиме и каретка располагается в месте обнаружения ошибки. Устранить такую ошибку можно двумя способами. Во- первых, можно, оставаясь в текстовом режиме, отредактировать область ввода таким образом, чтобы она содержала синтаксически правильный фрагмент. Во- вторых, можно выполнить команду undo из пункта edit командного меню, возвращающую редактор из текстового режима в режим синтаксического управления (при этом редактор возвращается в то состояние, в котором он находился до перехода в текстовый режим) и дальнейшее редактирование продолжать уже в синтаксически управляемом режиме. Второй способ наиболее удобен в тех ситуациях, когда пользователь нечетко помнит синтаксис языка и ему трудно устранить ошибку прямым редактированием текста.

Для устранения обнаруженной ошибки в нашем случае воспользуйтесь первым способом, введите с клавиатуры в текущую позицию области ввода имя T и нажмите клавишу RETURN. Полученный вид экрана иллюстрирует рисунок 9.

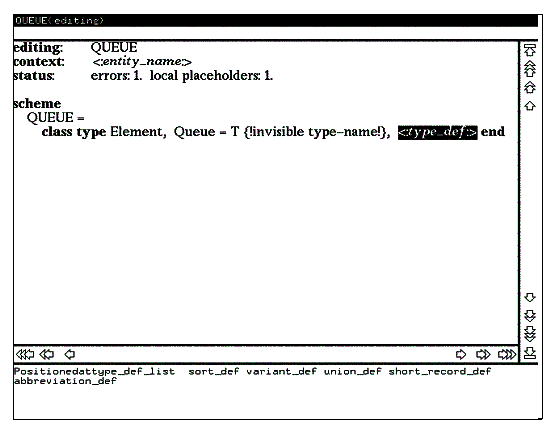
Рис. 9

Отображенное на рисунке 9 состояние редактора показывает, что введенный на предыдущем шаге редактирования фрагмент описания типа был синтаксически правильным, поэтому редактор вышел из текстового режима (по нажатию клавиши RETURN) и на экране появилось новое гнездо редактирования, соответствующее следующей в порядке обхода дерева метапеременной. Однако поскольку тип T не объявлен в данном модуле, редактор фиксирует ошибку описания типа, о чем свидетельствует выдаваемая им диагностика и значение счетчика ошибок в строке статуса.

Для устранения ошибок такого рода надо выделить с помощью мыши некорректную с точки зрения описания типа конструкцию (в нашем случае имя T) и выполнить команду cut- to- clipped из пункта edit командного меню. В результате выполнения этой команды выделенная конструкция удаляется из текста модуля и вместо нее появляется соответствующее гнездо редактирования (в нашем случае type_expr), которое и объявляется текущим. Аналогичный результат был бы получен при выполнении команды delete_selection из того же пункта командного меню. Заметим, что команда undo не может быть использована в данном случае, т.к. она вызывается только из текстового режима редактора.

В качестве следующего этапа редактирования завершим определение типа Queue как конечного списка из элементов типа Element. Для этого выберите в списке альтернатив для текущего гнезда редактирования сначала альтернативу list_type_expr и затем finite_list_type_expr. После этого в текстовом режиме наберите имя Element и нажмите клавишу RETURN. Вид экрана после выполнения указанных операций показан на рисунке 10.

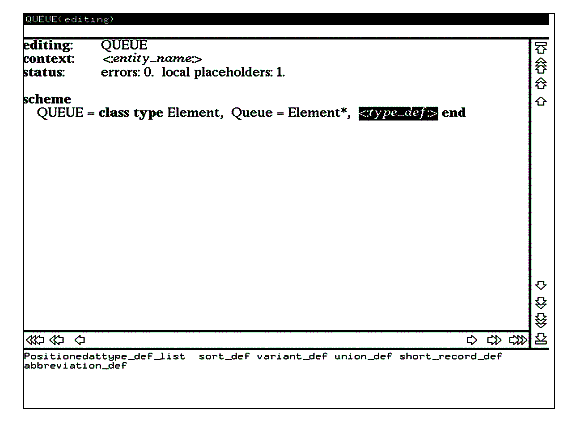
Рис. 10

3.5.         Завершение редактирования модуля

Теперь в модуле полностью закончено описание типов и можно переходить к описанию функций. Для этого нажмите клавишу RETURN, чтобы на экране появилось гнездо редактирования для нового раздела объявлений (см. рис. 11) и выберите в списке альтернатив метапеременную value_decl . При этом на экране появляется заголовок раздела описания функций value и гнездо редактирования value_def для описания очередной функции.

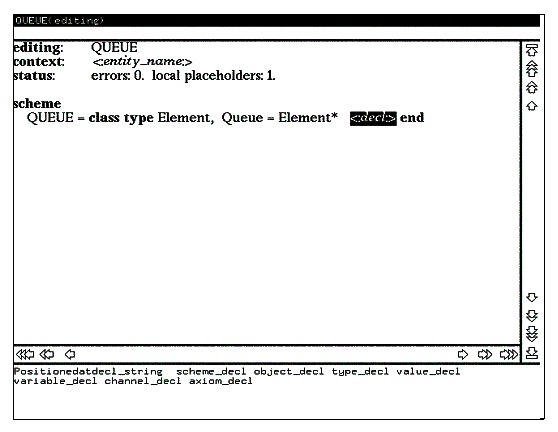
Рис. 11

В разделе описаний функций нашего модуля QUEUE должны находиться описания константы и двух функций, следовательно, полезно уметь вставлять в уже существующий список описаний новый элемент на то или иное место по желанию разработчика спецификации. Для выполнения подобных операций в редакторе предусмотрены следующие возможности:

·        вставка нового элемента между указанными элементами списка - выделить с помощью мыши место вставки нового элемента (два соседних элемента списка) и щелкнуть левой кнопкой мыши на разделителе элементов (на запятой в нашем случае);

·        вставка нового элемента перед указанным элементом списка - выделить с помощью мыши нужный элемент списка и нажать комбинацию клавиш ESC ^B;

·        добавить новый элемент в конец списка - выделить последний элемент списка и нажать комбинацию клавиш ESC RETURN.

Последние два способа добавления элемента в список основаны на том, что нажатие определенной комбинации управляющих клавиш меняет порядок движения по абстрактному синтаксическому дереву при переходе к очередному гнезду редактирования.

Для определения константы выберите в списке альтернатив метапеременную explicit_value_def, а затем с помощью описанных выше операций добавьте в список описаний функций два новых гнезда value_def, уточнив каждое из них метапеременной explicit_function_def. Обратите внимание на то, что у последней описанной в модуле QUEUE функции должно быть предусловие, для этого выделите в описании последней функции гнездо value_expr и нажмите клавишу RETURN. Вид экрана после выполнения всех этих операций представлен на рисунке 12.

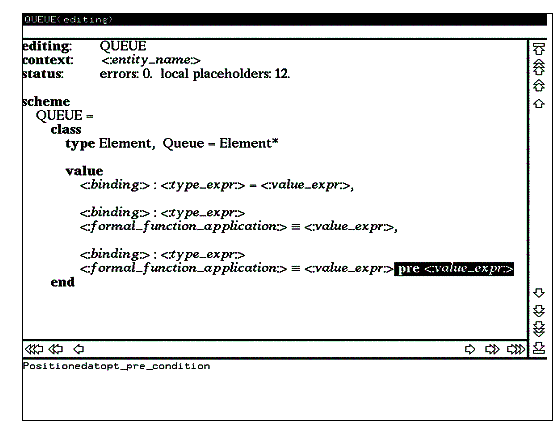
Рис. 12

На этом завершим сеанс работы с редактором. Перед выходом из редактора необходимо сохранить построенный модуль в текущей директории. Для этого выполните команду write- file из пункта save командного меню. По данной команде текст модуля будет записан в файл с именем QUEUE.rsl . Выход из редактора осуществляется по команде exit. После выхода из редактора текущая директория будет содержать наряду с файлом QUEUE.rsl еще несколько скрытых файлов со служебной информацией редактора для данного модуля.

Продолжить редактирование модуля можно в следующих сеансах работы, для чего следует указать имя файла с текстом модуля (в нашем случае QUEUE) в качестве параметра при вызове редактора. Читателям предлагается в качестве упражнения по использованию редактора eden довести до конца построение текста данного модуля.

Ответы и решения к упражнениям главы 1

1.1. (a) да

(b)       да

(c)       нет

(d)       нет

(e)       да

(f)        нет

(g)       нет

(h)       да

(i)        да

(j)        нет

(k)       да

1.2. (a) false (по свойству (1) раздела 1.1.2.)

(b)       a

Решение: if a then ~( a º chaos) else false end º (по свойству (3))

if a then ~( true º chaos) else false end º

if a then true else false end º (по свойству (3))

if a then a else a end º a

1.3. (a) да (для данного i выбираем j = - i)

(b) нет (не верно, например, для i > 0)

(c)       нет

1.4. " i : Int • $ j : Int • j > i или ~($ i : Int • " j : Int • i ³ j)

1.5. is_even : Nat ® Bool

is_even(n) º ($ m : Nat • n = 2 * m)

или альтернативное определение:

is_even : Nat ® Bool

is_even(n) º n \ 2 = 0

2.1. (a) type Complex = Real ´ Real

(b)       value zero : Complex = (0.0,0.0)

(c)         value c : Complex • let (x,y) = c in x = y end

(d)       value

add : Complex ´ Complex ® Complex

add((x₁,y₁), (x₂,y₂)) º (x₁ + x₂, y₁ + y₂),

mult : Complex ´ Complex ® Complex

mult((x₁,y₁), (x₂,y₂)) º (x₁ * x₂ - y₁ * y₂, x₁ * y₂ + y₁ * x₂)

(e)       value

f : Complex ® Complex

f(c₁) as c₂ post c₁ ¹ c₂

2.2. (a) type

Circle = Center ´ Radius,

Center = Position,

Radius = {| r : Real • r ³ 0.0 |}

(b)       value

on_circle : Circle ´ Position ® Bool

on_circle((c,r), p) º distance(c,p) = r

или альтернативное определение:

value

on_circle : Circle ´ Position ® Bool

on_circle(circ, p) º

let

(c,r) = circ

in

distance(c,p) = r

end

(c)       value

circle : Circle = (origin, 3.0)

(d)       value

pos : Position • on_circle(circle, pos)

2.3. (a) value

max : Int ´ Int ® Int

max(i,j) º if i ³ j then i else j end

(b)         value

max : Int ´ Int ® Int

max(i,j) as y

post (y = i Ù y ³ j) Ú (y = j Ù y ³ i)

(c)         value

max : Int ´ Int ® Int

axiom

" i,j : Int • max(i,j) º if i ³ j then i else j end

2.4. value

approx_sqrt : Real ´ Real - ~® Real

approx_sqrt(x, eps) as s

post s ­ 2 £ x Ù x < (s + eps) ­ 2

pre x ³ 0.0 Ù eps > 0.0

2.5.                Описание:

value

f : Int - ~® Int

f(x) º f(x)

является краткой формой описания:

value

f : Int - ~® Int

axiom

" x : Int • f(x) º f(x),

которое в силу истинности аксиомы эквивалентно:

value

f : Int - ~® Int

Следовательно, исходному описанию удовлетворяют все частично вычислимые (в частности, всюду вычислимые) функции из Int в Int.

3.1. {1,3,5,7,9} или {s | s : Nat • (s < 10) Ù ($ n : Nat • s = 2 * n)}

3.2. scheme

UNIVERSITY_SYSTEM =

    class

          type

               Student,

               Course,

               CourseInfo = Course ´ Student- set,

               University = Student- set ´ CourseInfo- set

          value

               allStudents : University ® Student- set

               allStudents(ss, cis) º ss,

               hasCourse : Course ´ University ® Bool

               hasCourse(c, (ss, cis)) º

                    ($ (c¢, ss¢) : CourseInfo • (c¢, ss¢) Î cis Ù c = c¢),

               numberOK : University ® Bool

               numberOK(ss, cis) º

                    (" (c, ss¢) : CourseInfo • (c, ss¢) Î cis Þ

                         (card ss¢ £ 100 Ù card ss¢ ³ 5)),

               studOf : Course ´ University - ~® Student- set

               studOf(c, (ss, cis)) º

                    {s | s : Student • $ ss¢ : Student- set • s Î ss¢ Ù (c, ss¢) Î cis }

                    pre hasCourse(c, (ss, cis)),

               attending : Student ´ University - ~® Course- set

               attending(s, (ss, cis)) º

                    {c | c : Course • $ ss¢ : Student- set • (c, ss¢) Î cis Ù s Î ss¢}

                    pre s Î allStudents(ss, cis),

               newStud : Student ´ University - ~® University

               newStud(s, (ss, cis)) º (ss È {s}, cis) pre s Ï ss,

               dropStud : Student ´ University - ~® University

               dropStud(s, (ss, cis)) º

                    (ss \ {s}, {(c, ss¢ \ {s}) | (c, ss¢) : CourseInfo • (c, ss¢) Î cis })

                    pre s Î ss

     end

4.1. type Elem

value

(a)   length : Elem^* ® Int

length(k) º if k = áñ then 0 else 1 + length(tl k) end

или

length : Elem^* ® Int

length(k) º card (inds k)

или

length : Elem^* ® Int

length(k) º

case k of

áñ ® 0,

áiñ ^ lr ® length(lr) + 1

end

(b)      rev : Elem^* ® Elem^*

rev(k) º if k = áñ then áñ else rev(tl k) ^ áhd kñ end

или

rev : Elem^* ® Elem^*

rev(k) º ák(len k - i + 1) | i in á1 .. len kññ

или

rev : Elem^* ® Elem^*

rev(k) º

case k of

áñ ® áñ,

áiñ ^ lr ® rev(lr) ^ áhd kñ

end

4.2.               type N1 = {| n : Nat • n ³ 1 |}

value

pascal : N1 ® (N1^*)^*

pascal(n) º

if n = 1 then áá1ññ

else

let p = pascal(n - 1) in

p ^ áá1ñ ^ áp(n - 1) (i - 1) + p(n - 1) (i) | i in á2 .. n - 1ññ ^ á1ññ

end

end

4.3.               scheme

PAGE =

class

type Page = Line^*, Line = Word^*, Word

value

is_on : Word ´ Page ® Bool

is_on(w, p) º ($ i : Nat • i Î inds p Ù w Î elems p(i)),

number_of : Word ´ Page ® Nat

number_of(w, p) º

card {(i, j) | i, j : Nat • i Î inds p Ù j Î inds p(i) Ù w = p(i)(j)}

end

5.1. scheme

MAP_UNIVERSITY_SYSTEM =

class

type

Student,

Course,

CourseInfos = Course - m® Student- set,

University = Student- set ´ CourseInfos

value

allStudents : University ® Student- set

allStudents(ss, cis) º ss,

hasCourse : Course ´ University ® Bool

hasCourse(c, (ss, cis)) º c Î dom cis,

numberOK : University ® Bool

numberOK(ss, cis) º

(" c : Course • c Î dom cis Þ

(card cis(c) £ 100 Ù card cis(c) ³ 5)),

studOf : Course ´ University - ~® Student- set

studOf(c, (ss, cis)) º cis(c) pre hasCourse(c, (ss, cis)),

attending : Student ´ University - ~® Course- set

attending(s, (ss, cis)) º

{c | c : Course • c Î dom cis Ù s Î cis(c)}

pre s Î allStudents(ss, cis),

newStud : Student ´ University - ~® University

newStud(s, (ss, cis)) º (ss È {s}, cis) pre s Ï ss,

dropStud : Student ´ University - ~® University

dropStud(s, (ss, cis)) º

(ss \ {s}, [ c ↦ cis(c) \ {s} | c : Course • c Î dom cis ])

pre s Î ss

end

Пример варианта письменного экзамена

и его решение

В этом разделе все специальные символы RSL указываются в ASCII представлении.

1. Дана неявная спецификация функции, описать ее в явной форме.

value

f : Nat ´ Nat ® Nat

f(a,b) as c

post

if (exists n : Nat :- is_divisor(a,n) /\ is_divisor(b,n)) then

is_divisor(a,c) /\ is_divisor(b,c) /\

all c1:Nat :- is_divisor(a,c1) /\ is_divisor(b,c1) => (c1<=c)

end,

is_divisor : Nat ><Nat - > Nat

is_divisor(a,b) is

b ~= 0 /\

a > b /\

a - (a / b) * b = a,

f : Nat ><Nat - > Nat

f(a,b) is

if a=b then a

elsif a- b > 0 then f(a- b,b) else f(a,b- a) end

Решение:

value

f : Nat ><Nat - > Nat

f(a,b) is

if a=b then a

elsif a- b > 0 then f(a- b,b) else f(a,b- a) end

2. Доказать, что схема S2 является уточнением схемы S1:

scheme

S1 =

class

type A,B,C

value

f1 : A >< B - > Bool,

f2 : A >< B - ~- > C,

f3 : C - ~- > A >< B

axiom

all a: A, b: B :-

f3( f2(a, b))is (a,b)

pre f1(a,b) = true

end

scheme

S2 =

class

type A=Int, B=Nat, C=Int

value

f1 : A >< B - > Bool

f1(i,n) is i * i = n,

f2 : A >< B - ~- > C

f2(i,n) is i,

f3 : C - ~- > A >< B

f3(cc) as (a,b)

post (cc = a) /\ b = (cc * cc)

end

Доказательство:

all a: A, b: B :-

f3( f2(a, b))is (a,b)

pre f1(a,b) = true

all_assumption_inf:

[[ if f1(a,b) = true then f3( f2(a, b)) is (a,b) end ]]

unfold_true:

[[ if f1(a,b) then f3( f2(a, b)) is (a,b) end ]]

unfold_f1:

[[ if a*a = b then f3( f2(a, b)) is (a,b) end ]]

unfold_f2:

[[ if a*a = b then f3( a ) is (a,b) end ]]

unfold_f3:

[[ if a*a = b then (a, a*a))is (a,b) end ]]

if_annihilation:

[[ (a, b)is (a,b) ]]

is_annihilation:

true

3. Дана алгебраическая спецификация группы функций, дать определение необходимых типов данных и явное определение функции get.

scheme

EXAM =

class

type R, Key, Val

value

empty : Unit - > R,

put : R >< Key >< Val - > R,

del : R >< Key >< Val - ~- > R,

get: R >< Key - ~- > Val- set,

find: R >< Key - > Bool,

axiom

forall r : R, k1, k2 : Key, v1, v2 : Val :-

[find_empty] find (empty(), k1) is false,

[find_put] find (put(r, k1, v1), k1) is true,

[get _put]

get (put(r, k1, v1), k1) is

if find (r, k1) then

get (r, k1) union {v1}

else

{v1}

end,

[del_put_1]

del(put(r, k1, v1), k1, v1) is

if find (r, k1) /\ v1 isin get (r, k1) then

del(r, k1, v1)

else

r

end,

[put_put]

put(put(r, k1, v1), k2, v2) is

if (k1 = k2) /\ (v1 = v2) then

put(r, k1, v1)

else

put(put(r, k2, v2), k1, v1)

end

end

Решение:

type R = Key- m- >Val- set, Key, Val

value

get: R >< Key - ~- > Val- set

get(r,k) as vs

post

vs = r(k)

pre k isin dom r

4. Упростить выражение

(b!2) || (y:=a?) || if (x:=1); (a!x); (true |^| false) then a!(b?)

else a!(1+b?) end

Решение:

x:=1; (y:=1) ; (a!2) |^|

x:=1; (y:=1) ; (a!3)

5. Определить классы эквивалентности в пространстве входных значений функции f, отвечающие разбиению пространства в соответствии с критерием полноты тестового покрытия "все достижимые дизъюнкты" (AFDNF)

post

if (a > 5) /\ (b < 3) then ...

elsif ((a > b) /\ (b=0)) \/ (b<3) then ...

else ...

end

Решение:

Ветвь 1: m1 m2

Ветвь 2: нет

Ветвь 3: m1~m2 m3~m4~m2

m1 ~m2 ~m3~m2

~m1 m3 ~m4

~m1~m3 m2

~m1 m3 ~m4 m2

~m1 m3 ~m4 ~m2

~m1 ~m3 ~m2

Ветви	m1 = a > 5	m2 = b < 3	m3 = a > b	m4 = b=0	m2 = b<3	a	b	Достижимые дизъюнкты
1	true	true				6	2	m1 m2
2	true	false	true	true
2	true	false	false	-	true
2	true	false	true	false	true
3	true	false	true	false	false	6	4	m1~m2 m3~m4~m2
3	true	false	false	-	false	6	6	m1 ~m2 ~m3~m2
3	false	-	true	false	true	5	1	~m1 m3 ~m4
3	false	-	false	-	true	1	2	~m1~m3 m2
3	false	-	true	false	true	5	2	~m1 m3 ~m4 m2
3	false	-	true	false	false	5	3	~m1 m3 ~m4 ~m2
3	false	-	false	-	false	3	3	~m1 ~m3 ~m2

Пояснение. Затененные клетки таблицы указывают на несовместимые условия. Дополнительные примеры заданий с решениями.

Темы.

1.      Определение классов эквивалентности для AFDNF критерия полноты тестового покрытия по неявным спецификациям.

2.      Упрощение параллельных и недетерминированных выражений.

Тема: Определение классов эквивалентности для AFDNF критерия полноты тестового покрытия по неявным спецификациям.

Цель: Определить классы эквивалентности в пространстве входных значений функции f, отвечающие разбиению пространства в соответствии с критерием полноты тестового покрытия "все достижимые дизъюнкты" (AFDNF).

1. value

f : Int >< Int- list >< Nat - ~- > Nat >< Bool

f (a,b,c) as (q,p)

post

if (a + len b > c) /\ (a isin elems b) then ...

elsif (a>=c) /\ (a isin inds b) then ...

else ...

end

pre (a < c) \/ (a isin inds b)

Ветвь	m1 (a < c)	m2 (a isin inds b)	m3 (a + len b > c)	m4 (a isin elems b)	a	b	с
1	true		true	false				m1m3m4
1	false	true	true	true				~m1m2m3m4
2	false	true	false					~m1m2~m3
2	false	true	true	false				~m1m2m3~m4
3	true		false					m1~m3
3	true		true	false				m1m3~m4

2. post

if (a > 4) /\ (b < 4) then ...

elsif (a > b) /\ (b=4) then ...

else ...

end

pre b<= 4

Решение:

post

if m2 /\ m3 then ...

elsif m4 /\ m5 then ...

else ...

end

pre m1

B1 - m1m2m3

B2 - m1m2~m3m4m5

B3 - m1~m2~m4 \/

m1~m2m4~m5

3. post

if (b > 5) /\ (a < 3) then ...

elsif ((a > b) /\ (b=0)) \/ (b<5) then ...

else ...

end

pre a+b<=7

Решение:

post

if m2 /\ m3 then ...

elsif (m4 /\ m5) \/ m6 then ...

else ...

end

pre m1

B1 - m1m2m3

B2 - m1~m2m4m5

m1~m2m4~m5m6

m1~m2~m4m6

B3 - m1~m2~m4~m6

4. post

if (a isin dom b) /\ (b (a) = a) then ...

elsif ((rng b inter dom b) = {}) \/ b(a+1) < 0 then ...

else ...

end

pre

(a isin dom b) /\ ((a+1) isin dom b)

Решение:

post

if m1 /\ m3 then ...

elsif m4 \/ m5 then ...

else ...

end

pre

m1 /\ m2

B1 - m1m2m3

B2 - m1m2~m3~m4m5

m1m2~m3m4

B3 - m1m2~m3~m4~m5

5. post

if (a > 5) /\ (b < 3) then ...

elsif (a > b) \/ (b<3) then ...

else ...

end

pre (a>2*b)

Решение:

post

if m2 /\ m3 then ...

elsif m4 \/ m3 then ...

else ...

end

pre m1

B1 - m1m2m3

B2 - m1m2~m3m4 \/

m1~m2m4 \/

m1~m2~m4m3

Тема: упрощение параллельных и недетерминированных выражений.

1. (b!2) || (x:=a?) || if (a!3; true) |^| ((a!b?+5); false) then a!(b?)

else a!(1+b?) end || (a!0)

Решение:

x:=3 || a!2 || a!0 |^|

x:=0 || a!3 ; a!2 |^|

x:=7 ; a!(1+b?) || a!0

x:=0 || a!7; a!(1+b?)

2. (if (a?)>0 then b!1 else b!2 end ++( a!1;x:=b?;b!4)) ||

(y:= if (b?)=1 then a? else (0- a?) end) || (a!0)

Решение:

x:=1; y:=0

3. (b!2) || (x:=a? |^| y:=b?) || (y:=a?) || if (true |^| false) then a!(b?)

else a!(1+b?) end

Решение:

x:=2 || (y:=a?) |^|

x:=3 || (y:=a?) |^|

y:=2 || x:=a? |^|

y:=3 || x:=a? |^|

y:=2 || y:=b? |^|

y:=3 || y:=b? |^|

y:=2 || y:=a? || a!b? |^|

y:=2 || y:=a? || a!(1+b?)

4. (b!2) || (a!4; x:=a?) || (y:=a?) || if (true |^| false) then a!(b?)

else a!(1+b?) end

Решение:

x:=2 || (y:=4) |^|

x:=3 || (y:=4) |^|

y:=2 || a!4; x:=a? |^|

y:=3 || a!4; x:=a?

5. a!(5+b?) || ((x:=(if true |^| false then x:=b?;1 else b!3;x:=2;6 end)+x) ++ (b!4 || y:=b?))

Решение:

a!(5+b?) || x:=5; y:=b? |^|

y:=3; x:=8; a!9 |^|

a!8 || x:=8 || y:=4

6. case (1 |^| b?) of

1 - > x:=a?+1,

2 - > x:=b?,

3 - > y:=a?+3,

4 - > y:=b?+a?,

5 - > x:=y:=a?;y

end ||

a!1 || b!(a?+2) || a!3

7. case (1 |^| b?) of

1 - > x:=a?+1,

2 - > x:=b? |^| a?,

3 - > y:=a?+3,

4 - > y:=b?+a?,

5 - > x:=y:=a?;y

end || a!0 || b!(a?+a?) || a!2 || a!3

8. (b!4 || y:=b?) || (a!(5+b?) ++ (x:=( x:=b!2; a? |^| b!3;x:=2;6)+x) )

Решение:

y:=4 || x:=14 |^|

y:=4 || x:=8 || a!8