Типичным представителем класса задач, для которых подходит представление (формализация) в пространстве состояний, является головоломка, известная как игра в пятнадцать. В ней используется пятнадцать пронумерованных (начиная с 1) подвижных фишек, расположенных в клетках квадрата 4x4. Одна клетка этого квадрата остается всегда пустой, так что одну из соседних с ней фишек можно передвинуть на место этой пустой клетки (изменив, тем самым, местоположение пустой клетки). На рис.1а изображены две конфигурации фишек. Рассмотрим задачу перевода начальной (первой) конфигурации в целевую (вторую) конфигурацию. Решением этой задачи будет подходящая последовательность сдвигов фишек, например: «передвинуть фишку 8 вверх, фишку 6 влево и т.д.». Более простым вариантом этой головоломки является квадрат 3x3 и восемь фишек на нем – пример соответствующей задачи показан на рис.1б.
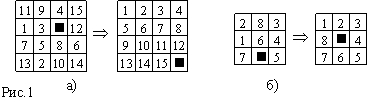
Основными особенностями класса задач, к которому принадлежит рассмотренная головоломка, является наличие в каждой задаче точно определенной начальной ситуации и точно определенной цели. Имеется также некоторое множество операций, или ходов, переводящих одну ситуацию в другую. Именно из таких ходов состоит искомое решение задачи., которое можно в принципе (теоретически) получить методом проб и ошибок. Действительно, отправляясь от начальной ситуации, можно построить все промежуточные конфигурации, возникающие в результате выполнения каждого из возможных ходов, затем построить множество конфигураций после применения следующего хода и так далее – пока не будет достигнут целевая конфигурация.
Ключевым понятием при формализации задачи в пространстве состояний является понятие состояния, характеризующего некоторый момент решения задачи. Например, для игры в пятнадцать состояние – это просто некоторая конкретная конфигурация фишек. Среди всех состояний выделяются начальное состояние и целевое состояние (целевая конфигурация), в совокупности определяющие задачу, которую надо решить.
Другим важным понятием для рассматриваемого представления является понятие оператора, или допустимого хода в задаче. Оператор преобразует одно состояние в другое, являясь по сути функцией, определенной на множестве состояний и принимающей значения из этого множества. Для игры в пятнадцать (или в восемь) удобнее выделить четыре оператора, соответствующие перемещениям пустой клетки влево, вправо, вверх, вниз. В некоторых случаях оператор может оказаться неприменимым к какому-то состоянию: например, операторы вправо и вниз неприменимы, если пустая клетка расположена в правом нижнем углу (соответствующая функция является частично определенной).
В терминах состояний и операторов решение задачи есть определенная последовательность операторов, преобразующая начальное состояние в целевое. Решение задачи ищется в пространстве состояний – множестве состояний, достижимых из начального состояния при помощи операторов. В игре в пятнадцать пространство состояний состоит из всех конфигураций фишек, которые могут быть образованы в результате допустимых перемещений фишек.
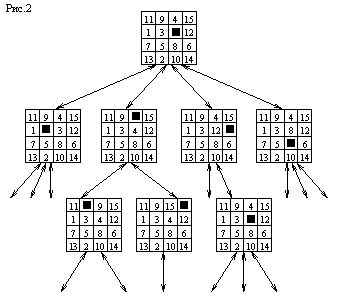
Пространство состояний можно представить в виде графа, вершины которого соответствуют состояниям, а дуги – применяемым операторам. Тогда решение задачи – это путь, ведущий от начального состояния к целевому. На рис.2 показана часть пространства состояний для игры в пятнадцать, в каждой вершине помещена та конфигурация фишек, которую она представляет. Пространства состояний могут быть большими и даже бесконечными, но в любом случае предполагается конечность множества допустимых операторов и счетность множества возможных состояний.
Итак, формализация задачи с использованием пространства состояний включает выявление и определение следующих составляющих:
Эти составляющие задают (неявно) пространство, в котором требуется провести поиск решения задачи.
Ясно, что решение задачи, представленной описанным способом, можно в принципе обнаружить, осуществляя последовательный поиск, или перебор вершин, в пространстве состояний. В начале этого процесса к начальному состоянию применяется тот или иной оператор. Затем на каждом шаге поиска к одному из уже полученных (просмотренных) состояний применяется допустимый оператор и строится новая вершина. Поиск заканчивается, когда построено целевое состояние. Заметим, что такой процесс построения вершин пространства состояний означает по сути преобразование в явную форму некоторой части графа, заданного начальным состоянием и операторами, определяющими правила получения новых вершин.
Рассмотрим дополнительно несколько характерных примеров представления задач в пространстве состояний, к числу которых относится задача об обезьяне и банане. В комнате находятся обезьяна, ящик и связка бананов, которая подвешена к потолку настолько высоко, что обезьяна может до нее дотянуться, только встав на ящик. Нужно найти последовательность действий, которая позволит обезьяне достать бананы. Предполагается, что обезьяна может ходить по комнате, двигать по полу ящик, взбираться на него и схватить бананы.
Описание состояния этой задачи должно включать следующие элементы: местоположение (координаты) обезьяны в комнате – в горизонтальной плоскости пола и по вертикали (на полу обезьяна или на ящике), местоположение ящика на полу и наличие у обезьяны бананов. Эти элементы можно представить в виде четырехэлементного списка (ПолОб, ВертОб, ПолЯщ, Цель), где ПолОб и ПолЯщ – соответственно положение обезьяны и ящика на полу, ВертОб – это П или Я в зависимости от того, где находится обезьяна, на полу или на ящике, а Цель – это 0 или 1 в зависимости от того, достала ли обезьяна бананы или нет.
Операторы в задаче об обезьяне соответствуют четырем ее возможным действиям:
По сути, для решения задачи значимы лишь три точки:
То - точка первоначального местоположения обезьяны;
Тя - точка первоначального расположения ящика;
Тб - точка, над которой подвешены бананы.
Рассмотрим теперь классическую задачу о коммивояжере. В ней коммивояжер, располагая картой дорог между несколькими городами, должен выстроить маршрут своей поездки так, чтобы побывать в каждом городе, но не более одного раза. На рис.4 показана карта дорог между 7 городами.
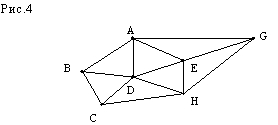
Получающееся пространство состояний представлено деревом, показанном на рис.5.
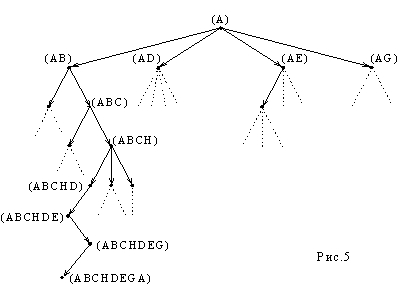
Алгоритмы поиска в пространстве состояний базируются на последовательном переборе вершин пространства состояния – до тех пор, пока не будет обнаружена целевая вершина.
Вершины и указатели, построенные в процессе перебора, образуют поддерево всего неявно определенного пространства состояний. Будем называть такое поддерево деревом перебора.
Известные алгоритмы поиска в пространстве состояний различаются несколькими характеристиками:
В соответствии с первой характеристикой алгоритмы делятся на два класса – слепые и эвристические. В слепых алгоритмах поиска в пространстве состояний местонахождение целевой вершины никак не влияет на порядок, в котором рассматриваются (раскрываются) вершины. В противоположность им, эвристические алгоритмы (методы) используют (для уменьшения возникающего перебора) априорную (эвристическую) информацию о том, где в пространстве состояний расположена цель, поэтому для раскрытия обычно выбирается более перспективная вершина.
Два основных вида слепых алгоритмов поиска, различающихся порядком раскрытия вершин – это алгоритмы поиска (перебора) вширь и поиска (перебора) вглубь. Как слепые, так и эвристические алгоритмы могут отличаться полнотой просмотра пространства состояний.
Полные алгоритмы перебора при необходимости осуществляют полный просмотр пространства. В отличие от них, неполные алгоритмы реализуют просмотр лишь некоторой части пространства, и если искомая целевая вершина не находится в этой части, то решение этим алгоритмом не будет найдено.
В соответствии с направлением поиска алгоритмы можно разделить на прямые (поиск ведется от начальной вершины к целевой), обратные (поиск от целевой вершины в направлении к начальной) и двунаправленные (чередование прямого и обратного поиска, или же одновременное их проведение). Наиболее употребительными (отчасти, в силу их простоты) являются прямые алгоритмы.
Двумя основными разновидностями слепого перебора являются алгоритмы перебора вширь и перебора вглубь.
В алгоритме перебора вширь вершины раскрываются в том порядке, в котором они строятся. В алгоритме перебора в глубину прежде всего раскрываются те вершины, которые были построены последними.
Рассмотрим вначале простой алгоритм перебора вширь на дереве, который состоит из следующей последовательности шагов:
Шаг 1. Поместить начальную вершину в список нераскрытых вершин Open.
Шаг 2. Если список Open пуст, то окончание алгоритма и выдача сообщения о неудаче поиска, в противном случае перейти к следующему шагу.
Шаг 3. Выбрать первую вершину из списка Open (назовем ее Current) и перенести ее в список Closed.
Шаг 4. Раскрыть вершину Current, образовав все ее дочерние вершины. Если дочерних вершин нет, то перейти к шагу 2, иначе поместить все дочерние вершины (в любом порядке) в конец списка Open и построить указатели, ведущие от этих вершин к родительской вершине Current.
Шаг 5. Проверить , нет ли среди дочерних вершин целевых. Если есть хотя бы одна целевая вершина, то окончание алгоритма и выдача решения задачи, получающегося просмотром указателей от найденной целевой вершины к начальной. В противном случае перейти к шагу 2.
Можно показать, что при переборе вширь непременно будет найден самый короткий путь к целевой вершине, при условии, что этот путь вообще существует. Если же такого пути нет, то будет сообщено о неуспехе поиска в случае конечных графов, а в случае бесконечных графов алгоритм никогда не кончит свою работу.
На рис.13 приведено дерево, полученное в результате применения алгоритма поиска вширь к некоторой начальной конфигурации игры в восемь, причем алгоритм работал только до глубины 4. В вершинах дерева помещены соответствующие описания состояний. Эти вершины занумерованы в том порядке, в котором они были раскрыты.
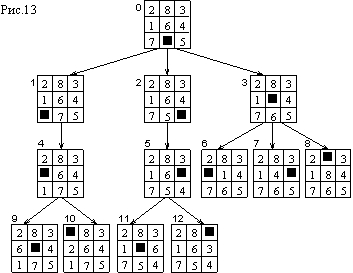
Глубину вершины в дереве можно определить следующим образом:
В алгоритме перебора вглубь раскрытию в первую очередь подлежит вершина, имеющая наибольшую глубину. Такой принцип может привести к бесконечному процессу – если пространство состояний бесконечно, и поиск вглубь пошел по ветви дерева, не содержащей целевое состояние. Поэтому необходимо то или иное ограничение этого процесса, самое распространенный способ – ограничить глубину просмотра дерева или графа. Это означает, что в ходе перебора раскрываются только вершины с глубиной, не превышающей некоторую заданную граничную глубину, т.е. в первую очередь раскрытию подлежит вершина наибольшей глубины, но не превышающей эту границу. Соответствующий алгоритм поиска называется ограниченным перебором вглубь.
Основные шаги алгоритма ограниченного перебора вглубь таковы:
Шаг 1. Поместить начальную вершину в список Open.
Шаг 2. Если список Open пуст, то окончание алгоритма и выдача сообщения о неудаче поиска, в противном случае перейти к следующему шагу.
Шаг 3. Выбрать первую вершину из списка Open (назовем ее Current) и перенести ее в список Closed.
Шаг 4. Если глубина вершины Current равна граничной глубине, то перейти к шагу 2, в ином случае перейти к следующему шагу.
Шаг 5. Раскрыть вершину Current, построив все ее дочерние вершины. Если дочерних вершин нет, то перейти к шагу 2, иначе поместить все дочерние вершины (в произвольном порядке) в начало списка Open и построить указатели, ведущие от этих вершин к родительской вершине Current.
Шаг 6. Если среди дочерних есть хотя бы одна целевая вершина, то окончание алгоритма и выдача решения задачи, получающегося просмотром указателей от найденной целевой вершины к начальной. В противном случае перейти к шагу 2.
В отличие от поиска вширь, алгоритм поиска в глубину с ограничением глубины является неполным алгоритмом, поскольку вершины пространства состояний, расположенные ниже граничной глубины, так и останутся нерассмотренными.
На рис.14 показано дерево, построенное алгоритмом поиска вглубь, граничная глубина установлена равной 4. Вершины занумерованы в том порядке, в котором они были раскрыты. В качестве начального состояния взята та же самая, что и в примере на рис.13, конфигурация игры в восемь В обоих этих деревьях раскрыто и построено вершин, но порядок их раскрытия различается. Видно, что в алгоритме поиска в глубину сначала идет поиск вдоль одного пути, пока не будет достигнута максимальная глубина, затем рассматриваются альтернативные пути той же или меньшей глубины, которые отличаются от него лишь последним шагом, после чего рассматриваются пути, отличающиеся последними двумя шагами, и т.д.
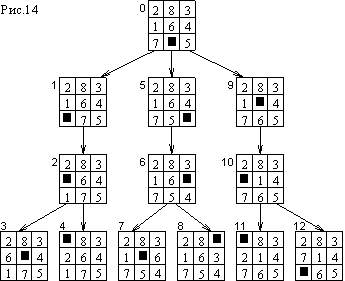
Если сравнивать алгоритмы поиска вширь и вглубь, то последний, несмотря на свою неполноту, может оказаться предпочтительнее – если он начат с удачной стороны, то целевая вершина будет обнаружена раньше, чем в алгоритме поиска вширь.
Если перебор осуществляется на графах, а не на деревьях, необходимо внести некоторые очевидные изменения в указанные алгоритмы. В алгоритме полного перебора следует дополнительно проверять, не находится ли уже вновь построенная вершина в списках Open и Closed по той причине, что она уже строилась раньше в результате раскрытия какой-то вершины. Если это так, то такую вершину не нужно снова помещать в список Open. В алгоритме же ограниченного поиска вглубь кроме рассмотренного изменения может оказаться необходимым пересчет глубины порождающейся вершины, уже имеющейся либо в списке Open, либо в списке Closed.
Заметим однако, что даже в случае перебора на полном графе дерево перебора, т.е. множество вершин и указателей, построенное в процессе перебора, тем не менее образует дерево, так как указатели по-прежнему указывают только на одну порождающую вершину. Иногда проще организовать процесс перебора так, что граф состояний разворачивается при поиске в дерево, в котором некоторые вершины, возможно, дублируются в разных частях этого дерева.
В целом алгоритмы слепого перебора являются неэффективными методами поиска решения, приводящими в случае нетривиальных задач к проблеме комбинаторной сложности. Действительно, если L − длина решающего пути, а B – количество ветвей (дочерних вершин) у каждой вершины, то для нахождения решения надо исследовать BL путей, ведущих из начальной вершины. Величина эта растет экспоненциально с ростом длины решающего пути, что приводит к ситуации, называемой комбинаторным взрывом.
Таким образом, для повышения эффективности поиска необходимо использовать информацию, отражающую специфику решаемой задачи и позволяющую более целенаправленно двигаться к цели. Такая информация обычно называется эвристической, а соответствующие алгоритмы – эвристическими.
Эвристический (упорядоченный) поиск
Идея, лежащая в основе большинства эвристических алгоритмов, состоит в том, чтобы оценивать (с помощью численных оценок) перспективность нераскрытых вершин пространства состояний (с точки зрения достижения цели), и выбирать для продолжения поиска наиболее перспективную вершину. Самый обычный способ использования эвристической информации – введение так называемой эвристической оценочной функции. Эта функция определяется на множестве вершин пространства состояний и принимает числовые значения. Значение оценочной функции Est(V) может интерпретироваться как перспективность раскрытия вершины, или вероятность ее расположения на решающем пути. Обычно считают, что меньшее значение Est(V) соответствует более перспективной вершине, и вершины раскрываются в порядке увеличения (возрастания) значения оценочной функции.
Таким образом, основные шаги алгоритма эвристического перебора таковы:
Шаг 1. Поместить начальную вершину в список Open и вычислить ее оценку (значение оценочной функции).
Шаг 2. Если список Open пуст, то окончание алгоритма и выдача сообщения о неудаче поиска, в противном случае перейти к шагу 3.
Шаг 3. Выбрать из списка Open вершину с минимальной оценкой (среди вершин с одинаковой минимальной оценкой выбирается любая); перенести эту вершину (назовем ее Current) в список Closed.
Шаг 4. Если Current – целевая вершина, то окончание алгоритма и выдача решения задачи, получающегося просмотром указателей от нее к начальной вершине, в противном случае перейти к следующему шагу.
Шаг 5. Раскрыть вершину Current, построив все ее дочерние вершины. Если таких вершин нет, то перейти к шагу 2, в ином случае – к шагу 6.
Шаг 6. Для каждой дочерней вершины вычислить оценку (значение оценочной функции), поместить все дочерние вершины в список Open, и построить указатели, ведущие от этих вершин к родительской вершине Current. Перейти к шагу 2.
Заметим, что поиск в глубину можно рассматривать как частный случай упорядоченного поиска с оценочной функцией Est(V) = D(V) , а поиск в ширину -- с Est(V) = 1/D(V) , где D – глубина вершины V.
Рассмотрим работу алгоритма эвристического поиска опять же на примере игры в восемь. В качестве оценочной функции можно взять следующую:
Est(V) = D(V) + K(V) где
D(V) – глубина вершины V, или число ребер дерева на пути от этой вершины к начальной вершине;
K(V) – число фишек позиции-вершины V, лежащих не на «своем» месте.
На рис.15 показано дерево, построенное алгоритмом упорядоченного перебора с указанной оценочной функцией (начальное состояние то же, что и в примерах рис. 13 и 14, а целевое показано на рис.3). Оценка каждой вершины приведена рядом с ней внутри кружка. Отдельно стоящие цифры, как и раньше, показывают порядок, в котором раскрывались вершины. Видно, что так как минимизация оценочной функции производится для всего пространства состояний, то раскрываемые друг за другом вершины могут располагаться в совершенно разных частях пространства состояний.
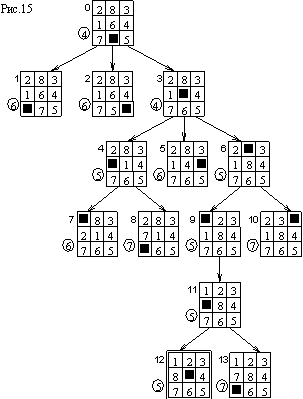
Найденный путь решения задачи длиною в пять ходов может быть получен и другими методами перебора, но использование оценочной функции приводит к существенно меньшему числу раскрытий вершин. Действительно, сравнение трех алгоритмов перебора показывает, что
В общем случае (в среднем) алгоритм эвристического поиска обнаруживает решение быстрее алгоритмов слепого перебора. Важно однако, что использование эвристической функции не может гарантировать сокращение поиска во всех случаях, и иногда (хотя и редко) решение задачи может искаться дольше, чем с использованием слепого метода.
Ясно, что подбор «хорошей» эвристической функции (существенно сокращающей поиск) – наиболее трудный момент при формализации задачи, особенно это важно в больших пространствах состояний. Можно сравнивать различные оценочные функции для одной задачи по их эвристической силе, т.е. по тому, насколько они сокращают (убыстряют) поиск.
Реализация алгоритмов слепого поиска на языке программирования Лисп не представляет особых затруднений. Ниже приводятся тексты лисп-функций BREADTH_FIRST_SEARCH (поиска вширь) и LIMITED_DEPTH_SEARCH (ограниченного поиска вглубь) от начального состояния StartState. Обе функции вырабатывают в качестве своего значения либо решающий путь (в виде лисповского списка) – если таковой существует, и список () в противном случае.
Точные определения использованных в них вспомогательных функций OPENING, SOLUTION, IS_GOAL, CONNECT зависят от конкретной поисковой задачи, поэтому дадим только их общую характеристику.
Функция CONNECT с двумя аргументами – списком порожденных дочерних вершин и текущей (только что раскрытой, родительской) вершиной – генерирует список указателей от каждой дочерней вершины к исходной родительской.
Функция SOLUTION с двумя аргументами – найденным целевым состоянием и списком всех указателей дерева перебора – вырабатывает список-решение задачи (решающий путь).
Предполагается, что функция OPENING порождает для своего единственного аргумента – описания состояния задачи – список дочерних вершин-состояний (который может оказаться пустым). Каждое описание состояние задается списком, первый элемент которого – это уникальный идентификатор состояния (число или атом), а второй элемент – собственно описание состояния задачи. Идентификаторы состояний необходимы для построения указателей функцией CONNECT.
Предикат IS_GOAL проверяет, является ли ее аргумент целевым состоянием. В случае положительного исхода проверки значением функции является само проверяемое состояние, в ином случае значение равно() .
В обоих алгоритмах поиска применяется также вспомогательная рекурсивная функция RETAIN_NEW, которая оставляет в списке дочерних состояний Dlist только те, которые не порождались ранее – тем самым исключается зацикливание при поиске в произвольном графе:
(defun RETAIN_NEW (Dlist)
(prog (D)
(cond( (null Dlist) (return()) )
(t (setq D (car Dlist))
(cond((or (member D Open)(member D Closed))
(return(RETAIN_NEW (cdr Dlist)) ))
(t (return(cons D
(RETAIN-NEW(cdr Dlist)))) )) )) ))
Другая вспомогательная рекурсивная функция CHECK_GOALS проверяет, есть ли среди дочерних состояний целевые. Значением этой функции является целевое состояние, если таковое найдено, и пустой список в ином случае:
(defun CHECK_GOALS (Dlist)
(cond((null Dlist) nil)
((IS_GOAL(car Dlist)) (car Dlist))
(t (CHECK_GOALS (cdr Dlist)) )) )
Приведем теперь текст лисп-функции поиска вширь. В этой функции, как и в последующих, идентификаторы Open, Closed, Current имеют тот же смысл, что и в неформальных описаниях базовых алгоритмов, комментариями предваряются основные шаги алгоритма. Отметим, что по сравнению с прежним описанием алгоритма добавлена операция исключения повторно порожденных состояний (функция RETAIN_NEW), а шаги 4 и 5 были соединены для упрощения программы.
(defun BREADTH_FIRST_SEARCH(StartState)
(prog (Open Closed Current
Deslist ;список дочерних вершин;
Reflist ;список указателей;
Goal ;целевая вершина;)
;Шаг 1:; (setq Open (list (list 'S0 StartState)))
;Шаг 2:; ВS (cond( (null Open) (return() )))
;Шаг 3:; (setq Current (car Open))
(setq Open (cdr Open))
(setq Closed (cons Current Closed))
;Шаги 4,5:; (setq Deslist (OPENING Current))
(cond( (setq Goal(CHECK_GOALS Deslist))
(return (SOLUTION Goal Reflist)) ))
; Исключение повторных вершин-состояний:
(setq Deslist (RETAIN_NEW Deslist))
(cond( (null Deslist) (go BS) ))
(setq Open (append Open Deslist))
; Построение указателей и занесение их в общий список:
(setq Reflist(append(CONNECT Deslist Current)
Reflist))
(go ВS) ))
Граф-пространство состояний для головоломки-игры в восемь достаточно велик (в игре в пятнадцать фишек он на порядок больше), поэтому хотя в принципе применимы алгоритмы слепого поиска, предпочтителен все же эвристический поиск. Опишем нужные для HEURISTIC_SEARCH вспомогательные лисп-функции IS_GOAL, EST, OPENING, SOLUTION, CONNECT для игры в восемь. В соответствии с предположениями, сделанными в предыдущем разделе, состояние задачи (конфигурация игры) представляется списком из следующих элементов:
идентификатор состояния (используются атомы S1,S2,S3, ... генерируемые встроенной лисповской функцией gensym);
собственно описание состояния – список из номеров фишек, записанных последовательно по рядам квадрата;
число-глубина состояния-вершины в дереве перебора;
числовая эвристическая оценка состояния.
В описание состояния включается также – в качестве первого элемента списка – обозначение того оператора движения пустой клетки, который привел к данному состоянию. Этот элемент нужен, чтобы исключить тривиальные повторы состояний при раскрытии вершин. Операторы будут обозначаться соответственно именами-атомами right, left, up, down; а "пустышка" (пустая клетка) – как # .
Например, (S3 ('left 2 8 3 1 6 4 # 7 5) 1 6) - цель S3, полученная сдвигом "пустышки" влево, находящаяся в дереве перебора на глубине 1 и имеющая эвристическую оценку 6. Отметим, что эвристическая оценка используется только в алгоритме эвристического перебора, а глубина вершины – в алгоритмах эвристического перебора и ограниченного перебора вглубь.
Описанные ниже лисп-функции для игры в восемь могут быть пригодны и для игры в пятнадцать, так как размер стороны игрового квадрата, равный 3, используется в них как глобальная переменная переменная Size. Другая глобальная переменная Goalstate, хранит описание целевого состояния (без идентификатора, глубины и эвристической оценки). Значение оценочной функции EST – сумма числа фишек, стоящих не на «своих» местах, и длины пути (глубины) оцениваемого состояния в дереве поиска.
(defun IS_GOAL(State)
(equal (cdadr State) Goalstate ))
(defun EST (S)
(prog(Len G N E1 E2)
(setq Len (cadr S)) (setq N 0)
(setq S (cdar S)) (setq G Goalstate0
;одновременный просмотр списков-описаний
; заданного и целевого состояний:
ES (cond((null S) (return (+ N Len)) ))
(pop E1 S) (pop E2 G)
(cond( (eql E1 E2) (setq N (add1 N)) ))
(go ES) ))
(defun OPENING (State)
(prog(Op St Dlist K I J El)
; выделение составных элементов описания состояния:
(setq St (cadr State))
(setq Op (car St)) (setq St (cdr St))
(setq State St) (setq K 0)
; поиск порядкового номера К "пустышки" в списке:
OP (setq El (car St))
(setq K (add1 K))
(cond ((neq El '#) (setq St(cdr St)) (go OP) ))
; вычисление номера ряда и номера столбца "пустышки":
(setq I(add1(mod K Size))) (setq J (rem K Size))
; поочередно проверка возможности движения «пустышки»
; вправо/влево/вверх/вниз (за счет анализа оператора Op
; исключаем в дереве поиска тривиальные циклы(т.е. возврат
; после применения двух операторов в исходное состояние):
(cond((and (neq Op 'left) (< J Size))
(ADD_STATE 'right K (add1 K)) ))
(cond((and (neq Op 'right) (> J 1))
(ADD_STATE 'left K (sub1 K)) ))
(cond((and (neq Op 'down) (> I 1))
(ADD_STATE 'up K (- K Size)) ))
(cond((and (neq Op 'up) (< I Size))
(ADD_STATE 'down K (+ K Size)) ))
(return Dlist) ))
При раскрытии использована вспомогательная функция ADD_STATE, добавляющая в список дочерних вершин список-описание новой вершины из 2 элементов: идентификатора этой вершины (его генерирует функция gensym) и списка номеров фишек. В ADD_STATE применяется встроенная лисповская функция NTH, выбирающая из заданного списка элемент с заданным порядковым номером.
(defun ADD_STATE (Op K1 K2)
(push(list(gensym)
(cons Op
(cond((< K1 K2)
(EXCHANGE State 1 '# K1 (NTH K2 State)K2))
(t (EXCHANGE State 1(NTH K2 State)K2 '# K1))) ))
Dlist))
Рекурсивная функция EXCHANGE, использованная в ADD_STATE, формирует новое состояние игры путем перестановки заданных элементов исходного состояния-списка List (переменная K служит для просмотра этого списка, и при обращении к функции ее значение равно1).
(defun EXCHANGE (List K Elem1 K1 Elem2 K2)
(cond((eql K K1) (cons Elem2
(EXCHANGE(cdr List)(add1 K)Elem1 K1 Elem2 K2) ))
((eql K K2)(cons Elem1 (cdr List)) )) )
Функция CONNECT формирует список указателей от текущей вершины-состояния Curr к заданным (в списке Dlist) дочерним вершинам-состояниям. Каждый указатель есть трехэлементный список из идентификатора родительской вершины, идентификатора дочерней вершины и названия связывающего их оператора.
(defun CONNECT (Dlist Curr)
(prog (D Di Ci Rlist)
C (setq D (car Dlist)) (setq Dlist (cdr Dlist))
(setq Di (car D)) (setq Ci (car Curr))
(setq Rlist(cons (list Ci Di (caadr D))Rlist))
(cond ((null Dlist) (return Rlist) ))
(go C) ))
Функция SOLUTION, выделяя решающий путь, строит последовательность (названий) операторов, преобразующих начальное состояние в целевое (ее аргумент Reflist – список всех указателей-связей между состояниями). Для поиска указателя к очередной вершине решающего пути функция использует вспомогательную функцию LOOK_FOR .
(defun SOLUTION (Goal Reflist)
(prog (Sollist ;список, в котором строится решение
Gi Edge)
(setq Gi (car G))
S (cond( (eq Gi 'S0) (return Sollist) ))
(setq Edge (LOOK_FOR Gi Reflist))
(setq Sollist (cons(caddr Edge) Sollist))
(setq Gi (car Edge))
(go S) ))
(defun LOOK_FOR (Id List)
(cond( (null List) (quote error))
((eq ID (cadar List)) (car List))
(t (LOOK_FOR Id (cdr List)) )) )
В заключение приведем блок, инициализирующий эвристический поиск решения игры в восемь: в самом его начале устанавливаются переменные-параметры встроенной функции gensym.
(prog(Goalstate Initstate Size)
(setq *gensym-prefix* 'S)
(setq *gensym-count* 1)
(setq Size 3)
(setq Goalstate '(1 2 3 8 # 4 7 6 5))
(setq Initstate '(? 2 8 3 1 6 4 7 # 5))
(HEURISTIC_SEARCH Initstate) )
Будем рассматривать класс игр двух лиц с полной информацией. В таких играх участвуют два игрока, которые поочередно делают свои ходы. В любой момент игры каждому игроку известно все, что произошло в игре к этому моменту и что может быть сделано в настоящий момент. Игра заканчивается либо выигрышем одного игрока (и проигрышем другого), либо ничьей.
Таким образом, в рассматриваемый класс не попадают игры, исход которых зависит хотя бы частично от случая − большинство карточных игр, игральные кости, «морской бой» и проч. Тем не менее класс достаточно широк: в него входят такие игры, как шахматы, шашки, реверси, калах, крестики-нолики и др.
Для формализации и изучения игровых стратегий в классе игр с полной информацией может быть использован подход, основанный на редукции задач. Напомним, что при этом должны быть определены следующие составляющие: форма описания задач и подзадач; операторы, сводящие задачи к подзадачам; элементарные задачи; а также задано описание исходной задачи.
Наиболее интересной представляется задача поиска выигрышной стратегии для одного из игроков, отправляясь от некоторой фиксированной конфигурации (позиции) игры (не обязательно начальной). При использовании подхода, основанного на редукции задач, выигрышная стратегия ищется в процессе доказательства того, что игра может быть выиграна. Аналогично, поиск ничейной стратегии, исходя из некоторой конкретной позиции, ведется в процессе доказательства того, что игра может быть сведена к ничьей.
Ясно, что описание решаемой задачи должно содержать описание конфигурации игры, для которой ищется нужная стратегия. Например, в шашках игровая позиция включает задание положений на доске всех шашек, в том числе дамок. Обычно описание конфигурации содержит также указание, кому принадлежит следующий ход.
Пусть именами игроков будут ПЛЮС и МИНУС. Будем использовать следующие обозначения:
XS (или YS) − некоторая конфигурация игры, причем индекс S принимает значения + или −, указывая тем самым, кому принадлежит следующий ход (т.е. в конфигурации X+ следующий ход должен делать игрок ПЛЮС, а в X− – игрок МИНУС);
W(XS) − задача доказательства того, что игрок ПЛЮС может выиграть, исходя из конфигурации XS;
V(XS) − задача доказательства того, что игрок МИНУС может выиграть, отправляясь от конфигурации XS.
Рассмотрим сначала игровую задачу W(XS). Операторы сведения этой задачи к подзадачам определяются исходя из ходов, допустимых в проводимой игре:
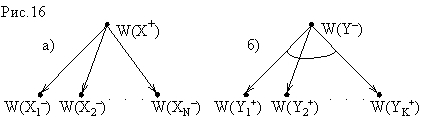
Последовательное применение для исходной конфигурации игры данной схемы сведения игровых задач к совокупности подзадач порождает И/ИЛИ-дерево (И/ИЛИ-граф), которое называют деревом (графом) игры. Дуги игрового дерева соответствуют ходам игроков, вершины − конфигурациям игры, причем листья дерева − это позиции, в которых игра завершается выигрышем, проигрышем или ничьей. Часть листьев являются заключительными вершинами, соответствующими элементарным задачам − позициям, выигрышным для игрока ПЛЮС. Заметим, что для конфигураций, где ход принадлежит ПЛЮСу, в игровом дереве получается ИЛИ-вершина, а для позиций, в которых ходит МИНУС, − И-вершина.
Цель построения игрового дерева или графа − получение решающего поддерева (подграфа) для задачи W(XS), показывающего, как игрок ПЛЮС может выиграть игру из позиции XS независимо от ответов противника. Для этого могут быть применены разные алгоритмы поиска на И/ИЛИ-графах. Решающее дерево или граф заканчивается на позициях, выигрышных для ПЛЮСа, и содержит полную стратегию достижения им выигрыша: для каждого возможного продолжения игры, выбранного противником, в дереве или графе есть ответный ход, приводящий к победе.
Для задачи V(XS) схема сведения игровых задач к подзадачам аналогична: ходам игрока ПЛЮС будут соответствовать И-вершины, а ходам МИНУСа − ИЛИ-вершины, заключительные же вершины будут соответствовать позициям, выигрышным для игрока МИНУС.
Конечно, подобная редукция задач применима и в случае, когда нужно доказать существование ничейной стратегии в игре. При этом определение заключительной вершины (элементарной задачи) должно быть соответствующим образом изменено.
В большинстве игр, представляющих интерес, таких как шашки и шахматы, построить полные решающие деревья или графы (и найти полные игровые стратегии) не представляется возможным. Например, для шашек число вершин в полном игровом дереве оценивается величиной порядка 1040, и просмотреть такое дерево практически нереально. Алгоритмы же упорядоченного перебора с применением эвристик не настолько уменьшают просматриваемую часть дерева игры, чтобы дать существенное (на несколько порядков) сокращение времени поиска.
Тем не менее в случае неполных игр в шашки и шахматы (например, для эндшпилей), так же как и для всех несложных игр, таких как «крестики-нолики» на фиксированном квадрате небольшого размера, можно успешно применять алгоритмы поиска на И/ИЛИ-графах, позволяющие обнаруживать выигрышные и ничейные игровые стратегии.
Рассмотрим, к примеру, игру «крестики-нолики» на квадрате 3×3. Игрок ПЛЮС ходит первым и ставит крестики, а МИНУС − нолики. Игра заканчивается, когда составлена либо строка, либо столбец, либо диагональ из крестиков (выигрывает ПЛЮС) или ноликов (выигрывает МИНУС). Оценим размер полного дерева игры: начальная вершина имеет 9 дочерних вершин, каждая из которых в свою очередь − 8 дочерних; каждая вершина глубины 2 имеет 7 дочерних и т.д. Таким образом, число концевых вершин в дереве игры равно 9!=362880, но многие пути в этом дереве обрываются раньше на заключительных вершинах. Значит, в этой игре возможен полный просмотр дерева и нахождение выигрышной стратегии. Однако ситуация изменится при существенном увеличении размеров квадрата или в случае неограниченного поля игры.
В таких случаях, как и во всех сложных играх вместо нереальной задачи поиска полной игровой стратегии решается, как правило, более простая задача − поиск для заданной позиции игры достаточно хорошего первого хода.
С целью поиска достаточно хорошего первого хода просматривается обычно часть игрового дерева, построенного от заданной конфигурации. Для этого применяется один из переборных алгоритмов (в глубину, в ширину или эвристический) и некоторое искусственное окончание перебора вершин в игровом дереве: например, ограничивается время перебора или же глубина поиска.
После построения таким образом частичного дерева игры вершины в нем оцениваются, и по этим оценкам определяется наилучший ход от заданной игровой конфигурации. При этом для получения оценок концевых вершин (листьев) полученного дерева используется так называемая статическая оценочная функция, а для оценивания остальных вершин – корневой (начальной) и промежуточных (между корневой и концевыми вершинами) – используется так называемый минимаксный принцип.
Статическая оценочная функция, будучи применена к некоторой вершине-позиции игры, дает числовое значение, оценивающее различные достоинства этой игровой позиции. Например, для шашек могут учитываться такие (статические) элементы конфигурации игры, как продвинутость и подвижность шашек, количество дамок, контроль ими центра и проч. По сути, статическая функция вычисляет эвристическую оценку шансов на выигрыш одного из игроков. Для определенности будем рассматривать задачу выигрыша игрока ПЛЮС и соответственно поиска достаточно хорошего его первого хода от заданной конфигурации.
Будем придерживаться общепринятого соглашения, по которому значение статической оценочной функции тем больше, чем больше преимуществ имеет игрок ПЛЮС (над игроком МИНУС) в оцениваемой позиции. Очень часто оценочная функция выбирается следующим образом:
Например, для шашек в качестве простейшей статической функции может быть взят перевес в количестве шашек (и дамок) у игрока ПЛЮС. Для игры «крестики-нолики» на фиксированном квадрате возможна такая статическая оценочная функция:
ì +∞ если P есть позиция выигрыша игрока ПЛЮС
E(P) = í −∞ если P есть позиция выигрыша МИНУСа
î (NL+ +NC+ +ND+ )−(NL− +NC− +ND−) в остальных случаях
где +∞ − очень большое положительное число;
−∞ − очень маленькое отрицательное число;
NL+, NC+, ND+ − соответственно число строк, столбцов и диагоналей, «открытых» для игрока ПЛЮС (т.е. где он еще может поставить выигрышные три крестика подряд),
NL−, NC−, ND− − аналогичные числа для игрока МИНУС.
На рис.18 приведены две игровые позиции (на квадрате 4×4) и соответствующие значения статической оценочной функции.
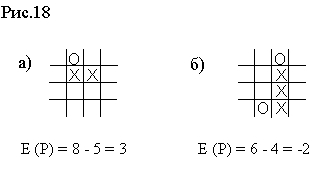
Подчеркнем, что с помощью статической оценочной функции оцениваются только концевые вершины дерева игры, для оценок же промежуточных вершин (и начальной вершины) используется минимаксный принцип, основанный на следующей простой идее. Если бы игроку ПЛЮС пришлось бы выбирать один из нескольких возможных ходов, то он выбрал бы наиболее сильный ход, т.е. ход, приводящий к позиции с наибольшей оценкой. Аналогично, если бы игроку МИНУС пришлось бы выбирать ход, то он выбрал бы ход, приводящий к позиции с наименьшей оценкой.
Сформулируем теперь сам минимаксный принцип:
Минимаксный принцип положен в основу минимаксной процедуры, предназначенной для определения наилучшего (достаточно хорошего) хода игрока исходя из заданной конфигурации игры S при фиксированной глубине поиска N в игровом дереве. Предполагается, что игрок ПЛЮС ходит первым (начальная вершина есть ИЛИ-вершина). Основные этапы этой процедуры таковы:
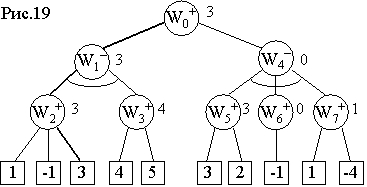
На рис.19 показано применение минимаксной процедуры для дерева игры, построенного до глубины N=3. Концевые вершины не имеют имен, они обозначены своими оценками − значениями статической оценочной функции. Числовые индексы имен остальных вершин показывают порядок, в котором эти вершины строились алгоритмом перебора вглубь. Рядом с этими вершинами находятся их минимаксные оценки, полученные при движении в обратном (по отношению к построению дерева) направлении. Таким образом, наилучший ход – первый из двух возможных.
На рассматриваемом игровом дереве выделена ветвь (последовательность ходов игроков), представляющая так называемую минимаксно-оптимальную игру (или основной вариант игры), при которой каждый из игроков всегда выбирает наилучший для себя ход. Заметим, что оценки всех вершин этой ветви дерева совпадают, и оценка начальной вершины равна оценке концевой вершины этой ветви.
В принципе статическую оценочную функцию можно было бы применить и к промежуточным вершинам, и на основе этих оценок осуществить выбор наилучшего первого хода, например, сразу выбрать ход, максимизирующий значение статической оценочной функции среди вершин, дочерних к исходной. Однако считается, что оценки, полученные с помощью минимаксной процедуры, есть более надежные меры относительного достоинства промежуточных вершин, чем оценки, полученные прямым применением статической оценочной функции. Действительно, минимаксные оценки основаны на просмотре игры вперед и учитывают разные особенности, которые могут возникнуть в последующем, в то время как простое применение оценочной функции учитывает лишь статические свойства позиции как таковой. Это отличие статических и минимаксных оценок существенно для «активных», динамичных позиций игры (например, в шашках и шахматах к ним относятся конфигурации, в которых возникает угроза взятия одной или нескольких фигур). В случае же так называемых «пассивных», спокойных позиций статическая оценка обычно мало отличается от оценки по минимаксному принципу.
Минимаксная процедура организована таким образом, что процесс построения частичного дерева игры отделен от процесса оценивания вершин. Такое разделение приводит к тому, что в целом минимаксная процедура − неэффективная стратегия поиска хорошего первого хода. Чтобы сделать процедуру более экономной, необходимо вычислять статические оценки концевых вершин и минимаксные оценки промежуточных вершин одновременно с построением игрового дерева. Этот путь приводит к так называемой альфа-бета процедуре поиска наилучшего первого хода от заданной позиции, на нем можно добиться существенного сокращения вычислительных затрат, прежде всего, времени вычисления оценок. В основе такого сокращения поиска лежит достаточно очевидное соображение: если есть два варианта хода одного игрока, то худший в ряде случаев можем сразу отбросить, не выясняя, насколько в точности он хуже.
Рассмотрим сначала идею работы альфа-бета процедуры на примере игрового дерева, приведенного на рис.19. Дерево игры строится до глубины N=3 алгоритмом перебора вглубь. Причем сразу, как это становится возможным, вычисляются не только статические оценки концевых вершин, но и предварительные минимаксные оценки промежуточных вершин. Предварительная оценка определяется соответственно как минимум или максимум уже известных (к настоящему моменту) оценок дочерних вершин, и она может быть получена при наличии оценки хотя бы одной дочерней вершины. Предварительные оценки затем постепенно уточняются по минимаксному принципу – по мере получения новых (предварительных и точных) оценок в ходе дальнейшего построения дерева.
Пусть таким образом построены вершины W1−, W2+ и первые три конечные вершины (листья) − см. рис.20. Эти листья оценены статической функцией, и вершина W2+ получила точную минимаксную оценку 3, а вершина W1− − предварительную оценку 3. Далее при построении и раскрытии вершины W3+ статическая оценка первой ее дочерней вершины дает величину 4, которая становится предварительной оценкой самой вершин W3+ . Эта предварительная оценка будет потом (после построения второй дочерней вершины) пересчитана, причем согласно минимаксному принципу она может только увеличиться (так как равна максимуму оценок дочерних вершин), но даже если она увеличится, это не повлияет на оценку вершины W1−, поскольку последняя при уточнении по минимаксному принципу может только уменьшаться (она равна минимуму оценок дочерних вершин). Следовательно, можно пренебречь второй дочерней вершиной для W3+, не строить и не оценивать ее (так как уточнение оценки вершины W3+ не повлияет на оценку вершины W1−). Такое сокращение процедуры поиска в дереве называется отсечением ветвей дерева.
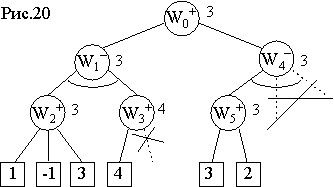
Продолжим для нашего примера процесс поиска в глубину с одновременным вычислением предварительных (и точных, где это возможно) оценок вершин вплоть до момента, когда построены уже вершины W4− , W5+ и две дочерних последней, которые оцениваются статической функцией. Исходя из оценки первой дочерней вершины начальная вершина W0+, соответствующая исходной позиции игры, к этому моменту уже предварительно оценена величиной 3. Вершина W5+ получила точную минимаксную оценку 3, а ее родительская W4− получила пока только предварительную оценку 3. Эта предварительная оценка вершины W4−может быть уточнена в дальнейшем, но в соответствии с минимаксным принципом возможно только ее уменьшение, а это уменьшение не повлияет на оценку вершины W0+, поскольку последняя, опять же согласно минимаксному принципу, может только увеличиваться. Таким образом, построение дерева можно прервать ниже вершины W4−, отсекая целиком выходящие из нее вторую и третью ветви (и оставляя ее оценку предварительной).
На этом построение рассматриваемого игрового дерева заканчивается, полученный результат − лучший первый ход − тот же самый, что и при минимаксной процедуре. У некоторых вершин дерева осталась неуточненная, предварительная оценка, однако этих приближенных оценок оказалось достаточно для того, чтобы определить точную минимаксную оценку начальной вершины и наилучший первый ход. В то же время произошло существенное сокращение поиска: вместо 17 вершин построено только 11, и вместо 10 обращений к статической оценочной функции понадобилось всего 6.
Обобщим рассмотренную идею сокращения перебора. Сформулируем сначала правила вычисления оценок вершин дерева игры, в том числе предварительных оценок промежуточных вершин, которые для удобства будем называть альфа- и бета-величинами:
Укажем очевидное следствие этих правил вычисления: альфа-величины не могут уменьшаться, а бета-величины не могут увеличиваться.
Сформулируем теперь правила прерывания перебора, или отсечения ветвей игрового дерева:.
При этом в случае А говорят, что имеет место альфа-отсечение (поскольку отсекаются ветви дерева, начиная с ИЛИ-вершин, которым приписана альфа-величина), а в случае В − бета-отсечение (поскольку отсекаются ветви, начинающиеся с бета-величин).
Важно, что рассмотренные правила работают в ходе построения игрового дерева вглубь; это означает, что предварительные оценки промежуточных вершин появляются лишь по мере продвижения от концевых вершин дерева вверх к корню и реально отсечения могут начаться только после того, как получена хотя бы одна точная минимаксная оценка промежуточной вершины.
В рассмотренном примере на рис. 20 первое прерывание перебора было бета-отсечением, а второе − альфа-отсечением. Причем в обоих случаях отсечение было неглубоким, поскольку необходимая для соблюдения соответствующего правила отсечения предварительная оценка (альфа- или бета-величина) находилась в непосредственно предшествующей (к точке отсечения) вершине. В общем же случае она может находиться существенно выше отсекаемой ветви – на пути от вершины, ниже которой производится отсечение, к начальной вершине, включая последнюю.
После прерывания перебора предварительные оценки вершин в точках отсечения остаются неуточненными, но, как уже отмечалось, это не препятствует правильному нахождению предварительных оценок всех предшествующих вершин, как и точной оценки корневой вершины и ее дочерних вершин, а значит, и искомого наилучшего первого хода.
На приведенных выше правилах вычисления оценок вершин и выполнения отсечений (всюду, где это возможно) основана альфа-бета процедура, являющаяся более эффективной реализацией минимаксного принципа. Несложно в принципе, используя математическую индукцию и рассуждая аналогично рассмотренному примеру, доказать следующее
Утверждение:
Альфа-бета процедура всегда приводит к тому же результату (наилучшему первому ходу), что и простая минимаксная процедура той же глубины.
Важным является вопрос, насколько в среднем альфа-бета процедура эффективнее обычной минимаксной процедуры. Нетрудно заметить, что количество отсечений в альфа-бета процедуре зависит от степени, в которой полученные первыми предварительные оценки (альфа- бета-величины) аппроксимируют окончательные минимаксные оценки: чем ближе эти оценки, тем больше отсечений и меньше перебор. Это положение иллюстрирует пример на рис.20, в котором основной вариант игры обнаруживается практически в самом начале поиска.
Таким образом, эффективность альфа-бета процедуры зависит от порядка построения и раскрытия вершин в дереве игры. В принципе возможен и неудачный порядок просмотра, при котором придется пройти (без отсечений) через все вершины дерева, и в этом, худшем случае, альфа-бета процедура не будет иметь никаких преимуществ против минимаксной процедуры.
Наилучший случай (наибольшее число отсечений) достигается, когда при переборе в глубину первой обнаруживается конечная вершина, статическая оценка которой станет в последствии минимаксной оценкой начальной вершины. При максимальном числе отсечений требуется строить и оценивать минимальное число концевых вершин. Показано, что в случае, когда самые сильные ходы всегда рассматриваются первыми, количество концевых вершин глубины N, которые будут построены и оценены альфа-бета процедурой, примерно равно числу концевых вершин, которые были бы построены и оценены на глубине N/2 обычной минимаксной процедурой. Таким образом, при фиксированном времени и памяти альфа-бета процедура сможет пройти при поиске вдвое глубже по сравнению с обычной минимаксной процедурой.
В заключение отметим, что статическая оценочная функция и альфа-бета процедура − две непременные составляющие подавляющего большинства компьютерных игровых программ (в том числе коммерческих). Часто используются также дополнительные эвристические приемы в самой альфа-бета процедуре:
Для усиления игры могут быть также использованы библиотека типовых игровых ситуаций и другие идеи.
Рассмотрим сначала написанную на Плэнере функцию MIN_MAX, реализующую минимаксную процедуру. Аргументы этой функции: Instate − исходная позиция игры, для которой ищется наилучший ход; N − глубина поиска (т.е. количество ходов вперед). Вырабатываемое функцией значение − это дочерняя для Instate позиция, соответствующая наилучшему ходу.
[define MIN_MAX (lambda (Instate N)
[SELECT_MAX [MM_EVALP .Instate 0 T ]] )]
Функция MIN_MAX использует две вспомогательные функции: SELECT_MAX и MM_EVALP. Первая функция, SELECT_MAX выбирает из своего аргумента-списка List, каждый элемент которого – позиция (ход) и ее оценка, позицию (ход) с наибольшей оценкой:
[define SELECT_MAX (lambda (List)
[prog (Elem Max_elem )
[fin Max_elem .List]
SM [cond([fin Elem List] [return [2 .Max_elem]])
([gt [1 .Elem] [1 .Max_elem]]
[set Max_elem .Elem]) ]
[go SM] ] )]
Функция MM_EVALP с тремя аргументами является главной рекурсивной функцией, оценивающей вершины дерева игры по минимаксному принципу. На каждом шаге рекурсии она оценивает вершину-позицию Position, находящуюся на глубине Depth и имеющую тип Deptype ("ИЛИ" при Deptype=Т и "И" при Deptype=() ). Исходная позиция (корневая вершина) имеет тип Т и находится на глубине 0. Значением функции MM_EVALP является либо вычисленная оценка Position (при Depth>0 ) либо список ходов (точнее, дочерних для Position позиций) с их числовыми оценками (при Depth=0).
При работе MM_EVALP используются вспомогательные функции, определение которых зависит от конкретной игры: OPENING, вычисляющая для заданной позиции игры список дочерних вершин-позиций, и STAT_EST − статическая оценочная функция. Основные этапы вычислений предваряются комментарием.
[define MM_EVALP (lambda (Position Depth Deptype)
[prog (D %дочерняя позиция;
(Movelist()) %список ходов-позиций);
Pvalue Dvalue) %оценки текущей и дочерней
позиций;
% 1:установка развилки, включающей все дочерние вершины текущей позиции(список () добавлен в развилку, чтобы "поймать" момент ее закрытия);
[set D [among (<OPENING .Position> ())]]
% 2: если развилка закрыта - возврат функцией подсчитанной оценки;
[cond ([empty .D]
[return [cond ([eq .Depth 0] .Movelist)
(t .Pvalue) ]] )]
% 3: вычисление оценки очередной дочерней позиции: либо применение статической функции, либо рекурсивный спуск;
[cond ([eq .Depth [- .N 1]]
[set Dvalue [STAT_EST .D]])
(t [set Dvalue [MM_EVALP .D
[+ 1 .Depth]
[not .Deptype]]] )]
% 4:пересчет оценки текущей позиции по минимаксному принципу;
[cond ([hasval Pvalue] [pset Pvalue
[cond(.Deptype [max .Pvalue .Dvalue])
(t [min .Pvalue .Dvalue]) ]])
(t [pset Pvalue .Dvalue]) ]
% 5: при необходимости пересчет для исходной позиции списка ходов(дочерних позиций) с их оценками;
[cond([eq .Depth 0]
[pset Movelist(!.Movelist (.Dvalue .D)) ])]
% 6: возврат к другой альтернативе развилки;
[fail] ])]