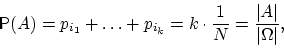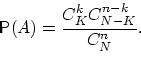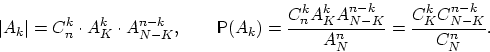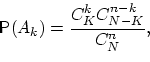



Next: Геометрическая вероятность
Up: Классическая вероятностная схема
Previous: Основные формулы комбинаторики
Теория вероятностей изучает закономерности, возникающие в случайных
экспериментах. Случайным называют эксперимент,
результат которого нельзя предсказать заранее. Невозможность предсказать
результат отличает случайное явление от детерминированного.
Не все случайные явления (эксперименты)
можно изучать методами теории вероятностей, а лишь те, которые
могут быть воспроизведены в одних и тех же условиях. Случайность и хаос —
не одно и то же. Оказывается, что и в случайных экспериментах наблюдаются
некоторые закономерности, например
свойство «статистической устойчивости»:
если  — некоторое событие, могущее произойти или не произойти в результате эксперимента,
то доля
— некоторое событие, могущее произойти или не произойти в результате эксперимента,
то доля 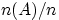 экспериментов, в которых данное событие произошло, имеет тенденцию стабилизироваться
с ростом общего числа экспериментов
экспериментов, в которых данное событие произошло, имеет тенденцию стабилизироваться
с ростом общего числа экспериментов 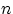 , приближаясь к некоторому
числу
, приближаясь к некоторому
числу 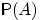 . Это число служит объективной характеристикой
«степени возможности» событию
. Это число служит объективной характеристикой
«степени возможности» событию  произойти.
произойти.
Следует помнить, что мы занимаемся
математикой и имеем дело не с реальностью, а лишь с её математической
моделью. Мы и будем изучать только математические модели, а приложение
их к реальности оставим на долю математической и практической статистики.
Определение 1.
Пространством элементарных исходов 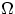
(«омега») называется
множество, содержащее все возможные результаты данного случайного
эксперимента, из которых в эксперименте происходит ровно один.
Элементы этого множества называют
элементарными исходами
и обозначают буквой
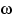
(«омега»).
Определение 2.
Событиями мы будем называть подмножества
множества
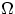
. Говорят, что в результате эксперимента
произошло событие
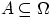
, если в эксперименте произошел один из элементарных исходов,
входящих в множество

.
Пример 1.
Один раз подбрасывается кубик — игральная кость.
Рассмотрим пространство элементарных исходов
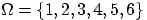
, элементарные исходы здесь
соответствуют числу выпавших очков.
Примеры событий:
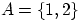 — выпало одно или два очка;
— выпало одно или два очка;
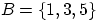 — выпало нечётное число очков.
— выпало нечётное число очков.
Пример 2.
Два раза подбрасывается игральная кость.
Или, что то же самое, один раз подбрасываются две игральные кости.
Будем считать пространством элементарных исходов множество пар чисел
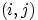
, где
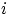
(сответственно,
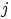
) есть число очков, выпавших при первом (втором)
подбрасывании:
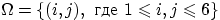
.
Примеры событий:
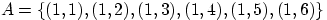 —
при первом подбрасывании выпало одно очко;
—
при первом подбрасывании выпало одно очко;
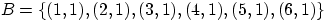 —
при втором подбрасывании выпало одно очко;
—
при втором подбрасывании выпало одно очко;
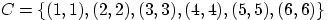 —
на костях выпало одинаковое число очков;
—
на костях выпало одинаковое число очков;
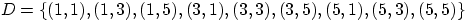 —
на обеих костях выпало нечётное число очков.
—
на обеих костях выпало нечётное число очков.
Пример 3.
На поверхность стола бросается монета. Результатом эксперимента
можно считать координату центра монеты.
Пространство элементарных исходов — множество точек стола.
Если нам не безразличен
угол поворота монеты, то можно добавить к множеству положений центра
величину этого угла. В этом случае
есть
множество пар
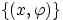
,
где
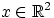
— точка стола и
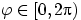
— угол поворота.
Число элементарных исходов такого эксперимента
несчётно.
Пример 4.
Монета подбрасывается до тех пор, пока не выпадет вверх гербом.
Пространство элементарных исходов состоит из бесконечного, но
счётного
числа исходов:
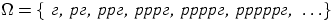
,
где
р означает выпадение решки, а
г — герба
при одном подбрасывании.
Определение 3.
1. Достоверным называется
событие, которое обязательно происходит в результате эксперимента,
т.е. единственное событие, включающее все
элементарные исходы — событие 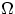 .
.
2. Невозможным называется
событие, которое не может произойти в результате эксперимента,
т.е. событие, не содержащее ни одного элементарного исхода
(«пустое множество» 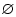 ). Заметим, что всегда
). Заметим, что всегда
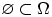 .
.
В теории вероятностей существуют ровно те же операции над множествами, что и в теории множеств.
Определение 4.
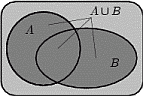
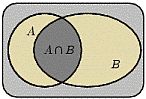 1. Объединением
1. Объединением 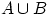 событий
событий  и
и 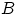 называется событие, состоящее в том, что произошло либо
называется событие, состоящее в том, что произошло либо  , либо
, либо 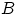 , либо оба события одновременно. На языке теории множеств
, либо оба события одновременно. На языке теории множеств
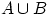 есть множество, содержащее как элементарные исходы из
множества
есть множество, содержащее как элементарные исходы из
множества  , так и элементарные исходы из множества
, так и элементарные исходы из множества 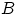 .
.
2. Пересечением 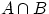 событий
событий  и
и 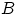 называется событие, состоящее в том, что произошли
оба события
называется событие, состоящее в том, что произошли
оба события  и
и 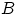 одновременно. На языке теории множеств
одновременно. На языке теории множеств
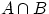 есть множество, содержащее элементарные исходы, входящие
в пересечение множеств
есть множество, содержащее элементарные исходы, входящие
в пересечение множеств  и
и 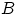 .
.
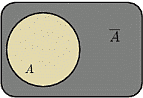
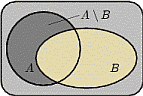 3. Противоположным (или дополнительным)
к событию
3. Противоположным (или дополнительным)
к событию  называется событие
называется событие
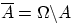 , состоящее в том, что событие
, состоящее в том, что событие  в результате эксперимента не произошло.
Т.е. множество
в результате эксперимента не произошло.
Т.е. множество 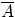 состоит из элементарных исходов, не входящих
в
состоит из элементарных исходов, не входящих
в  .
.
4. Дополнением 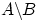 события
события 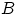 до
до  называется событие, состоящее в том, что произошло
событие
называется событие, состоящее в том, что произошло
событие  , но не произошло
, но не произошло 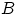 . Т.е.
множество
. Т.е.
множество 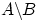 содержит элементарные исходы, входящие
в множество
содержит элементарные исходы, входящие
в множество  , но не входящие в
, но не входящие в 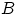 .
.
Определение 5.
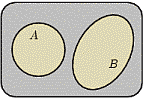 1. События
1. События  и
и  называют несовместными,
если
называют несовместными,
если 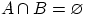 .
.
 2. События
2. События 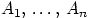 называют попарно несовместными,
если для любых
называют попарно несовместными,
если для любых 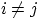 , где
, где 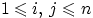 , события
, события 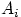 и
и 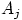 несовместны.
несовместны.
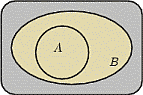
3. Говорят, что событие  влечёт событие
влечёт событие 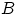 ,
и пишут
,
и пишут 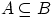 , если всегда, как только происходит событие
, если всегда, как только происходит событие
 ,
происходит и событие
,
происходит и событие 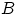 . На языке теории множеств это означает,
что любой элементарный исход, входящий в множество
. На языке теории множеств это означает,
что любой элементарный исход, входящий в множество  ,
одновременно входит и в множество
,
одновременно входит и в множество 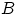 , т.е.
, т.е.  содержится в
содержится в 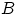 .
.
Пространство элементарных исходов назовём
дискретным,
если оно конечно или счётно:
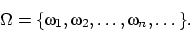
Так, эксперименты из примеров
1, 2 и 4 (но не 3) приводят к дискретным пространствам
элементарных исходов.
Чтобы определить вероятность любого события на дискретном пространстве элементарных
исходов, достаточно присвоить вероятность каждому элементарному исходу.
Тогда вероятность любого события определяется как сумма вероятностей
входящих в него элементарных исходов.
Определение 6.
Поставим каждому элементарному исходу
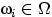
в соответствие число
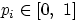
так, что
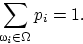
Назовём число 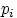 вероятностью элементарного исхода
вероятностью элементарного исхода 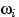 .
Вероятностью события
.
Вероятностью события  назовём число
назовём число
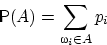 ,
,
равное сумме вероятностей элементарных исходов, входящих в множество  . В случае
. В случае 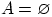 положим
положим 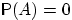 .
.
Рассмотрим частный случай такой вероятности —
так называемую «классическую вероятность».
Предположим, что мы имеем дело с пространством элементарных
исходов, состоящим из конечного числа
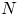
элементов:
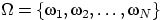
.
Предположим, что из каких-либо соображений
мы можем считать элементарные исходы равновозможными.
Тогда вероятность любого из них принимается равной
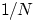
.
Эти соображения не имеют отношения к математической
модели и основаны на какой-либо симметрии
в эксперименте (симметричная монета, хорошо перемешанная колода карт,
правильная кость).
Если событие  состоит из
состоит из 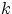 элементарных исходов, то вероятность этого события
равняется отношению
элементарных исходов, то вероятность этого события
равняется отношению 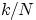 :
:
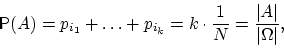
где символом 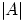 обозначено число элементов конечного множества
обозначено число элементов конечного множества  .
.
Определение 7.
Говорят, что эксперимент удовлетворяет
классическому
определению вероятности, если пространство элементарных исходов состоит из конечного
числа
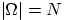
равновозможных исходов.
В этом случае вероятность любого события

вычисляется по формуле
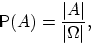
называемой классическим определением
вероятности.
Формулу
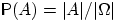
читают так:
«вероятность события

равна отношению числа исходов,
благоприятствующих событию

, к общему числу исходов».
Полезно сравнить это определение с классической формулировкой Якоба
Бернулли
(1):
«Вероятность есть степень достоверности и отличается от неё как часть
от целого» (Ars Conjectandi, 1713 г.)
Мы видим теперь, что подсчёт вероятности в классической схеме
сводится к подсчёту общего числа «шансов» и числа шансов,
благоприятствующих какому-либо событию.
Число шансов считают с помощью формул комбинаторики.
Рассмотрим описанные в параграфе 1
урновые схемы.
Три схемы: с возвращением и с учётом порядка,
без возвращения и с учётом порядка, а также
без возвращения и без учёта порядка, удовлетворяют классическому
определению вероятности. Общее число элементарных исходов в этих
схемах подсчитано в теоремах 4, 2, 3
и равно соответственно 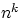 ,
, 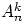 ,
, 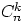 .
Четвёртая же схема — схема выбора с возвращением и без учёта
порядка — имеет заведомо неравновозможные исходы.
.
Четвёртая же схема — схема выбора с возвращением и без учёта
порядка — имеет заведомо неравновозможные исходы.
Пример 5.
Рассмотрим выбор двух шариков из двух или, что то же самое,
дважды подбросим монету.
Если учитывать порядок, то исходов получится четыре, и все они равновозможны,
т.е. имеют вероятность по 1/4:
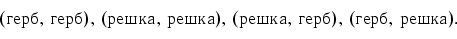
Если порядок не учитывать, то следует объявить два последних
исхода одним и тем же результатом эксперимента,
и получить не четыре, а три исхода:
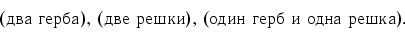
Первые два исхода имеют вероятности по 1/4, а последний —
вероятность 1/4+1/4=1/2.
Упражнение 9.
Посчитать число элементарных исходов в
примере 2
(при подбрасывании двух игральных костей).
Каким станет пространство элементарных исходов,
если порядок костей не учитывать? Посчитать число элементарных
исходов в таком пространстве (пользуясь
теоремой 5 или прямым
подсчётом). Убедиться, что их ровно
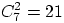
. Равновозможны ли эти исходы?
Посчитать вероятность каждого.
Пример 6.
Из урны, в которой
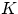
белых и
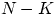
чёрных шаров,
наудачу и без возвращения вынимают
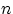
шаров,
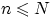
.
Термин «наудачу» означает, что появление любого набора
из
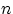
шаров равновозможно. Найти вероятность того, что
будет выбрано
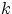
белых и
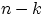
чёрных шаров.
Решение. При 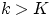 или
или 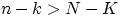 искомая вероятность равна нулю, так как соответствующее событие
невозможно. Пусть
искомая вероятность равна нулю, так как соответствующее событие
невозможно. Пусть 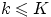 и
и 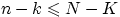 .
.
Результатом эксперимента является набор из 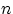 шаров.
Можно не учитывать или учитывать порядок следования шаров, вероятность не должна
зависеть от способа подсчёта.
шаров.
Можно не учитывать или учитывать порядок следования шаров, вероятность не должна
зависеть от способа подсчёта.
Выбор без учёта порядка. Общее число элементарных исходов есть число
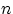 -элементных подмножеств множества, состоящего из
-элементных подмножеств множества, состоящего из 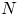 элементов:
элементов: 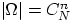 (по теореме 3).
(по теореме 3).
Обозначим через 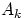 событие, вероятность которого требуется найти.
Событию
событие, вероятность которого требуется найти.
Событию 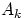 благоприятствует появление любого набора,
содержащего
благоприятствует появление любого набора,
содержащего 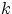 белых шаров и
белых шаров и 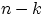 чёрных.
Число благоприятных исходов равно произведению (по теореме 1)
числа способов выбрать
чёрных.
Число благоприятных исходов равно произведению (по теореме 1)
числа способов выбрать 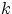 белых шаров из
белых шаров из 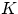 и числа способов выбрать
и числа способов выбрать 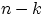 чёрных шаров из
чёрных шаров из 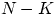 , т.е.
, т.е.
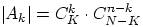 .
Вероятность события
.
Вероятность события 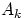 равна
равна
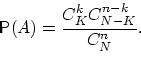 | (1) |
Выбор с учётом порядка. Общее число элементарных исходов есть число
способов разместить 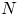 элементов на
элементов на 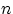 местах: по теореме 2,
местах: по теореме 2,
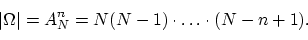
При подсчёте числа благоприятных исходов нужно учесть число
способов выбрать 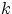 белых и
белых и 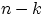 чёрных шаров и число способов расположить
эти шары среди
чёрных шаров и число способов расположить
эти шары среди 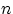 . Можно, скажем, посчитать число способов
выбрать
. Можно, скажем, посчитать число способов
выбрать 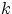 мест среди
мест среди 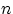 (равное
(равное 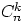 ), затем число
способов разместить на этих
), затем число
способов разместить на этих 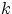 местах
местах 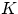 белых шаров
(равное
белых шаров
(равное 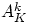 ),
и затем число способов разместить на оставшихся
),
и затем число способов разместить на оставшихся 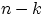 местах
местах
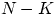 чёрных шаров (равное
чёрных шаров (равное 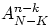 ).
Перемножив (почему?) эти числа, получим
).
Перемножив (почему?) эти числа, получим
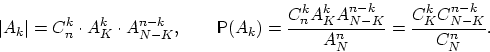
В рассмотренной задаче мы сопоставили каждому набору
из
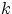
белых и
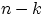
чёрных шаров вероятность
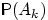
получить этот набор при выборе
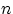
шаров из урны, содержащей
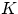
белых и
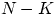
чёрных шаров.
Определение 8.
Соответствие между числом
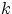
и вероятностью
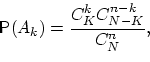
(где 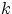 таково, что
таково, что 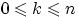 ,
, 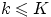 и
и 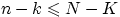 )
называется гипергеометрическим распределением.
)
называется гипергеометрическим распределением.
Здесь мы в первый, но далеко не в последний раз встретились с термином
«распределение» вероятностей. Это слово всегда обозначает некий способ разделить
(распределить) общую единичную вероятность между какими-то точками
или множествами на вещественной прямой.
В гипергеометрическом распределении
единичная вероятность распределена между подходящими целыми числами 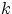 неравномерно.
Каждому целому числу
неравномерно.
Каждому целому числу 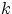 сопоставлена своя вероятность
сопоставлена своя вероятность 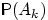 .
На вещественной прямой можно единичную вероятность распределить
по-разному. Этим одно распределение отличается от другого: тем,
на каком множестве чисел «распределена» общая единичная вероятность,
и тем, какие веса, или вероятности, присвоены отдельным точкам или
частям этого множества.
.
На вещественной прямой можно единичную вероятность распределить
по-разному. Этим одно распределение отличается от другого: тем,
на каком множестве чисел «распределена» общая единичная вероятность,
и тем, какие веса, или вероятности, присвоены отдельным точкам или
частям этого множества.
Упражнение 10.
Понять последний абзац.




Next: Геометрическая вероятность
Up: Классическая вероятностная схема
Previous: Основные формулы комбинаторики
1Jacob Bernoulli (27.12.1654 — 16.08.1705, Basel, Switzerland)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
N.Ch.
![]() — некоторое событие, могущее произойти или не произойти в результате эксперимента,
то доля
— некоторое событие, могущее произойти или не произойти в результате эксперимента,
то доля ![]() экспериментов, в которых данное событие произошло, имеет тенденцию стабилизироваться
с ростом общего числа экспериментов
экспериментов, в которых данное событие произошло, имеет тенденцию стабилизироваться
с ростом общего числа экспериментов ![]() , приближаясь к некоторому
числу
, приближаясь к некоторому
числу ![]() . Это число служит объективной характеристикой
«степени возможности» событию
. Это число служит объективной характеристикой
«степени возможности» событию ![]() произойти.
произойти.

 1. Объединением
1. Объединением 
 3. Противоположным (или дополнительным)
к событию
3. Противоположным (или дополнительным)
к событию  1. События
1. События  2. События
2. События