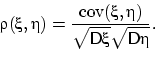
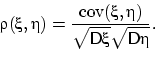
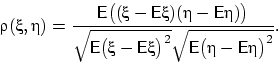
Здесь математикам уместно провести аналогии с «косинусом
угла» между двумя элементами ![]() и
и ![]() гильбертова пространства, образованного
случайными величинами с нулевым математическим ожиданием и
конечным вторым моментом, снабженного скалярным
произведением
гильбертова пространства, образованного
случайными величинами с нулевым математическим ожиданием и
конечным вторым моментом, снабженного скалярным
произведением ![]() и «нормой», равной корню из дисперсии,
или корню из скалярного произведения
и «нормой», равной корню из дисперсии,
или корню из скалярного произведения ![]() .
.
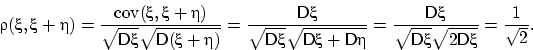
Коэффициент корреляции величин ![]() и
и ![]() равен
косинусу угла
равен
косинусу угла ![]() , образованного «векторами»
, образованного «векторами» ![]() и
и ![]() , когда «
, когда «![]() » и их «длина» одинакова.
» и их «длина» одинакова.
а) нулю, если ![]() имеет нормальное распределение с нулевым средним;
имеет нормальное распределение с нулевым средним;
б) ![]() , если
, если ![]() имеет показательное распределение с любым
параметром.
имеет показательное распределение с любым
параметром.
N.Ch.