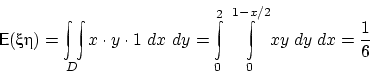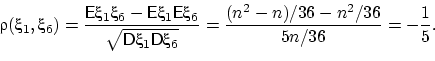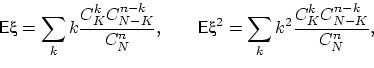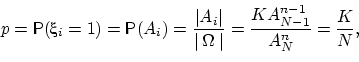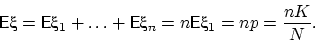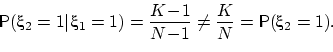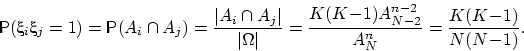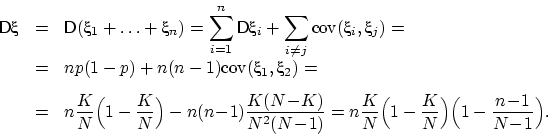Пример 51.
Если
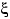
и
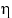
суть координаты точки, брошенной
наудачу в треугольник
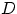
с вершинами
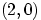
,

и
, то их
коэффициент корреляции 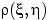 отрицателен
отрицателен.
Это можно объяснить так: чем больше
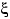
, тем меньше у
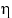
возможностей быть большой.
Предлагаю убедиться в этом, проверив справедливость следующих
высказываний. Во-первых,
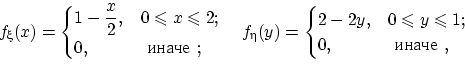
и вычисленные по этим плотностям средние (вычислить!) равны соответственно
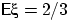 и
и 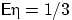 .
.
Во-вторых, по определению многомерного равномерного распределения в области  ,
,
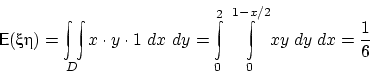
(кажется). Т.е. ковариация (а с ней и
коэффициент корреляции) отрицательна.
Пример 52.
Найдём коэффициент корреляции между
числом выпадений единицы и
числом
выпадений шестерки при
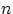
подбрасываниях правильной игральной кости.
Обозначим для  через
через  случайную величину,
равную числу выпадений грани с
случайную величину,
равную числу выпадений грани с 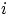 очками при
очками при 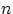 подбрасываниях кубика.
Посчитаем
подбрасываниях кубика.
Посчитаем 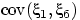 . Каждая из случайных величин
. Каждая из случайных величин  имеет биномиальное
распределение с параметрами
имеет биномиальное
распределение с параметрами 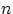 и 1/6, поэтому
и 1/6, поэтому 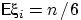 ,
, 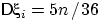 .
.
Далее заметим, что 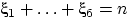 . Из-за симметрии кубика математические
ожидания
. Из-за симметрии кубика математические
ожидания 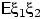 ,
, 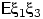 , ...,
, ..., 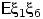 одинаковы (но, надо думать, отличаются от
одинаковы (но, надо думать, отличаются от
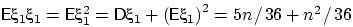 ).
).
Посчитаем 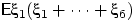 . С одной стороны, это равно
. С одной стороны, это равно
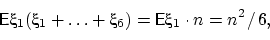
с другой стороны,
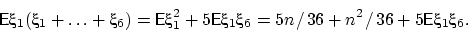
Отсюда 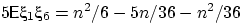 , т.е.
, т.е.
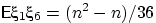 .
.
Следовательно, искомый коэффициент корреляции равен
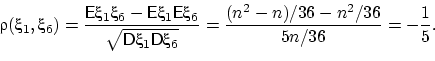
Интересно, что полученный коэффициент корреляции не зависит от 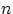 .
.
Пример 53.
Вычислим
математическое ожидание и
дисперсию гипергеометрического распределения.
Мы не могли сделать это раньше, так как очень не хотели вычислять следующие
суммы:
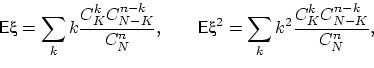
где, напомним (чтобы читатель окончательно отказался от мысли вычислить эти суммы напрямую),
суммирование ведётся по целым 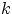 таким, что
таким, что 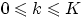 и
и 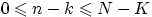 .
.
Рассмотрим урну, содержащую 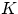 белых шаров и
белых шаров и 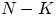 не белых, и пусть
из неё наудачу и без возвращения выбирают по одному
не белых, и пусть
из неё наудачу и без возвращения выбирают по одному 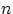 шаров.
Свяжем случайную величину
шаров.
Свяжем случайную величину 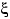 , равную числу белых шаров среди
, равную числу белых шаров среди 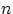 выбранных, с результатами отдельных извлечений шаров.
выбранных, с результатами отдельных извлечений шаров.
Обозначим через  , где
, где 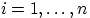 , «индикатор» того, что
, «индикатор» того, что 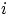 -й по счёту вынутый шар оказался белым:
-й по счёту вынутый шар оказался белым:
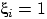 , если при
, если при 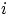 -м извлечении появился белый шар, иначе
-м извлечении появился белый шар, иначе 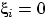 . Тогда
. Тогда 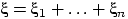 — число появившихся белых шаров, и математическое
ожидание считается просто:
— число появившихся белых шаров, и математическое
ожидание считается просто:
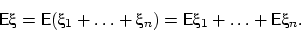
Убедимся, что случайные величины 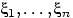 имеют одно и то же
распределение Бернулли
имеют одно и то же
распределение Бернулли  , где
, где 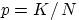 .
.
Пронумеруем шары: белые — номерами от одного до 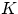 , остальные — номерами от
, остальные — номерами от 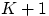 до
до 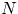 .
Элементарным исходом опыта является набор из
.
Элементарным исходом опыта является набор из 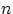 номеров шаров в схеме
выбора
номеров шаров в схеме
выбора 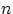 элементов из
элементов из 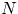 без возвращения и с учётом порядка.
Общее число исходов равно
без возвращения и с учётом порядка.
Общее число исходов равно 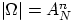 по теореме 2.
по теореме 2.
Вычислим вероятность события 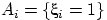 . Событие
. Событие  включает в себя
элементарные исходы (наборы), в которых на
включает в себя
элементарные исходы (наборы), в которых на 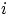 -м месте стоит любой из
номеров белых шаров, а остальные
-м месте стоит любой из
номеров белых шаров, а остальные 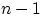 место занимают любые из оставшихся
место занимают любые из оставшихся
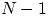 номеров.
По теореме 1 о перемножении шансов число благоприятных
событию
номеров.
По теореме 1 о перемножении шансов число благоприятных
событию  исходов есть произведение
исходов есть произведение 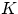 и
и 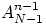 .
Здесь
.
Здесь 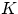 есть число способов поставить
на
есть число способов поставить
на 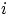 -е место один из номеров белых шаров,
-е место один из номеров белых шаров,
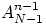 — число способов после этого
разместить на оставшихся
— число способов после этого
разместить на оставшихся 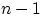 местах остальные
местах остальные 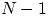 номеров шаров. Но тогда
номеров шаров. Но тогда
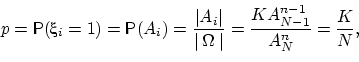
что совершенно очевидно: вероятность двадцатому шару быть белым, если мы ничего
не знаем про первые девятнадцать, точно такая же, как вероятность
первому шару быть белым и равна отношению числа белых шаров к числу всех.
Вернёмся к математическому ожиданию:
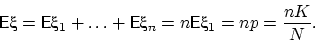
Вычислим дисперсию 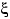 .
До сих пор мы не интересовались совместным распределением
.
До сих пор мы не интересовались совместным распределением 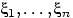 : для вычисления математического ожидания их суммы нам было достаточно знания
маргинальных распределений этих величин. Но дисперсия суммы уже не всегда
равна сумме дисперсий. Зависимость величин
: для вычисления математического ожидания их суммы нам было достаточно знания
маргинальных распределений этих величин. Но дисперсия суммы уже не всегда
равна сумме дисперсий. Зависимость величин 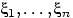 очевидна:
если, скажем, случилось событие
очевидна:
если, скажем, случилось событие 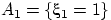 , то вероятность второму шару быть
белым уже не равна
, то вероятность второму шару быть
белым уже не равна 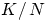 :
:
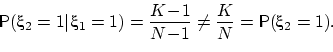
Поэтому при вычислении дисперсии будем пользоваться свойством 14. Вычислим
ковариацию величин  и
и 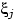 ,
, 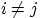 . Для этого сначала посчитаем
. Для этого сначала посчитаем 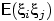 . Произведение
. Произведение
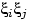 снова имеет распределение Бернулли:
снова имеет распределение Бернулли:
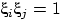 , если при
, если при 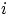 -м и
-м и 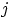 -м извлечениях появились белые шары.
Вероятность этого события равна
-м извлечениях появились белые шары.
Вероятность этого события равна
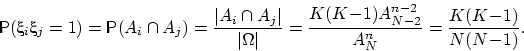
Тогда
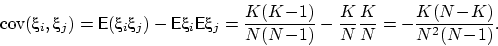
Подставляя одинаковые дисперсии  и эти не зависящие от
и эти не зависящие от
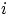 и
и 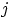 ковариации в формулу дисперсии суммы, получим:
ковариации в формулу дисперсии суммы, получим:
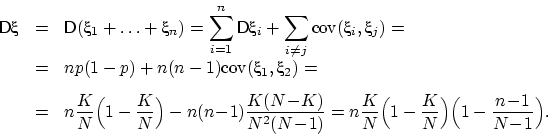
Заметим любопытнейшую вещь: если вынимать шары с возвращением, то
испытания станут независимыми испытаниями в схеме Бернулли, а
ставшие независимыми величины  в сумме дадут число белых
шаров, имеющее биномиальное распределение с параметрами
в сумме дадут число белых
шаров, имеющее биномиальное распределение с параметрами 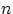 и
и  и точно такое же математическое ожидание
и точно такое же математическое ожидание 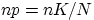 , как и у числа белых шаров при выборе без возвращения.
, как и у числа белых шаров при выборе без возвращения.
Дисперсия же у числа белых шаров при выборе без возвращения меньше,
чем при выборе с возвращением — за счёт отрицательной коррелированности
слагаемых  и
и 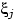 при
при 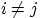 .
.
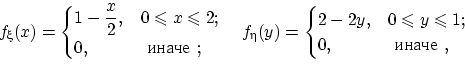
![]() и
и ![]() .
.
![]() ,
,