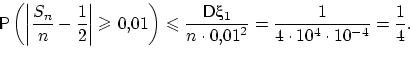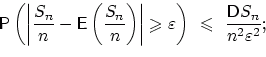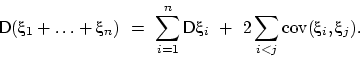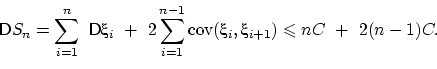Пример 55.
Монета подбрасывается 10000 раз. Оценим вероятность того, что
частота выпадения герба отличается от половины более чем на 0,01.
Требуется оценить
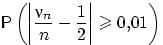 , где
, где 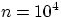 ,
, 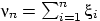 — число выпадений герба, а
— число выпадений герба, а
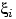 — независимые случайные величины, каждая из которых имеет
распределение Бернулли с параметром 1/2 и равна
единице, если при соответствующем подбрасывании выпал герб, и нулю иначе.
Поскольку
— независимые случайные величины, каждая из которых имеет
распределение Бернулли с параметром 1/2 и равна
единице, если при соответствующем подбрасывании выпал герб, и нулю иначе.
Поскольку 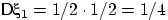 , искомая оценка сверху
выглядит так:
, искомая оценка сверху
выглядит так:
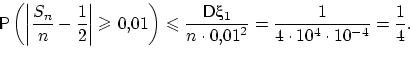
Иначе говоря, неравенство Чебышёва позволяет заключить,
что в среднем не более чем в четверти случаев при 10000 подбрасываниях
монеты частота выпадения герба будет отличаться от 1/2 на одну сотую или больше.
Мы увидим, насколько это грубая оценка, когда познакомимся с
центральной предельной теоремой.
Пример 56.
Пусть
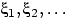
— последовательность
случайных
величин,
дисперсии которых ограничены одной и той же постоянной
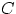
, а
ковариации любых двух
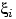
и
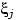
(
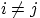
), не являющихся соседними в последовательности,
равны нулю.
Удовлетворяет ли эта последовательность ЗБЧ?
Воспользуемся подходящим неравенством в (24)
и свойством 14:
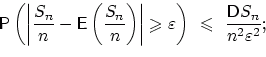
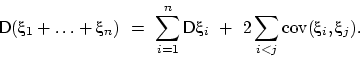 | (26) |
Но при 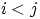 по условию
по условию 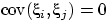 для
для 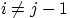 .
Следовательно, все ковариации в равенстве (26) равны нулю,
кроме, может быть,
.
Следовательно, все ковариации в равенстве (26) равны нулю,
кроме, может быть, 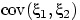 ,
, 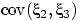 , ...,
, ..., 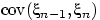 (их ровно
(их ровно 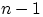 штука).
штука).
Оценим каждую из них, используя тот факт, что коэффициент корреляции
по модулю не превосходит единицы:
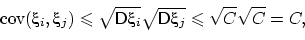
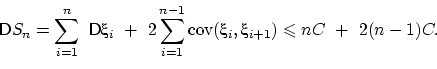
Получаем, что последовательность  удовлетворяет ЗБЧ, так как
удовлетворяет ЗБЧ, так как
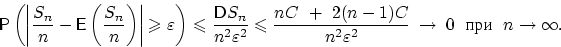
![]() , где
, где ![]() ,
, ![]() — число выпадений герба, а
— число выпадений герба, а
![]() — независимые случайные величины, каждая из которых имеет
распределение Бернулли с параметром 1/2 и равна
единице, если при соответствующем подбрасывании выпал герб, и нулю иначе.
Поскольку
— независимые случайные величины, каждая из которых имеет
распределение Бернулли с параметром 1/2 и равна
единице, если при соответствующем подбрасывании выпал герб, и нулю иначе.
Поскольку ![]() , искомая оценка сверху
выглядит так:
, искомая оценка сверху
выглядит так: