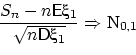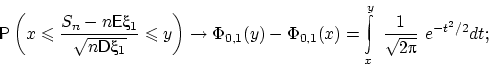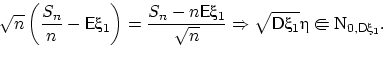Мы будем называть следующее утверждение «ЦПТ Ляпунова
(1)»,
но сформулируем и докажем теорему Ляпунова только в частном случае — для последовательности
независимых и
одинаково распределённых случайных величин.
Как и ранее, через
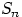
обозначена сумма первых
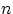
случайных величин в последовательности:
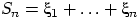
.
Пользуясь
определением и свойствами слабой сходимости,
и заметив, что
функция распределения 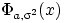
любого нормального закона
непрерывна всюду на
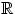
(
почему?), утверждение ЦПТ можно сформулировать любым из следующих способов:
Мы докажем ЦПТ и ЗБЧ в форме Хинчина чуть
позднее. Нам потребуется для этого познакомиться с мощным
математическим инструментом, который в математике обычно называют
«преобразованиями Фурье»,
а в теории вероятностей — «характеристическими функциями».
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.