next up previous contents index
Next:  Свойства характеристических функций   Up:  Характеристические функции   Previous:  Характеристические функции

§ 1. Примеры вычисления

Пример 59. Пусть случайная величина имеет распределение Бернулли с параметром . Её характеристическая функция равна

Пример 60. Пусть случайная величина имеет биномиальное распределение с параметрами и . Её характеристическая функция равна

Последнее равенство есть бином Ньютона.

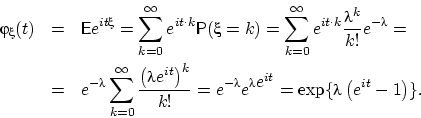
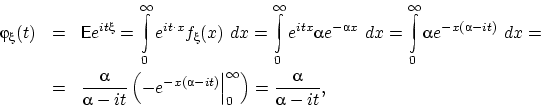
Пример 61. Пусть случайная величина имеет распределение Пуассона с параметром . Её характеристическая функция равна

Пример 62. Пусть случайная величина имеет показательное распределение с параметром . Её характеристическая функция равна

поскольку при модуль величины стремится к нулю: .

Пример 63. Пусть случайная величина имеет гамма-распределение с параметрами и . Её характеристическая функция равна

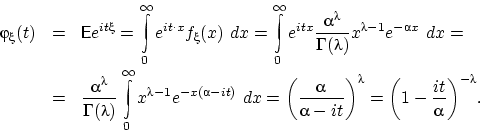
Интеграл мы вычислили с помощью гамма-функции: замена даёт

Пример 64. Пусть случайная величина имеет стандартное нормальное распределение. Её характеристическая функция равна

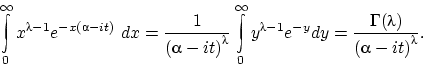
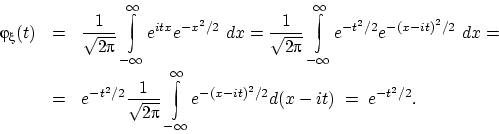
Как всегда, при интегрировании мы выделили полный квадрат в показателе экспоненты и вспомнили, чему равен интеграл по всей прямой от функции (а чему он равен?).

Самое время остановиться и спросить: «Ну и что? Зачем нам эти функции и какой от них прок?» Приглашаю читателя познакомиться с замечательными свойствами характеристических функций.

N.Ch.