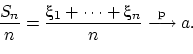
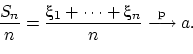
![]()
Найдём характеристическую функцию случайной величины ![]() .
Пользуясь свойствами (Ф3) и (Ф4), получим
.
Пользуясь свойствами (Ф3) и (Ф4), получим
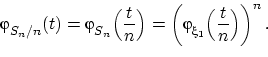
Вспомним, что первый момент ![]() существует, поэтому свойство (Ф6) позволяет
разложить
существует, поэтому свойство (Ф6) позволяет
разложить ![]() в ряд Тейлора в окрестности нуля:
в ряд Тейлора в окрестности нуля:
![]()
В точке ![]() , соответственно,
, соответственно,
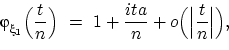
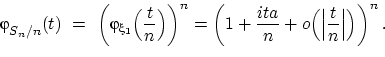
При ![]() , пользуясь «замечательным пределом»
, пользуясь «замечательным пределом»
![]() , получим
, получим
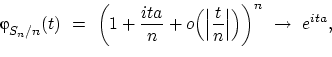
что и требовалось доказать.
QED
N.Ch.