В этом примере мы построим множество на отрезке, «длина» которого не существует. Нам понадобятся лишь следующие очевидные свойства «длины» множества: длина множества остается неизменной при сдвиге всех точек этого множества; длина множества, составленного из счётного объединения попарно непересекающихся множеств, равняется сумме длин этих множеств.

Рассмотрим окружность единичного радиуса (то же, что отрезок ). Возьмём любое иррациональное число . Поскольку оно иррационально, число не является целым ни при каком целом (т.е. число равно лишь при ).

Поэтому если взять произвольную точку на окружности и перечислить все точки, которые получаются поворотом точки на угол , , то мы ни разу не вернёмся в точку . Точек, получившихся из точки такими поворотами, счётное число. Объединим их в один класс точек. С любой другой точкой окружности можно тоже связать класс точек, получающихся из неё поворотами на при целых . Таким образом, вся окружность разбивается на классы точек. В каждом классе счётное число точек, и все точки в одном классе получаются друг из друга такими поворотами. Разные классы не пересекаются. Заметим, что таких классов несчётное число, т.к. объединением счётного числа счётных множеств нельзя получить несчётное число точек окружности (доказать, что объединение счётного числа счётных множеств счётно!).

Искомое множество определим так: возьмём из каждого такого класса ровно по одной точке. Пусть множество получается поворотом всех точек множества на угол , .

Так как все точки одного класса можно получить, поворачивая любую из них на угол , , а в множестве собрано по одной точке из каждого класса, то поворачивая это множество, получим все точки окружности.

Очевидно, что . Предположим, что «длина» множества существует. Тогда все множества имеют ту же длину, так как получены из поворотом. И так как все эти множества не пересекаются, то «длина» их объединения равна сумме их длин:

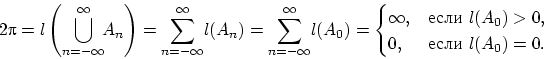
Полученное противоречие означает, что длина множества просто не существует.