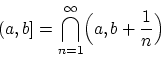Next: Мера и вероятностная мера
Up: Аксиоматика теории вероятностей
Previous: Аксиоматика теории вероятностей
Пусть

— пространство элементарных исходов
некоторого случайного эксперимента (т.е. непустое множество
произвольной природы). Мы собираемся определить набор подмножеств

, которые будут называться событиями, и
затем задать вероятность как функцию, определённую
только на
множестве событий (
каждый третий студент 1 курса ЭФ не знает, что такое область определения функции. А вы знаете?).
Итак, событиями мы будем называть не любые подмножества
 , а лишь элементы некоторого выделенного
набора подмножеств
, а лишь элементы некоторого выделенного
набора подмножеств  . При этом необходимо позаботиться,
чтобы этот набор подмножеств был
замкнут относительно введённых в параграфе 2 главы 1
операций над событиями, т.е. чтобы объединение, пересечение,
дополнение событий снова давало событие. Сначала введём понятие алгебры событий.
. При этом необходимо позаботиться,
чтобы этот набор подмножеств был
замкнут относительно введённых в параграфе 2 главы 1
операций над событиями, т.е. чтобы объединение, пересечение,
дополнение событий снова давало событие. Сначала введём понятие алгебры событий.
Определение 10.
Множество

, элементами которого являются подмножества множества

(не обязательно все) называется
алгеброй (алгеброй событий), если оно удовлетворяет следующим условиям:
(A1) 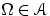 (алгебра событий содержит достоверное событие);
(алгебра событий содержит достоверное событие);
(A2) если  , то
, то  (вместе с любым событием алгебра содержит противоположное
событие);
(вместе с любым событием алгебра содержит противоположное
событие);
(A3) если  и
и  , то
, то
 (вместе с любыми двумя событиями алгебра содержит их объединение).
(вместе с любыми двумя событиями алгебра содержит их объединение).
Из свойств
(A1) и
(A2) следует, что пустое множество

также содержится в

.
Из (A3) следует, что вместе с любым конечным
набором событий алгебра содержит их объединение: для любого  ,
для любых
,
для любых  , ...,
, ...,  выполнено
выполнено  .
.
Вместо замкнутости относительно операции объединения можно требовать
замкнутость относительно операции пересечения.
Свойство 1.
Свойство
(A3) в определении
10
можно заменить на
(A4) если  и
и  , то
, то
 .
.
Доказательство.
Докажем, что при выполнении
(A1) и
(A2) из
(A3) следует
(A4).
Если

,

, то

,

по свойству
(A2). Тогда из
(A3) следует, что

,
и, по
(A2), дополнение

к этому множеству также принадлежит

.
В силу формул двойственности, дополнение
к объединению как раз и есть пересечение дополнений:

Аналогично доказывается, что при выполнении (A1) и (A2) из (A4) следует (A3),
т.е. эти два свойства в определении взаимозаменяемы.
Пример 11.
Пусть

— пространство элементарных
исходов. Следующие наборы подмножеств

являются алгебрами (проверьте это по определению):
1.  — тривиальная алгебра.
— тривиальная алгебра.
2.  .
.
3.  ,
где
,
где  — произвольное подмножество
— произвольное подмножество  (в предыдущем примере
(в предыдущем примере  ).
).
4.  — множество всех подмножеств
— множество всех подмножеств  .
.
Упражнение 11.
Доказать, что если

состоит из

элементов,
то в множестве всех его подмножеств ровно

элементов.
В теории вероятностей часто возникает необходимость объединять счётные наборы
событий и считать событием результат такого объединения.
При этом свойства (A3) алгебры оказывается недостаточно: из него не вытекает,
что объединение счётной последовательности
множеств из алгебры снова принадлежит алгебре. Поэтому разумно наложить
более суровые ограничения на класс событий.
Упражнение 12.
- а)
- Доказать, что вместо (S1) достаточно предположить непустоту
множества
 .
.
- б)
- Вывести из (S1) и (S2), что
 .
.
Этого набора аксиом достаточно для замкнутости множества

относительно счётного числа любых других операций над событиями.
В частности, аналогично
свойству 1 проверяется
следующее свойство.
Свойство 2.
Свойство
(S3) в
определении 11
можно заменить на
(S4) если  ,
,  , то
, то
 .
.
Как показывает следующее свойство, всякая

-алгебра автоматически является алгеброй.
Свойство 3.
Если

—

-алгебра,
то она удовлетворяет свойству
(A3), т.е. для любых

и

выполняется

.
Доказательство.
Превратим пару

в счётную последовательность событий так:

, т.е. положим

,

при всех

.
Объединение

совпадает с объединением
всех множеств

из этой бесконечной последовательности. А так как

—

-алгебра, то

Упражнение 13.
Докажите, что для любых

выполнено

.
Обратное, вообще говоря, неверно: не всякая алгебра является сигма-алгеброй.
Чтобы показать это, приведём пример алгебры, не являющейся

-алгеброй.
Пример 12.
Пусть

,
и пусть

— множество, содержащее любые
конечные подмножества

(т.е. состоящие из конечного числа точек, в том числе пустое)
и их дополнения. В частности, множество

принадлежит

, множество

также принадлежит

.
Легко проверить, что множество  является алгеброй.
Действительно, пустое множество и само
является алгеброй.
Действительно, пустое множество и само  там содержатся,
дополнение к любому конечному подмножеству множества вещественных
чисел содержится в
там содержатся,
дополнение к любому конечному подмножеству множества вещественных
чисел содержится в  по определению,
дополнение к множеству вида
по определению,
дополнение к множеству вида  для конечных
для конечных  совпадает с
совпадает с  и также принадлежит
и также принадлежит  по определению. Свойство (A3)
проверяется непосредственно: объединение любых конечных множеств снова конечно
и поэтому принадлежит
по определению. Свойство (A3)
проверяется непосредственно: объединение любых конечных множеств снова конечно
и поэтому принадлежит  . Объединение конечного множества
с множеством вида
. Объединение конечного множества
с множеством вида  , где
, где  конечно, есть снова множество
вида
конечно, есть снова множество
вида  , где
, где  конечно (или пусто). Объединение двух множеств
конечно (или пусто). Объединение двух множеств  и
и
 , являющихся дополнениями до
, являющихся дополнениями до  конечных множеств
конечных множеств  и
и  , есть снова множество такого же вида.
, есть снова множество такого же вида.
Однако алгебра  не содержит ни одного счётного множества
точек. Действительно, объединяя конечные множества в конечном числе, мы можем
получить только конечное множество. Например, натуральный ряд
не содержит ни одного счётного множества
точек. Действительно, объединяя конечные множества в конечном числе, мы можем
получить только конечное множество. Например, натуральный ряд  не принадлежит
не принадлежит  . Поэтому
. Поэтому  не является
не является  -алгеброй:
для бесконечной, но счётной последовательности одноточечных множеств
-алгеброй:
для бесконечной, но счётной последовательности одноточечных множеств  из
из  их объединение
их объединение  не принадлежит
не принадлежит  .
.
Все алгебры из
примера 11 являются

-алгебрами, поскольку
содержат лишь конечное число элементов. Вообще, на конечном множестве

понятия алгебры и

-алгебры совпадают. Множество
всех подмножеств

является

-алгеброй для любого

.
Борелевская(1)  -алгебра в
-алгебра в  .
.
Приведём пример

-алгебры, которая
нам будет необходима в дальнейшем, —

-алгебры
борелевских множеств на вещественной прямой.
Борелевской сигма-алгеброй в  называется самая маленькая среди
всех возможных
называется самая маленькая среди
всех возможных  -алгебр, содержащих любые интервалы на прямой.
Разумеется,
-алгебр, содержащих любые интервалы на прямой.
Разумеется,  -алгебры, содержащие все интервалы, существуют. Например,
таково множество всех подмножеств
-алгебры, содержащие все интервалы, существуют. Например,
таково множество всех подмножеств  .
Чтобы сделать эти слова — про самую маленькую
.
Чтобы сделать эти слова — про самую маленькую  -алгебру — понятными, поработаем с примерами.
-алгебру — понятными, поработаем с примерами.
Пример 13.
Пусть

— вещественная прямая.
Рассмотрим некоторые наборы множеств, не являющиеся

-алгебрами, и увидим, как их можно дополнить до

-алгебр.
1. Множество  не является
не является  -алгеброй, так как, например,
-алгеброй, так как, например,
 . Самый маленький набор множеств, содержащий
. Самый маленький набор множеств, содержащий  и являющийся
и являющийся
 -алгеброй (минимальная
-алгеброй (минимальная  -алгебра),
получится, если включить в него всевозможные
объединения, пересечения и дополнения множеств из
-алгебра),
получится, если включить в него всевозможные
объединения, пересечения и дополнения множеств из  :
:
 .
.
Более точно:
Определение 12.
Минимальной 
-алгеброй, содержащей некоторый
набор множеств

, называется пересечение
всех

-алгебр, содержащих

.
Ещё раз напомним, что пересекать в
определении 12 есть что: хотя бы одна

-алгебра, содержащая данный набор множеств, всегда найдётся — это

-алгебра всех подмножеств

.
Упражнение 14.
Доказать, что пересечение двух

-алгебр, содержащих
набор множеств

, снова является

-алгеброй (
невероятно!), содержащей

.
Упражнение 15.
Найти минимальную

-алгебру, содержащую следующий набор подмножеств

:

.
2.
Пусть множество

подмножеств вещественной прямой

состоит из всевозможных открытых интервалов

, где

:

Определение 13.
Минимальная

-алгебра, содержащая множество

всех интервалов на вещественной прямой,
называется
борелевской сигма-алгеброй в

и обозначается

.
Перечислим некоторые множества на прямой, содержащиеся
в

по определению. Таковы все привычные нам множества. Чтобы получить
множество, не содержащееся в

,
требуются специальные построения.
Итак, мы знаем, что все интервалы на прямой принадлежат  ,
и
,
и  —
—  -алгебра. Отсюда сразу следует, что
-алгебра. Отсюда сразу следует, что
 содержит любое множество,
которое можно получить из интервалов с помощью счётного числа операций объединения
или пересечения, а также взятием дополнения.
содержит любое множество,
которое можно получить из интервалов с помощью счётного числа операций объединения
или пересечения, а также взятием дополнения.
В частности,

принадлежит

.
Доказательство. Это сразу следует из свойства
(S1) 
-алгебры,
но может быть доказано и исходя из свойств
(S2),
(S3).
Интервал

принадлежит

, а значит, принадлежит и

при любом

, т.е.

.
Но

—

-алгебра, и содержит счётное объединение любых своих элементов, поэтому

Далее, любой интервал вида

(или

, или

),
где

, принадлежит

.
Доказательство. Интервал

принадлежит

при любом

.
Тогда счётное пересечение этих интервалов
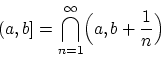
по свойству
(S4) также принадлежит

.
Любое одноточечное подмножество

принадлежит

.
Доказательство. Действительно,

, а разность

двух множеств из

-алгебры снова принадлежит

-алгебре.
Упражнение 17.
Докажите, что множества вида

принадлежат

, что
множество натуральных чисел

принадлежит

,
множество рациональных чисел

принадлежит

.
3.
Борелевская

-алгебра в

строится совершенно
так же, как в

. Это должна быть минимальная

-алгебра, содержащая все множества
вида

— уже не интервалы, как в

,
а прямоугольники в

, параллелепипеды в

и т.д.
Вместе с ними

содержит
любые множества, являющиеся «предельными» для объединений измельчающихся
прямоугольников. Например, круг в

является борелевским множеством —
можно изнутри или снаружи приблизить его объединениями прямоугольников.
Итак, мы определили специальный класс

подмножеств пространства
элементарных исходов

, названный

-алгеброй событий,
причём применение счётного числа любых операций
(объединений, пересечений, дополнений)
к множествам из

снова дает множество
из

, т.е. не выводит за рамки этого класса.
Событиями будем называть
только множества

.
Определим теперь понятие вероятности как функции, определённой
на множестве событий (функции, которая каждому событию ставит в соответствие число — вероятность этого события).
А чтобы читателю сразу стало понятно, о чём пойдёт речь, добавим: вероятность мы определим как
неотрицательную нормированную меру, заданную на  -алгебре
-алгебре  подмножеств
подмножеств  .
. 
Следующий параграф познакомит нас с понятиями меры и вероятностной меры.





Next: Мера и вероятностная мера
Up: Аксиоматика теории вероятностей
Previous: Аксиоматика теории вероятностей
1
Félix Edouard Justin Emile Borel (7.01.1871 — 3.02.1956, France)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
N.Ch.
![]() , а лишь элементы некоторого выделенного
набора подмножеств
, а лишь элементы некоторого выделенного
набора подмножеств ![]() . При этом необходимо позаботиться,
чтобы этот набор подмножеств был
замкнут относительно введённых в параграфе 2 главы 1
операций над событиями, т.е. чтобы объединение, пересечение,
дополнение событий снова давало событие. Сначала введём понятие алгебры событий.
. При этом необходимо позаботиться,
чтобы этот набор подмножеств был
замкнут относительно введённых в параграфе 2 главы 1
операций над событиями, т.е. чтобы объединение, пересечение,
дополнение событий снова давало событие. Сначала введём понятие алгебры событий.