Мера и вероятностная мера

Next: Условная вероятность, независимость Up: Аксиоматика теории вероятностей Previous: Алгебра и сигма-алгебра событий

§ 2. Мера и вероятностная мера

Мера как неотрицательная -аддитивная функция множеств

Определение 14. Пусть

— некоторое множество и

—

-алгебра его подмножеств. Функция

называется мерой на

, если она удовлетворяет условиям:

(1) для любого множества его мера неотрицательна: ;

(2) для любого счётного набора попарно непересекающихся множеств (т.е. такого, что при всех ) мера их объединения равна сумме их мер:

(«счётная аддитивность» или «сигма-аддитивность» меры).

Пример 14.

Пусть , — множество всех подмножеств . Зададим меру на так: , , , , , , , . Для краткости записи мы вместо писали всюду .

Пример 15.

Пусть , — множество всех подмножеств натурального ряда. Зададим меру на так: — число элементов в множестве (или бесконечность, если множество не является конечным).

Пример 16 (мера Лебега⁽¹⁾). Когда мы говорили о геометрической вероятности, мы использовали термин «мера области

», имея в виду «длину» на прямой, «площадь» на плоскости, «объем» в трёхмерном пространстве. Являются ли все эти «длины-площади-объемы» настоящими мерами в смысле определения 14? Мы решим этот вопрос для прямой, оставляя плоскость и пространство большей размерности читателю.

Замечание 6.

Если вам уже расхотелось читать дальше, сообщаем: мерой Лебега в задачниках и учебниках называют как раз «длину-площадь-объем», так что всё в порядке, дальнейшее до параграфа 2 можно смело пропустить.

Рассмотрим вещественную прямую с

-алгеброй борелевских множеств. Эта

-алгебра, по определению, есть наименьшая

-алгебра, содержащая любые интервалы. Для каждого интервала

число

назовём длиной интервала

Мы не станем доказывать следующее утверждение:

Лемма 1. Существует единственная мера

на

, значение которой на любом интервале равно его длине:

. Эта мера называется мерой Лебега.

Замечание 7. Это утверждение является следствием теоремы Каратеодори⁽²⁾ о продолжении меры с алгебры на

-алгебру, применительно к

. Пользуясь процедурой лебеговского продолжения (пополнения) меры, можно распространить меру

на более широкую

-алгебру, нежели борелевская, — на

-алгебру измеримых по Лебегу множеств. Для этого достаточно присвоить нулевую меру любым подмножествам борелевских множеств с нулевой мерой Лебега.

Нам пригодится свойство, которым обладает любая мера. Это свойство непрерывности меры иногда называют аксиомой непрерывности, имея в виду, что ею можно заменить (

2) в определении 14.

Лемма 2 (непрерывность меры). Пусть дана убывающая последовательность

вложенных друг в друга множеств из

такая, что

. Тогда

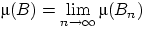
Доказательство.

Обозначим через

кольца:

. Множества

попарно не пересекаются. Тогда из представлений

в силу аксиомы (2) следует, что

Первая сумма в силу условия есть сумма абсолютно сходящегося ряда (составленного из неотрицательных слагаемых). Из сходимости этого ряда следует, что «хвост» ряда, равный , стремится к нулю при . Поэтому

QED

В полезности этого свойства легко убедиться упражнениями.

Упражнение 18.

Используя аксиому непрерывности меры для множеств , доказать, что мера Лебега одноточечного подмножества вещественной прямой равна нулю: . Используя этот факт, доказать, что , , , .

Замечание. В отсутствие предположения

(или

для некоторого

), заставляющего меры вложенных множеств быть конечными, свойство

может не выполняться.

Например, зададим меру на так: , если не более чем счётно, иначе . Тогда для множеств имеем:

И вот наконец мы в состоянии определить понятие вероятности.

Вероятность как нормированная мера.

Определение 15. Пусть

— множество и

—

-алгебра его подмножеств. Мера

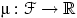
называется нормированной, если

. Другое название нормированной меры — вероятность или вероятностная мера.

То же самое ещё раз и подробно:

Определение 16. Пусть

— пространство элементарных исходов,

—

-алгебра его подмножеств (событий). Вероятностью или вероятностной мерой на

называется функция

, обладающая свойствами:

(P1) для любого события выполняется неравенство ;

(P2) для любого счётного набора попарно несовместных событий имеет место равенство

(P3) вероятность достоверного события равна единице: .

Свойства (P1) — (P3) называют аксиомами вероятности.

Определение 17. Тройка

, в которой

— пространство элементарных исходов,

—

-алгебра его подмножеств и

— вероятностная мера на

, называется вероятностным пространством.

Докажем свойства вероятности, вытекающие из аксиом. Ниже мы не будем всякий раз оговаривать, но будем иметь в виду, что имеем дело только с событиями.

Свойство 0.

Доказательство. События

, где

, попарно несовместны, и их объединение есть также пустое множество. По аксиоме (P2),

Это возможно только в случае .

Аксиома счётной аддитивности вероятности (P2) тем более верна для конечного набора попарно несовместных событий.

Свойство 1. Для любого конечного набора попарно несовместных событий

имеет место равенство

Доказательство. Положим

при любом

. Вероятности этих событий, по свойству 0, равны нулю. События

попарно несовместны, и по аксиоме (P2),

Сразу несколько следствий можно получить из этого свойства.

Свойство 2. Для любого события

выполнено:

Доказательство. Поскольку

, и события

несовместны, из аксиомы (P3) и свойства 1 получим

Свойство 3. Если

, то

Доказательство. Представим

в виде объединения двух несовместных событий:

. По свойству 1,

Сразу же заметим, что по аксиоме (P1) выражение в правой части равенства

больше либо равно

, что доказывает следующее свойство монотонности вероятности.

Свойство 4. Если

, то

Свойство 5. Для любого события

выполнено:

Доказательство.

по (P1). А так как

, то

Свойство 6. Всегда

Доказательство. Имеем

, поэтому

по свойству 3 Но

, причём

несовместны. Снова пользуясь свойством 1, получим:

Из этого свойства и аксиомы (P1) следуют два полезных свойства. Свойство 8 читатель докажет с помощью свойства 7.

Свойство 7. Всегда

Свойство 8. Совершенно всегда

Следующее свойство называют формулой включения и исключения. Она оказывается весьма полезной в случае, когда для вычисления вероятности некоторого события

нельзя разбить это событие на удобные попарно несовместные события, но удаётся разбить событие

на простые составляющие, которые, однако, совместны.

Свойство 9. Для любого конечного набора событий

имеет место равенство:

(2)

Доказательство. Воспользуемся методом математической индукции. Базис индукции при

— свойство 6. Пусть свойство 9 верно при

. Докажем, что тогда оно верно при

. По свойству 6,

(3)

По предположению индукции, первое слагаемое в правой части (3) равно

(4)

Вычитаемое в правой части (3) равно

(5)

Упражнение 19. Подставить (4), (5) в (3) и довести до конца шаг индукции.

QED

Приведём пример задачи, в которой использование свойства 9 — самый простой путь решения. Это известная «задача о рассеянной секретарше».

Пример 17. Есть

писем и

подписанных конвертов. Письма раскладываются в конверты наудачу по одному. Найти вероятность того, что хотя бы одно письмо попадет в предназначенный ему конверт, и предел этой вероятности при

Решение. Пусть событие , , означает, что -е письмо попало в свой конверт. Тогда

Так как события , , совместны, придётся использовать формулу (2). По классическому определению вероятности вычислим вероятности всех событий и их пересечений. Элементарными исходами будут всевозможные перестановки (размещения) писем по конвертам. Их общее число есть , и событию благоприятны из них, а именно любые перестановки всех писем, кроме -го, лежащего в своём конверте. Поэтому для всех .

Совершенно так же получим, что при любых

Вероятность пересечения любых трёх событий равна

Аналогично посчитаем вероятности пересечений любого другого числа событий, в том числе

Вычислим количество слагаемых в каждой сумме в формуле (2). Например, в сумме по ровно слагаемых — ровно столько трёхэлементных множеств можно образовать из элементов, и каждое такое множество встречается в индексах данной суммы единожды. Подставляя все вероятности в формулу (2), получим:

Упражнение 20. Выписать разложение

в ряд Тейлора и убедиться в том, что

при

¹Henri Léon Lebesgue (28.06.1875 — 26.07.1941, France)

²Constantin Carathéodory (13.09.1873 — 2.02.1950, Germany)

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

N.Ch.