Пример 21.
Есть три завода, производящих одну и ту же продукцию.
При этом первый завод производит 25%,
второй завод — 35% и третий — 40%
всей производимой продукции.
Брак составляет 5% от продукции первого завода, 3% от продукции второго
и 4% от продукции третьего завода.
Вся продукция смешивается и поступает в продажу.
Найти а) вероятность купить бракованное изделие; б) условную вероятность
того, что купленное изделие изготовлено первым заводом, если это изделие
бракованное.
Первая вероятность равна доле бракованных изделий
в объеме всей продукции, т.е.
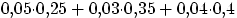 .
Вторая вероятность равна доле брака первого завода
среди всего брака, т.е.
.
Вторая вероятность равна доле брака первого завода
среди всего брака, т.е.
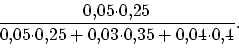
Заметим, что найти эти вероятности можно
безо всякого знания теории вероятностей вообще.
Достаточно элементарного
здравого смысла.
События
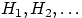
, образующие полную группу событий,
часто называют гипотезами. При подходящем
выборе гипотез для произвольного события
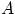
могут быть сравнительно просто
вычислены
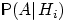
(вероятность событию
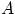
произойти при выполнении «гипотезы»
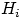
) и собственно
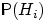
(вероятность выполнения «гипотезы»
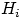
).
Как, используя эти данные, посчитать вероятность события
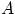
?
![]() .
Вторая вероятность равна доле брака первого завода
среди всего брака, т.е.
.
Вторая вероятность равна доле брака первого завода
среди всего брака, т.е.
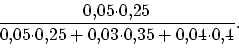
![]() .
Вторая вероятность равна доле брака первого завода
среди всего брака, т.е.
.
Вторая вероятность равна доле брака первого завода
среди всего брака, т.е.
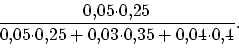
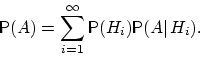
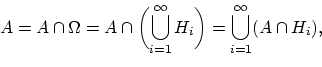
![]() ,
, ![]() попарно несовместны.
Поэтому
попарно несовместны.
Поэтому 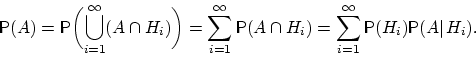
![]() -аддитивность вероятностной меры (а что это?), а в третьем — теорему 6 умножения вероятностей.
-аддитивность вероятностной меры (а что это?), а в третьем — теорему 6 умножения вероятностей.