![]() .
.
QED
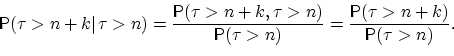 | (7) |
Последнее равенство следует из того, что событие ![]() влечёт событие
влечёт событие ![]() , поэтому пересечение этих
событий есть
, поэтому пересечение этих
событий есть ![]() .
Найдём для целого
.
Найдём для целого ![]() вероятность
вероятность ![]() :
:
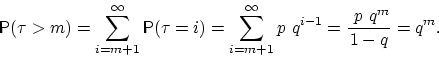
Можно получить ![]() и ещё проще:
событие
и ещё проще:
событие ![]() означает в точности,
что в схеме Бернулли первые
означает в точности,
что в схеме Бернулли первые ![]() испытаний завершились «неудачами»,
т.е. его вероятность равна
испытаний завершились «неудачами»,
т.е. его вероятность равна ![]() .
Возвращаясь к (7), получим
.
Возвращаясь к (7), получим
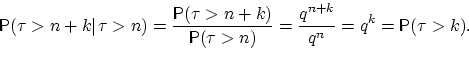
QED
N.Ch.