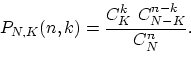
Если число шаров в урне очень велико, то извлечение одного, двух, трёх
шаров почти не меняет пропорцию белых и чёрных шаров в урне, так что
вероятности ![]() не очень отличаются от вероятностей в процедуре
выбора с возвращением:
не очень отличаются от вероятностей в процедуре
выбора с возвращением:
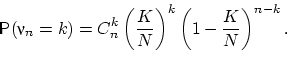
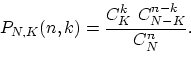
Если число шаров в урне очень велико, то извлечение одного, двух, трёх
шаров почти не меняет пропорцию белых и чёрных шаров в урне, так что
вероятности ![]() не очень отличаются от вероятностей в процедуре
выбора с возвращением:
не очень отличаются от вероятностей в процедуре
выбора с возвращением:
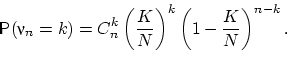
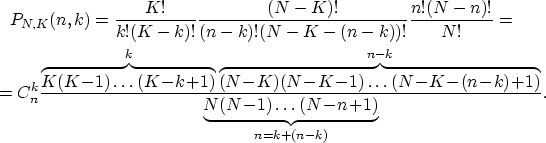
И в числителе, и в знаменателе дроби — произведение фиксированного числа
![]() сомножителей, поэтому и дробь есть произведение
сомножителей, поэтому и дробь есть произведение ![]() сомножителей.
Каждый из первых
сомножителей.
Каждый из первых ![]() сомножителей имеет вид
сомножителей имеет вид ![]() при некоторых
фиксированных
при некоторых
фиксированных ![]() и
и ![]() и стремится к
и стремится к ![]() при
при ![]() .
Каждый из оставшихся
.
Каждый из оставшихся ![]() сомножителей имеет вид
сомножителей имеет вид ![]() и стремится к
и стремится к ![]() при
при ![]() . Окончательно имеем
. Окончательно имеем
![]()
QED
N.Ch.