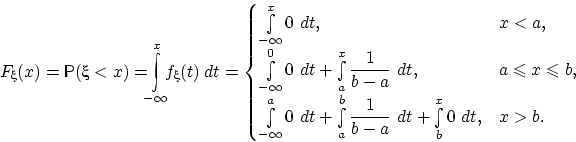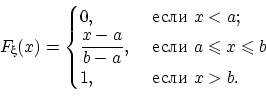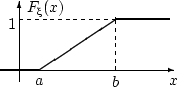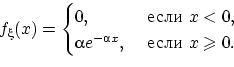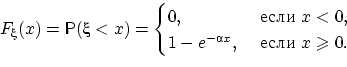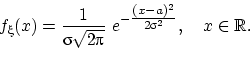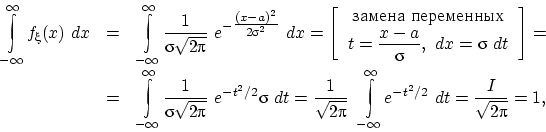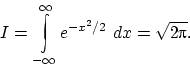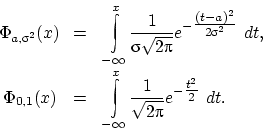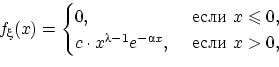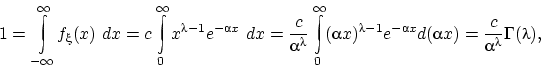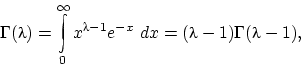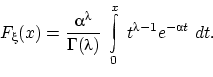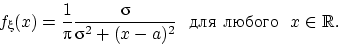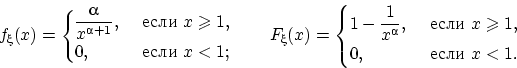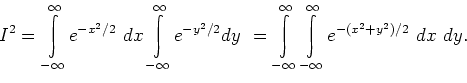Next: Свойства функций распределения
Up: Случайные величины и их
Previous: Примеры дискретных распределений
Говорят, что
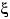
имеет
равномерное распределение на отрезке
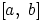
, и пишут:

,
если
плотность распределения 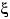
постоянна на отрезке
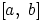
и равна нулю вне него:
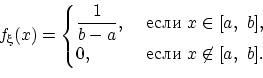
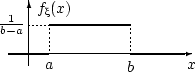
Очевидно, что площадь под графиком этой функции равна единице и 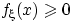 .
Поэтому
.
Поэтому 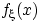 является плотностью распределения.
является плотностью распределения.
Случайная величина  имеет
смысл координаты точки, выбранной наудачу на отрезке
имеет
смысл координаты точки, выбранной наудачу на отрезке 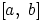 .
Вычислим по определению 30 функцию распределения случайной величины
.
Вычислим по определению 30 функцию распределения случайной величины 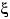 :
:
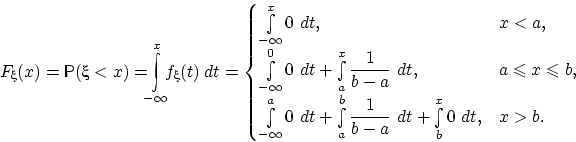
Получим следующую непрерывную функцию распределения:
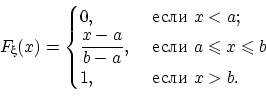
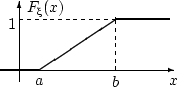
Говорят, что
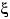
имеет
показательное (экспоненциальное) распределение с параметром
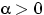
, и пишут:
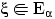
,
если
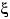
имеет следующую
плотность распределения:
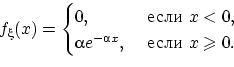
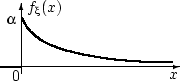
Функция распределения случайной величины 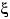 непрерывна:
непрерывна:
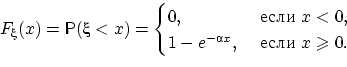
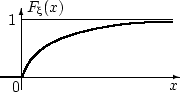
Показательное распределение является единственным абсолютно непрерывным
распределением, для которого выполнено свойство «нестарения»
(и в этом смысле оно является непрерывным
аналогом дискретного геометрического распределения).
Теорема 19.
Пусть
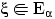
. Тогда для любых
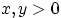
 | (11) |
Упражнение 27.
Доказать
теорему 19.
Доказать далее, что если неотрицательная случайная величина
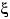
с абсолютно
непрерывным распределением обладает свойством
(11) при любых
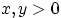
,
то она имеет показательное распределение с некоторым параметром
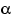
.
Говорят, что
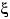
имеет
гамма-распределение с параметрами
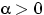
,
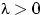
,
и пишут:
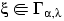
,
если
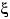
имеет следующую
плотность распределения:
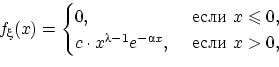
где постоянная 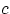 вычисляется из свойства (f2) плотности так:
вычисляется из свойства (f2) плотности так:
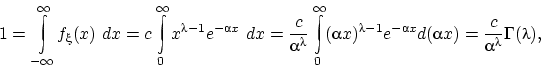
откуда 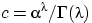 .
Здесь через
.
Здесь через 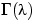 обозначен интеграл
обозначен интеграл
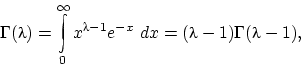
называемый гамма-функцией Эйлера(3); 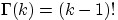 при целых
положительных
при целых
положительных 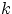 ,
, 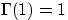 .
Замена в интеграле Пуассона даст
.
Замена в интеграле Пуассона даст 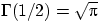 .
.
Показательное распределение — частный случай гамма-распределения:
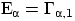 .
.
Упражнение 28.
Нарисовать график плотности распределения
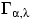
при
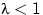
, при
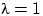
и при
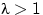
, отметить на этом графике точки экстремума,
точки перегиба и иные особенности графика.
Функцию распределения гамма-распределения можно записать, вообще говоря,
только в виде интеграла:
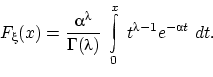
Но при целых значениях параметра 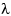 интегрированием по частям
этот интеграл можно превратить в сумму:
интегрированием по частям
этот интеграл можно превратить в сумму:
 | (12) |
Упражнение 29.
Доказать первое из равенств
(12)
при целых значениях
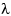
.
Доказать следующее забавное равенство:
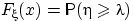
,
где
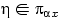
.
Говорят, что
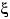
имеет
распределение Коши(4)
с параметрами
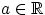
,
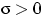
,
и пишут:
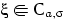
,
если
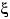
имеет следующую плотность распределения:
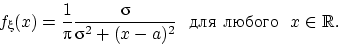
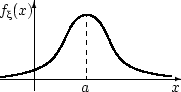
Плотность распределения Коши симметрична относительно прямой 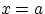 и похожа на плотность нормального распределения,
но имеет более толстые «хвосты» на
и похожа на плотность нормального распределения,
но имеет более толстые «хвосты» на 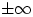 .
Функция распределения случайной величины
.
Функция распределения случайной величины 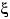 с распределением Коши
равна
с распределением Коши
равна 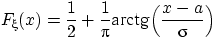 при всех
при всех 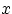 .
.
Говорят, что
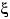
имеет
распределение Парето(5) с параметром
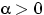
,
если
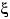
имеет следующие
плотность и
функцию распределения:
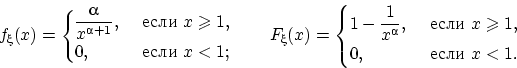
Часто рассматривают более широкий класс распределений
Парето, сосредоточенных не на 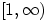 , а на
, а на 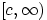 при
при 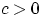 .
.
С другими абсолютно непрерывными распределениями (хи-квадрат
Пирсона, распределениями Стьюдента, Фишера, Колмогорова, Лапласа) мы познакомимся при изучении
математической статистики. С распределениями Вейбулла, логарифмически
нормальным и некоторыми другими читатель познакомится в дальнейших курсах.





Next: Свойства функций распределения
Up: Случайные величины и их
Previous: Примеры дискретных распределений
1Johann Carl Friedrich Gauss (30.04.1777 — 23.02.1855, Germany)
2Этот интеграл вычисляется так:
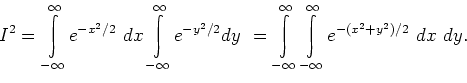
Далее полярная замена переменных: 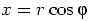 ,
,
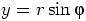 ,
, 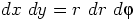 ,
, 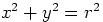 :
:

3Leonhard Euler (15.04.1707 — 18.09.1783, Switzerland, Россия)
4Augustin Louis Cauchy (21.08.1789 — 23.05.1857, France)
5Vilfredo Pareto (15.07.1848 — 20.08.1923, France, Italy, Switzerland)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
N.Ch.
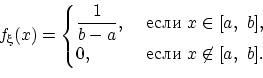
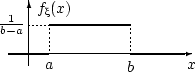
![]() .
Поэтому
.
Поэтому ![]() является плотностью распределения.
является плотностью распределения.
![]() имеет
смысл координаты точки, выбранной наудачу на отрезке
имеет
смысл координаты точки, выбранной наудачу на отрезке ![]() .
Вычислим по определению 30 функцию распределения случайной величины
.
Вычислим по определению 30 функцию распределения случайной величины ![]() :
: