Пусть задано вероятностное пространство
![]() .
.
Пусть задано вероятностное пространство
![]() .
.
Если задана случайная величина ![]() , нам может потребоваться вычислить
вероятности вида
, нам может потребоваться вычислить
вероятности вида ![]() ,
,
![]() ,
, ![]() ,
,
![]() (и вообще самые разные
вероятности попадания в борелевские множества на прямой).
Это возможно лишь если множества, стоящие под знаком вероятности,
являются событиями — ведь
вероятность есть функция, определённая только на
(и вообще самые разные
вероятности попадания в борелевские множества на прямой).
Это возможно лишь если множества, стоящие под знаком вероятности,
являются событиями — ведь
вероятность есть функция, определённая только на ![]() -алгебре событий.
Требование измеримости равносильно тому, что для любого борелевского множества
-алгебре событий.
Требование измеримости равносильно тому, что для любого борелевского множества
![]() определена вероятность
определена вероятность ![]() .
.
Можно потребовать в определении 26 чего-нибудь другого.
Например, чтобы событием было попадание в любой интервал:
![]() ,
или в любой полуинтервал:
,
или в любой полуинтервал: ![]() .
.
Если ![]() — случайная величина в смысле определения 26, то
она будет случайной величиной и в смысле определения 27,
поскольку любой интервал
— случайная величина в смысле определения 26, то
она будет случайной величиной и в смысле определения 27,
поскольку любой интервал ![]() является борелевским множеством.
является борелевским множеством.
Докажем, что верно и обратное.
Пусть для любого интервала ![]() выполнено
выполнено ![]() .
Мы должны доказать, что то же самое верно и для любых борелевских множеств.
.
Мы должны доказать, что то же самое верно и для любых борелевских множеств.
Соберём в множестве ![]() все подмножества вещественной прямой, прообразы которых являются
событиями. Множество
все подмножества вещественной прямой, прообразы которых являются
событиями. Множество ![]() уже содержит все интервалы
уже содержит все интервалы ![]() .
Покажем теперь, что множество
.
Покажем теперь, что множество ![]() является
является ![]() -алгеброй.
По определению,
-алгеброй.
По определению, ![]() тогда и только тогда, когда множество
тогда и только тогда, когда множество
![]() принадлежит
принадлежит ![]() .
.
1. Убедимся, что ![]() .
Но
.
Но ![]() и, следовательно,
и, следовательно, ![]() .
.
2. Убедимся, что ![]() для любого
для любого ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда
![]() , так как
, так как ![]() —
— ![]() -алгебра.
-алгебра.
3. Убедимся, что ![]() для любых
для любых
![]() .
Пусть
.
Пусть ![]() для всех
для всех ![]() . Но
. Но ![]() —
— ![]() -алгебра, поэтому
-алгебра, поэтому
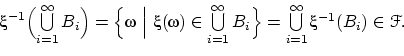
Мы доказали, что ![]() —
— ![]() -алгебра и содержит все интервалы
на прямой. Но
-алгебра и содержит все интервалы
на прямой. Но ![]() — наименьшая из
— наименьшая из ![]() -алгебр, содержащих все интервалы на прямой. Следовательно,
-алгебр, содержащих все интервалы на прямой. Следовательно,
![]() содержит
содержит ![]() :
: ![]() .
.
QED
1. Если ![]() есть множество всех подмножеств
есть множество всех подмножеств
![]() , то
, то ![]() и
и ![]() являются случайными величинами,
поскольку любое множество элементарных исходов принадлежит
являются случайными величинами,
поскольку любое множество элементарных исходов принадлежит ![]() ,
в том числе и
,
в том числе и ![]() или
или
![]() .
Можно записать соответствие между значениями случайных величин
.
Можно записать соответствие между значениями случайных величин
![]() и
и ![]() и вероятностями принимать эти значения в виде
«таблицы распределения вероятностей» или, коротко, «таблицы распределения»:
и вероятностями принимать эти значения в виде
«таблицы распределения вероятностей» или, коротко, «таблицы распределения»:
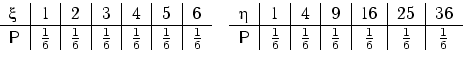
Здесь ![]() .
.
2. Пусть ![]() -алгебра событий
-алгебра событий ![]() состоит из четырёх множеств:
состоит из четырёх множеств:
![]() ,
,
т.е. событием является, кроме достоверного и невозможного событий,
выпадение чётного или нечётного числа очков.
Убедимся, что при такой сравнительно бедной ![]() -алгебре ни
-алгебре ни ![]() , ни
, ни ![]() не являются случайными величинами, поскольку они неизмеримы. Возьмём, скажем,
не являются случайными величинами, поскольку они неизмеримы. Возьмём, скажем, ![]() .
Видим, что
.
Видим, что ![]() и
и ![]() .
.
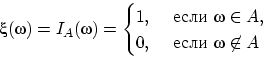
не является случайной величиной, поскольку, например, прообраз единицы
![]() не принадлежит
не принадлежит ![]() .
И вероятность для
.
И вероятность для ![]() попасть в единицу
попасть в единицу ![]() просто не существует.
просто не существует.
N.Ch.