 | (17) |
Убедимся, что эта функция является плотностью распределения:
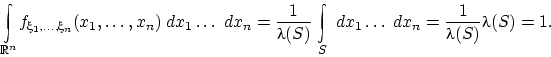
 | (17) |
Убедимся, что эта функция является плотностью распределения:
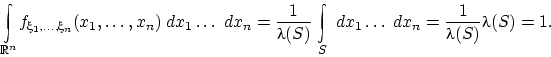
Говорят, что вектор ![]() имеет
многомерное нормальное распределение
имеет
многомерное нормальное распределение ![]() с вектором средних
с вектором средних ![]() и матрицей ковариаций
и матрицей ковариаций ![]() ,
если плотность совместного распределения
,
если плотность совместного распределения ![]() равна
равна

Мы не будем проверять, что эта функция является
плотностью совместного распределения, поскольку для этого требуется
умение заменять переменные в многомерном интеграле.
Выражение ![]() в показателе
экспоненты является квадратичной формой от переменных
в показателе
экспоненты является квадратичной формой от переменных ![]() :
действительно, для матрицы
:
действительно, для матрицы ![]() с элементами
с элементами ![]()
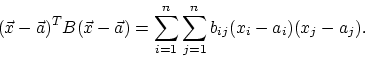
Подробно
с многомерным нормальным распределением мы познакомимся в курсе
математической статистики, и там же выясним, что означают слова
«с вектором средних ![]() и матрицей ковариаций
и матрицей ковариаций ![]() ».
».
В частном случае, когда ![]() — диагональная матрица
с элементами
— диагональная матрица
с элементами ![]() на диагонали, совместная
плотность превращается в произведение плотностей нормальных случайных
величин:
на диагонали, совместная
плотность превращается в произведение плотностей нормальных случайных
величин:
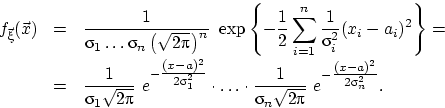
N.Ch.