| (16) |
Доказательство всех этих свойств совершенно аналогично одномерному случаю.
Но теперь свойств (F0)—(F3) не хватает для описания
класса функций совместного распределения. Т.е.
выполнение этих свойств для некоторой функции ![]() не гарантирует, что эта функция является функцией распределения
некоторого случайного вектора.
не гарантирует, что эта функция является функцией распределения
некоторого случайного вектора.
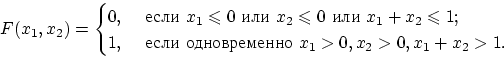
удовлетворяет всем свойствам (F0)—(F3), но
не является функцией распределения никакого вектора ![]() хотя бы потому, что, найдись такой вектор, найдётся и прямоугольник
хотя бы потому, что, найдись такой вектор, найдётся и прямоугольник
![]() , «вероятность» попасть в который
(вычисленная с помощью этой «функции распределения»)
отрицательна:
, «вероятность» попасть в который
(вычисленная с помощью этой «функции распределения»)
отрицательна:
![]()
![]() .
.
Дополнительно к свойствам (F0)—(F3) от функции ![]() требуют неотрицательности этого выражения
(при любых
требуют неотрицательности этого выражения
(при любых ![]() ,
, ![]() ).
).
N.Ch.