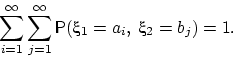
Таблицу, на пересечении
![]() -й строки и
-й строки и ![]() -го столбца которой стоит
вероятность
-го столбца которой стоит
вероятность ![]() , называют
таблицей совместного распределения случайных величин
, называют
таблицей совместного распределения случайных величин
![]() и
и ![]() .
.
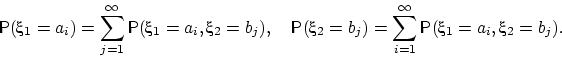
Так, первое равенство следует из того, что набор
![]() ,
, ![]() , ... есть полная группа событий,
и поэтому событие
, ... есть полная группа событий,
и поэтому событие ![]() раскладывается в объединение попарно несовместных
событий:
раскладывается в объединение попарно несовместных
событий:
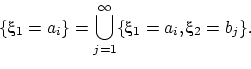
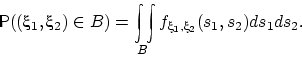
Если такая функция ![]() существует, она называется
плотностью совместного распределения случайных величин
существует, она называется
плотностью совместного распределения случайных величин
![]() .
.
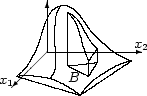 Достаточно, если двойной интеграл по множеству
Достаточно, если двойной интеграл по множеству Если случайные величины ![]() ,
, ![]() имеют абсолютно непрерывное совместное распределение,
то для любых
имеют абсолютно непрерывное совместное распределение,
то для любых ![]() имеет место равенство:
имеет место равенство:
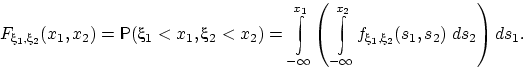
Плотность совместного распределения обладает такими же свойствами, как и плотность распределения одной случайной величины:
Справедливо и обратное: любая функция, обладающая этими свойствами, является плотностью некоторого совместного распределения. Доказательство этого факта ничем не отличается от одномерного случая.
По функции совместного распределения его плотность находится как смешанная частная производная:
Из существования плотностей ![]() и
и ![]() не следует абсолютная непрерывность
совместного распределения этих случайных величин. Например, вектор
не следует абсолютная непрерывность
совместного распределения этих случайных величин. Например, вектор ![]() принимает значения только на диагонали в
принимает значения только на диагонали в ![]() и уже поэтому не имеет плотности
совместного распределения (его совместное распределение сингулярно).
и уже поэтому не имеет плотности
совместного распределения (его совместное распределение сингулярно).
Обратное же свойство, как показывает следующая теорема, всегда верно: если совместное распределение абсолютно непрерывно, то и частные распределения тоже таковы.


Аналогично устанавливается и справедливость второго равенства.
QED
N.Ch.