




Next: Функции от двух случайных
Up: Многомерные распределения
Previous: Роль совместного распределения
Определение 38.
Случайные величины

называют
попарно
независимыми,
если независимы
любые две из них.
Оба этих определения годятся не только для конечного набора
случайных величин, но и для их бесконечной последовательности.
Пример 29.
Вспомним
пример Бернштейна. Свяжем с событиями

,

и

случайные величины

,

и

—
индикаторы этих событий. Например,

, если

произошло, и

, если

не произошло.
Случайные величины

,

и

независимы попарно (проверить),
но зависимы в совокупности:

Попарная независимость случайных величин встречается редко. Поэтому всюду,
где мы будем употреблять термин «независимы», будет подразумеваться
независимость в совокупности.
Определение независимости
можно сформулировать в терминах функций распределения:
Определение 39.
Случайные величины

независимы (в совокупности),
если
для любых 
имеет место равенство:

Для случайных величин с
дискретным распределением
эквивалентное определение независимости выглядит так:
Определение 40.
Случайные величины

с дискретным распределением независимы (в совокупности),
если
для любых чисел

имеет место равенство:

Упражнение 38.
Доказать, что из независимости в смысле
определения 37 следует независимость в смысле
определения 39 (доказательство в обратную сторону
см. в § 4 гл. 3 учебника А.А.Боровкова
«Теория вероятностей»).
Упражнение 39.
Доказать, что для случайных величин с дискретным распределением
определения
37 и
40
эквивалентны.
Для случайных величин с
абсолютно непрерывным совместным распределением
определение независимости можно сформулировать так:
Определение 41.
Случайные величины

с абсолютно непрерывным совместным распределением
независимы (в совокупности), если плотность совместного распределения
равна произведению плотностей случайных величин

,
т.е.
для любых 
имеет место равенство:
 .
.
Докажем эквивалентность определений
39 и
41.
Доказательство. По теореме
27, если совместное распределение

абсолютно непрерывно, то и в отдельности

также имеют абсолютно непрерывные распределения.
Пусть случайные величины

независимы в смысле определения
39,
т.е. для любых


Но функция совместного распределения равна

а произведение функций распределения записывается произведением
интегралов, или одним  -мерным интегралом:
-мерным интегралом:

Равенство интегралов 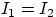 при всех значениях
при всех значениях
 влечёт, после дифференцирования по
влечёт, после дифференцирования по
 , равенство подынтегральных выражений почти всюду (дифференцировать
можно почти всюду),
т.е. независимость в смысле определения 41.
Для доказательства в обратную сторону можно использовать те же равенства, но в обратном порядке.
, равенство подынтегральных выражений почти всюду (дифференцировать
можно почти всюду),
т.е. независимость в смысле определения 41.
Для доказательства в обратную сторону можно использовать те же равенства, но в обратном порядке.
QED
N.Ch.
![]()
![]()

![]()
![]()
![]() .
. ![]()

![]() -мерным интегралом:
-мерным интегралом:

![]() при всех значениях
при всех значениях
![]() влечёт, после дифференцирования по
влечёт, после дифференцирования по
![]() , равенство подынтегральных выражений почти всюду (дифференцировать
можно почти всюду),
т.е. независимость в смысле определения 41.
Для доказательства в обратную сторону можно использовать те же равенства, но в обратном порядке.
, равенство подынтегральных выражений почти всюду (дифференцировать
можно почти всюду),
т.е. независимость в смысле определения 41.
Для доказательства в обратную сторону можно использовать те же равенства, но в обратном порядке.