



Next: Примеры использования формулы свёртки
Up: Многомерные распределения
Previous: Независимость случайных величин
Пусть
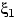
и
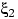
— случайные величины с
плотностью совместного
распределения 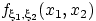
, и задана
борелевская функция 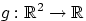
. Требуется найти
функцию (а если существует, то и
плотность)
распределения случайной величины
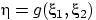
.
Пользуясь тем, что вероятность случайному вектору попасть в некоторую область
можно вычислить как объем под графиком плотности распределения
вектора над этой областью, сформулируем утверждение.
Теорема 28.
Пусть
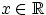
, и область
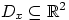
состоит из точек
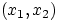
таких, что
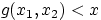
. Тогда
случайная величина
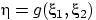
имеет функцию распределения
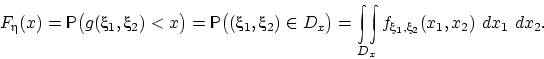
Далее в этой главе предполагается, что случайные величины
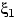
и
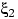 независимы
независимы, т.е.
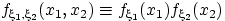
.
В этом случае распределение величины
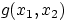
полностью
определяется частными распределениями величин
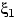
и
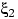
.
Следствие 9 (формула свёртки).
Если случайные величины
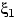
и
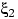
независимы и имеют
абсолютно непрерывные распределения с плотностями
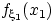
и
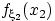
,
то плотность распределения суммы
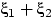
равна
«свёртке»
плотностей
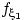
и

:
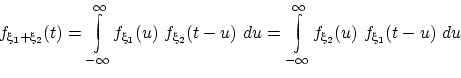 | (18) |
Доказательство.
Воспользуемся утверждением
теоремы 28 для борелевской функции
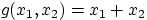
. Интегрирование по области
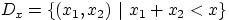
можно заменить последовательным вычислением
двух интегралов: наружного — по переменной
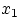
, меняющейся в пределах от
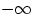
до
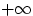
, и внутреннего — по переменной
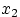
, которая при каждом
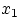
должна быть меньше, чем
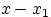
.
Здесь
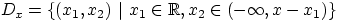
.
Поэтому
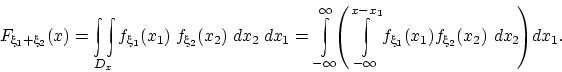
Сделаем в последнем интеграле замену переменной 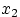 на
на 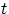 так:
так:
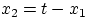 . При этом
. При этом  перейдёт в
перейдёт в
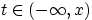 ,
, 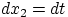 .
В полученном интеграле меняем порядок интегрирования: функция распределения
.
В полученном интеграле меняем порядок интегрирования: функция распределения 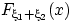 равна
равна

Итак, мы представили функцию распределения
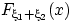 в виде
в виде 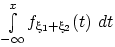 , где
, где
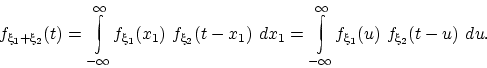
Второе равенство получается либо из первого заменой переменных,
либо просто из-за возможности поменять местами 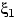 и
и 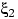 .
.
QED
Следствие
9 не только предлагает формулу
для вычисления плотности распределения суммы, но и утверждает
(
заметьте!), что сумма двух независимых случайных величин
с абсолютно непрерывными распределениями также имеет
абсолютно непрерывное распределение.
Упражнение 40. Для тех, кто уже ничему не удивляется:
привести пример двух случайных величин с абсолютно
непрерывными распределениями таких, что их сумма имеет
вырожденное распределение.
Если даже одна из двух независимых случайных величин имеет
дискретное, а вторая —
абсолютно непрерывное распределение,
то их сумма тоже имеет абсолютно непрерывное распределение:
Упражнение 41.
Пусть
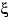
имеет таблицу распределения
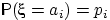
, а
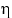
имеет плотность распределения
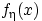
,
и эти величины независимы. Доказать, что
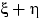
имеет плотность
распределения
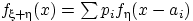
. Для вычисления функции распределения суммы
использовать
формулу полной вероятности.
N.Ch.
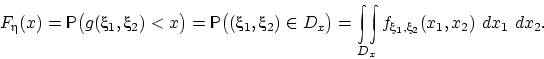
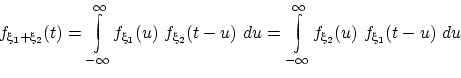
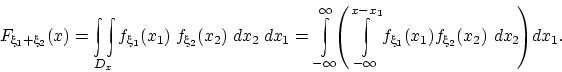
![]() на
на ![]() так:
так:
![]() . При этом
. При этом ![]() перейдёт в
перейдёт в
![]() ,
, ![]() .
В полученном интеграле меняем порядок интегрирования: функция распределения
.
В полученном интеграле меняем порядок интегрирования: функция распределения ![]() равна
равна

![]() в виде
в виде ![]() , где
, где
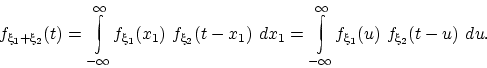
![]() и
и ![]() .
.