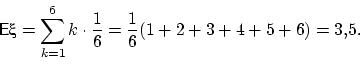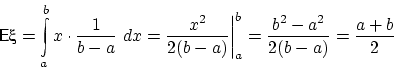Определение 42.
Математическим ожиданием 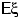
(средним значением, первым моментом)
случайной величины 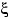
с
дискретным распределением, задаваемым
таблицей
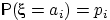
,
где
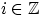
,
называется
число
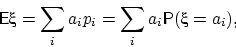
если данный ряд абсолютно сходится, т.е. если 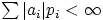 . В противном случае говорят, что математическое
ожидание не существует.
. В противном случае говорят, что математическое
ожидание не существует.
Определение 43.
Математическим ожиданием 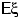
(средним значением, первым моментом)
случайной величины
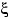
с
абсолютно непрерывным распределением с плотностью
распределения
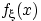
называется
число
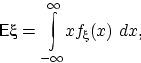
если этот интеграл абсолютно сходится, т.е. если
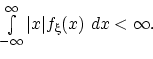 В противном случае математическое ожидание не существует.
В противном случае математическое ожидание не существует.
Математическое ожидание имеет простой физический смысл: если на прямой
разместить единичную массу, поместив в точки
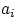
массу
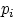
(для дискретного распределения), или «размазав» её с плотностью
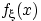
(для абсолютно непрерывного распределения),
то точка
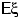
будет координатой «центра тяжести» прямой.
Пример 32.
Пусть случайная величина
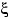
равна числу очков, выпадающих при одном
подбрасывании кубика. Тогда
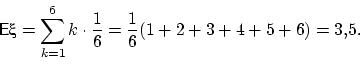
В среднем при одном подбрасывании кубика выпадает 3,5 очка.
Пример 33.
Пусть случайная величина
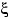
— координата точки, брошенной наудачу
на отрезок
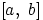
. Тогда
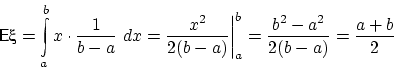
Центр тяжести равномерного распределения есть середина отрезка.
![]()
![]() . В противном случае говорят, что математическое
ожидание не существует.
. В противном случае говорят, что математическое
ожидание не существует.![]()
![]() . В противном случае говорят, что математическое
ожидание не существует.
. В противном случае говорят, что математическое
ожидание не существует.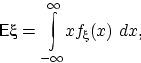
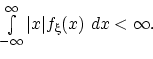 В противном случае математическое ожидание не существует.
В противном случае математическое ожидание не существует.