- E1.
- Для произвольной борелевской функции
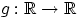
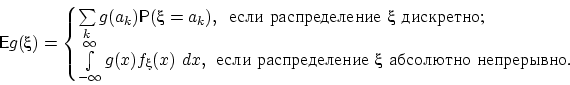
Доказательство.
Мы докажем это свойство (как и почти все дальнейшие) только для дискретного распределения.
Пусть 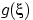 принимает значения
принимает значения 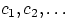 с вероятностями
с вероятностями
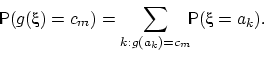
Тогда
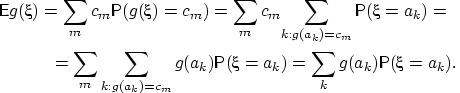
QED
Следствие 10.
Математическое ожидание 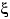 существует тогда и только тогда, когда
существует тогда и только тогда, когда 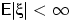 .
.
Доказательство.
Условием существование математического ожидания является
абсолютная сходимость ряда или интеграла
в определениях 42 и 43.
По свойству (E1) это и есть условие 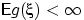 при
при 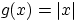 .
.
QED
Доказательство.
Пусть случайные величины 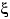 и
и 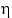 имеют дискретные распределения со значениями
имеют дискретные распределения со значениями
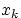 и
и  соответственно.
Для борелевской функции
соответственно.
Для борелевской функции 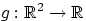 можно доказать свойство, аналогичное (E1) (сделать это!).
Воспользуемся этим свойством для
можно доказать свойство, аналогичное (E1) (сделать это!).
Воспользуемся этим свойством для 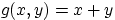 :
:
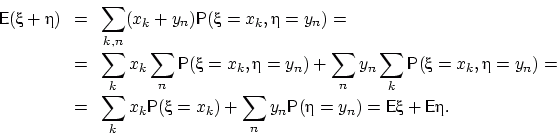
QED
- E5.
- Если
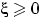 п.н., т.е. если
п.н., т.е. если 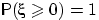 , то
, то 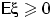 .
.
Упражнение 42.
Доказать для дискретного и для абсолютно непрерывного распределений.
Замечание 18.
Сокращение «п.н.» читается как «почти наверное» и означает «с вероятностью 1».
По определению, математическое ожидание — это числовая характеристика распределения. Распределение
же не изменится от изменения случайной величины на множестве нулевой вероятности.
Поэтому, например, даже если 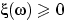 не при всех
не при всех 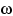 , а на множестве единичной вероятности,
математическое ожидание
, а на множестве единичной вероятности,
математическое ожидание 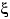 всё равно неотрицательно.
всё равно неотрицательно.
- E6.
- Если
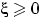 п.н., и при этом
п.н., и при этом 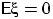 , то
, то 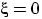 п.н., т.е.
п.н., т.е. 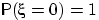 .
.
Доказательство. Это свойство мы докажем, заранее предполагая, что 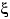 имеет дискретное распределение
с неотрицательными значениями
имеет дискретное распределение
с неотрицательными значениями 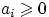 . Равенство
. Равенство 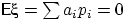 означает, что все слагаемые в этой сумме равны нулю, т.е. все вероятности
означает, что все слагаемые в этой сумме равны нулю, т.е. все вероятности 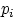 нулевые, кроме вероятности,
соответствующей значению
нулевые, кроме вероятности,
соответствующей значению 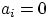 .
.
QED
Из свойств (E5) и (E6) вытекает множество полезных
утверждений:
- E7.
- Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий:
если
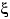 и
и 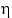 независимы и их математические ожидания существуют, то
независимы и их математические ожидания существуют, то
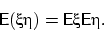
Доказательство. В дискретном случае:
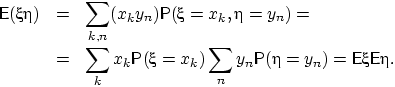
QED
Замечание 19.
Обратное утверждение к свойству (E7) неверно: из равенства 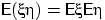 не следует независимость величин
не следует независимость величин 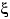 и
и 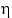 .
.
Пример 34.
Пусть 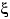 принимает значения 0 и
принимает значения 0 и 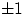 с вероятностями по 1/3 каждое,
и
с вероятностями по 1/3 каждое,
и 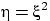 . Это зависимые случайные величины:
. Это зависимые случайные величины:
![]()
Однако ![]() и
и ![]() , поэтому
, поэтому
![]() .
.
Пример 35.
Пусть 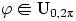 , и пусть
, и пусть 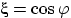 и
и 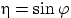 — заведомо зависимые случайные величины (доказать!).
Но математическое ожидание их произведения
равно произведению их математических ожиданий из-за симметричности распределений
— заведомо зависимые случайные величины (доказать!).
Но математическое ожидание их произведения
равно произведению их математических ожиданий из-за симметричности распределений
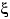 ,
, 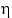 и
и 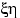 относительно нуля. Действительно, по свойству
(E1) имеем:
относительно нуля. Действительно, по свойству
(E1) имеем:
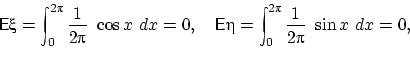
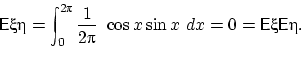
N.Ch.