next up previous contents index
Next:  Свойства дисперсии   Up:  Числовые характеристики распределений   Previous:  Свойства математического ожидания

§ 3. Дисперсия и моменты старших порядков

Определение 44. Пусть .

Число называется моментом порядка или -м моментом случайной величины ,

число называется абсолютным -м моментом,

называется центральным -м моментом, и

— абсолютным центральным -м моментом случайной величины .

Число (центральный момент второго порядка) называется дисперсией случайной величины .

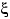
Пример 36. Пусть, скажем, случайная величина принимает значение 0 с вероятностью 0,99999 и значение 100 с вероятностью 0,00001. Посмотрим, как моменты разных порядков реагируют на большие, но маловероятные значения случайной величины:

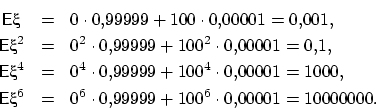
Пример 37. Дисперсия есть «среднее значение квадрата отклонения случайной величины от своего среднего». Посмотрим, за что эта величина отвечает.

Пусть случайная величина принимает значения с равными вероятностями, а случайная величина — значения с равными вероятностями. Тогда , поэтому , . Говорят, что дисперсия характеризует степень разброса значений случайной величины вокруг её математического ожидания.

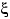
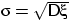
Определение 45. Если дисперсия величины конечна, то число называют среднеквадратическим отклонением случайной величины .
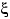
Чтобы прояснить связь моментов разных порядков, докажем несколько неравенств. Во-первых, очевидное утверждение, обеспечивающее существование моментов меньших порядков, если существуют моменты более высокого порядка:
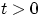
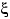
Теорема 29. Если существует момент порядка случайной величины , то существуют и её моменты порядка , .
Доказательство. Для любого числа верно неравенство:

Действительно, при , и при . Из этого неравенства следует, что для всех . Но следствие 11 позволяет из неравенства для случайных величин получить такое же неравенство для их математических ожиданий:

Момент порядка существует, т.е. . Поэтому и .

QED

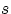
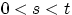
Докажем ещё одно чрезвычайно полезное неравенство.
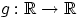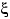
Теорема 30   (неравенство Йенсена(1)). Пусть функция выпукла («выпукла вниз», т.е. её надграфик есть выпуклое множество). Тогда для любой случайной величины с конечным первым моментом верно неравенство:

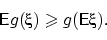
Доказательство. Нам понадобится следующее свойство.
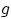
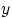
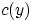
Лемма 8. Пусть функция выпукла. Тогда для всякого найдётся число такое, что при всех

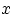
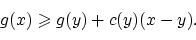
Это свойство очевидно и означает, что график выпуклой функции лежит полностью выше любой из касательных к этому графику.

Возьмём в условиях леммы 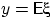, 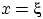. Тогда

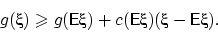
Вычислим математическое ожидание обеих частей неравенства. Так как 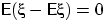, и неравенство между математическими ожиданиями сохраняется по следствию 11, то .

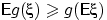QED

Следующее неравенство связывает моменты разных порядков.
Следствие 14. Если , то для любого

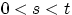
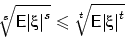
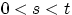
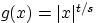
Доказательство. Поскольку , то — выпуклая функция. По неравенству Йенсена для ,

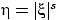
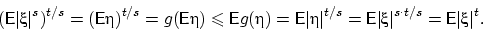
Осталось извлечь из обеих частей корень степени .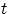

QED


(1) Johan Ludwig William Valdemar Jensen (8.05.1859 — 5.03.1925, Denmark) .

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

N.Ch.