Математическое ожидание и дисперсию этого распределения мы знаем из свойств
(E2) и (D3): ![]() ,
, ![]() .
.
Математическое ожидание и дисперсию этого распределения мы знаем из свойств
(E2) и (D3): ![]() ,
, ![]() .
.
Используем свойство устойчивости биномиального распределения
относительно суммирования.
Возьмём на каком-нибудь вероятностном пространстве ![]() независимых случайных величин
независимых случайных величин ![]() с распределением Бернулли
с распределением Бернулли ![]() .
Тогда их сумма
.
Тогда их сумма ![]() имеет распределение
имеет распределение
![]() , и по свойству (E4) имеем:
, и по свойству (E4) имеем:
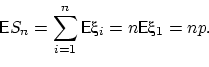
А поскольку ![]() независимы, и дисперсия каждой равна
независимы, и дисперсия каждой равна ![]() , то
, то
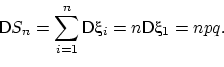
Итак, ![]() ,
, ![]() для
для ![]() .
.
Вычислим математическое ожидание ![]() :
:

Вычислим так называемый «второй факториальный момент» ![]() :
:
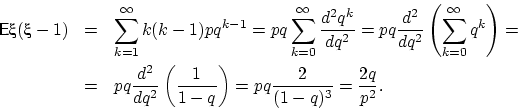
Найдём дисперсию через второй факториальный момент:
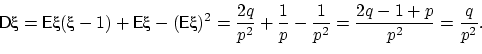
Вычислим математическое ожидание ![]() :
:
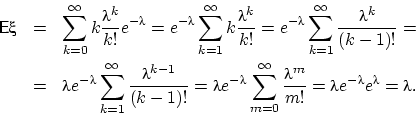
Моменты более высоких порядков легко находятся через факториальные моменты
![]() порядка
порядка ![]() .
Так, второй факториальный момент
.
Так, второй факториальный момент ![]() равен
равен
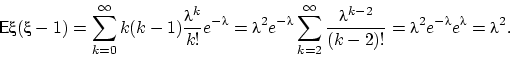
Поэтому ![]() и
и ![]() .
.
Математическое ожидание этого распределения существует в силу конечности
![]() :
:
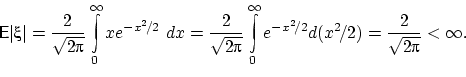
Математическое ожидание ![]() равно
равно
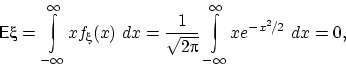
так как под сходящимся интегралом стоит нечётная функция. Далее,
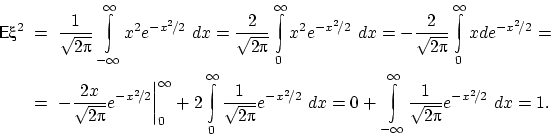
Поэтому ![]()
Если ![]() , то
, то
![]() .
.
Мы только что вычислили
![]() ,
, ![]() .
Тогда (над каждым равенством подписать, каким свойствам оно обязано)
.
Тогда (над каждым равенством подписать, каким свойствам оно обязано)
![]()
Найдём для произвольного ![]() момент порядка
момент порядка ![]() .
.
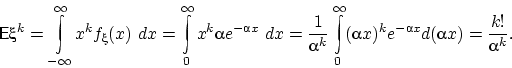
В последнем равенстве мы воспользовались гамма-функцией Эйлера:
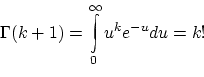
Тогда
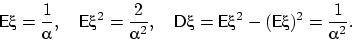
Математическое ожидание распределения Коши не существует, так как расходится интеграл
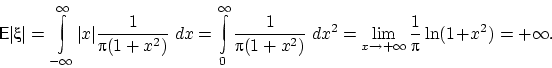
Расходится он из-за того, что подынтегральная функция ведёт себя на бесконечности как ![]() .
Поэтому не существуют ни дисперсия, ни моменты более высоких порядков этого распределения.
То же самое можно сказать про распределение Коши
.
Поэтому не существуют ни дисперсия, ни моменты более высоких порядков этого распределения.
То же самое можно сказать про распределение Коши ![]() .
.
У распределения Парето существуют только моменты порядка ![]() , поскольку
, поскольку
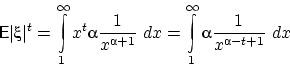
сходится при ![]() , когда подынтегральная функция на бесконечности
ведёт себя как
, когда подынтегральная функция на бесконечности
ведёт себя как ![]() , где
, где ![]() .
.