Выясним сначала, когда выполнен ЗБЧ для последовательности независимых и одинаково распределённых случайных величин.
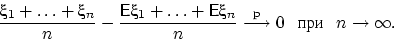 | (22) |
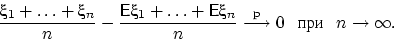 | (22) |
Выясним сначала, когда выполнен ЗБЧ для последовательности независимых и одинаково распределённых случайных величин.
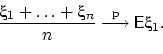 | (23) |
ЗБЧ утверждает, что среднее арифметическое большого числа случайных слагаемых «стабилизируется» с ростом этого числа. Как бы сильно каждая случайная величина не отклонялась от своего среднего значения, при суммировании эти отклонения «взаимно гасятся», так что среднее арифметическое приближается к постоянной величине.
В дальнейшем мы увидим, что требование конечности второго момента (или дисперсии) связано исключительно со способом доказательства, и что утверждение останется верным, если требовать существования только первого момента.
Обозначим через
![]() сумму первых
сумму первых ![]() случайных величин.
Из линейности математического ожидания получим:
случайных величин.
Из линейности математического ожидания получим:
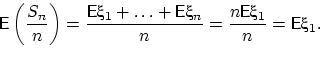
Пусть ![]() .
Воспользуемся неравенством Чебышёва:
.
Воспользуемся неравенством Чебышёва:
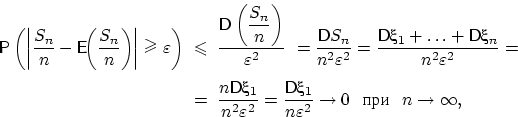 |
(24) |
так как ![]() .
Заметим, что дисперсия суммы превратилась в сумму дисперсий в силу попарной
независимости слагаемых, из-за которой все ковариации
.
Заметим, что дисперсия суммы превратилась в сумму дисперсий в силу попарной
независимости слагаемых, из-за которой все ковариации ![]() в свойстве 14 обратились в нуль при
в свойстве 14 обратились в нуль при ![]() .
Сумма же дисперсий слагаемых равняется
.
Сумма же дисперсий слагаемых равняется ![]() из-за их одинаковой
распределённости.
из-за их одинаковой
распределённости.
QED
| (25) |
Сильная зависимость слагаемых приводит обычно
к невыполнению ЗБЧ. Если, например, ![]() и
и ![]() , то
, то ![]() , и свойство (23)
не выполнено (убедиться!).
В этом случае
, и свойство (23)
не выполнено (убедиться!).
В этом случае ![]() ; для одинаково распределённых
слагаемых дисперсия суммы быстрее расти не может.
; для одинаково распределённых
слагаемых дисперсия суммы быстрее расти не может.
Следующее утверждение мы докажем чуть позже. Сравните его условия с условиями ЗБЧ Чебышёва.
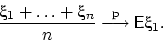
Получим в качестве следствия из ЗБЧ Чебышёва закон больших чисел Я. Бернулли. В отличие от ЗБЧ Чебышёва, описывающего предельное поведение среднего арифметического случайных величин с произвольными распределениями, ЗБЧ Бернулли имеет дело лишь со схемой Бернулли.
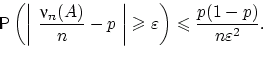

и ![]() ,
,
![]() .
Осталось воспользоваться ЗБЧ в форме Чебышёва и неравенством
(25).
.
Осталось воспользоваться ЗБЧ в форме Чебышёва и неравенством
(25).
QED
1Александр Яковлевич Хинчин (19.07.1894 — 18.11.1959)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.