ЛЕКЦИЯ
4. Силы в магнитном поле.
действие магнитного поля
на вещество
 4.1. Действие магнитного поля на движущийся заряд.
Сила Лоренца
4.1. Действие магнитного поля на движущийся заряд.
Сила Лоренца

 Как показывает опыт, на
заряд, движущийся в магнитном поле, действует сила, величина которой зависит
прямо пропорционально от величины заряда
q, величины индукции В
Как показывает опыт, на
заряд, движущийся в магнитном поле, действует сила, величина которой зависит
прямо пропорционально от величины заряда
q, величины индукции В  магнитного поля в том месте пространства, где находится заряд и от
проекции его скорости v на
плоскость, перпендикулярную вектору В.
Будем называть эту силу магнитной. Если измерять заряд в кулонах, индукцию магнитного поля в теслах, а скорость в метрах в
секунду, то величину магнитной силы в ньютонах
можно вычислить по формуле
магнитного поля в том месте пространства, где находится заряд и от
проекции его скорости v на
плоскость, перпендикулярную вектору В.
Будем называть эту силу магнитной. Если измерять заряд в кулонах, индукцию магнитного поля в теслах, а скорость в метрах в
секунду, то величину магнитной силы в ньютонах
можно вычислить по формуле
![]() , (4.1.1)
, (4.1.1)
где a - угол между векторами
скорости и индукции.
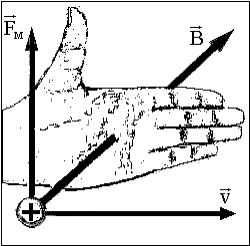
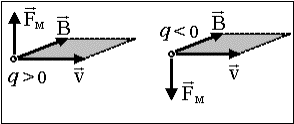
Магнитная сила всегда направлена перпендикулярно векторам скорости заряда и магнитной индукции и образует с ними правую тройку векторов (при q>0), поэтому ее векторное выражение имеет вид
![]() . (4.1.2)
. (4.1.2)
Направление этой силы можно найти по известному правилу левой руки (см. рис. 4.1.2).
Отметим
два важных свойства магнитной силы. Во-первых, она равна нулю, если скорость
заряда параллельна или антипараллельна
магнитной индукции (![]() или
или ![]() , соответственно). Во-вторых, из-за того, что магнитная сила
всегда перпендикулярна скорости заряда, она способна только искривить
траекторию заряда, но не может изменить величину его скорости. Работа магнитной силы всегда равна нулю.
, соответственно). Во-вторых, из-за того, что магнитная сила
всегда перпендикулярна скорости заряда, она способна только искривить
траекторию заряда, но не может изменить величину его скорости. Работа магнитной силы всегда равна нулю.
Магнитная сила используется, например, для отклонения электронов в кинескопах телевизоров, для отклонения ионов в масс-спектрометрах, для отклонения заряженных частиц в циклических ускорителях.
Если в том месте, где
находится заряд, существует не только магнитное, но и электрическое поле с
напряженностью Е, то действующая на
частицу сила равна
![]() . (4.1.3)
. (4.1.3)
Это выражение было получено Х. Лоренцем путем
обобщения экспериментальных данных и носит название силы Лоренца. Первое слагаемое Fэ в выражении (4.1.3)
называют электрической, а второе Fм – магнитной составляющими полной
силы Лоренца.
4.2. Действие магнитного поля на провод с током. Сила Ампера. Работа
перемещения провода с током в постоянном магнитном поле
При помещении провода с
током в магнитное поле действующая на носители тока магнитная сила передается
проводу. Получим выражение для магнитной силы, действующей на элементарный
отрезок провода длиной dl в магнитном
поле с индукцией В.
Обозначим заряд одного
носителя q1, концентрацию
носителей n , скорость упорядоченного
движения носителей u , скорость
хаотического движения v. Магнитная
сила, действующая на один носитель
![]() , (4.2.1)
, (4.2.1)
ее среднее значение равно
![]() .
.
Здесь![]() , так как все направления скорости хаотического движения
равновероятны.
, так как все направления скорости хаотического движения
равновероятны.
Пусть площадь сечения
провода S , тогда объем отрезка
провода равен Sdl и общее число
носителей nSdl. Суммарная магнитная
сила, действующая на элементарный отрезок провода, равна
![]() .
.
Здесь ![]() плотность тока.
плотность тока.
 Величина плотности тока j связана с силой тока I и площадью сечения S: j=I/S . Введем вектор элемента длины
проводника dl , сонаправленный с вектором плотности тока j, тогда jSdl=Idl и для магнитной силы, действующей на
элемент тока, получаем
Величина плотности тока j связана с силой тока I и площадью сечения S: j=I/S . Введем вектор элемента длины
проводника dl , сонаправленный с вектором плотности тока j, тогда jSdl=Idl и для магнитной силы, действующей на
элемент тока, получаем
![]() . (4.2.2)
. (4.2.2)
 Это соотношение было получено
экспериментально Ампером и называется законом
Ампера. Исторически оно было получено раньше, чем выражение для магнитной
части силы Лоренца. В действительности, Лоренц получил выражение для магнитной
силы, основываясь на законе Ампера.
Это соотношение было получено
экспериментально Ампером и называется законом
Ампера. Исторически оно было получено раньше, чем выражение для магнитной
части силы Лоренца. В действительности, Лоренц получил выражение для магнитной
силы, основываясь на законе Ампера.
Для прямого отрезка провода
с током I, помещенного в однородное
магнитное поле B, сила Ампера равна
![]() . (4.2.3)
. (4.2.3)
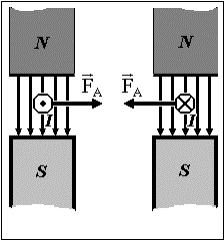
Здесь вектор l направлен по току (в
сторону переноса положительного заряда), а его модуль равен длине провода.
Направление амперовой силы определяется так же, как направление магнитной силы
для положительного заряда (см. рис. 4.2.3).
Элементарная работа dА, совершаемая силой Ампера dFА при перемещении на dr в магнитном поле элемента проводника dl, равна
![]() . (4.2.4)
. (4.2.4)
Здесь мы, подставив выражение для амперовой силы
(4.2.2), вынесли скалярную величину – силу тока I и воспользовались известным свойством смешанного произведения
векторов: оно не изменяется при циклической перестановке сомножителей.
Векторное произведение перемещения и элемента проводника есть вектор площадки,
прочерченной проводником при его перемещении (см. рис. 4.2.4):
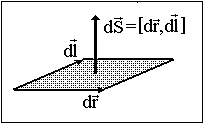
![]() . (4.2.5)
. (4.2.5)
Скалярное произведение вектора площадки и вектора
магнитной индукции – это магнитный поток через площадку dS
![]() , (4.2.6)
, (4.2.6)
![]() поэтому для работы получаем
поэтому для работы получаем
![]() . (4.2.7)
. (4.2.7)
Если проводник, сила тока I в котором поддерживается
постоянной, совершает конечное перемещение из положения 1 в положение 2, то
работа амперовых сил при таком перемещении
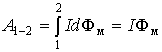 , (4.2.8)
, (4.2.8)
где Фм – магнитный поток через поверхность, прочерченную проводником при
рассматриваемом перемещении.
Если в постоянном магнитном поле перемещается замкнутый контур, то поток, прочерченный всеми элементами контура, равен изменению потока пронизывающего контур (так называемого потокосцепления Y). Докажем это.
![]()
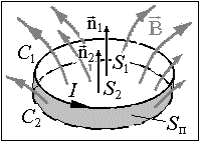 На
рисунке 4.2.5 изображены два последовательных состояния контура С1 и
С2. Поверхности S1
и S2,
которые ограничивает контур в положениях С1 и С2 и
поверхность Sп,
прочерченная контуром, составляют замкнутую поверхность. По теореме
Остроградского-Гаусса для магнитной индукции суммарный поток через эту
замкнутую поверхность равен нулю. Выберем нормали n1
и n2 к поверхностям S1 и S2 при вычислении
потокосцеплений Y1
и Y2 в каждом из положений так, чтобы они были согласованы с направлением тока в контуре по
правилу правого винта (из конца вектора нормали ток в контуре виден идущим
против часовой стрелки). При этом поток наружу из замкнутой поверхности
складывается из потока через S1
в направлении n1 (равен Y1),
потока через S2 в
направлении противоположном n2
(равен -Y2)
и потока через прочерченную поверхность Sп
(Фм). Таким образом, получаем
На
рисунке 4.2.5 изображены два последовательных состояния контура С1 и
С2. Поверхности S1
и S2,
которые ограничивает контур в положениях С1 и С2 и
поверхность Sп,
прочерченная контуром, составляют замкнутую поверхность. По теореме
Остроградского-Гаусса для магнитной индукции суммарный поток через эту
замкнутую поверхность равен нулю. Выберем нормали n1
и n2 к поверхностям S1 и S2 при вычислении
потокосцеплений Y1
и Y2 в каждом из положений так, чтобы они были согласованы с направлением тока в контуре по
правилу правого винта (из конца вектора нормали ток в контуре виден идущим
против часовой стрелки). При этом поток наружу из замкнутой поверхности
складывается из потока через S1
в направлении n1 (равен Y1),
потока через S2 в
направлении противоположном n2
(равен -Y2)
и потока через прочерченную поверхность Sп
(Фм). Таким образом, получаем
![]() , (4.2.9)
, (4.2.9)
откуда ![]() . Следовательно, соотношение (4.2.8) для замкнутого контура
можно записать так
. Следовательно, соотношение (4.2.8) для замкнутого контура
можно записать так
![]() . (4.2.10)
. (4.2.10)
При выводе этой формулы мы рассмотрели простое перемещение контура, но она оказывается справедливой и при более сложных изменениях состояния контура, например, при вращении и при деформации. В приведенном виде она выполняется для движении не только одиночного контура, но и катушки, состоящей из нескольких витков, в частности, для катушки из N одинаковых витков. В последнем случае потокосцепление равно Y = NFм, где Fм – магнитный поток через один виток.
4.3. Результирующая сила и момент сил, действующие на контур с током во
внешнем магнитном поле. Магнитный момент контура с током
Рассмотрим замкнутый плоский
проводник с током (контур с током). Выберем вектор n, перпендикулярный плоскости контура и согласованный с
направлением тока по правилу правого винта (см. рис. 3.4.3). Пусть сила тока в
контуре I и площадь, охваченная
контуром S. Введем вектор
![]() , (4.3.1)
, (4.3.1)
который, как мы увидим в дальнейшем, определяет
взаимодействие контура с магнитным полем. Этот вектор называется магнитным дипольным моментом контура с
током и в СИ имеет размерность А×м2 .
Поместим этот контур в
однородное магнитное поле с индукцией В,
тогда на каждый элемент контура dl будет действовать сила
![]() . (4.3.2)
. (4.3.2)
Суммируя силы, приложенные к элементам контура, получим для результирующей силы
![]() . (4.3.3)
. (4.3.3)
Здесь сила тока и магнитная индукция для всех
элементов контура одинаковы, поэтому их можно вынести из-под знака интеграла.
Интегрирование всех векторов dl, составляющих контур, дает
вектор перемещения вдоль тока, который
для замкнутого контура равен нулю, т. е. ![]() . Поэтому полная сила, действующая на замкнутый контур с
током в однородном поле, тоже равна нулю:
. Поэтому полная сила, действующая на замкнутый контур с
током в однородном поле, тоже равна нулю:
![]() . (4.3.4)
. (4.3.4)
Найдем далее момент сил
(вращательный момент), действующий на контур с током в однородном магнитном
поле. При этом учтем известный из механики факт, что если результирующая сил
равна нулю, то момент сил не зависит от выбора точки, относительно которой он
вычисляется.
Рассмотрим прямоугольный
контур ABCD, расположенный в однородном магнитном поле так, что вектор нормали n образует с вектором В угол a , и стороны AB и CD
перпендикулярны вектору В (см.
рис.4.3.1).

![]()
 Обозначим силы Ампера,
действующие на стороны контура F1,F2,F3,F4 . Найдем суммарный момент этих сил относительно
точки О (центра контура). Линии действия сил F3,F4
проходят через точку О, следовательно,
моменты этих сил равны нулю. Две другие силы: F1 и F2 и радиус-векторы точек их
приложения r1 и r2 лежат в плоскости,
образованной векторами B и n . Расположение векторов в
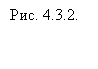
этой плоскости изображено на рисунке 4.3.2.
Обозначим силы Ампера,
действующие на стороны контура F1,F2,F3,F4 . Найдем суммарный момент этих сил относительно
точки О (центра контура). Линии действия сил F3,F4
проходят через точку О, следовательно,
моменты этих сил равны нулю. Две другие силы: F1 и F2 и радиус-векторы точек их
приложения r1 и r2 лежат в плоскости,
образованной векторами B и n . Расположение векторов в
этой плоскости изображено на рисунке 4.3.2.
Каждая из сил F1, F2 перпендикулярна вектору В, а радиус-векторы r1, r2 перпендикулярны вектору n. Поэтому силы F1, F2 образуют с радиус-векторами
r1, r2 тот же угол a, что и вектор B с нормалью n.
Момент этих сил M равен
![]() . (4.3.5)
. (4.3.5)
Слагаемые в этой сумме направлены в одну сторону
(перпендикулярно плоскости рисунка от нас). По формуле (4.2.3) обе силы равны F1=F2=IaB,
кроме того, r1=r2=b/2.
Поэтому слагаемые в (4.3.5) одинаковы по величине и равны
![]() , (4.3.6)
, (4.3.6)
а величина результирующего момента
![]() , (4.3.7)
, (4.3.7)
где S = ab – площадь рамки.
Воспользовавшись определением магнитного момента контура (4.3.1.), можно
записать величину момента сил Ампера,
действующих на этот контур:
![]() . (4.3.8)
. (4.3.8)
Векторы pm, B, M составляют правую тройку
векторов, поэтому в общем виде получаем
![]() . (4.3.9)
. (4.3.9)
Можно доказать, что формула
(4.3.9) справедлива в однородном магнитном поле для контура произвольной формы.
Как следует из формулы (4.3.8)
для момента амперовых сил, существует два
положения a = 0 и a = p, в которых этот момент обращается в нуль. В остальных случаях (см. рис.4.3.2)
вращающий момент, действующий на контур с
током, стремится развернуть контур так,
чтобы направление магнитного момента контура совпало с направлением магнитной
индукции внешнего поля, т.е. к состоянию a = 0. Поэтому при a = 0 контур оказывается в устойчивом равновесии, а при a = p – в неустойчивом.
Выше было доказано, что в однородном поле результирующая сила, действующая на контур, равна нулю. Можно показать, что на контур в неоднородном магнитном поле действует сила
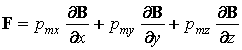 . (4.3.10)
. (4.3.10)
Здесь pmx,
pmy, pmz проекции вектора магнитного момента на координатные
оси x, y, z. Векторное уравнение
(4.3.10) в проекции, например, на ось х
означает, что
 , (4.3.11)
, (4.3.11)
![]()
 где
Bx, By, Bz – проекции магнитной индукции на
координатные оси. В частном случае, если вектор магнитной индукции изменяется
только в том же направлении, в котором направлен вектор B, можно направить ось x по вектору B. Пусть кроме того
величина вектора магнитной индукции возрастает в направлении оси x , т. е.
где
Bx, By, Bz – проекции магнитной индукции на
координатные оси. В частном случае, если вектор магнитной индукции изменяется
только в том же направлении, в котором направлен вектор B, можно направить ось x по вектору B. Пусть кроме того
величина вектора магнитной индукции возрастает в направлении оси x , т. е. ![]() . При этом знак проекции силы, действующей на контур, будет
определяется знаком проекции pmx. Иными словами,
если угол между магнитным моментом контура и осью x острый (pmx>0), то сила
направлена в сторону оси, т.е. в сторону возрастания величины индукции. Если
угол тупой (pmx<0), то сила
направлена в противоположную сторону. Рисунок 4.3.3 иллюстрирует, почему это
происходит. На каждый элемент провода действует сила dF, проекция dFx
которой (рис. 4.3.3a) для всех
элементов направлена в одну сторону и складывается в общую силу. Если магнитный
момент направлен параллельно магнитной индукции (рис. 4.3.3б,
. При этом знак проекции силы, действующей на контур, будет
определяется знаком проекции pmx. Иными словами,
если угол между магнитным моментом контура и осью x острый (pmx>0), то сила
направлена в сторону оси, т.е. в сторону возрастания величины индукции. Если
угол тупой (pmx<0), то сила
направлена в противоположную сторону. Рисунок 4.3.3 иллюстрирует, почему это
происходит. На каждый элемент провода действует сила dF, проекция dFx
которой (рис. 4.3.3a) для всех
элементов направлена в одну сторону и складывается в общую силу. Если магнитный
момент направлен параллельно магнитной индукции (рис. 4.3.3б, ![]() ), результирующая сила
F направлена в сторону возрастания модуля магнитной индукции.
Если же магнитный момент направлен антипараллельно (рис. 4.3.3в,
), результирующая сила
F направлена в сторону возрастания модуля магнитной индукции.
Если же магнитный момент направлен антипараллельно (рис. 4.3.3в, ![]() ), сила направлена в сторону убывания модуля B.
), сила направлена в сторону убывания модуля B.
![]()
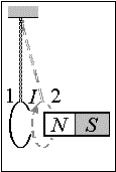 В общем
случае под действием силы F незакрепленный
контур с током втягивается в область более сильного магнитного поля, если угол a между векторами pm и B острый. Если же угол a тупой, то контур с током
выталкивается в область более слабого поля, поворачивается под действием
момента сил Ампера, так, что угол a становится острым, и затем втягивается в область
более сильного поля.
В общем
случае под действием силы F незакрепленный
контур с током втягивается в область более сильного магнитного поля, если угол a между векторами pm и B острый. Если же угол a тупой, то контур с током
выталкивается в область более слабого поля, поворачивается под действием
момента сил Ампера, так, что угол a становится острым, и затем втягивается в область
более сильного поля.
Рис.
4.3.5
 Поведение контура с током
можно наблюдать в опыте, схема которого показана на рис.4.3.4. Через катушку из медной проволоки, подвешенную
вблизи одного из концов полосового магнита, пропускают ток. При этом катушка
поворачивается вокруг вертикальной оси так, чтобы ее магнитный момент был
сонаправлен вектору В магнита, и
притягивается к магниту, занимая положение 2, т.е. перемещается туда где
магнитное поле сильнее.
Поведение контура с током
можно наблюдать в опыте, схема которого показана на рис.4.3.4. Через катушку из медной проволоки, подвешенную
вблизи одного из концов полосового магнита, пропускают ток. При этом катушка
поворачивается вокруг вертикальной оси так, чтобы ее магнитный момент был
сонаправлен вектору В магнита, и
притягивается к магниту, занимая положение 2, т.е. перемещается туда где
магнитное поле сильнее.
Сила
Ампера, действующая на замкнутый проводник с током со стороны магнитного поля,
кроме того вызывают деформацию проводника (см. рис 4.3.5.).
4.4. Магнитное поле в веществе. Намагниченность. Напряженность магнитного
поля
История открытия магнитных свойств веществ уходит в глубь веков. Более двух тысяч лет назад магнитные материалы использовались в качестве компаса. В современной физике магнетизм – обширный раздел, связанный с большинством областей физической науки и ее техническими приложениями.
Важнейшую роль в учении о
магнетизме сыграла гипотеза Ампера, согласно которой магнитные свойства вещества обусловлены элементарными замкнутыми
токами, циркулирующими внутри небольших частиц вещества – атомов, молекул или
их групп. Все вещества по отношению к воздействию на них магнитного поля
принято называть магнетиками. При описании магнитного поля в веществе –
магнетике можно, не вдаваясь в природу этих элементарных токов, для простоты
считать их все одинаковыми. Пусть каждая молекула вещества характеризуется
некоторым магнитным моментом
![]() , (4.4.1)
, (4.4.1)
где Iмол
элементарный молекулярный ток, а Sмол
– площадь, охваченная его контуром. Количественной характеристикой
намагниченного состояния вещества служит векторная величина намагниченность J, равная отношению магнитного момента Pm
макроскопически малого объёма DV
вещества к этому объему:
![]() , (4.4.2)
, (4.4.2)
где pmi – магнитный момент i- молекулы из общего числа N молекул, содержащихся в
объеме DV.
Этот объем должен быть столь малым, чтобы в его пределах магнитное поле можно
было считать однородным. В то же время в нем должно содержаться столь большое
число молекул (N>>1), чтобы к ним
можно было применять статистические методы.
Если магнетик не намагничен,
молекулярные токи ориентированы хаотически и средняя намагниченность равна нулю. Под действием магнитного поля В0, создаваемого внешними
токами, происходят различные процессы намагничивания вещества при этом
возникает дополнительное усредненное магнитное поле В1 молекулярных токов, так что суммарное поле В, действующее в магнетике,
характеризуется магнитной индукцией
 В = В0 + В1. (4.4.3)
В = В0 + В1. (4.4.3)
Закон полного тока для магнитного поля в веществе имеет вид
![]() , (4.4.4)
, (4.4.4)
![]()
 где
Iмакро и Iмикро – алгебраические
суммы соответственно макро- и микротоков, проходящих через замкнутый контур L , т.е. результирующие макро- и микротоки пересекающие
поверхность, натянутую на этот контур.
где
Iмакро и Iмикро – алгебраические
суммы соответственно макро- и микротоков, проходящих через замкнутый контур L , т.е. результирующие макро- и микротоки пересекающие
поверхность, натянутую на этот контур.
![]() Найдем связь между
Iмикро и намагниченностью вещества. Вклад в этот
ток дают только те молекулярные токи I’мол (см рис.
4.4.1.), которые «нанизаны» на контур L как бусы на нитку.
Найдем связь между
Iмикро и намагниченностью вещества. Вклад в этот
ток дают только те молекулярные токи I’мол (см рис.
4.4.1.), которые «нанизаны» на контур L как бусы на нитку.
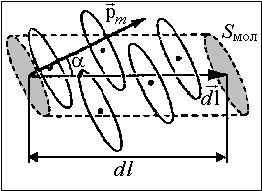
Будем полагать, что магнитные моменты всех молекулярных токов pmi ориентированы одинаково. Пусть a угол между вектором dl малого элемента замкнутого контура L и векторами pmi . На элемент контура dl «нанизаны» молекулярные токи dn молекул, находящихся в объеме косого цилиндра (рис. 4.4.2.) с образующей dl и
основанием, равным Sмол, нормаль к которой составляет угол a с образующей цилиндра:
![]() , (4.4.5.)
, (4.4.5.)
где n концентрация молекулярных токов.
Таким образом, малому элементу dl контура L соответствует охватываемый этим контуром микроток, который с учетом (4.4.1) можно записать в виде
![]() . (4.4.6)
. (4.4.6)
Интегрируя это выражение по всему замкнутому контуру L, находим полный микроток
![]() , (4.4.7)
, (4.4.7)
следовательно, микроток Iмикро , охваченный замкнутым контуром L равен циркуляции намагниченности J по этому контуру. Справедливость этого утверждения можно доказать и в том случае, когда молекулярные токи ориентированы хаотично.
С учетом выражения (4.4.7) закон полного тока (4.4.4) можно преобразовать к следующему виду:
![]() . (4.4.8)
. (4.4.8)
Вектор
H=B/m0 - J (4.4.9)
называется напряженностью магнитного поля (магнитной напряженностью). Используя напряженность магнитного поля H, закон полного тока для магнитного поля в веществе можно записать в виде
![]() . (4.4.10)
. (4.4.10)
Таким образом, циркуляция напряженности магнитного поля вдоль произвольного контура равна результирующему макротоку сквозь поверхность, натянутую на этот контур.
В случае многих однородных изотропных веществ, как показывает эксперимент, между намагниченностью и магнитной индукцией есть прямая пропорциональность:
![]() . (4.4.11)
. (4.4.11)
С учетом этого из формулы (4.4.9) находим, что напряженность магнитного поля также пропорциональна магнитной индукции. Соотношение между этими величинами принято записывать в виде
![]() . (4.4.12)
. (4.4.12)
Входящая в коэффициент пропорциональности константа m называется относительной магнитной проницаемостью вещества.
Подставив преобразованное соотношение (4.4.12)
![]() (4.4.13)
(4.4.13)
в (4.4.9), получим
![]() . (4.4.14)
. (4.4.14)
Величина
c
называется магнитной восприимчивостью
вещества и связана с магнитной
проницаемостью соотношением
![]() . (4.4.15)
. (4.4.15)
4.5. Магнитное поле в веществе. Виды
магнетиков

 Измерения
показывают, что для большинства веществ магнитная проницаемость m
близка к единице и не зависит от величины магнитного поля. Все такие вещества
могут быть разбиты на два класса:
Измерения
показывают, что для большинства веществ магнитная проницаемость m
близка к единице и не зависит от величины магнитного поля. Все такие вещества
могут быть разбиты на два класса:
1)

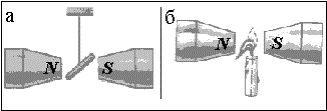 m>1 – парамагнетики,
в которых намагниченность вещества увеличивает суммарное магнитное поле;
парамагнетики втягиваются в область сильного неоднородного магнитного поля (см.
рис.4.5.1);
m>1 – парамагнетики,
в которых намагниченность вещества увеличивает суммарное магнитное поле;
парамагнетики втягиваются в область сильного неоднородного магнитного поля (см.
рис.4.5.1);
2)
m<1 – диамагнетики, в которых намагниченность уменьшает суммарное поле;
диамагнетики выталкиваются из области сильного неоднородного поля (см. рис.4.5.2)
У обоих типов магнетиков магнитная проницаемость слабо отличается от единицы. Кроме этих двух классов имеется класс веществ, в которых величина магнитной проницаемости (и магнитной восприимчивости) может быть очень большой и сильно зависит от величины магнитного поля, а также от температуры вещества. Это, так называемые, магнитоупорядоченные состояния – ферромагнетики, антиферромагнетики и ферримагнетики.
Как объясняется такое поведение веществ с точки зрения современного строения материи?
Как известно, атом вещества состоит из ядра и электронной оболочки. Если электронную орбиту с движущимся по ней электроном представить как контур с током, то легко понять, что каждая электронная орбита имеет свой магнитный момент. К тому же, благодаря собственному механическому моменту вращения (спину), электрон обладает и собственным магнитным моментом.
Спином и собственным магнитным моментом обладают и ядерные частицы – протон и нейтрон. Но так как масса протона в 1836 раз больше массы электрона, то при том же спине его магнитный момент много меньше, чем у электрона. Электрически нейтральный нейтрон также имеет магнитный момент, сравнимый по величине с магнитным моментом протона.
Магнитные моменты атомов векторно складываются из магнитных моментов входящих в них частиц. При этом определяющим является суммарный магнитный момент электронной оболочки.
![]()
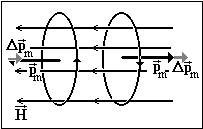 Как
возникает диамагнетизм? Если
рассматривать электронную оболочку как контур с током, то при наложении
внешнего магнитного поля H в соответствии с
правилом Ленца в контуре должна индуцироваться электродвижущая сила (ЭДС) и
возникать индукционный ток. Магнитный момент Dpm индукционного тока независимо от направления
магнитного момента pm
контура всегда направлен против напряженности внешнего поля H (см. рис. 4.5.3.). Возникающее при
этом магнитное поле индукционного тока также направлено против внешнего поля.
Внутри материала суммарное магнитное поле будет при этом уменьшаться. Его
относительное уменьшение порядка 10-8 . Диамагнетизмом
обладают все вещества, его величина не зависит от температуры.
Как
возникает диамагнетизм? Если
рассматривать электронную оболочку как контур с током, то при наложении
внешнего магнитного поля H в соответствии с
правилом Ленца в контуре должна индуцироваться электродвижущая сила (ЭДС) и
возникать индукционный ток. Магнитный момент Dpm индукционного тока независимо от направления
магнитного момента pm
контура всегда направлен против напряженности внешнего поля H (см. рис. 4.5.3.). Возникающее при
этом магнитное поле индукционного тока также направлено против внешнего поля.
Внутри материала суммарное магнитное поле будет при этом уменьшаться. Его
относительное уменьшение порядка 10-8 . Диамагнетизмом
обладают все вещества, его величина не зависит от температуры.
Если атом не имеет собственного магнитного момента,
диамагнитный эффект - определяющий, и вещество является диамагнетиком.
Индуцированный магнитный момент направлен против внешнего магнитного поля, и
атомы такого вещества выталкиваются из области сильного поля.
Парамагнетизм. В общем случае атом вещества может иметь собственный результирующий магнитный момент, например, если число электронов нечетно. В отсутствии внешнего поля магнитный момент макроскопического тела равен нулю из-за беспорядочного распределения по направлениям атомных магнитных моментов (см. рис. 4.5.4а). Под действием внешнего магнитного поля атомные магнитные моменты ориентируются в направлении приложенного поля. За счет полей атомных моментов магнитное поле внутри вещества увеличивается. Сами атомы стремятся переместится в область более сильного поля. Вещество является парамагнетиком. Поскольку тепловое движение мешает упорядочению направлений атомных моментов парамагнетика, его магнитная восприимчивость уменьшается с температурой. Магнитная восприимчивость парамагнетиков имеет величину порядка 10 – 4 – 10–6.
Парамагнетизм и диамагнетизм – сравнительно слабые эффекты. Исключение составляет вещество в сверхпроводящем состоянии. В этом случае при наложении магнитного поля индуцируются незатухающие макроскопические токи, магнитные моменты которых направлены против внешнего магнитного поля и полностью его компенсируют. Диамагнитный эффект здесь очень большой. Сверхпроводники называют идеальными диамагнетиками, для которых
![]() . (4.5.1)
. (4.5.1)
 Магнитоупорядоченные
состояния
имеют квантово-механическую природу. Среди твердых тел есть такие, которые
самопроизвольно под действием внутренних сил намагничены. В них, не зависимо от
внешнего поля, магнитные моменты спинов электронов выстроены параллельно (ферромагнетизм) или антипараллельно (антиферромагнетизм). Схематично их
внутренняя структура в атомном масштабе изображена на рис. 4.5.4 .
Магнитоупорядоченные
состояния
имеют квантово-механическую природу. Среди твердых тел есть такие, которые
самопроизвольно под действием внутренних сил намагничены. В них, не зависимо от
внешнего поля, магнитные моменты спинов электронов выстроены параллельно (ферромагнетизм) или антипараллельно (антиферромагнетизм). Схематично их
внутренняя структура в атомном масштабе изображена на рис. 4.5.4 .
Наличие внутри
ферромагнетика магнитного поля не всегда проявляется внешне по следующей
причине. Ферромагнетик внутри обычно разбивается на макроскопически малые
(размером ~ 10–4 ¸ 10–6 м) области – домéны, внутри которых атомные магнитные моменты
сонаправлены и намагниченность велика. Но если векторы намагниченности доменов
ориентированы по отношению друг к другу под разными углами, то средняя
намагниченность может быть равна нулю, и магнитное поле вещества будет
незаметно (например, железо с малым содержанием примесей .
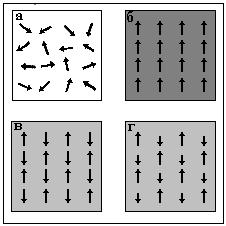
При наложении даже
относительно слабого поля атомные магнитные моменты стремятся выстроиться вдоль
поля. При этом границы между доменами смещаются так, что увеличиваются те
домены, магнитный момент которых направлен вдоль поля (см. рис 4.5.5). В
результате весь объем материала намагничивается, достигая магнитного насыщения Js,
когда все атомные моменты всех доменов выстроены вдоль поля. Из химических
элементов максимальное магнитное насыщение при комнатной температуре имеет
железо.
Если после намагничивания
уменьшить до нуля напряженность
внешнего магнитного поля, не все домены вернутся к прежней ориентации,
некоторые останутся ориентированными близко к направлению «выключенного»
внешнего поля, материал будет иметь остаточную
намагниченность Jr. Остаточная намагниченность особенно велика у
сплавов магния, никеля, кобальта, из которых делают постоянные магниты.
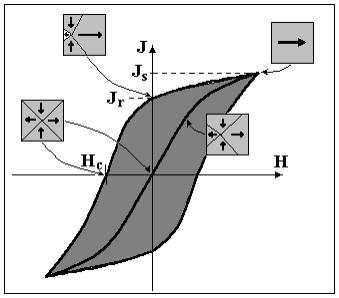
![]() Для того чтобы сделать
намагниченность ферромагнетика нулевой необходимо приложить магнитное поле
противоположного направления. Напряженность такого поля называют коэрцитивной силой Hc.
Увеличивая обратное поле, затем, уменьшая его и накладывая в первоначальном
направлении, т.е. изменяя его величину и направление периодически, можно
получить в координатах J-H петлю гистерезиса
(рис. 4.5.5).
Для того чтобы сделать
намагниченность ферромагнетика нулевой необходимо приложить магнитное поле
противоположного направления. Напряженность такого поля называют коэрцитивной силой Hc.
Увеличивая обратное поле, затем, уменьшая его и накладывая в первоначальном
направлении, т.е. изменяя его величину и направление периодически, можно
получить в координатах J-H петлю гистерезиса
(рис. 4.5.5).
Упорядоченное выстраивание спинов электронов в объеме каждого атома есть результат взаимодействия электронов. В атомах ферромагнетика энергетически выгодным оказывается такое взаимное расположение электронов, когда они находятся на максимальном расстоянии друг от друга со спинами (и спиновыми магнитными моментами), ориентированными в одну сторону. При определенных расстояниях между атомами в кристаллической решетке взаимодействие магнитных моментов спинов и орбит электронов в соседних атомах также делает энергетически выгодным ориентацию атомных моментов в одном направлении. Причем это направление спонтанного намагничивания фиксировано относительно кристаллической решетки. Например, у железа оно совпадает с ребром элементарной кубической ячейки.
Тепловое движение мешает упорядочению расположения магнитных моментов атомов в кристаллической решетке и, кроме того, с ростом температуры меняются расстояния между атомами, поэтому при определенной для каждого ферромагнетика температуре (она называется температурой или точкой Кюри) правильный порядок нарушается, и ферромагнетик становится парамагнетиком.
В некоторых антиферромагнетиках,
например, в оксиде железа, вследствие того, что антипараллельные магнитные
моменты не равны между собой, возникает явление некомпенсированного
антиферромагнетизма, или ферримагнетизм.
Ферримагнетик ведет
себя так же, как ферромагнетик, только результирующая намагниченность его
гораздо меньше. Такие вещества называют ферритами.
![]()
 Качественные зависимости
намагниченности от напряженности магнитного поля для разных типов магнетиков
приведены на рисунке 4.5.6.
Качественные зависимости
намагниченности от напряженности магнитного поля для разных типов магнетиков
приведены на рисунке 4.5.6.
4.6. Условия для магнитного поля на границе раздела двух изотропных сред
(граничные условия)
![]()
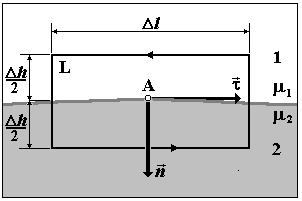 Найдем соотношение между
магнитной индукцией B и
напряженностью H магнитного поля в некоторой
точке А на границе двух сред (см. рис 4.6.1). Проведем в точке А единичные
векторы: t – по
касательной вдоль границы раздела сред и n – по нормали к
границе, направленной от первой среды ко второй. Построим вблизи точки А
небольшой замкнутый прямоугольный контур L, две стороны которого параллельны
вектору t и
равны Dl,
а две - вектору n и равны Dh. Предположим, что по
границе раздела внутри контура вблизи точки А не текут макротоки. Из теоремы о
циркуляции вектора напряженности магнитного поля следует, что
Найдем соотношение между
магнитной индукцией B и
напряженностью H магнитного поля в некоторой
точке А на границе двух сред (см. рис 4.6.1). Проведем в точке А единичные
векторы: t – по
касательной вдоль границы раздела сред и n – по нормали к
границе, направленной от первой среды ко второй. Построим вблизи точки А
небольшой замкнутый прямоугольный контур L, две стороны которого параллельны
вектору t и
равны Dl,
а две - вектору n и равны Dh. Предположим, что по
границе раздела внутри контура вблизи точки А не текут макротоки. Из теоремы о
циркуляции вектора напряженности магнитного поля следует, что
![]() . (4.6.1)
. (4.6.1)
Это равенство должно выполняться при любом значении Dh и тогда в пределе при ![]() получаем
получаем
![]() .
(4.6.2)
.
(4.6.2)
Здесь H1t и H2t - проекции напряженности H на
направление касательного орта в точке А. Поскольку последнее равенство в
(4.6.2) должно выполняться при произвольном Dl,
находим
![]() .
(4.6.3)
.
(4.6.3)
Таким образом, касательная
к поверхности раздела двух сред составляющая напряженности магнитного поля не
изменяется при переходе из одной среды в другую.
Второе условие получим с
помощью теоремы Гаусса для магнитной индукции B. Возьмем охватывающую окрестность точки А небольшую цилиндрическую
поверхность S, основания DS которой параллельны границе
раздела и лежат по разные стороны от нее (см. рис 4.6.2), а образующая
параллельна вектору нормали n. По
теореме Остроградского-Гаусса имеем для потока В через всю поверхность S

![]() . (4.6.4)
. (4.6.4)
Это равенство должно
выполняться при любом значении высоты цилиндра Dh и
в пределе получим
![]() . (4.6.5)
. (4.6.5)
Рис.4.6.2
Поскольку
это соотношение должно выполняться при любой площади основания DS, отличной от нуля, получаем
![]() , (4.6.6)
, (4.6.6)
т.е. при переходе через границу раздела двух сред, нормальная составляющая
вектора магнитной индукции не изменяется.
Из граничных условий (4.6.3)
и (4.6.6) можно сделать следующие выводы:
-
если
граница раздела ортогональна линиям магнитной индукции, то вектор магнитной
индукции не изменяется при переходе через границу.
-
если
граница раздела касается линий магнитной индукции, то напряженность магнитного
поля не изменяется при переходе через границу раздела сред.
-
Если
первая среда - вакуум, т. е. m1=1, то из (4.4.13) и (4.6.3)
получаем
![]() . (4.6.7)
. (4.6.7)
Таким образом, относительная магнитная проницаемость среды показывает, во сколько раз увеличивается касательная составляющая вектора магнитной индукции при переходе из вакуума в данную среду (нормальная - не меняется). В этом проявляется существенное отличие магнитных материалов от диэлектрических. Для последних диэлектрическая проницаемость показывает во сколько раз уменьшается нормальная компонента напряженности электрического поля при переходе из вакуума в диэлектрик (касательная – не меняется).
Отметим, что
напряженность электрического поля E и
магнитная индукция B являются
основными характеристиками поля, тогда как электрическая индукция D и напряженность магнитного поля H – вспомогательные характеристики
электромагнитного поля, вводимые для удобства его описания в различных средах.
Рекомендуемая литература:
1. Савельев И.В. Курс общей физики: Учеб. Пособие: для вузов. В 5 кн. Кн.2. Электричество и магнетизм – 4-е изд., перераб.– М.: Наука, Физматлит,, 1998, сс. 146–151, 158–164, 167–171, 181–214.
2. Трофимова Т.И. Курс физики: Учеб. Пособие: для вузов.– 5-е изд., стер.– М.: Высш. шк., 1998, сс. 209–210, 212–214, 221–222, 236–247.
3. Детлаф А. А., Яворский Б. М. Курс физики: Учеб. пособие для вузов.– 2-е изд., испр. и доп.– М.: Высш. шк., 1999, сс. 272–280, 291–293,312–327.
4. Иродов И. Е. Электромагнетизм. Основные законы.– 3-е изд., испр.–М.: Лаборатория базовых знаний, 2000, сс. 154–158, 170–178, 189–210.
Вопросы для самоподготовки.
1.
 На рисунке В4.1 изображено
преломление линий магнитной индукции на границе двух магнетиков, с
проницаемостями m1 и m2. Определите, у какой из
сред больше магнитная проницаемость. Найдите отношение
На рисунке В4.1 изображено
преломление линий магнитной индукции на границе двух магнетиков, с
проницаемостями m1 и m2. Определите, у какой из
сред больше магнитная проницаемость. Найдите отношение ![]() .
.
2.
![]() Чем различается действие на
точечный электрический заряд электрического и магнитного поля?
Чем различается действие на
точечный электрический заряд электрического и магнитного поля?
3.
Каково
происхождение сил Ампера, действующих на проводник с током в магнитном поле?
4. Как будет вести себя замкнутый контур с током, помещенный в некоторое магнитное поле?
5.
Какую работу совершают силы Ампера при повороте кругового
витка радиуса R в
однородном магнитном поле с индукцией В,
если сила тока в витке I ?
6.
За счет какого источника энергии совершают работу амперовы
силы при перемещении в магнитном поле проводника или замкнутого контура с током?
7.
В каких приборах и устройствах используется действие
магнитного поля на замкнутый контур с током?
8.
Чем различаются и в чем сходны макро- и микротоки?
9. Что общего между намагниченностью и поляризованностью?
10. Зачем при описании магнитного поля в веществе вводится вектор напряженности магнитного поля?
11. В чем состоит различие между диамагнитным и парамагнитным эффектом?
12. Имеет ли место диамагнитный эффект в парамагнетиках и парамагнитный - в диамагнетиках?
13. В чем состоит существенное отличие ферромагнетиков от диа- и парамагнетиков?
14. Держали ли Вы в руках ферромагнетик и в чем его отличие от других магнетиков (в теории и на практике)?
15. Какая разница между током проводимости и током намагничивания?
16. Какая разница между диамагнитным и парамагнитным эффектами?
17. Какие токи (проводимости, намагничивания или те и другие)определяют поле векторов В и Н?
18. Объясните зависимость ферромагнитных свойств вещества от температуры.
19. Определить магнитный момент кольца с током радиусом 1 см, если на оси кольца на расстоянии 1 м от его центра индукция магнитного поля равна 10 мкТл.
20. Прямолинейный проводник, длиной 0,5 м и током 10 А, расположен перпендикулярно силовым линиям однородного магнитного поля с индукцией 0,1 Тл. Найти работу силы Ампера при перемещении проводника на 5 см в направлении действия этой силы.
21. Пучок протонов проходит через область скрещенных электрического и магнитного полей. Протоны движутся перпендикулярно силовым линиям. Напряженность электрического поля Е=3·105 В/м, индукция магнитного поля В=0,08 Тл. Определить скорость протонов, которые не будут отклоняться.
22. В однородном магнитном поле, индукция которого 0,5 Тл, находится плоская катушка радиусом 10 см, содержащая 75 витков. Плоскость катушки составляет угол 45º с направлением вектора индукции. Какую работу надо совершить, чтобы удалить катушку из магнитного поля, если по виткам течет ток 1 А?
23. Чему равен период обращения электрона, движущегося со скоростью 4·105 м/с в однородном магнитном поле с индукцией В=12 мкТл?
24. Заряженная частица, прошедшая разность потенциалов 5 кВ двигается по окружности радиусом 10 см в магнитном поле с индукцией 1 Тл . Определить скорость частицы и отношение ее заряда к массе.
25. Протон, движущийся вертикально вверх со скоростью 5·106 м/с в однородном магнитном поле, испытывает действие силы 8·10–14 Н, направленной на запад. Когда протон движется горизонтально на север, сила равна нулю. Определить величину и направление вектора магнитной индукции в этой области.